分类回归#
在此示例中,我们将对具有两个以上类别的结果进行建模。
import os
import warnings
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pymc_bart as pmb
import seaborn as sns
warnings.simplefilter(action="ignore", category=FutureWarning)
# set formats
RANDOM_SEED = 8457
az.style.use("arviz-darkgrid")
鹰数据集#
在此示例中,我们将使用一个数据集,其中包含关于 3 种鹰类的信息(CH=库珀鹰, RT=红尾鹰, SS=夏普-辛鹰)。该数据集总共包含 908 个个体的的信息,每个个体包含 16 个变量,以及物种信息。为了简化示例,我们将使用以下 5 个协变量
Wing: 初级飞羽从尖端到与腕部连接处的长度(毫米)。
Weight: 体重(克)。
Culmen: 上喙从尖端到与鸟类肉质部分碰撞处的长度(毫米)。
Hallux: 杀戮爪的长度(毫米)。
Tail: 与尾巴长度相关的测量值(毫米)。
此外,我们将消除数据集中的 NaN 值。有了这些,我们将预测鹰的“物种”,换句话说,这些是我们的因变量,我们想要预测的类别。
# Load data and eliminate NANs
try:
Hawks = pd.read_csv(os.path.join("..", "data", "Hawks.csv"))[
["Wing", "Weight", "Culmen", "Hallux", "Tail", "Species"]
].dropna()
except FileNotFoundError:
Hawks = pd.read_csv(pm.get_data("Hawks.csv"))[
["Wing", "Weight", "Culmen", "Hallux", "Tail", "Species"]
].dropna()
Hawks.head()
| Wing | Weight | Culmen | Hallux | Tail | Species | |
|---|---|---|---|---|---|---|
| 0 | 385.0 | 920.0 | 25.7 | 30.1 | 219 | RT |
| 2 | 381.0 | 990.0 | 26.7 | 31.3 | 235 | RT |
| 3 | 265.0 | 470.0 | 18.7 | 23.5 | 220 | CH |
| 4 | 205.0 | 170.0 | 12.5 | 14.3 | 157 | SS |
| 5 | 412.0 | 1090.0 | 28.5 | 32.2 | 230 | RT |
EDA#
以下比较协变量,以快速可视化 3 个物种的数据。
sns.pairplot(Hawks, hue="Species");
/home/osvaldo/anaconda3/envs/pymc/lib/python3.11/site-packages/seaborn/axisgrid.py:123: UserWarning: The figure layout has changed to tight
self._figure.tight_layout(*args, **kwargs)
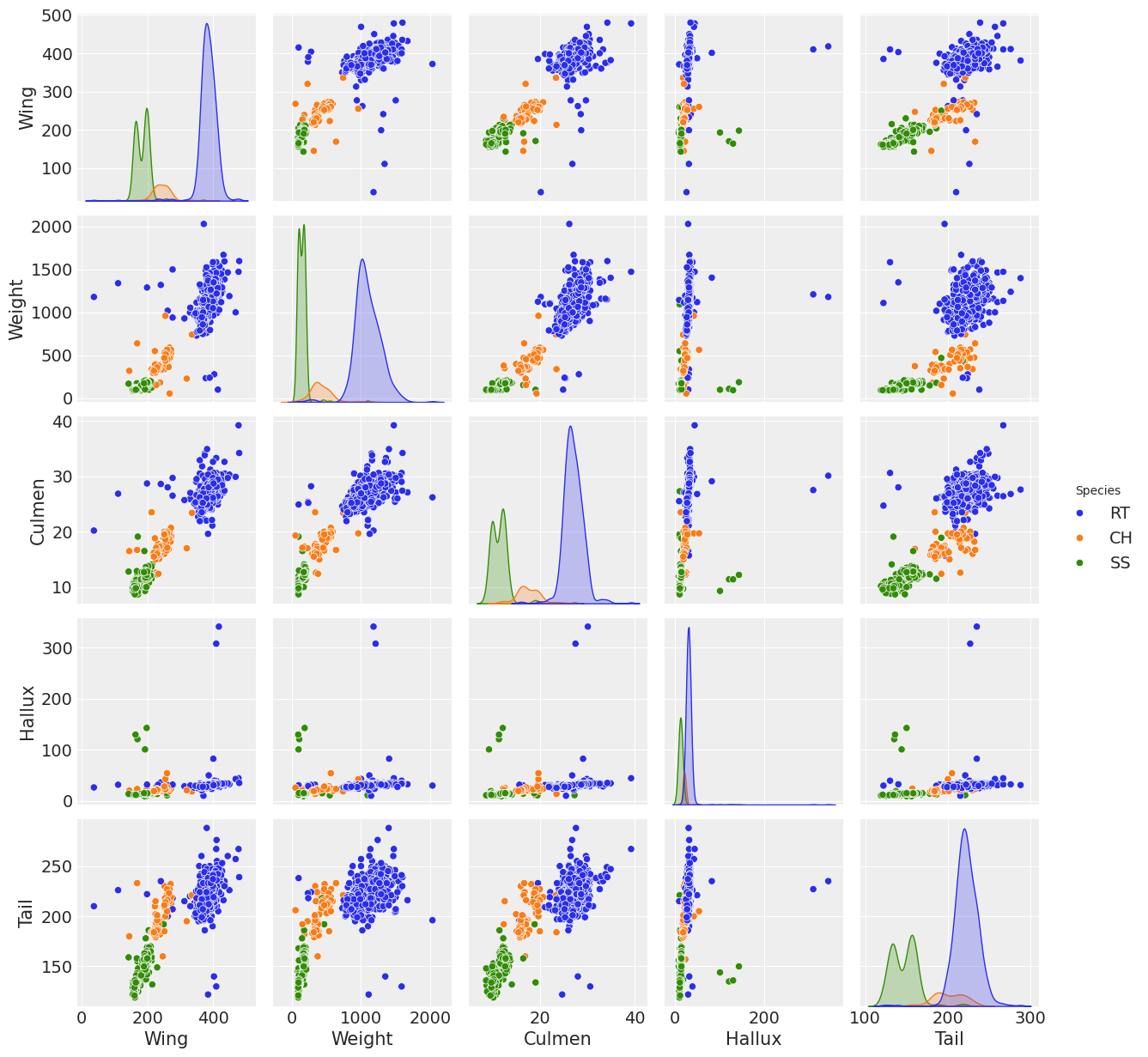
可以看出,在几乎所有协变量中,RT 物种的分布都比其他两个物种更具区分度,并且协变量 wing、weight 和 culmen 在物种之间呈现出一定的分离。 然而,没有一个变量在物种分布之间有明显的区分,以至于它们可以完全将它们分开。 可以组合协变量,可能是 wing、weight 和 culmen,以实现分类。 这些是进行回归分析的主要原因。
模型规范#
首先,我们将准备模型的数据,使用“Species”作为响应变量,以及“Wing”、“Weight”、“Culmen”、“Hallux”和“Tail”作为预测变量。 使用 pd.Categorical(Hawks['Species']).codes 我们可以将物种名称编码为 0 到 2 之间的整数,其中 0=”CH”,1=”RT” 和 2=”SS”。
y_0 = pd.Categorical(Hawks["Species"]).codes
x_0 = Hawks[["Wing", "Weight", "Culmen", "Hallux", "Tail"]]
print(len(x_0), x_0.shape, y_0.shape)
891 (891, 5) (891,)
在每个 pymc 模型中,我们只能有一个 BART() 实例(目前是这样),因此为了对 3 个物种进行建模,我们可以使用坐标和维度名称来指定变量的形状,指示有 891 行信息用于 3 个物种。 此步骤有助于稍后从 InferenceData 中选择组。
_, species = pd.factorize(Hawks["Species"], sort=True)
species
Index(['CH', 'RT', 'SS'], dtype='object')
coords = {"n_obs": np.arange(len(x_0)), "species": species}
在此模型中,我们使用 pm.math.softmax() 函数,用于来自 pmb.BART() 的 \(\mu\),因为它保证向量沿 axis=0(在本例中)求和为 1。
with pm.Model(coords=coords) as model_hawks:
μ = pmb.BART("μ", x_0, y_0, m=50, dims=["species", "n_obs"])
θ = pm.Deterministic("θ", pm.math.softmax(μ, axis=0))
y = pm.Categorical("y", p=θ.T, observed=y_0)
pm.model_to_graphviz(model=model_hawks)
现在拟合模型并从后验分布中获取样本。
with model_hawks:
idata = pm.sample(chains=4, compute_convergence_checks=False, random_seed=123)
pm.sample_posterior_predictive(idata, extend_inferencedata=True)
Multiprocess sampling (4 chains in 4 jobs)
PGBART: [μ]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 91 seconds.
Sampling: [y]
结果#
变量重要性#
可能某些输入变量对于按物种分类没有信息量,因此为了简约并降低模型估计的计算成本,量化数据集中每个变量的重要性很有用。 PyMC-BART 提供了函数 plot_variable_importance(),它生成一个图,该图在其 x 轴上显示协变量的数量,在其 y 轴上显示 R\(^2\) (皮尔逊相关系数的平方),表示完整模型(包括所有变量)的预测值与受限模型(仅包含变量子集)的预测值之间的关系。误差条表示来自后验预测分布的 94% HDI。
vi_results = pmb.compute_variable_importance(idata, μ, x_0, method="VI", random_seed=RANDOM_SEED)
pmb.plot_variable_importance(vi_results);
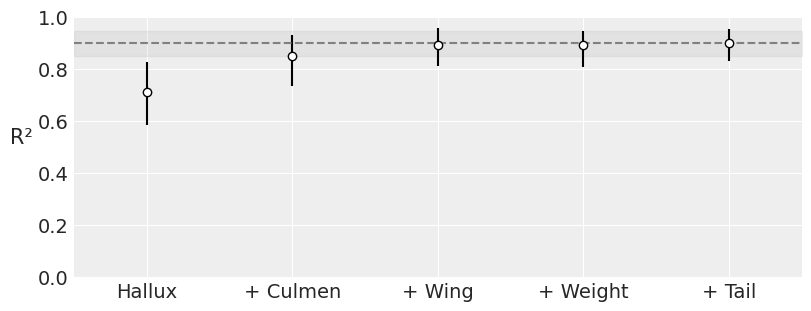
可以观察到,使用协变量 Hallux、Culmen 和 Wing,我们获得了与使用所有协变量相同的 R\(^2\) 值,这意味着最后两个协变量对分类的贡献小于其他三个。 我们必须考虑到的一件事是,HDI 非常宽,这降低了我们结果的精度,稍后我们将看到一种减少这种情况的方法。
偏依赖图#
让我们使用 pmb.plot_pdp() 检查每个协变量对每个物种的行为,它显示了协变量对预测变量的边际效应,同时我们对所有其他协变量进行平均。
pmb.plot_pdp(μ, X=x_0, Y=y_0, grid=(5, 3), figsize=(12, 7));
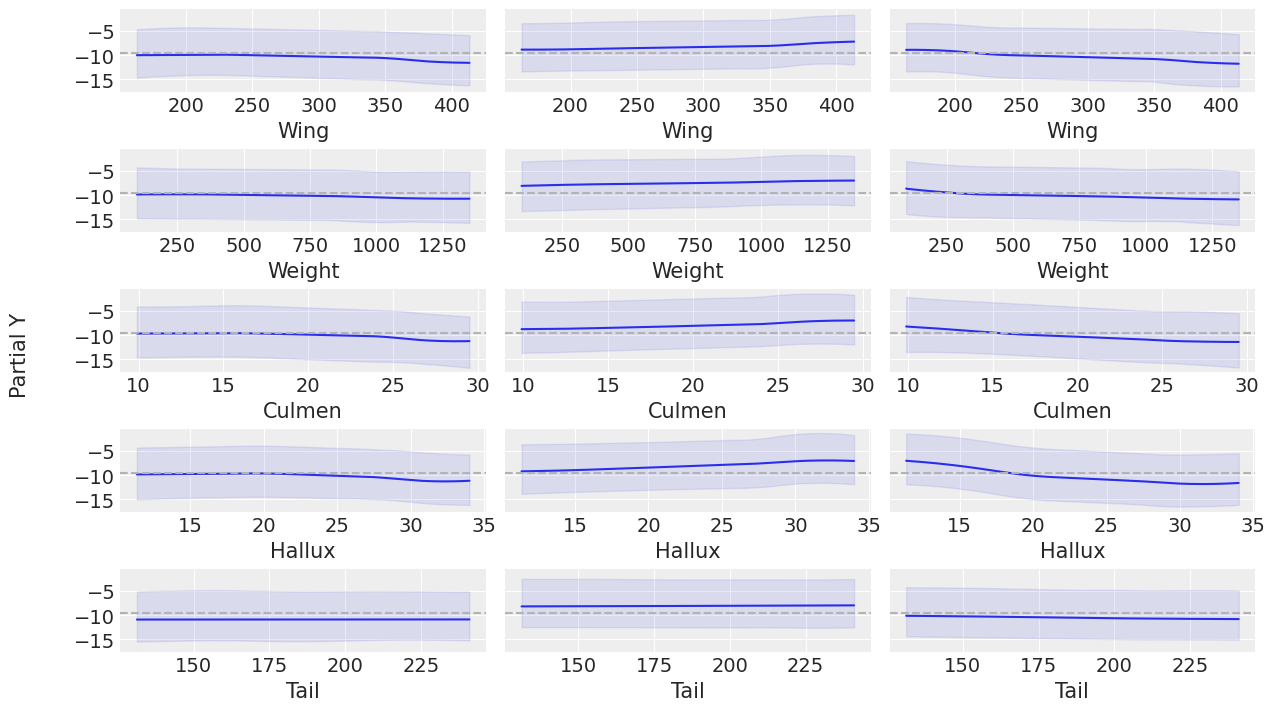
pdp 图以及变量重要性图证实,Tail 是对预测变量影响最小的协变量。 在变量重要性图中,Tail 是最后一个添加的协变量,并且没有改善结果,在 pdp 图中,Tail 具有最平坦的响应。 对于此图中的其余协变量,很难看出哪个协变量对预测变量的影响更大,因为它们具有很大的变异性,如 HDI 宽度所示,稍后我们将看到一种减少这种变异性的方法。 最后,一些变异性取决于每个物种的数据量,我们可以在使用 Pandas .describe() 并使用 .groupby("Species") 对来自“Species”的数据进行分组的协变量之一的 counts 中看到这一点。
预测值 vs 观测值#
现在我们将比较预测数据与观测数据,以评估模型的拟合度,我们使用 Arviz 函数 az.plot_ppc() 来做到这一点。
ax = az.plot_ppc(idata, kind="kde", num_pp_samples=200, random_seed=123)
# plot aesthetics
ax.set_ylim(0, 0.7)
ax.set_yticks([0, 0.2, 0.4, 0.6])
ax.set_ylabel("Probability")
ax.set_xticks([0.5, 1.5, 2.5])
ax.set_xticklabels(["CH", "RT", "SS"])
ax.set_xlabel("Species");
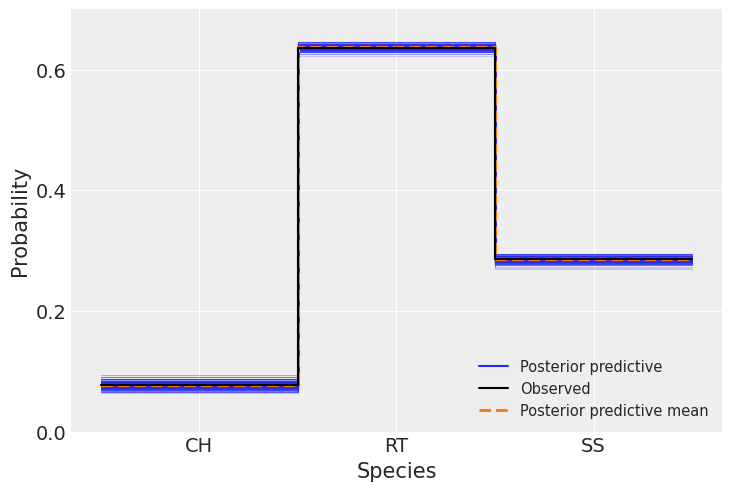
我们可以看到观测数据(黑线)和模型预测的数据(蓝线和橙线)之间有很好的一致性。 正如我们之前提到的,物种之间值的差异受每个物种数据量的影响。 这里,正如我们在前两个图中看到的那样,预测数据中没有观察到离散性。
下面我们看到,样本内预测与观测值提供了非常好的协议。
np.mean((idata.posterior_predictive["y"] - y_0) == 0) * 100
<xarray.DataArray 'y' ()> Size: 8B array(96.56689113)
all = 0
for i in range(3):
perct_per_class = np.mean(idata.posterior_predictive["y"].where(y_0 == i) == i) * 100
all += perct_per_class
print(perct_per_class)
all
<xarray.DataArray 'y' ()> Size: 8B
array(6.16102694)
<xarray.DataArray 'y' ()> Size: 8B
array(62.72738496)
<xarray.DataArray 'y' ()> Size: 8B
array(27.67847924)
<xarray.DataArray 'y' ()> Size: 8B array(96.56689113)
到目前为止,我们在基于 5 个协变量对物种进行分类方面取得了非常好的结果。 但是,如果我们想选择协变量的子集来进行未来的分类,那么选择哪些协变量不是很清楚。 也许可以肯定的是,可以消除 Tail。 在开始时,当我们绘制每个协变量的分布时,我们说进行分类的最重要变量可能是 Wing、Weight 和 Culmen,然而,在运行模型后,我们看到 Hallux、Culmen 和 Wing 被证明是最重要的。
不幸的是,偏依赖图显示出非常广泛的离散性,使结果看起来可疑。 减少这种变异性的一种方法是调整独立树,下面我们将看到如何做到这一点并获得更准确的结果。
拟合独立树#
使用 pymc-bart 拟合独立树的选项通过参数 pmb.BART(..., separate_trees=True, ...) 设置。 正如我们将看到的,对于此示例,使用此选项在预测中并没有产生很大的差异,但有助于我们减少 ppc 中的变异性,并在样本内比较中获得小的改进。 如果将此选项用于更大的数据集,则必须考虑到模型拟合速度较慢,因此您可以以计算成本为代价获得更好的结果。 以下代码运行与之前相同的模型和分析,但拟合的是独立的树。 比较运行此模型与前一个模型的时间。
with pm.Model(coords=coords) as model_t:
μ_t = pmb.BART("μ", x_0, y_0, m=50, separate_trees=True, dims=["species", "n_obs"])
θ_t = pm.Deterministic("θ", pm.math.softmax(μ_t, axis=0))
y_t = pm.Categorical("y", p=θ_t.T, observed=y_0)
idata_t = pm.sample(chains=4, compute_convergence_checks=False, random_seed=123)
pm.sample_posterior_predictive(idata_t, extend_inferencedata=True)
Multiprocess sampling (4 chains in 4 jobs)
PGBART: [μ]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 262 seconds.
Sampling: [y]
现在我们将重现与之前相同的分析。
vi_results = pmb.compute_variable_importance(
idata_t, μ_t, x_0, method="VI", random_seed=RANDOM_SEED
)
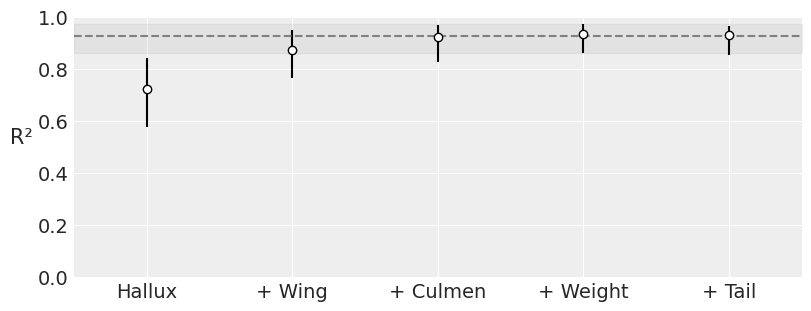
pmb.plot_variable_importance(vi_results);
pmb.plot_pdp(μ_t, X=x_0, Y=y_0, grid=(5, 3), figsize=(12, 7));
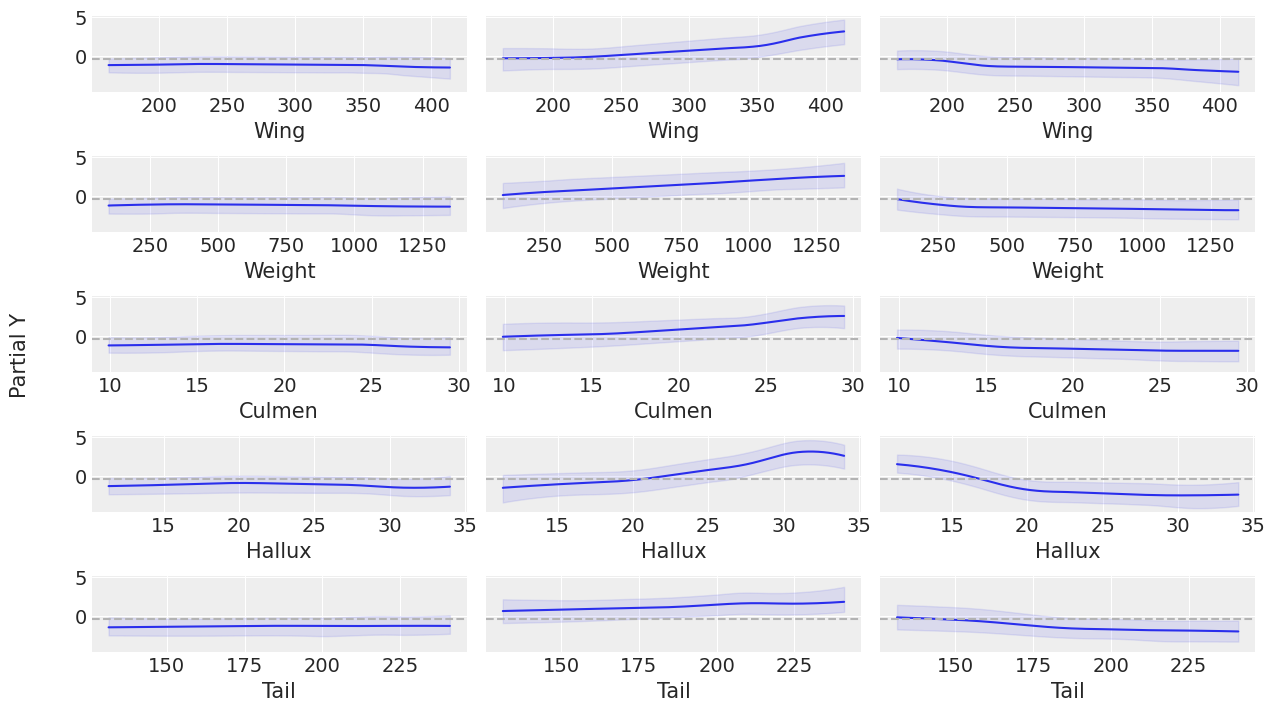
将这两个图与之前的图进行比较,可以看出每个图的方差都显着降低。 在 pmb.plot_variable_importance() 的情况下,误差带更小,R\(^{2}\) 值更接近 1。 对于 pm.plot_pdp(),我们可以看到更细的带和 y 轴上限的减小,这代表了由于分别调整树而导致的不确定性降低。 这样做的好处是,每个协变量对每个物种的行为更加可见。
将所有这些结合在一起,我们可以选择 Hallux、Culmen 和 Wing 作为协变量来进行分类。
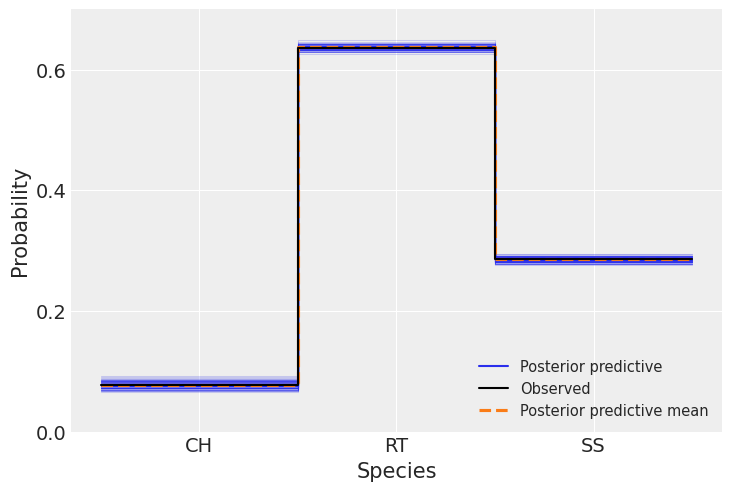
关于观测数据和预测数据之间的比较,我们获得了相同的好结果,预测值(蓝线)的不确定性更小。 样本内比较的计数相同。
ax = az.plot_ppc(idata_t, kind="kde", num_pp_samples=100, random_seed=123)
ax.set_ylim(0, 0.7)
ax.set_yticks([0, 0.2, 0.4, 0.6])
ax.set_ylabel("Probability")
ax.set_xticks([0.5, 1.5, 2.5])
ax.set_xticklabels(["CH", "RT", "SS"])
ax.set_xlabel("Species");
np.mean((idata_t.posterior_predictive["y"] - y_0) == 0) * 100
<xarray.DataArray 'y' ()> Size: 8B array(97.39806397)
all = 0
for i in range(3):
perct_per_class = np.mean(idata_t.posterior_predictive["y"].where(y_0 == i) == i) * 100
all += perct_per_class
print(perct_per_class)
all
<xarray.DataArray 'y' ()> Size: 8B
array(6.51882716)
<xarray.DataArray 'y' ()> Size: 8B
array(62.99374299)
<xarray.DataArray 'y' ()> Size: 8B
array(27.88549383)
<xarray.DataArray 'y' ()> Size: 8B array(97.39806397)
参考文献#
水印#
%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor
Last updated: Mon Dec 23 2024
Python implementation: CPython
Python version : 3.11.5
IPython version : 8.16.1
pytensor: 2.26.4
pymc : 5.19.1
matplotlib: 3.8.4
seaborn : 0.13.2
pandas : 2.1.2
pymc_bart : 0.6.0
numpy : 1.26.4
arviz : 0.20.0.dev0
Watermark: 2.4.3
