GenExtreme

class pymc_extras.distributions.GenExtreme(name: str, *args, rng=None, dims: str | Sequence[str | None] | None = None, initval=None, observed=None, total_size=None, transform=UNSET, default_transform=UNSET, **kwargs)

单变量广义极值对数似然函数

此分布的累积分布函数 (cdf) 为

\[G(x \mid \mu, \sigma, \xi) = \exp\left[ -\left(1 + \xi z\right)^{-\frac{1}{\xi}} \right]\]

其中

\[z = \frac{x - \mu}{\sigma}\]

且定义在以下集合上

\[\left\{x: 1 + \xi\left(\frac{x-\mu}{\sigma}\right) > 0 \right\}.\]

请注意，此参数化方法遵循 Coles (2001)，并且与 Scipy 的参数化方法在形状参数 \(\xi\) 的符号上有所不同。

(Source code, png, hires.png, pdf)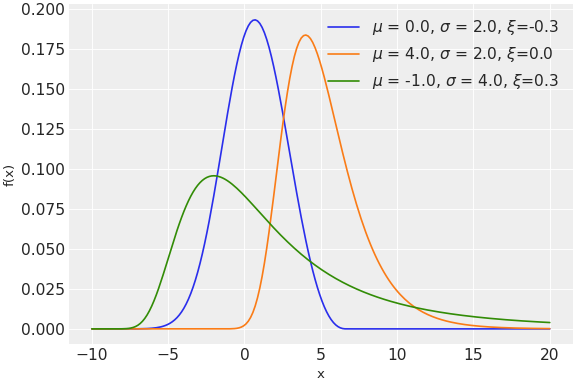

支持	\(x \in [\mu - \sigma/\xi, +\infty]\)，当 \(\xi > 0\) 时 \(x \in \mathbb{R}\) 当 \(\xi = 0\) 时 \(x \in [-\infty, \mu - \sigma/\xi]\)，当 \(\xi < 0\) 时
均值	\(\mu + \sigma(g_1 - 1)/\xi\)，当 \(\xi \neq 0, \xi < 1\) 时 \(\mu + \sigma \gamma\)，当 \(\xi = 0\) 时 \(\infty\)，当 \(\xi \geq 1\) 时，其中 \(\gamma\) 是欧拉-马歇罗尼常数，且 \(g_k = \Gamma (1-k\xi)\)
方差	\(\sigma^2 (g_2 - g_1^2)/\xi^2\)，当 \(\xi \neq 0, \xi < 0.5\) 时 \(\frac{\pi^2}{6} \sigma^2\)，当 \(\xi = 0\) 时 \(\infty\)，当 \(\xi \geq 0.5\) 时

参数:

• mu (float) – 位置参数。

• sigma (float) – 尺度参数 (sigma > 0)。

• xi (float) – 形状参数

• scipy (bool) – 是否使用 Scipy 对形状参数的解释（默认为 False）。

参考文献

[Coles2001]

Coles, S.G. (2001). 极端值统计建模导论 Springer-Verlag, London

__init__()

方法

__init__()
dist([mu, sigma, xi, scipy])	创建与 cls 分布对应的张量变量。
logcdf(mu, sigma, xi)	计算广义极值分布在指定值的累积分布函数的对数。
logp(mu, sigma, xi)	计算广义极值分布在指定值的对数概率。
support_point(size, mu, sigma, xi)	使用众数，因为当 \(\xi > 1\) 时，均值可能为无穷大

属性

rv_op