import arviz as az
import numpy as np

import pymc as pm

print(f"Running on PyMC v{pm.__version__}")

Running on PyMC v5.15.1+68.gc0b060b98.dirty

az.style.use("arviz-darkgrid")

模型比较#

为了演示 PyMC 中模型比较标准的使用，我们实现了 Gelman 等人 (2003) 第 5.5 节中的 8 所学校 示例，该示例试图推断辅导对来自 8 所学校的学生的 SAT 分数的影响。下面，我们拟合一个 pooled 模型 ，该模型假设所有学校都具有单一固定效应，以及一个 分层模型 ，该模型允许随机效应部分地汇集数据。

数据包括 8 所学校中观察到的处理效应 (y) 和相关的标准差 (sigma)。

y = np.array([28, 8, -3, 7, -1, 1, 18, 12])
sigma = np.array([15, 10, 16, 11, 9, 11, 10, 18])
J = len(y)

Pooled 模型#

with pm.Model() as pooled:
    # Latent pooled effect size
    mu = pm.Normal("mu", 0, sigma=1e6)

    obs = pm.Normal("obs", mu, sigma=sigma, observed=y)

    trace_p = pm.sample(2000)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [mu]





Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 6 seconds.













az.plot_trace(trace_p);








../../_images/69bd250de55dfb612954797a0838bf15f33d8001365fbede3ae19d1656a495da.png









分层模型#






with pm.Model() as hierarchical:
    eta = pm.Normal("eta", 0, 1, shape=J)
    # Hierarchical mean and SD
    mu = pm.Normal("mu", 0, sigma=10)
    tau = pm.HalfNormal("tau", 10)

    # Non-centered parameterization of random effect
    theta = pm.Deterministic("theta", mu + tau * eta)

    obs = pm.Normal("obs", theta, sigma=sigma, observed=y)

    trace_h = pm.sample(2000, target_accept=0.9)









Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [eta, mu, tau]









Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 24 seconds.













az.plot_trace(trace_h, var_names="mu");








../../_images/8de0e384eab51e9d473bc0601bec2a3640d476ae273ee51edcf7b7bc57c0b17d.png









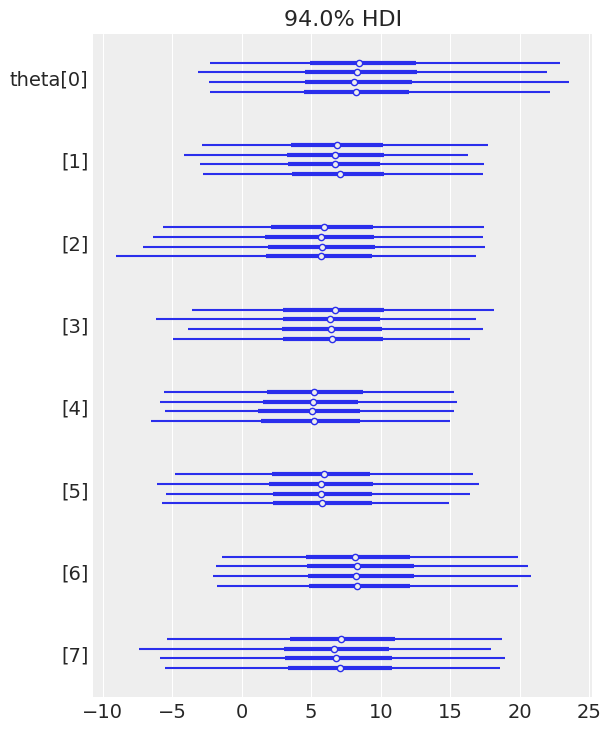
az.plot_forest(trace_h, var_names="theta");








../../_images/220695e8447f0651dc133a3389ef5d6f586b78e08421f0a2371928118cc909f1.png









留一法交叉验证 (LOO)#


LOO 交叉验证是对样本外预测拟合的估计。在交叉验证中，数据被重复划分为训练集和保留集，迭代地使用前者拟合模型，并使用保留数据评估拟合度。Vehtari 等人 (2016) 引入了一种从 MCMC 样本中有效计算 LOO 的方法（无需重新拟合数据）。这种近似基于重要性抽样。重要性权重使用一种称为 Pareto 平滑重要性抽样 (PSIS) 的方法进行稳定。






广泛适用信息准则 (WAIC)#


WAIC (Watanabe 2010) 是一种完全贝叶斯准则，用于估计样本外期望，使用计算出的点对数后验预测密度 (LPPD) 并校正有效参数的数量以调整过拟合。


默认情况下，ArviZ 使用 LOO，但也提供 WAIC。






模型对数似然#


为了计算 LOO 和 WAIC，ArviZ 需要访问每个后验样本的模型元素级对数似然。我们可以通过 compute_log_likelihood() 添加它。或者，我们可以将 idata_kwargs={"log_likelihood": True} 传递给 sample()，以便在采样结束时自动计算它。






with pooled:
    pm.compute_log_likelihood(trace_p)





















pooled_loo = az.loo(trace_p)

pooled_loo









Computed from 8000 posterior samples and 8 observations log-likelihood matrix.

         Estimate       SE
elpd_loo   -30.58     1.11
p_loo        0.69        -
------

Pareto k diagnostic values:
                         Count   Pct.
(-Inf, 0.5]   (good)        8  100.0%
 (0.5, 0.7]   (ok)          0    0.0%
   (0.7, 1]   (bad)         0    0.0%
   (1, Inf)   (very bad)    0    0.0%













with hierarchical:
    pm.compute_log_likelihood(trace_h)





















hierarchical_loo = az.loo(trace_h)

hierarchical_loo









Computed from 8000 posterior samples and 8 observations log-likelihood matrix.

         Estimate       SE
elpd_loo   -30.82     1.08
p_loo        1.17        -
------

Pareto k diagnostic values:
                         Count   Pct.
(-Inf, 0.5]   (good)        4   50.0%
 (0.5, 0.7]   (ok)          4   50.0%
   (0.7, 1]   (bad)         0    0.0%
   (1, Inf)   (very bad)    0    0.0%









ArviZ 包括两个方便的函数，以帮助比较不同模型的 LOO。其中第一个函数是 compare，它从一组迹和模型计算 LOO（或 WAIC），并返回 DataFrame。






df_comp_loo = az.compare({"hierarchical": trace_h, "pooled": trace_p})
df_comp_loo













  
    

      
      排名
      elpd_loo
      p_loo
      elpd_diff
      权重
      se
      dse
      警告
      尺度
    

  
  
    

      pooled
      0
      -30.578116
      0.686645
      0.000000
      1.0
      1.105891
      0.000000
      False
      log
    

    

      hierarchical
      1
      -30.820005
      1.167010
      0.241889
      0.0
      1.080954
      0.231679
      False
      log
    

  







我们有很多列，所以让我们逐个检查它们的含义


    

  1. 索引是从传递给 compare(.) 的字典的键中获取的模型名称。
    2. 

  2. 排名，模型的排名，从 0（最佳模型）到模型数量。
    3. 

  3. loo，LOO（或 WAIC）的值。DataFrame 始终从最佳 LOO/WAIC 到最差排序。
    4. 

  4. p_loo，惩罚项的值。我们可以粗略地将此值视为估计的有效参数数量（但不要太认真对待）。
    5. 

  5. d_loo，排名最高的模型的 LOO/WAIC 值与每个模型的 LOO/WAIC 值之间的相对差异。因此，对于第一个模型，我们总是得到值 0。
    6. 

  6. 权重，分配给每个模型的权重。这些权重可以粗略地解释为在给定数据的情况下，每个模型为真的概率（在比较的模型中）。
    7. 

  7. se，LOO/WAIC 计算的标准误差。标准误差可用于评估 LOO/WAIC 估计的不确定性。默认情况下，这些误差使用堆叠法计算。
    8. 

  8. dse，两个 LOO/WAIC 值之间差异的标准误差。与我们可以计算每个 LOO/WAIC 值的标准误差的方式相同，我们可以计算两个 LOO/WAIC 值之间差异的标准误差。请注意，这两个量不一定相同，原因是关于 LOO/WAIC 的不确定性在模型之间是相关的。对于排名最高的模型，此量始终为 0。
    9. 

  9. warning，如果 True，则 LOO/WAIC 的计算可能不可靠。
    10. 

  10. loo_scale，报告值的尺度。默认值是如前所述的对数尺度。其他选项包括偏差 (deviance) – 这是对数分数乘以 -2（这会反转顺序：较低的 LOO/WAIC 会更好）– 和负对数 (negative-log) – 这是对数分数乘以 -1（与偏差尺度一样，较低的值更好）。
    11. 



第二个方便函数采用 compare 的输出，并生成一个摘要图，其风格类似于 Richard McElreath 的 Statistical Rethinking 一书中所使用的风格（另请查看 本书示例到 PyMC 的移植）。






az.plot_compare(df_comp_loo, insample_dev=False);








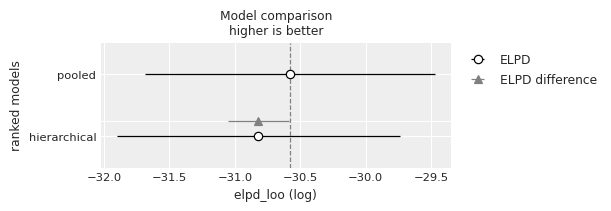
../../_images/270be4d73a90733f93abe34f7f15e76428600d61b57df128acb78d2096a7c058.png





空心圆圈表示 LOO 的值，与其关联的黑色误差线是 LOO 标准偏差的值。


最高 LOO 的值，即最佳估计模型，也用垂直虚线灰色线表示，以方便与其他 LOO 值进行比较。


对于除排名最高的模型之外的所有模型，我们还会得到一个三角形，指示该模型与顶级模型之间 WAIC 差异的值，以及一个灰色误差线，指示排名最高的 WAIC 与每个模型的 WAIC 之间差异的标准误差。






解释#


虽然我们可能期望分层模型优于完全 pooled 模型，但在这种情况下，模型之间几乎没有选择，因为这两个模型都给出了非常相似的信息准则值。当我们考虑到 LOO 和 WAIC 的不确定性（以标准误差衡量）时，这一点会更加明显。






参考#


Gelman, A., Hwang, J., & Vehtari, A. (2014). 理解贝叶斯模型的预测信息准则。《统计与计算》，24(6), 997–1016。


Vehtari, A, Gelman, A, Gabry, J. (2016). 使用留一法交叉验证和 WAIC 的实用贝叶斯模型评估。《统计与计算》






%load_ext watermark

%watermark -n -u -v -iv -w -p xarray,pytensor









Last updated: Tue Jun 25 2024

Python implementation: CPython
Python version       : 3.11.8
IPython version      : 8.22.2

xarray  : 2024.2.0
pytensor: 2.20.0+3.g66439d283.dirty

matplotlib: 3.8.3
numpy     : 1.26.4
pymc      : 5.15.0+1.g58927d608
arviz     : 0.17.1

Watermark: 2.4.3