PyMC 简介#

注意：本文部分基于 John Salvatier、Thomas V. Wiecki 和 Christopher Fonnesbeck 在 PeerJ CS 上发表的关于 PyMC 的文章。

摘要#

概率编程允许对用户定义的概率模型进行自动贝叶斯推断。用于马尔可夫链蒙特卡洛 (MCMC) 采样的基于梯度的算法，称为哈密顿蒙特卡洛 (HMC)，允许对日益复杂的模型进行推断，但这需要通常不易计算的梯度信息。PyMC 是一个用 Python 编写的开源概率编程框架，它使用 PyTensor 通过自动微分计算梯度，以及将概率程序即时编译到计算后端的套件之一，以提高速度。PyMC 允许在 Python 代码中进行模型规范，而不是在特定领域的语言中，使其易于学习、自定义和调试。本文是对这个软件包的教程式介绍，适用于那些已经对贝叶斯统计学有些熟悉的人。

引言#

概率编程 (PP) 允许在代码中灵活地指定贝叶斯统计模型。PyMC 是一个 PP 框架，它具有直观且可读，但功能强大的语法，该语法与统计学家用来描述模型的自然语法非常接近。它具有下一代马尔可夫链蒙特卡洛 (MCMC) 采样算法，例如无调优采样器 (NUTS; Hoffman, 2014)，它是哈密顿蒙特卡洛 (HMC; Duane, 1987) 的自调优变体。这类采样器在高维和复杂后验分布上效果良好，并允许拟合许多复杂模型，而无需关于拟合算法的专门知识。HMC 和 NUTS 利用来自似然的梯度信息来实现比传统采样方法快得多的收敛速度，尤其是对于较大的模型。NUTS 还具有几种自调优策略，用于自适应地设置哈密顿蒙特卡洛的可调参数，这意味着您通常不需要具备关于算法如何工作的专门知识。

Python 中的概率编程具有许多优点，包括多平台兼容性、富有表现力但简洁且可读的语法、易于与其他科学库集成，以及通过 C、C++、Fortran 或 Cython 进行扩展。这些特性使得编写和使用自定义统计分布、采样器和转换函数相对简单，这是贝叶斯分析所要求的。

虽然 PyMC 的大多数面向用户的功能都是用纯 Python 编写的，但它利用 PyTensor（Theano 项目的一个分支）将模型透明地转码为 C 并将其编译为机器代码，从而提高性能。PyTensor 是一个库，它允许使用称为张量的广义向量数据结构来定义表达式，这些张量与流行的 NumPy ndarray 数据结构紧密集成，并且类似地允许广播和高级索引，就像 NumPy 数组一样。PyTensor 还自动优化似然的计算图以提高速度，并允许编译到计算后端的套件，包括 Jax 和 Numba。

在这里，我们介绍如何使用 PyMC 解决一般贝叶斯统计推断和预测问题。我们将首先通过一个简单的例子了解如何使用 PyMC 的基础知识：安装、数据创建、模型定义、模型拟合和后验分析。然后，我们将介绍两个案例研究，并使用它们来展示如何定义和拟合更复杂的模型。最后，我们将讨论其他一些有用的功能：自定义分布和任意确定性节点。

安装#

运行 PyMC 需要相对较新的 Python 解释器，最好是 3.8 或更高版本。对于 macOS、Linux 和 Windows 的完整 Python 安装，最容易的方法是下载并安装 ContinuumIO 的免费 Anaconda Python Distribution 或开源 Miniforge。

安装 Python 后，请按照 PyMC 文档站点上的安装指南进行操作。

PyMC 在宽松的 Apache License 2.0 下分发。在 GitHub 站点上，用户还可以报告错误和其他问题，以及为项目贡献文档或代码，我们积极鼓励这样做。

一个动机示例：线性回归#

为了介绍模型定义、拟合和后验分析，我们首先考虑一个简单的贝叶斯线性回归模型，其参数具有正态分布先验。我们有兴趣将结果 \(Y\) 预测为正态分布的观测值，其期望值 \(\mu\) 是两个预测变量 \(X_1\) 和 \(X_2\) 的线性函数

\[\begin{split}\begin{aligned} Y &\sim \mathcal{N}(\mu, \sigma^2) \\ \mu &= \alpha + \beta_1 X_1 + \beta_2 X_2 \end{aligned}\end{split}\]

其中 \(\alpha\) 是截距，\(\beta_i\) 是协变量 \(X_i\) 的系数，而 \(\sigma\) 表示观测误差。由于我们正在构建贝叶斯模型，因此我们必须为模型中的未知变量分配先验分布。我们为两个回归系数选择均值为零、方差为 100 的正态先验，这对应于关于真实参数值的弱信息。我们选择半正态分布（以零为界的正态分布）作为 \(\sigma\) 的先验。

\[\begin{split}\begin{aligned} \alpha &\sim \mathcal{N}(0, 100) \\ \beta_i &\sim \mathcal{N}(0, 100) \\ \sigma &\sim \lvert\mathcal{N}(0, 1){\rvert} \end{aligned}\end{split}\]

生成数据#

我们可以仅使用 NumPy 的 random 模块从此模型模拟一些人工数据，然后使用 PyMC 尝试恢复相应的参数。我们有意生成与 PyMC 模型结构紧密对应的数据。

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

%config InlineBackend.figure_format = 'retina'
# Initialize random number generator
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")

# True parameter values
alpha, sigma = 1, 1
beta = [1, 2.5]

# Size of dataset
size = 100

# Predictor variable
X1 = np.random.randn(size)
X2 = np.random.randn(size) * 0.2

# Simulate outcome variable
Y = alpha + beta[0] * X1 + beta[1] * X2 + rng.normal(size=size) * sigma

以下是模拟数据的样子。我们使用绘图库 matplotlib 可视化数据。

fig, axes = plt.subplots(1, 2, sharex=True, figsize=(10, 4))
axes[0].scatter(X1, Y, alpha=0.6)
axes[1].scatter(X2, Y, alpha=0.6)
axes[0].set_ylabel("Y")
axes[0].set_xlabel("X1")
axes[1].set_xlabel("X2");

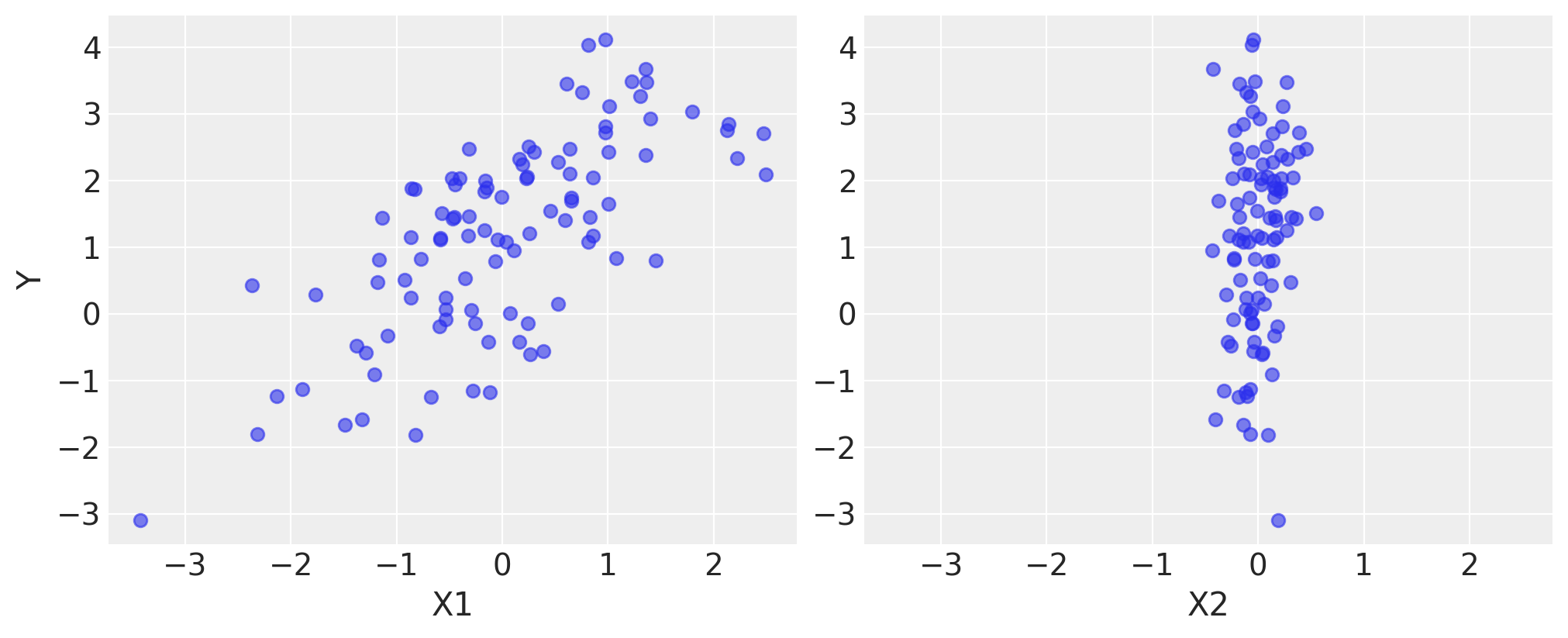
../../_images/e4d51c3aa30152870ac3e856061f670d5512689f02bc26426b537e1ce695e010.png

后验分析#

PyMC 的绘图和诊断功能现在由一个专门的、平台无关的软件包 Arviz 处理。可以使用 plot_trace 创建一个简单的后验图。

az.plot_trace(idata, combined=True);

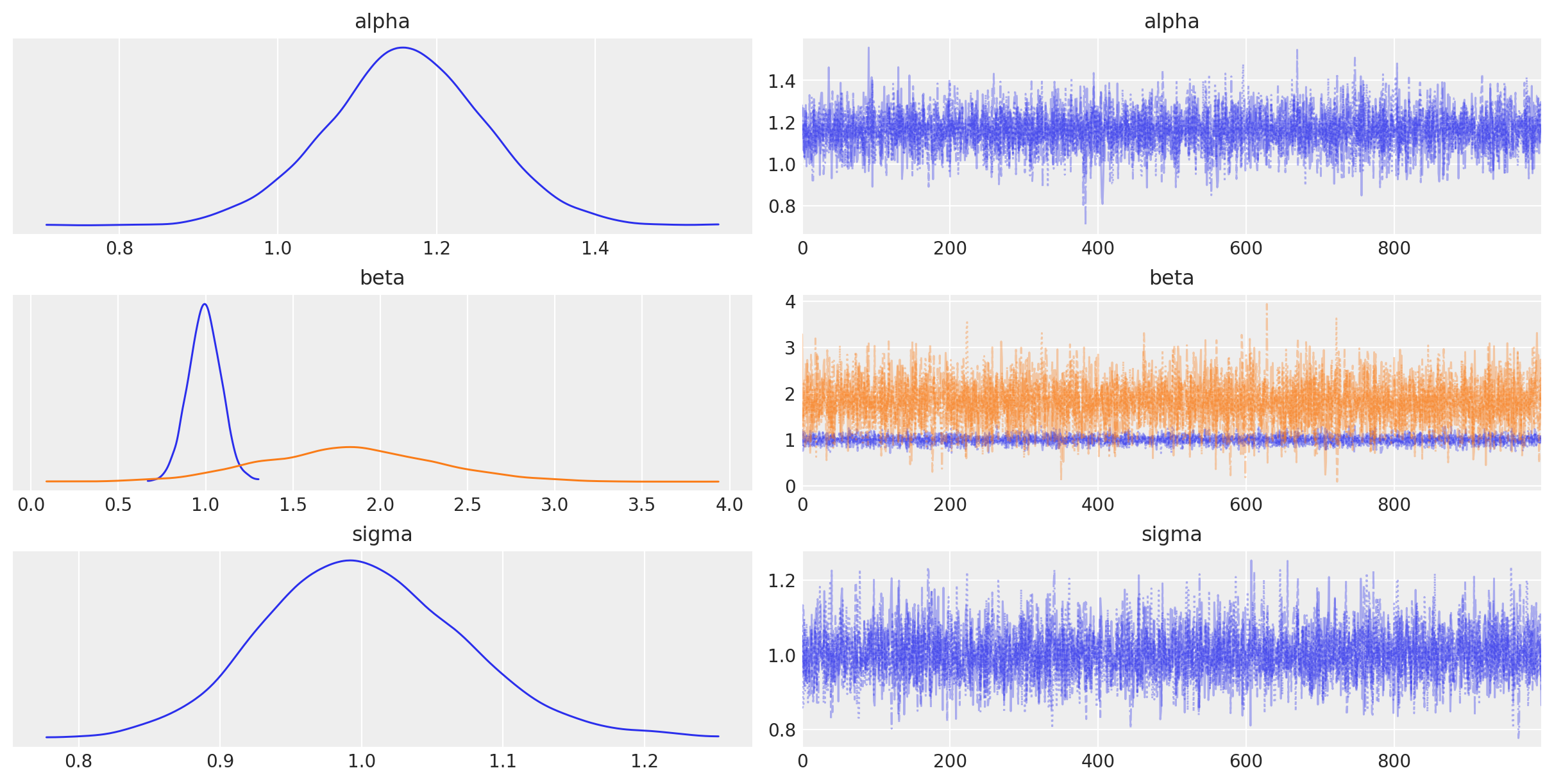
../../_images/62c5aea3c37f61509a61881c3121fac71d94179b9d000495d09c10c94dbaa4e4.png

左列由每个随机随机变量的边际后验的平滑直方图（使用核密度估计）组成，而右列包含按顺序绘制的马尔可夫链的样本。beta 变量是向量值的，因此生成两个密度图和两个迹线图，分别对应于两个预测变量系数。

此外，summary 函数提供了常用后验统计信息的基于文本的输出

az.summary(idata, round_to=2)

	均值	标准差	hdi_3%	hdi_97%	mcse_mean	ess_bulk	ess_tail	r_hat
alpha	1.16	0.10	0.98	1.35	0.00	6594.07	3334.89	1.0
beta[0]	0.99	0.09	0.81	1.16	0.00	6137.67	2892.81	1.0
beta[1]	1.82	0.50	0.93	2.78	0.01	5768.56	3287.63	1.0
sigma	1.00	0.07	0.86	1.13	0.00	5709.96	3233.70	1.0

案例研究 1：听力障碍儿童的教育成果#

作为一个动机示例，我们将使用听力障碍儿童的教育成果数据集。在这里，我们有兴趣确定与更好或更差的学习成果相关的因素。

数据#

这个匿名数据集取自听力和口语语言数据存储库 (LSL-DR)，这是一个国际数据存储库，它跟踪患有听力损失并 enrolled in programs focused on supporting listening and spoken language development 的儿童的人口统计和纵向结果。研究人员有兴趣发现与这些计划中教育成果的改进相关的因素。

有一套可用的预测变量，包括

性别 (male)
家庭中的兄弟姐妹数量 (siblings)
家庭参与度指数 (family_inv)
主要家庭语言是否不是英语 (non_english)
是否存在先前的残疾 (prev_disab)
非白人种族 (non_white)
测试时的年龄（以月为单位，age_test）
听力损失是否不严重 (non_severe_hl)
受试者的母亲是否获得了高中毕业文凭或更高学历 (mother_hs)
听力障碍是否在 3 个月大时被识别出来 (early_ident)。

结果变量是几个学习领域之一的标准化测试分数。

test_scores = pd.read_csv(pm.get_data("test_scores.csv"), index_col=0)
test_scores.head()

	分数	男性	兄弟姐妹	家庭参与度	非英语	先前残疾	测试年龄	非重度听力损失	母亲高中学历	早期识别	非白人
0	40	0	2.0	2.0	False	NaN	55	1.0	NaN	False	False
1	31	1	0.0	NaN	False	0.0	53	0.0	0.0	False	False
2	83	1	1.0	1.0	True	0.0	52	1.0	NaN	False	True
3	75	0	3.0	NaN	False	0.0	55	0.0	1.0	False	False
5	62	0	0.0	4.0	False	1.0	50	0.0	NaN	False	False

test_scores["score"].hist();

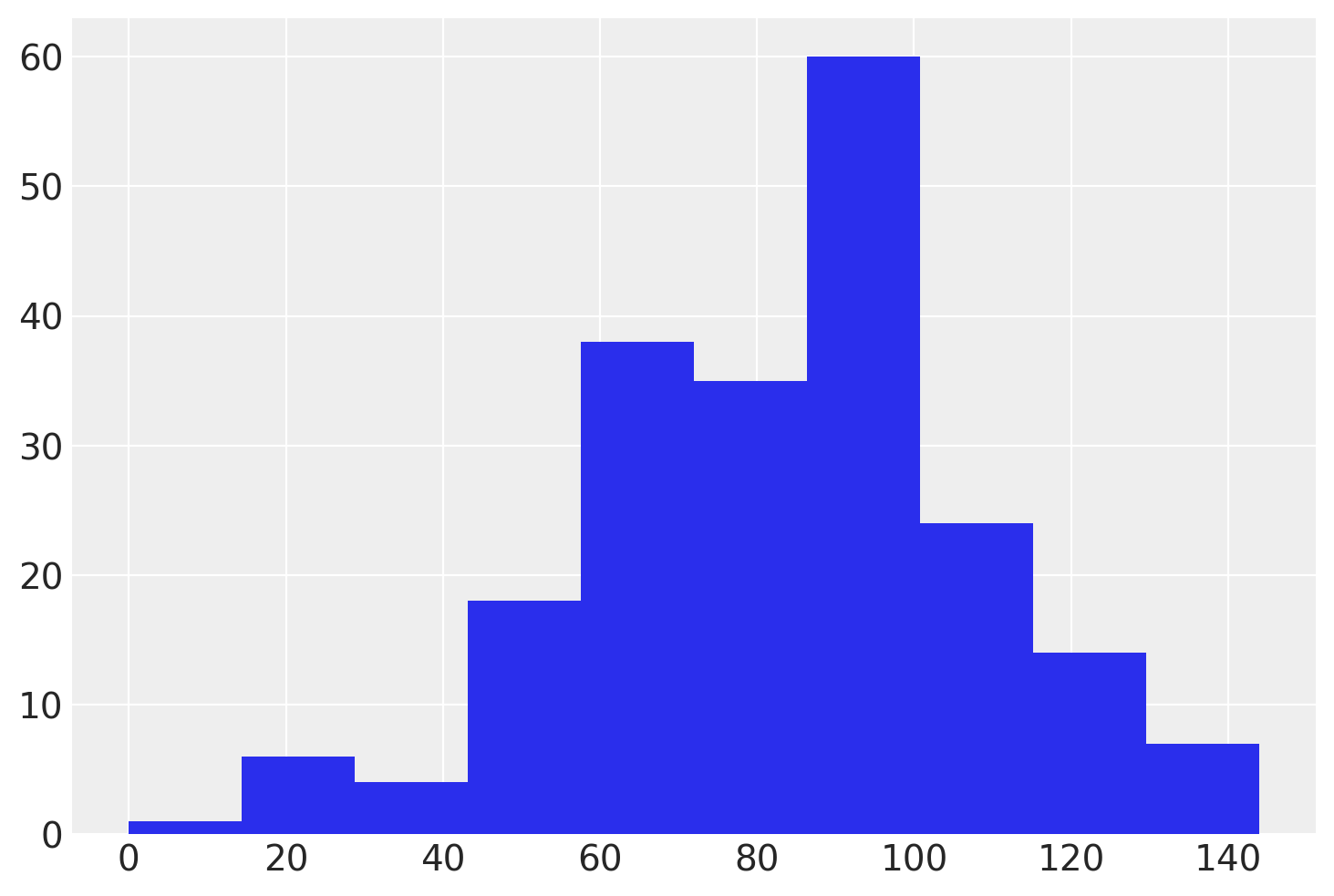
../../_images/bb1c4825f48677febc3973755646376e27a308a78ca80810c95025f6e01e4c38.png

# Dropping missing values is a very bad idea in general, but we do so here for simplicity
X = test_scores.dropna().astype(float)
y = X.pop("score")

# Standardize the features
X -= X.mean()
X /= X.std()

N, D = X.shape

模型#

这是一个比第一个回归示例更实际的问题，因为我们现在正在处理多元回归模型。然而，虽然 LSL-DR 数据集中有几个潜在的预测变量，但先验地很难确定哪些变量与构建有效的统计模型相关。有很多方法可以进行变量选择，但一种流行的自动化方法是正则化，如果无效的协变量无助于预测结果，则通过正则化（一种惩罚形式）将它们向零收缩。

您可能从机器学习或经典统计应用程序中听说过正则化，其中 lasso 或岭回归等方法通过对回归参数的大小施加惩罚来将参数向零收缩。在贝叶斯上下文中，我们对回归系数应用适当的先验分布。一种这样的先验是分层正则化马蹄，它使用两种正则化策略，一种是全局参数，一组是局部参数，每个系数一个。使其工作的关键是选择长尾分布作为收缩先验，这允许一些非零，同时将其余的推向零。

每个回归系数 \(\beta_i\) 的马蹄先验如下所示

\[\beta_i \sim N\left(0, \tau^2 \cdot \tilde{\lambda}_i^2\right)\]

其中 \(\sigma\) 是误差标准差的先验，它也将用于模型似然。在这里，\(\tau\) 是全局收缩参数，\(\tilde{\lambda}_i\) 是局部收缩参数。让我们从全局开始：对于 \(\tau\) 的先验，我们将使用半学生 t 分布，这是一个合理的选择，因为它具有重尾。

\[ \tau \sim \textrm{Half-StudentT}_{2} \left(\frac{D_0}{D - D_0} \cdot \frac{\sigma}{\sqrt{N}}\right). \]

一个问题是先验的参数化需要预先指定的值 \(D_0\)，它表示非零系数的真实数量。幸运的是，对此值的合理猜测是所需要的全部，它只需要在真实数量的数量级范围内即可。让我们使用预测变量数量的一半作为我们的猜测

D0 = int(D / 2)

同时，局部收缩参数由比率定义

\[\tilde{\lambda}_i^2 = \frac{c^2 \lambda_i^2}{c^2 + \tau^2 \lambda_i^2}.\]

为了完成此规范，我们需要 \(\lambda_i\) 和 \(c\) 的先验；与全局收缩一样，我们在 \(\lambda_i\) 上使用长尾 \(\textrm{Half-StudentT}_5(1)\)。我们需要 \(c^2\) 严格为正，但不一定长尾，因此 \(c^2\) 的逆伽玛先验 \(c^2 \sim \textrm{InverseGamma}(1, 1)\) 正好符合要求。

最后，为了使 NUTS 采样器更有效地采样 \(\beta_i\)，我们将对其进行重新参数化，如下所示

\[\begin{split} \begin{align*} z_i & \sim N(0, 1), \\ \beta_i & = z_i \cdot \tau \cdot \tilde{\lambda_i}. \end{align*} \end{split}\]

您将在实践中经常遇到这种重新参数化。

模型规范#

在 PyMC 中指定模型反映了其统计规范。此模型采用了一些新的分布：HalfStudentT 分布用于 \(\tau\) 和 \(\lambda\) 先验，InverseGamma 分布用于 \(c^2\) 变量。

在 PyMC 中，具有纯正先验的变量（如 InverseGamma）使用对数变换进行变换。这使得采样更加稳健。在幕后，一个在非约束空间中的变量（名为 <variable-name>_log）被添加到模型中进行采样。具有在两侧约束它们的先验的变量，如 Beta 或 Uniform，也被变换为非约束的，但使用对数优势比变换。

我们还将通过将输入变量名称作为名为“predictors”的坐标传递到模型中，来利用 PyMC 和 ArviZ 中的命名维度。这将允许我们传递此名称向量，以替代向量值参数中的 shape 整数参数。然后，模型会将适当的名称与它正在估计的每个潜在参数相关联。设置这个需要做更多的工作，但在我们处理模型输出时，它将带来回报。

让我们在 PyMC 中编码此模型

import pytensor.tensor as pt

with pm.Model(coords={"predictors": X.columns.values}) as test_score_model:
    # Prior on error SD
    sigma = pm.HalfNormal("sigma", 25)

    # Global shrinkage prior
    tau = pm.HalfStudentT("tau", 2, D0 / (D - D0) * sigma / np.sqrt(N))
    # Local shrinkage prior
    lam = pm.HalfStudentT("lam", 5, dims="predictors")
    c2 = pm.InverseGamma("c2", 1, 1)
    z = pm.Normal("z", 0.0, 1.0, dims="predictors")
    # Shrunken coefficients
    beta = pm.Deterministic(
        "beta", z * tau * lam * pt.sqrt(c2 / (c2 + tau**2 * lam**2)), dims="predictors"
    )
    # No shrinkage on intercept
    beta0 = pm.Normal("beta0", 100, 25.0)

    scores = pm.Normal("scores", beta0 + pt.dot(X.values, beta), sigma, observed=y.values)

请注意，我们已将 beta 的计算包装在 Deterministic PyMC 类中。您可以在下面阅读有关此内容的更多详细信息，但这确保了此确定性变量的值保留在样本轨迹中。

另请注意，我们在上下文管理器的第一次出现中声明了 Model 名称 test_score_model，而不是像第一个示例那样将其拆分为两行。

模型完成后，我们可以使用 GraphViz 查看其结构，GraphViz 绘制模型图。它有助于确保您编码的模型中的关系是正确的，因为很容易犯编码错误。

pm.model_to_graphviz(test_score_model)

../../_images/ac30f30b2297ec4f2bb798b4f28d2cbba2d0502dbaae4a5f78fdd5cccacda517.svg

在我们继续之前，让我们看看模型在看到任何数据之前会做什么。我们可以进行先验预测采样，以从模型生成模拟数据。然后，让我们将这些模拟与数据集中的实际测试分数进行比较。

with test_score_model:
    prior_samples = pm.sample_prior_predictive(100)

Sampling: [beta0, c2, lam, scores, sigma, tau, z]

az.plot_dist(
    test_scores["score"].values,
    kind="hist",
    color="C1",
    hist_kwargs={"alpha": 0.6},
    label="observed",
)
az.plot_dist(
    prior_samples.prior_predictive["scores"],
    kind="hist",
    hist_kwargs={"alpha": 0.6},
    label="simulated",
)
plt.xticks(rotation=45);

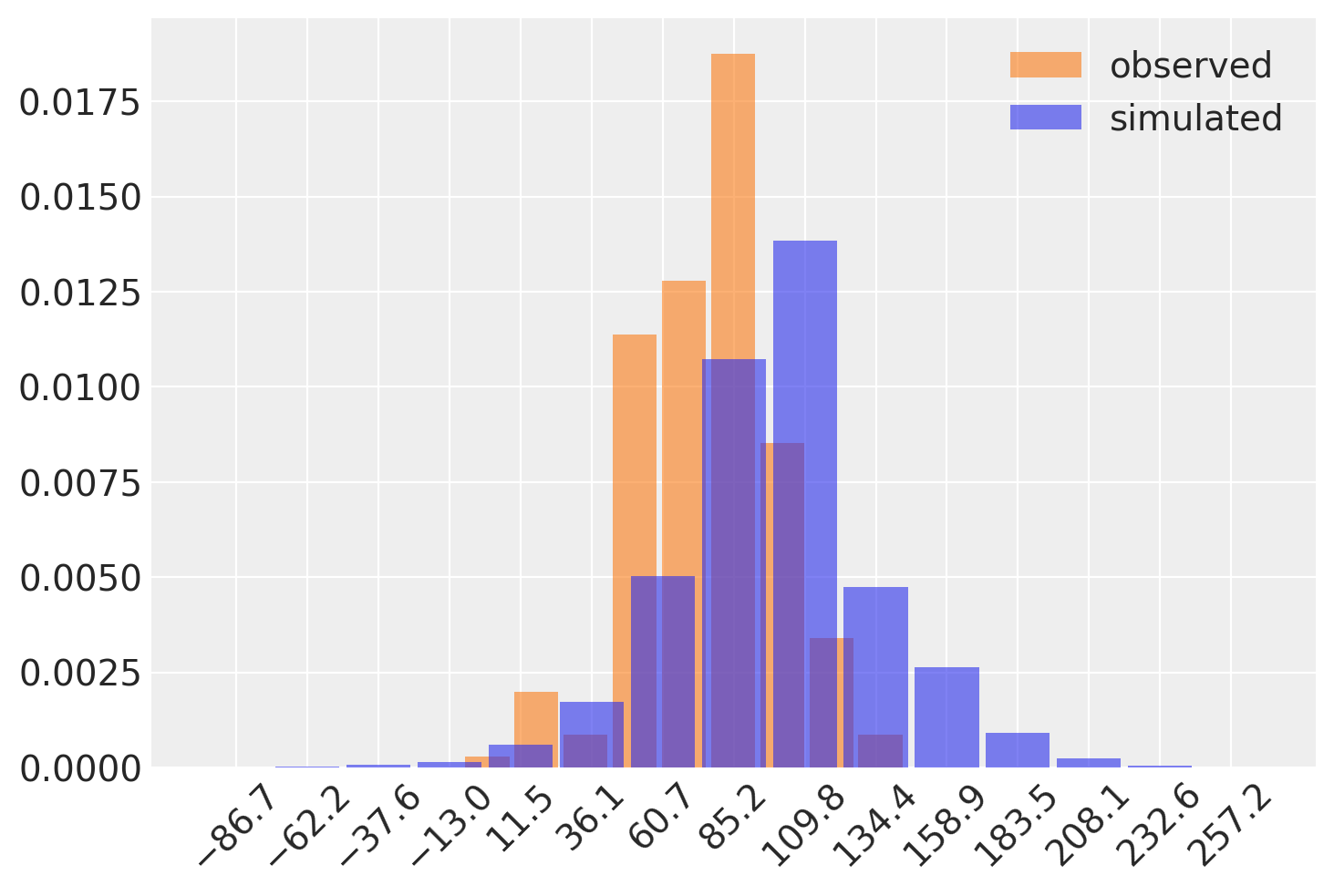
../../_images/c360fbe88ec35949249dd90e419fd69b12be7f3e0c2eef805f6c764a8d878d25.png

我们如何知道这是否合理？这需要一些关于该问题的领域知识。在这里，我们试图预测测试分数的 outcome。如果我们的模型预测数千个值，或大量负值，同时排除合理的 scores，那么我们就错误地指定了模型。您可以在这里看到，模拟数据的分布的支持完全重叠观测到的分数分布的支持；这是一个好兆头！有一些负值，还有一些可能太大而不合理，但没什么可担心的。

模型拟合#

现在到了容易的部分：PyMC 的“Inference Button”是对 sample 的调用。我们将让此模型调整的时间比默认值（1000 次迭代）稍长。这使 NUTS 采样器有更多时间充分调整自身。

with test_score_model:
    idata = pm.sample(1000, tune=2000, random_seed=42)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [sigma, tau, lam, c2, z, beta0]

Sampling 4 chains for 2_000 tune and 1_000 draw iterations (8_000 + 4_000 draws total) took 92 seconds.
There were 2 divergences after tuning. Increase `target_accept` or reparameterize.

请注意，我们在此处收到一些关于发散的警告。这些是 NUTS 无法在后验分布中进行有效移动的样本，因此生成的点可能不是后验的代表性样本。在此示例中没有很多，所以没什么可担心的，但让我们继续听取建议，并将 target_accept 从其默认值 0.9 增加到 0.99。

with test_score_model:
    idata = pm.sample(1000, tune=2000, random_seed=42, target_accept=0.99)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [sigma, tau, lam, c2, z, beta0]

Sampling 4 chains for 2_000 tune and 1_000 draw iterations (8_000 + 4_000 draws total) took 275 seconds.

由于目标接受率更大，因此算法在跨步步长时更加保守，使其更小。我们为此付出的代价是，每个样本都需要更长的时间才能完成。但是，警告现在消失了，我们得到了干净的后验样本！

模型检查#

模型检查的简单第一步是目视检查我们的样本，方法是查看单变量潜在参数的迹线图，以检查是否存在明显的题。这些名称可以作为 var_names 参数传递给 plot_trace。

az.plot_trace(idata, var_names=["tau", "sigma", "c2"]);

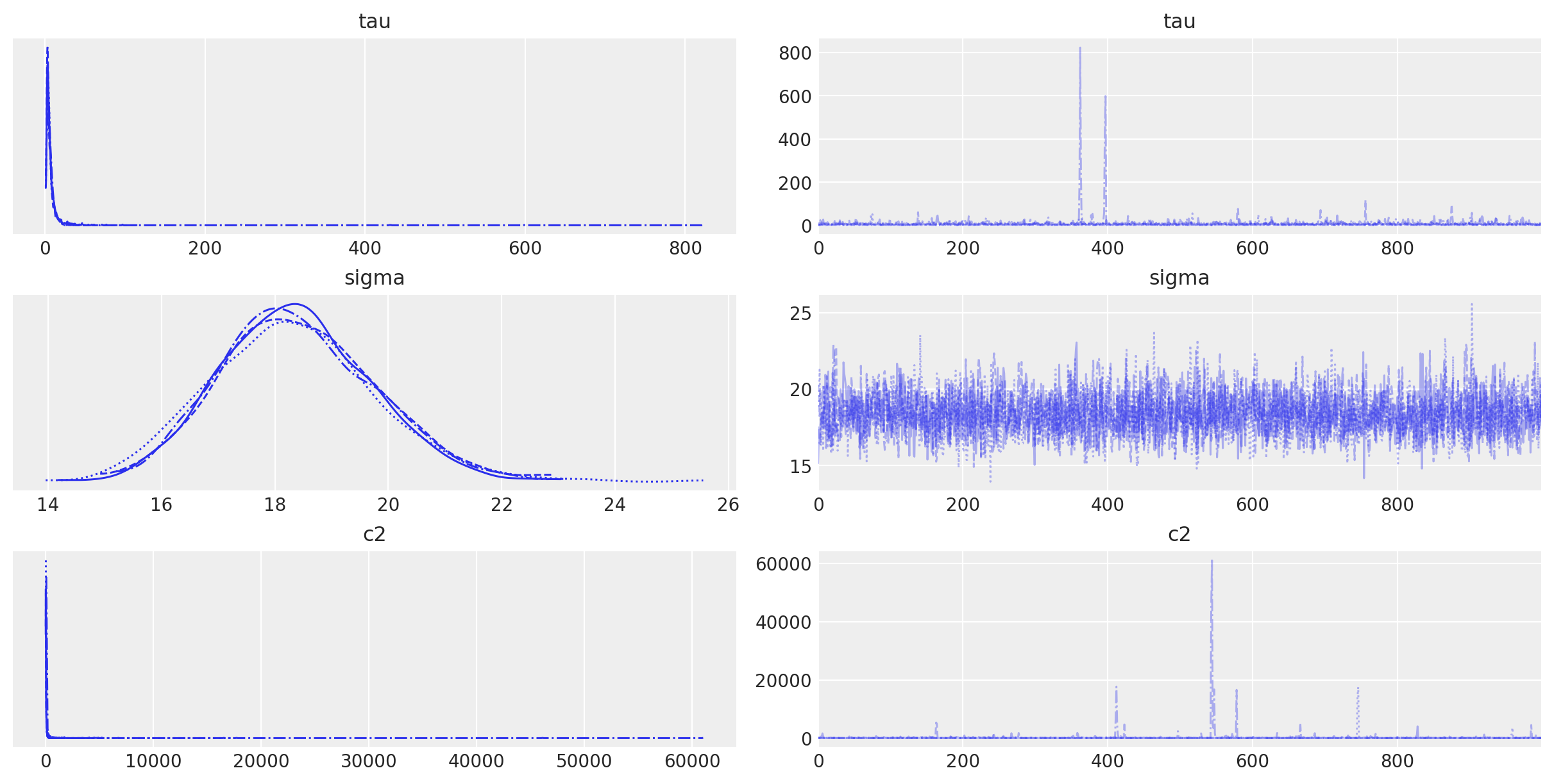
../../_images/bc0f9c018c59950b83d7a6541331c6bfa719cfd7634e38fbcbef70c806de8d7c.png

这些看起来可以吗？嗯，每个参数左侧的每个密度看起来都与其他密度非常相似，这意味着它们已收敛到相同的后验分布（无论是正确的还是不正确的）。右侧迹线图的同质性也是一个好兆头；采样值的时间序列没有趋势或模式。请注意，c2 和 tau 偶尔会采样极端值，但这对于重尾分布是预期的。

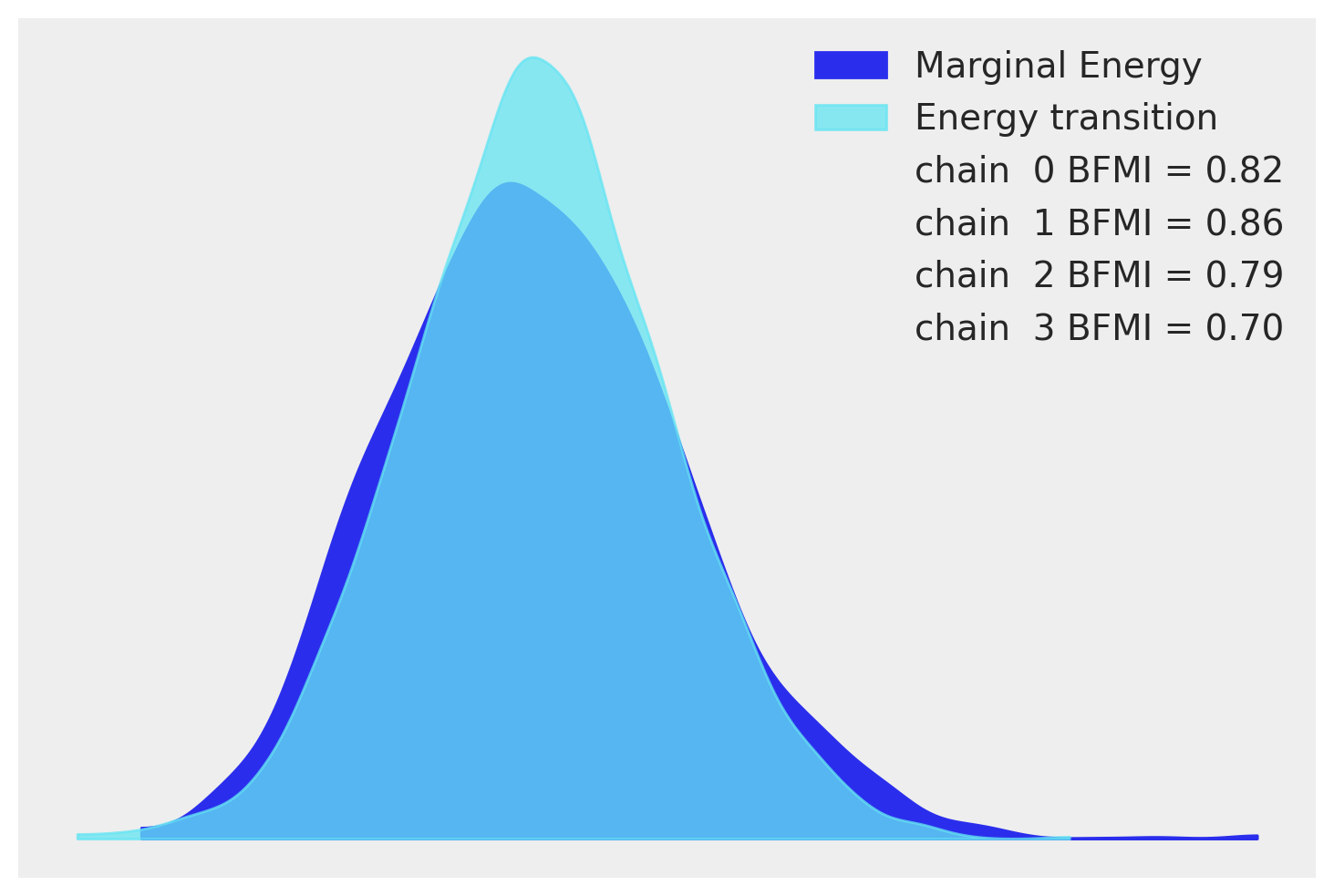
下一个简单的模型检查步骤是查看 NUTS 采样器是否按预期执行。能量图是检查 NUTS 算法是否能够充分探索后验分布的一种方法。如果不是，则当后验的某些部分没有被充分频繁地访问时，可能会冒着有偏后验估计的风险。该图显示了两个密度估计：一个是采样运行的边际能量分布，另一个是步骤之间能量跃迁的分布。这一切有点抽象，但我们所要寻找的是分布彼此相似。我们的看起来还不错。

az.plot_energy(idata);

../../_images/ebec467a18d6db85f2aabb7744c245f639e4dec07375a166c72f6fdb1d36a406.png

最终，我们对 beta 的估计感兴趣，即预测变量系数集。将 beta 传递给 plot_trace 将生成一个非常拥挤的图，因此我们将改用 plot_forest，它旨在处理向量值参数。

az.plot_forest(idata, var_names=["beta"], combined=True, hdi_prob=0.95, r_hat=True);

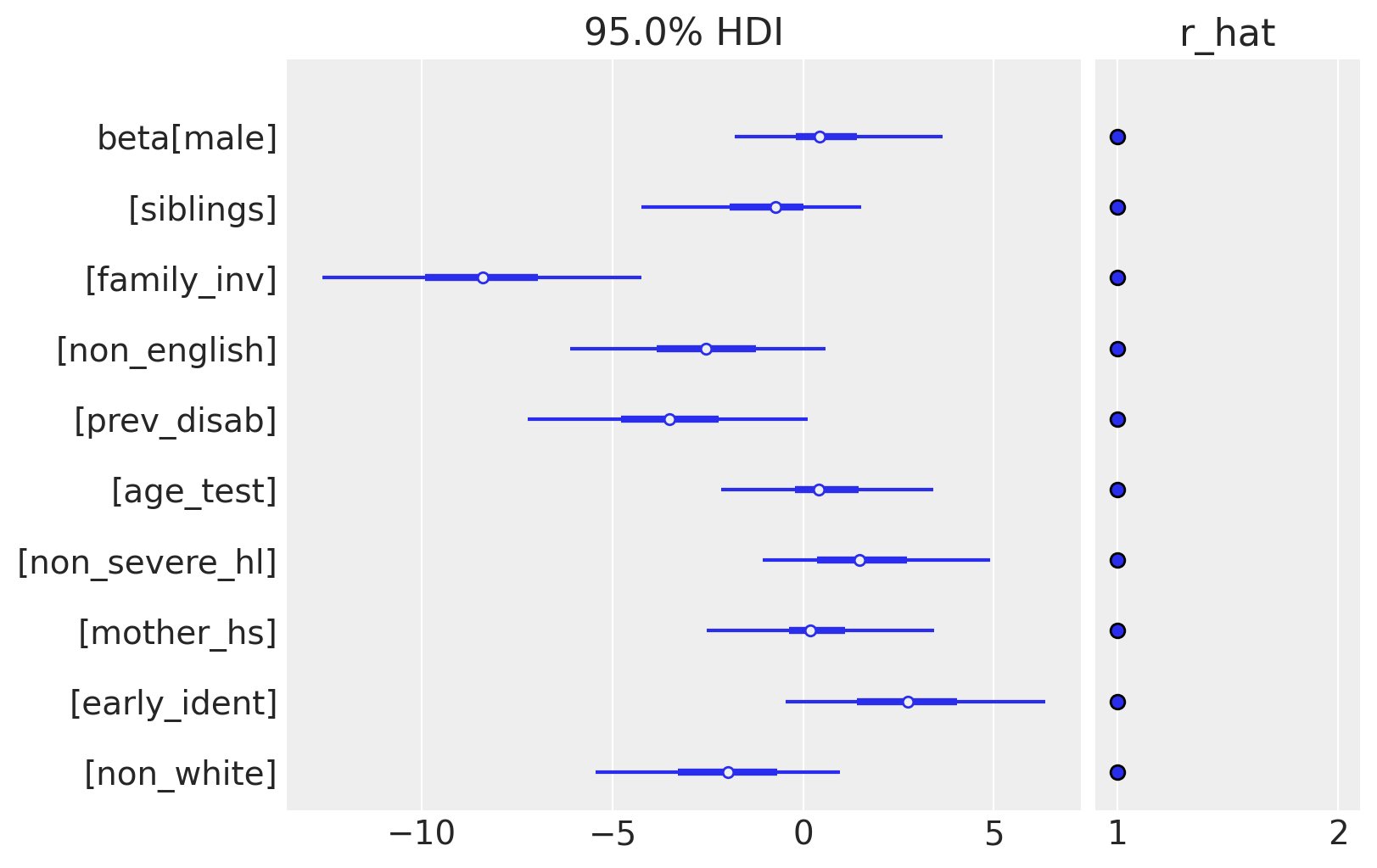
../../_images/0472d976afb9af1297b3608ae1a7a9f3d8ec21eaf80fe0a376db70c103fb3bed.png

系数的后验分布揭示了一些在预测测试分数方面显得重要的因素。家庭参与度 (family_inv) 的系数很大且为负，这意味着分数越高（与较差的参与度相关）会导致更差的测试分数。另一方面，早期识别听力障碍是积极的，这意味着尽早发现问题可以带来更好的教育成果，这也很直观。请注意，其他变量，特别是性别 (male)、测试时的年龄 (age_test) 和母亲的教育程度 (mother_hs) 基本上都被缩减为零。

案例研究 2：煤矿灾难#

考虑以下 1851 年至 1962 年英国记录的煤矿灾难时间序列 (Jarrett, 1979)。据认为，灾难的数量受到此期间安全法规变化的影响。不幸的是，我们还有一对年份的数据缺失，在 pandas Series 中用 nan 标识为缺失值。这些缺失值将由 PyMC 自动插补。

接下来，我们将为此序列构建一个模型，并尝试估计变化发生的时间。同时，我们将了解如何处理缺失数据，使用多个采样器以及从离散随机变量中采样。

# fmt: off
disaster_data = pd.Series(
    [4, 5, 4, 0, 1, 4, 3, 4, 0, 6, 3, 3, 4, 0, 2, 6,
    3, 3, 5, 4, 5, 3, 1, 4, 4, 1, 5, 5, 3, 4, 2, 5,
    2, 2, 3, 4, 2, 1, 3, np.nan, 2, 1, 1, 1, 1, 3, 0, 0,
    1, 0, 1, 1, 0, 0, 3, 1, 0, 3, 2, 2, 0, 1, 1, 1,
    0, 1, 0, 1, 0, 0, 0, 2, 1, 0, 0, 0, 1, 1, 0, 2,
    3, 3, 1, np.nan, 2, 1, 1, 1, 1, 2, 4, 2, 0, 0, 1, 4,
    0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1]
)
# fmt: on
years = np.arange(1851, 1962)

plt.plot(years, disaster_data, "o", markersize=8, alpha=0.4)
plt.ylabel("Disaster count")
plt.xlabel("Year");

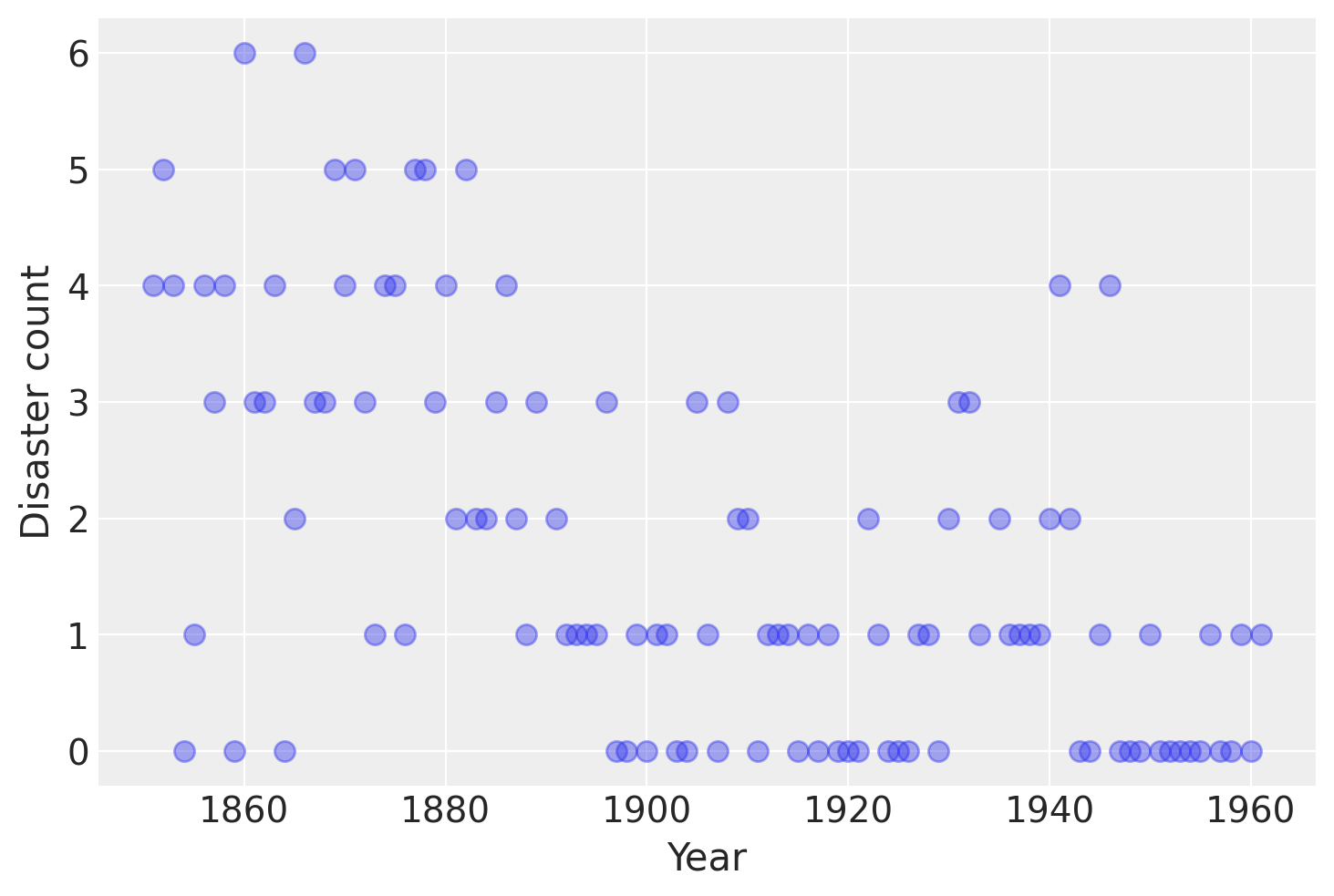
../../_images/036b4f6ecc0a774b2648c66e486f4bad431038ee492a4b5bbcadd2cd6d8d8bde.png

时间序列中灾难的发生被认为遵循泊松过程，在时间序列的早期部分具有较大的速率参数，而在后期部分具有较小的速率参数。我们有兴趣找到序列中的变化点，这可能与采矿安全法规的变化有关。

在我们的模型中，

\[\begin{split} \begin{aligned} D_t &\sim \text{Pois}(r_t), r_t= \begin{cases} e, & \text{if } t \le s \\ l, & \text{if } t \gt s \end{cases} \\ s &\sim \text{Unif}(t_l, t_h)\\ e &\sim \text{exp}(1)\\ l &\sim \text{exp}(1) \end{aligned} \end{split}\]

参数定义如下

\(D_t\)：年份 \(t\) 的灾难数量
\(r_t\)：年份 \(t\) 灾难的泊松分布的速率参数。
\(s\)：速率参数发生变化的年份（切换点）。
\(e\)：切换点 \(s\) 之前的速率参数。
\(l\)：切换点 \(s\) 之后的速率参数。
\(t_l\), \(t_h\)：年份 \(t\) 的下限和上限。

此模型的构建方式与我们之前的模型非常相似。主要区别在于引入了具有泊松先验和离散均匀先验的离散变量，以及确定性随机变量 rate 的新颖形式。

with pm.Model() as disaster_model:
    switchpoint = pm.DiscreteUniform("switchpoint", lower=years.min(), upper=years.max())

    # Priors for pre- and post-switch rates number of disasters
    early_rate = pm.Exponential("early_rate", 1.0)
    late_rate = pm.Exponential("late_rate", 1.0)

    # Allocate appropriate Poisson rates to years before and after current
    rate = pm.math.switch(switchpoint >= years, early_rate, late_rate)

    disasters = pm.Poisson("disasters", rate, observed=disaster_data)

速率随机变量的逻辑，

rate = switch(switchpoint >= year, early_rate, late_rate)

是使用 switch 实现的，switch 是一个类似于 if 语句的函数。它使用第一个参数在接下来的两个参数之间切换。

缺失值通过将 NumPy MaskedArray 或带有 NaN 值的 DataFrame 传递给创建观测随机变量时的 observed 参数来透明地处理。在幕后，创建了另一个随机变量 disasters.missing_values 来模拟缺失值。

不幸的是，由于它们是离散变量，因此没有有意义的梯度，因此我们不能使用 NUTS 对 switchpoint 或缺失的灾难观测值进行采样。相反，我们将使用 Metropolis 步长方法进行采样，该方法实现了自适应 Metropolis-Hastings 算法，因为它旨在处理离散值。PyMC 自动分配正确的采样算法。

with disaster_model:
    idata = pm.sample(10000)

Multiprocess sampling (4 chains in 4 jobs)
CompoundStep
>CompoundStep
>>Metropolis: [switchpoint]
>>Metropolis: [disasters_unobserved]
>NUTS: [early_rate, late_rate]

Sampling 4 chains for 1_000 tune and 10_000 draw iterations (4_000 + 40_000 draws total) took 193 seconds.

在下面的迹图 (trace plot) 中，我们可以看到大约有 10 年的跨度对于安全性的重大变化来说是合理的，但是 5 年的跨度包含了大部分概率质量。分布是锯齿状的，这是因为年份切换点和似然性之间的跳跃关系；锯齿状不是由于采样误差造成的。

axes_arr = az.plot_trace(idata)
plt.draw()
for ax in axes_arr.flatten():
    if ax.get_title() == "switchpoint":
        labels = [label.get_text() for label in ax.get_xticklabels()]
        ax.set_xticklabels(labels, rotation=45, ha="right")
        break
plt.draw()

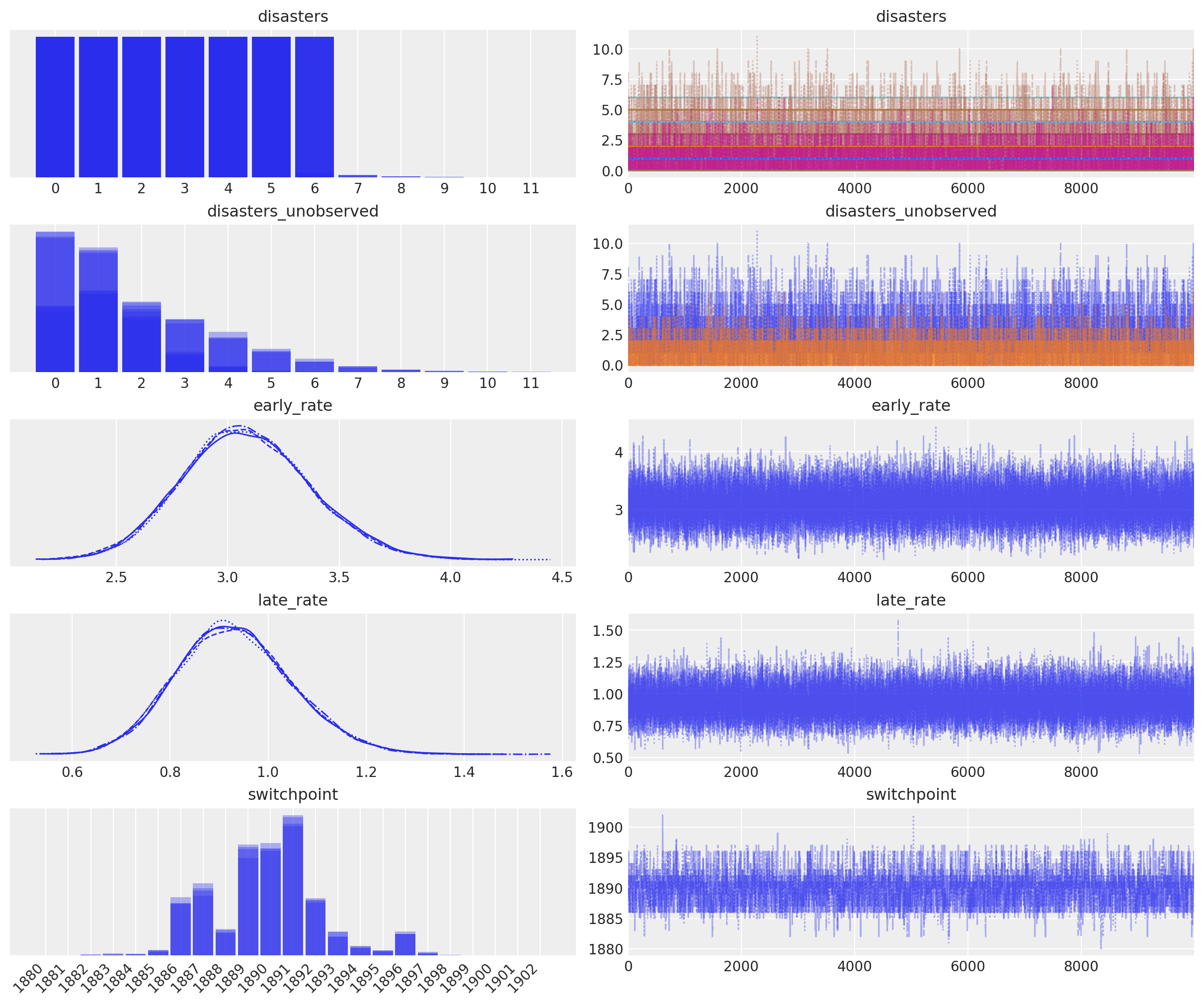
../../_images/9ea5b043586ce226d8dcf2bfbe9e5634c0b28c20e1129728d9753c1cb54777a3.png

请注意，rate 随机变量未出现在迹 (trace) 中。在这种情况下，这没问题，因为它本身并不受关注。请记住之前的示例，我们将通过将其包装在 Deterministic 类中并为其命名来追踪该变量。

下图显示了作为橙色垂直线的切换点，以及作为半透明带的最高后验密度 (HPD)。虚线黑线显示了事故率。

plt.figure(figsize=(10, 8))
plt.plot(years, disaster_data, ".", alpha=0.6)
plt.ylabel("Number of accidents", fontsize=16)
plt.xlabel("Year", fontsize=16)

trace = idata.posterior.stack(draws=("chain", "draw"))

plt.vlines(trace["switchpoint"].mean(), disaster_data.min(), disaster_data.max(), color="C1")
average_disasters = np.zeros_like(disaster_data, dtype="float")
for i, year in enumerate(years):
    idx = year < trace["switchpoint"]
    average_disasters[i] = np.mean(np.where(idx, trace["early_rate"], trace["late_rate"]))

sp_hpd = az.hdi(idata, var_names=["switchpoint"])["switchpoint"].values
plt.fill_betweenx(
    y=[disaster_data.min(), disaster_data.max()],
    x1=sp_hpd[0],
    x2=sp_hpd[1],
    alpha=0.5,
    color="C1",
)
plt.plot(years, average_disasters, "k--", lw=2);

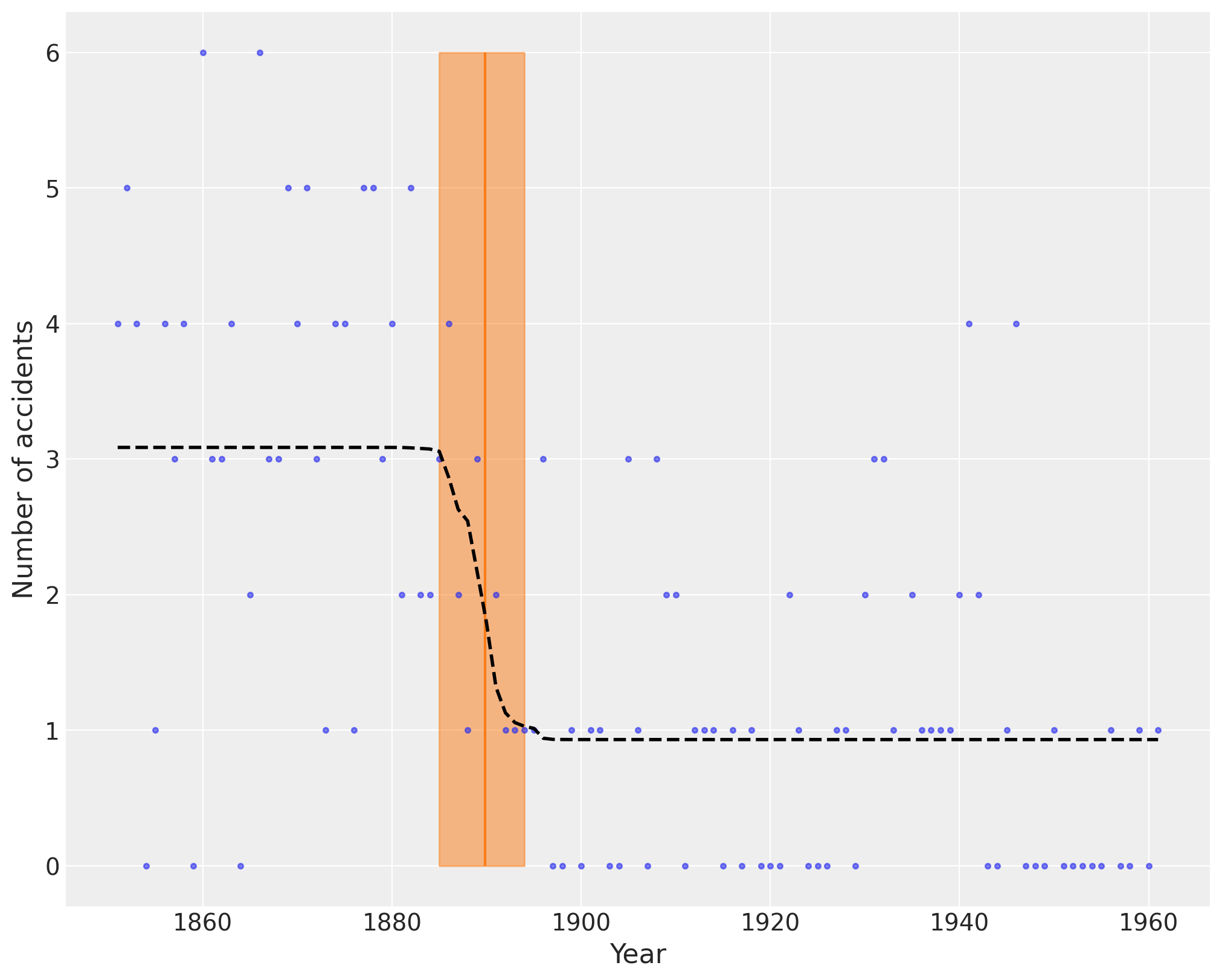
../../_images/a2136bb63dfea4a9d1cd44c3fef5a311ab7925f62a37ce36f6bb18910ec4bbbc.png

任意确定性变量#

由于 PyMC 依赖于 PyTensor，因此它提供了许多数学函数和运算符，用于将随机变量转换为新的随机变量。但是，PyTensor 中的函数库并非详尽无遗，因此 PyTensor 和 PyMC 提供了在纯 Python 中创建任意函数并将这些函数包含在 PyMC 模型中的功能。这通过 as_op 函数装饰器来支持。

PyTensor 需要知道函数的输入和输出类型，这些类型通过 as_op 的 itypes 指定输入，otypes 指定输出。

from pytensor.compile.ops import as_op


@as_op(itypes=[pt.lscalar], otypes=[pt.lscalar])
def crazy_modulo3(value):
    if value > 0:
        return value % 3
    else:
        return (-value + 1) % 3


with pm.Model() as model_deterministic:
    a = pm.Poisson("a", 1)
    b = crazy_modulo3(a)

这种方法的一个重要缺点是 pytensor 无法检查这些函数以计算基于哈密顿量的采样器所需的梯度。因此，对于使用此类运算符的模型，不可能使用 HMC 或 NUTS 采样器。但是，如果我们从 Op 继承而不是使用 as_op，则可以添加梯度。PyMC 示例集包含 as_op 用法的更详细示例。

任意分布#

类似地，PyMC 中的统计分布库并非详尽无遗，但 PyMC 允许为任意概率分布创建用户定义的函数。CustomDist 类对于简单的统计分布，接受任何计算对数概率 \(log(p(x))\) 的函数作为参数。此函数可以在其计算中使用其他随机变量。这是一个受 Jake Vanderplas 关于线性回归应使用哪些先验的博客文章 (Vanderplas, 2014) 启发的示例。

import pytensor.tensor as pt

with pm.Model() as model:
    alpha = pm.Uniform('intercept', -100, 100)
    
    # Create variables with custom log-densities
    beta = pm.CustomDist('beta', logp=lambda value: -1.5 * pt.log(1 + value**2))
    eps = pm.CustomDist('eps', logp=lambda value: -pt.log(pt.abs_(value)))
    
    # Create likelihood
    like = pm.Normal('y_est', mu=alpha + beta * X, sigma=eps, observed=Y)

对于更复杂的分布，可以创建 Continuous 或 Discrete 的子类，并根据需要提供自定义的 logp 函数。这就是 PyMC 中内置分布的指定方式。例如，心理学和天体物理学等领域对于可能需要数值近似的特定过程具有复杂的似然函数。

下面显示了将上面的 beta 变量实现为 Continuous 子类，以及相关的 RandomVariable 对象，该对象的实例成为分布的属性。

class BetaRV(pt.random.op.RandomVariable):
    name = "beta"
    ndim_supp = 0
    ndims_params = []
    dtype = "floatX"

    @classmethod
    def rng_fn(cls, rng, size):
        raise NotImplementedError("Cannot sample from beta variable")


beta = BetaRV()

class Beta(pm.Continuous):
    rv_op = beta

    @classmethod
    def dist(cls, mu=0, **kwargs):
        mu = pt.as_tensor_variable(mu)
        return super().dist([mu], **kwargs)

    def logp(self, value):
        mu = self.mu
        return beta_logp(value - mu)


def beta_logp(value):
    return -1.5 * pt.log(1 + (value) ** 2)


with pm.Model() as model:
    beta = Beta("beta", mu=0)

如果您的 logp 无法在 PyTensor 中表达，则可以使用 as_op 修饰器修饰该函数，如下所示：@as_op(itypes=[pt.dscalar], otypes=[pt.dscalar])。请注意，这将创建一个黑盒 Python 函数，该函数将慢得多，并且不提供例如 NUTS 所需的梯度。

讨论#

概率编程是统计学习中一种新兴的范式，其中贝叶斯建模是重要的子学科。概率编程的标志性特征——将变量指定为概率分布，并将变量条件化于其他变量和观测值——使其成为在各种设置和模型复杂度范围内构建模型的强大工具。伴随着概率编程的兴起，用于拟合贝叶斯模型的方法也出现了创新浪潮，这些方法代表了对现有 MCMC 方法的显着改进。然而，尽管这种扩展，但只有少数软件包能够跟上方法论创新的步伐，而且允许非专家用户实施模型的软件包就更少了。

PyMC 为定量研究人员提供了一个概率编程平台，以灵活而简洁地实施统计模型。大量的统计分布和几种预定义的拟合算法使用户能够专注于手头的科学问题，而不是贝叶斯建模的实施细节。选择 Python 作为开发语言，而不是特定领域的语言，意味着 PyMC 用户能够以交互方式构建模型、内省模型对象以及调试或分析他们的工作，使用一种动态、高级且易于学习的编程语言。PyMC 的模块化、面向对象的设计意味着添加新的拟合算法或其他功能非常简单。此外，PyMC 还具有大多数其他软件包中没有的几个功能，最值得注意的是基于哈密顿量的采样器以及对受约束随机变量的自动转换，后者仅由 Stan 提供。然而，与 Stan 不同，PyMC 支持离散变量以及非基于梯度的采样算法，如 Metropolis-Hastings 和 Slice 采样。

PyMC 的开发是一项持续的努力，并且计划在未来的版本中加入几个功能。最值得注意的是，变分推断技术通常比 MCMC 采样更有效，但以通用性为代价。然而，最近，已经开发了黑盒变分推断算法，例如自动微分变分推断（ADVI；Kucukelbir et al., 2017）。该算法计划添加到 PyMC 中。作为开源科学计算工具包，我们鼓励开发贝叶斯模型新拟合算法的研究人员在 PyMC 中提供参考实现。由于采样器可以用纯 Python 代码编写，因此可以对其进行通用实现，使其适用于任意 PyMC 模型，从而为作者提供更大的受众来使用其方法。

参考文献#

Bastien, F., Lamblin, P., Pascanu, R., Bergstra, J., Goodfellow, I., Bergeron, A., Bouchard, N., Warde-Farley, D., and Bengio, Y. (2012) “Theano: new features and speed improvements”. NIPS 2012 deep learning workshop.

Bergstra, J., Breuleux, O., Bastien, F., Lamblin, P., Pascanu, R., Desjardins, G., Turian, J., Warde-Farley, D., and Bengio, Y. (2010) “Theano: A CPU and GPU Math Expression Compiler”. Proceedings of the Python for Scientific Computing Conference (SciPy) 2010. June 30 - July 3, Austin, TX

Duane, S., Kennedy, A. D., Pendleton, B. J., and Roweth, D. (1987) “Hybrid Monte Carlo”, Physics Letters, vol. 195, pp. 216-222.

Hoffman, M. D., & Gelman, A. (2014). The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo. The Journal of Machine Learning Research, 30.

Jarrett, R.G. A note on the intervals between coal mining disasters. Biometrika, 66:191–193, 1979.

Kucukelbir A, Dustin Tran, Ranganath R, Gelman A, and Blei DM. Automatic differentiation variational inference, The Journal of Machine Learning Research. 18 , pp. 430-474.

Lunn, D.J., Thomas, A., Best, N., and Spiegelhalter, D. (2000) WinBUGS – a Bayesian modelling framework: concepts, structure, and extensibility. Statistics and Computing, 10:325–337.

Neal, R.M. Slice sampling. Annals of Statistics. (2003). doi:10.2307/3448413. Patil, A., D. Huard and C.J. Fonnesbeck. (2010) PyMC: Bayesian Stochastic Modelling in Python. Journal of Statistical Software, 35(4), pp. 1-81

Piironen, J., & Vehtari, A. (2017). Sparsity information and regularization in the horseshoe and other shrinkage priors. Electronic Journal of Statistics, 11(2), 5018-5051.

Stan Development Team. (2014). Stan: A C++ Library for Probability and Sampling, Version 2.5.0.

Vanderplas, Jake. “Frequentism and Bayesianism IV: How to be a Bayesian in Python.” Pythonic Perambulations. N.p., 14 Jun 2014. Web. 27 May. 2015.

%load_ext watermark
%watermark -n -u -v -iv -w -p xarray

Last updated: Fri Aug 09 2024

Python implementation: CPython
Python version       : 3.11.8
IPython version      : 8.26.0

xarray: 2024.7.0

numpy     : 1.26.4
pytensor  : 2.22.1
pandas    : 2.2.1
matplotlib: 3.8.3
arviz     : 0.18.0
pymc      : 5.15.1

Watermark: 2.4.3