分类回归#
在此示例中,我们将对具有两个以上类别的结果进行建模。
注意
此 notebook 使用了非 PyMC 依赖项的库,因此需要专门安装才能运行此 notebook。打开下面的下拉菜单以获取更多指导。
额外依赖项安装说明
为了运行此 notebook(本地或在 binder 上),您不仅需要安装所有可选依赖项的 PyMC 工作环境,还需要安装一些额外的依赖项。 有关安装 PyMC 本身的建议,请参阅安装
您可以使用首选的软件包管理器安装这些依赖项,我们在此处提供 pip 和 conda 命令示例。
$ pip install pymc-bart
请注意,如果您想(或需要)从 notebook 内部而不是命令行安装软件包,则可以通过运行 pip 命令的变体来安装软件包
import sys
!{sys.executable} -m pip install pymc-bart
您不应运行 !pip install,因为它可能会将软件包安装在不同的环境中,即使已安装,也无法从 Jupyter notebook 中访问。
另一种选择是使用 conda 代替
$ conda install pymc-bart
当使用 conda 安装科学 Python 软件包时,我们建议使用 conda forge
import os
import warnings
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pymc_bart as pmb
import seaborn as sns
from scipy.special import softmax
warnings.simplefilter(action="ignore", category=FutureWarning)
# set formats
RANDOM_SEED = 8457
az.style.use("arviz-darkgrid")
鹰数据集#
在这里,我们将使用一个数据集,其中包含关于 3 种鹰(CH=库珀鹰,RT=红尾鹰,SS=锐尾鹰)的信息。 此数据集总共包含 908 个个体的信息,每个个体包含 16 个变量,以及物种信息。 为了简化示例,我们将使用以下 5 个协变量
Wing:初级飞羽从尖端到与腕部连接处的长度(单位:毫米)。
Weight:体重(单位:克)。
Culmen:上喙从尖端到与鸟类肉质部分碰撞处的长度(单位:毫米)。
Hallux:杀戮爪的长度(单位:毫米)。
Tail:与尾巴长度相关的测量值(单位:毫米)。
此外,我们将消除数据集中的 NaN 值。 通过这些,我们将预测鹰的“物种”,换句话说,这些是我们的因变量,我们想要预测的类别。
# Load data and eliminate NANs
try:
Hawks = pd.read_csv(os.path.join("..", "data", "Hawks.csv"))[
["Wing", "Weight", "Culmen", "Hallux", "Tail", "Species"]
].dropna()
except FileNotFoundError:
Hawks = pd.read_csv(pm.get_data("Hawks.csv"))[
["Wing", "Weight", "Culmen", "Hallux", "Tail", "Species"]
].dropna()
Hawks.head()
| 翅膀 | 体重 | 上喙 | 杀戮爪 | 尾巴 | 物种 | |
|---|---|---|---|---|---|---|
| 0 | 385.0 | 920.0 | 25.7 | 30.1 | 219 | RT |
| 2 | 381.0 | 990.0 | 26.7 | 31.3 | 235 | RT |
| 3 | 265.0 | 470.0 | 18.7 | 23.5 | 220 | CH |
| 4 | 205.0 | 170.0 | 12.5 | 14.3 | 157 | SS |
| 5 | 412.0 | 1090.0 | 28.5 | 32.2 | 230 | RT |
EDA#
以下比较了协变量,以快速可视化 3 个物种的数据。
sns.pairplot(Hawks, hue="Species");
/Users/alex_andorra/mambaforge/envs/pymc-examples/lib/python3.12/site-packages/seaborn/axisgrid.py:123: UserWarning: The figure layout has changed to tight
self._figure.tight_layout(*args, **kwargs)
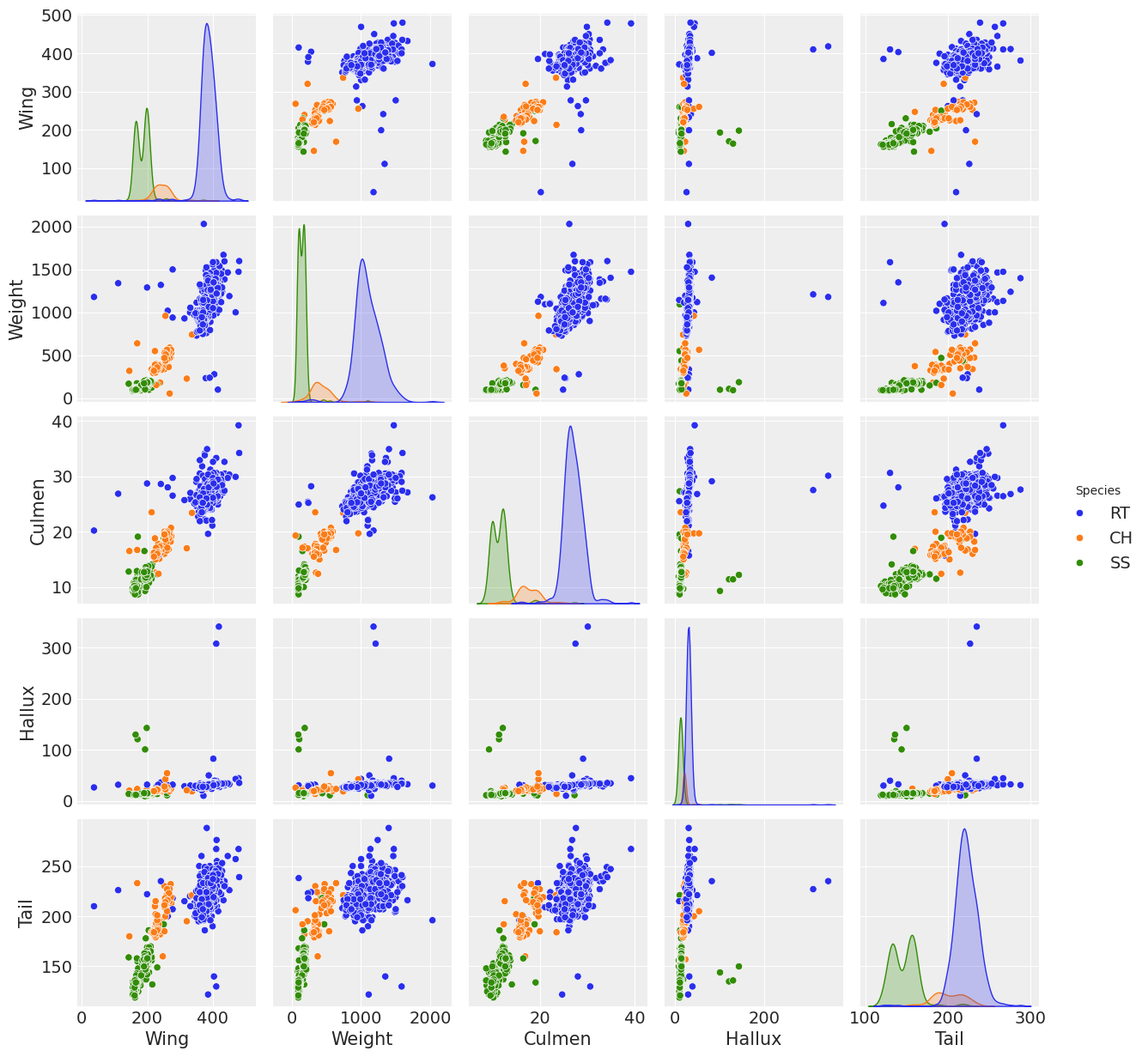
可以看出,在几乎所有协变量中,RT 物种的分布都比其他两个物种更具差异性,并且协变量翅膀、体重和上喙呈现出物种之间的一定分离。 然而,没有一个变量在物种分布之间具有明显的区分,以至于它们可以清晰地将它们分开。 可以组合协变量,可能是翅膀、体重和上喙,以实现分类。 这些是进行回归的主要原因。
模型规范#
首先,我们将准备用于模型的数据,使用“物种”作为响应变量,以及“翅膀”、“体重”、“上喙”、“杀戮爪”和“尾巴”作为预测变量。 使用 pd.Categorical(Hawks['Species']).codes 我们可以将物种名称编码为介于 0 和 2 之间的整数,其中 0=”CH”,1=”RT” 和 2=”SS”。
y_0 = pd.Categorical(Hawks["Species"]).codes
x_0 = Hawks[["Wing", "Weight", "Culmen", "Hallux", "Tail"]]
print(len(x_0), x_0.shape, y_0.shape)
891 (891, 5) (891,)
在每个 pymc 模型中,我们只能有一个 BART() 实例(目前),因此为了对 3 个物种进行建模,我们可以使用坐标和维度名称来指定变量的形状,表明有 891 行信息用于 3 个物种。 此步骤有助于稍后从 InferenceData 中选择组。
_, species = pd.factorize(Hawks["Species"], sort=True)
species
Index(['CH', 'RT', 'SS'], dtype='object')
coords = {"n_obs": np.arange(len(x_0)), "species": species}
在此模型中,我们对来自 pmb.BART() 的 \(\mu\) 使用 pm.math.softmax() 函数,因为它可以保证向量在 axis=0 方向上求和为 1(在本例中)。
with pm.Model(coords=coords) as model_hawks:
μ = pmb.BART("μ", x_0, y_0, m=50, dims=["species", "n_obs"])
θ = pm.Deterministic("θ", pm.math.softmax(μ, axis=0))
y = pm.Categorical("y", p=θ.T, observed=y_0)
pm.model_to_graphviz(model=model_hawks)
现在拟合模型并从后验中获取样本。
with model_hawks:
idata = pm.sample(chains=4, compute_convergence_checks=False, random_seed=123)
pm.sample_posterior_predictive(idata, extend_inferencedata=True)
Multiprocess sampling (4 chains in 4 jobs)
PGBART: [μ]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 58 seconds.
Sampling: [y]
结果#
变量重要性#
可能某些输入变量对于按物种分类没有信息量,因此为了简洁起见并降低模型估计的计算成本,量化数据集中每个变量的重要性很有用。 PyMC-BART 提供了函数 plot_variable_importance(),该函数生成一个图,其 x 轴显示协变量的数量,y 轴显示完整模型(包括所有变量)和受限模型(仅包含变量子集)的预测之间的 R\(^2\)(皮尔逊相关系数的平方)。 误差线表示来自后验预测分布的 94% HDI。
vi_results = pmb.compute_variable_importance(idata, μ, x_0, method="VI", random_seed=RANDOM_SEED)
pmb.plot_variable_importance(vi_results);
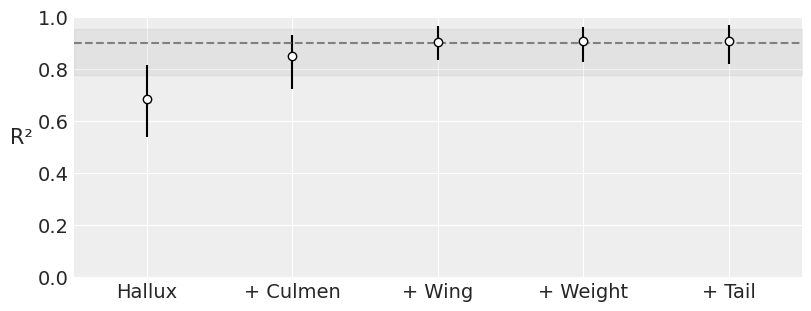
可以观察到,使用协变量 Hallux、Culmen 和 Wing,我们获得了与使用所有协变量相同的 \(R^2\) 值,这意味着最后两个协变量对分类的贡献小于其他三个。 我们必须考虑的一件事是 HDI 非常宽,这降低了我们结果的精度; 稍后我们将看到一种减少这种情况的方法。
我们还可以绘制子模型的预测与完整模型的预测的散点图,以了解每个新的协变量如何改进子模型的预测。
axes = pmb.plot_scatter_submodels(
vi_results, grid=(5, 3), figsize=(12, 14), plot_kwargs={"alpha_scatter": 0.05}
)
plt.suptitle("Comparison of submodels' predictions to full model's\n", fontsize=18)
for ax, cat in zip(axes, np.repeat(species, len(vi_results["labels"]))):
ax.set(title=f"Species {cat}")
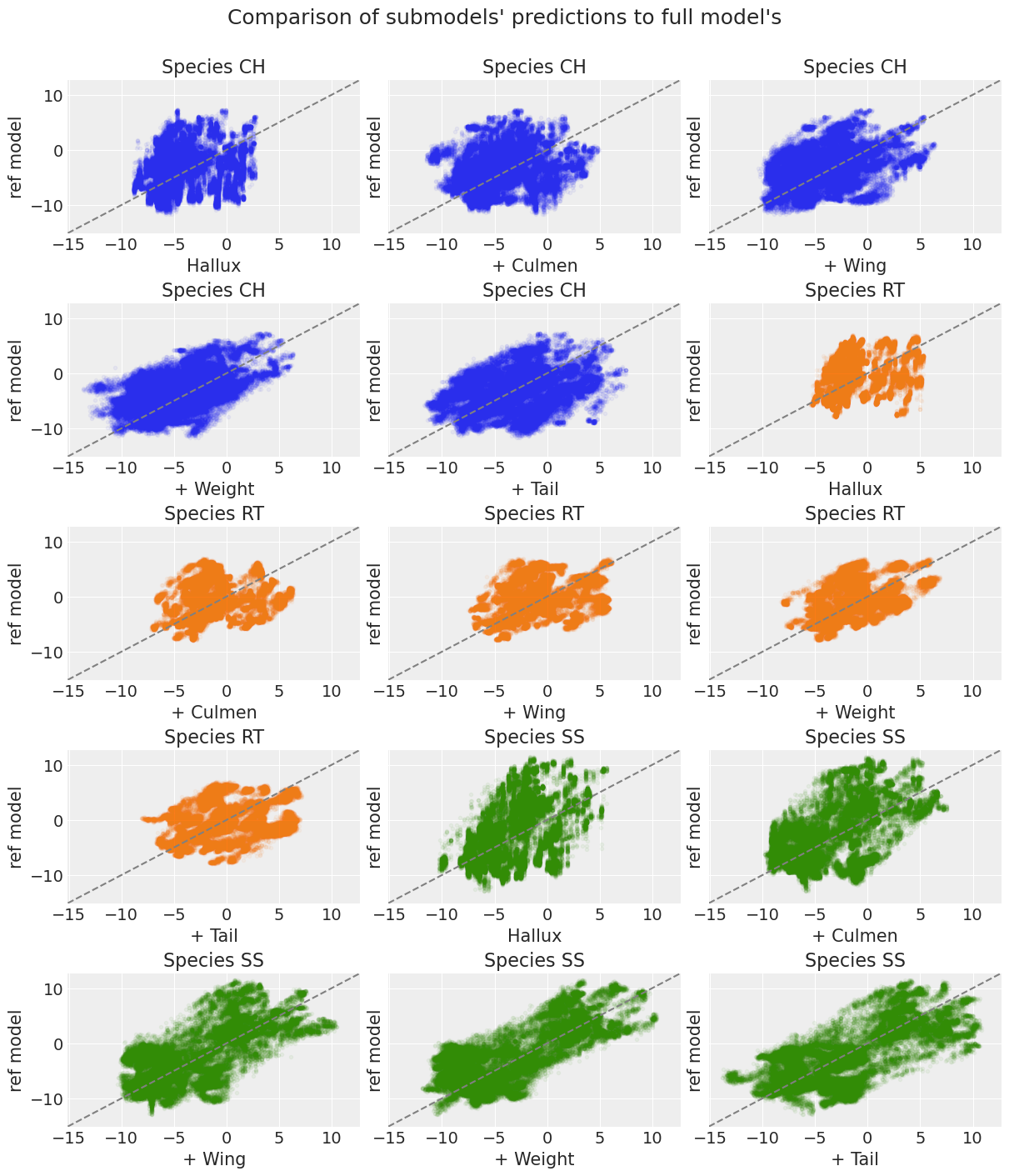
Partial Dependence Plot(部分依赖图)#
让我们使用 pmb.plot_pdp() 检查每个协变量对每个物种的行为,该函数显示协变量对预测变量的边际效应,同时我们对所有其他协变量进行平均。 由于我们的响应变量是分类变量,我们将传递 softmax 作为反向链接函数传递给 plot_pdp。
您可以看到我们必须小心 softmax 函数,因为它不是向量化的:它考虑元素之间的关系,因此应用它的特定轴很重要。 默认情况下,scipy 应用于所有轴,但我们希望将其应用于最后一个轴,因为类别在那里。 为了确保这一点,我们使用 np.apply_along_axis 并在 lambda 函数中传递它。
axes = pmb.plot_pdp(
μ,
X=x_0,
Y=y_0,
grid=(5, 3),
figsize=(12, 12),
func=lambda x: np.apply_along_axis(softmax, axis=-1, arr=x),
)
plt.suptitle("Partial Dependence Plots\n", fontsize=18)
for (i, ax), cat in zip(enumerate(axes), np.tile(species, len(vi_results["labels"]))):
ax.set(title=f"Species {cat}")
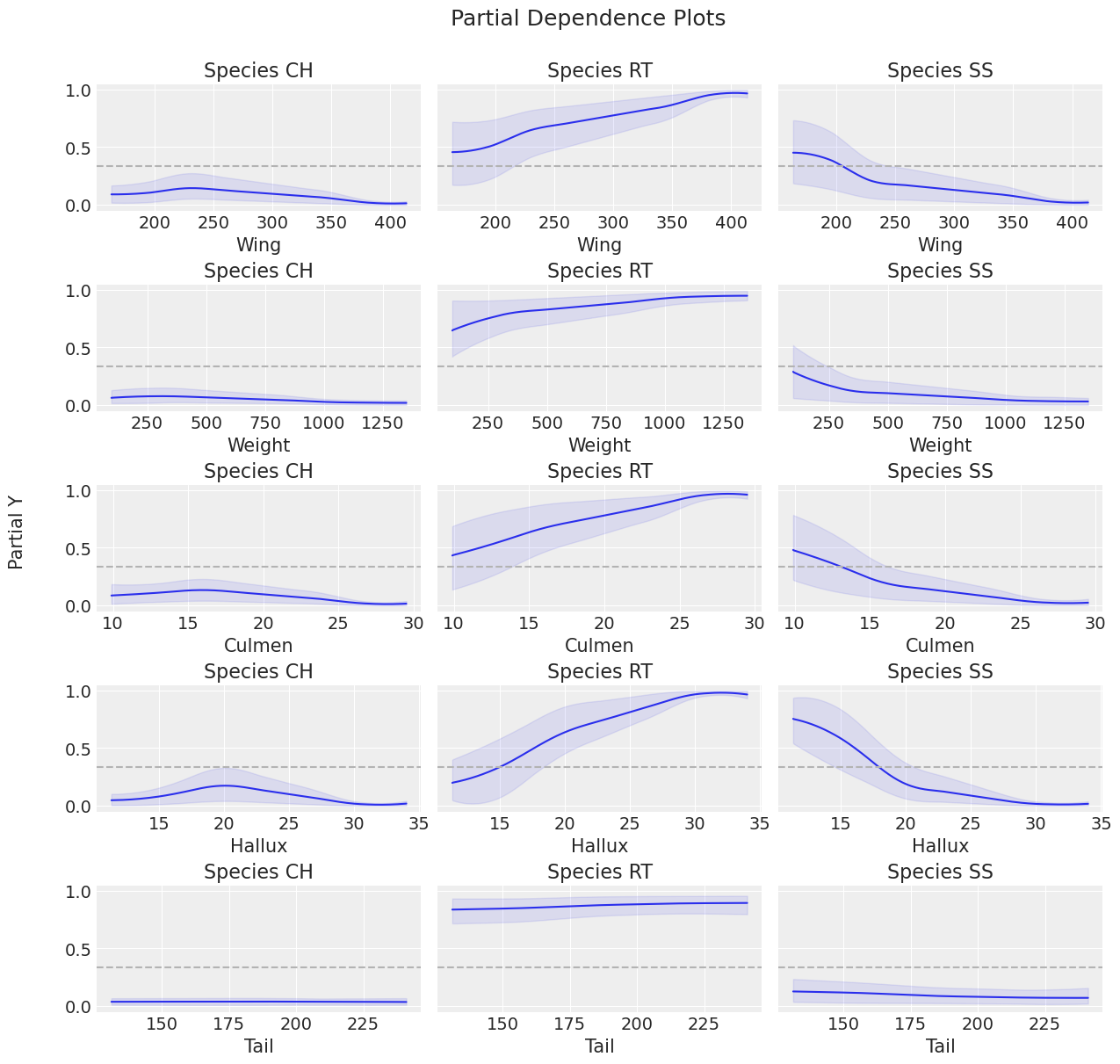
Partial Dependence Plot(部分依赖图)与 Variable Importance plot(变量重要性图)一起证实,Tail 是对预测变量影响最小的协变量:在 Variable Importance plot(变量重要性图)中,Tail 是最后一个添加的协变量,并且没有改进结果; 在 PDP 图中,Tail 具有最平坦的响应。
对于此图中的其余协变量,很难看出哪个协变量对预测变量的影响更大,因为它们具有很大的变异性,这在 HDI 宽度中显示出来。
最后,一些变异性取决于每个物种的数据量,我们可以在每个物种的每个协变量的 counts 中看到这一点
Hawks.groupby("Species").count()
| 翅膀 | 体重 | 上喙 | 杀戮爪 | 尾巴 | |
|---|---|---|---|---|---|
| 物种 | |||||
| CH | 69 | 69 | 69 | 69 | 69 |
| RT | 567 | 567 | 567 | 567 | 567 |
| SS | 255 | 255 | 255 | 255 | 255 |
Predicted vs Observed(预测值与观测值)#
现在我们将比较预测数据与观测数据,以评估模型的拟合度,我们使用 Arviz 函数 az.plot_ppc() 来完成此操作。
ax = az.plot_ppc(idata, kind="kde", num_pp_samples=200, random_seed=123)
# plot aesthetics
ax.set_ylim(0, 0.7)
ax.set_yticks([0, 0.2, 0.4, 0.6])
ax.set_ylabel("Probability")
ax.set_xticks([0.5, 1.5, 2.5])
ax.set_xticklabels(["CH", "RT", "SS"])
ax.set_xlabel("Species");
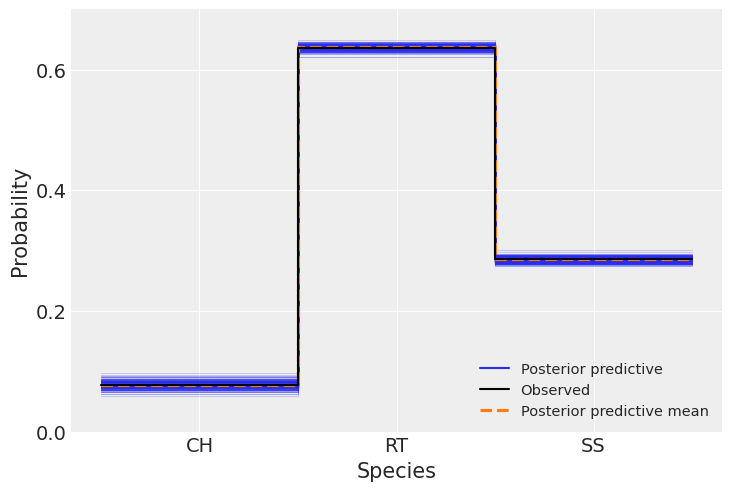
我们可以看到观测数据(黑线)和模型预测的数据(蓝线和橙线)之间有良好的一致性。 正如我们之前提到的,物种之间值的差异受每个物种数据量的影响。 这里在预测数据中没有观察到分散性,正如我们在前两个图中看到的那样。
下面我们看到样本内预测与观测结果提供了非常良好的一致性。
np.mean((idata.posterior_predictive["y"] - y_0) == 0) * 100
<xarray.DataArray 'y' ()> Size: 8B array(96.3900954)
all = 0
for i in range(3):
perct_per_class = np.mean(idata.posterior_predictive["y"].where(y_0 == i) == i) * 100
all += perct_per_class
print(perct_per_class)
all
<xarray.DataArray 'y' ()> Size: 8B
array(6.13838384)
<xarray.DataArray 'y' ()> Size: 8B
array(62.69332211)
<xarray.DataArray 'y' ()> Size: 8B
array(27.55838945)
<xarray.DataArray 'y' ()> Size: 8B array(96.3900954)
到目前为止,我们在基于 5 个协变量对物种进行分类方面取得了非常好的结果。 但是,如果我们想选择协变量子集以进行未来的分类,则不太清楚应该选择哪些协变量。 也许可以肯定的是可以消除 Tail。 在开始绘制每个协变量的分布时,我们说过用于分类的最重要变量可能是 Wing、Weight 和 Culmen,但是,在运行模型后,我们看到 Hallux、Culmen 和 Wing 被证明是最重要的。
不幸的是,部分依赖图显示出非常广泛的分散性,使得结果看起来可疑。 减少这种变异性的一种方法是调整独立树,下面我们将看到如何执行此操作并获得更准确的结果。
拟合独立树#
使用 pymc-bart 拟合独立树的选项通过参数 pmb.BART(..., separate_trees=True, ...) 设置。 正如我们将看到的,对于此示例,使用此选项在预测中没有产生很大的差异,但有助于我们减少 ppc 中的变异性,并在样本内比较中获得小的改进。 如果将此选项用于更大的数据集,则必须考虑到模型的拟合速度较慢,因此您可以以计算成本为代价获得更好的结果。 以下代码运行与之前相同的模型和分析,但拟合独立树。 将运行此模型的时间与之前的模型进行比较。
with pm.Model(coords=coords) as model_t:
μ_t = pmb.BART("μ", x_0, y_0, m=50, separate_trees=True, dims=["species", "n_obs"])
θ_t = pm.Deterministic("θ", pm.math.softmax(μ_t, axis=0))
y_t = pm.Categorical("y", p=θ_t.T, observed=y_0)
idata_t = pm.sample(chains=4, compute_convergence_checks=False, random_seed=123)
pm.sample_posterior_predictive(idata_t, extend_inferencedata=True)
Multiprocess sampling (4 chains in 4 jobs)
PGBART: [μ]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 136 seconds.
Sampling: [y]
现在我们将重现与之前相同的分析。
vi_results = pmb.compute_variable_importance(
idata_t, μ_t, x_0, method="VI", random_seed=RANDOM_SEED
)
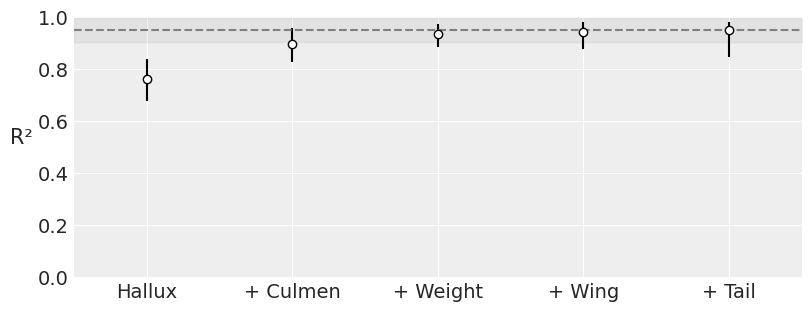
pmb.plot_variable_importance(vi_results);
axes = pmb.plot_pdp(
μ_t,
X=x_0,
Y=y_0,
grid=(5, 3),
figsize=(12, 12),
func=lambda x: np.apply_along_axis(softmax, axis=-1, arr=x),
)
plt.suptitle("Partial Dependence Plots\n", fontsize=18)
for (i, ax), cat in zip(enumerate(axes), np.tile(species, len(vi_results["labels"]))):
ax.set(title=f"Species {cat}")
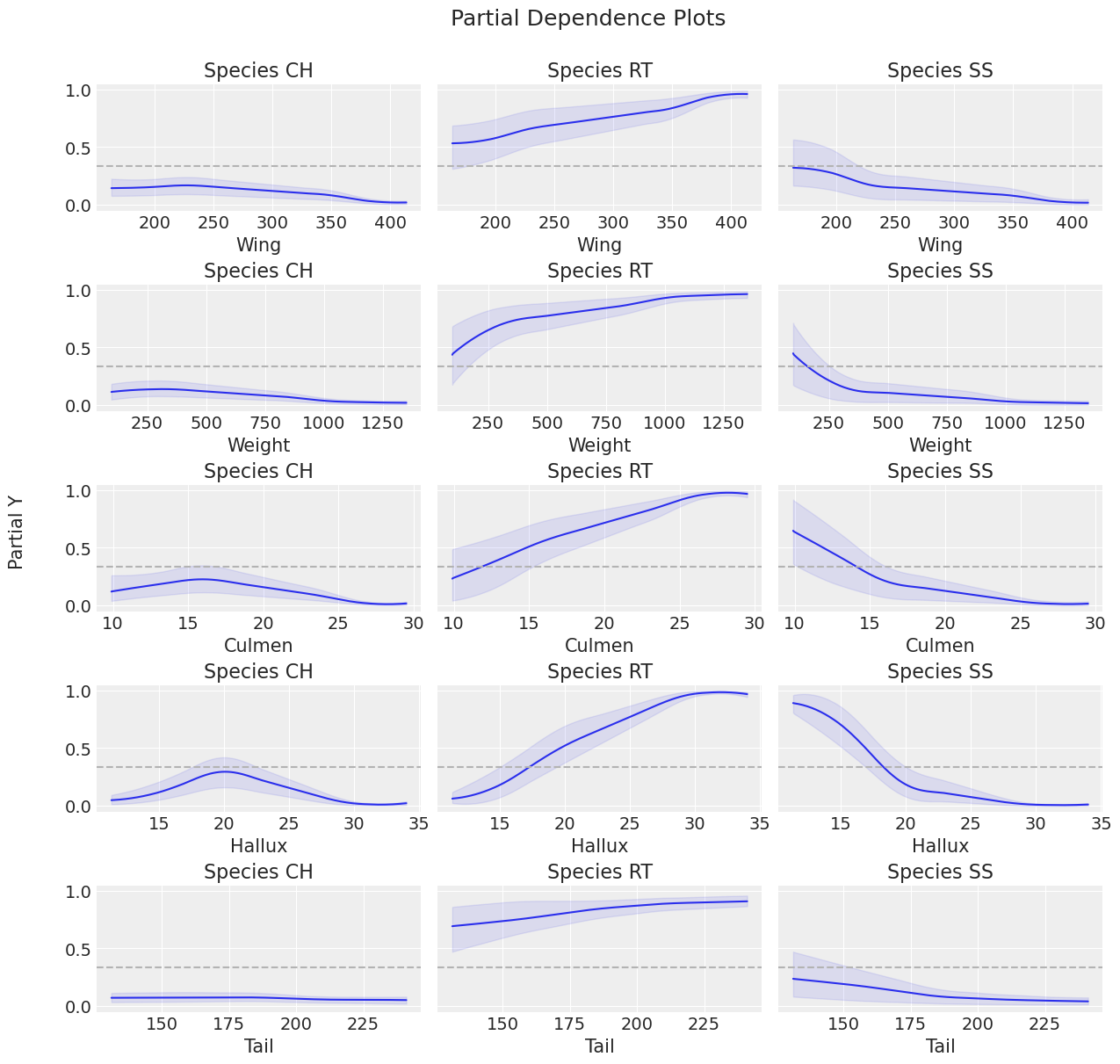
将这两个图与之前的图进行比较,可以发现在每个图的方差方面都有明显的减少。 在 pmb.plot_variable_importance() 的情况下,误差带较小,\(R^{2}\) 值更接近 1。 对于 pmb.plot_pdp(),我们可以看到更细的 HDI 带。 这表示由于分别调整树而减少了不确定性。 这样做的另一个好处是,每个物种的每个协变量的行为更加可见。
将所有这些结合在一起,我们可以选择 Hallux、Culmen 和 Wing 作为协变量来进行分类。
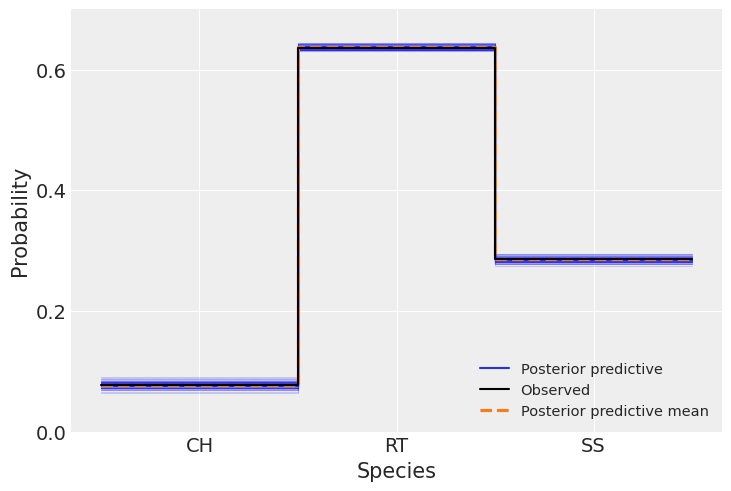
关于观测数据和预测数据之间的比较,我们获得了相同的良好结果,但预测值(蓝线)的不确定性较小。 样本内比较的计数相同。
ax = az.plot_ppc(idata_t, kind="kde", num_pp_samples=100, random_seed=123)
ax.set_ylim(0, 0.7)
ax.set_yticks([0, 0.2, 0.4, 0.6])
ax.set_ylabel("Probability")
ax.set_xticks([0.5, 1.5, 2.5])
ax.set_xticklabels(["CH", "RT", "SS"])
ax.set_xlabel("Species");
np.mean((idata_t.posterior_predictive["y"] - y_0) == 0) * 100
<xarray.DataArray 'y' ()> Size: 8B array(97.29281706)
all = 0
for i in range(3):
perct_per_class = np.mean(idata_t.posterior_predictive["y"].where(y_0 == i) == i) * 100
all += perct_per_class
print(perct_per_class)
all
<xarray.DataArray 'y' ()> Size: 8B
array(6.47943322)
<xarray.DataArray 'y' ()> Size: 8B
array(62.92943322)
<xarray.DataArray 'y' ()> Size: 8B
array(27.88395062)
<xarray.DataArray 'y' ()> Size: 8B array(97.29281706)
参考文献#
水印#
%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor
Last updated: Sat Feb 22 2025
Python implementation: CPython
Python version : 3.12.3
IPython version : 8.22.2
pytensor: 2.26.4
pandas : 2.2.1
pymc_bart : 0.8.2
seaborn : 0.13.2
matplotlib: 3.8.3
pymc : 5.19.1
arviz : 0.20.0
numpy : 1.26.4
Watermark: 2.4.3