BART 分位数回归#

from pathlib import Path

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pymc_bart as pmb

from scipy import stats

print(f"Running on PyMC v{pm.__version__}")

Running on PyMC v5.19.1

%config InlineBackend.figure_format = "retina"
RANDOM_SEED = 5781
np.random.seed(RANDOM_SEED)
az.style.use("arviz-darkgrid")

通常，当我们进行回归时，我们对某些分布的条件均值进行建模。常见的情况是连续无界响应的正态分布、计数数据的泊松分布等。

相反，分位数回归估计响应变量的条件分位数。如果分位数为 0.5，那么我们将估计中位数（而不是均值），这可以用作执行稳健回归的一种方法，类似于使用 Student-t 分布而不是正态分布。但是对于某些问题，我们实际上关心的是响应在远离均值（或中位数）时的行为。例如，在医学研究中，病理学或潜在的健康风险发生在较高或较低的分位数，例如，超重和体重不足。在生态学等其他领域，由于变量之间存在复杂的相互作用，分位数回归是合理的，其中一个变量对另一个变量的影响对于变量的不同范围是不同的。

非对称拉普拉斯分布#

起初，考虑我们应该使用哪个分布作为分位数回归的可能性或如何为分位数回归编写贝叶斯模型可能会很奇怪。但事实证明答案很简单，我们只需要使用非对称拉普拉斯分布。此分布有一个参数控制均值，另一个参数控制尺度，第三个参数控制不对称性。关于这个不对称参数，至少有两种替代参数化方法。以 \(\kappa\) 为参数，范围从 0 到 \(\infty\)，以 \(q\) 为参数，范围在 0 到 1 之间。后一种参数化对于分位数回归更直观，因为我们可以直接将其解释为感兴趣的分位数。

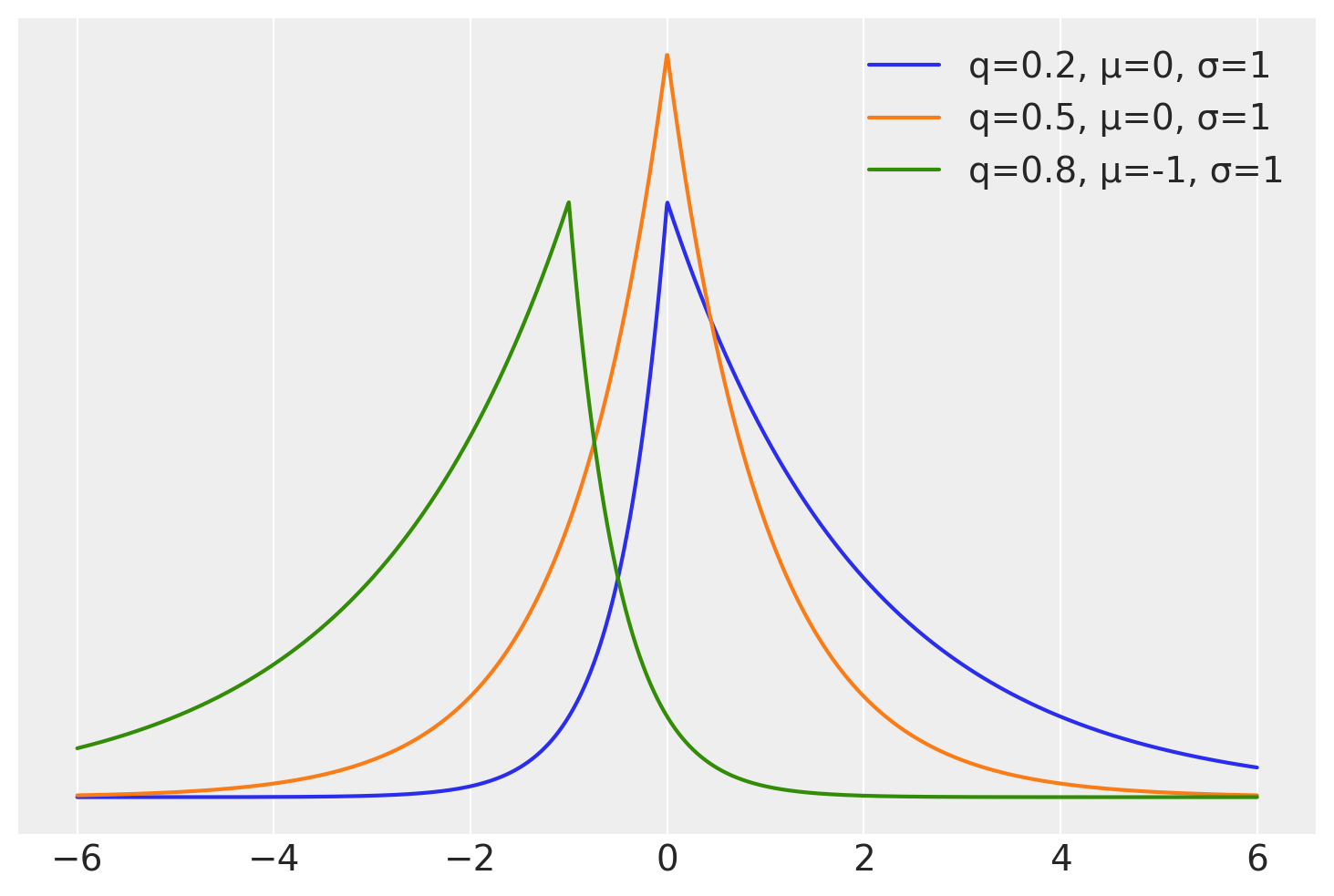
在下一个单元格中，我们计算来自非对称拉普拉斯族的 3 个分布的 pdf

x = np.linspace(-6, 6, 2000)
for q, m in zip([0.2, 0.5, 0.8], [0, 0, -1]):
    κ = (q / (1 - q)) ** 0.5
    plt.plot(x, stats.laplace_asymmetric(κ, m, 1).pdf(x), label=f"q={q:}, μ={m}, σ=1")
plt.yticks([])
plt.legend();

../_images/db057b16cc6507be0bf4e84b884be162f7f37c6622887347e3b616418e3b79fe.png

我们将使用一个简单的数据集来模拟荷兰儿童和年轻男性的体重指数，作为他们年龄的函数。

try:
    bmi = pd.read_csv(Path("..", "data", "bmi.csv"))
except FileNotFoundError:
    bmi = pd.read_csv(pm.get_data("bmi.csv"))

bmi.plot(x="age", y="bmi", kind="scatter");

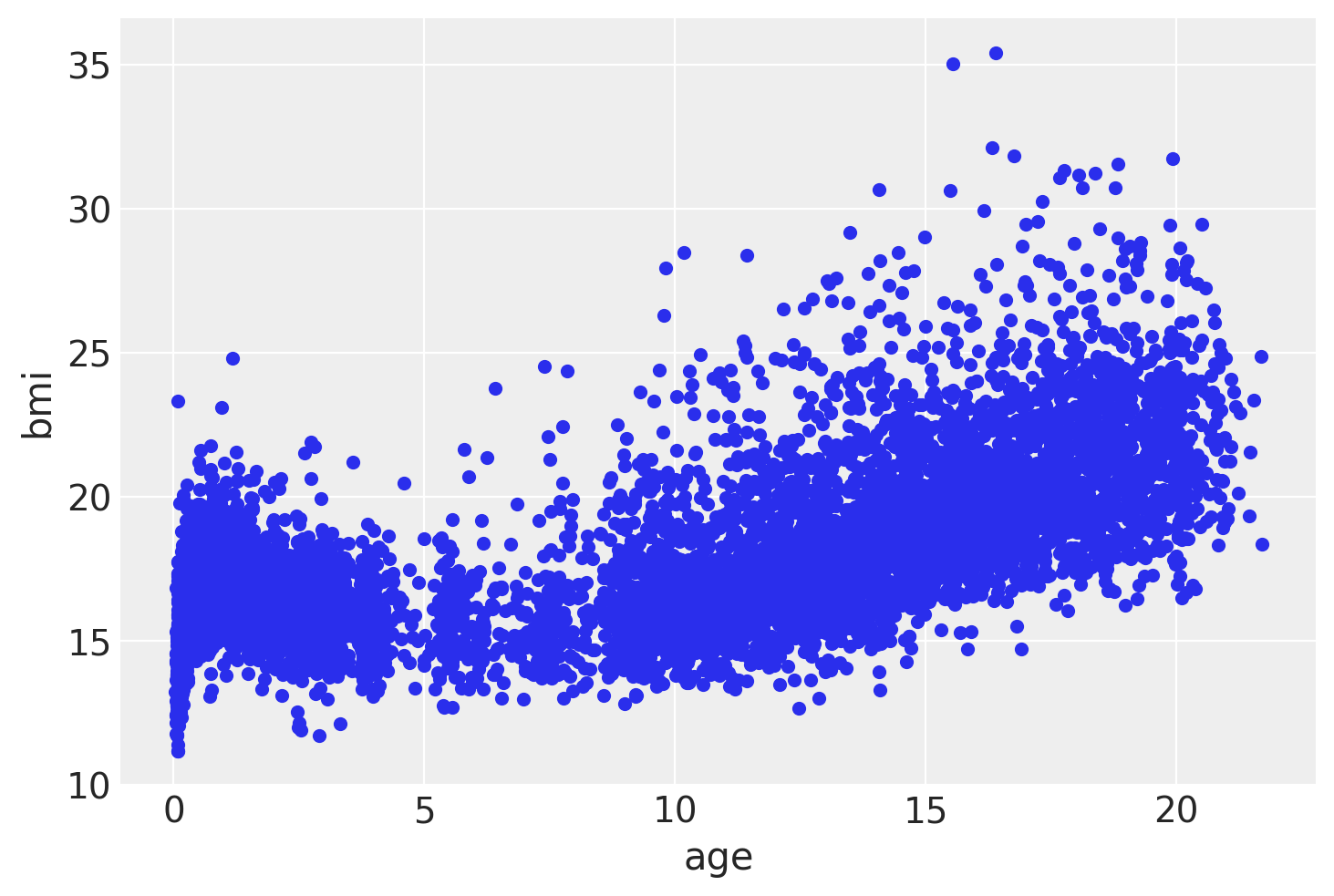
../_images/02fd8c10f92b70b6972286e64ca3ed546252968ac8c50cd8302923009e50e242.png

正如我们从前面的图中看到的那样，BMI 和年龄之间的关系远非线性，因此我们将使用 BART。

我们将对 0.1、0.5 和 0.9 这 3 个分位数进行建模。我们可以通过拟合 3 个分离的模型来计算此数量，唯一的不同是非对称拉普拉斯分布的 q 值。或者我们可以像 y_stack 中那样堆叠观察值并拟合单个模型。

y = bmi.bmi.values
X = bmi.age.values[:, None]


y_stack = np.stack([bmi.bmi.values] * 3)
quantiles = np.array([[0.1, 0.5, 0.9]]).T
quantiles

array([[0.1],
       [0.5],
       [0.9]])

with pm.Model() as model:
    μ = pmb.BART("μ", X, y, shape=(3, 7294))
    σ = pm.HalfNormal("σ", 5)
    obs = pm.AsymmetricLaplace("obs", mu=μ, b=σ, q=quantiles, observed=y_stack)

    idata = pm.sample(compute_convergence_checks=False)

Multiprocess sampling (4 chains in 4 jobs)
CompoundStep
>PGBART: [μ]
>NUTS: [σ]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 337 seconds.

我们可以在下图看到 3 条拟合曲线的结果。一个突出的特点是中位数（橙色）线与其他两条线之间的间隙或距离不相同。此外，曲线的形状虽然遵循相似的模式，但并不完全相同。

plt.plot(bmi.age, bmi.bmi, ".", color="0.5")
for idx, q in enumerate(quantiles[:, 0]):
    plt.plot(
        bmi.age,
        idata.posterior["μ"].mean(("chain", "draw")).sel(μ_dim_0=idx),
        label=f"q={q:}",
        lw=3,
    )

plt.legend();

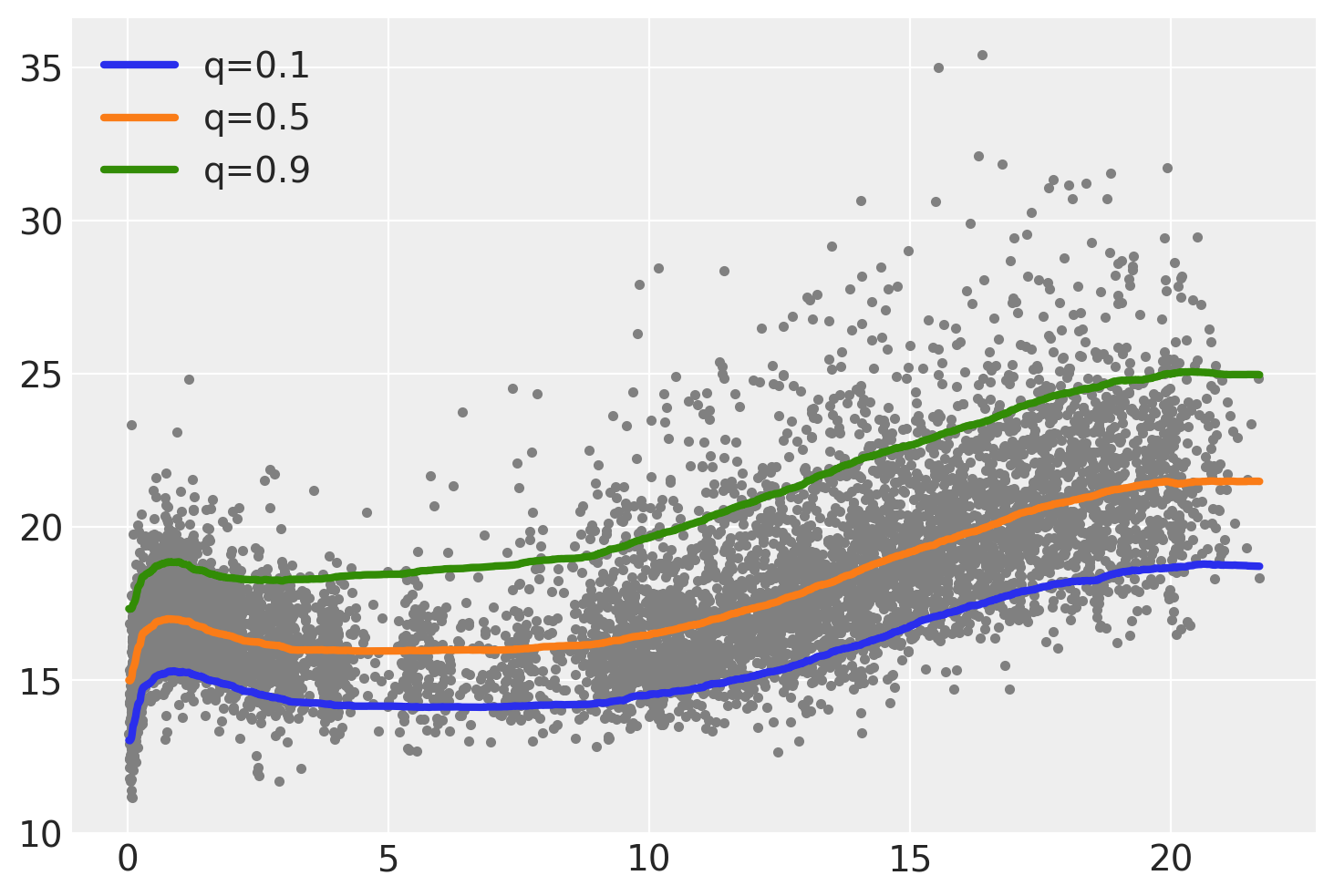
../_images/12cb97be279d4a47470186cfae554294221722f2196e78a5c29186781dceb08c.png

为了更好地理解这些评论，让我们用正态似然计算 BART 回归，然后从该拟合中计算相同的 3 个分位数。

y = bmi.bmi.values
x = bmi.age.values[:, None]
with pm.Model() as model:
    μ = pmb.BART("μ", x, y)
    σ = pm.HalfNormal("σ", 5)
    obs = pm.Normal("obs", mu=μ, sigma=σ, observed=y)

    idata_g = pm.sample(compute_convergence_checks=False)
    idata_g.extend(pm.sample_posterior_predictive(idata_g))

Multiprocess sampling (4 chains in 4 jobs)
CompoundStep
>PGBART: [μ]
>NUTS: [σ]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 78 seconds.
Sampling: [obs]

idata_g_mean_quantiles = idata_g.posterior_predictive["obs"].quantile(
    quantiles[:, 0], ("chain", "draw")
)

plt.plot(bmi.age, bmi.bmi, ".", color="0.5")
for q in quantiles[:, 0]:
    plt.plot(bmi.age.values, idata_g_mean_quantiles.sel(quantile=q), label=f"q={q:}")

plt.legend()
plt.xlabel("Age")
plt.ylabel("BMI");

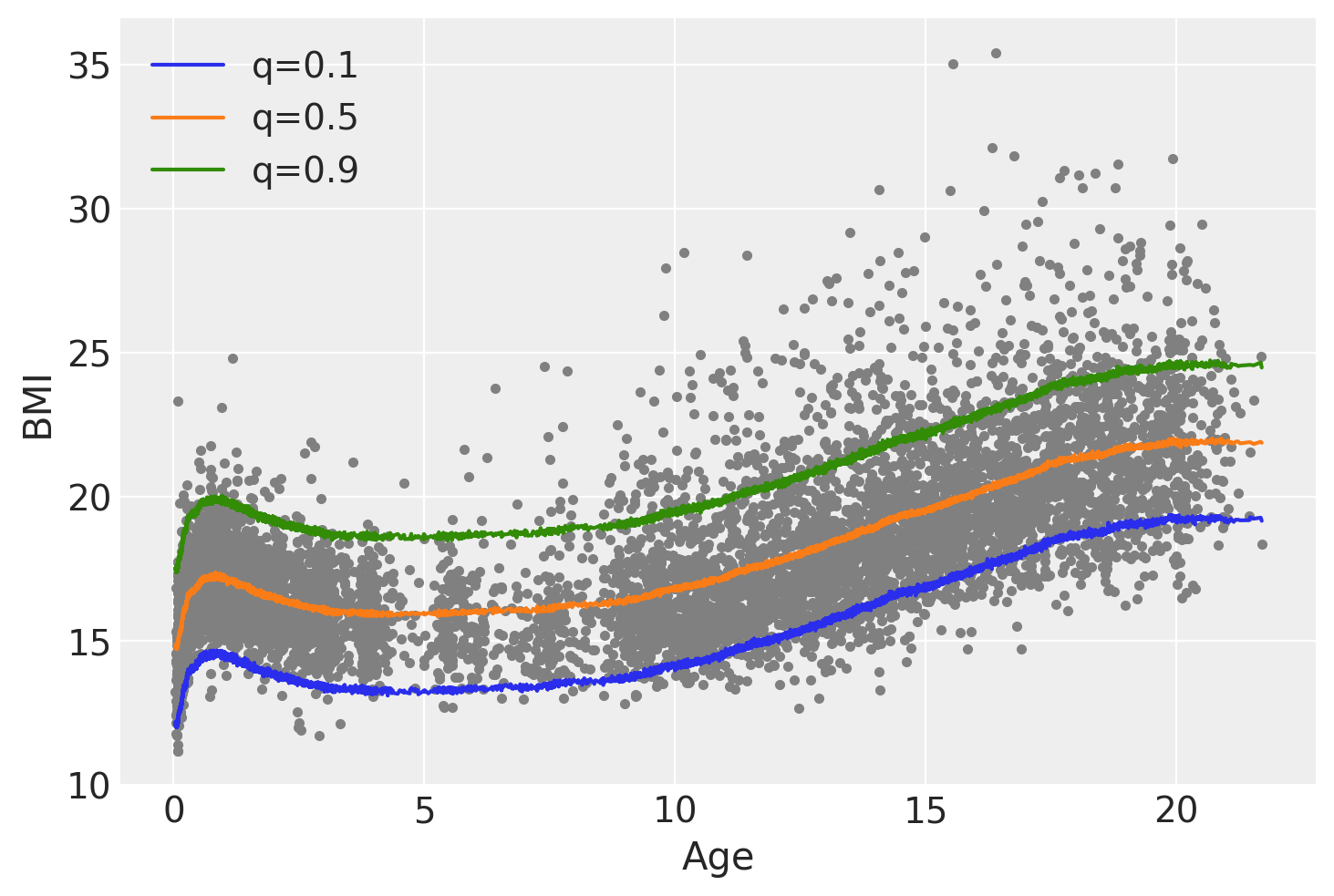
../_images/fb1ceee1bf080b9b2898554db2ae70ddf1367040306c834e2c43a1a12f79d5bb.png

我们可以看到，当我们使用正态似然，并从中计算分位数时，分位数 q=0.1 和 q=0.9 相对于 q=0.5 是对称的，曲线的形状也基本相同，只是向上或向下移动。此外，非对称拉普拉斯族允许模型解释 BMI 随年龄增长而增加的变异性，而对于高斯族，这种变异性始终保持不变。

作者#

作者：Osvaldo Martin，2023 年 1 月
重新运行者：Osvaldo Martin，2023 年 3 月
重新运行者：Osvaldo Martin，2023 年 11 月
重新运行者：Osvaldo Martin，2024 年 12 月

参考文献#

[1]

Miriana Quiroga, Pablo G Garay, Juan M. Alonso, Juan Martin Loyola, and Osvaldo A Martin. Bayesian additive regression trees for probabilistic programming. 2022. URL: https://arxiv.org/abs/2206.03619, doi:10.48550/ARXIV.2206.03619.

[2]

Osvaldo A Martin, Ravin Kumar, and Junpeng Lao. Bayesian Modeling and Computation in Python. Chapman and Hall/CRC, 2021. doi:10.1201/9781003019169.

水印#

%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,xarray

Last updated: Mon Dec 23 2024

Python implementation: CPython
Python version       : 3.11.5
IPython version      : 8.16.1

pytensor: 2.26.4
xarray  : 2024.9.0

pymc_bart : 0.6.0
pandas    : 2.1.2
scipy     : 1.11.4
numpy     : 1.26.4
pymc      : 5.19.1
arviz     : 0.20.0.dev0
matplotlib: 3.8.4

Watermark: 2.4.3

许可声明#

此示例 галерея 中的所有笔记本均根据 MIT 许可证提供，该许可证允许修改和再分发以用于任何用途，前提是保留版权和许可声明。

引用 PyMC 示例#

要引用此笔记本，请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。

重要提示

许多笔记本都改编自其他来源：博客、书籍……在这种情况下，您也应该引用原始来源。

另请记住引用您的代码使用的相关库。

这是一个 bibtex 中的引用模板

@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}

渲染后可能看起来像

分类

标签