因子分析#
因子分析是一种广泛使用的概率模型,用于识别多元数据中以潜在变量编码的低秩结构。它与主成分分析非常相关,仅在于对这些潜在变量假设的先验分布不同。它也是线性高斯模型的一个很好的例子,因为它可以完全描述为底层高斯变量的线性变换。要了解因子分析与其他模型之间的高级关系,您可以查看 此图,最初由 Ghahramani 和 Roweis 发表。
注意
此 notebook 使用的库不是 PyMC 依赖项,因此需要专门安装才能运行此 notebook。打开下面的下拉菜单以获取更多指导。
额外的依赖项安装说明
为了运行此 notebook(在本地或 binder 上),您不仅需要安装所有可选依赖项的 PyMC 工作环境,还需要安装一些额外的依赖项。有关安装 PyMC 本身的建议,请参阅 安装
您可以使用您喜欢的包管理器安装这些依赖项,我们提供 pip 和 conda 命令作为示例,如下所示。
$ pip install seaborn
请注意,如果您想(或需要)从 notebook 内部而不是命令行安装软件包,您可以通过运行 pip 命令的变体来安装软件包
import sys
!{sys.executable} -m pip install seaborn
您不应运行 !pip install,因为它可能会将软件包安装在不同的环境中,即使已安装,也无法从 Jupyter notebook 中使用。
另一种选择是使用 conda 代替
$ conda install seaborn
当使用 conda 安装科学 python 软件包时,我们建议使用 conda forge
import arviz as az
import numpy as np
import pymc as pm
import pytensor.tensor as pt
import scipy as sp
import seaborn as sns
import xarray as xr
from matplotlib import pyplot as plt
from matplotlib.lines import Line2D
from numpy.random import default_rng
from xarray_einstats import linalg
from xarray_einstats.stats import XrContinuousRV
print(f"Running on PyMC v{pm.__version__}")
Running on PyMC v5.10.2
%config InlineBackend.figure_format = 'retina'
az.style.use("arviz-darkgrid")
np.set_printoptions(precision=3, suppress=True)
RANDOM_SEED = 31415
rng = default_rng(RANDOM_SEED)
模拟数据生成#
为了完成几个示例,我们首先生成一些数据。数据将不遵循因子分析模型假设的精确生成过程,因为潜在变量将不是高斯的。我们假设我们有一个观察到的数据集,其中包含 \(N\) 行和 \(d\) 列,这些列实际上是 \(k_{true}\) 个潜在变量的噪声线性函数。
n = 250
k_true = 4
d = 10
下一个代码单元通过创建潜在变量数组 M 和线性变换 Q 来生成数据。然后,矩阵乘积 \(QM\) 被方差参数 err_sd 控制的加性高斯噪声扰动。
由于我们生成数据的方式,表示 \(Y\) 列之间相关性的协方差矩阵将等于 \(QQ^T\)。PCA 和因子分析的基本假设是 \(QQ^T\) 不是满秩的。如果我们绘制协方差矩阵,我们可以看到一些提示
plt.figure(figsize=(4, 3))
sns.heatmap(np.corrcoef(Y));
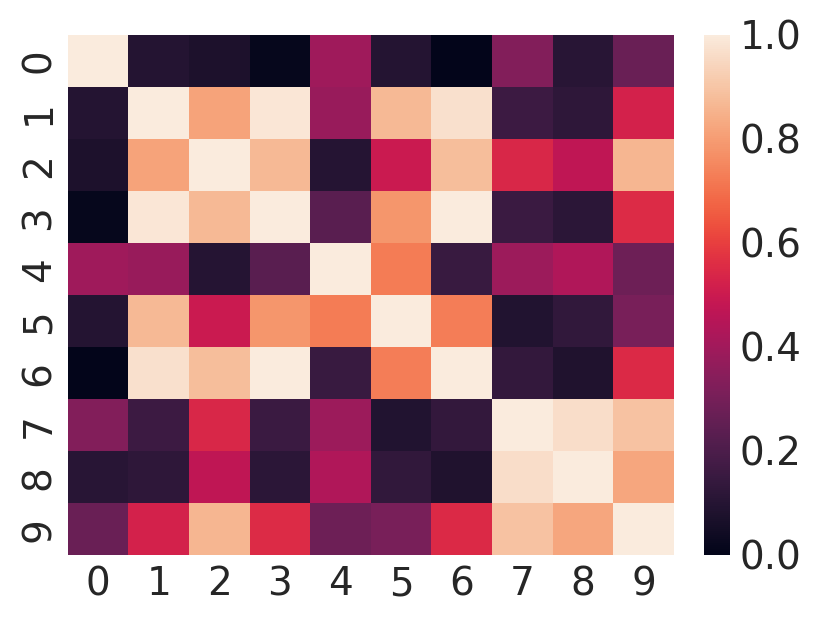
如果您眯起眼睛看足够长的时间,您可能会瞥见一些地方,其中不同的列可能是彼此的线性函数。
模型#
概率 PCA (PPCA) 和因子分析 (FA) 是 PyMC Discourse 上常见的主题来源。下面链接的帖子处理了问题的不同方面,包括
直接实现#
因子分析的模型是概率矩阵分解
\(X_{(d,n)}|W_{(d,k)}, F_{(k,n)} \sim \mathcal{N}(WF, \Psi)\)
其中 \(\Psi\) 是对角矩阵。下标表示矩阵的维度。概率 PCA 是一种变体,它设置 \(\Psi = \sigma^2 I\)。基本实现(取自 此 gist)显示在下一个单元格中。不幸的是,它在模型拟合方面具有不良特性。
k = 2
coords = {"latent_columns": np.arange(k), "rows": np.arange(n), "observed_columns": np.arange(d)}
with pm.Model(coords=coords) as PPCA:
W = pm.Normal("W", dims=("observed_columns", "latent_columns"))
F = pm.Normal("F", dims=("latent_columns", "rows"))
sigma = pm.HalfNormal("sigma", 1.0)
X = pm.Normal("X", mu=W @ F, sigma=sigma, observed=Y, dims=("observed_columns", "rows"))
trace = pm.sample(tune=2000, random_seed=rng) # target_accept=0.9
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [W, F, sigma]
Sampling 4 chains for 2_000 tune and 1_000 draw iterations (8_000 + 4_000 draws total) took 29 seconds.
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details
The effective sample size per chain is smaller than 100 for some parameters. A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details
此时,已经有几个关于收敛检查失败的警告。我们可以在下面的迹线图中看到更多问题。此图显示了矩阵 \(W\) 中单个条目的每个采样器链所采用的路径,以及每个链的样本平均值。
for i in trace.posterior.chain.values:
samples = trace.posterior["W"].sel(chain=i, observed_columns=3, latent_columns=1)
plt.plot(samples, label="Chain {}".format(i + 1))
plt.axhline(samples.mean(), color=f"C{i}")
plt.legend(ncol=4, loc="upper center", fontsize=12, frameon=True), plt.xlabel("Sample");
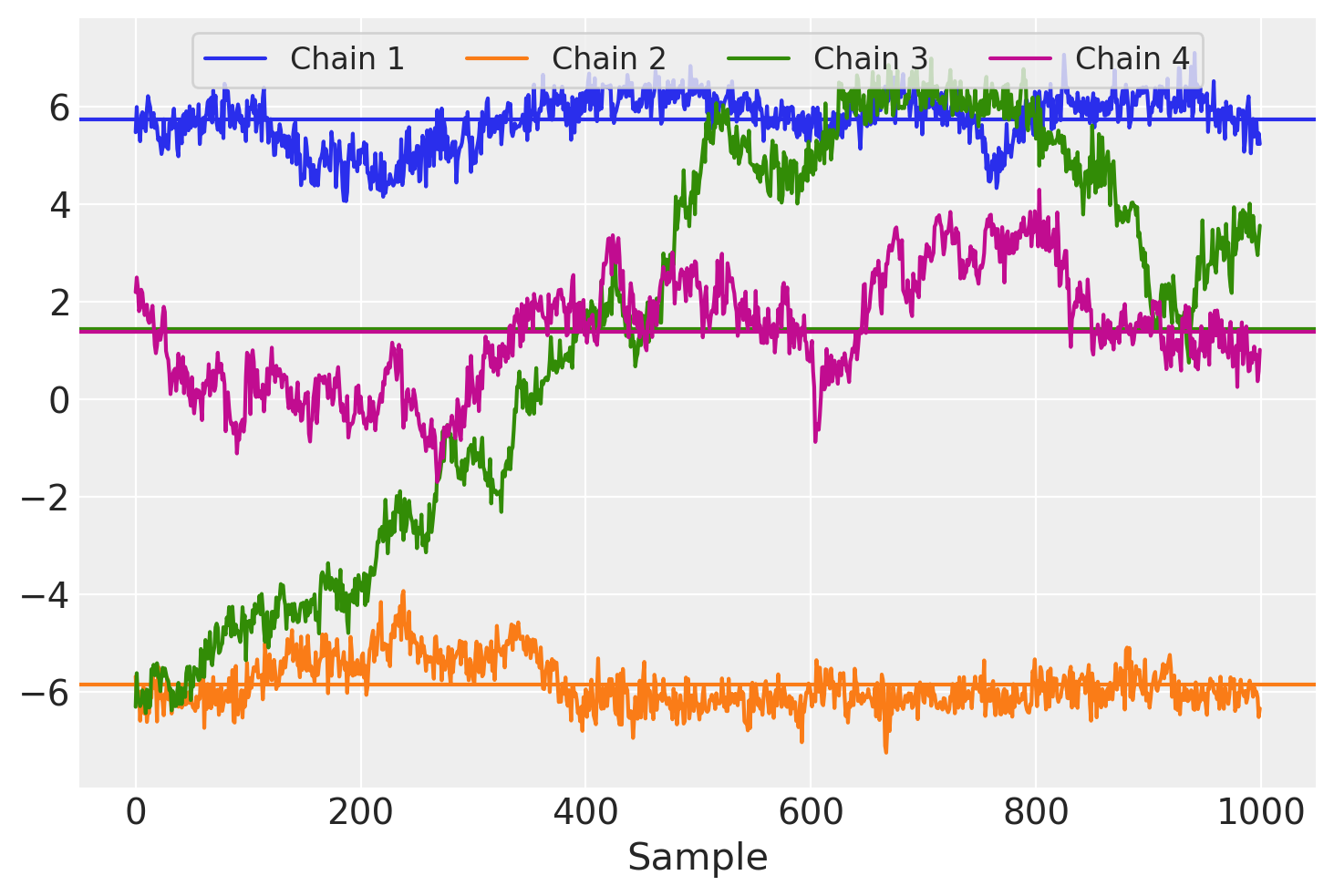
每个链似乎都有不同的样本均值,我们还可以看到链之间存在大量的自相关,表现为采样迭代中的长期趋势。
此模型公式的主要缺点之一是缺乏可识别性。使用此模型表示,只有乘积 \(WF\) 对 \(X\) 的似然性很重要,因此对于任何可逆矩阵 \(\Omega\),\(P(X|W, F) = P(X|W\Omega, \Omega^{-1}F)\)。虽然 \(W\) 和 \(F\) 上的先验约束 \(|\Omega|\) 既不太大也不太小,但因子和载荷仍然可以旋转、反射和/或置换而不会改变模型似然性。预计它会在采样器的运行之间发生,甚至在运行中发生参数化“漂移”,并产生上面高度自相关的 \(W\) 迹线图。
替代参数化#
这可以通过约束 W 的形式为以下形式来解决
下三角
沿对角线的正值和递增值
我们可以调整 expand_block_triangular 以填充非方阵。此函数模仿 pm.expand_packed_triangular,但后者仅适用于方阵的压缩版本(即模型中的 \(d=k\),前者也可以用于非方阵。
def expand_packed_block_triangular(d, k, packed, diag=None, mtype="pytensor"):
# like expand_packed_triangular, but with d > k.
assert mtype in {"pytensor", "numpy"}
assert d >= k
def set_(M, i_, v_):
if mtype == "pytensor":
return pt.set_subtensor(M[i_], v_)
M[i_] = v_
return M
out = pt.zeros((d, k), dtype=float) if mtype == "pytensor" else np.zeros((d, k), dtype=float)
if diag is None:
idxs = np.tril_indices(d, m=k)
out = set_(out, idxs, packed)
else:
idxs = np.tril_indices(d, k=-1, m=k)
out = set_(out, idxs, packed)
idxs = (np.arange(k), np.arange(k))
out = set_(out, idxs, diag)
return out
我们还将定义另一个函数,该函数有助于创建沿主对角线具有递增条目的对角矩阵。
def makeW(d, k, dim_names):
# make a W matrix adapted to the data shape
n_od = int(k * d - k * (k - 1) / 2 - k)
# trick: the cumulative sum of z will be positive increasing
z = pm.HalfNormal("W_z", 1.0, dims="latent_columns")
b = pm.Normal("W_b", 0.0, 1.0, shape=(n_od,), dims="packed_dim")
L = expand_packed_block_triangular(d, k, b, pt.ones(k))
W = pm.Deterministic("W", L @ pt.diag(pt.extra_ops.cumsum(z)), dims=dim_names)
return W
通过这些修改,我们重新制作模型并再次运行 MCMC 采样器。
with pm.Model(coords=coords) as PPCA_identified:
W = makeW(d, k, ("observed_columns", "latent_columns"))
F = pm.Normal("F", dims=("latent_columns", "rows"))
sigma = pm.HalfNormal("sigma", 1.0)
X = pm.Normal("X", mu=W @ F, sigma=sigma, observed=Y, dims=("observed_columns", "rows"))
trace = pm.sample(tune=2000, random_seed=rng) # target_accept=0.9
for i in range(4):
samples = trace.posterior["W"].sel(chain=i, observed_columns=3, latent_columns=1)
plt.plot(samples, label="Chain {}".format(i + 1))
plt.legend(ncol=4, loc="lower center", fontsize=8), plt.xlabel("Sample");
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [W_z, W_b, F, sigma]
Sampling 4 chains for 2_000 tune and 1_000 draw iterations (8_000 + 4_000 draws total) took 39 seconds.
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details
The effective sample size per chain is smaller than 100 for some parameters. A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details
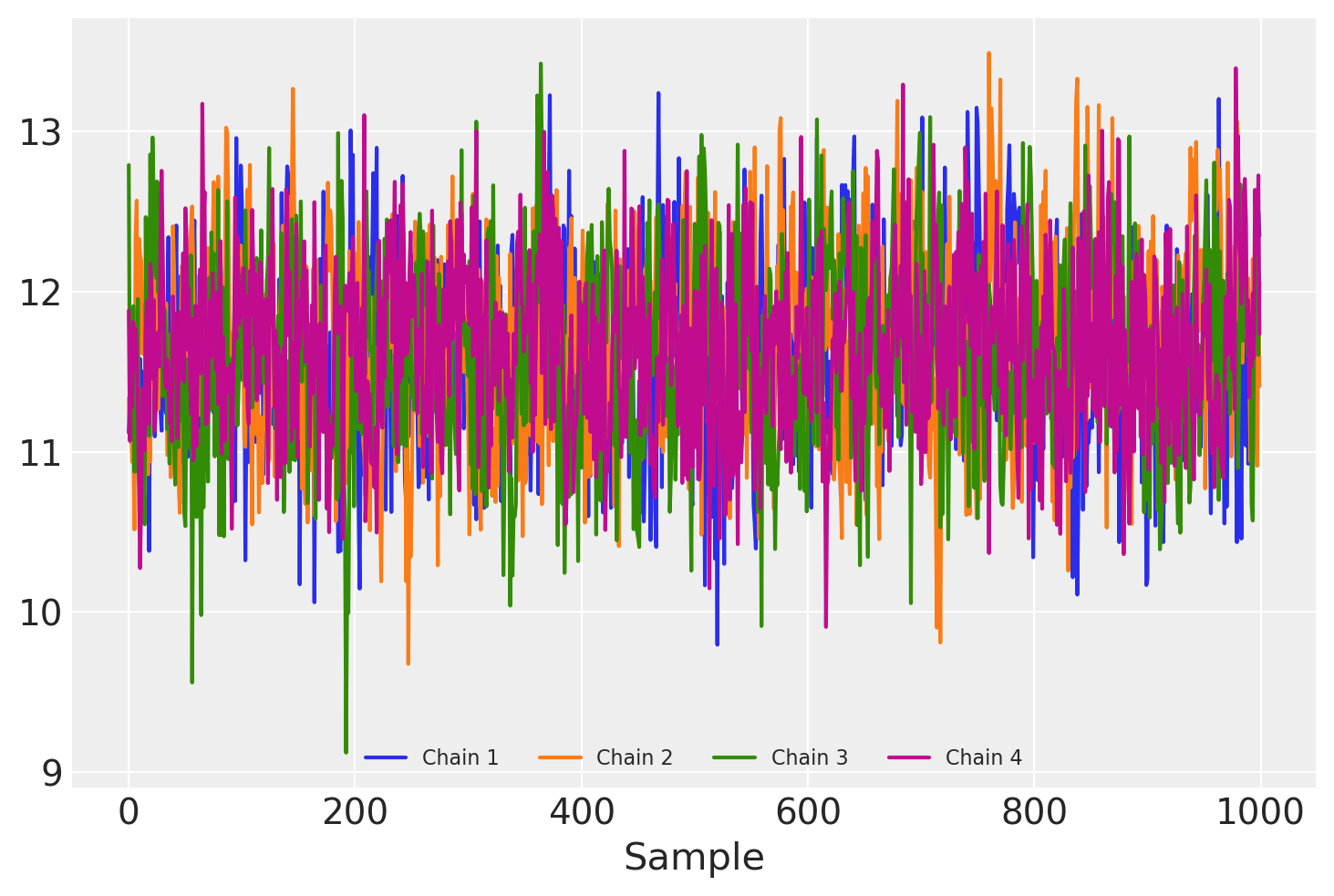
与采样器链之间相比,\(W\)(和 \(F\)!)现在具有具有相同后验分布的条目,尽管显然仍然存在一些自相关。
由于 F 中的 \(k \times n\) 个参数都需要采样,因此对于非常大的 n 来说,采样可能会变得非常昂贵。此外,观察到的数据点 \(X_i\) 和关联的潜在值 \(F_i\) 之间的链接意味着无法执行使用小批量的流式推理。
可以通过分析地将 \(F\) 从模型中积分出来来解决此可伸缩性问题。通过这样做,我们将任何单个 \(F_i\) 值的计算推迟到以后。因此,这种方法通常被描述为摊销推理。但是,这会固定 \(F\) 上的先验,从而降低建模灵活性。与 \(F_{ij} \sim \mathcal{N}(0, I)\) 保持一致,我们有
\(X|WF \sim \mathcal{N}(WF, \sigma^2 I).\)
因此,我们可以将 \(X\) 写为
\(X = WF + \sigma I \epsilon,\)
其中 \(\epsilon \sim \mathcal{N}(0, I)\)。固定 \(W\) 但将 \(F\) 和 \(\epsilon\) 视为随机变量,两者都 \(\sim\mathcal{N}(0, I)\),我们看到 \(X\) 是两个多元正态变量的总和,其均值分别为 \(0\) 和协方差 \(WW^T\) 和 \(\sigma^2 I\)。由此可见
\(X|W \sim \mathcal{N}(0, WW^T + \sigma^2 I )\).
with pm.Model(coords=coords) as PPCA_amortized:
W = makeW(d, k, ("observed_columns", "latent_columns"))
sigma = pm.HalfNormal("sigma", 1.0)
cov = W @ W.T + sigma**2 * pt.eye(d)
# MvNormal parametrizes covariance of columns, so transpose Y
X = pm.MvNormal("X", 0.0, cov=cov, observed=Y.T, dims=("rows", "observed_columns"))
trace_amortized = pm.sample(tune=30, draws=100, random_seed=rng)
Only 100 samples in chain.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [W_z, W_b, sigma]
Sampling 4 chains for 30 tune and 100 draw iterations (120 + 400 draws total) took 52 seconds.
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details
The effective sample size per chain is smaller than 100 for some parameters. A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details
不幸的是,此模型的采样速度非常慢,可能是因为计算 MvNormal 的 logprob 需要反转协方差矩阵。但是,显式积分 \(F\) 还允许批量处理观测值,以便更快地计算 ADVI 和 FullRankADVI 近似值。
coords["observed_columns2"] = coords["observed_columns"]
with pm.Model(coords=coords) as PPCA_amortized_batched:
W = makeW(d, k, ("observed_columns", "latent_columns"))
Y_mb = pm.Minibatch(
Y.T, batch_size=50
) # MvNormal parametrizes covariance of columns, so transpose Y
sigma = pm.HalfNormal("sigma", 1.0)
cov = W @ W.T + sigma**2 * pt.eye(d)
X = pm.MvNormal("X", 0.0, cov=cov, observed=Y_mb)
trace_vi = pm.fit(n=50000, method="fullrank_advi", obj_n_mc=1).sample()
Finished [100%]: Average Loss = 1,759.7
/home/erik/miniforge3/envs/pymc_env/lib/python3.11/site-packages/pymc/backends/arviz.py:65: UserWarning: Could not extract data from symbolic observation X
warnings.warn(f"Could not extract data from symbolic observation {obs}")
结果#
当我们比较使用 MCMC 和 VI 计算的后验时,我们发现(至少对于我们正在查看的这个特定参数)这两个分布很接近,但它们的均值确实不同。两个 MCMC 后验彼此非常吻合,而 ADVI 估计值也相差不远。
col_selection = dict(observed_columns=3, latent_columns=1)
ax = az.plot_kde(
trace.posterior["W"].sel(**col_selection).values,
label="MCMC posterior for the explicit model".format(0),
plot_kwargs={"color": f"C{1}"},
)
az.plot_kde(
trace_amortized.posterior["W"].sel(**col_selection).values,
label="MCMC posterior for amortized inference",
plot_kwargs={"color": f"C{2}", "linestyle": "--"},
)
az.plot_kde(
trace_vi.posterior["W"].sel(**col_selection).squeeze().values,
label="FR-ADVI posterior for amortized inference",
plot_kwargs={"alpha": 0},
fill_kwargs={"alpha": 0.5, "color": f"C{0}"},
)
ax.set_title(rf"PDFs of $W$ estimate at {col_selection}")
ax.legend(loc="upper left", fontsize=10);
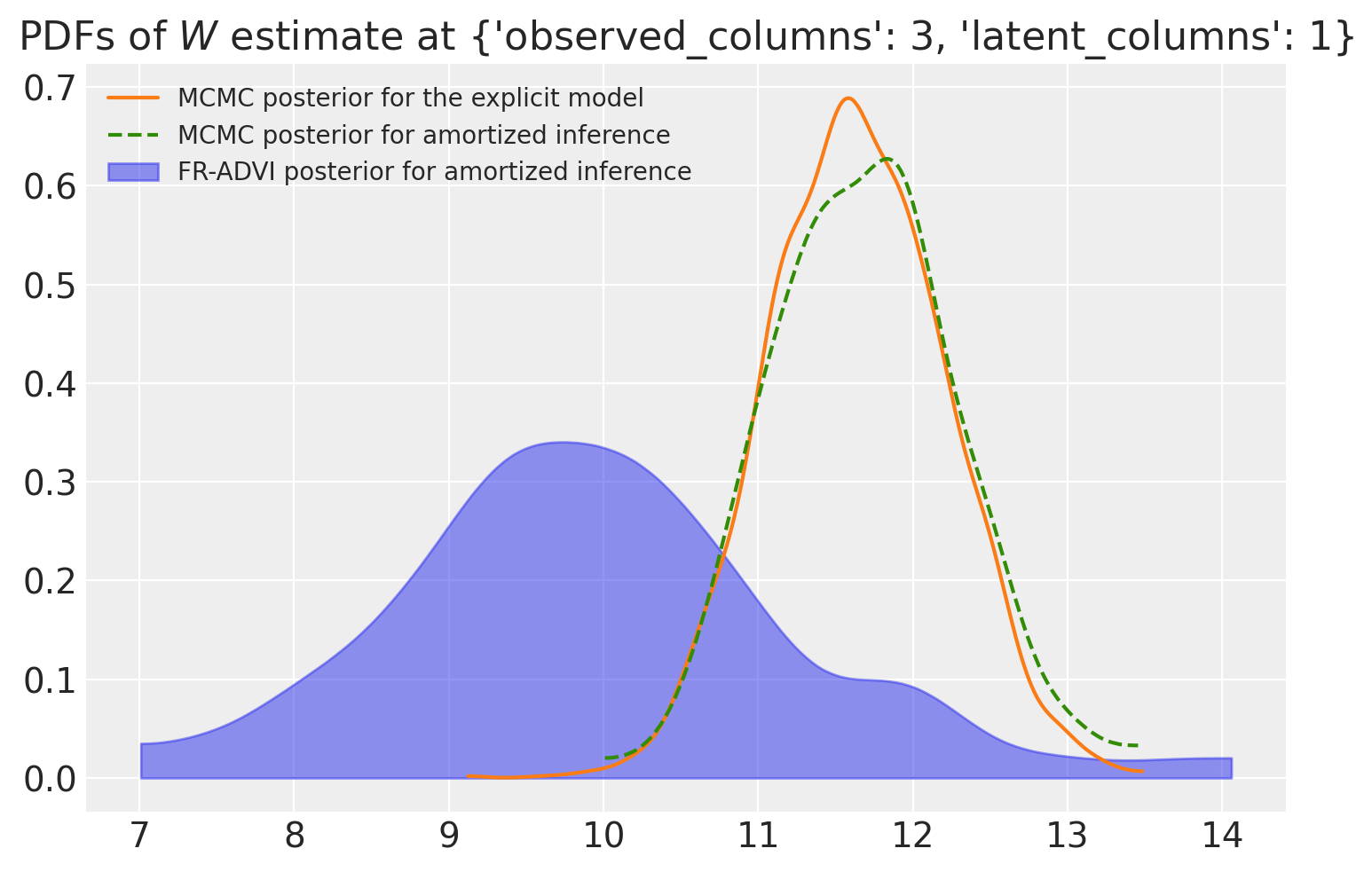
F 的事后识别#
矩阵 \(F\) 通常是因子分析感兴趣的,并且通常用作降维的特征矩阵。但是,\(F\) 已被边缘化,以便更容易拟合模型;现在我们需要它回来。转换
\(X|WF \sim \mathcal{N}(WF, \sigma^2)\)
为
\((W^TW)^{-1}W^T X|W,F \sim \mathcal{N}(F, \sigma^2(W^TW)^{-1})\)
我们将 \(F\) 表示为具有已知协方差矩阵的多元正态分布的均值。使用先验 \( F \sim \mathcal{N}(0, I) \) 并根据 共轭先验 的表达式进行更新,我们发现
\( F | X, W \sim \mathcal{N}(\mu_F, \Sigma_F) \),
其中
\(\mu_F = \left(I + \sigma^{-2} W^T W\right)^{-1} \sigma^{-2} W^T X\)
\(\Sigma_F = \left(I + \sigma^{-2} W^T W\right)^{-1}\)
对于在迹线中找到的 \(W\) 和 \(X\) 的每个值,我们现在从此分布中抽取一个样本。
# configure xarray-einstats
def get_default_dims(dims, dims2):
proposed_dims = [dim for dim in dims if dim not in {"chain", "draw"}]
assert len(proposed_dims) == 2
if dims2 is None:
return proposed_dims
linalg.get_default_dims = get_default_dims
post = trace_vi.posterior
obs = trace.observed_data
WW = linalg.matmul(
post["W"], post["W"], dims=("latent_columns", "observed_columns", "latent_columns")
)
# Constructing an identity matrix following https://einstats.python.arviz.org/en/latest/tutorials/np_linalg_tutorial_port.html
I = xr.zeros_like(WW)
idx = xr.DataArray(WW.coords["latent_columns"])
I.loc[{"latent_columns": idx, "latent_columns2": idx}] = 1
Sigma_F = linalg.inv(I + post["sigma"] ** (-2) * WW)
X_transform = linalg.matmul(
Sigma_F,
post["sigma"] ** (-2) * post["W"],
dims=("latent_columns2", "latent_columns", "observed_columns"),
)
mu_F = xr.dot(X_transform, obs["X"], dims="observed_columns").rename(
latent_columns2="latent_columns"
)
Sigma_chol = linalg.cholesky(Sigma_F)
norm_dist = XrContinuousRV(sp.stats.norm, xr.zeros_like(mu_F)) # the zeros_like defines the shape
F_sampled = mu_F + linalg.matmul(
post["sigma"] * Sigma_F,
norm_dist.rvs(),
dims=(("latent_columns", "latent_columns2"), ("latent_columns", "rows")),
)
与原始数据比较#
为了检查我们的模型捕捉原始数据的程度,我们将测试我们从采样的 \(W\) 和 \(F\) 矩阵中重建数据的效果。对于 \(Y\) 的每个元素,我们绘制 \(X = W F\) 的均值和标准差,这是基于我们模型的重建值。
X_sampled_amortized = linalg.matmul(
post["W"],
F_sampled,
dims=("observed_columns", "latent_columns", "rows"),
)
reconstruction_mean = X_sampled_amortized.mean(dim=("chain", "draw")).values
reconstruction_sd = X_sampled_amortized.std(dim=("chain", "draw")).values
plt.errorbar(
Y.ravel(),
reconstruction_mean.ravel(),
yerr=reconstruction_sd.ravel(),
marker=".",
ls="none",
alpha=0.3,
)
slope, intercept, r_value, p_value, std_err = sp.stats.linregress(
Y.ravel(), reconstruction_mean.ravel()
)
plt.plot(
[Y.min(), Y.max()],
np.array([Y.min(), Y.max()]) * slope + intercept,
"k--",
label=f"Linear regression for the mean, R²={r_value**2:.2f}",
)
plt.plot([Y.min(), Y.max()], [Y.min(), Y.max()], "k:", label="Perfect reconstruction")
plt.xlabel("Elements of Y")
plt.ylabel("Model reconstruction")
plt.legend(loc="upper left");

我们发现我们的模型在捕捉原始数据的变化方面做得相当不错,尽管只使用了两个潜在因子而不是实际的四个。
水印#
%load_ext watermark
%watermark -n -u -v -iv -w
Last updated: Wed Dec 27 2023
Python implementation: CPython
Python version : 3.11.7
IPython version : 8.16.0
pytensor : 2.18.3
scipy : 1.11.4
arviz : 0.16.1
seaborn : 0.12.2
numpy : 1.26.2
pymc : 5.10.2
xarray : 2023.12.0
xarray_einstats: 0.6.0
matplotlib : 3.8.2
Watermark: 2.4.3
许可声明#
此示例库中的所有 notebook 均根据 MIT 许可证 提供,该许可证允许修改和再分发以用于任何用途,前提是保留版权和许可声明。
引用 PyMC 示例#
要引用此 notebook,请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。
重要提示
许多 notebook 改编自其他来源:博客、书籍... 在这种情况下,您也应该引用原始来源。
还请记住引用您的代码使用的相关库。
这是一个 bibtex 中的引用模板
@incollection{citekey,
author = "<notebook authors, see above>",
title = "<notebook title>",
editor = "PyMC Team",
booktitle = "PyMC examples",
doi = "10.5281/zenodo.5654871"
}
一旦呈现,它可能看起来像