分层部分池化#

假设您的任务是评估几位棒球运动员的击球技能。其中一项性能指标是击球率。由于球员参加的比赛场次不同，并且在击球顺序中的位置也不同，因此每位球员的击球次数也不同。但是，您想评估所有球员的技能，包括那些击球机会相对较少的球员。

那么，假设一名球员只击球了 4 次，而且一次也没有击中球。他们是糟糕的球员吗？

作为免责声明，此笔记本的作者假设对棒球及其规则知之甚少或一无所知。他一生中的击球次数大约是“4”次。

数据#

我们将使用棒球 数据 [Efron and Morris, 1975]。

方法#

我们将使用 PyMC 来估计每位球员的击球率。在估计了数据集中所有球员的平均值后，我们可以使用此信息来告知对另一名球员的估计，该球员的数据很少（即 4 次击球）。

在没有贝叶斯分层模型的情况下，解决此问题有两种方法

  1. 独立计算每位球员的击球率（无池化）

  2. 计算总体平均值，假设每个人的基本平均值都相同（完全池化）

当然，这两种方法都不现实。显然，并非所有球员的击球技巧都相同，因此全局平均值是不合理的。与此同时，职业棒球运动员在许多方面都很相似，因此他们的平均值也不是完全独立的。

可能可以对“相似”球员的群体进行聚类，并估计群体平均值，但是使用分层建模方法是共享信息的自然方式，无需识别 ad hoc 聚类。

分层部分池化的思想是模拟全局表现，并使用该估计来参数化球员群体，以解释球员表现之间的差异。全局表现和个人表现之间的这种权衡将由模型自动调整。此外，由于每位球员的击球次数不同（即 信息）而导致的不确定性将自动考虑在内，方法是将这些估计值缩小到更接近全局均值。

有关更深入的讨论，请参阅 Stan 教程 [Carpenter et al., 2016] 关于该主题。模型和参数值取自该示例。

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pytensor.tensor as pt

%matplotlib inline

RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")

现在我们可以使用 pandas 加载数据集

data = pd.read_csv(pm.get_data("efron-morris-75-data.tsv"), sep="\t")
at_bats, hits = data[["At-Bats", "Hits"]].to_numpy().T

现在让我们为这些数据开发一个生成模型。

我们将假设存在一个隐藏因子 (phi) 与所有球员（不限于我们的 18 位）的预期表现相关。由于人口平均值是 0 到 1 之间的未知值，因此它必须有下限和上限。此外，我们假设对全局平均值一无所知。因此，先验分布的自然选择是均匀分布。

接下来，我们引入一个超参数 kappa 以解释人口击球率的方差，为此我们将使用有界帕累托分布。这将确保估计值落在合理的范围内。这些超参数将反过来用于参数化 beta 分布，这非常适合对单位区间上的量进行建模。beta 分布通常通过尺度和形状参数进行参数化，也可以根据其均值 \(\mu \in [0,1]\) 和样本大小（方差的代理）\(\nu = \alpha + \beta (\nu > 0)\) 进行参数化。

最后一步是为每位球员的数据（击中或未击中）指定一个抽样分布，使用二项分布。这是将数据引入模型的地方。

我们可以使用 pm.Pareto('kappa', m=1.5)，来定义我们对 kappa 的先验，但帕累托分布具有非常长的尾部。对于采样器来说，正确探索这些尾部非常困难，因此我们使用等效但更快的参数化，即使用指数分布。我们使用帕累托分布随机变量的对数遵循指数分布的事实。

N = len(hits)
player_names = data["FirstName"] + " " + data["LastName"]
coords = {"player_names": player_names.tolist()}

with pm.Model(coords=coords) as baseball_model:
    phi = pm.Uniform("phi", lower=0.0, upper=1.0)

    kappa_log = pm.Exponential("kappa_log", lam=1.5)
    kappa = pm.Deterministic("kappa", pt.exp(kappa_log))

    theta = pm.Beta("theta", alpha=phi * kappa, beta=(1.0 - phi) * kappa, dims="player_names")
    y = pm.Binomial("y", n=at_bats, p=theta, dims="player_names", observed=hits)

回想一下我们最初的问题是关于只有 4 次击球且没有击中的球员的真实击球率。我们可以将其作为模型中的附加变量添加

with baseball_model:
    theta_new = pm.Beta("theta_new", alpha=phi * kappa, beta=(1.0 - phi) * kappa)
    y_new = pm.Binomial("y_new", n=4, p=theta_new, observed=0)

模型可以像这样可视化

pm.model_to_graphviz(baseball_model)
../_images/ebc23400283c5ac276dcac1cb83402a474a679bf3963131b9f20349b2c052dea.svg

我们现在可以使用 MCMC 拟合模型

with baseball_model:
    idata = pm.sample(2000, tune=2000, chains=2, target_accept=0.95)

    # check convergence diagnostics
    assert all(az.rhat(idata) < 1.03)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [phi, kappa_log, theta, theta_new]
100.00% [8000/8000 00:26<00:00 采样 2 个链，0 个发散]
Sampling 2 chains for 2_000 tune and 2_000 draw iterations (4_000 + 4_000 draws total) took 34 seconds.

现在我们可以绘制参数的后验分布。首先，是人口超参数

az.plot_trace(idata, var_names=["phi", "kappa"]);
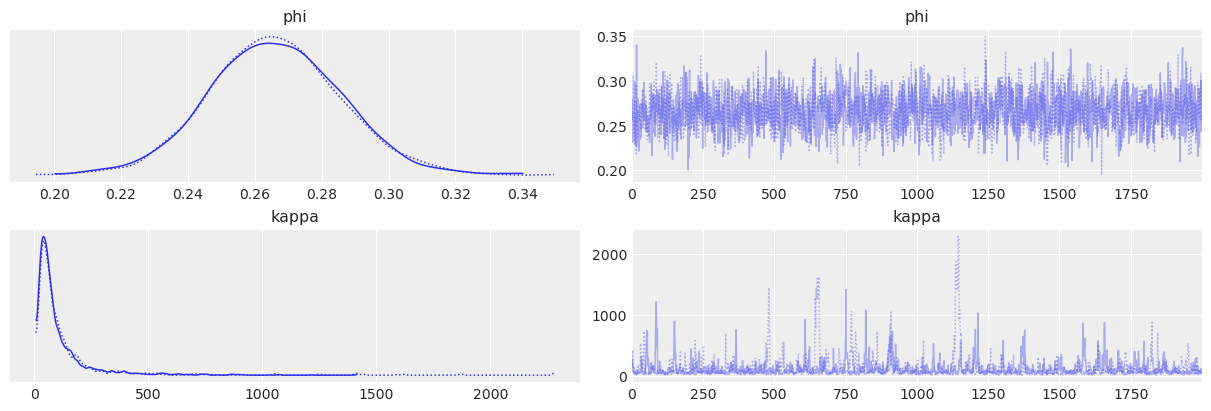
../_images/3881064d5b655660775e0b004bfc4a3fe4ee43eabb74af9c39eefb76248e1e0f.png

因此，人口平均击球率在 0.22-0.31 范围内，预期值约为 0.26。

接下来，是数据集中所有 18 位球员的估计值

az.plot_forest(idata, var_names="theta");
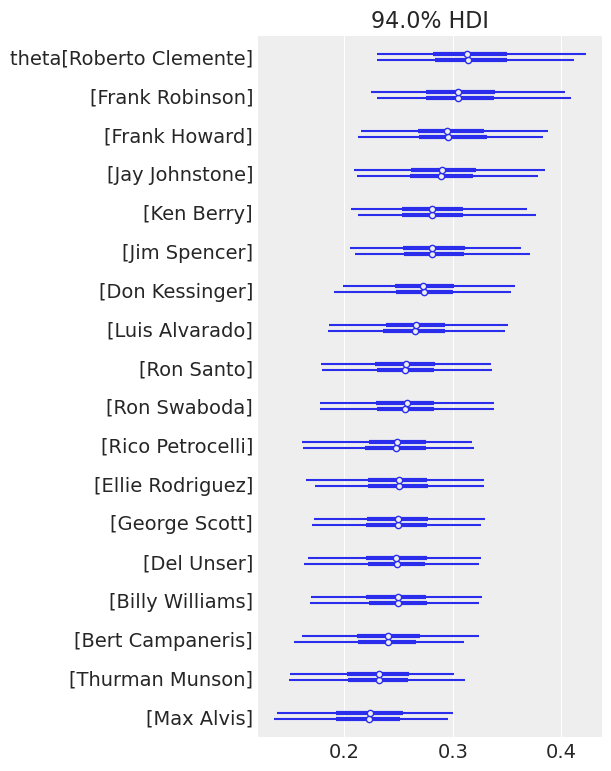
../_images/c723373ea236a4a93a129dff0c5864c0ceaa03f661ca396f00f58b9a81ee30da.png

最后，让我们获取我们 0 投 4 中的球员的估计值

az.plot_trace(idata, var_names=["theta_new"]);
../_images/d8a2dfa5e05e22432f7528394a8929da951e0512be1214df930585240abcca5f.png

请注意，尽管我们的额外球员没有击中任何球，但对他的平均值的估计值不是零——零甚至不是一个高概率值。这是因为我们假设该球员是从一个由我们估计的超参数指定的分布的人口中抽取的。但是，该球员的估计均值接近我们数据集中球员均值的低端，这表明 4 次击球为该估计贡献了一些信息。

作者#

  • 由 Vladislavs Dovgalecs 于 2016 年 11 月撰写 (pymc#1546)

  • 由 Adrian Seybolt 于 2017 年 6 月更新 (pymc#2288)

  • 由 Christian Luhmann 于 2020 年 8 月更新 (pymc#4068)

  • 由 Reshama Shaikh 于 2023 年 1 月使用 PyMC v5 运行

参考文献#

[1]

Bradley Efron 和 Carl Morris。Data analysis using stein's estimator and its generalizations。《美国统计协会杂志》，70(350):311–319, 1975。

[2]

Bob Carpenter, J Gabry, 和 B Goodrich。Hierarchical partial pooling for repeated binary trials。2016。

水印#

%load_ext watermark
%watermark -n -u -v -iv -w -p xarray

Last updated: Sat Jan 28 2023

Python implementation: CPython
Python version       : 3.11.0
IPython version      : 8.8.0

xarray: 2022.12.0

matplotlib: 3.6.2
pandas    : 1.5.2
arviz     : 0.14.0
pytensor  : 2.8.11
pymc      : 5.0.1
numpy     : 1.24.1

Watermark: 2.3.1

许可声明#

此示例画廊中的所有笔记本均根据 MIT 许可证 提供，该许可证允许修改和再分发以用于任何用途，前提是保留版权和许可声明。

引用 PyMC 示例#

要引用此笔记本，请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。

重要提示

许多笔记本都改编自其他来源：博客、书籍……在这种情况下，您也应该引用原始来源。

还请记住引用您的代码使用的相关库。

这是一个 bibtex 中的引用模板

@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}

渲染后可能看起来像这样