可靠性统计和预测校准#
注意
此 notebook 使用的库不是 PyMC 的依赖项，因此需要专门安装才能运行此 notebook。 打开下面的下拉菜单以获取更多指导。
额外依赖项安装说明
为了运行此 notebook（本地或在 binder 上），您不仅需要安装可用的 PyMC 以及所有可选依赖项，还需要安装一些额外的依赖项。 有关安装 PyMC 本身的建议，请参阅 安装
您可以使用您喜欢的包管理器安装这些依赖项，我们提供以下 pip 和 conda 命令作为示例。
$ pip install lifelines
请注意，如果您想（或需要）从 notebook 内部而不是命令行安装软件包，您可以通过运行 pip 命令的变体来安装软件包
import sys
!{sys.executable} -m pip install lifelines
您不应运行 !pip install，因为它可能会将软件包安装在不同的环境中，即使已安装，也无法从 Jupyter notebook 中使用。
另一种选择是使用 conda 代替
$ conda install lifelines
当使用 conda 安装科学 python 包时，我们建议使用 conda forge
import os
import random
from io import StringIO
import arviz as az
import matplotlib.cm as cm
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
from lifelines import KaplanMeierFitter, LogNormalFitter, WeibullFitter
from lifelines.utils import survival_table_from_events
from scipy.stats import binom, lognorm, norm, weibull_min
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
%config InlineBackend.figure_format = 'retina'
可靠性统计#
当我们想要推断生产线中可能发生的故障时，根据行业、商品的性质或我们寻求回答的具体问题的具体性，我们可能拥有大型或小型样本数据集。 但在所有情况下，都存在成本问题和可容忍的故障数量。
因此，可靠性研究必须考虑观察故障的重要时期、故障成本和运行错误指定研究的成本。 对问题定义的精确度和建模练习的性质的要求至关重要。
失效时间数据的关键特征是其被删失的方式，以及这如何偏置传统的统计摘要和估计技术。 在此 notebook 中，我们将重点关注失效时间的预测，并将校准预测区间的贝叶斯概念与一些频率学替代方案进行比较。 我们借鉴了 Statistical Methods for Reliability Data 这本书中的工作。 有关详细信息（请参阅 Meeker et al. [2022]）
预测类型#
我们可能想了解失效时间分布的不同视图，例如
新项目的失效时间
未来 m 个单元样本中发生 k 次失效的时间
虽然可以使用非参数和描述性方法来评估这些类型的问题，但我们将重点关注我们拥有概率模型的情况，例如，失效时间的对数正态分布 \(F(t: \mathbf{\theta})\)，由未知 \(\mathbf{\theta}\) 参数化。
演示结构#
我们将
讨论可靠性数据的累积密度函数 CDF 的非参数估计
展示如何推导出相同函数的频率学或 MLE 以告知我们的预测区间
展示如何在信息稀疏的情况下使用贝叶斯方法来增强对相同 CDF 的分析。
始终关注理解 CDF 如何帮助我们理解可靠性设置中的失效风险。 特别是 CDF 如何用于推导出良好校准的预测区间。
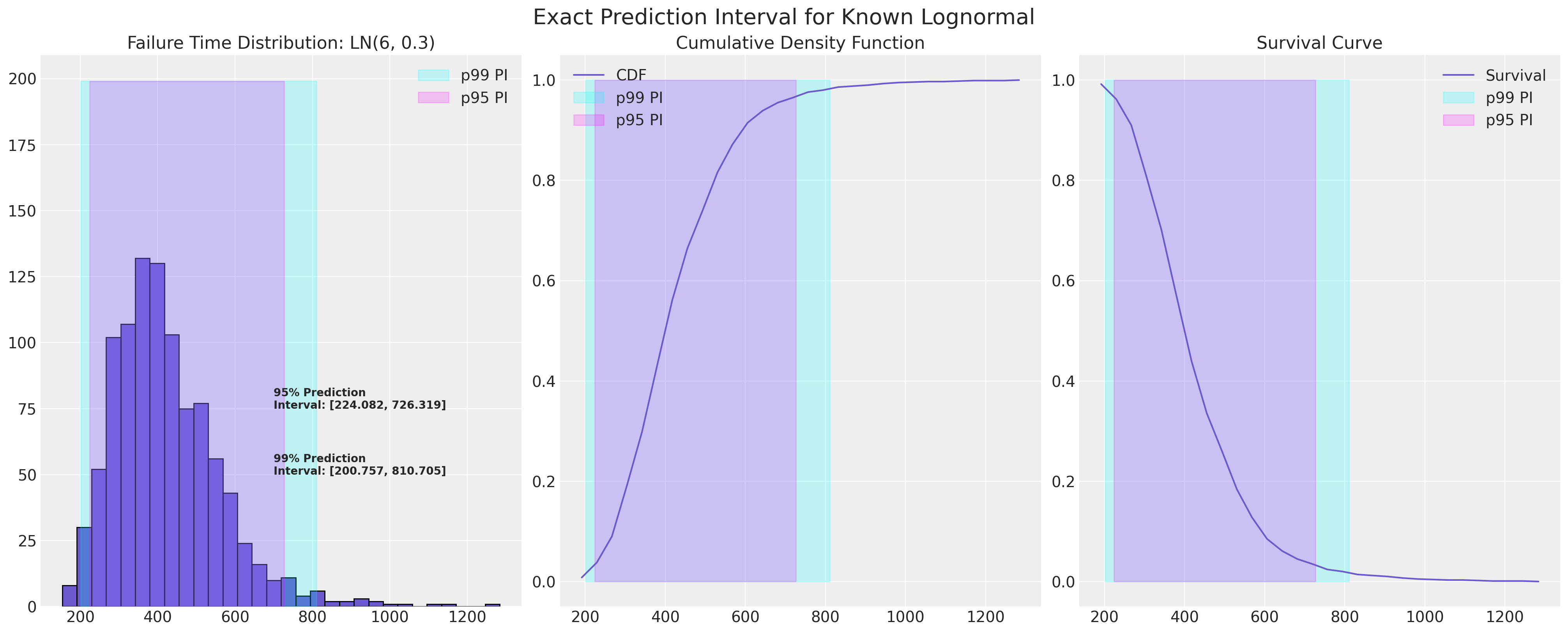
示例失效分布#
在可靠性统计研究中，重点是具有长尾的位置-尺度分布。 在理想的世界中，我们将确切知道哪个分布描述了我们的失效过程，并且可以精确定义下一次失效的预测区间。
mu, sigma = 6, 0.3
def plot_ln_pi(mu, sigma, xy=(700, 75), title="Exact Prediction Interval for Known Lognormal"):
failure_dist = lognorm(s=sigma, scale=np.exp(mu))
samples = failure_dist.rvs(size=1000, random_state=100)
fig, axs = plt.subplots(1, 3, figsize=(20, 8))
axs = axs.flatten()
axs[0].hist(samples, ec="black", color="slateblue", bins=30)
axs[0].set_title(f"Failure Time Distribution: LN({mu}, {sigma})")
count, bins_count = np.histogram(samples, bins=30)
pdf = count / sum(count)
cdf = np.cumsum(pdf)
axs[1].plot(bins_count[1:], cdf, label="CDF", color="slateblue")
axs[2].plot(bins_count[1:], 1 - cdf, label="Survival", color="slateblue")
axs[2].legend()
axs[1].legend()
axs[1].set_title("Cumulative Density Function")
axs[2].set_title("Survival Curve")
lb = failure_dist.ppf(0.01)
ub = failure_dist.ppf(0.99)
axs[0].annotate(
f"99% Prediction \nInterval: [{np.round(lb, 3)}, {np.round(ub, 3)}]",
xy=(xy[0], xy[1] - 25),
fontweight="bold",
)
axs[0].fill_betweenx(y=range(200), x1=lb, x2=ub, alpha=0.2, label="p99 PI", color="cyan")
axs[1].fill_betweenx(y=range(2), x1=lb, x2=ub, alpha=0.2, label="p99 PI", color="cyan")
axs[2].fill_betweenx(y=range(2), x1=lb, x2=ub, alpha=0.2, label="p99 PI", color="cyan")
lb = failure_dist.ppf(0.025)
ub = failure_dist.ppf(0.975)
axs[0].annotate(
f"95% Prediction \nInterval: [{np.round(lb, 3)}, {np.round(ub, 3)}]",
xy=(xy[0], xy[1]),
fontweight="bold",
)
axs[0].fill_betweenx(y=range(200), x1=lb, x2=ub, alpha=0.2, label="p95 PI", color="magenta")
axs[1].fill_betweenx(y=range(2), x1=lb, x2=ub, alpha=0.2, label="p95 PI", color="magenta")
axs[2].fill_betweenx(y=range(2), x1=lb, x2=ub, alpha=0.2, label="p95 PI", color="magenta")
axs[0].legend()
axs[1].legend()
axs[2].legend()
plt.suptitle(title, fontsize=20)
plot_ln_pi(mu, sigma)
从数据估计失效分布#
在现实世界中，我们很少有如此精确的知识。 相反，我们从完全不太清晰的数据开始。 我们将首先检查关于三个工厂的热交换器的失效数据，并汇集信息以量化三个工厂的热交换器的寿命。
数据刻意很小，因此我们可以专注于评估失效时间数据所涉及的描述性统计信息。 特别是，我们将估计经验 CDF 和生存函数。 然后，我们将把这种分析风格推广到更大的数据集。
热交换器数据#
关于删失数据的说明：请参阅下面失效数据如何标记观察结果是否已被删失，即我们是否观察到热交换器完整生命周期。 这是失效时间数据的关键特征。 太简单的统计摘要会因以下事实而偏离其对故障发生率的估计，即我们的研究尚未看到每个项目生命周期的完整过程。 最常见的删失形式是所谓的“右删失”数据，我们没有看到一部分观察结果的“失效”事件。 由于过早结束数据收集，我们的历史记录不完整。
左删失（我们没有从项目历史记录的开始观察项目）和区间删失（左删失和右删失）也可能发生，但不太常见。
显示代码单元格源
heat_exchange_df = pd.read_csv(
StringIO(
"""Years Lower,Years Upper,Censoring Indicator,Count,Plant
0,1,Left,1,1
1,2,Interval,2,1
2,3,Interval,2,1
3, ,Right,95,1
0,1,Left,2,2
1,2,Interval,3,2
2, ,Right,95,2
0,1,Left,1,3
1, ,Right,99,3
"""
)
)
heat_exchange_df["year_interval"] = (
heat_exchange_df["Years Lower"].astype(str) + "," + heat_exchange_df["Years Upper"].astype(str)
)
heat_exchange_df["failed"] = np.where(
heat_exchange_df["Censoring Indicator"] != "Right", heat_exchange_df["Count"], 0
)
heat_exchange_df["censored"] = np.where(
heat_exchange_df["Censoring Indicator"] == "Right", heat_exchange_df["Count"], 0
)
heat_exchange_df["risk_set"] = [100, 99, 97, 0, 100, 98, 0, 100, 0]
heat_exchange_df
| 年份下限 | 年份上限 | 删失指示符 | 计数 | 工厂 | 年_间隔 | 已失效 | 截尾数据 | 风险集 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 左 | 1 | 1 | 0,1 | 1 | 0 | 100 |
| 1 | 1 | 2 | 区间 | 2 | 1 | 1,2 | 2 | 0 | 99 |
| 2 | 2 | 3 | 区间 | 2 | 1 | 2,3 | 2 | 0 | 97 |
| 3 | 3 | 右 | 95 | 1 | 3, | 0 | 95 | 0 | |
| 4 | 0 | 1 | 左 | 2 | 2 | 0,1 | 2 | 0 | 100 |
| 5 | 1 | 2 | 区间 | 3 | 2 | 1,2 | 3 | 0 | 98 |
| 6 | 2 | 右 | 95 | 2 | 2, | 0 | 95 | 0 | |
| 7 | 0 | 1 | 左 | 1 | 3 | 0,1 | 1 | 0 | 100 |
| 8 | 1 | 右 | 99 | 3 | 1, | 0 | 99 | 0 |
actuarial_table = heat_exchange_df.groupby(["Years Upper"])[["failed", "risk_set"]].sum()
actuarial_table = actuarial_table.tail(3)
def greenwood_variance(df):
### Used to estimate the variance in the CDF
n = len(df)
ps = [df.iloc[i]["p_hat"] / (df.iloc[i]["risk_set"] * df.iloc[i]["1-p_hat"]) for i in range(n)]
s = [(df.iloc[i]["S_hat"] ** 2) * np.sum(ps[0 : i + 1]) for i in range(n)]
return s
def logit_transform_interval(df):
### Used for robustness in the estimation of the Confidence intervals in the CDF
df["logit_CI_95_lb"] = df["F_hat"] / (
df["F_hat"]
+ df["S_hat"] * np.exp((1.960 * df["Standard_Error"]) / (df["F_hat"] * df["S_hat"]))
)
df["logit_CI_95_ub"] = df["F_hat"] / (
df["F_hat"]
+ df["S_hat"] / np.exp((1.960 * df["Standard_Error"]) / (df["F_hat"] * df["S_hat"]))
)
df["logit_CI_95_lb"] = np.where(df["logit_CI_95_lb"] < 0, 0, df["logit_CI_95_lb"])
df["logit_CI_95_ub"] = np.where(df["logit_CI_95_ub"] > 1, 1, df["logit_CI_95_ub"])
return df
def make_actuarial_table(actuarial_table):
### Actuarial lifetables are used to describe the nature of the risk over time and estimate
actuarial_table["p_hat"] = actuarial_table["failed"] / actuarial_table["risk_set"]
actuarial_table["1-p_hat"] = 1 - actuarial_table["p_hat"]
actuarial_table["S_hat"] = actuarial_table["1-p_hat"].cumprod()
actuarial_table["CH_hat"] = -np.log(actuarial_table["S_hat"])
### The Estimate of the CDF function
actuarial_table["F_hat"] = 1 - actuarial_table["S_hat"]
actuarial_table["V_hat"] = greenwood_variance(actuarial_table)
actuarial_table["Standard_Error"] = np.sqrt(actuarial_table["V_hat"])
actuarial_table["CI_95_lb"] = (
actuarial_table["F_hat"] - actuarial_table["Standard_Error"] * 1.960
)
actuarial_table["CI_95_lb"] = np.where(
actuarial_table["CI_95_lb"] < 0, 0, actuarial_table["CI_95_lb"]
)
actuarial_table["CI_95_ub"] = (
actuarial_table["F_hat"] + actuarial_table["Standard_Error"] * 1.960
)
actuarial_table["CI_95_ub"] = np.where(
actuarial_table["CI_95_ub"] > 1, 1, actuarial_table["CI_95_ub"]
)
actuarial_table["plotting_position"] = actuarial_table["F_hat"].rolling(1).median()
actuarial_table = logit_transform_interval(actuarial_table)
return actuarial_table
actuarial_table_heat = make_actuarial_table(actuarial_table)
actuarial_table_heat = actuarial_table_heat.reset_index()
actuarial_table_heat.rename({"Years Upper": "t"}, axis=1, inplace=True)
actuarial_table_heat["t"] = actuarial_table_heat["t"].astype(int)
actuarial_table_heat
| t | 已失效 | 风险集 | p_hat | 1-p_hat | S_hat | CH_hat | F_hat | V_hat | 标准误差 | CI_95_lb | CI_95_ub | plotting_position | logit_CI_95_lb | logit_CI_95_ub | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 4 | 300 | 0.013333 | 0.986667 | 0.986667 | 0.013423 | 0.013333 | 0.000044 | 0.006622 | 0.000354 | 0.026313 | 0.013333 | 0.005013 | 0.034977 |
| 1 | 2 | 5 | 197 | 0.025381 | 0.974619 | 0.961624 | 0.039131 | 0.038376 | 0.000164 | 0.012802 | 0.013283 | 0.063468 | 0.038376 | 0.019818 | 0.073016 |
| 2 | 3 | 2 | 97 | 0.020619 | 0.979381 | 0.941797 | 0.059965 | 0.058203 | 0.000350 | 0.018701 | 0.021550 | 0.094856 | 0.058203 | 0.030694 | 0.107629 |
值得花一些时间来了解这个示例，因为它建立了失效时间建模中一些关键量的估计。
首先请注意我们如何将时间视为一系列离散的间隔。 数据格式为离散的期间格式，因为它记录了随时间推移的汇总失效。 我们将在下面看到另一种失效数据格式 - 项目-期间格式，它记录了所有期间的每个单独项目及其相应的状态。 在这种格式中，关键量是每期中 failed 项目的集合和 risk_set。 其他一切都源于这些事实。
首先，我们已经确定了在连续三年中所有三家公司生产的热交换器的数量以及随后 failed 的数量。 这提供了对当年失效概率的估计：p_hat 及其倒数 1-p_hat。 这些在一年中进一步组合以估计生存曲线 S_hat，可以进一步转换以恢复累积风险 CH_hat 和累积密度函数 F_hat 的估计值。
接下来，我们需要一种快速而粗略的方法来量化我们对 CDF 估计的不确定性程度。 为此，我们使用 Greenwood 公式来估计我们估计 F_hat 的 V_hat 的方差。 这为我们提供了标准误差和文献中推荐的两种置信区间。
我们将相同的技术应用于更大的数据集，并在下面绘制其中一些量。
减震器数据：频率学可靠性分析研究#
减震器数据为期间格式，但它记录了随时间推移不断减少的风险集，每个时间点有一个项目被删失或失效，即由于成功（批准）或由于失效而被移除测试。 这是 期间 格式数据的特例。
显示代码单元格源
shockabsorbers_df = pd.read_csv(
StringIO(
"""Kilometers,Failure Mode,Censoring Indicator
6700,Mode1,Failed
6950,Censored,Censored
7820,Censored,Censored
8790,Censored,Censored
9120,Mode2,Failed
9660,Censored,Censored
9820,Censored,Censored
11310,Censored,Censored
11690,Censored,Censored
11850,Censored,Censored
11880,Censored,Censored
12140,Censored,Censored
12200,Mode1,Failed
12870,Censored,Censored
13150,Mode2,Failed
13330,Censored,Censored
13470,Censored,Censored
14040,Censored,Censored
14300,Mode1,Failed
17520,Mode1,Failed
17540,Censored,Censored
17890,Censored,Censored
18450,Censored,Censored
18960,Censored,Censored
18980,Censored,Censored
19410,Censored,Censored
20100,Mode2,Failed
20100,Censored,Censored
20150,Censored,Censored
20320,Censored,Censored
20900,Mode2,Failed
22700,Mode1,Failed
23490,Censored,Censored
26510,Mode1,Failed
27410,Censored,Censored
27490,Mode1,Failed
27890,Censored,Censored
28100,Censored,Censored
"""
)
)
shockabsorbers_df["failed"] = np.where(shockabsorbers_df["Censoring Indicator"] == "Failed", 1, 0)
shockabsorbers_df["t"] = shockabsorbers_df["Kilometers"]
shockabsorbers_events = survival_table_from_events(
shockabsorbers_df["t"], shockabsorbers_df["failed"]
).reset_index()
shockabsorbers_events.rename(
{"event_at": "t", "observed": "failed", "at_risk": "risk_set"}, axis=1, inplace=True
)
actuarial_table_shock = make_actuarial_table(shockabsorbers_events)
actuarial_table_shock
| t | 已移除 | 已失效 | 截尾数据 | 入口 | 风险集 | p_hat | 1-p_hat | S_hat | CH_hat | F_hat | V_hat | 标准误差 | CI_95_lb | CI_95_ub | plotting_position | logit_CI_95_lb | logit_CI_95_ub | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | 0 | 0 | 0 | 38 | 38 | 0.000000 | 1.000000 | 1.000000 | -0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | NaN | NaN |
| 1 | 6700.0 | 1 | 1 | 0 | 0 | 38 | 0.026316 | 0.973684 | 0.973684 | 0.026668 | 0.026316 | 0.000674 | 0.025967 | 0.000000 | 0.077212 | 0.026316 | 0.003694 | 0.164570 |
| 2 | 6950.0 | 1 | 0 | 1 | 0 | 37 | 0.000000 | 1.000000 | 0.973684 | 0.026668 | 0.026316 | 0.000674 | 0.025967 | 0.000000 | 0.077212 | 0.026316 | 0.003694 | 0.164570 |
| 3 | 7820.0 | 1 | 0 | 1 | 0 | 36 | 0.000000 | 1.000000 | 0.973684 | 0.026668 | 0.026316 | 0.000674 | 0.025967 | 0.000000 | 0.077212 | 0.026316 | 0.003694 | 0.164570 |
| 4 | 8790.0 | 1 | 0 | 1 | 0 | 35 | 0.000000 | 1.000000 | 0.973684 | 0.026668 | 0.026316 | 0.000674 | 0.025967 | 0.000000 | 0.077212 | 0.026316 | 0.003694 | 0.164570 |
| 5 | 9120.0 | 1 | 1 | 0 | 0 | 34 | 0.029412 | 0.970588 | 0.945046 | 0.056521 | 0.054954 | 0.001431 | 0.037831 | 0.000000 | 0.129103 | 0.054954 | 0.013755 | 0.195137 |
| 6 | 9660.0 | 1 | 0 | 1 | 0 | 33 | 0.000000 | 1.000000 | 0.945046 | 0.056521 | 0.054954 | 0.001431 | 0.037831 | 0.000000 | 0.129103 | 0.054954 | 0.013755 | 0.195137 |
| 7 | 9820.0 | 1 | 0 | 1 | 0 | 32 | 0.000000 | 1.000000 | 0.945046 | 0.056521 | 0.054954 | 0.001431 | 0.037831 | 0.000000 | 0.129103 | 0.054954 | 0.013755 | 0.195137 |
| 8 | 11310.0 | 1 | 0 | 1 | 0 | 31 | 0.000000 | 1.000000 | 0.945046 | 0.056521 | 0.054954 | 0.001431 | 0.037831 | 0.000000 | 0.129103 | 0.054954 | 0.013755 | 0.195137 |
| 9 | 11690.0 | 1 | 0 | 1 | 0 | 30 | 0.000000 | 1.000000 | 0.945046 | 0.056521 | 0.054954 | 0.001431 | 0.037831 | 0.000000 | 0.129103 | 0.054954 | 0.013755 | 0.195137 |
| 10 | 11850.0 | 1 | 0 | 1 | 0 | 29 | 0.000000 | 1.000000 | 0.945046 | 0.056521 | 0.054954 | 0.001431 | 0.037831 | 0.000000 | 0.129103 | 0.054954 | 0.013755 | 0.195137 |
| 11 | 11880.0 | 1 | 0 | 1 | 0 | 28 | 0.000000 | 1.000000 | 0.945046 | 0.056521 | 0.054954 | 0.001431 | 0.037831 | 0.000000 | 0.129103 | 0.054954 | 0.013755 | 0.195137 |
| 12 | 12140.0 | 1 | 0 | 1 | 0 | 27 | 0.000000 | 1.000000 | 0.945046 | 0.056521 | 0.054954 | 0.001431 | 0.037831 | 0.000000 | 0.129103 | 0.054954 | 0.013755 | 0.195137 |
| 13 | 12200.0 | 1 | 1 | 0 | 0 | 26 | 0.038462 | 0.961538 | 0.908698 | 0.095742 | 0.091302 | 0.002594 | 0.050927 | 0.000000 | 0.191119 | 0.091302 | 0.029285 | 0.250730 |
| 14 | 12870.0 | 1 | 0 | 1 | 0 | 25 | 0.000000 | 1.000000 | 0.908698 | 0.095742 | 0.091302 | 0.002594 | 0.050927 | 0.000000 | 0.191119 | 0.091302 | 0.029285 | 0.250730 |
| 15 | 13150.0 | 1 | 1 | 0 | 0 | 24 | 0.041667 | 0.958333 | 0.870836 | 0.138302 | 0.129164 | 0.003756 | 0.061285 | 0.009046 | 0.249282 | 0.129164 | 0.048510 | 0.301435 |
| 16 | 13330.0 | 1 | 0 | 1 | 0 | 23 | 0.000000 | 1.000000 | 0.870836 | 0.138302 | 0.129164 | 0.003756 | 0.061285 | 0.009046 | 0.249282 | 0.129164 | 0.048510 | 0.301435 |
| 17 | 13470.0 | 1 | 0 | 1 | 0 | 22 | 0.000000 | 1.000000 | 0.870836 | 0.138302 | 0.129164 | 0.003756 | 0.061285 | 0.009046 | 0.249282 | 0.129164 | 0.048510 | 0.301435 |
| 18 | 14040.0 | 1 | 0 | 1 | 0 | 21 | 0.000000 | 1.000000 | 0.870836 | 0.138302 | 0.129164 | 0.003756 | 0.061285 | 0.009046 | 0.249282 | 0.129164 | 0.048510 | 0.301435 |
| 19 | 14300.0 | 1 | 1 | 0 | 0 | 20 | 0.050000 | 0.950000 | 0.827294 | 0.189595 | 0.172706 | 0.005191 | 0.072047 | 0.031495 | 0.313917 | 0.172706 | 0.072098 | 0.359338 |
| 20 | 17520.0 | 1 | 1 | 0 | 0 | 19 | 0.052632 | 0.947368 | 0.783752 | 0.243662 | 0.216248 | 0.006455 | 0.080342 | 0.058778 | 0.373717 | 0.216248 | 0.098254 | 0.411308 |
| 21 | 17540.0 | 1 | 0 | 1 | 0 | 18 | 0.000000 | 1.000000 | 0.783752 | 0.243662 | 0.216248 | 0.006455 | 0.080342 | 0.058778 | 0.373717 | 0.216248 | 0.098254 | 0.411308 |
| 22 | 17890.0 | 1 | 0 | 1 | 0 | 17 | 0.000000 | 1.000000 | 0.783752 | 0.243662 | 0.216248 | 0.006455 | 0.080342 | 0.058778 | 0.373717 | 0.216248 | 0.098254 | 0.411308 |
| 23 | 18450.0 | 1 | 0 | 1 | 0 | 16 | 0.000000 | 1.000000 | 0.783752 | 0.243662 | 0.216248 | 0.006455 | 0.080342 | 0.058778 | 0.373717 | 0.216248 | 0.098254 | 0.411308 |
| 24 | 18960.0 | 1 | 0 | 1 | 0 | 15 | 0.000000 | 1.000000 | 0.783752 | 0.243662 | 0.216248 | 0.006455 | 0.080342 | 0.058778 | 0.373717 | 0.216248 | 0.098254 | 0.411308 |
| 25 | 18980.0 | 1 | 0 | 1 | 0 | 14 | 0.000000 | 1.000000 | 0.783752 | 0.243662 | 0.216248 | 0.006455 | 0.080342 | 0.058778 | 0.373717 | 0.216248 | 0.098254 | 0.411308 |
| 26 | 19410.0 | 1 | 0 | 1 | 0 | 13 | 0.000000 | 1.000000 | 0.783752 | 0.243662 | 0.216248 | 0.006455 | 0.080342 | 0.058778 | 0.373717 | 0.216248 | 0.098254 | 0.411308 |
| 27 | 20100.0 | 2 | 1 | 1 | 0 | 12 | 0.083333 | 0.916667 | 0.718440 | 0.330673 | 0.281560 | 0.009334 | 0.096613 | 0.092199 | 0.470922 | 0.281560 | 0.133212 | 0.499846 |
| 28 | 20150.0 | 1 | 0 | 1 | 0 | 10 | 0.000000 | 1.000000 | 0.718440 | 0.330673 | 0.281560 | 0.009334 | 0.096613 | 0.092199 | 0.470922 | 0.281560 | 0.133212 | 0.499846 |
| 29 | 20320.0 | 1 | 0 | 1 | 0 | 9 | 0.000000 | 1.000000 | 0.718440 | 0.330673 | 0.281560 | 0.009334 | 0.096613 | 0.092199 | 0.470922 | 0.281560 | 0.133212 | 0.499846 |
| 30 | 20900.0 | 1 | 1 | 0 | 0 | 8 | 0.125000 | 0.875000 | 0.628635 | 0.464205 | 0.371365 | 0.014203 | 0.119177 | 0.137778 | 0.604953 | 0.371365 | 0.178442 | 0.616380 |
| 31 | 22700.0 | 1 | 1 | 0 | 0 | 7 | 0.142857 | 0.857143 | 0.538830 | 0.618356 | 0.461170 | 0.017348 | 0.131711 | 0.203016 | 0.719324 | 0.461170 | 0.232453 | 0.707495 |
| 32 | 23490.0 | 1 | 0 | 1 | 0 | 6 | 0.000000 | 1.000000 | 0.538830 | 0.618356 | 0.461170 | 0.017348 | 0.131711 | 0.203016 | 0.719324 | 0.461170 | 0.232453 | 0.707495 |
| 33 | 26510.0 | 1 | 1 | 0 | 0 | 5 | 0.200000 | 0.800000 | 0.431064 | 0.841499 | 0.568936 | 0.020393 | 0.142806 | 0.289037 | 0.848835 | 0.568936 | 0.296551 | 0.805150 |
| 34 | 27410.0 | 1 | 0 | 1 | 0 | 4 | 0.000000 | 1.000000 | 0.431064 | 0.841499 | 0.568936 | 0.020393 | 0.142806 | 0.289037 | 0.848835 | 0.568936 | 0.296551 | 0.805150 |
| 35 | 27490.0 | 1 | 1 | 0 | 0 | 3 | 0.333333 | 0.666667 | 0.287376 | 1.246964 | 0.712624 | 0.022828 | 0.151089 | 0.416490 | 1.000000 | 0.712624 | 0.368683 | 0.913267 |
| 36 | 27890.0 | 1 | 0 | 1 | 0 | 2 | 0.000000 | 1.000000 | 0.287376 | 1.246964 | 0.712624 | 0.022828 | 0.151089 | 0.416490 | 1.000000 | 0.712624 | 0.368683 | 0.913267 |
| 37 | 28100.0 | 1 | 0 | 1 | 0 | 1 | 0.000000 | 1.000000 | 0.287376 | 1.246964 | 0.712624 | 0.022828 | 0.151089 | 0.416490 | 1.000000 | 0.712624 | 0.368683 | 0.913267 |
失效数据的最大似然拟合#
除了对我们的数据进行描述性摘要外，我们还可以使用寿命表数据来估计对我们的失效时间分布的单变量模型拟合。 这样的拟合（如果良好）将使我们能够更清楚地了解预测分布和特定的预测区间集。 在这里，我们将使用 lifelines 包中的函数来估计右删失数据的 MLE 拟合。
lnf = LogNormalFitter().fit(actuarial_table_shock["t"] + 1e-25, actuarial_table_shock["failed"])
lnf.print_summary()
| 模型 | lifelines.LogNormalFitter |
|---|---|
| 观测数量 | 38 |
| 观察到的事件数 | 11 |
| 对数似然 | -124.20 |
| 假设 | mu_ != 0, sigma_ != 1 |
| 系数 | se(系数) | 系数下限 95% | 系数上限 95% | 比较到 | z | p | -log2(p) | |
|---|---|---|---|---|---|---|---|---|
| mu_ | 10.13 | 0.14 | 9.85 | 10.41 | 0.00 | 71.08 | <0.005 | inf |
| sigma_ | 0.53 | 0.11 | 0.31 | 0.74 | 1.00 | -4.26 | <0.005 | 15.58 |
| AIC | 252.41 |
|---|
尽管很想使用此模型并运行它，但对于数据有限的情况，我们需要谨慎。 例如，在热交换器数据中，我们有三年的数据，总共有 11 次失效。 太简单的模型可能会完全弄错这一点。 目前，我们将重点关注减震器数据 - 其非参数描述以及对此数据的简单单变量拟合。
显示代码单元格源
def plot_cdfs(actuarial_table, dist_fits=True, ax=None, title="", xy=(3000, 0.5), item_period=None):
if item_period is None:
lnf = LogNormalFitter().fit(actuarial_table["t"] + 1e-25, actuarial_table["failed"])
wbf = WeibullFitter().fit(actuarial_table["t"] + 1e-25, actuarial_table["failed"])
else:
lnf = LogNormalFitter().fit(item_period["t"] + 1e-25, item_period["failed"])
wbf = WeibullFitter().fit(item_period["t"] + 1e-25, item_period["failed"])
if ax is None:
fig, ax = plt.subplots(figsize=(20, 10))
ax.plot(
actuarial_table["t"],
actuarial_table["F_hat"],
"-o",
color="black",
label="Non-Parametric Estimate of CDF",
)
ax.plot(
actuarial_table["t"],
actuarial_table["CI_95_lb"],
color="darkorchid",
linestyle="--",
label="Non-Parametric 95% CI based on Normal Approx",
)
ax.plot(actuarial_table["t"], actuarial_table["CI_95_ub"], color="darkorchid", linestyle="--")
ax.fill_between(
actuarial_table["t"].values,
actuarial_table["CI_95_lb"].values,
actuarial_table["CI_95_ub"].values,
color="darkorchid",
alpha=0.2,
)
ax.plot(
actuarial_table["t"],
actuarial_table["logit_CI_95_lb"],
color="royalblue",
linestyle="--",
label="Non-Parametric 95% CI based on Logit Approx",
)
ax.plot(
actuarial_table["t"], actuarial_table["logit_CI_95_ub"], color="royalblue", linestyle="--"
)
ax.fill_between(
actuarial_table["t"].values,
actuarial_table["logit_CI_95_lb"].values,
actuarial_table["logit_CI_95_ub"].values,
color="royalblue",
alpha=0.2,
)
if dist_fits:
lnf.plot_cumulative_density(ax=ax, color="crimson", alpha=0.8)
wbf.plot_cumulative_density(ax=ax, color="cyan", alpha=0.8)
ax.annotate(
f"Lognormal Fit: mu = {np.round(lnf.mu_, 3)}, sigma = {np.round(lnf.sigma_, 3)} \nWeibull Fit: lambda = {np.round(wbf.lambda_, 3)}, rho = {np.round(wbf.rho_, 3)}",
xy=(xy[0], xy[1]),
fontsize=12,
weight="bold",
)
ax.set_title(
f"Estimates of the Cumulative Density Function \n derived from our {title} Failure Data",
fontsize=20,
)
ax.set_ylabel("Fraction Failing")
ax.set_xlabel("Time Scale")
ax.legend()
return ax
plot_cdfs(actuarial_table_shock, title="Shock Absorber");
这表明与数据非常吻合，并且正如您可能预期的那样，减震器的失效比例随着使用年限的增加而增加，因为它们会磨损。 但是，给定估计模型，我们如何量化预测？
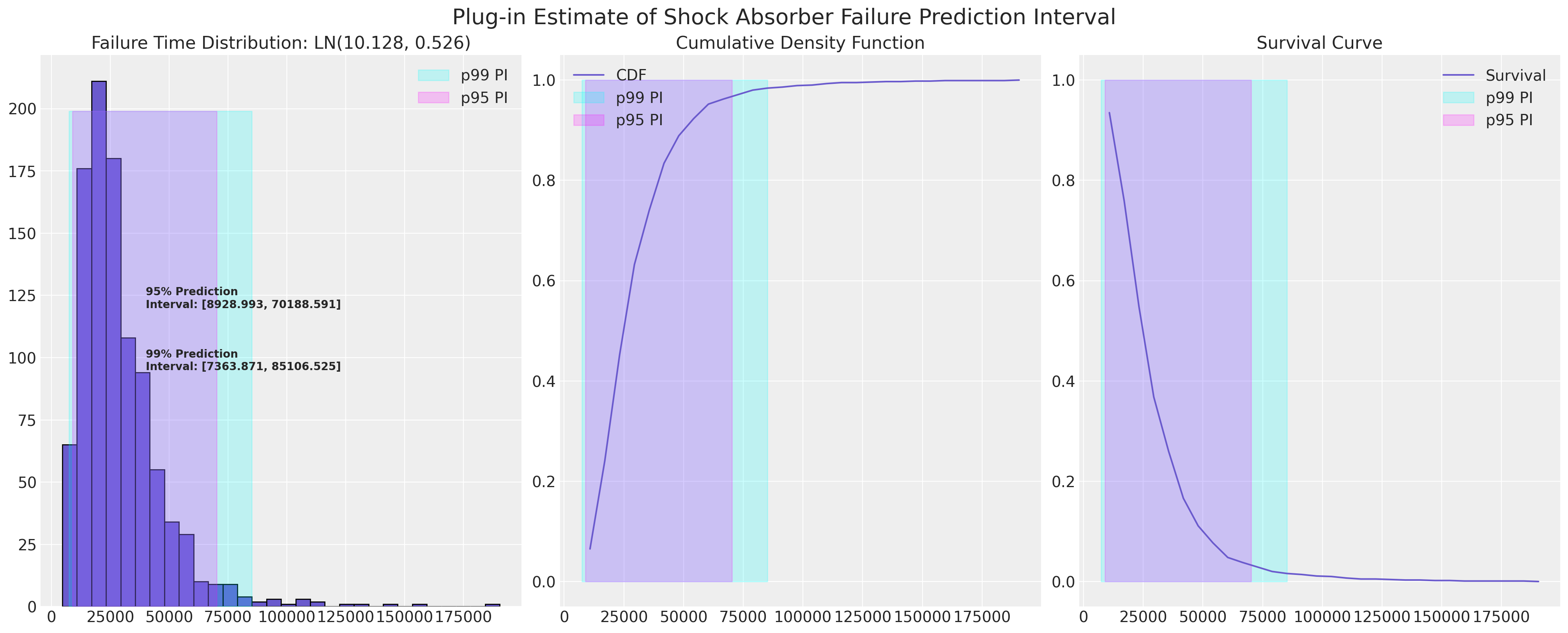
用于计算近似统计预测区间的插入程序#
由于我们已经估计了减震器数据 CDF 的对数正态拟合，我们可以绘制其近似预测区间。 这里的兴趣可能在于预测区间的下限，因为作为制造商，我们可能希望了解保修索赔以及如果下限太低而面临退款风险。
plot_ln_pi(
10.128,
0.526,
xy=(40000, 120),
title="Plug-in Estimate of Shock Absorber Failure Prediction Interval",
)
Bootstrap 校准和覆盖率估计#
我们现在想要估计此预测区间隐含的覆盖率，为此，我们将引导估计 95% 置信区间的下限和上限，并最终评估它们在 MLE 拟合条件下的覆盖率。 我们将使用分数加权（贝叶斯）bootstrap。 我们将报告两种估计覆盖率统计量的方法 - 第一种是基于从已知范围内采样随机值并评估其是否落在 95% MLE 下限和上限之间的经验覆盖率。
我们将用于评估覆盖率的第二种方法是引导估计 95% 下限和上限，然后评估这些引导值在 MLE 拟合条件下将覆盖多少。
def bayes_boot(df, lb, ub, seed=100):
w = np.random.dirichlet(np.ones(len(df)), 1)[0]
lnf = LogNormalFitter().fit(df["t"] + 1e-25, df["failed"], weights=w)
rv = lognorm(s=lnf.sigma_, scale=np.exp(lnf.mu_))
## Sample random choice from implied bootstrapped distribution
choices = rv.rvs(1000)
future = random.choice(choices)
## Check if choice is contained within the MLE 95% PI
contained = (future >= lb) & (future <= ub)
## Record 95% interval of bootstrapped dist
lb = rv.ppf(0.025)
ub = rv.ppf(0.975)
return lb, ub, contained, future, lnf.sigma_, lnf.mu_
CIs = [bayes_boot(actuarial_table_shock, 8928, 70188, seed=i) for i in range(1000)]
draws = pd.DataFrame(
CIs, columns=["Lower Bound PI", "Upper Bound PI", "Contained", "future", "Sigma", "Mu"]
)
draws
| 下限 PI | 上限 PI | 包含 | 未来 | Sigma | Mu | |
|---|---|---|---|---|---|---|
| 0 | 9539.612509 | 52724.144855 | 真 | 12721.873679 | 0.436136 | 10.018018 |
| 1 | 11190.287884 | 70193.514908 | 真 | 37002.708820 | 0.468429 | 10.240906 |
| 2 | 12262.816075 | 49883.853578 | 真 | 47419.786326 | 0.357947 | 10.115890 |
| 3 | 10542.933491 | 119175.518677 | 假 | 82191.111953 | 0.618670 | 10.475782 |
| 4 | 9208.478350 | 62352.752208 | 真 | 25393.072528 | 0.487938 | 10.084221 |
| ... | ... | ... | ... | ... | ... | ... |
| 995 | 9591.084003 | 85887.280659 | 真 | 53836.013839 | 0.559245 | 10.264690 |
| 996 | 9724.522689 | 45044.965713 | 真 | 19481.035376 | 0.391081 | 9.948911 |
| 997 | 8385.673724 | 104222.628035 | 真 | 16417.930907 | 0.642870 | 10.294282 |
| 998 | 11034.708453 | 56492.385175 | 真 | 42085.798578 | 0.416605 | 10.125331 |
| 999 | 9408.619310 | 51697.495907 | 真 | 19253.676200 | 0.434647 | 10.001273 |
1000 行 × 6 列
我们可以使用这些引导统计量来进一步计算预测分布的量。 在我们的例子中，我们可以使用参数 CDF 来表示我们的简单参数模型，但我们将在此处采用经验 cdf 来展示当我们有更复杂的模型时如何使用此技术。
def ecdf(sample):
# convert sample to a numpy array, if it isn't already
sample = np.atleast_1d(sample)
# find the unique values and their corresponding counts
quantiles, counts = np.unique(sample, return_counts=True)
# take the cumulative sum of the counts and divide by the sample size to
# get the cumulative probabilities between 0 and 1
cumprob = np.cumsum(counts).astype(np.double) / sample.size
return quantiles, cumprob
fig, axs = plt.subplots(1, 2, figsize=(20, 6))
axs = axs.flatten()
ax = axs[0]
ax1 = axs[1]
hist_data = []
for i in range(1000):
samples = lognorm(s=draws.iloc[i]["Sigma"], scale=np.exp(draws.iloc[i]["Mu"])).rvs(1000)
qe, pe = ecdf(samples)
ax.plot(qe, pe, color="skyblue", alpha=0.2)
lkup = dict(zip(pe, qe))
hist_data.append([lkup[0.05]])
hist_data = pd.DataFrame(hist_data, columns=["p05"])
samples = lognorm(s=draws["Sigma"].mean(), scale=np.exp(draws["Mu"].mean())).rvs(1000)
qe, pe = ecdf(samples)
ax.plot(qe, pe, color="red", label="Expected CDF for Shock Absorbers Data")
ax.set_xlim(0, 30_000)
ax.set_title("Bootstrapped CDF functions for the Shock Absorbers Data", fontsize=20)
ax1.hist(hist_data["p05"], color="slateblue", ec="black", alpha=0.4, bins=30)
ax1.set_title("Estimate of Uncertainty in the 5% Failure Time", fontsize=20)
ax1.axvline(
hist_data["p05"].quantile(0.025), color="cyan", label="Lower Bound CI for 5% failure time"
)
ax1.axvline(
hist_data["p05"].quantile(0.975), color="cyan", label="Upper Bound CI for 5% failure time"
)
ax1.legend()
ax.legend();
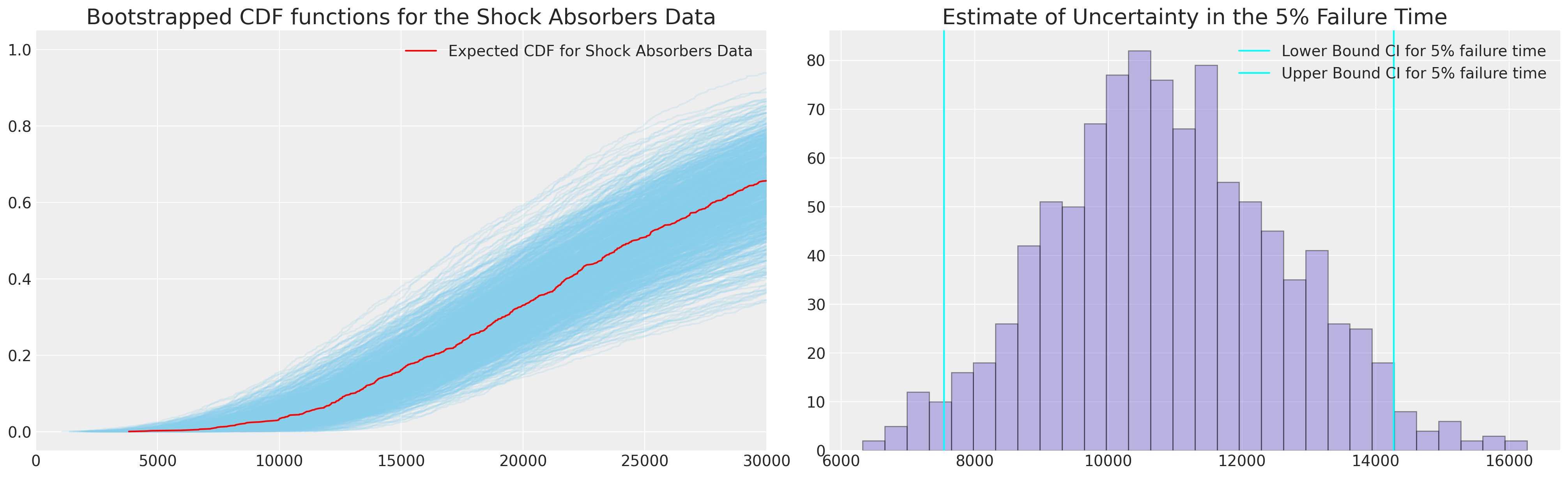
接下来，我们将绘制引导数据以及我们在 MLE 拟合条件下实现的覆盖率的两个估计值。 换句话说，当我们想要评估基于我们的 MLE 拟合的预测区间的覆盖率时，我们还可以引导估计此量。
显示代码单元格源
mosaic = """AABB
CCCC"""
fig, axs = plt.subplot_mosaic(mosaic=mosaic, figsize=(20, 12))
mle_rv = lognorm(s=0.53, scale=np.exp(10.128))
axs = [axs[k] for k in axs.keys()]
axs[0].scatter(
draws["Mu"],
draws["Lower Bound PI"],
c=draws["Contained"],
cmap=cm.cool,
alpha=0.3,
label="Fits in MLE 95% CI",
)
axs[1].scatter(
draws["Sigma"],
draws["Lower Bound PI"],
c=draws["Contained"],
cmap=cm.cool,
alpha=0.3,
label="Fits in MLE 95% CI",
)
axs[0].set_title("Bootstrapped Mu against Bootstrapped 95% Lower Bound")
prop = draws["Contained"].sum() / len(draws)
axs[0].annotate(
f"Estimated Prediction \nEmpirical Coverage \nBased on Sampling : {np.round(prop, 3)}",
xy=(10.4, 12000),
fontweight="bold",
)
axs[1].set_title("Bootstrapped Sigma against Bootstrapped 95% Lower Bound")
axs[0].legend()
axs[0].set_xlabel("Mu")
axs[1].set_xlabel("Sigma")
axs[0].set_ylabel("Estimated Lower 95% PI")
axs[1].legend()
axs[2].hist(
mle_rv.cdf(draws["Lower Bound PI"]),
bins=50,
label="Bootstrap 95% LB",
ec="k",
color="royalblue",
alpha=0.2,
)
axs[2].hist(
mle_rv.cdf(draws["Upper Bound PI"]),
bins=50,
label="Bootstrap 95% UB",
ec="k",
color="darkorchid",
alpha=0.2,
)
axs[2].hist(
np.abs(mle_rv.cdf(draws["Lower Bound PI"]) - mle_rv.cdf(draws["Upper Bound PI"])),
alpha=0.2,
bins=50,
color="slateblue",
ec="black",
label="Bootstrap Abs Diff",
)
axs[2].axvline(
np.abs(mle_rv.cdf(draws["Lower Bound PI"]) - mle_rv.cdf(draws["Upper Bound PI"])).mean(),
label="Expected Coverage",
)
axs[2].set_title("Difference in LB and UB | MLE(mu, sigma)")
axs[2].legend()
plug_in = np.abs(
np.mean(mle_rv.cdf(draws["Lower Bound PI"])) - np.mean(mle_rv.cdf(draws["Upper Bound PI"]))
)
lb = np.round(draws["Lower Bound PI"].mean(), 3)
ub = np.round(draws["Upper Bound PI"].mean(), 3)
axs[2].annotate(
f"Estimated Prediction Interval \n Coverage Based on Plug in Method : {np.round(plug_in, 3)} \n with [{lb, ub}]",
xy=(0.6, 80),
fontweight="bold",
);
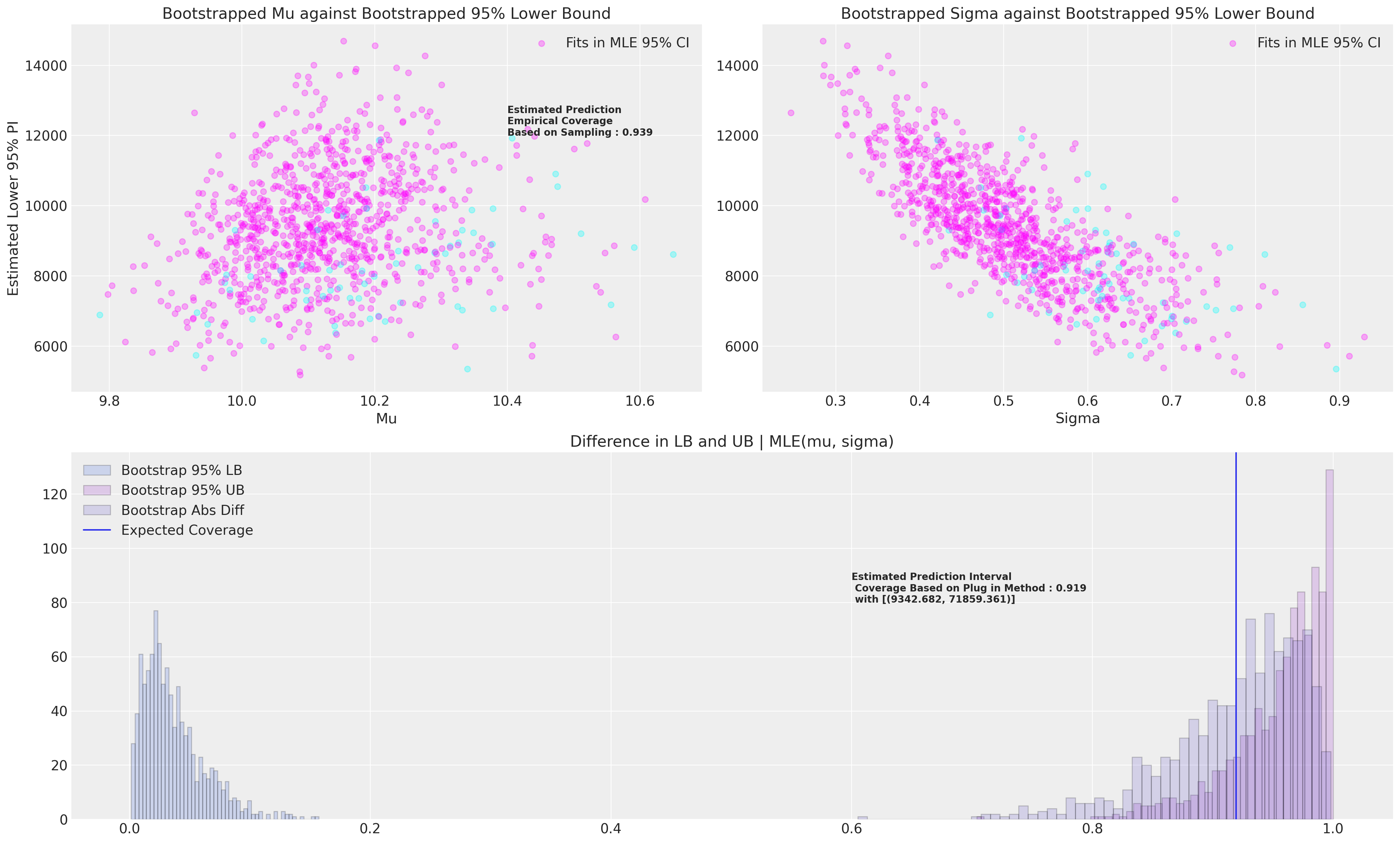
这些模拟应该重复比我们在此处进行的次数多得多的次数。 应该清楚地看到我们如何也可以改变 MLE 区间大小以实现所需的覆盖率水平。
轴承保持器数据：贝叶斯可靠性分析研究#
接下来，我们将查看一个参数拟合稍微不太干净的数据集。 此数据最明显的特征是失效记录的数量很少。 数据以 期间 格式记录，计数显示每期 risk set 的范围。
我们希望花一些时间来研究这个例子，以展示在轴承保持器数据的情况下，如何增强效果良好的 频率学 技术来估计减震器数据。 特别是，我们将展示如何使用 贝叶斯 方法解决出现的问题。
显示代码单元格源
bearing_cage_df = pd.read_csv(
StringIO(
"""Hours,Censoring Indicator,Count
50,Censored,288
150,Censored,148
230,Failed,1
250,Censored,124
334,Failed,1
350,Censored,111
423,Failed,1
450,Censored,106
550,Censored,99
650,Censored,110
750,Censored,114
850,Censored,119
950,Censored,127
990,Failed,1
1009,Failed,1
1050,Censored,123
1150,Censored,93
1250,Censored,47
1350,Censored,41
1450,Censored,27
1510,Failed,1
1550,Censored,11
1650,Censored,6
1850,Censored,1
2050,Censored,2"""
)
)
bearing_cage_df["t"] = bearing_cage_df["Hours"]
bearing_cage_df["failed"] = np.where(bearing_cage_df["Censoring Indicator"] == "Failed", 1, 0)
bearing_cage_df["censored"] = np.where(
bearing_cage_df["Censoring Indicator"] == "Censored", bearing_cage_df["Count"], 0
)
bearing_cage_events = survival_table_from_events(
bearing_cage_df["t"], bearing_cage_df["failed"], weights=bearing_cage_df["Count"]
).reset_index()
bearing_cage_events.rename(
{"event_at": "t", "observed": "failed", "at_risk": "risk_set"}, axis=1, inplace=True
)
actuarial_table_bearings = make_actuarial_table(bearing_cage_events)
actuarial_table_bearings
| t | 已移除 | 已失效 | 截尾数据 | 入口 | 风险集 | p_hat | 1-p_hat | S_hat | CH_hat | F_hat | V_hat | 标准误差 | CI_95_lb | CI_95_ub | plotting_position | logit_CI_95_lb | logit_CI_95_ub | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | 0 | 0 | 0 | 1703 | 1703 | 0.000000 | 1.000000 | 1.000000 | -0.000000 | 0.000000 | 0.000000e+00 | 0.000000 | 0.0 | 0.000000 | 0.000000 | NaN | NaN |
| 1 | 50.0 | 288 | 0 | 288 | 0 | 1703 | 0.000000 | 1.000000 | 1.000000 | -0.000000 | 0.000000 | 0.000000e+00 | 0.000000 | 0.0 | 0.000000 | 0.000000 | NaN | NaN |
| 2 | 150.0 | 148 | 0 | 148 | 0 | 1415 | 0.000000 | 1.000000 | 1.000000 | -0.000000 | 0.000000 | 0.000000e+00 | 0.000000 | 0.0 | 0.000000 | 0.000000 | NaN | NaN |
| 3 | 230.0 | 1 | 1 | 0 | 0 | 1267 | 0.000789 | 0.999211 | 0.999211 | 0.000790 | 0.000789 | 6.224491e-07 | 0.000789 | 0.0 | 0.002336 | 0.000789 | 0.000111 | 0.005581 |
| 4 | 250.0 | 124 | 0 | 124 | 0 | 1266 | 0.000000 | 1.000000 | 0.999211 | 0.000790 | 0.000789 | 6.224491e-07 | 0.000789 | 0.0 | 0.002336 | 0.000789 | 0.000111 | 0.005581 |
| 5 | 334.0 | 1 | 1 | 0 | 0 | 1142 | 0.000876 | 0.999124 | 0.998336 | 0.001666 | 0.001664 | 1.386254e-06 | 0.001177 | 0.0 | 0.003972 | 0.001664 | 0.000415 | 0.006641 |
| 6 | 350.0 | 111 | 0 | 111 | 0 | 1141 | 0.000000 | 1.000000 | 0.998336 | 0.001666 | 0.001664 | 1.386254e-06 | 0.001177 | 0.0 | 0.003972 | 0.001664 | 0.000415 | 0.006641 |
| 7 | 423.0 | 1 | 1 | 0 | 0 | 1030 | 0.000971 | 0.999029 | 0.997367 | 0.002637 | 0.002633 | 2.322113e-06 | 0.001524 | 0.0 | 0.005620 | 0.002633 | 0.000846 | 0.008165 |
| 8 | 450.0 | 106 | 0 | 106 | 0 | 1029 | 0.000000 | 1.000000 | 0.997367 | 0.002637 | 0.002633 | 2.322113e-06 | 0.001524 | 0.0 | 0.005620 | 0.002633 | 0.000846 | 0.008165 |
| 9 | 550.0 | 99 | 0 | 99 | 0 | 923 | 0.000000 | 1.000000 | 0.997367 | 0.002637 | 0.002633 | 2.322113e-06 | 0.001524 | 0.0 | 0.005620 | 0.002633 | 0.000846 | 0.008165 |
| 10 | 650.0 | 110 | 0 | 110 | 0 | 824 | 0.000000 | 1.000000 | 0.997367 | 0.002637 | 0.002633 | 2.322113e-06 | 0.001524 | 0.0 | 0.005620 | 0.002633 | 0.000846 | 0.008165 |
| 11 | 750.0 | 114 | 0 | 114 | 0 | 714 | 0.000000 | 1.000000 | 0.997367 | 0.002637 | 0.002633 | 2.322113e-06 | 0.001524 | 0.0 | 0.005620 | 0.002633 | 0.000846 | 0.008165 |
| 12 | 850.0 | 119 | 0 | 119 | 0 | 600 | 0.000000 | 1.000000 | 0.997367 | 0.002637 | 0.002633 | 2.322113e-06 | 0.001524 | 0.0 | 0.005620 | 0.002633 | 0.000846 | 0.008165 |
| 13 | 950.0 | 127 | 0 | 127 | 0 | 481 | 0.000000 | 1.000000 | 0.997367 | 0.002637 | 0.002633 | 2.322113e-06 | 0.001524 | 0.0 | 0.005620 | 0.002633 | 0.000846 | 0.008165 |
| 14 | 990.0 | 1 | 1 | 0 | 0 | 354 | 0.002825 | 0.997175 | 0.994549 | 0.005466 | 0.005451 | 1.022444e-05 | 0.003198 | 0.0 | 0.011718 | 0.005451 | 0.001722 | 0.017117 |
| 15 | 1009.0 | 1 | 1 | 0 | 0 | 353 | 0.002833 | 0.997167 | 0.991732 | 0.008303 | 0.008268 | 1.808196e-05 | 0.004252 | 0.0 | 0.016603 | 0.008268 | 0.003008 | 0.022519 |
| 16 | 1050.0 | 123 | 0 | 123 | 0 | 352 | 0.000000 | 1.000000 | 0.991732 | 0.008303 | 0.008268 | 1.808196e-05 | 0.004252 | 0.0 | 0.016603 | 0.008268 | 0.003008 | 0.022519 |
| 17 | 1150.0 | 93 | 0 | 93 | 0 | 229 | 0.000000 | 1.000000 | 0.991732 | 0.008303 | 0.008268 | 1.808196e-05 | 0.004252 | 0.0 | 0.016603 | 0.008268 | 0.003008 | 0.022519 |
| 18 | 1250.0 | 47 | 0 | 47 | 0 | 136 | 0.000000 | 1.000000 | 0.991732 | 0.008303 | 0.008268 | 1.808196e-05 | 0.004252 | 0.0 | 0.016603 | 0.008268 | 0.003008 | 0.022519 |
| 19 | 1350.0 | 41 | 0 | 41 | 0 | 89 | 0.000000 | 1.000000 | 0.991732 | 0.008303 | 0.008268 | 1.808196e-05 | 0.004252 | 0.0 | 0.016603 | 0.008268 | 0.003008 | 0.022519 |
| 20 | 1450.0 | 27 | 0 | 27 | 0 | 48 | 0.000000 | 1.000000 | 0.991732 | 0.008303 | 0.008268 | 1.808196e-05 | 0.004252 | 0.0 | 0.016603 | 0.008268 | 0.003008 | 0.022519 |
| 21 | 1510.0 | 1 | 1 | 0 | 0 | 21 | 0.047619 | 0.952381 | 0.944506 | 0.057093 | 0.055494 | 2.140430e-03 | 0.046265 | 0.0 | 0.146173 | 0.055494 | 0.010308 | 0.248927 |
| 22 | 1550.0 | 11 | 0 | 11 | 0 | 20 | 0.000000 | 1.000000 | 0.944506 | 0.057093 | 0.055494 | 2.140430e-03 | 0.046265 | 0.0 | 0.146173 | 0.055494 | 0.010308 | 0.248927 |
| 23 | 1650.0 | 6 | 0 | 6 | 0 | 9 | 0.000000 | 1.000000 | 0.944506 | 0.057093 | 0.055494 | 2.140430e-03 | 0.046265 | 0.0 | 0.146173 | 0.055494 | 0.010308 | 0.248927 |
| 24 | 1850.0 | 1 | 0 | 1 | 0 | 3 | 0.000000 | 1.000000 | 0.944506 | 0.057093 | 0.055494 | 2.140430e-03 | 0.046265 | 0.0 | 0.146173 | 0.055494 | 0.010308 | 0.248927 |
| 25 | 2050.0 | 2 | 0 | 2 | 0 | 2 | 0.000000 | 1.000000 | 0.944506 | 0.057093 | 0.055494 | 2.140430e-03 | 0.046265 | 0.0 | 0.146173 | 0.055494 | 0.010308 | 0.248927 |
为了估计单变量或非参数 CDF，我们需要将 期间 格式数据分解为 项目-期间 格式。
项目期间数据格式#
item_period = bearing_cage_df["Hours"].to_list() * bearing_cage_df["Count"].sum()
ids = [[i] * 25 for i in range(bearing_cage_df["Count"].sum())]
ids = [int(i) for l in ids for i in l]
item_period_bearing_cage = pd.DataFrame(item_period, columns=["t"])
item_period_bearing_cage["id"] = ids
item_period_bearing_cage["failed"] = np.zeros(len(item_period_bearing_cage))
## Censor appropriate number of ids
unique_ids = item_period_bearing_cage["id"].unique()
censored = bearing_cage_df[bearing_cage_df["Censoring Indicator"] == "Censored"]
i = 0
stack = []
for hour, count, idx in zip(censored["Hours"], censored["Count"], censored["Count"].cumsum()):
temp = item_period_bearing_cage[
item_period_bearing_cage["id"].isin(unique_ids[i:idx])
& (item_period_bearing_cage["t"] == hour)
]
stack.append(temp)
i = idx
censored_clean = pd.concat(stack)
### Add appropriate number of failings
stack = []
unique_times = censored_clean["t"].unique()
for id, fail_time in zip(
[9999, 9998, 9997, 9996, 9995, 9994],
bearing_cage_df[bearing_cage_df["failed"] == 1]["t"].values,
):
temp = pd.DataFrame(unique_times[unique_times < fail_time], columns=["t"])
temp["id"] = id
temp["failed"] = 0
temp = pd.concat([temp, pd.DataFrame({"t": [fail_time], "id": [id], "failed": [1]}, index=[0])])
stack.append(temp)
failed_clean = pd.concat(stack).sort_values(["id", "t"])
censored_clean
item_period_bearing_cage = pd.concat([failed_clean, censored_clean])
## Transpose for more concise visual
item_period_bearing_cage.head(30).T
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ... | 4 | 5 | 6 | 7 | 8 | 9 | 0 | 0 | 1 | 2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| t | 50.0 | 150.0 | 250.0 | 350.0 | 450.0 | 550.0 | 650.0 | 750.0 | 850.0 | 950.0 | ... | 450.0 | 550.0 | 650.0 | 750.0 | 850.0 | 950.0 | 1009.0 | 50.0 | 150.0 | 250.0 |
| ID | 9994.0 | 9994.0 | 9994.0 | 9994.0 | 9994.0 | 9994.0 | 9994.0 | 9994.0 | 9994.0 | 9994.0 | ... | 9995.0 | 9995.0 | 9995.0 | 9995.0 | 9995.0 | 9995.0 | 9995.0 | 9996.0 | 9996.0 | 9996.0 |
| 已失效 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
3 行 × 30 列
assert item_period_bearing_cage["id"].nunique() == 1703
assert item_period_bearing_cage["failed"].sum() == 6
assert item_period_bearing_cage[item_period_bearing_cage["t"] >= 1850]["id"].nunique() == 3
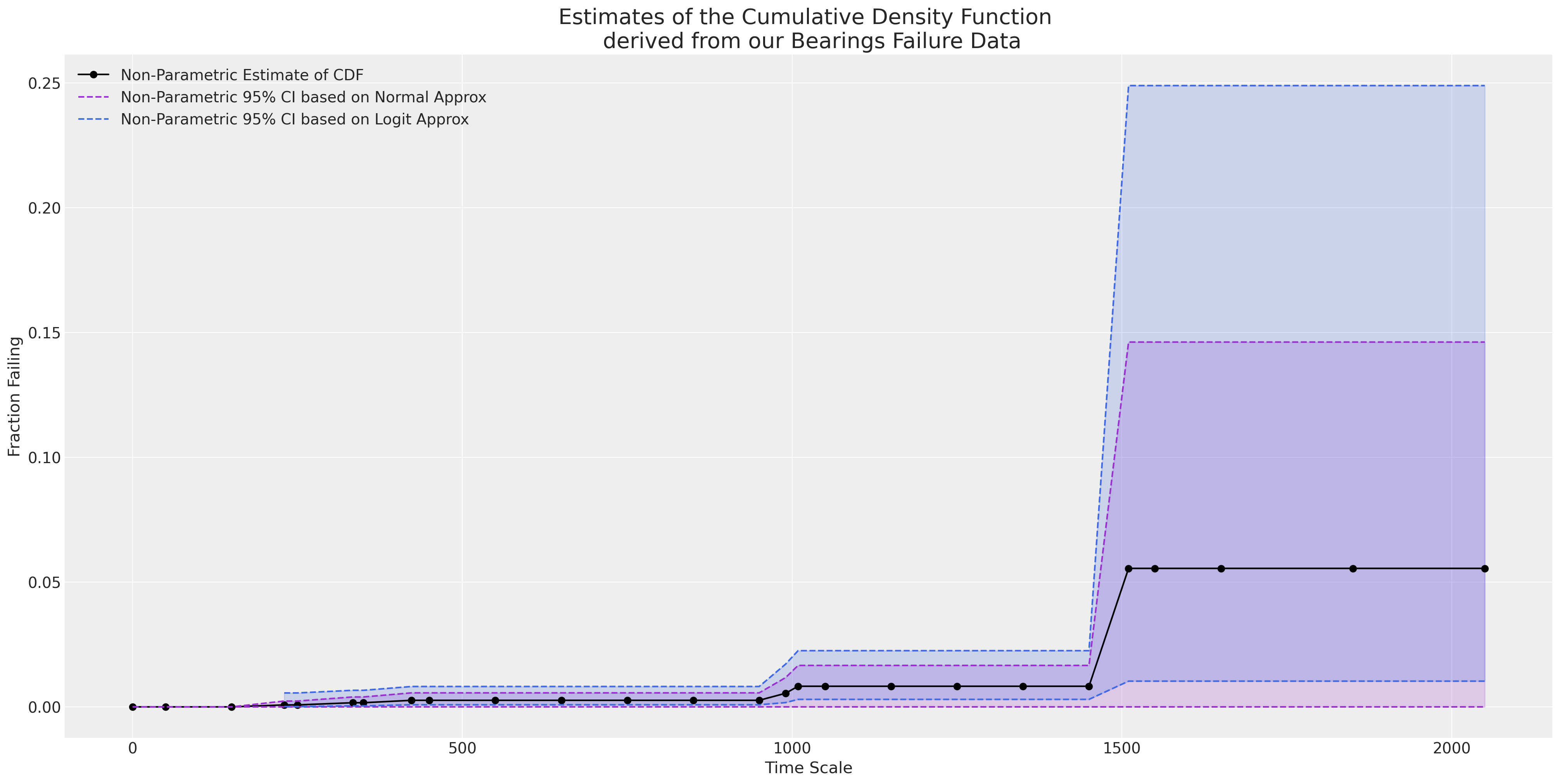
当我们绘制经验 CDF 时，我们看到 y 轴的最大高度仅达到 0.05。 天真的 MLE 拟合在推断超出观察到的数据范围时会严重错误。
ax = plot_cdfs(
actuarial_table_bearings,
title="Bearings",
dist_fits=False,
xy=(20, 0.7),
item_period=item_period_bearing_cage,
)
概率图：在受限线性范围内比较 CDF#
在本节中，我们将使用线性化 MLE 拟合的技术，以便可以执行目视“拟合优度”检查。 这些类型的图依赖于可以应用于位置和尺度分布的转换，以将其 CDF 转换为线性空间。
对于对数正态拟合和威布尔拟合，我们都可以在线性空间中将其 CDF 表示为对数 t 值与适当的 \(CDF^{-1}\) 之间的关系。
显示代码单元格源
def sev_ppf(p):
return np.log(-np.log(1 - p))
mosaic = """AABB
CCCC"""
fig, axs = plt.subplot_mosaic(mosaic=mosaic, figsize=(20, 15))
axs = [axs[k] for k in axs.keys()]
ax = axs[0]
ax2 = axs[1]
ax3 = axs[2]
ax.plot(
np.log(actuarial_table_bearings["t"]),
norm.ppf(actuarial_table_bearings["logit_CI_95_ub"]),
"-o",
label="Non-Parametric CI UB",
color="slateblue",
)
ax.scatter(
np.log(actuarial_table_bearings["t"]),
norm.ppf(actuarial_table_bearings["plotting_position"]),
label="Non-Parametric CDF",
color="black",
)
ax.plot(
np.log(actuarial_table_bearings["t"]),
norm.ppf(actuarial_table_bearings["logit_CI_95_lb"]),
"-o",
label="Non-Parametric CI LB",
color="slateblue",
)
for mu in np.linspace(10, 12, 3):
for sigma in np.linspace(1.6, 1.9, 3):
rv = lognorm(s=sigma, scale=np.exp(mu))
ax.plot(
np.log(actuarial_table_bearings["t"]),
norm.ppf(rv.cdf(actuarial_table_bearings["t"])),
"--",
label=f"LN({np.round(mu, 3)}, {np.round(sigma, 3)})",
color="grey",
)
lnf = LogNormalFitter().fit(item_period_bearing_cage["t"], item_period_bearing_cage["failed"])
rv = lognorm(s=lnf.sigma_, scale=np.exp(lnf.mu_))
ax.plot(
np.log(actuarial_table_bearings["t"]),
norm.ppf(rv.cdf(actuarial_table_bearings["t"])),
"--",
label=f"MLE LN({np.round(lnf.mu_, 3)}, {np.round(lnf.sigma_, 3)})",
color="RED",
)
for r in np.linspace(1, 2, 3):
for s in np.linspace(12000, 25000, 2):
rv = weibull_min(c=r, scale=s)
ax2.plot(
np.log(actuarial_table_bearings["t"]),
sev_ppf(rv.cdf(actuarial_table_bearings["t"])),
"--",
label=f"Wb({np.round(s, 3)}, {np.round(r, 3)})",
color="lightblue",
)
wbf = WeibullFitter().fit(item_period_bearing_cage["t"], item_period_bearing_cage["failed"])
rv = weibull_min(c=wbf.rho_, scale=wbf.lambda_)
ax2.plot(
np.log(actuarial_table_bearings["t"]),
sev_ppf(rv.cdf(actuarial_table_bearings["t"])),
"--",
label=f"MLE Wb({np.round(wbf.lambda_, 3)}, {np.round(wbf.rho_, 3)})",
color="red",
)
ax2.plot(
np.log(actuarial_table_bearings["t"]),
sev_ppf(actuarial_table_bearings["logit_CI_95_ub"]),
"-o",
label="Non-Parametric CI UB",
color="slateblue",
)
ax2.scatter(
np.log(actuarial_table_bearings["t"]),
sev_ppf(actuarial_table_bearings["plotting_position"]),
label="Non-Parametric CDF",
color="black",
)
ax2.plot(
np.log(actuarial_table_bearings["t"]),
sev_ppf(actuarial_table_bearings["logit_CI_95_lb"]),
"-o",
label="Non-Parametric CI LB",
color="slateblue",
)
ax3.plot(
actuarial_table_bearings["t"],
actuarial_table_bearings["logit_CI_95_ub"],
"-o",
label="Non-Parametric CI UB",
color="slateblue",
)
ax3.scatter(
actuarial_table_bearings["t"],
actuarial_table_bearings["F_hat"],
label="Non-Parametric CDF",
color="black",
)
ax3.plot(
actuarial_table_bearings["t"],
actuarial_table_bearings["logit_CI_95_lb"],
"-o",
label="Non-Parametric CI LB",
color="slateblue",
)
lnf.plot_cumulative_density(ax=ax3, color="cyan")
wbf.plot_cumulative_density(ax=ax3, color="darkorchid")
ax2.set_title("Linearizing the Weibull CDF", fontsize=20)
ax.set_title("Linearizing the Lognormal CDF", fontsize=20)
ax3.set_title("MLE CDF Fits", fontsize=20)
ax.legend()
ax.set_xlabel("Time")
ax2.set_xlabel("Time")
xticks = np.round(np.linspace(0, actuarial_table_bearings["t"].max(), 10), 1)
yticks = np.round(np.linspace(0, actuarial_table_bearings["F_hat"].max(), 10), 4)
ax.set_xticklabels(xticks)
ax.set_yticklabels(yticks)
ax2.set_xticklabels(xticks)
ax2.set_yticklabels([])
ax2.legend()
ax.set_ylabel("Fraction Failing");
/home/oriol/bin/miniconda3/envs/releases/lib/python3.10/site-packages/pandas/core/arraylike.py:402: RuntimeWarning: divide by zero encountered in log
result = getattr(ufunc, method)(*inputs, **kwargs)
/home/oriol/bin/miniconda3/envs/releases/lib/python3.10/site-packages/pandas/core/arraylike.py:402: RuntimeWarning: divide by zero encountered in log
result = getattr(ufunc, method)(*inputs, **kwargs)
/tmp/ipykernel_29435/2628457585.py:2: RuntimeWarning: divide by zero encountered in log
return np.log(-np.log(1 - p))
/home/oriol/bin/miniconda3/envs/releases/lib/python3.10/site-packages/pandas/core/arraylike.py:402: RuntimeWarning: divide by zero encountered in log
result = getattr(ufunc, method)(*inputs, **kwargs)
/tmp/ipykernel_29435/2628457585.py:2: RuntimeWarning: divide by zero encountered in log
return np.log(-np.log(1 - p))
/tmp/ipykernel_29435/2628457585.py:128: UserWarning: FixedFormatter should only be used together with FixedLocator
ax.set_xticklabels(xticks)
/tmp/ipykernel_29435/2628457585.py:129: UserWarning: FixedFormatter should only be used together with FixedLocator
ax.set_yticklabels(yticks)
/tmp/ipykernel_29435/2628457585.py:130: UserWarning: FixedFormatter should only be used together with FixedLocator
ax2.set_xticklabels(xticks)
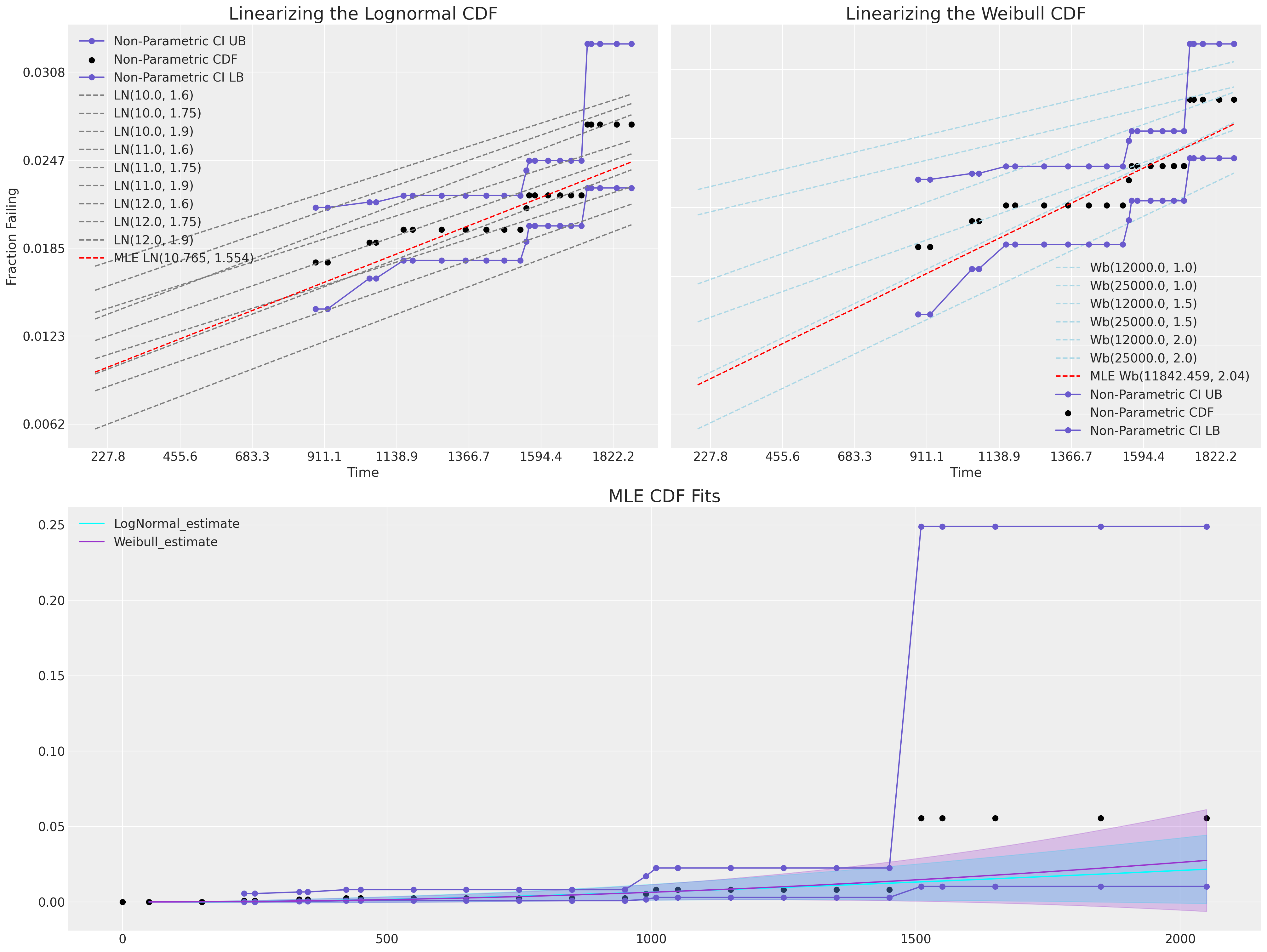
我们可以在这里看到，MLE 拟合都无法覆盖观察到的数据范围。
可靠性数据的贝叶斯建模#
我们现在已经了解了如何使用频率学或 MLE 框架对稀疏可靠性的参数模型拟合进行建模和可视化。 我们现在想展示如何在贝叶斯范例中实现相同风格的推断。
与 MLE 范例一样，我们需要对删失似然性进行建模。 对于我们上面看到的大多数对数位置分布，似然性表示为分布 pdf \(\phi\) 和 cdf \(\Phi\) 的组合函数，具体取决于数据点是否在时间窗口中被完全观察到或被删失，并适当应用。
\[ L(\mu, \sigma) = \prod_{i = 1}^{n} \Bigg(\dfrac{1}{\sigma t_{i}} \phi\Bigg[ \dfrac{log(t_{i}) - \mu}{\sigma} \Bigg] \Bigg)^{\delta_{i}} \cdot \Bigg(1 - \Phi \Bigg[ \dfrac{log(t_{i}) - \mu}{\sigma} \Bigg] \Bigg)^{1-\delta}\]
其中 \(\delta_{i}\) 是指示观测值是失效还是右删失观测值的指示符。 更复杂的删失类型可以通过对 CDF 进行类似的修改来包含，具体取决于删失观测值的性质。
威布尔生存的直接 PYMC 实现#
我们拟合了此模型的两个版本，先验规范不同，一个在数据上采用 模糊 均匀先验，另一个指定更接近 MLE 拟合的先验。 我们将在下面展示先验规范对模型与观察数据的校准的影响。
def weibull_lccdf(y, alpha, beta):
"""Log complementary cdf of Weibull distribution."""
return -((y / beta) ** alpha)
item_period_max = item_period_bearing_cage.groupby("id")[["t", "failed"]].max()
y = item_period_max["t"].values
censored = ~item_period_max["failed"].values.astype(bool)
priors = {"beta": [100, 15_000], "alpha": [4, 1, 0.02, 8]}
priors_informative = {"beta": [10_000, 500], "alpha": [2, 0.5, 0.02, 3]}
def make_model(p, info=False):
with pm.Model() as model:
if info:
beta = pm.Normal("beta", p["beta"][0], p["beta"][1])
else:
beta = pm.Uniform("beta", p["beta"][0], p["beta"][1])
alpha = pm.TruncatedNormal(
"alpha", p["alpha"][0], p["alpha"][1], lower=p["alpha"][2], upper=p["alpha"][3]
)
y_obs = pm.Weibull("y_obs", alpha=alpha, beta=beta, observed=y[~censored])
y_cens = pm.Potential("y_cens", weibull_lccdf(y[censored], alpha, beta))
idata = pm.sample_prior_predictive()
idata.extend(pm.sample(random_seed=100, target_accept=0.95))
idata.extend(pm.sample_posterior_predictive(idata))
return idata, model
idata, model = make_model(priors)
idata_informative, model = make_model(priors_informative, info=True)
/tmp/ipykernel_29435/305144286.py:28: UserWarning: The effect of Potentials on other parameters is ignored during prior predictive sampling. This is likely to lead to invalid or biased predictive samples.
idata = pm.sample_prior_predictive()
Sampling: [alpha, beta, y_obs]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [beta, alpha]
100.00% [8000/8000 00:06<00:00 采样 4 条链，1 个偏差]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 6 seconds.
/tmp/ipykernel_29435/305144286.py:30: UserWarning: The effect of Potentials on other parameters is ignored during posterior predictive sampling. This is likely to lead to invalid or biased predictive samples.
idata.extend(pm.sample_posterior_predictive(idata))
Sampling: [y_obs]
100.00% [4000/4000 00:00<00:00]
/tmp/ipykernel_29435/305144286.py:28: UserWarning: The effect of Potentials on other parameters is ignored during prior predictive sampling. This is likely to lead to invalid or biased predictive samples.
idata = pm.sample_prior_predictive()
Sampling: [alpha, beta, y_obs]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [beta, alpha]
100.00% [8000/8000 00:06<00:00 采样 4 条链，0 个偏差]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 6 seconds.
/tmp/ipykernel_29435/305144286.py:30: UserWarning: The effect of Potentials on other parameters is ignored during posterior predictive sampling. This is likely to lead to invalid or biased predictive samples.
idata.extend(pm.sample_posterior_predictive(idata))
Sampling: [y_obs]
100.00% [4000/4000 00:00<00:00]
idata
arviz.InferenceData
-
<xarray.Dataset> Dimensions: (chain: 4, draw: 1000) Coordinates: * chain (chain) int64 0 1 2 3 * draw (draw) int64 0 1 2 3 4 5 6 7 8 ... 992 993 994 995 996 997 998 999 Data variables: beta (chain, draw) float64 7.427e+03 8.514e+03 ... 1.013e+04 5.044e+03 alpha (chain, draw) float64 2.232 2.385 2.49 2.55 ... 2.437 2.503 2.898 Attributes: created_at: 2023-01-15T20:06:41.169437 arviz_version: 0.13.0 inference_library: pymc inference_library_version: 5.0.0 sampling_time: 6.423727989196777 tuning_steps: 1000 -
<xarray.Dataset> Dimensions: (chain: 4, draw: 1000, y_obs_dim_2: 6) Coordinates: * chain (chain) int64 0 1 2 3 * draw (draw) int64 0 1 2 3 4 5 6 7 ... 993 994 995 996 997 998 999 * y_obs_dim_2 (y_obs_dim_2) int64 0 1 2 3 4 5 Data variables: y_obs (chain, draw, y_obs_dim_2) float64 6.406e+03 ... 5.59e+03 Attributes: created_at: 2023-01-15T20:06:42.789072 arviz_version: 0.13.0 inference_library: pymc inference_library_version: 5.0.0 -
<xarray.Dataset> Dimensions: (chain: 4, draw: 1000) Coordinates: * chain (chain) int64 0 1 2 3 * draw (draw) int64 0 1 2 3 4 5 ... 994 995 996 997 998 999 Data variables: (12/17) perf_counter_diff (chain, draw) float64 0.0008238 ... 0.002601 n_steps (chain, draw) float64 3.0 3.0 7.0 ... 11.0 7.0 9.0 acceptance_rate (chain, draw) float64 0.9404 1.0 ... 0.9876 0.9424 smallest_eigval (chain, draw) float64 nan nan nan nan ... nan nan nan largest_eigval (chain, draw) float64 nan nan nan nan ... nan nan nan lp (chain, draw) float64 -80.96 -79.7 ... -81.05 -79.99 ... ... step_size_bar (chain, draw) float64 0.1791 0.1791 ... 0.1591 0.1591 reached_max_treedepth (chain, draw) bool False False False ... False False diverging (chain, draw) bool False False False ... False False process_time_diff (chain, draw) float64 0.0008239 ... 0.002601 index_in_trajectory (chain, draw) int64 -2 2 -3 -2 2 -2 ... -2 -1 -3 1 -6 perf_counter_start (chain, draw) float64 1.153e+04 ... 1.153e+04 Attributes: created_at: 2023-01-15T20:06:41.180463 arviz_version: 0.13.0 inference_library: pymc inference_library_version: 5.0.0 sampling_time: 6.423727989196777 tuning_steps: 1000 -
<xarray.Dataset> Dimensions: (chain: 1, draw: 500) Coordinates: * chain (chain) int64 0 * draw (draw) int64 0 1 2 3 4 5 6 7 8 ... 492 493 494 495 496 497 498 499 Data variables: alpha (chain, draw) float64 3.896 5.607 4.329 5.377 ... 3.828 4.875 3.723 beta (chain, draw) float64 6.915e+03 1.293e+04 ... 6.599e+03 1.244e+04 Attributes: created_at: 2023-01-15T20:06:29.497052 arviz_version: 0.13.0 inference_library: pymc inference_library_version: 5.0.0 -
<xarray.Dataset> Dimensions: (chain: 1, draw: 500, y_obs_dim_0: 6) Coordinates: * chain (chain) int64 0 * draw (draw) int64 0 1 2 3 4 5 6 7 ... 493 494 495 496 497 498 499 * y_obs_dim_0 (y_obs_dim_0) int64 0 1 2 3 4 5 Data variables: y_obs (chain, draw, y_obs_dim_0) float64 6.422e+03 ... 1.476e+04 Attributes: created_at: 2023-01-15T20:06:29.500007 arviz_version: 0.13.0 inference_library: pymc inference_library_version: 5.0.0 -
<xarray.Dataset> Dimensions: (y_obs_dim_0: 6) Coordinates: * y_obs_dim_0 (y_obs_dim_0) int64 0 1 2 3 4 5 Data variables: y_obs (y_obs_dim_0) float64 1.51e+03 1.009e+03 990.0 ... 334.0 230.0 Attributes: created_at: 2023-01-15T20:06:29.501343 arviz_version: 0.13.0 inference_library: pymc inference_library_version: 5.0.0
az.plot_trace(idata, kind="rank_vlines");
az.plot_trace(idata_informative, kind="rank_vlines");
az.summary(idata)
| 均值 | 标准差 | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| beta | 8149.835 | 2916.378 | 3479.929 | 13787.447 | 111.293 | 78.729 | 612.0 | 371.0 | 1.01 |
| alpha | 2.626 | 0.558 | 1.779 | 3.631 | 0.030 | 0.025 | 616.0 | 353.0 | 1.01 |
az.summary(idata_informative)
| 均值 | 标准差 | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| beta | 10031.200 | 491.768 | 9110.601 | 10975.705 | 10.891 | 7.742 | 2045.0 | 1940.0 | 1.0 |
| alpha | 2.181 | 0.166 | 1.875 | 2.487 | 0.004 | 0.003 | 2240.0 | 1758.0 | 1.0 |
joint_draws = az.extract(idata, num_samples=1000)[["alpha", "beta"]]
alphas = joint_draws["alpha"].values
betas = joint_draws["beta"].values
joint_draws_informative = az.extract(idata_informative, num_samples=1000)[["alpha", "beta"]]
alphas_informative = joint_draws_informative["alpha"].values
betas_informative = joint_draws_informative["beta"].values
mosaic = """AAAA
BBCC"""
fig, axs = plt.subplot_mosaic(mosaic=mosaic, figsize=(20, 13))
axs = [axs[k] for k in axs.keys()]
ax = axs[0]
ax1 = axs[2]
ax2 = axs[1]
hist_data = []
for i in range(1000):
draws = pm.draw(pm.Weibull.dist(alpha=alphas[i], beta=betas[i]), 1000)
qe, pe = ecdf(draws)
lkup = dict(zip(pe, qe))
hist_data.append([lkup[0.1], lkup[0.05]])
ax.plot(qe, pe, color="slateblue", alpha=0.1)
hist_data_info = []
for i in range(1000):
draws = pm.draw(pm.Weibull.dist(alpha=alphas_informative[i], beta=betas_informative[i]), 1000)
qe, pe = ecdf(draws)
lkup = dict(zip(pe, qe))
hist_data_info.append([lkup[0.1], lkup[0.05]])
ax.plot(qe, pe, color="pink", alpha=0.1)
hist_data = pd.DataFrame(hist_data, columns=["p10", "p05"])
hist_data_info = pd.DataFrame(hist_data_info, columns=["p10", "p05"])
draws = pm.draw(pm.Weibull.dist(alpha=np.mean(alphas), beta=np.mean(betas)), 1000)
qe, pe = ecdf(draws)
ax.plot(qe, pe, color="purple", label="Expected CDF Uninformative Prior")
draws = pm.draw(
pm.Weibull.dist(alpha=np.mean(alphas_informative), beta=np.mean(betas_informative)), 1000
)
qe, pe = ecdf(draws)
ax.plot(qe, pe, color="magenta", label="Expected CDF Informative Prior")
ax.plot(
actuarial_table_bearings["t"],
actuarial_table_bearings["logit_CI_95_ub"],
"--",
label="Non-Parametric CI UB",
color="black",
)
ax.plot(
actuarial_table_bearings["t"],
actuarial_table_bearings["F_hat"],
"-o",
label="Non-Parametric CDF",
color="black",
alpha=1,
)
ax.plot(
actuarial_table_bearings["t"],
actuarial_table_bearings["logit_CI_95_lb"],
"--",
label="Non-Parametric CI LB",
color="black",
)
ax.set_xlim(0, 2500)
ax.set_title(
"Bayesian Estimation of Uncertainty in the Posterior Predictive CDF \n Informative and Non-Informative Priors",
fontsize=20,
)
ax.set_ylabel("Fraction Failing")
ax.set_xlabel("Time")
ax1.hist(
hist_data["p10"], bins=30, ec="black", color="skyblue", alpha=0.4, label="Uninformative Prior"
)
ax1.hist(
hist_data_info["p10"],
bins=30,
ec="black",
color="slateblue",
alpha=0.4,
label="Informative Prior",
)
ax1.set_title("Distribution of 10% failure Time", fontsize=20)
ax1.legend()
ax2.hist(
hist_data["p05"], bins=30, ec="black", color="cyan", alpha=0.4, label="Uninformative Prior"
)
ax2.hist(
hist_data_info["p05"], bins=30, ec="black", color="pink", alpha=0.4, label="Informative Prior"
)
ax2.legend()
ax2.set_title("Distribution of 5% failure Time", fontsize=20)
wbf = WeibullFitter().fit(item_period_bearing_cage["t"] + 1e-25, item_period_bearing_cage["failed"])
wbf.plot_cumulative_density(ax=ax, color="cyan", label="Weibull MLE Fit")
ax.legend()
ax.set_ylim(0, 0.25);
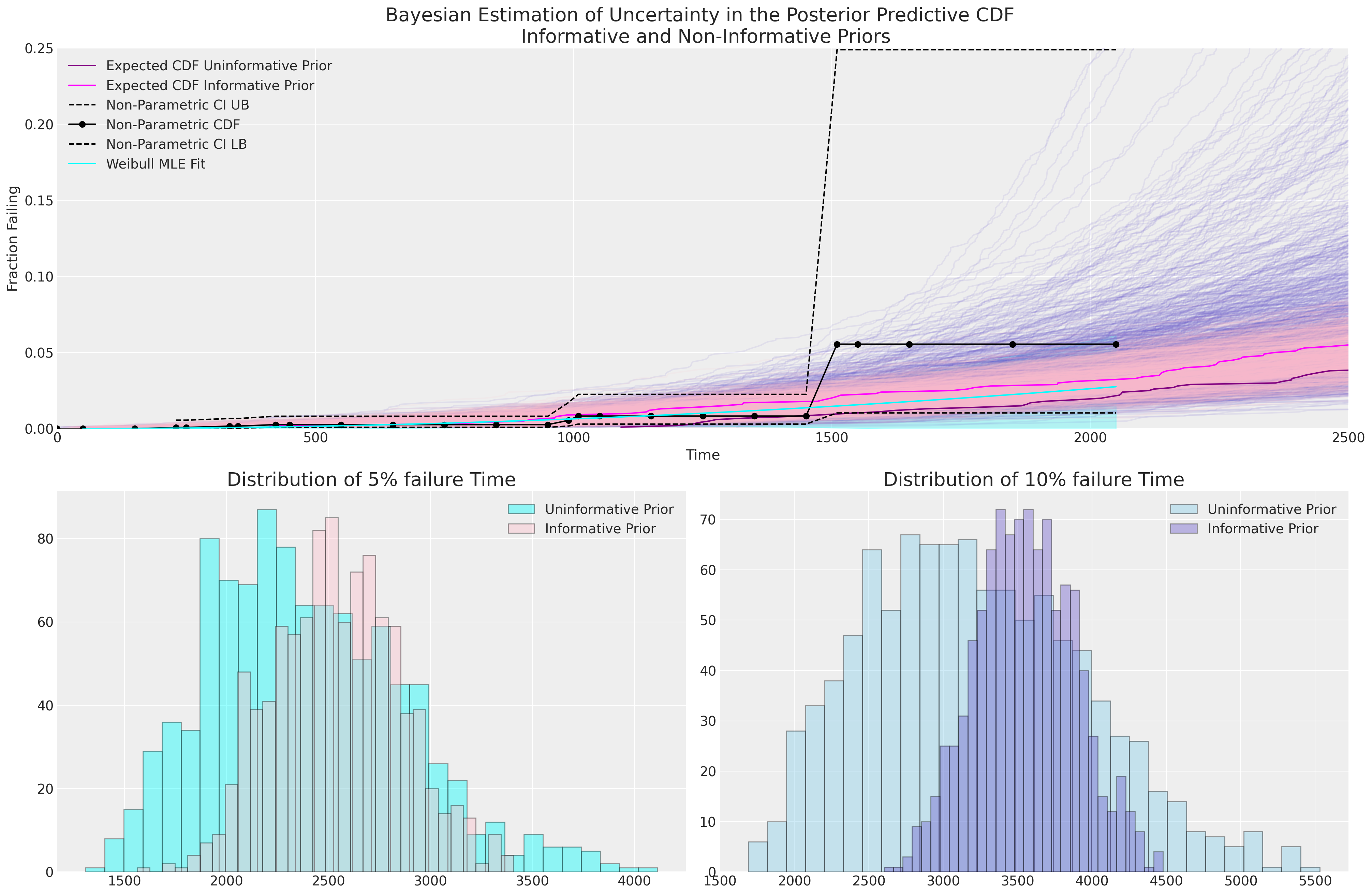
我们可以在这里看到，由我们刻意模糊的先验驱动的贝叶斯不确定性估计比我们的 MLE 拟合包含更多的不确定性，并且信息量不足的先验意味着 5% 和 10% 失效时间的更广泛的预测分布。 具有信息量不足的先验的贝叶斯模型似乎在捕获我们的 CDF 非参数估计中的不确定性方面做得更好，但如果没有更多信息，很难判断哪个模型更合适。
每个模型拟合的随时间推移的失效百分比的具体估计值在数据稀疏的情况下尤其重要。 我们可以咨询主题专家，了解其产品的 10% 失效时间的预期和范围是否合理，这是一种有意义的理智检查。
预测区间内的失效次数#
由于我们关于观察到的失效数据非常稀疏，因此我们必须非常小心地推断超出观察到的时间范围，但我们可以询问关于 cdf 下尾可预测的失效次数。 这提供了对此数据的另一种看法，可能有助于与主题事项专家进行讨论。
插件估计#
假设我们想知道基于服务 150 到 600 小时之间的失效轴承数量。 我们可以根据估计的 CDF 和未来新轴承的数量来计算这一点。 我们首先计算
\[ \hat{\rho} = \dfrac{\hat{F}(t_1) - \hat{F}(t_0)}{1 - \hat{F}(t_0)} \]
以建立区间内发生失效的概率，然后区间内失效次数的点预测由 risk_set*\(\hat{\rho}\) 给出。
mle_fit = weibull_min(c=2, scale=10_000)
rho = mle_fit.cdf(600) - mle_fit.cdf(150) / (1 - mle_fit.cdf(150))
print("Rho:", rho)
print("N at Risk:", 1700)
print("Expected Number Failing in between 150 and 600 hours:", 1700 * rho)
print("Lower Bound 95% PI :", binom(1700, rho).ppf(0.05))
print("Upper Bound 95% PI:", binom(1700, rho).ppf(0.95))
Rho: 0.0033685024546080927
N at Risk: 1700
Expected Number Failing in between 150 and 600 hours: 5.7264541728337575
Lower Bound 95% PI : 2.0
Upper Bound 95% PI: 10.0
在贝叶斯后验上应用相同的程序#
我们将使用信息量不足模型的后验预测分布。 我们在这里展示了如何推导出时间间隔内失效次数的 95% 预测区间估计中的不确定性。 正如我们在上面看到的，此过程的 MLE 替代方案是从 bootstrap 抽样生成预测分布。 bootstrap 程序倾向于与使用 MLE 估计的插件程序一致，并且缺乏指定先验信息的灵活性。
import xarray as xr
from xarray_einstats.stats import XrContinuousRV, XrDiscreteRV
def PI_failures(joint_draws, lp, up, n_at_risk):
fit = XrContinuousRV(weibull_min, joint_draws["alpha"], scale=joint_draws["beta"])
rho = fit.cdf(up) - fit.cdf(lp) / (1 - fit.cdf(lp))
lub = XrDiscreteRV(binom, n_at_risk, rho).ppf([0.05, 0.95])
lb, ub = lub.sel(quantile=0.05, drop=True), lub.sel(quantile=0.95, drop=True)
point_prediction = n_at_risk * rho
return xr.Dataset(
{"rho": rho, "n_at_risk": n_at_risk, "lb": lb, "ub": ub, "expected": point_prediction}
)
output_ds = PI_failures(joint_draws, 150, 600, 1700)
output_ds
<xarray.Dataset>
Dimensions: (sample: 1000)
Coordinates:
* sample (sample) object MultiIndex
* chain (sample) int64 1 0 0 0 2 1 1 2 1 3 0 2 ... 1 3 2 3 0 1 3 3 0 1 2
* draw (sample) int64 776 334 531 469 19 675 ... 437 470 242 662 316 63
Data variables:
rho (sample) float64 0.0007735 0.004392 ... 0.001465 0.001462
n_at_risk int64 1700
lb (sample) float64 0.0 3.0 0.0 0.0 0.0 1.0 ... 0.0 1.0 0.0 0.0 0.0
ub (sample) float64 3.0 12.0 5.0 5.0 4.0 7.0 ... 5.0 7.0 6.0 5.0 5.0
expected (sample) float64 1.315 7.466 2.24 2.518 ... 2.835 2.491 2.486def cost_func(failures, power):
### Imagined cost function for failing item e.g. refunds required
return np.power(failures, power)
mosaic = """AAAA
BBCC"""
fig, axs = plt.subplot_mosaic(mosaic=mosaic, figsize=(20, 12))
axs = [axs[k] for k in axs.keys()]
ax = axs[0]
ax1 = axs[1]
ax2 = axs[2]
ax.scatter(
joint_draws["alpha"],
output_ds["expected"],
c=joint_draws["beta"],
cmap=cm.cool,
alpha=0.3,
label="Coloured by function of Beta values",
)
ax.legend()
ax.set_ylabel("Expected Failures")
ax.set_xlabel("Alpha")
ax.set_title(
"Posterior Predictive Expected Failure Count between 150-600 hours \nas a function of Weibull(alpha, beta)",
fontsize=20,
)
ax1.hist(
output_ds["lb"],
ec="black",
color="slateblue",
label="95% PI Lower Bound on Failure Count",
alpha=0.3,
)
ax1.axvline(output_ds["lb"].mean(), label="Expected 95% PI Lower Bound on Failure Count")
ax1.axvline(output_ds["ub"].mean(), label="Expected 95% PI Upper Bound on Failure Count")
ax1.hist(
output_ds["ub"],
ec="black",
color="cyan",
label="95% PI Upper Bound on Failure Count",
bins=20,
alpha=0.3,
)
ax1.hist(
output_ds["expected"], ec="black", color="pink", label="Expected Count of Failures", bins=20
)
ax1.set_title("Uncertainty in the Posterior Prediction Interval of Failure Counts", fontsize=20)
ax1.legend()
ax2.set_title("Expected Costs Distribution(s) \nbased on implied Failure counts", fontsize=20)
ax2.hist(
cost_func(output_ds["expected"], 2.3),
label="Cost(failures,2)",
color="royalblue",
alpha=0.3,
ec="black",
bins=20,
)
ax2.hist(
cost_func(output_ds["expected"], 2),
label="Cost(failures,2.3)",
color="red",
alpha=0.5,
ec="black",
bins=20,
)
ax2.set_xlabel("$ cost")
# ax2.set_xlim(-60, 0)
ax2.legend();
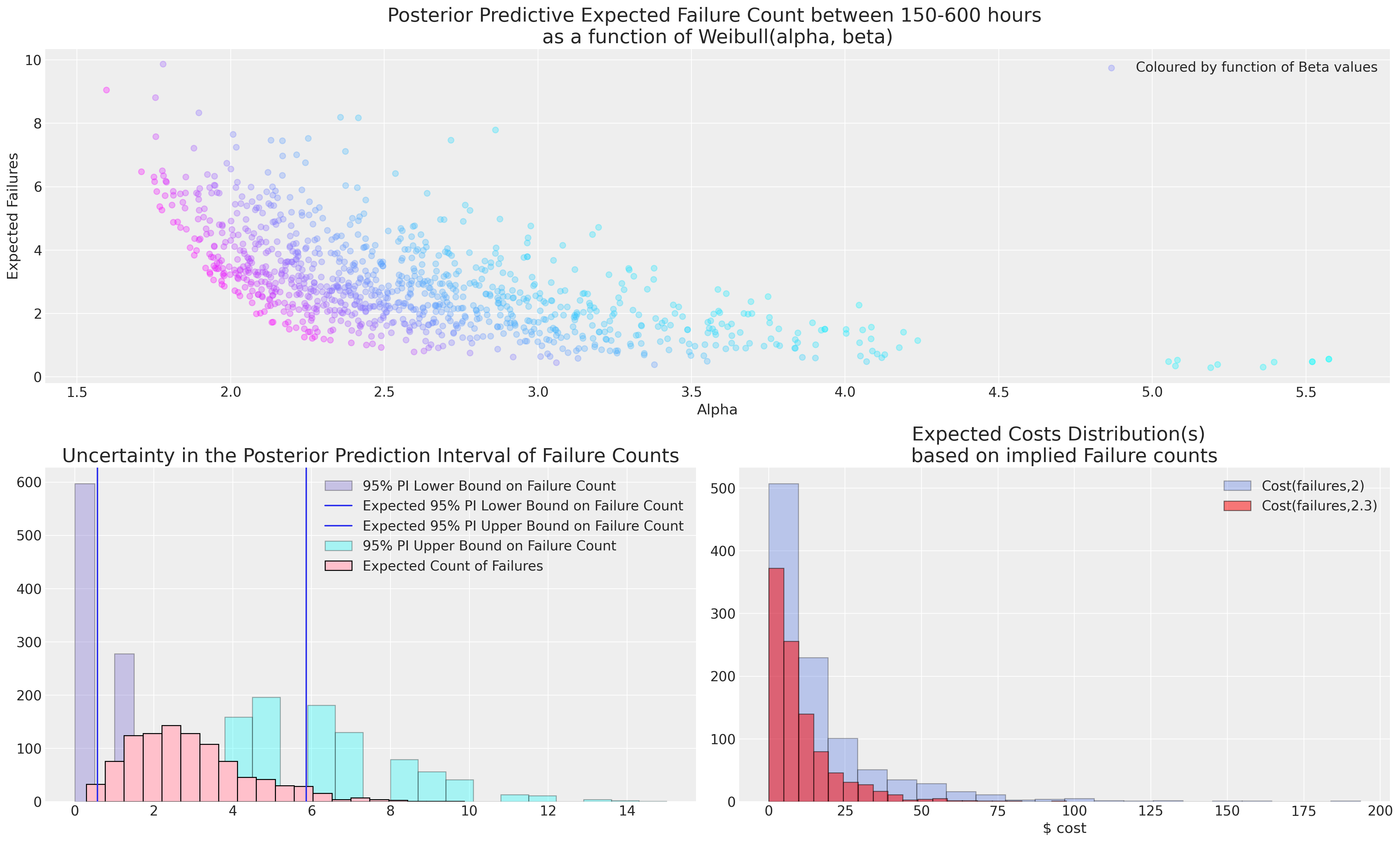
在这种情况下，模型的选择至关重要。 关于哪个失效概况合适的决定必须由主题事项专家告知，因为从如此稀疏的数据中进行推断始终是冒险的。 如果实际成本与失效相关联，那么对不确定性的理解至关重要，并且主题事项专家通常更适合判断在 600 小时的服务时间内是否可以合理预期 2 次或 7 次失效。
结论#
我们已经了解了如何从频率学和贝叶斯角度分析和建模可靠性，并与非参数估计进行比较。 我们已经展示了如何通过 bootstrap 和贝叶斯方法推导出许多关键统计量的预测区间。 我们已经看到了通过重采样方法和信息丰富的先验规范来校准这些预测区间的方法。 对问题的这些看法是互补的，适当的技术选择应由感兴趣问题的因素驱动，而不是某些意识形态的承诺。
特别是，我们已经看到 MLE 拟合我们的方位数据如何为贝叶斯分析中先验的建立提供一个不错的初步猜测方法。我们还看到如何通过从隐含模型中推导出关键量，并将这些推论置于审查之下，从而引出主题 matter 专家知识。贝叶斯预测区间的选择是根据我们对先验的期望进行校准的，在我们没有期望的地方，我们可以提供模糊的或非信息性的先验。这些先验的推论可以再次被检查，并根据适当的成本函数进行分析。
参考文献#
[1]
W.Q. Meeker, L.A. Escobar, and F.G Pascual. 可靠性数据统计方法. Wiley, 2022.
水印#
%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,xarray_einstats
Last updated: Sun Jan 15 2023
Python implementation: CPython
Python version : 3.10.8
IPython version : 8.7.0
pytensor : 2.8.10
xarray_einstats: 0.5.0.dev0
pandas : 1.5.2
pymc : 5.0.0
matplotlib: 3.6.2
xarray : 2022.12.0
numpy : 1.24.0
arviz : 0.13.0
Watermark: 2.3.1
许可声明#
本示例库中的所有笔记本均根据 MIT 许可证 提供，该许可证允许修改和再分发以用于任何用途，前提是版权和许可声明得以保留。
引用 PyMC 示例#
要引用此笔记本，请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。
重要提示
许多笔记本改编自其他来源：博客、书籍…… 在这种情况下，您也应该引用原始来源。
另请记住引用您的代码使用的相关库。
这是一个 bibtex 中的引用模板
@incollection{citekey,
author = "<notebook authors, see above>",
title = "<notebook title>",
editor = "PyMC Team",
booktitle = "PyMC examples",
doi = "10.5281/zenodo.5654871"
}
渲染后可能看起来像