橄榄球预测的分层模型#
在此示例中,我们将重现 Baio 和 Blangiardo [2010] 中描述的第一个模型,使用 PyMC。然后展示如何从后验预测分布中抽样,以模拟从得分进球(建模量)得出的锦标赛结果。
我们将论文的结果应用于六国锦标赛,这是意大利、爱尔兰、苏格兰、英格兰、法国和威尔士之间的比赛。
动机#
您对球队实力的估计取决于您对其他球队实力的估计
例如,爱尔兰队比意大利队更强 - 但强多少?
2014 年的结果来源是维基百科。我添加了随后的年份,2015 年、2016 年、2017 年。手动从维基百科拉取。
我们想要推断一个潜在参数 - 即仅基于球队的得分强度的球队“实力”,而我们拥有的只是他们的得分和结果,我们无法准确衡量球队的“实力”。
概率编程是为这些潜在参数建模的绝佳范例
目标是为即将到来的 2018 年六国赛建立模型。
注意
此笔记本使用非 PyMC 依赖项的库,因此需要专门安装才能运行此笔记本。打开下面的下拉菜单以获取更多指导。
额外依赖项安装说明
为了运行此笔记本(本地或在 binder 上),您不仅需要安装可用的 PyMC 以及所有可选依赖项,还需要安装一些额外的依赖项。有关安装 PyMC 本身的建议,请参阅安装
您可以使用您喜欢的软件包管理器安装这些依赖项,我们提供以下 pip 和 conda 命令作为示例。
$ pip install seaborn numba
请注意,如果您想(或需要)从笔记本内部而不是命令行安装软件包,您可以通过运行 pip 命令的变体来安装软件包
import sys
!{sys.executable} -m pip install seaborn numba
您不应运行 !pip install,因为它可能会将软件包安装在不同的环境中,即使已安装,也无法从 Jupyter 笔记本中使用。
另一种选择是使用 conda 代替
$ conda install seaborn numba
当使用 conda 安装科学 python 软件包时,我们建议使用 conda forge
!date
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pytensor.tensor as pt
import seaborn as sns
from matplotlib.ticker import StrMethodFormatter
%matplotlib inline
sáb 02 abr 2022 03:24:55 EEST
az.style.use("arviz-darkgrid")
plt.rcParams["figure.constrained_layout.use"] = False
这是一个橄榄球预测练习。所以我们将输入一些数据。我们从维基百科和 BBC 体育获取了这些数据。
try:
df_all = pd.read_csv("../data/rugby.csv", index_col=0)
except:
df_all = pd.read_csv(pm.get_data("rugby.csv"), index_col=0)
我们想要推断什么?#
我们想要推断生成我们观察到的数据(比分)的潜在参数(每个球队的实力)。
此外,我们知道比分是对球队实力的噪声测量,因此理想情况下,我们希望模型可以轻松量化我们对潜在实力的不确定性。
通常我们不明确知道贝叶斯模型是什么,因此我们必须“估计”贝叶斯模型
如果我们无法解决某些问题,请近似它。
马尔可夫链蒙特卡洛 (MCMC) 而是从后验分布中抽取样本。
幸运的是,此算法几乎可以应用于任何模型。
我们想要什么?#
我们想要量化我们的不确定性
我们还想使用它来生成模型
我们想要的是分布而不是点估计
可视化/EDA#
我们应该对这个数据集进行一些探索性数据分析。
这些图应该相当不言自明,我们将查看球队之间得分差异之类的内容。
df_all.describe()
| 主场得分 | 客场得分 | 年份 | |
|---|---|---|---|
| 计数 | 60.000000 | 60.000000 | 60.000000 |
| 均值 | 23.500000 | 19.983333 | 2015.500000 |
| 标准差 | 14.019962 | 12.911028 | 1.127469 |
| 最小值 | 0.000000 | 0.000000 | 2014.000000 |
| 25% | 16.000000 | 10.000000 | 2014.750000 |
| 50% | 20.500000 | 18.000000 | 2015.500000 |
| 75% | 27.250000 | 23.250000 | 2016.250000 |
| 最大值 | 67.000000 | 63.000000 | 2017.000000 |
# Let's look at the tail end of this dataframe
df_all.tail()
| 主队 | 客队 | 主场得分 | 客场得分 | 年份 | |
|---|---|---|---|---|---|
| 55 | 意大利 | 法国 | 18 | 40 | 2017 |
| 56 | 英格兰 | 苏格兰 | 61 | 21 | 2017 |
| 57 | 苏格兰 | 意大利 | 29 | 0 | 2017 |
| 58 | 法国 | 威尔士 | 20 | 18 | 2017 |
| 59 | 爱尔兰 | 英格兰 | 13 | 9 | 2017 |
这里有一些我们不需要的东西。我们的模型不需要年份。但这可能会改进未来的模型。
首先,让我们看看按年份划分的得分差异。
df_all["difference"] = np.abs(df_all["home_score"] - df_all["away_score"])
(
df_all.groupby("year")["difference"]
.mean()
.plot(
kind="bar",
title="Average magnitude of scores difference Six Nations",
yerr=df_all.groupby("year")["difference"].std(),
)
.set_ylabel("Average (abs) point difference")
);
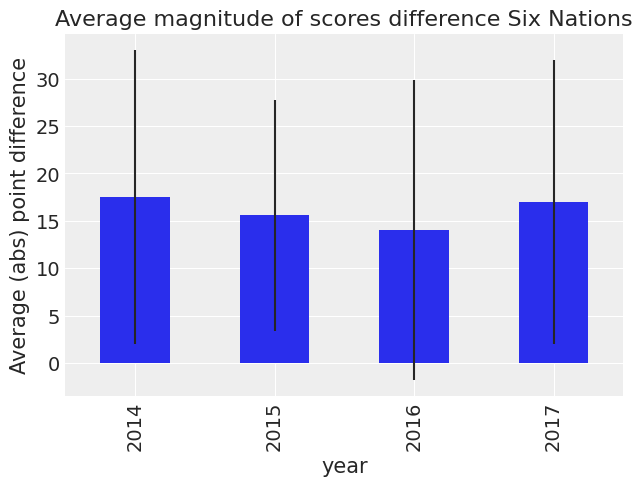
我们可以看到标准误差很大。所以我们不能说任何关于差异的事情。让我们按国家/地区查看。
df_all["difference_non_abs"] = df_all["home_score"] - df_all["away_score"]
让我们首先看一个数据透视表,其中包含此总和,按年份细分。
df_all.pivot_table("difference_non_abs", "home_team", "year")
| 年份 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|
| 主队 | ||||
| 英格兰 | 7.000000 | 20.666667 | 7.500000 | 21.333333 |
| 法国 | 6.666667 | 0.000000 | -2.333333 | 4.000000 |
| 爱尔兰 | 28.000000 | 8.500000 | 17.666667 | 7.000000 |
| 意大利 | -21.000000 | -31.000000 | -23.500000 | -33.666667 |
| 苏格兰 | -11.000000 | -12.000000 | 2.500000 | 16.666667 |
| 威尔士 | 25.666667 | 1.000000 | 22.000000 | 4.000000 |
现在让我们首先绘制按主队(不包括年份)划分的图。
(
df_all.pivot_table("difference_non_abs", "home_team")
.rename_axis("Home_Team")
.plot(kind="bar", rot=0, legend=False)
.set_ylabel("Score difference Home team and away team")
);
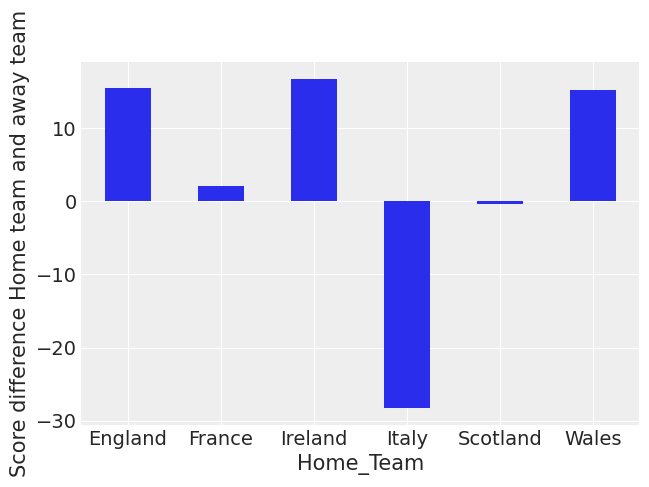
您可以看到意大利和苏格兰的平均得分是负数。您还可以看到,英格兰、爱尔兰和威尔士最近在主场是最强的球队。
(
df_all.pivot_table("difference_non_abs", "away_team")
.rename_axis("Away_Team")
.plot(kind="bar", rot=0, legend=False)
.set_ylabel("Score difference Home team and away team")
);
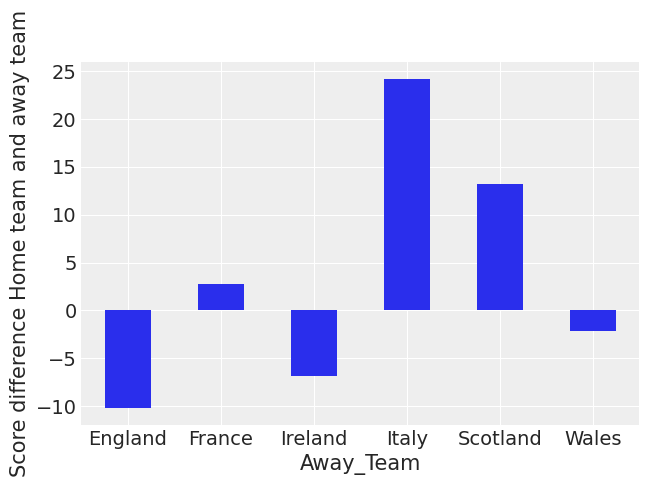
这表明意大利、苏格兰和法国的客场表现都很差。英格兰在客场比赛时受到的影响最小。这种汇总视图没有考虑球队的实力。
让我们更详细地看一下多年来平均得分差异的时间序列图。
我们看到球队行为发生了一些变化,我们也看到意大利是一支弱队。
g = sns.FacetGrid(df_all, col="home_team", col_wrap=2, height=5)
g.map(sns.scatterplot, "year", "difference_non_abs")
g.fig.autofmt_xdate()
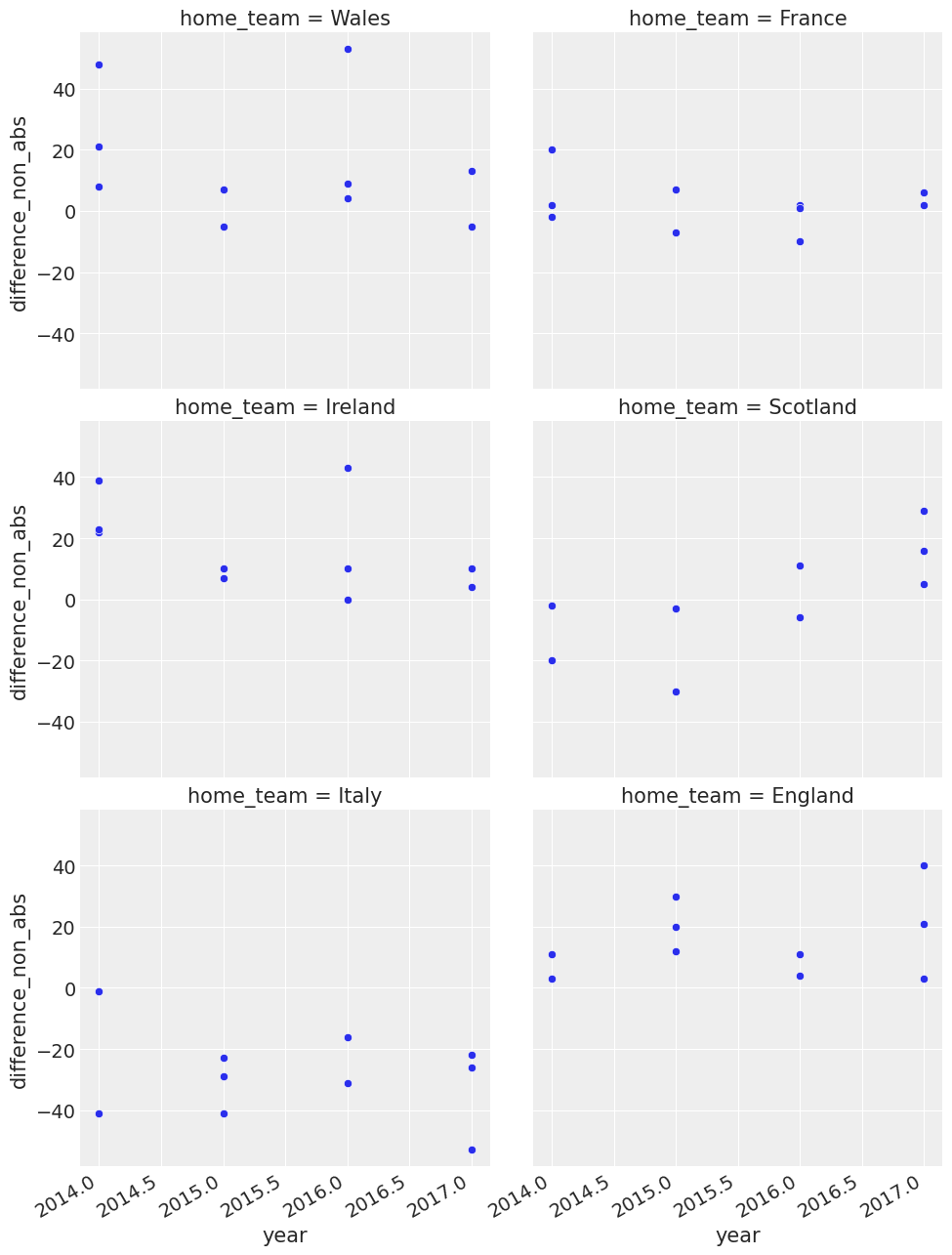
g = sns.FacetGrid(df_all, col="away_team", col_wrap=2, height=5)
g = g.map(plt.scatter, "year", "difference_non_abs").set_axis_labels("Year", "Score Difference")
g.fig.autofmt_xdate()
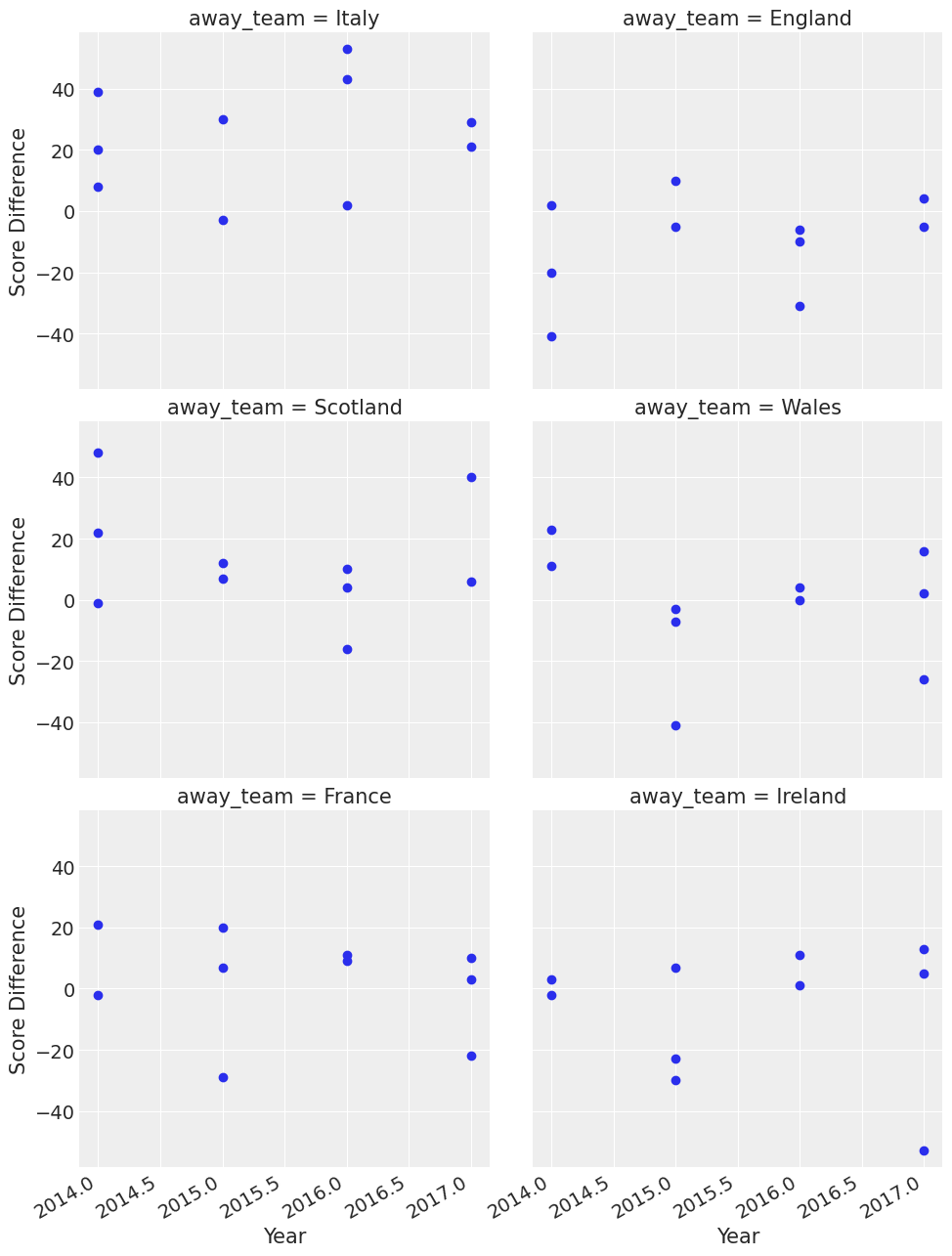
您可以在这里看到一些有趣的事情,例如威尔士在 2015 年的客场表现不错。那一年,他们在客场赢了三场比赛,并在客场对阵意大利的比赛中赢了大约 40 分。
现在我们对数据有了一定的了解,我们可以继续描述模型。
我们对“生成故事”有哪些已知假设?#
我们知道橄榄球六国赛只有 6 支球队 - 他们每赛季彼此比赛一次
我们有过去几年的数据
我们还知道,在体育运动中,得分被建模为泊松分布
我们认为主场优势在体育运动中是一个强大的影响因素
模型。#
联赛由总共 T= 6 支球队组成,每赛季彼此比赛一次。我们将赛季第 g 场比赛(15 场比赛)中主队和客队的得分分别表示为 \(y_{g1}\) 和 \(y_{g2}\)。
观察到的计数向量 \(\mathbb{y} = (y_{g1}, y_{g2})\) 被建模为独立的泊松分布:\(y_{gi}| \theta_{gj} \tilde\;\; Poisson(\theta_{gj})\),其中 theta 参数分别表示主队 (j=1) 和客队 (j=2) 在第 g 场比赛中的得分强度。我们根据已广泛用于统计文献中的公式对这些参数进行建模,假设对数线性随机效应模型
参数 home 表示主队在比赛中的优势,我们假设这种效应对于所有球队并且在整个赛季中都是恒定的
得分强度由两支参赛球队的进攻和防守能力共同决定,分别由参数 att 和 def 表示
相反,对于每个 t = 1, …, T,特定于球队的效应是从共同分布中建模为可交换的
\(att_{t} \; \tilde\;\; Normal(\mu_{att},\tau_{att})\) 和 \(def_{t} \; \tilde\;\;Normal(\mu_{def},\tau_{def})\)
我们在上面做了一些数据整理和调整,使数据对于我们的模型来说更整洁。
对客场得分和主场得分使用对数函数是体育分析文献中的标准技巧
构建模型#
我们现在在 PyMC 中构建模型,指定全局参数、球队特定参数和似然函数
plt.rcParams["figure.constrained_layout.use"] = True
home_idx, teams = pd.factorize(df_all["home_team"], sort=True)
away_idx, _ = pd.factorize(df_all["away_team"], sort=True)
coords = {"team": teams}
with pm.Model(coords=coords) as model:
# constant data
home_team = pm.ConstantData("home_team", home_idx, dims="match")
away_team = pm.ConstantData("away_team", away_idx, dims="match")
# global model parameters
home = pm.Normal("home", mu=0, sigma=1)
sd_att = pm.HalfNormal("sd_att", sigma=2)
sd_def = pm.HalfNormal("sd_def", sigma=2)
intercept = pm.Normal("intercept", mu=3, sigma=1)
# team-specific model parameters
atts_star = pm.Normal("atts_star", mu=0, sigma=sd_att, dims="team")
defs_star = pm.Normal("defs_star", mu=0, sigma=sd_def, dims="team")
atts = pm.Deterministic("atts", atts_star - pt.mean(atts_star), dims="team")
defs = pm.Deterministic("defs", defs_star - pt.mean(defs_star), dims="team")
home_theta = pt.exp(intercept + home + atts[home_idx] + defs[away_idx])
away_theta = pt.exp(intercept + atts[away_idx] + defs[home_idx])
# likelihood of observed data
home_points = pm.Poisson(
"home_points",
mu=home_theta,
observed=df_all["home_score"],
dims=("match"),
)
away_points = pm.Poisson(
"away_points",
mu=away_theta,
observed=df_all["away_score"],
dims=("match"),
)
trace = pm.sample(1000, tune=1500, cores=4)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
/home/oriol/miniconda3/envs/arviz/lib/python3.9/site-packages/pymc/pytensorf.py:1005: UserWarning: The parameter 'updates' of pytensor.function() expects an OrderedDict, got <class 'dict'>. Using a standard dictionary here results in non-deterministic behavior. You should use an OrderedDict if you are using Python 2.7 (collections.OrderedDict for older python), or use a list of (shared, update) pairs. Do not just convert your dictionary to this type before the call as the conversion will still be non-deterministic.
pytensor_function = pytensor.function(
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [home, sd_att, sd_def, intercept, atts_star, defs_star]
Sampling 4 chains for 1_500 tune and 1_000 draw iterations (6_000 + 4_000 draws total) took 25 seconds.
我们指定了模型和似然函数
所有这些都在底层 PyTensor 图上运行
az.plot_trace(trace, var_names=["intercept", "home", "sd_att", "sd_def"], compact=False);

让我们应用良好的统计工作流程实践,并查看各种评估指标,以查看我们的 NUTS 采样器是否收敛。
az.plot_energy(trace, figsize=(6, 4));
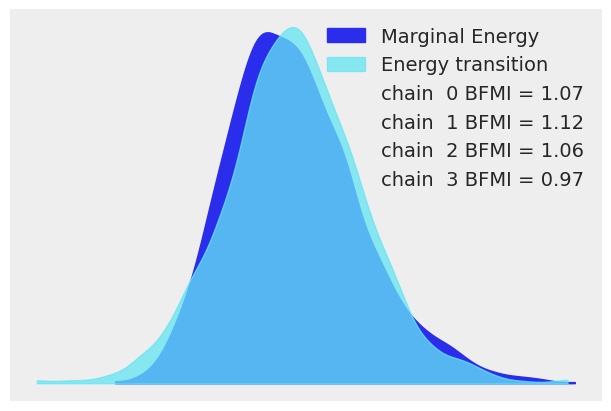
az.summary(trace, kind="diagnostics")
| mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|
| 主场 | 0.001 | 0.001 | 2694.0 | 2250.0 | 1.0 |
| 截距 | 0.001 | 0.000 | 2743.0 | 2455.0 | 1.0 |
| atts_star[英格兰] | 0.004 | 0.003 | 1243.0 | 1121.0 | 1.0 |
| atts_star[法国] | 0.004 | 0.003 | 1247.0 | 1111.0 | 1.0 |
| atts_star[爱尔兰] | 0.004 | 0.003 | 1208.0 | 1160.0 | 1.0 |
| atts_star[意大利] | 0.004 | 0.003 | 1352.0 | 1375.0 | 1.0 |
| atts_star[苏格兰] | 0.004 | 0.003 | 1318.0 | 1178.0 | 1.0 |
| atts_star[威尔士] | 0.004 | 0.003 | 1252.0 | 1122.0 | 1.0 |
| defs_star[英格兰] | 0.007 | 0.005 | 1110.0 | 899.0 | 1.0 |
| defs_star[法国] | 0.007 | 0.006 | 1091.0 | 876.0 | 1.0 |
| defs_star[爱尔兰] | 0.007 | 0.005 | 1113.0 | 881.0 | 1.0 |
| defs_star[意大利] | 0.007 | 0.006 | 1075.0 | 846.0 | 1.0 |
| defs_star[苏格兰] | 0.007 | 0.006 | 1081.0 | 854.0 | 1.0 |
| defs_star[威尔士] | 0.007 | 0.006 | 1098.0 | 889.0 | 1.0 |
| sd_att | 0.004 | 0.003 | 1767.0 | 1709.0 | 1.0 |
| sd_def | 0.006 | 0.004 | 1762.0 | 1662.0 | 1.0 |
| atts[英格兰] | 0.001 | 0.000 | 5489.0 | 3204.0 | 1.0 |
| atts[法国] | 0.001 | 0.000 | 5441.0 | 3286.0 | 1.0 |
| atts[爱尔兰] | 0.001 | 0.000 | 5257.0 | 3260.0 | 1.0 |
| atts[意大利] | 0.001 | 0.001 | 5157.0 | 2957.0 | 1.0 |
| atts[苏格兰] | 0.001 | 0.001 | 4926.0 | 3003.0 | 1.0 |
| atts[威尔士] | 0.001 | 0.000 | 4537.0 | 3306.0 | 1.0 |
| defs[英格兰] | 0.001 | 0.001 | 4779.0 | 3293.0 | 1.0 |
| defs[法国] | 0.001 | 0.001 | 4183.0 | 2917.0 | 1.0 |
| defs[爱尔兰] | 0.001 | 0.001 | 4766.0 | 3227.0 | 1.0 |
| defs[意大利] | 0.001 | 0.000 | 4419.0 | 3561.0 | 1.0 |
| defs[苏格兰] | 0.001 | 0.000 | 4068.0 | 3290.0 | 1.0 |
| defs[威尔士] | 0.001 | 0.001 | 4177.0 | 3164.0 | 1.0 |
我们的模型已良好收敛,并且 \(\hat{R}\) 看起来不错。
让我们看一些统计数据,以验证我们的模型是否返回了正确的属性。我们可以看到有些球队比其他球队更强。这是我们对进攻的期望
trace_hdi = az.hdi(trace)
trace_hdi["atts"]
<xarray.DataArray 'atts' (team: 6, hdi: 2)>
array([[ 0.18302232, 0.33451681],
[-0.16672247, 0.00056686],
[ 0.02480029, 0.18070957],
[-0.44275554, -0.2336128 ],
[-0.20865349, -0.03104828],
[ 0.09821099, 0.25031702]])
Coordinates:
* team (team) <U8 'England' 'France' 'Ireland' 'Italy' 'Scotland' 'Wales'
* hdi (hdi) <U6 'lower' 'higher'trace.posterior["atts"].median(("chain", "draw"))
<xarray.DataArray 'atts' (team: 6)>
array([ 0.25676819, -0.08392998, 0.10809197, -0.33498374, -0.11633869,
0.17182582])
Coordinates:
* team (team) <U8 'England' 'France' 'Ireland' 'Italy' 'Scotland' 'Wales'结果#
从上面我们可以开始理解进攻强度和防守强度的不同分布。这些是概率估计,有助于我们更好地理解体育分析中的不确定性
_, ax = plt.subplots(figsize=(12, 6))
ax.scatter(teams, trace.posterior["atts"].median(dim=("chain", "draw")), color="C0", alpha=1, s=100)
ax.vlines(
teams,
trace_hdi["atts"].sel({"hdi": "lower"}),
trace_hdi["atts"].sel({"hdi": "higher"}),
alpha=0.6,
lw=5,
color="C0",
)
ax.set_xlabel("Teams")
ax.set_ylabel("Posterior Attack Strength")
ax.set_title("HDI of Team-wise Attack Strength");
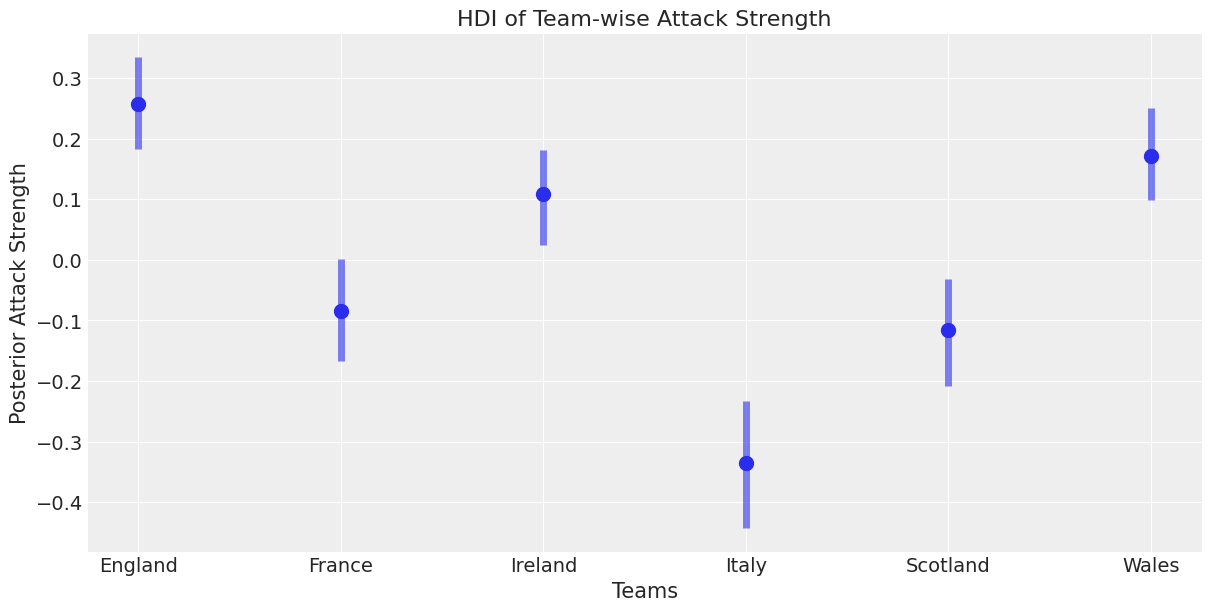
这是贝叶斯建模的强大之处之一,我们可以对我们的一些估计进行不确定性量化。我们获得了不同国家进攻强度的贝叶斯可信区间。
我们可以看到爱尔兰、威尔士和英格兰之间存在重叠,这符合您的预期,因为这些球队近年来都赢得了比赛。
意大利远远落后于其他球队 - 这符合我们的预期,苏格兰和法国之间存在重叠,这似乎也大致正确。
可能有一些我们想要在此处添加的效果,例如更强烈地加权最近的结果。然而,这将是一个更复杂的模型。
# subclass arviz labeller to omit the variable name
class TeamLabeller(az.labels.BaseLabeller):
def make_label_flat(self, var_name, sel, isel):
sel_str = self.sel_to_str(sel, isel)
return sel_str
ax = az.plot_forest(trace, var_names=["atts"], labeller=TeamLabeller())
ax[0].set_title("Team Offense");
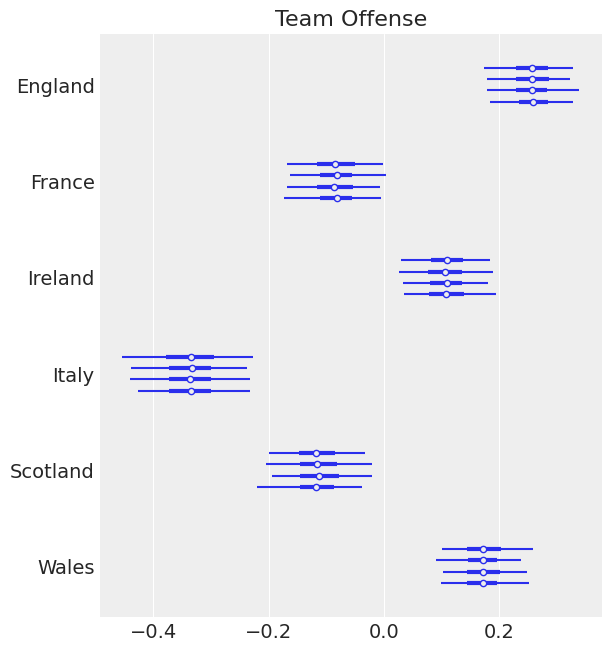
ax = az.plot_forest(trace, var_names=["defs"], labeller=TeamLabeller())
ax[0].set_title("Team Defense");
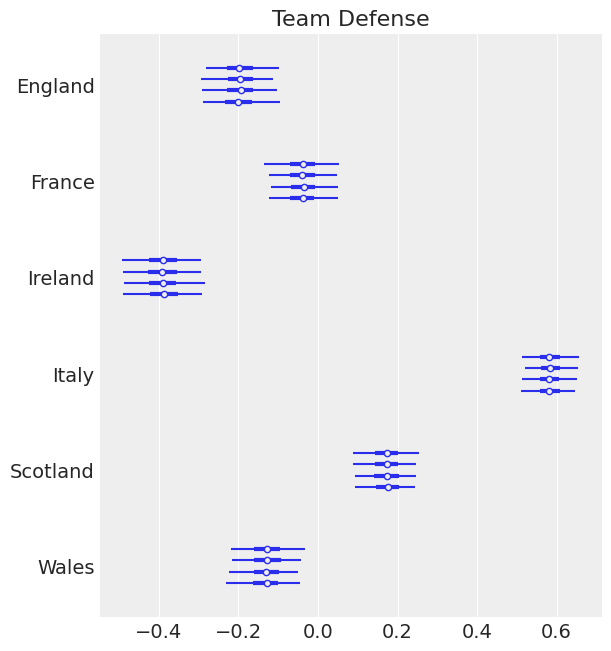
像爱尔兰和英格兰这样的强队对防守有很强的负面影响。这符合我们的预期。我们期望我们的强队在进攻方面有强大的积极影响,在防守方面有强大的消极影响。
我们正在使用的这种查看参数并检查它们的方法是良好统计工作流程的一部分。我们还认为,也许我们的先验可以更好地指定。然而,这超出了本文的范围。我们建议您访问 使用 RStan 的稳健统计工作流程,以获得关于“统计工作流程”的良好讨论
让我们做一些其他图。因此,我们可以看到我们的防守效果范围。我也会在下面打印球队以供参考
az.plot_posterior(trace, var_names=["defs"]);
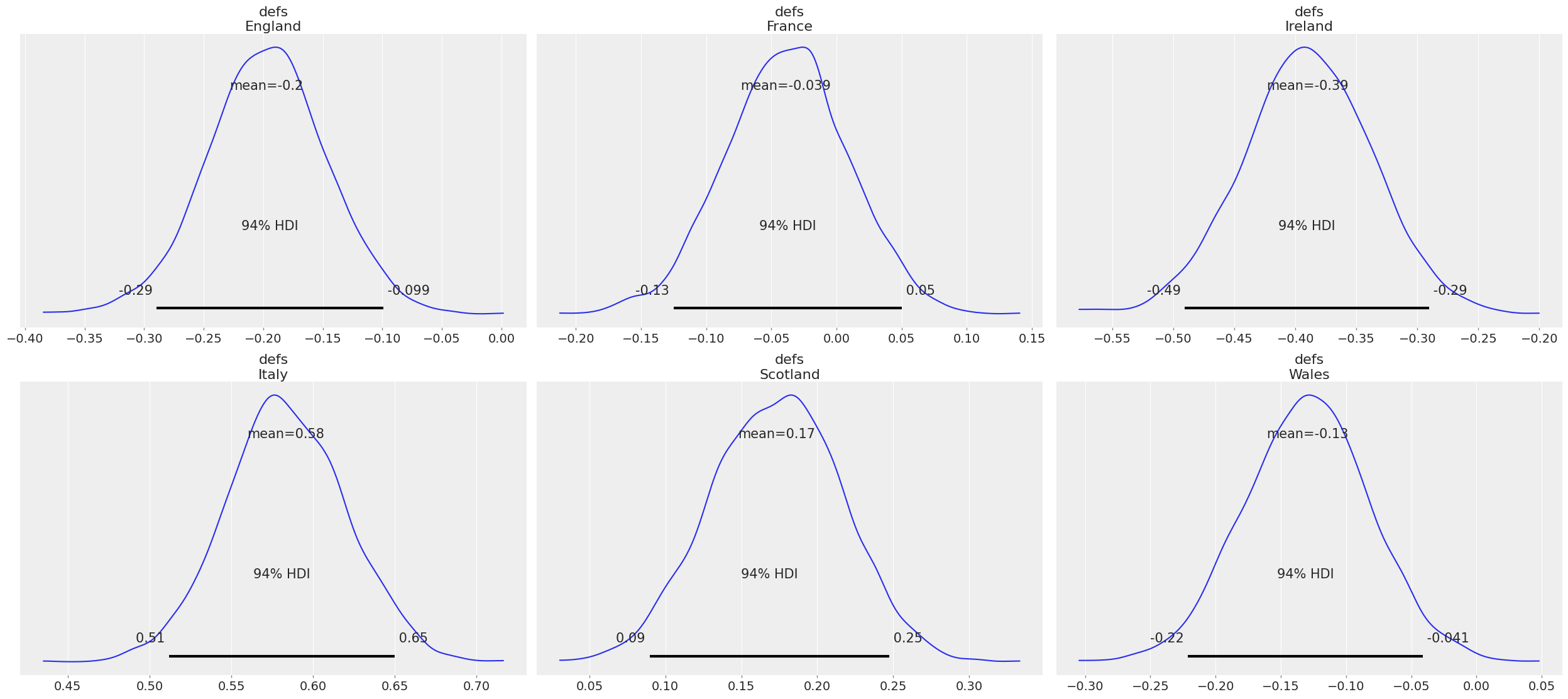
我们可以看到爱尔兰的平均值为 -0.39,这意味着我们预计爱尔兰的防守会很强。这符合我们的预期,爱尔兰通常即使在输掉比赛的情况下也不会输掉 50 分。我们可以看到 94% HDI 在 -0.491 和 -0.28 之间
与意大利相比,我们看到强烈的积极影响,平均值为 0.58,HDI 为 0.51 和 0.65。这意味着我们预计意大利会失分很多,相对于它的得分而言。鉴于意大利经常输掉 30 - 60 分,这似乎是正确的。
我们在这里也看到,这告知了我们可以引入的其他先验。我们可以引入某种世界排名作为先验。
截至 2017 年 12 月,橄榄球排名 表明英格兰排名世界第二,爱尔兰排名第三,苏格兰排名第五,威尔士排名第七,法国排名第九,意大利排名第十四。我们可以将此纳入模型,它可以解释意大利与其他许多球队不同的部分事实。
现在让我们模拟谁在总共 4000 次模拟中获胜,后验分布中的每个样本一次模拟。
with model:
pm.sample_posterior_predictive(trace, extend_inferencedata=True)
pp = trace.posterior_predictive
const = trace.constant_data
team_da = trace.posterior.team
/home/oriol/miniconda3/envs/arviz/lib/python3.9/site-packages/pymc/pytensorf.py:1005: UserWarning: The parameter 'updates' of pytensor.function() expects an OrderedDict, got <class 'dict'>. Using a standard dictionary here results in non-deterministic behavior. You should use an OrderedDict if you are using Python 2.7 (collections.OrderedDict for older python), or use a list of (shared, update) pairs. Do not just convert your dictionary to this type before the call as the conversion will still be non-deterministic.
pytensor_function = pytensor.function(
后验预测样本包含每支球队在每场比赛中的得分。我们使用进球作为观察变量,根据得分和防守能力进行建模和模拟。
我们现在的目标是看看谁赢得比赛,因此我们可以估计每支球队赢得整个比赛的概率。从中我们需要将得分进球转换为积分
# fmt: off
pp["home_win"] = (
(pp["home_points"] > pp["away_points"]) * 3 # home team wins and gets 3 points
+ (pp["home_points"] == pp["away_points"]) * 2 # tie -> home team gets 2 points
)
pp["away_win"] = (
(pp["home_points"] < pp["away_points"]) * 3
+ (pp["home_points"] == pp["away_points"]) * 2
)
# fmt: on
然后添加每支球队在所有比赛中获得的积分
groupby_sum_home = pp.home_win.groupby(team_da[const.home_team]).sum()
groupby_sum_away = pp.away_win.groupby(team_da[const.away_team]).sum()
pp["teamscores"] = groupby_sum_home + groupby_sum_away
并最终生成 4000 次模拟中每支球队的排名。由于我们的数据存储在 InferenceData 类中的 xarray 对象中,我们将使用 xarray-einstats
from xarray_einstats.stats import rankdata
pp["rank"] = rankdata(-pp["teamscores"], dims="team", method="min")
pp[["rank"]].sel(team="England")
<xarray.Dataset>
Dimensions: (chain: 4, draw: 1000)
Coordinates:
* chain (chain) int64 0 1 2 3
* draw (draw) int64 0 1 2 3 4 5 6 7 8 ... 992 993 994 995 996 997 998 999
team <U7 'England'
Data variables:
rank (chain, draw) int64 2 1 2 2 2 1 1 1 2 1 1 ... 1 1 1 1 2 1 3 1 2 2 1
Attributes:
created_at: 2022-04-02T00:25:59.622442
arviz_version: 0.12.0
inference_library: pymc
inference_library_version: 4.0.0b6正如您所见,我们现在为每支球队收集了 4000 个介于 1 和 6 之间的整数,其中 1 表示他们赢得比赛。我们可以使用以半整数为箱体边缘的直方图来计数和归一化每支球队在每个位置完成的次数
from xarray_einstats.numba import histogram
bin_edges = np.arange(7) + 0.5
data_sim = (
histogram(pp["rank"], dims=("chain", "draw"), bins=bin_edges, density=True)
.rename({"bin": "rank"})
.assign_coords(rank=np.arange(6) + 1)
)
现在我们已将数据简化为二维数组,我们将将其转换为 pandas DataFrame,这现在是处理我们数据的更合适的选择
idx_dim, col_dim = data_sim.dims
sim_table = pd.DataFrame(data_sim, index=data_sim[idx_dim], columns=data_sim[col_dim])
fig, ax = plt.subplots(figsize=(8, 4))
ax = sim_table.T.plot(kind="barh", ax=ax)
ax.xaxis.set_major_formatter(StrMethodFormatter("{x:.1%}"))
ax.set_xlabel("Rank-wise Probability of results for all six teams")
ax.set_yticklabels(np.arange(1, 7))
ax.set_ylabel("Ranks")
ax.invert_yaxis()
ax.legend(loc="best", fontsize="medium");
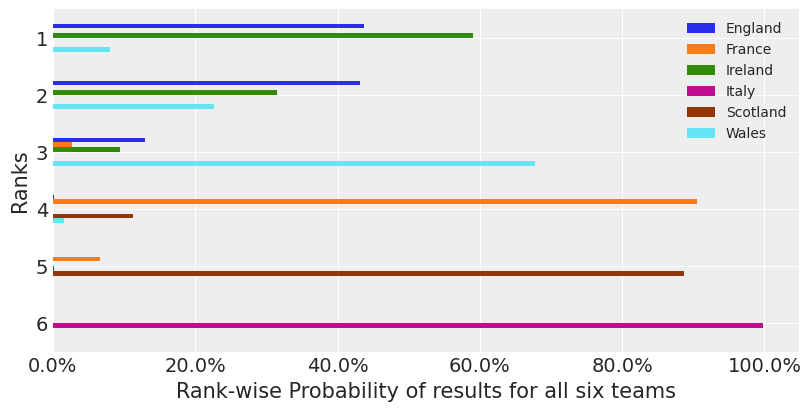
根据此模型,我们看到爱尔兰队大约 60% 的时间获得最多积分,英格兰队大约 45% 的时间获得最多积分,威尔士队大约 10% 的时间获得最多积分。(请注意,这些概率的总和不为 100%,因为在积分榜首位出现平局的可能性不为零。)
作为爱尔兰橄榄球迷 - 我喜欢这个模型。但是它表明收缩和偏差存在一些问题。因为最近的形式表明英格兰将获胜。
然而,此模型的重点是说明如何将分层模型应用于体育分析问题,并说明 PyMC 的强大功能。
协变量#
我们应该对变量进行一些探索
az.plot_pair(
trace,
var_names=["atts"],
kind="scatter",
divergences=True,
textsize=25,
marginals=True,
),
figsize = (10, 10)
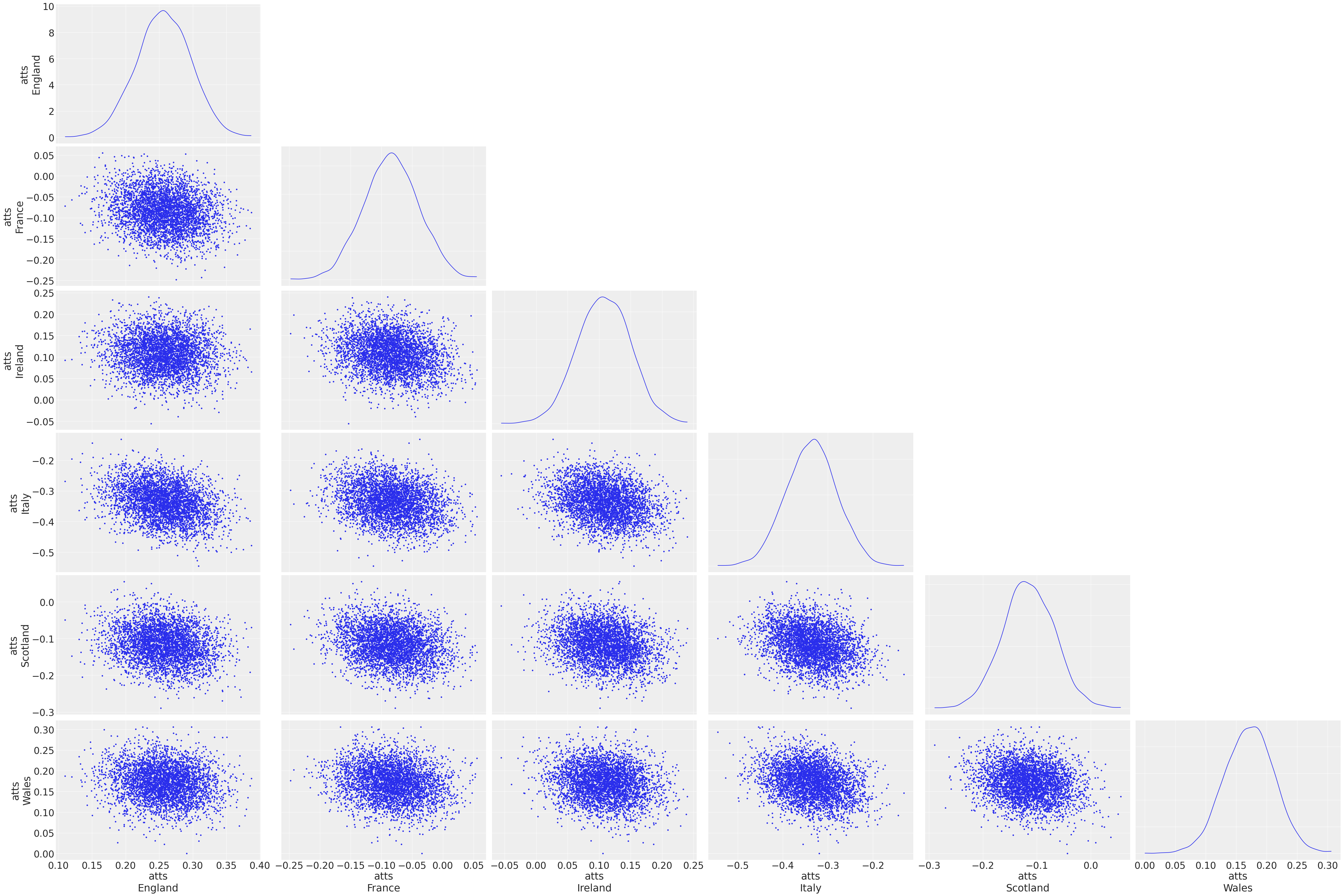
我们观察到这些协变量之间没有太多相关性,除了像意大利这样的较弱球队的这些变量的分布更负面。尽管如此,这仍然是深入了解变量行为的好方法。
参考文献#
水印#
%load_ext watermark
%watermark -n -u -v -iv -w -p xarray,aeppl,numba,xarray_einstats
Last updated: Sat Apr 02 2022
Python implementation: CPython
Python version : 3.9.10
IPython version : 8.0.1
xarray : 2022.3.0
aeppl : 0.0.27
numba : 0.55.1
xarray_einstats: 0.2.0
matplotlib: 3.5.1
numpy : 1.21.5
pandas : 1.4.1
seaborn : 0.11.2
pymc : 4.0.0b6
pytensor : 2.5.1
arviz : 0.12.0
Watermark: 2.3.0
许可声明#
此示例库中的所有笔记本均根据 MIT 许可证 提供,该许可证允许修改和再分发以用于任何用途,前提是保留版权和许可声明。
引用 PyMC 示例#
要引用此笔记本,请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。
重要提示
许多笔记本都改编自其他来源:博客、书籍……在这种情况下,您也应该引用原始来源。
另请记住引用您的代码使用的相关库。
这是一个 bibtex 中的引用模板
@incollection{citekey,
author = "<notebook authors, see above>",
title = "<notebook title>",
editor = "PyMC Team",
booktitle = "PyMC examples",
doi = "10.5281/zenodo.5654871"
}
渲染后可能看起来像