回归不连续性设计分析#

准实验 涉及实验干预和定量测量。然而，准实验不 涉及将单元（例如细胞、人、公司、学校、州）随机分配到测试组或对照组。当提出因果关系主张时，这种无法进行随机分配的情况会带来问题，因为它使得更难以论证对照组和测试组之间的任何差异是由于干预措施造成的，而不是由于混淆因素造成的。

回归不连续性设计 是一种特殊的准实验设计形式。它由对照组和测试组组成，但单元分配到条件是根据阈值标准选择的，而不是随机的。

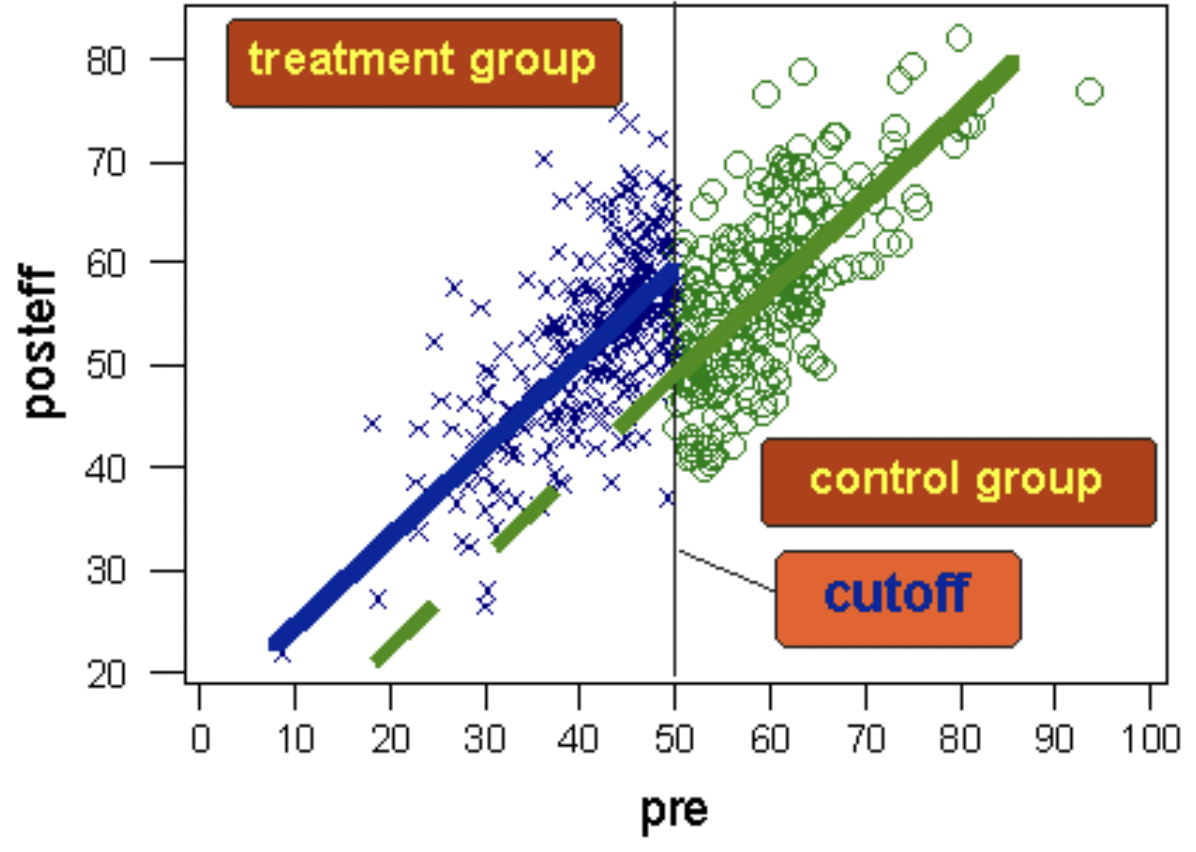
regression discontinuity design schematic

回归不连续性设计的示意图。 绿色虚线显示了如果测试组未接受治疗，我们预期测试组的后测分数所处的位置。 图像取自 https://conjointly.com/kb/regression-discontinuity-design/。#

得分非常低的单元可能在某些维度上与得分非常高的单元存在系统性差异。 例如，如果我们查看得分最高和得分最低的学生，那么很可能存在混淆变量。 高分学生可能比低分学生来自更优越的背景。

如果我们对得分在后一半的学生进行额外辅导（我们的实验干预），那么我们可以很容易地想象，测试组和对照组之间在某些特权衡量标准上存在巨大差异。 乍一看，这似乎使回归不连续性设计毫无用处——随机分配的全部意义在于减少或消除对照组和测试组之间​​的系统偏差。 但是使用阈值似乎会最大限度地扩大组间混淆变量的差异。 这难道不是一件奇怪的事情吗？

然而，关键在于，得分刚好低于和刚好高于阈值的学生，在特权程度上发生系统性差异的可能性要小得多。 因此，如果 我们发现证据表明，刚好高于和刚好低于阈值的学生的后测分数存在有意义的不连续性，那么干预（根据阈值标准应用）更有可能是因果关系的原因。

锐利与模糊回归不连续性设计#

请注意，回归不连续性设计分为两类。 本笔记本侧重于锐利 回归不连续性设计，但重要的是要了解锐利和模糊变体

  • 锐利： 在这里，分配到对照组或治疗组完全由阈值决定。 哪些单元属于哪个组不存在不确定性。

  • 模糊： 在某些情况下，基于阈值的控制和治疗之间可能没有明确的界限。 例如，如果实验人员在根据阈值将单元分配到组时不够严格，则可能会发生这种情况。 或者，在实际研究的单元方面可能存在不合规性。 例如，患者可能并非始终完全遵守服药规定，因此由于不合规性，分配到测试组的患者中，一些未知比例的患者实际上可能在对照组中。

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm

RANDOM_SEED = 123
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
%config InlineBackend.figure_format = 'retina'

生成模拟数据#

请注意，这里我们假设测量噪声可忽略不计/为零，但真实值从前测到后测存在一些变异性。 可以考虑前测和后测结果的测量噪声，但我们不在本笔记本中讨论这个问题。

隐藏代码单元格源 
# define true parameters
threshold = 0.0
treatment_effect = 0.7
N = 1000
sd = 0.3  # represents change between pre and post test with zero measurement error

# No measurement error, but random change from pre to post
df = (
    pd.DataFrame.from_dict({"x": rng.normal(size=N)})
    .assign(treated=lambda x: x.x < threshold)
    .assign(y=lambda x: x.x + rng.normal(loc=0, scale=sd, size=N) + treatment_effect * x.treated)
)

df
x 已治疗 y
0 -0.989121 真 0.050794
1 -0.367787 真 -0.181418
2 1.287925 假 1.345912
3 0.193974 假 0.430915
4 0.920231 假 1.229825
... ... ... ...
995 -1.246726 真 -0.819665
996 0.090428 假 0.006909
997 0.370658 假 -0.027703
998 -1.063268 真 0.008132
999 0.239116 假 0.604780

1000 行 × 3 列

隐藏代码单元格源 
def plot_data(df):
    fig, ax = plt.subplots(figsize=(12, 7))
    ax.plot(df.x[~df.treated], df.y[~df.treated], "o", alpha=0.3, label="untreated")
    ax.plot(df.x[df.treated], df.y[df.treated], "o", alpha=0.3, label="treated")
    ax.axvline(x=threshold, color="k", ls="--", lw=3, label="treatment threshold")
    ax.set(xlabel=r"observed $x$ (pre-test)", ylabel=r"observed $y$ (post-test)")
    ax.legend()
    return ax


plot_data(df);
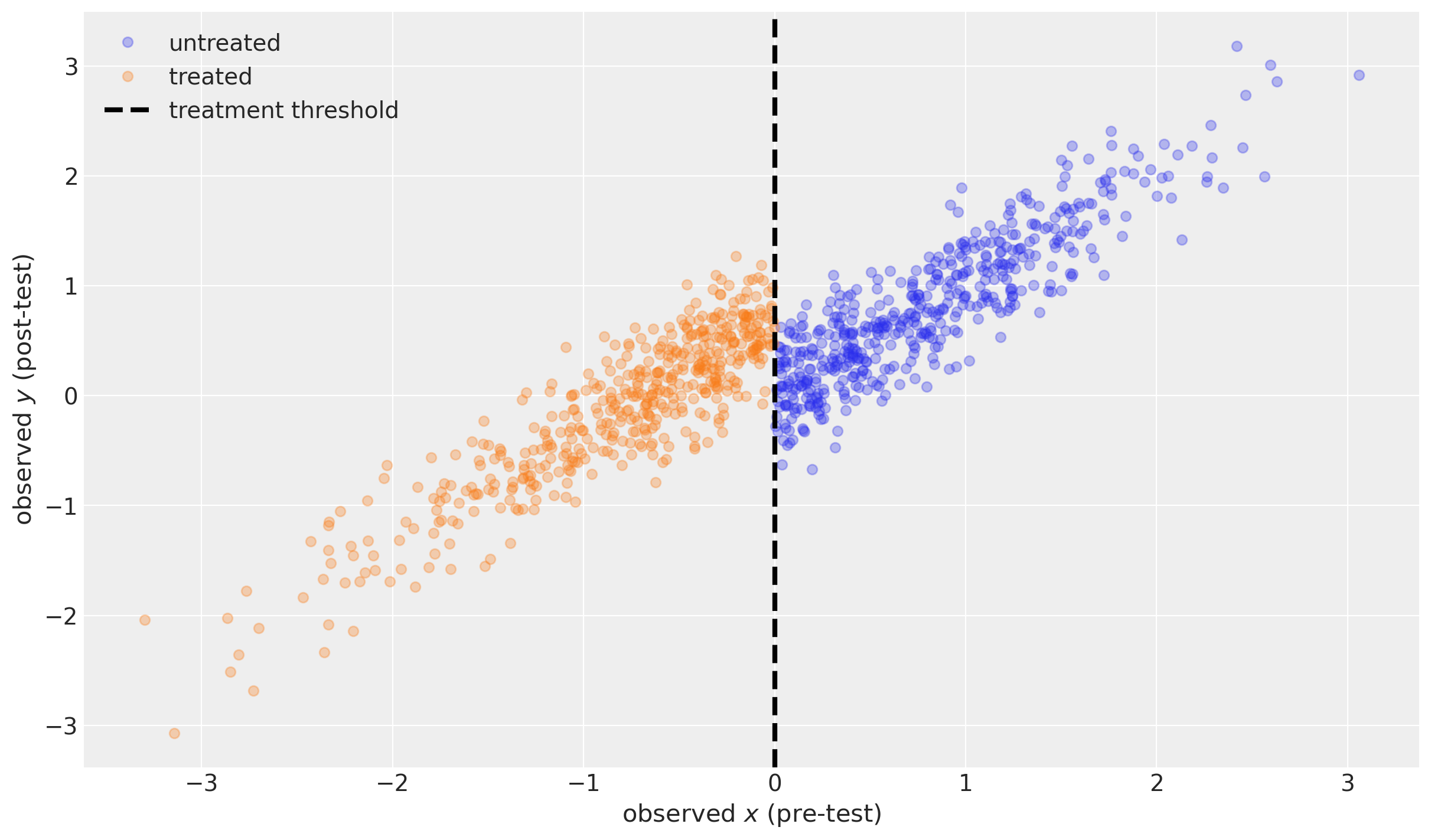
../_images/0615b106487e7d8fc900fda79bc7046210a227de9997b6289ce324fa8a95c078.png

锐利回归不连续性模型#

我们可以将贝叶斯回归不连续性模型定义为

\[\begin{split} \begin{aligned} \Delta & \sim \text{Cauchy}(0, 1) \\ \sigma & \sim \text{HalfNormal}(0, 1) \\ \mu & = x_i + \underbrace{\Delta \cdot treated_i}_{\text{治疗效果}} \\ y_i & \sim \text{Normal}(\mu, \sigma) \end{aligned} \end{split}\]

其中

  • \(\Delta\) 是不连续性的大小，

  • \(\sigma\) 是前测到后测分数变化的标准差，

  • \(x_i\) 和 \(y_i\) 是单元 \(i\) 的观测前测和后测指标，以及

  • \(treated_i\) 是观测到的指标变量（对照组为 0，测试组为 1）。

注释

  • 我们做出没有测量误差的简化假设。

  • 在这里，我们将自己限制在使用相同指标（例如心率、教育程度、上臂围）进行前测 (\(x\)) 和后测 (\(y\)) 的情况。 因此，未治疗 的后测指标可以建模为 \(y \sim \text{Normal}(\mu=x, \sigma)\)。

  • 如果前测和后测测量工具不相同，那么我们希望将斜率和截距参数构建到 \(\mu\) 中，以捕获前测和后测指标之间的“兑换率”。

  • 我们假设我们已准确观察到单元是否已接受治疗。 也就是说，该模型假设不连续性是锐利的，没有不确定性。

with pm.Model() as model:
    x = pm.MutableData("x", df.x, dims="obs_id")
    treated = pm.MutableData("treated", df.treated, dims="obs_id")
    sigma = pm.HalfNormal("sigma", 1)
    delta = pm.Cauchy("effect", alpha=0, beta=1)
    mu = pm.Deterministic("mu", x + (delta * treated), dims="obs_id")
    pm.Normal("y", mu=mu, sigma=sigma, observed=df.y, dims="obs_id")

pm.model_to_graphviz(model)
../_images/349723bfe8e021a180590d168f76eb888b1ac871e07108b407c4c396c894ab9a.svg

推断#

with model:
    idata = pm.sample(random_seed=RANDOM_SEED)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [sigma, effect]
100.00% [8000/8000 00:00<00:00 采样 4 条链，0 个发散]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.

我们可以看到，我们没有收到采样警告，并且绘制 MCMC 轨迹图显示没有问题。

az.plot_trace(idata, var_names=["effect", "sigma"]);
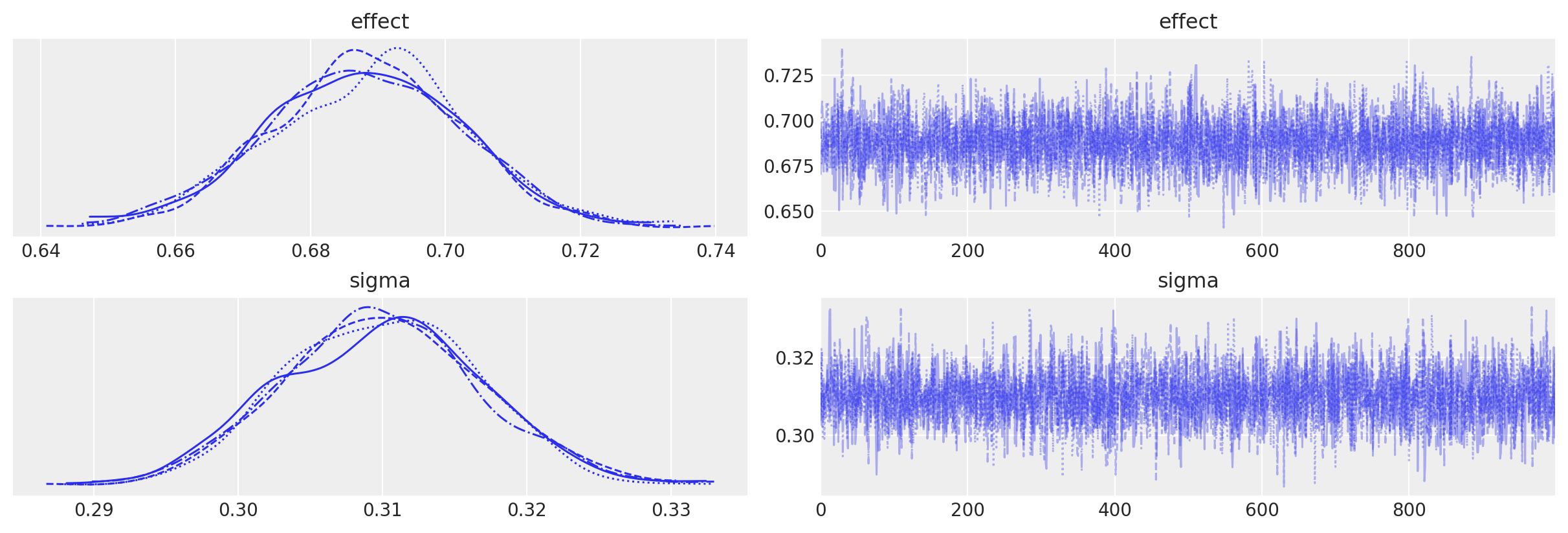
../_images/76103b825978fd64ac7d9a96c1a7142a3b23f8a999eb2a2a9f82ed2948b681d9.png

我们还可以看到，我们能够准确地恢复真实的不连续性幅度（左图）以及单位在前测和后测之间变化的​​标准差（右图）。

az.plot_posterior(
    idata, var_names=["effect", "sigma"], ref_val=[treatment_effect, sd], hdi_prob=0.95
);
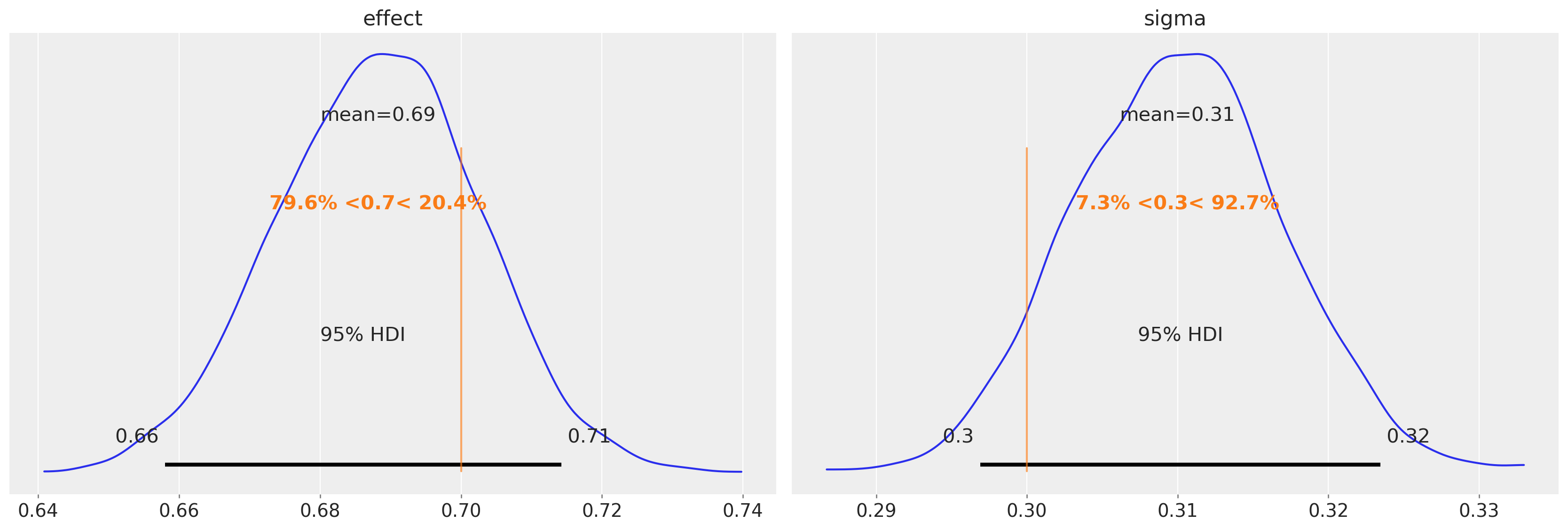
../_images/0bff9be0ca34ed04e3f19fd76f65a0678ccd201bb95855f1fe6e7cae59da941d.png

最重要的是 effect 参数的后验分布。 我们可以使用它来判断效果的强度（例如，通过 95% 可信区间）或效果的存在/不存在（例如，通过贝叶斯因子或 ROPE）。

反事实问题#

我们可以使用后验预测来询问，如果我们

  • 没有单元接受治疗（蓝色阴影区域，非常窄）

  • 所有单元都接受了治疗（橙色阴影区域）。

技术说明： 形式上，我们正在进行 y 的后验预测。 多次使用不同的随机种子运行 pm.sample_posterior_predictive 将导致每次 y 的新的和不同的样本。 但是，对于 mu 而言，情况并非如此（我们没有正式进行后验预测）。 这是因为 mu 是一个确定性函数（mu = x + delta*treated），因此对于我们已经获得的 delta 的后验样本，mu 的值将完全由 x 和 treated 数据的值确定）。

# MODEL EXPECTATION WITHOUT TREATMENT ------------------------------------
# probe data
_x = np.linspace(np.min(df.x), np.max(df.x), 500)
_treated = np.zeros(_x.shape)

# posterior prediction (see technical note above)
with model:
    pm.set_data({"x": _x, "treated": _treated})
    ppc = pm.sample_posterior_predictive(idata, var_names=["mu", "y"])

# plotting
ax = plot_data(df)
az.plot_hdi(
    _x,
    ppc.posterior_predictive["mu"],
    color="C0",
    hdi_prob=0.95,
    ax=ax,
    fill_kwargs={"label": r"$\mu$ untreated"},
)

# MODEL EXPECTATION WITH TREATMENT ---------------------------------------
# probe data
_x = np.linspace(np.min(df.x), np.max(df.x), 500)
_treated = np.ones(_x.shape)

# posterior prediction (see technical note above)
with model:
    pm.set_data({"x": _x, "treated": _treated})
    ppc = pm.sample_posterior_predictive(idata, var_names=["mu", "y"])

# plotting
az.plot_hdi(
    _x,
    ppc.posterior_predictive["mu"],
    color="C1",
    hdi_prob=0.95,
    ax=ax,
    fill_kwargs={"label": r"$\mu$ treated"},
)
ax.legend()

Sampling: [y]
100.00% [4000/4000 00:00<00:00] 
Sampling: [y]
100.00% [4000/4000 00:00<00:00] 
<matplotlib.legend.Legend at 0x12ff8bfd0>
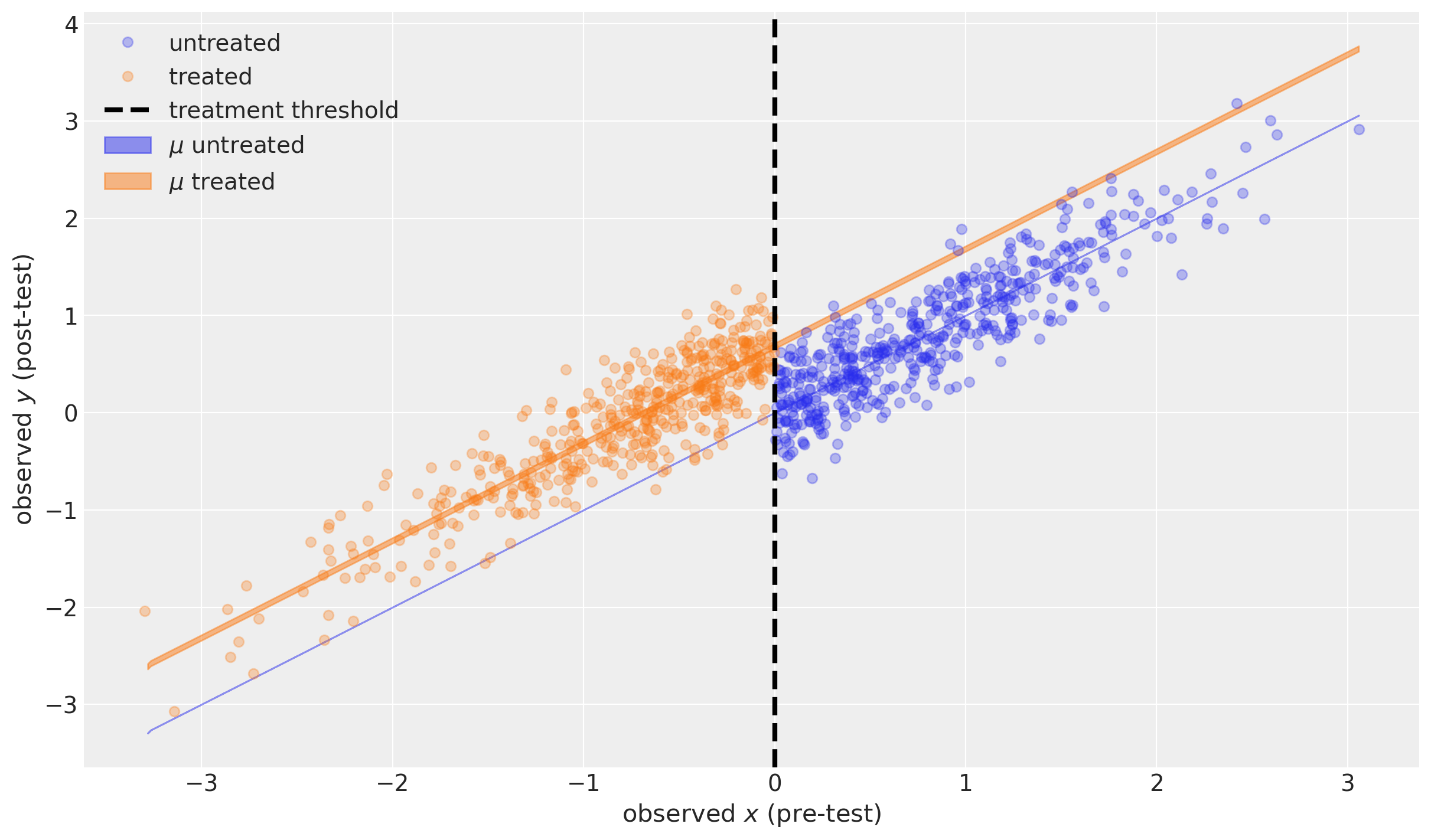
../_images/824076ccdb239564ecff17303a90ec60d34065ac9e23f902c1576fce336bdb9d.png

蓝色阴影区域显示了在没有治疗的情况下，一系列可能的前测指标的后测测量预期值的 95% 可信区域。 这实际上是无限窄的，因为这个特定模型假设 \(\mu=x\)（见上文）。

橙色阴影区域显示了在治疗情况下，一系列可能的前测指标的后测测量预期值的 95% 可信区域。

两者实际上都是反事实推断的非常有趣的例子。 我们没有观察到任何阈值以下的未治疗单元，也没有观察到任何阈值以上的已治疗单元。 但是，假设我们的模型是对现实的良好描述，我们可以提出反事实问题“如果阈值以上的单元接受治疗会怎样？”以及“如果阈值以下的单元接受治疗会怎样？”

总结#

在本笔记本中，我们仅触及了如何分析来自回归不连续性设计的数据的表面。 可以说，我们将重点限制在几乎最简单的情况下，以便我们可以专注于允许提出因果关系主张的方法的核心属性。

作者#

  • 由 Benjamin T. Vincent 于 2022 年 4 月创作

  • Benjamin T. Vincent 于 2023 年 2 月更新，以在 PyMC v5 上运行

水印#

%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,aeppl,xarray

Last updated: Wed Feb 01 2023

Python implementation: CPython
Python version       : 3.11.0
IPython version      : 8.9.0

pytensor: 2.8.11
aeppl   : not installed
xarray  : 2023.1.0

arviz     : 0.14.0
pandas    : 1.5.3
pymc      : 5.0.1
matplotlib: 3.6.3
numpy     : 1.24.1

Watermark: 2.3.1

许可声明#

本示例库中的所有笔记本均根据 MIT 许可证 提供，该许可证允许修改和再分发用于任何用途，前提是保留版权和许可声明。

引用 PyMC 示例#

要引用本笔记本，请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。

重要提示

许多笔记本都改编自其他来源：博客、书籍…… 在这种情况下，您也应该引用原始来源。

另请记住引用您的代码使用的相关库。

这是一个 bibtex 中的引用模板

@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}

渲染后可能看起来像