异方差高斯过程#
我们通常可以将模型中的不确定性来源分为两类。“偶然性”不确定性（来自拉丁语中骰子或随机性的词语）源于我们系统固有的变异性。“认知性”不确定性（来自希腊语中知识的词语）源于我们的观测结果在我们感兴趣的领域中的位置。
高斯过程 (GP) 模型是捕捉这两种不确定性来源的强大工具。通过考虑满足协方差核和数据指定条件的所有函数的分布，这些模型表达了在观测值附近较低的认知不确定性，以及在更远处较高的认知不确定性。为了纳入偶然性不确定性，标准 GP 模型假设在整个域中具有恒定幅度的加性白噪声。然而，如果某些区域比其他区域具有更高的方差，则这种“同方差”模型可能无法很好地表示您的系统。在其他领域中，这在实验科学中尤为常见，在实验科学中，改变实验参数会影响响应的幅度和变异性。显式地结合噪声对输入和输出的依赖性（和相互依赖性）可以更好地理解平均行为，并为优化提供更丰富的信息，例如。
本笔记本将介绍几种使用 GP 进行异方差建模的方法。我们将使用玩具数据，这些数据代表在系统上的一系列输入值上进行的（独立）重复测量，其中噪声的幅度随着响应变量的增加而增加。我们将从简单的建模方法开始，例如将 GP 拟合到每个点的均值，并按每个点的方差进行加权（如果单个测量是通过具有已知不确定性的方法进行的，这可能很有用），并将此与典型的同方差 GP 进行对比。然后，我们将构建一个模型，该模型使用一个潜在 GP 对响应均值进行建模，并使用第二个（独立的）潜在 GP 对响应方差进行建模。为了提高此模型的效率和可扩展性，我们将以稀疏框架重新制定它。最后，我们将使用共区域化核来允许噪声和平均响应之间存在相关性。
数据#
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc3 as pm
import theano.tensor as tt
from scipy.spatial.distance import pdist
%config InlineBackend.figure_format ='retina'
%load_ext watermark
SEED = 2020
rng = np.random.default_rng(SEED)
az.style.use("arviz-darkgrid")
def signal(x):
return x / 2 + np.sin(2 * np.pi * x) / 5
def noise(y):
return np.exp(y) / 20
X = np.linspace(0.1, 1, 20)[:, None]
X = np.vstack([X, X + 2])
X_ = X.flatten()
y = signal(X_)
σ_fun = noise(y)
y_err = rng.lognormal(np.log(σ_fun), 0.1)
y_obs = rng.normal(y, y_err, size=(5, len(y)))
y_obs_ = y_obs.T.flatten()
X_obs = np.tile(X.T, (5, 1)).T.reshape(-1, 1)
X_obs_ = X_obs.flatten()
idx = np.tile(np.array([i for i, _ in enumerate(X_)]), (5, 1)).T.flatten()
Xnew = np.linspace(-0.15, 3.25, 100)[:, None]
Xnew_ = Xnew.flatten()
ynew = signal(Xnew)
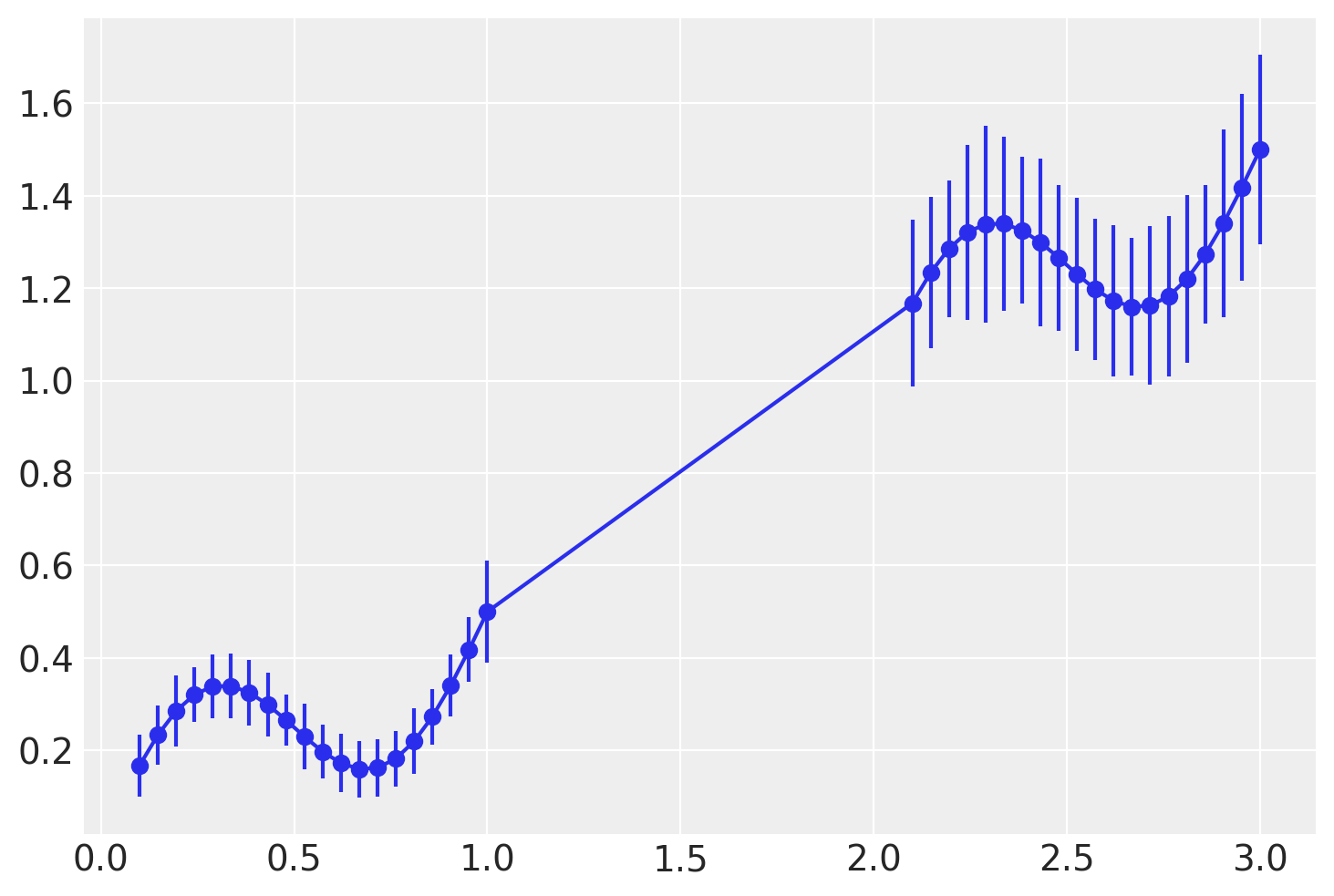
plt.plot(X, y, "C0o")
plt.errorbar(X_, y, y_err, color="C0")
<ErrorbarContainer object of 3 artists>
辅助和绘图函数#
def get_ℓ_prior(points):
"""Calculates mean and sd for InverseGamma prior on lengthscale"""
distances = pdist(points[:, None])
distinct = distances != 0
ℓ_l = distances[distinct].min() if sum(distinct) > 0 else 0.1
ℓ_u = distances[distinct].max() if sum(distinct) > 0 else 1
ℓ_σ = max(0.1, (ℓ_u - ℓ_l) / 6)
ℓ_μ = ℓ_l + 3 * ℓ_σ
return ℓ_μ, ℓ_σ
ℓ_μ, ℓ_σ = [stat for stat in get_ℓ_prior(X_)]
def plot_inducing_points(ax):
yl = ax.get_ylim()
yu = -np.subtract(*yl) * 0.025 + yl[0]
ax.plot(Xu, np.full(Xu.shape, yu), "xk", label="Inducing Points")
ax.legend(loc="upper left")
def get_quantiles(samples, quantiles=[2.5, 50, 97.5]):
return [np.percentile(samples, p, axis=0) for p in quantiles]
def plot_mean(ax, mean_samples):
"""Plots the median and 95% CI from samples of the mean
Note that, although each individual GP exhibits a normal distribution at each point
(by definition), we are sampling from a mixture of GPs defined by the posteriors of
our hyperparameters. As such, we use percentiles rather than mean +/- stdev to
represent the spread of predictions from our models.
"""
l, m, u = get_quantiles(mean_samples)
ax.plot(Xnew, m, "C0", label="Median")
ax.fill_between(Xnew_, l, u, facecolor="C0", alpha=0.5, label="95% CI")
ax.plot(Xnew, ynew, "--k", label="Mean Function")
ax.plot(X, y, "C1.", label="Observed Means")
ax.set_title("Mean Behavior")
ax.legend(loc="upper left")
def plot_var(ax, var_samples):
"""Plots the median and 95% CI from samples of the variance"""
if var_samples.squeeze().ndim == 1:
ax.plot(Xnew, var_samples, "C0", label="Median")
else:
l, m, u = get_quantiles(var_samples)
ax.plot(Xnew, m, "C0", label="Median")
ax.fill_between(Xnew.flatten(), l, u, facecolor="C0", alpha=0.5, label="95% CI")
ax.plot(Xnew, noise(signal(Xnew_)) ** 2, "--k", label="Noise Function")
ax.plot(X, y_err**2, "C1.", label="Observed Variance")
ax.set_title("Variance Behavior")
ax.legend(loc="upper left")
def plot_total(ax, mean_samples, var_samples=None, bootstrap=True, n_boots=100):
"""Plots the overall mean and variance of the aggregate system
We can represent the overall uncertainty via explicitly sampling the underlying normal
distributrions (with `bootstrap=True`) or as the mean +/- the standard deviation from
the Law of Total Variance. For systems with many observations, there will likely be
little difference, but in cases with few observations and informative priors, plotting
the percentiles will likely give a more accurate representation.
"""
if (var_samples is None) or (var_samples.squeeze().ndim == 1):
samples = mean_samples
l, m, u = get_quantiles(samples)
ax.plot(Xnew, m, "C0", label="Median")
elif bootstrap:
# Estimate the aggregate behavior using samples from each normal distribution in the posterior
samples = (
rng.normal(
mean_samples.T[:, :, None],
np.sqrt(var_samples).T[:, :, None],
(*mean_samples.T.shape, n_boots),
)
.reshape(len(Xnew_), -1)
.T
)
l, m, u = get_quantiles(samples)
ax.plot(Xnew, m, "C0", label="Median")
else:
m = mean_samples.mean(axis=0)
ax.plot(Xnew, m, "C0", label="Mean")
sd = np.sqrt(mean_samples.var(axis=0) + var_samples.mean(axis=0))
l, u = m - 2 * sd, m + 2 * sd
ax.fill_between(Xnew.flatten(), l, u, facecolor="C0", alpha=0.5, label="Total 95% CI")
ax.plot(Xnew, ynew, "--k", label="Mean Function")
ax.plot(X_obs, y_obs_, "C1.", label="Observations")
ax.set_title("Aggregate Behavior")
ax.legend(loc="upper left")
同方差 GP#
首先，让我们使用 PyMC3 的 Marginal Likelihood 实现拟合同方差 GP。在本笔记本中，我们将始终使用 Michael Betancourt 建议的信息性先验作为长度尺度的先验。我们可以使用 pm.find_MAP() 和 .predict 以获得更快的推理和预测，结果类似，但为了与其他模型进行直接比较，我们将使用 NUTS 和 .conditional，它们运行速度足够快。
with pm.Model() as model_hm:
ℓ = pm.InverseGamma("ℓ", mu=ℓ_μ, sigma=ℓ_σ)
η = pm.Gamma("η", alpha=2, beta=1)
cov = η**2 * pm.gp.cov.ExpQuad(input_dim=1, ls=ℓ)
gp_hm = pm.gp.Marginal(cov_func=cov)
σ = pm.Exponential("σ", lam=1)
ml_hm = gp_hm.marginal_likelihood("ml_hm", X=X_obs, y=y_obs_, noise=σ)
trace_hm = pm.sample(return_inferencedata=True, random_seed=SEED)
with model_hm:
mu_pred_hm = gp_hm.conditional("mu_pred_hm", Xnew=Xnew)
noisy_pred_hm = gp_hm.conditional("noisy_pred_hm", Xnew=Xnew, pred_noise=True)
samples_hm = pm.sample_posterior_predictive(trace_hm, var_names=["mu_pred_hm", "noisy_pred_hm"])
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [σ, η, ℓ]
100.00% [8000/8000 01:50<00:00 采样 4 条链, 0 个发散]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 112 seconds.
100.00% [4000/4000 01:09<00:00]
_, axs = plt.subplots(1, 3, figsize=(18, 4))
mu_samples = samples_hm["mu_pred_hm"]
noisy_samples = samples_hm["noisy_pred_hm"]
plot_mean(axs[0], mu_samples)
plot_var(axs[1], noisy_samples.var(axis=0))
plot_total(axs[2], noisy_samples)
在这里，我们绘制了我们对均值行为的理解（在左侧带有相应的认知不确定性），我们对中间方差或偶然性不确定性的理解，以及右侧整合所有不确定性来源。该模型很好地捕捉了均值行为，但我们可以看到，它高估了较低区域的噪声，同时低估了较高区域的噪声，正如预期的那样。
方差加权 GP#
对异方差系统进行建模的最简单方法是在域中每个点的均值上拟合 GP，并提供标准差作为权重。
with pm.Model() as model_wt:
ℓ = pm.InverseGamma("ℓ", mu=ℓ_μ, sigma=ℓ_σ)
η = pm.Gamma("η", alpha=2, beta=1)
cov = η**2 * pm.gp.cov.ExpQuad(input_dim=1, ls=ℓ)
gp_wt = pm.gp.Marginal(cov_func=cov)
ml_wt = gp_wt.marginal_likelihood("ml_wt", X=X, y=y, noise=y_err)
trace_wt = pm.sample(return_inferencedata=True, random_seed=SEED)
with model_wt:
mu_pred_wt = gp_wt.conditional("mu_pred_wt", Xnew=Xnew)
samples_wt = pm.sample_posterior_predictive(trace_wt, var_names=["mu_pred_wt"])
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [η, ℓ]
100.00% [8000/8000 00:18<00:00 采样 4 条链, 0 个发散]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 18 seconds.
100.00% [4000/4000 00:20<00:00]
_, axs = plt.subplots(1, 3, figsize=(18, 4))
mu_samples = samples_wt["mu_pred_wt"]
plot_mean(axs[0], mu_samples)
axs[0].errorbar(X_, y, y_err, ls="none", color="C1", label="STDEV")
plot_var(axs[1], mu_samples.var(axis=0))
plot_total(axs[2], mu_samples)
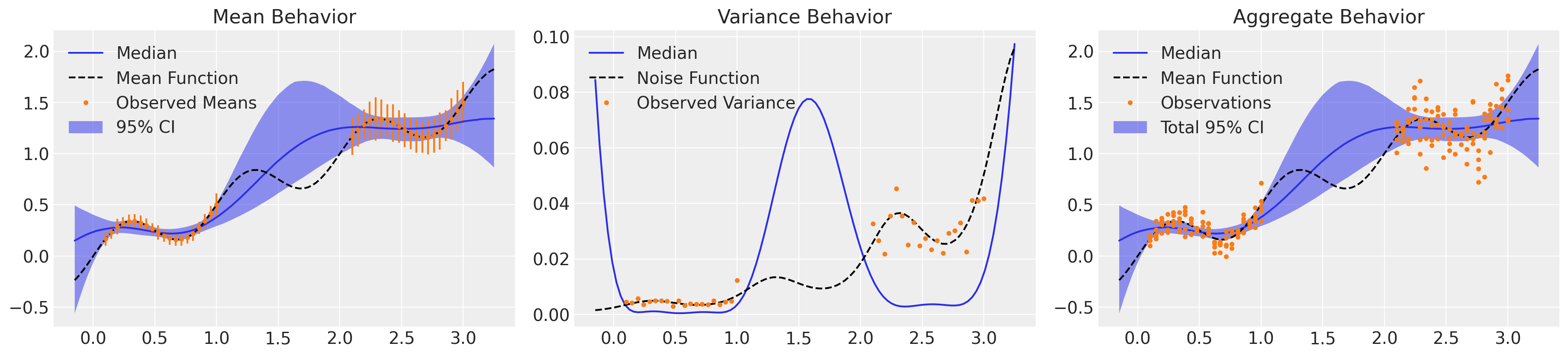
这种方法比同方差 GP 在整体不确定性中捕捉到更多细微之处，但仍然低估了观察到的两种状态下的方差。请注意，此模型显示的方差纯粹是认知性的：我们对均值行为的理解受我们观测结果中不确定性的加权，但我们没有包含一个用于解释偶然噪声的组成部分。
异方差 GP：潜在方差模型#
现在，让我们通过 PyMC3 的 Latent 实现将均值和方差的对数建模为单独的 GP，并将两者都馈送到 Normal 似然函数中。请注意，我们在各个协方差中添加少量对角噪声，以使其反演稳定。
with pm.Model() as model_ht:
ℓ = pm.InverseGamma("ℓ", mu=ℓ_μ, sigma=ℓ_σ)
η = pm.Gamma("η", alpha=2, beta=1)
cov = η**2 * pm.gp.cov.ExpQuad(input_dim=1, ls=ℓ) + pm.gp.cov.WhiteNoise(sigma=1e-6)
gp_ht = pm.gp.Latent(cov_func=cov)
μ_f = gp_ht.prior("μ_f", X=X_obs)
σ_ℓ = pm.InverseGamma("σ_ℓ", mu=ℓ_μ, sigma=ℓ_σ)
σ_η = pm.Gamma("σ_η", alpha=2, beta=1)
σ_cov = σ_η**2 * pm.gp.cov.ExpQuad(input_dim=1, ls=σ_ℓ) + pm.gp.cov.WhiteNoise(sigma=1e-6)
σ_gp = pm.gp.Latent(cov_func=σ_cov)
lg_σ_f = σ_gp.prior("lg_σ_f", X=X_obs)
σ_f = pm.Deterministic("σ_f", pm.math.exp(lg_σ_f))
lik_ht = pm.Normal("lik_ht", mu=μ_f, sd=σ_f, observed=y_obs_)
trace_ht = pm.sample(target_accept=0.95, chains=2, return_inferencedata=True, random_seed=SEED)
with model_ht:
μ_pred_ht = gp_ht.conditional("μ_pred_ht", Xnew=Xnew)
lg_σ_pred_ht = σ_gp.conditional("lg_σ_pred_ht", Xnew=Xnew)
samples_ht = pm.sample_posterior_predictive(trace_ht, var_names=["μ_pred_ht", "lg_σ_pred_ht"])
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 4 jobs)
NUTS: [lg_σ_f_rotated_, σ_η, σ_ℓ, μ_f_rotated_, η, ℓ]
100.00% [4000/4000 2:07:31<00:00 采样 2 条链, 26 个发散]
Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 7652 seconds.
There were 9 divergences after tuning. Increase `target_accept` or reparameterize.
There were 17 divergences after tuning. Increase `target_accept` or reparameterize.
100.00% [2000/2000 00:37<00:00]
_, axs = plt.subplots(1, 3, figsize=(18, 4))
μ_samples = samples_ht["μ_pred_ht"]
σ_samples = np.exp(samples_ht["lg_σ_pred_ht"])
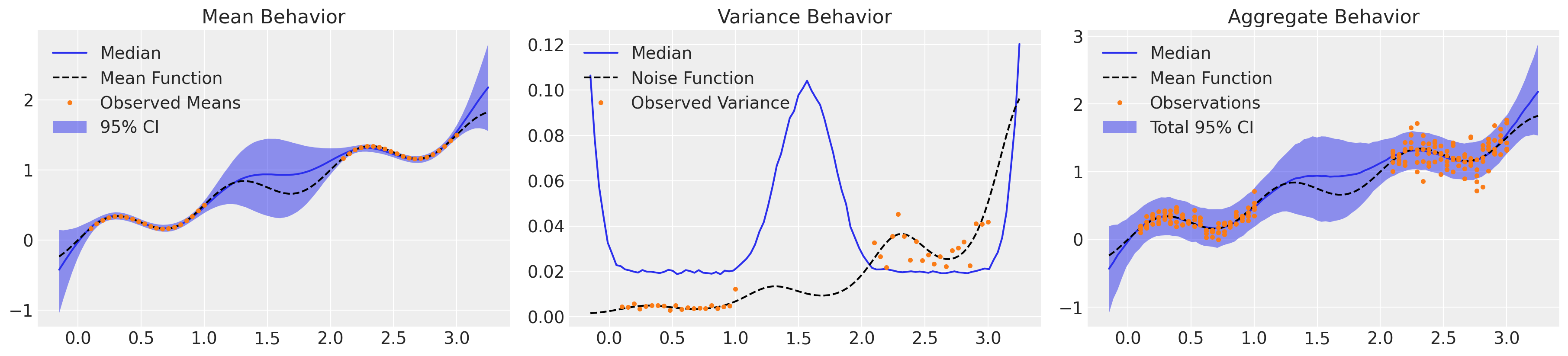
plot_mean(axs[0], μ_samples)
plot_var(axs[1], σ_samples**2)
plot_total(axs[2], μ_samples, σ_samples**2)
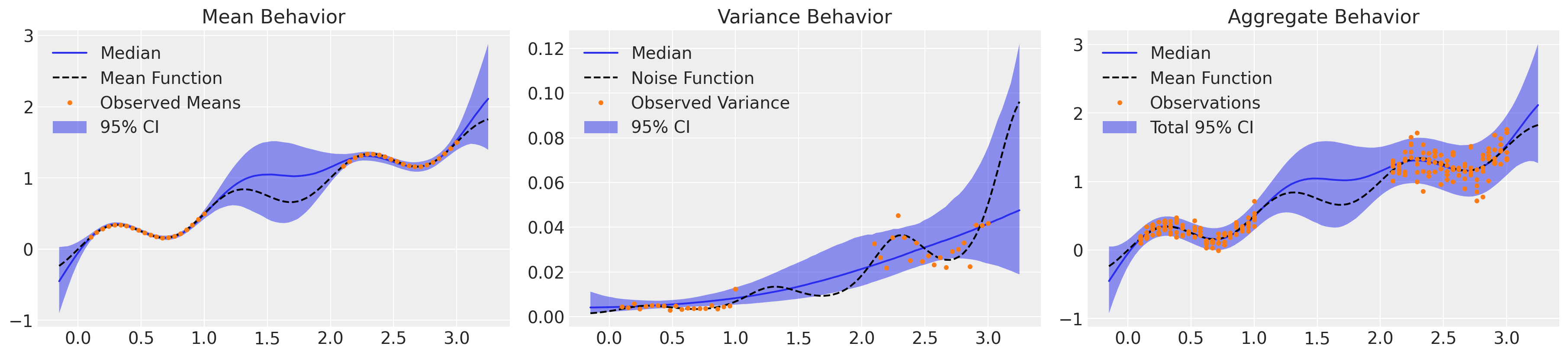
看起来好多了！我们准确地捕捉了系统的均值行为以及对潜在方差趋势的理解，并具有适当的不确定性。至关重要的是，模型的总体行为整合了认知性和偶然性不确定性，并且我们大约 5% 的观测值落在 2σ 带之外，并且或多或少均匀分布在整个域中。然而，仅采样 4k NUTS 迭代就花费了两个多小时。由于所需矩阵求逆的成本，GP 对于大型数据集来说效率非常低。让我们使用稀疏近似重新制定此模型。
稀疏异方差 GP#
GP 的稀疏近似使用一小组诱导点来调节模型，大大提高了推理速度，并在一定程度上提高了内存消耗。PyMC3 没有稀疏潜在 GP 的实现（尚未），但我们可以使用 Bill Engel 的 DTC 潜在 GP 示例快速组合我们自己的实现。这些诱导点可以通过多种方式指定，例如通过流行的 k-means 初始化，甚至可以作为模型的一部分进行优化，但由于我们的观测结果均匀分布，我们可以简单地使用我们唯一输入值的子集来完成。
class SparseLatent:
def __init__(self, cov_func):
self.cov = cov_func
def prior(self, name, X, Xu):
Kuu = self.cov(Xu)
self.L = pm.gp.util.cholesky(pm.gp.util.stabilize(Kuu))
self.v = pm.Normal(f"u_rotated_{name}", mu=0.0, sd=1.0, shape=len(Xu))
self.u = pm.Deterministic(f"u_{name}", tt.dot(self.L, self.v))
Kfu = self.cov(X, Xu)
self.Kuiu = tt.slinalg.solve_upper_triangular(
self.L.T, tt.slinalg.solve_lower_triangular(self.L, self.u)
)
self.mu = pm.Deterministic(f"mu_{name}", tt.dot(Kfu, self.Kuiu))
return self.mu
def conditional(self, name, Xnew, Xu):
Ksu = self.cov(Xnew, Xu)
mus = tt.dot(Ksu, self.Kuiu)
tmp = tt.slinalg.solve_lower_triangular(self.L, Ksu.T)
Qss = tt.dot(tmp.T, tmp) # Qss = tt.dot(tt.dot(Ksu, tt.nlinalg.pinv(Kuu)), Ksu.T)
Kss = self.cov(Xnew)
Lss = pm.gp.util.cholesky(pm.gp.util.stabilize(Kss - Qss))
mu_pred = pm.MvNormal(name, mu=mus, chol=Lss, shape=len(Xnew))
return mu_pred
# Explicitly specify inducing points by downsampling our input vector
Xu = X[1::2]
with pm.Model() as model_hts:
ℓ = pm.InverseGamma("ℓ", mu=ℓ_μ, sigma=ℓ_σ)
η = pm.Gamma("η", alpha=2, beta=1)
cov = η**2 * pm.gp.cov.ExpQuad(input_dim=1, ls=ℓ)
μ_gp = SparseLatent(cov)
μ_f = μ_gp.prior("μ", X_obs, Xu)
σ_ℓ = pm.InverseGamma("σ_ℓ", mu=ℓ_μ, sigma=ℓ_σ)
σ_η = pm.Gamma("σ_η", alpha=2, beta=1)
σ_cov = σ_η**2 * pm.gp.cov.ExpQuad(input_dim=1, ls=σ_ℓ)
lg_σ_gp = SparseLatent(σ_cov)
lg_σ_f = lg_σ_gp.prior("lg_σ_f", X_obs, Xu)
σ_f = pm.Deterministic("σ_f", pm.math.exp(lg_σ_f))
lik_hts = pm.Normal("lik_hts", mu=μ_f, sd=σ_f, observed=y_obs_)
trace_hts = pm.sample(target_accept=0.95, return_inferencedata=True, random_seed=SEED)
with model_hts:
μ_pred = μ_gp.conditional("μ_pred", Xnew, Xu)
lg_σ_pred = lg_σ_gp.conditional("lg_σ_pred", Xnew, Xu)
samples_hts = pm.sample_posterior_predictive(trace_hts, var_names=["μ_pred", "lg_σ_pred"])
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [u_rotated_lg_σ_f, σ_η, σ_ℓ, u_rotated_μ, η, ℓ]
100.00% [8000/8000 32:49<00:00 采样 4 条链, 20 个发散]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1971 seconds.
There were 4 divergences after tuning. Increase `target_accept` or reparameterize.
There were 10 divergences after tuning. Increase `target_accept` or reparameterize.
There were 2 divergences after tuning. Increase `target_accept` or reparameterize.
There were 4 divergences after tuning. Increase `target_accept` or reparameterize.
The number of effective samples is smaller than 25% for some parameters.
100.00% [4000/4000 00:40<00:00]
_, axs = plt.subplots(1, 3, figsize=(18, 4))
μ_samples = samples_hts["μ_pred"]
σ_samples = np.exp(samples_hts["lg_σ_pred"])
plot_mean(axs[0], μ_samples)
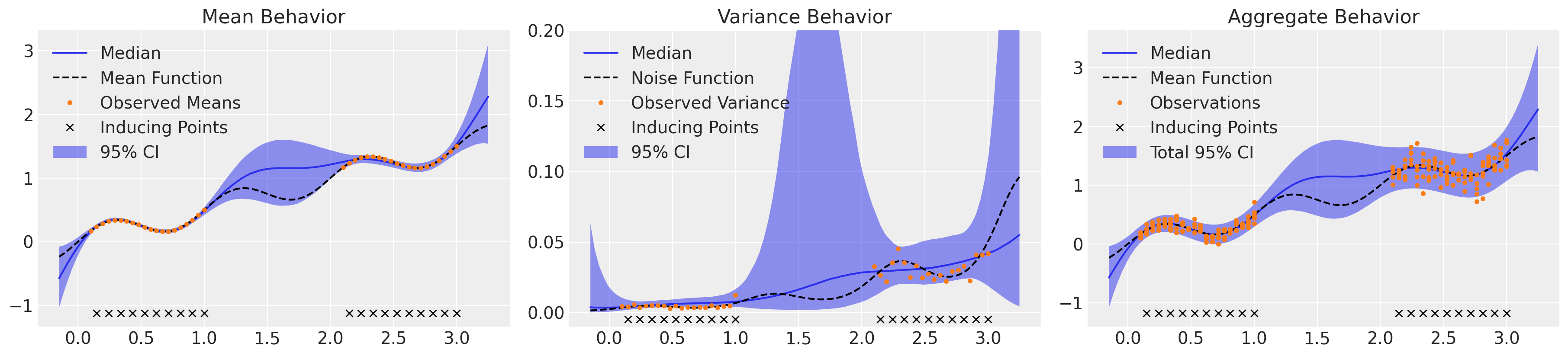
plot_inducing_points(axs[0])
plot_var(axs[1], σ_samples**2)
plot_inducing_points(axs[1])
plot_total(axs[2], μ_samples, σ_samples**2)
plot_inducing_points(axs[2])
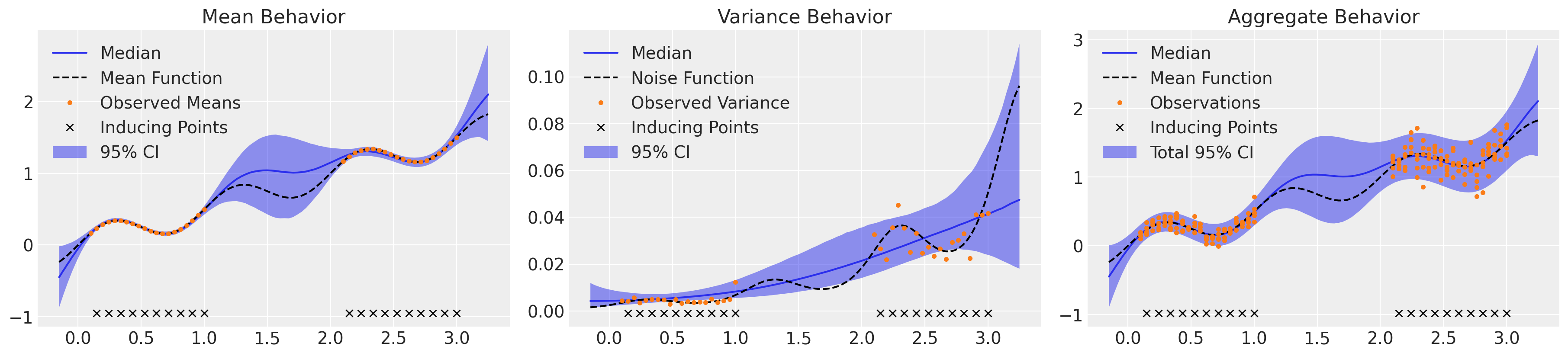
速度快了大约 8 倍，结果几乎没有区别，发散也更少。
具有相关噪声和均值响应的异方差 GP：线性共区域化模型#
到目前为止，我们将系统的均值和噪声建模为独立的。但是，在某些情况下，我们可能期望它们是相关的，例如，如果预期较高的测量值具有更大的噪声。在这里，我们将通过协方差函数显式地对此相关性进行建模，该协方差函数是我们之前使用的空间核和 Coregion 核的克罗内克积，正如 Bill Engels 在 此处 建议的那样。这是线性共区域化模型的实现，该模型将每个相关的 GP 视为少量独立基函数的线性组合，而这些基函数本身就是 GP。我们首先向观测值的域添加一个分类维度，以指示正在考虑均值还是方差，然后在将各个组成部分馈送到上面的 Normal 似然函数之前解包它们。
def add_coreg_idx(x):
return np.hstack([np.tile(x, (2, 1)), np.vstack([np.zeros(x.shape), np.ones(x.shape)])])
Xu_c, X_obs_c, Xnew_c = [add_coreg_idx(x) for x in [Xu, X_obs, Xnew]]
with pm.Model() as model_htsc:
ℓ = pm.InverseGamma("ℓ", mu=ℓ_μ, sigma=ℓ_σ)
η = pm.Gamma("η", alpha=2, beta=1)
EQcov = η**2 * pm.gp.cov.ExpQuad(input_dim=1, active_dims=[0], ls=ℓ)
D_out = 2 # two output dimensions, mean and variance
rank = 2 # two basis GPs
W = pm.Normal("W", mu=0, sd=3, shape=(D_out, rank), testval=np.full([D_out, rank], 0.1))
kappa = pm.Gamma("kappa", alpha=1.5, beta=1, shape=D_out)
coreg = pm.gp.cov.Coregion(input_dim=1, active_dims=[0], kappa=kappa, W=W)
cov = pm.gp.cov.Kron([EQcov, coreg])
gp_LMC = SparseLatent(cov)
LMC_f = gp_LMC.prior("LMC", X_obs_c, Xu_c)
μ_f = LMC_f[: len(y_obs_)]
lg_σ_f = LMC_f[len(y_obs_) :]
σ_f = pm.Deterministic("σ_f", pm.math.exp(lg_σ_f))
lik_htsc = pm.Normal("lik_htsc", mu=μ_f, sd=σ_f, observed=y_obs_)
trace_htsc = pm.sample(target_accept=0.95, return_inferencedata=True, random_seed=SEED)
with model_htsc:
c_mu_pred = gp_LMC.conditional("c_mu_pred", Xnew_c, Xu_c)
samples_htsc = pm.sample_posterior_predictive(trace_htsc, var_names=["c_mu_pred"])
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [u_rotated_LMC, kappa, W, η, ℓ]
100.00% [8000/8000 2:14:23<00:00 采样 4 条链, 49 个发散]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 8065 seconds.
There were 7 divergences after tuning. Increase `target_accept` or reparameterize.
There were 27 divergences after tuning. Increase `target_accept` or reparameterize.
There were 7 divergences after tuning. Increase `target_accept` or reparameterize.
There were 8 divergences after tuning. Increase `target_accept` or reparameterize.
The number of effective samples is smaller than 10% for some parameters.
100.00% [4000/4000 00:35<00:00]
μ_samples = samples_htsc["c_mu_pred"][:, : len(Xnew)]
σ_samples = np.exp(samples_htsc["c_mu_pred"][:, len(Xnew) :])
_, axs = plt.subplots(1, 3, figsize=(18, 4))
plot_mean(axs[0], μ_samples)
plot_inducing_points(axs[0])
plot_var(axs[1], σ_samples**2)
axs[1].set_ylim(-0.01, 0.2)
axs[1].legend(loc="upper left")
plot_inducing_points(axs[1])
plot_total(axs[2], μ_samples, σ_samples**2)
plot_inducing_points(axs[2])
我们可以通过检查通过 \(\mathbf{B} \equiv \mathbf{WW}^T+diag(\kappa)\) 构建的协方差矩阵 \(\bf{B}\) 来查看均值和方差之间学习到的相关性
with model_htsc:
B_samples = pm.sample_posterior_predictive(trace_htsc, var_names=["W", "kappa"])
100.00% [4000/4000 00:00<00:00]
# Keep in mind that the first dimension in all arrays is the sampling dimension
W = B_samples["W"]
W_T = np.swapaxes(W, 1, 2)
WW_T = np.matmul(W, W_T)
kappa = B_samples["kappa"]
I = np.tile(np.identity(2), [kappa.shape[0], 1, 1])
# einsum is just a concise way of doing multiplication and summation over arbitrary axes
diag_kappa = np.einsum("ij,ijk->ijk", kappa, I)
B = WW_T + diag_kappa
B.mean(axis=0)
array([[15.72083568, -0.98047927],
[-0.98047927, 11.53955904]])
sd = np.sqrt(np.diagonal(B, axis1=1, axis2=2))
outer_sd = np.einsum("ij,ik->ijk", sd, sd)
correlation = B / outer_sd
print(f"2.5%ile correlation: {np.percentile(correlation,2.5,axis=0)[0,1]:0.3f}")
print(f"Median correlation: {np.percentile(correlation,50,axis=0)[0,1]:0.3f}")
print(f"97.5%ile correlation: {np.percentile(correlation,97.5,axis=0)[0,1]:0.3f}")
2.5%ile correlation: -0.888
Median correlation: -0.086
97.5%ile correlation: 0.889
该模型无意中学习到均值和噪声略微负相关，尽管具有较宽的可信区间。
比较#
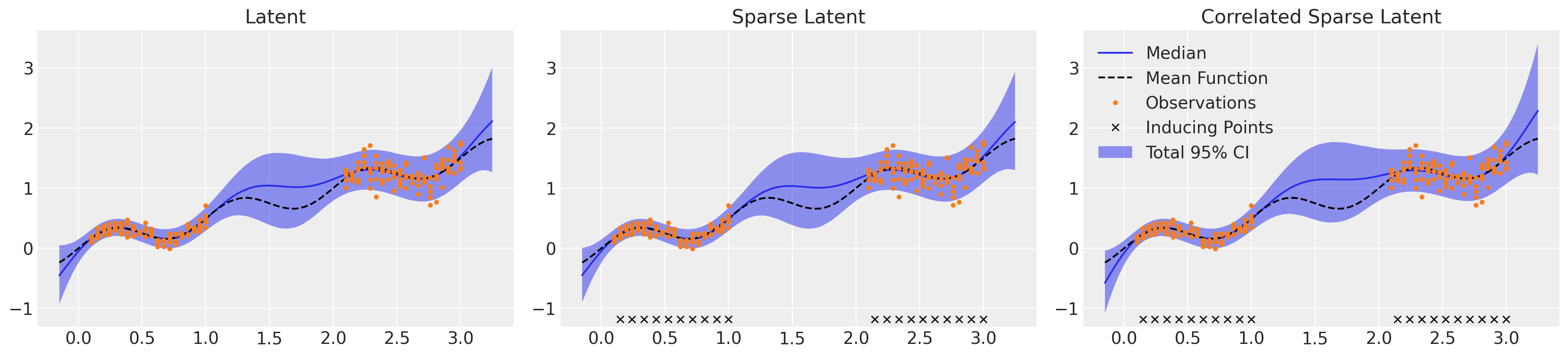
此处显示的三个潜在方法在复杂性和效率方面有所不同，但最终产生了非常相似的回归面，如下所示。所有三种方法都显示出对偶然性和认知性不确定性的细致理解。值得注意的是，我们必须将 target_accept 从默认值 0.8 增加到 0.95，以避免过多的发散，但这具有减慢 NUTS 评估速度的缺点。可以通过降低 target_accept 来缩短采样时间，但代价是可能由于发散而导致有偏差的推断，或者通过进一步减少稀疏近似中使用的诱导点数量来缩短采样时间。检查每种方法的收敛统计信息，所有方法的 r_hat 值都较低，为 1.01 或更低，但 LMC 模型显示某些参数的有效样本量较小，特别是 η 和 ℓ 参数的 ess_tail。为了对该模型的 95% CI 边界有信心，我们应该运行更多迭代的采样，理想情况下至少要运行到最小的 ess_tail 高于 200，但越高越好。
回归面#
_, axs = plt.subplots(1, 3, figsize=(18, 4))
μ_samples = samples_ht["μ_pred_ht"]
σ_samples = np.exp(samples_ht["lg_σ_pred_ht"])
plot_total(axs[0], μ_samples, σ_samples**2)
axs[0].set_title("Latent")
μ_samples = samples_hts["μ_pred"]
σ_samples = np.exp(samples_hts["lg_σ_pred"])
plot_total(axs[1], μ_samples, σ_samples**2)
axs[1].set_title("Sparse Latent")
μ_samples = samples_htsc["c_mu_pred"][:, : len(Xnew)]
σ_samples = np.exp(samples_htsc["c_mu_pred"][:, len(Xnew) :])
plot_total(axs[2], μ_samples, σ_samples**2)
axs[2].set_title("Correlated Sparse Latent")
yls = [ax.get_ylim() for ax in axs]
yl = [np.min([l[0] for l in yls]), np.max([l[1] for l in yls])]
for ax in axs:
ax.set_ylim(yl)
plot_inducing_points(axs[1])
plot_inducing_points(axs[2])
axs[0].legend().remove()
axs[1].legend().remove()
潜在模型收敛性#
display(az.summary(trace_ht).sort_values("ess_bulk").iloc[:5])
| 均值 | 标准差 | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| η | 1.886 | 0.731 | 0.749 | 3.311 | 0.028 | 0.020 | 659.0 | 812.0 | 1.0 |
| μ_f_rotated_[0] | 0.101 | 0.042 | 0.034 | 0.178 | 0.002 | 0.001 | 770.0 | 933.0 | 1.0 |
| ℓ | 0.581 | 0.061 | 0.472 | 0.700 | 0.002 | 0.001 | 920.0 | 846.0 | 1.0 |
| μ_f_rotated_[5] | 0.545 | 0.177 | 0.235 | 0.872 | 0.006 | 0.004 | 921.0 | 927.0 | 1.0 |
| σ_η | 1.939 | 0.748 | 0.882 | 3.303 | 0.020 | 0.014 | 1346.0 | 1176.0 | 1.0 |
稀疏潜在模型收敛性#
display(az.summary(trace_hts).sort_values("ess_bulk").iloc[:5])
| 均值 | 标准差 | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| η | 1.857 | 0.681 | 0.777 | 3.183 | 0.022 | 0.016 | 850.0 | 1122.0 | 1.0 |
| u_rotated_μ[0] | 0.147 | 0.053 | 0.061 | 0.242 | 0.002 | 0.001 | 887.0 | 1276.0 | 1.0 |
| u_rotated_μ[1] | 0.345 | 0.110 | 0.157 | 0.548 | 0.004 | 0.003 | 929.0 | 1447.0 | 1.0 |
| u_rotated_μ[2] | -1.019 | 0.312 | -1.606 | -0.463 | 0.009 | 0.006 | 1232.0 | 1866.0 | 1.0 |
| u_rotated_μ[10] | 0.984 | 0.400 | 0.191 | 1.684 | 0.011 | 0.008 | 1264.0 | 2338.0 | 1.0 |