均值和协方差函数#
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import pytensor.tensor as pt
%config InlineBackend.figure_format = "retina"
WARNING (pytensor.tensor.blas): Using NumPy C-API based implementation for BLAS functions.
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
plt.rcParams["figure.figsize"] = (10, 4)
PyMC 中提供了大量的均值和协方差函数。定义自定义的均值和协方差函数相对容易。由于 PyMC 使用 PyTensor，因此用户无需定义它们的梯度。
均值函数#
以下均值函数在 PyMC 中可用。
所有均值函数都遵循类似的使用模式。首先，指定均值函数。然后可以针对某些输入对其进行评估。前两个均值函数非常简单。无论输入如何，gp.mean.Zero 都会返回一个零向量，其长度与输入值的数量相同。
零值#
zero_func = pm.gp.mean.Zero()
X = np.linspace(0, 1, 5)[:, None]
print(zero_func(X).eval())
[0. 0. 0. 0. 0.]
PyMC 中所有 GP 实现的默认均值函数是 Zero。
常数#
gp.mean.Constant 返回一个向量，其值由用户提供。
const_func = pm.gp.mean.Constant(25.2)
print(const_func(X).eval())
[25.2 25.2 25.2 25.2 25.2]
只要形状与它将接收的输入匹配，gp.mean.Constant 也可以接受 PyTensor 张量或 PyMC 随机变量的向量。
const_func_vec = pm.gp.mean.Constant(pt.ones(5))
print(const_func_vec(X).eval())
[1. 1. 1. 1. 1.]
线性#
gp.mean.Linear 接受系数矩阵和截距向量（或一维情况下的斜率和标量截距）作为输入。
beta = rng.normal(size=3)
b = 0.0
lin_func = pm.gp.mean.Linear(coeffs=beta, intercept=b)
X = rng.normal(size=(5, 3))
print(lin_func(X).eval())
[ 1.03424803 -2.25903687 0.78030931 0.9880038 -3.45565466]
定义自定义均值函数#
要定义自定义均值函数，请继承 gp.mean.Mean，并提供 __call__ 和 __init__ 方法。例如，Constant 均值函数的代码是
import theano.tensor as tt
class Constant(pm.gp.mean.Mean):
def __init__(self, c=0):
Mean.__init__(self)
self.c = c
def __call__(self, X):
return tt.alloc(1.0, X.shape[0]) * self.c
请记住必须使用 PyTensor 而不是 NumPy。
协方差函数#
PyMC 包含了更大套件的内置 协方差 函数。以下展示了从具有给定协方差函数的 GP 先验中抽取的函数，并演示了如何以直接的方式使用 Python 运算符构建复合协方差函数。我们的目标是使我们的 API 尽可能地遵循核代数（参见 Rasmussen 和 Williams [2006] 的第 4 章）。有关它们在 PyMC 中的用法的概述，请参见主文档页面。
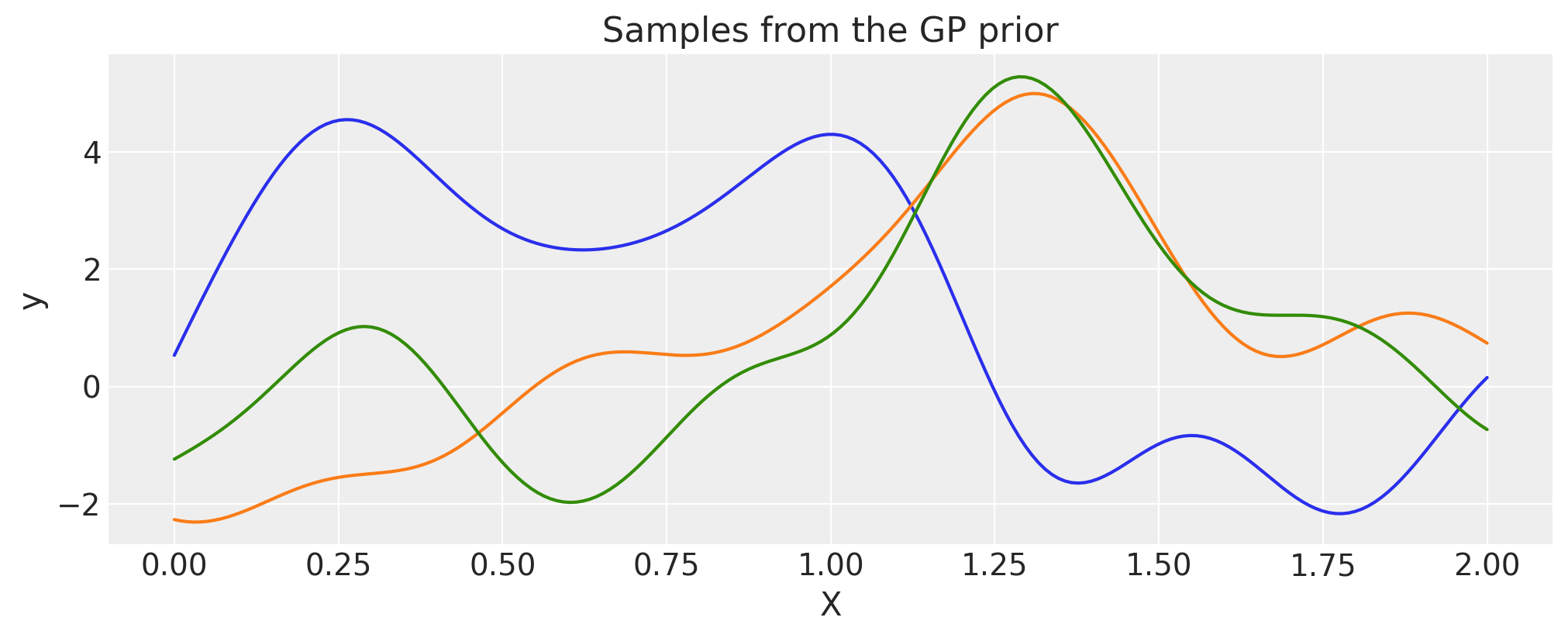
指数平方#
\[ k(x, x') = \mathrm{exp}\left[ -\frac{(x - x')^2}{2 \ell^2} \right] \]
lengthscale = 0.2
eta = 2.0
cov = eta**2 * pm.gp.cov.ExpQuad(1, lengthscale)
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)
X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()
plt.plot(
X,
pm.draw(
pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=K.shape[0]), draws=3, random_seed=rng
).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
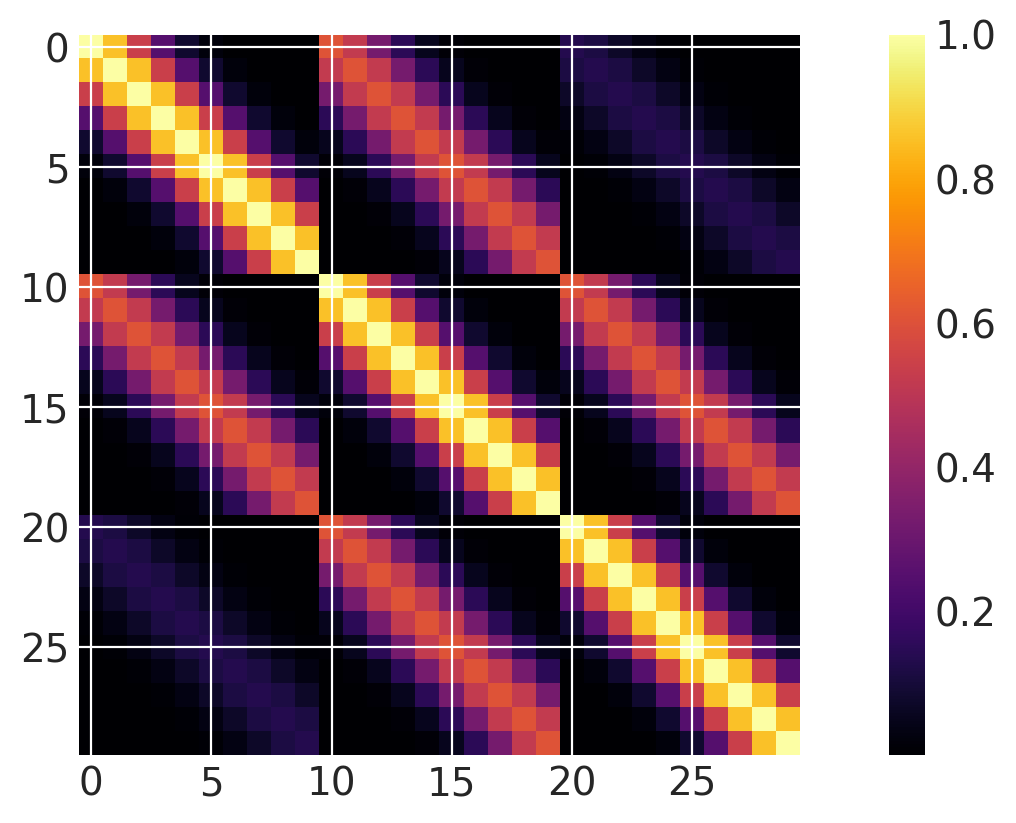
二维（和更高维）输入#
两个维度都激活#
可以轻松定义具有更高维度输入的核函数。请注意，ls（长度尺度）参数是一个长度为 2 的数组。PyMC 随机变量的列表可用于自动相关性确定 (ARD)。
x1 = np.linspace(0, 1, 10)
x2 = np.arange(1, 4)
# Cartesian product
X2 = np.dstack(np.meshgrid(x1, x2)).reshape(-1, 2)
ls = np.array([0.2, 1.0])
cov = pm.gp.cov.ExpQuad(input_dim=2, ls=ls)
m = plt.imshow(cov(X2).eval(), cmap="inferno", interpolation="none")
plt.colorbar(m);
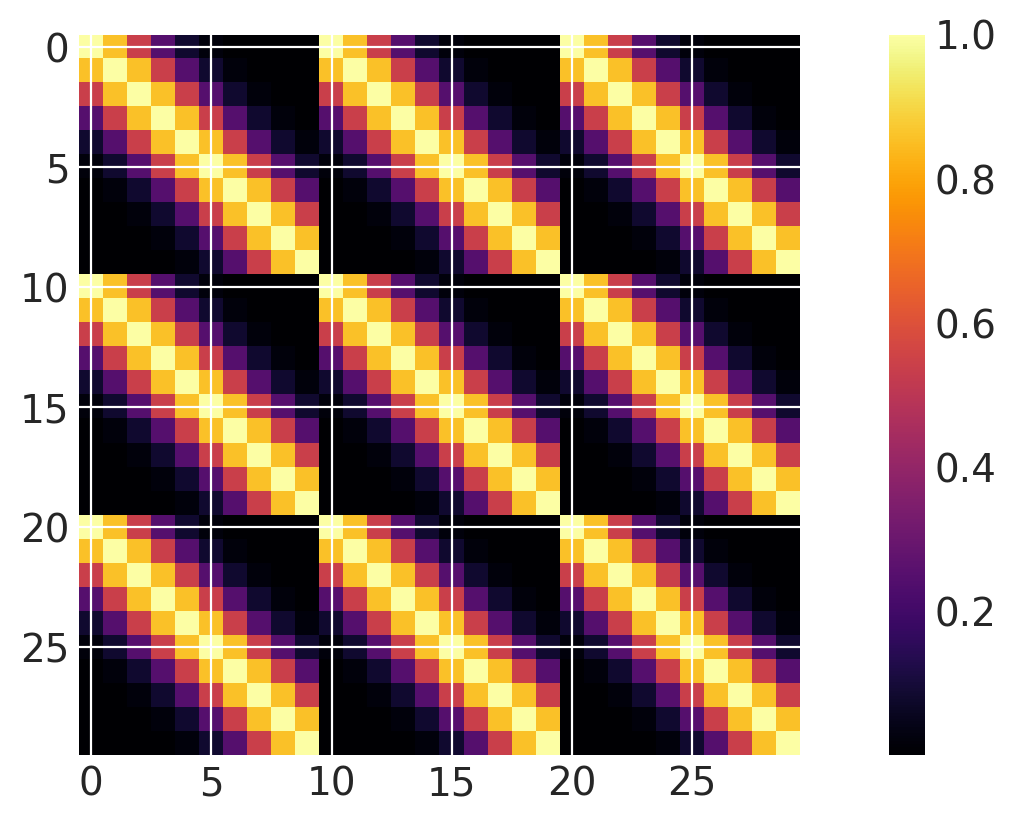
一个维度激活#
ls = 0.2
cov = pm.gp.cov.ExpQuad(input_dim=2, ls=ls, active_dims=[0])
m = plt.imshow(cov(X2).eval(), cmap="inferno", interpolation="none")
plt.colorbar(m);
不同维度上的协方差乘积#
请注意，这等效于使用二维 ExpQuad，其中每个维度都有单独的长度尺度参数。
ls1 = 0.2
ls2 = 1.0
cov1 = pm.gp.cov.ExpQuad(2, ls1, active_dims=[0])
cov2 = pm.gp.cov.ExpQuad(2, ls2, active_dims=[1])
cov = cov1 * cov2
m = plt.imshow(cov(X2).eval(), cmap="inferno", interpolation="none")
plt.colorbar(m);
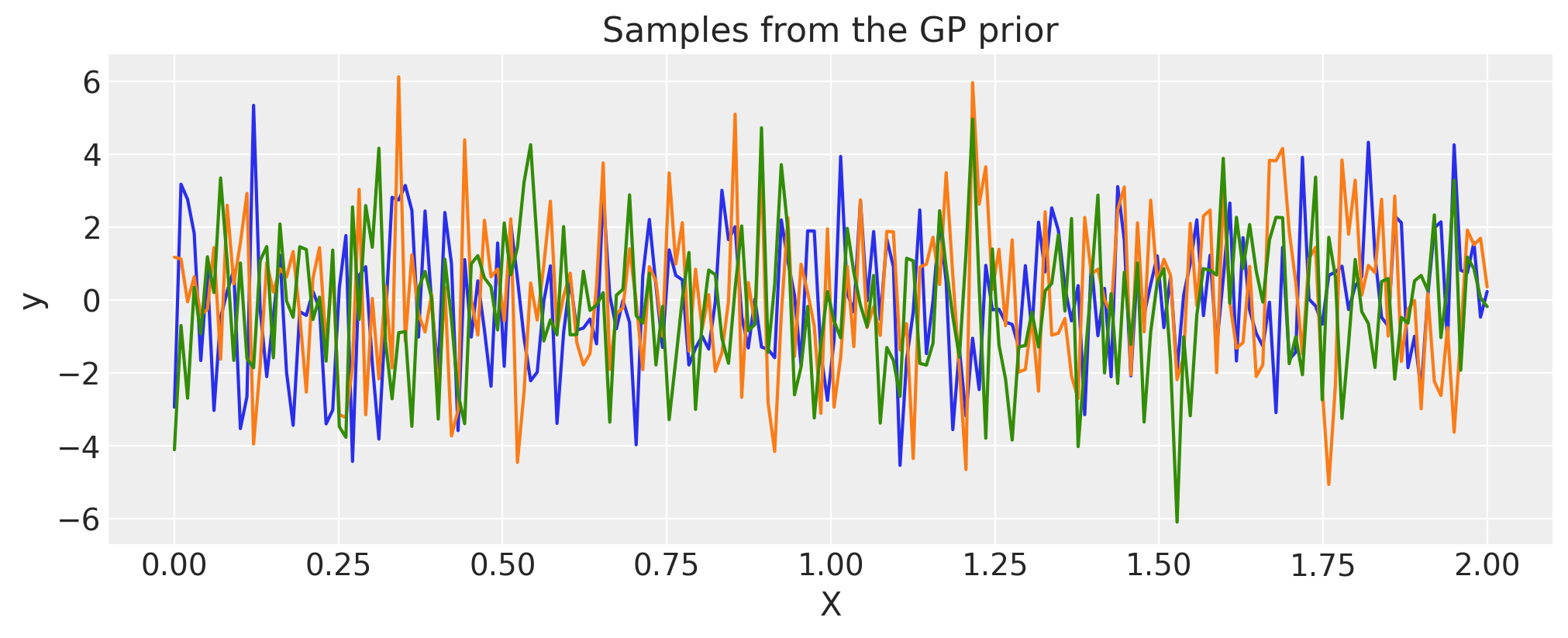
白噪声#
\[ k(x, x') = \sigma^2 \mathrm{I}_{xx} \]
sigma = 2.0
cov = pm.gp.cov.WhiteNoise(sigma)
X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()
plt.plot(
X,
pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
常数#
\[ k(x, x') = c \]
c = 2.0
cov = pm.gp.cov.Constant(c)
X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()
plt.plot(
X,
pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
有理二次#
\[ k(x, x') = \left(1 + \frac{(x - x')^2}{2\alpha\ell^2} \right)^{-\alpha} \]
alpha = 0.1
ls = 0.2
tau = 2.0
cov = tau * pm.gp.cov.RatQuad(1, ls, alpha)
X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()
plt.plot(
X,
pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
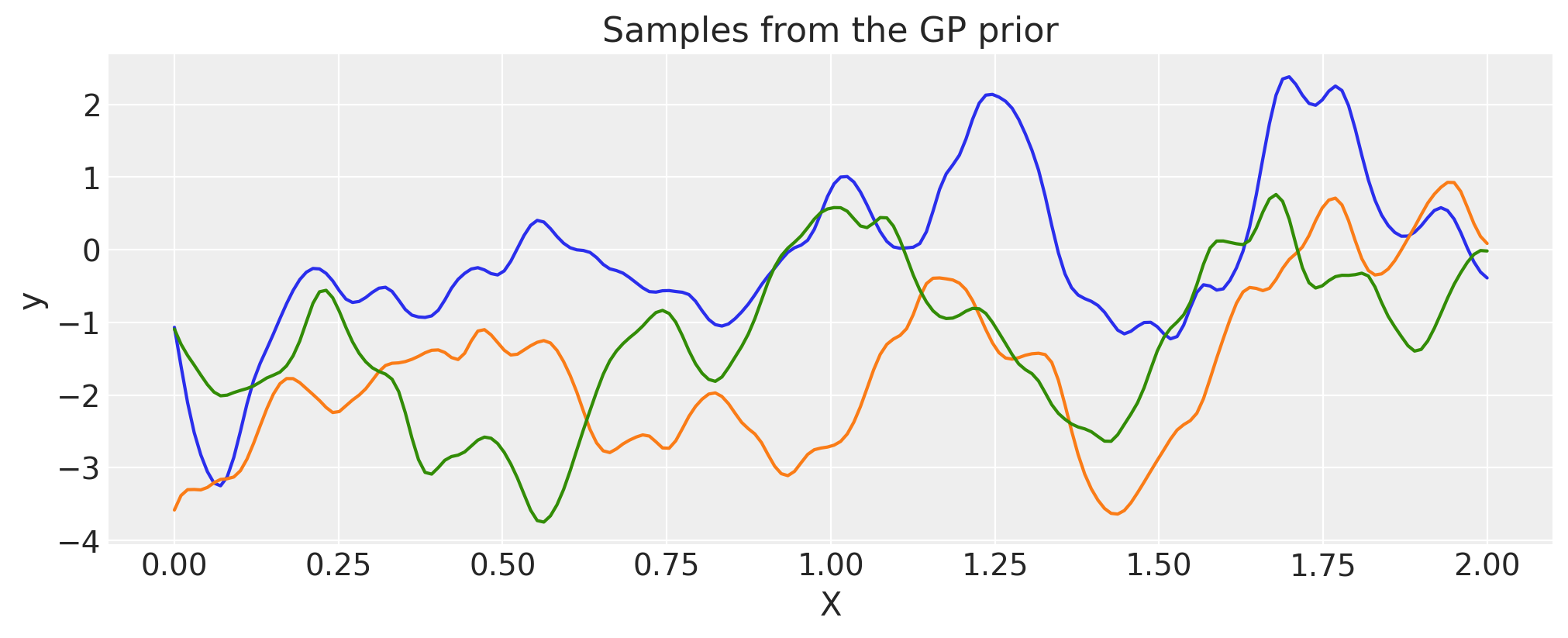
指数#
\[ k(x, x') = \mathrm{exp}\left[ -\frac{||x - x'||}{2\ell^2} \right] \]
inverse_lengthscale = 5
cov = pm.gp.cov.Exponential(1, ls_inv=inverse_lengthscale)
X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()
plt.plot(
X,
pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
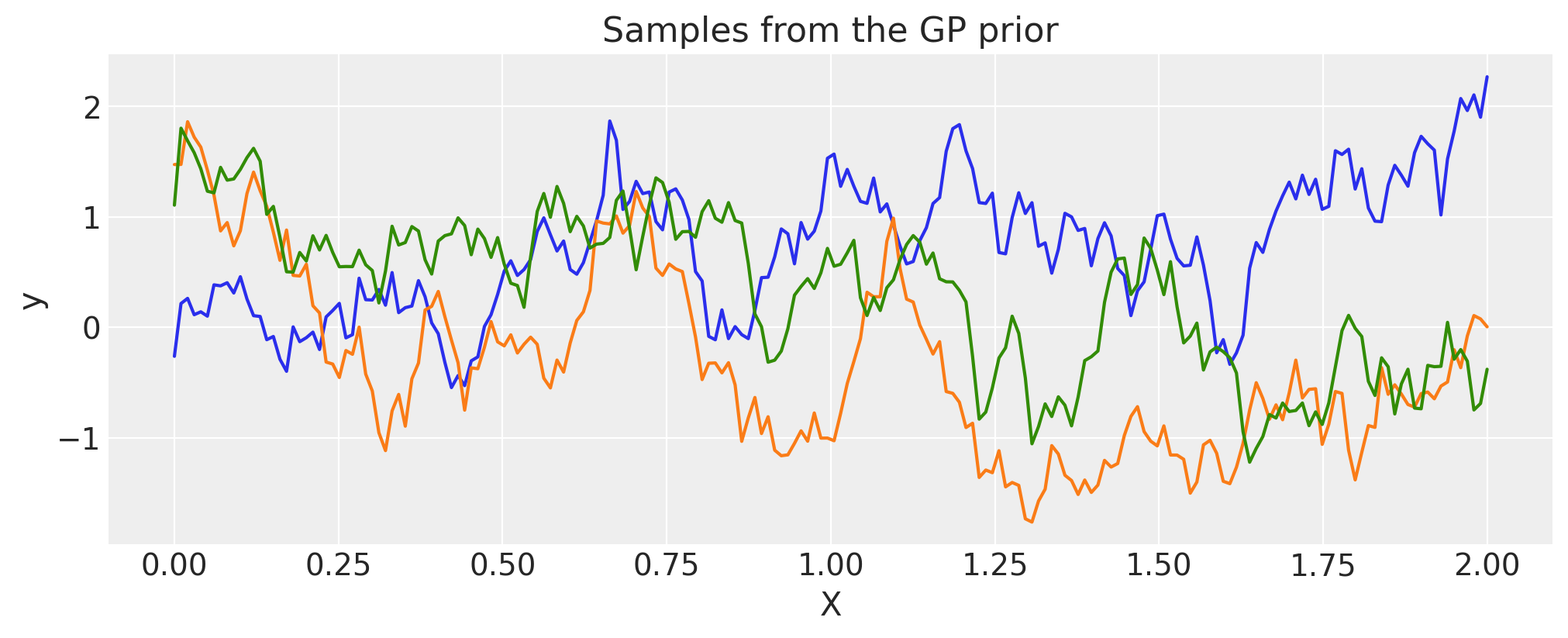
Matern 5/2#
\[ k(x, x') = \left(1 + \frac{\sqrt{5(x - x')^2}}{\ell} + \frac{5(x-x')^2}{3\ell^2}\right) \mathrm{exp}\left[ - \frac{\sqrt{5(x - x')^2}}{\ell} \right] \]
ls = 0.2
tau = 2.0
cov = tau * pm.gp.cov.Matern52(1, ls)
X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()
plt.plot(
X,
pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
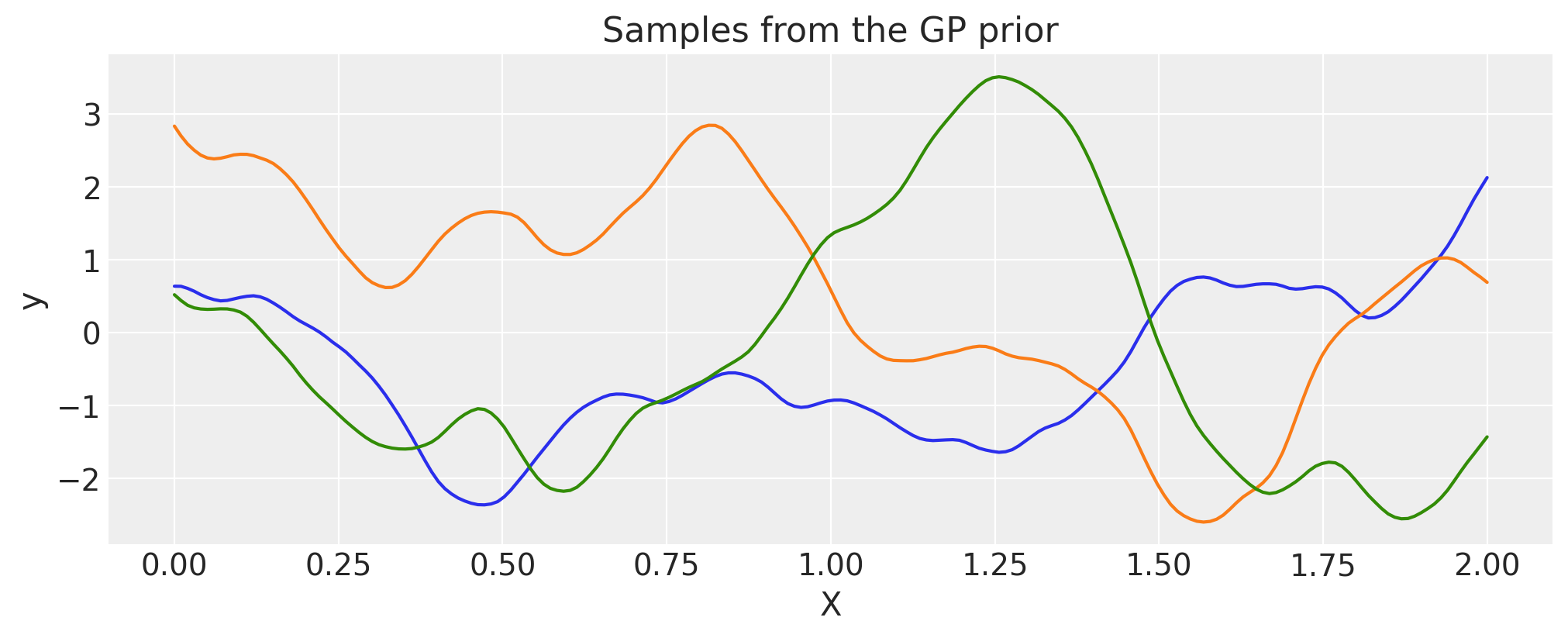
Matern 3/2#
\[ k(x, x') = \left(1 + \frac{\sqrt{3(x - x')^2}}{\ell}\right) \mathrm{exp}\left[ - \frac{\sqrt{3(x - x')^2}}{\ell} \right] \]
ls = 0.2
tau = 2.0
cov = tau * pm.gp.cov.Matern32(1, ls)
X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()
plt.plot(
X,
pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
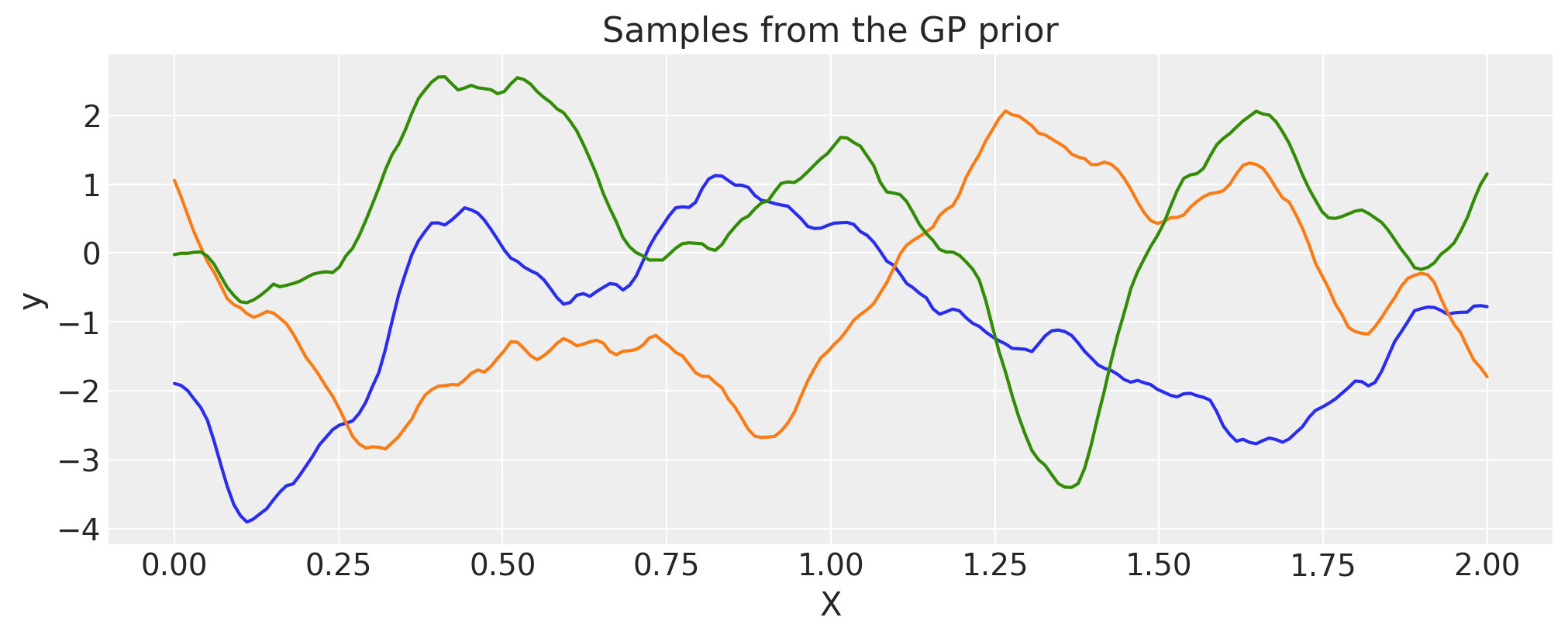
Matern 1/2#
\[k(x, x') = \mathrm{exp}\left[ -\frac{(x - x')^2}{\ell} \right]\]
ls = 0.2
tau = 2.0
cov = tau * pm.gp.cov.Matern12(1, ls)
X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()
plt.plot(
X,
pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
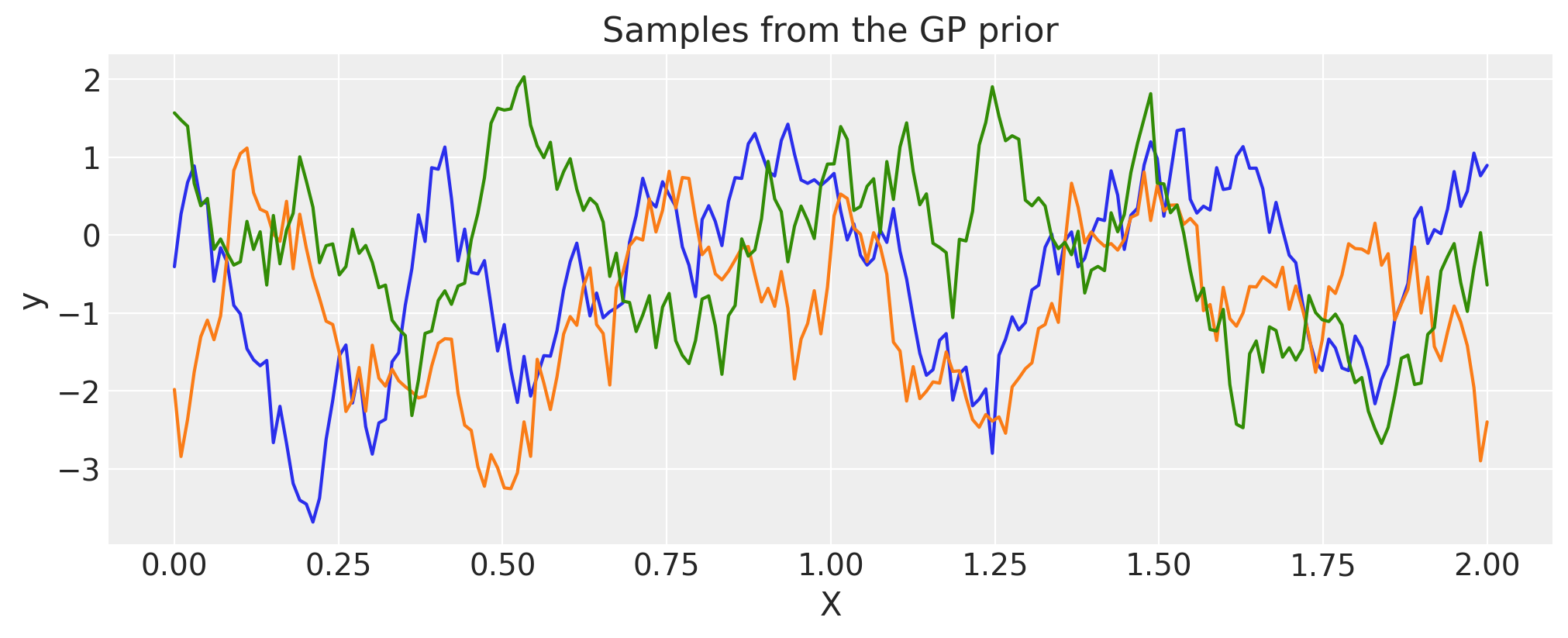
余弦#
\[ k(x, x') = \mathrm{cos}\left( 2 \pi \frac{||x - x'||}{ \ell^2} \right) \]
period = 0.5
cov = pm.gp.cov.Cosine(1, period)
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-4)
X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()
plt.plot(
X,
pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
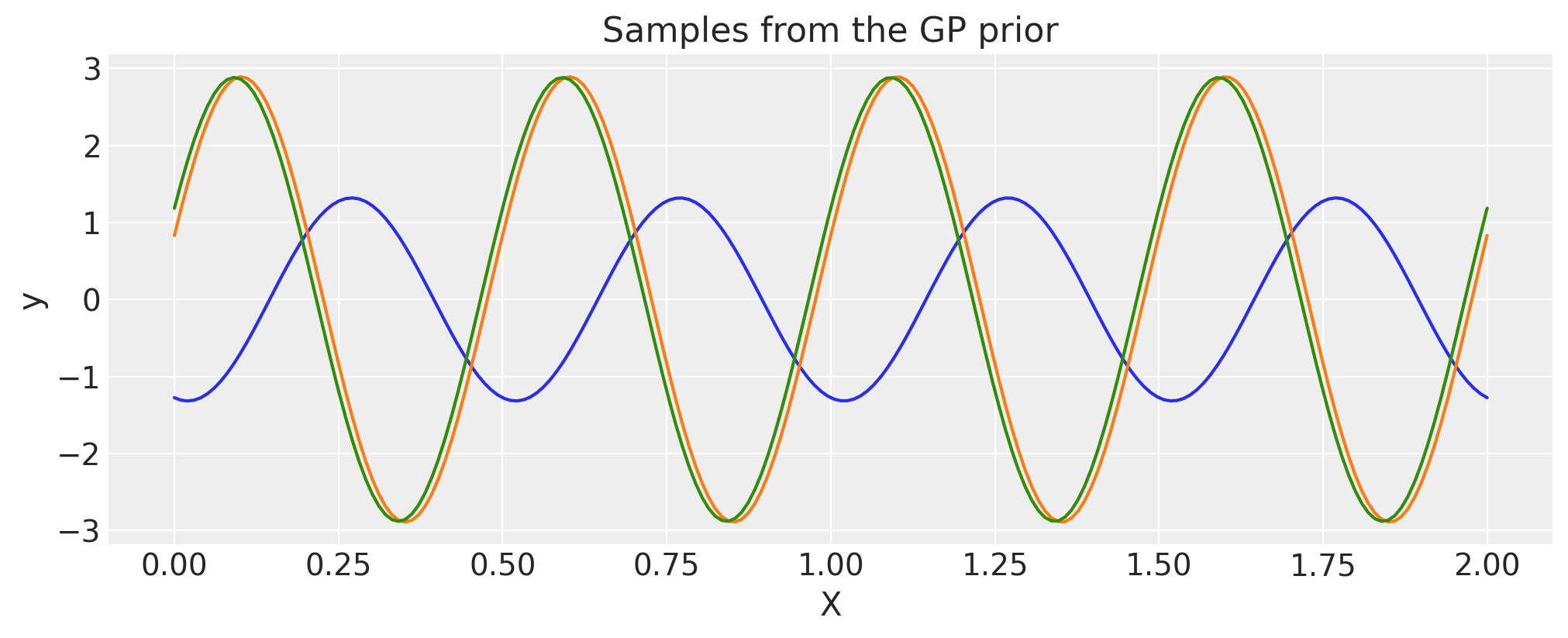
线性#
\[ k(x, x') = (x - c)(x' - c) \]
c = 1.0
tau = 2.0
cov = tau * pm.gp.cov.Linear(1, c)
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)
X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()
plt.plot(
X,
pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
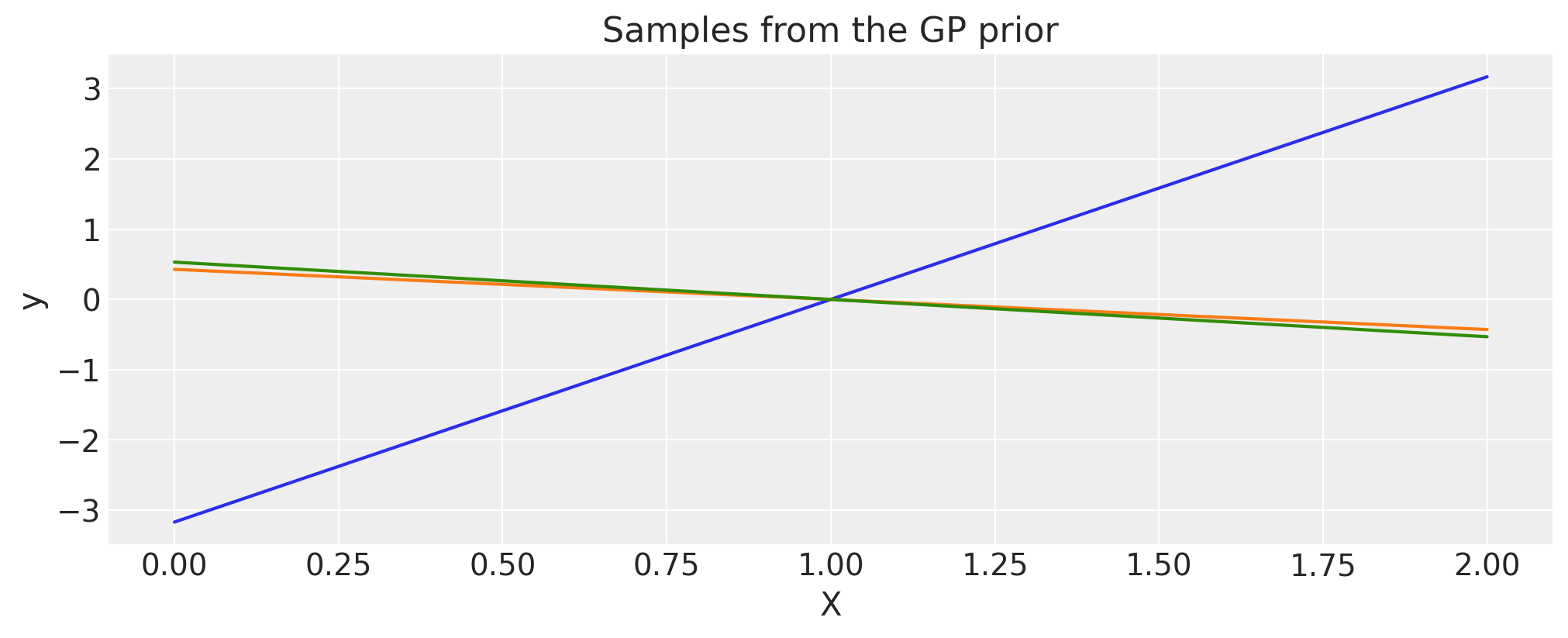
多项式#
\[ k(x, x') = [(x - c)(x' - c) + \mathrm{offset}]^{d} \]
c = 1.0
d = 3
offset = 1.0
tau = 0.1
cov = tau * pm.gp.cov.Polynomial(1, c=c, d=d, offset=offset)
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)
X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()
plt.plot(
X,
pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
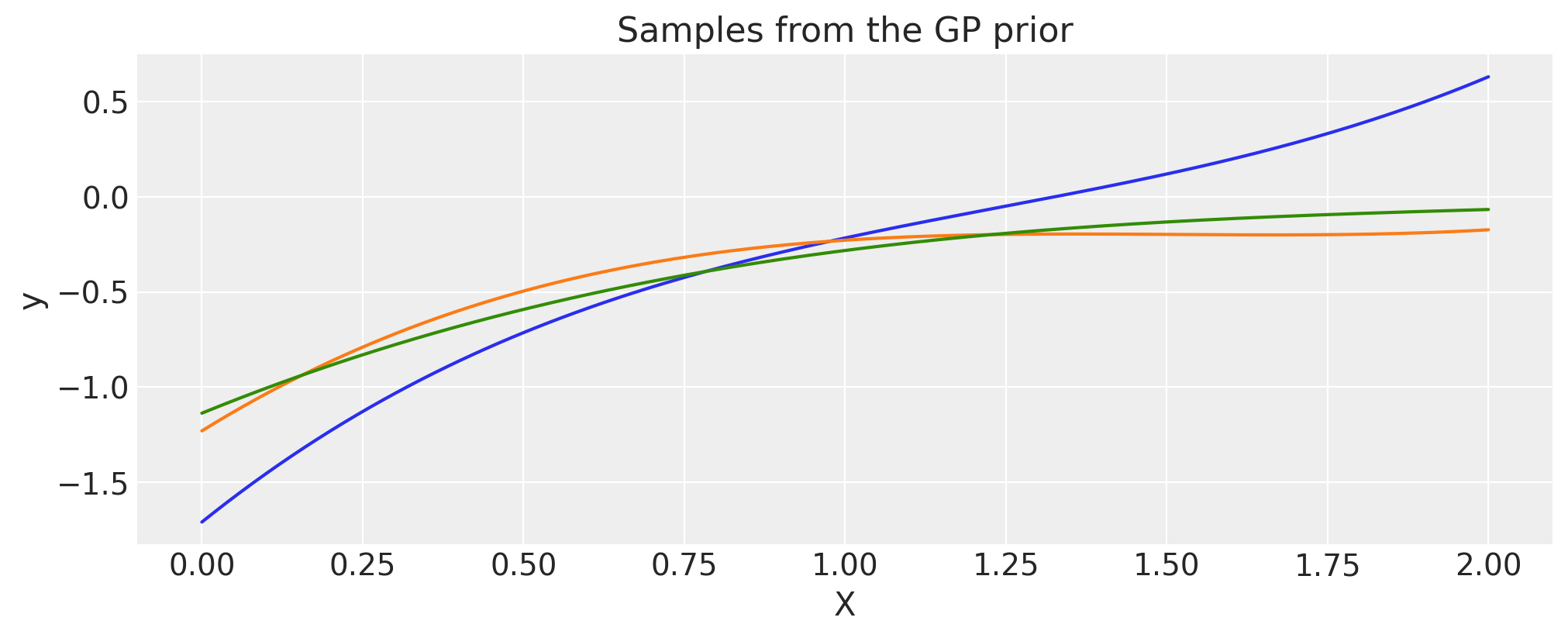
与预计算协方差矩阵相乘#
协方差函数 cov 可以与 numpy 矩阵 K_cos 相乘，只要形状适当即可。
# first evaluate a covariance function into a matrix
period = 0.2
cov_cos = pm.gp.cov.Cosine(1, period)
K_cos = cov_cos(X).eval()
# now multiply it with a covariance *function*
cov = pm.gp.cov.Matern32(1, 0.5) * K_cos
X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()
plt.plot(
X,
pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
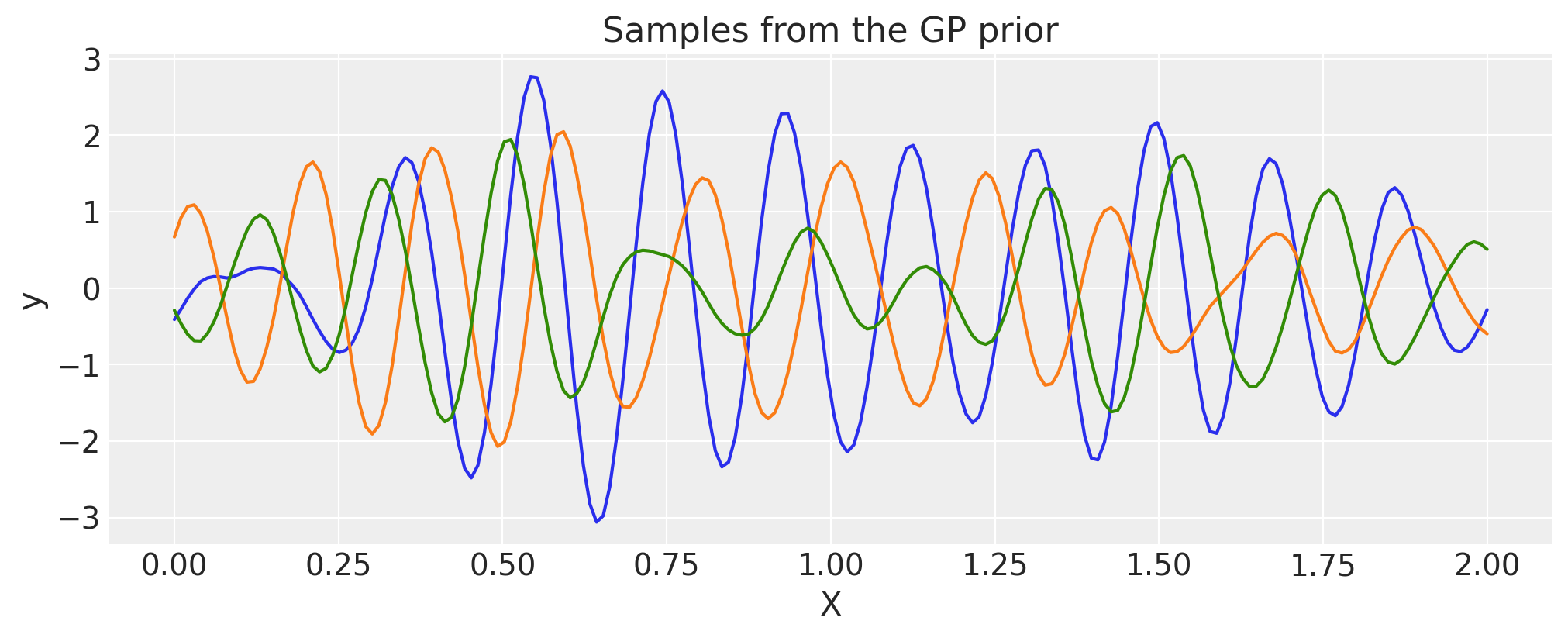
在输入上应用任意扭曲函数#
如果 \(k(x, x')\) 是有效的协方差函数，那么 \(k(w(x), w(x'))\) 也是。
扭曲函数的第一个参数必须是输入 X。其余参数可以是任何其他内容，包括随机变量。
def warp_func(x, a, b, c):
return 1.0 + x + (a * pt.tanh(b * (x - c)))
a = 1.0
b = 5.0
c = 1.0
cov_exp = pm.gp.cov.ExpQuad(1, 0.2)
cov = pm.gp.cov.WarpedInput(1, warp_func=warp_func, args=(a, b, c), cov_func=cov_exp)
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)
X = np.linspace(0, 2, 400)[:, None]
wf = warp_func(X.flatten(), a, b, c).eval()
plt.plot(X, wf)
plt.xlabel("X")
plt.ylabel("warp_func(X)")
plt.title("The warping function used")
K = cov(X).eval()
plt.plot(
X,
pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
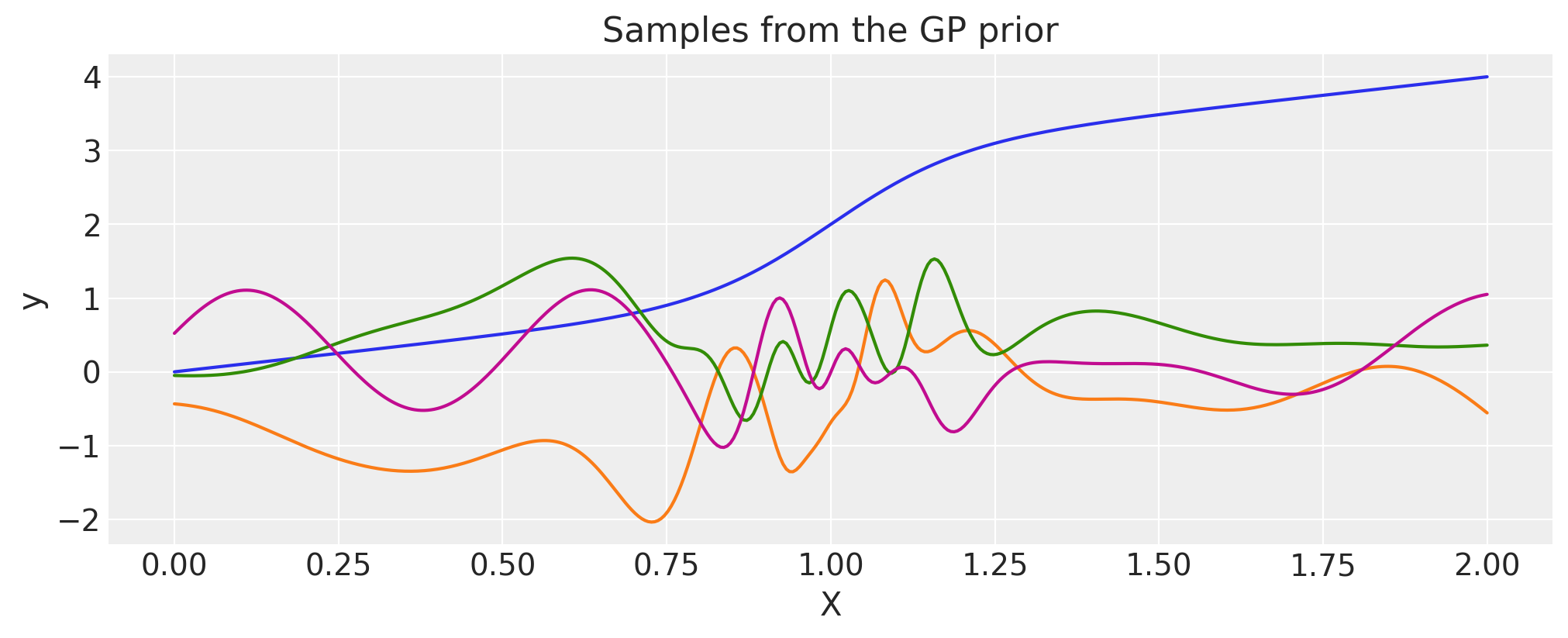
使用 WarpedInput 构建 Periodic#
WarpedInput 核函数可用于创建 Periodic 协方差。此协方差对周期性函数进行建模，但不是精确的正弦波（如 Cosine 核函数）。
周期核函数由下式给出
\[ k(x, x') = \exp\left( -\frac{2 \sin^{2}(\pi |x - x'|\frac{1}{T})}{\ell^2} \right) \]
其中 T 是周期，\(\ell\) 是长度尺度。它可以通过使用函数 \(\mathbf{u}(x) = (\sin(2\pi x \frac{1}{T})\,, \cos(2 \pi x \frac{1}{T}))\) 扭曲 ExpQuad 核函数的输入来导出。在这里，我们使用 WarpedInput 核函数来构建它。
输入 X 在此页面顶部定义，长度为 2 “秒”。我们使用 \(0.5\) 的周期，这意味着从此 GP 先验中抽取的函数将在 2 秒内重复 4 次。
def mapping(x, T):
c = 2.0 * np.pi * (1.0 / T)
u = pt.concatenate((pt.sin(c * x), pt.cos(c * x)), 1)
return u
T = 0.6
ls = 0.4
# note that the input of the covariance function taking
# the inputs is 2 dimensional
cov_exp = pm.gp.cov.ExpQuad(2, ls)
cov = pm.gp.cov.WarpedInput(1, cov_func=cov_exp, warp_func=mapping, args=(T,))
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)
K = cov(X).eval()
plt.plot(
X,
pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
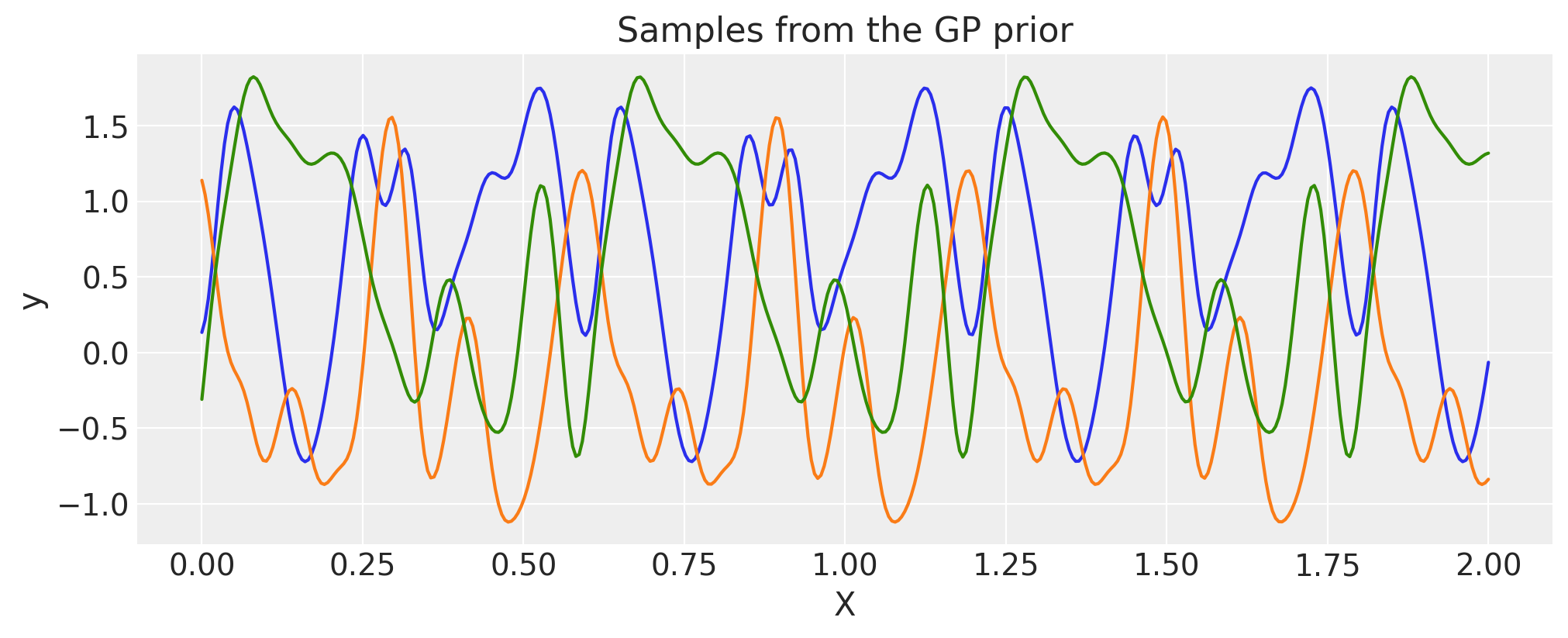
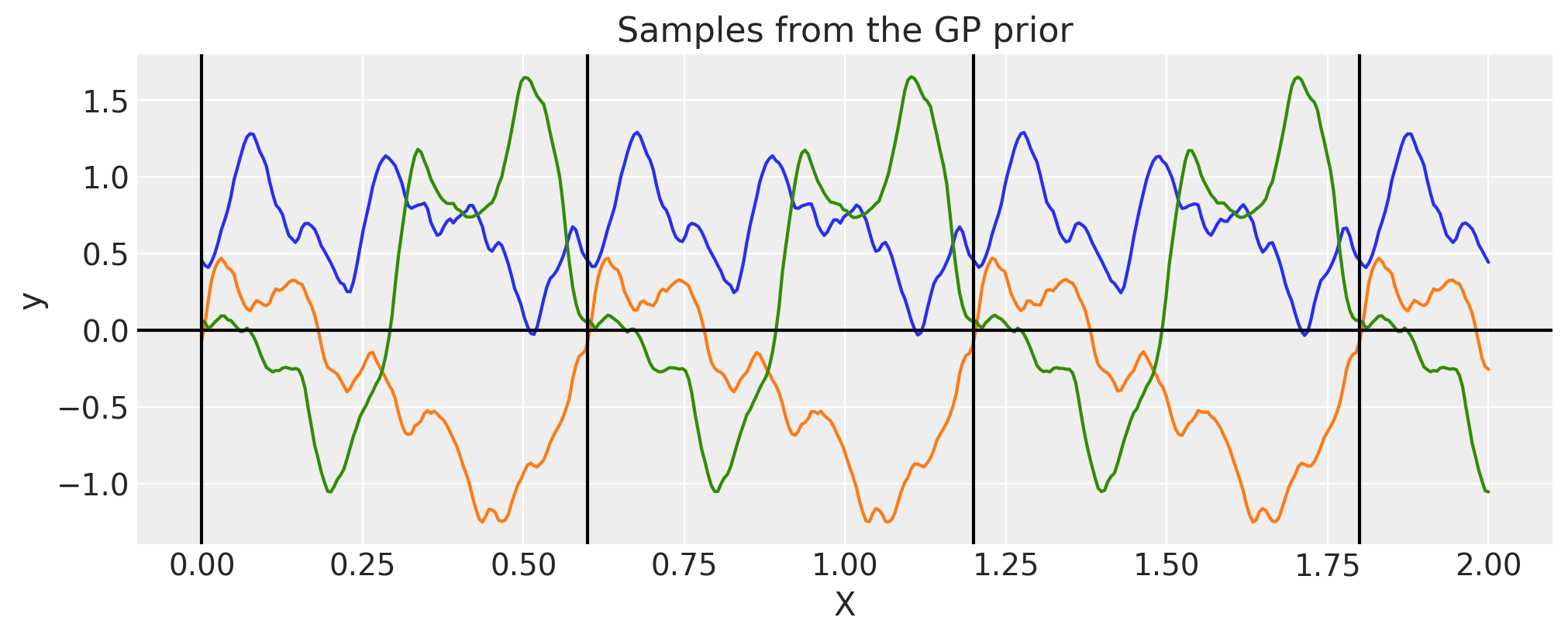
周期性#
没有必要每次都以这种方式构建周期协方差。此协方差函数的更有效实现已内置。
period = 0.6
ls = 0.4
cov = pm.gp.cov.Periodic(1, period=period, ls=ls)
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)
K = cov(X).eval()
plt.plot(
X,
pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
for p in np.arange(0, 2, period):
plt.axvline(p, color="black")
plt.axhline(0, color="black")
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
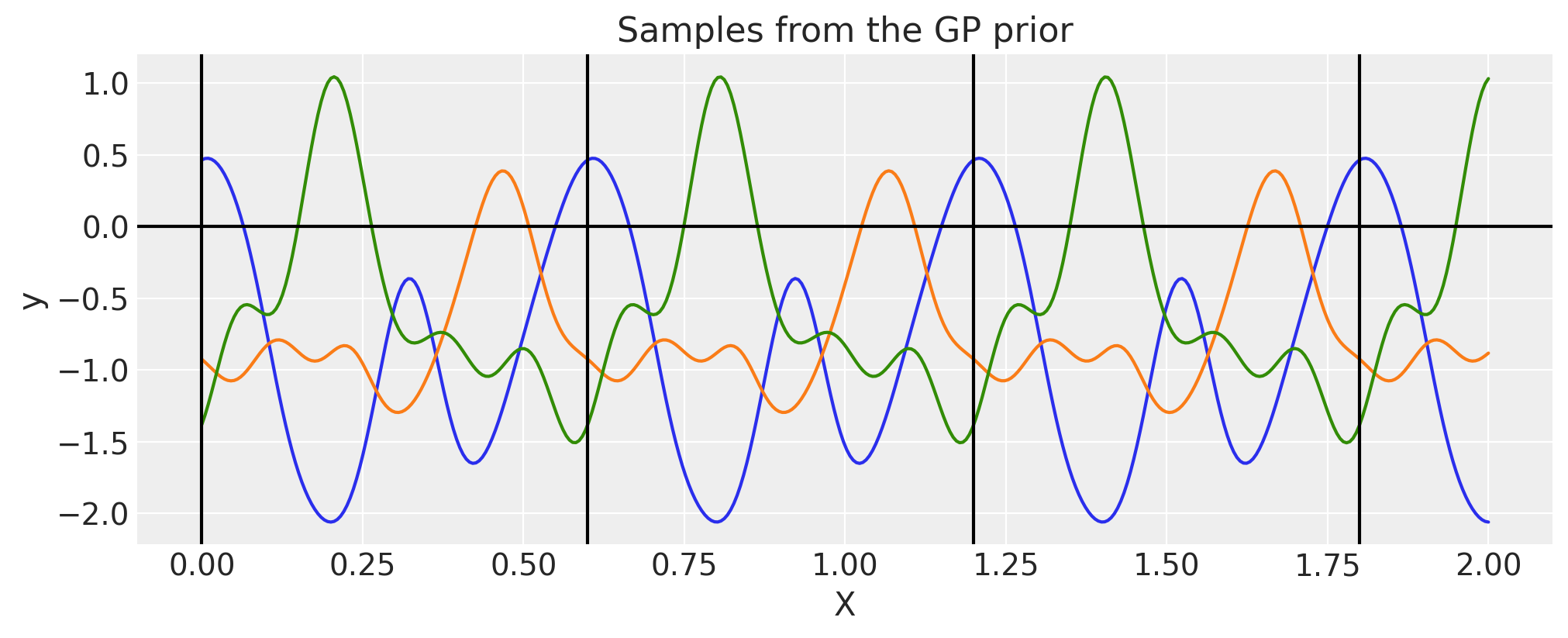
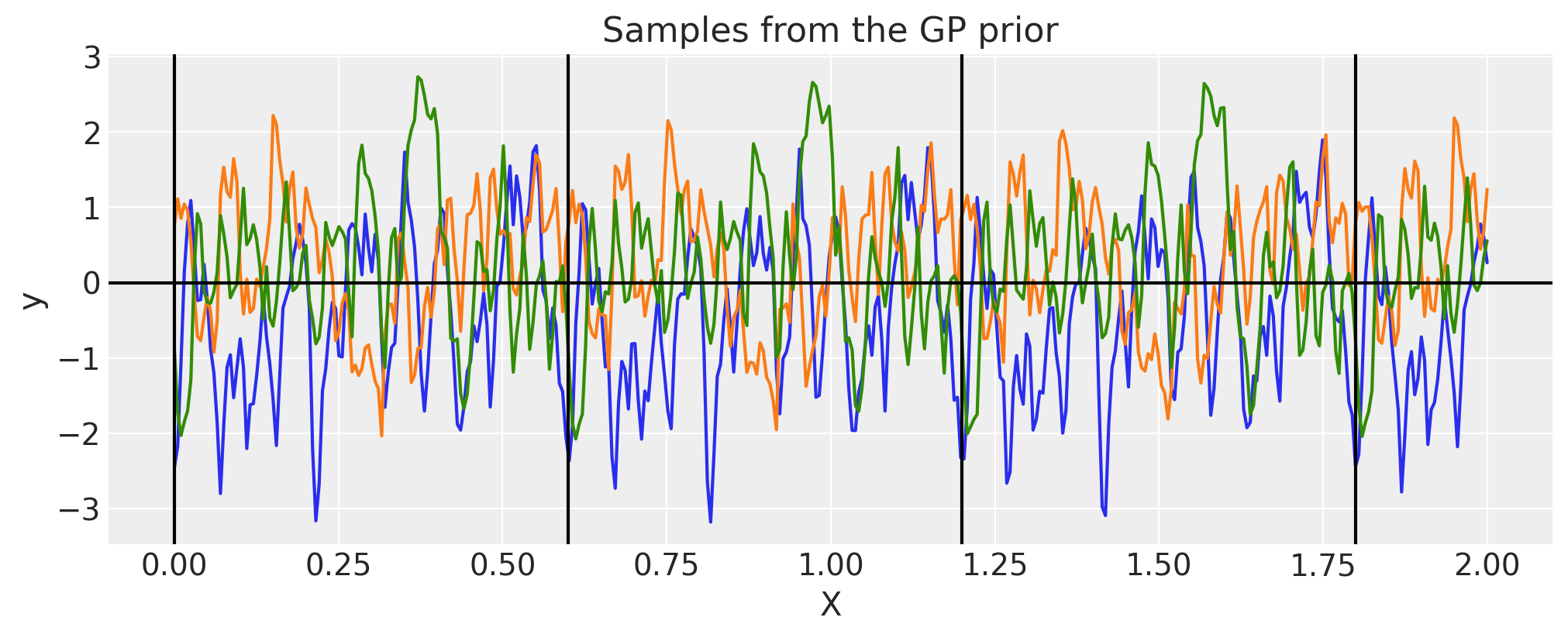
循环#
循环核函数类似于周期核函数，但有一个额外的 nuisance 参数 \(\tau\)
在 Padonou 和 Roustant [2015] 中，Weinland 函数用于解决该问题，并确保循环域（以及不仅限于循环域）上的正定核。
\[ W_c(t) = \left(1 + \tau \frac{t}{c}\right)\left(1-\frac{t}{c}\right)_+^\tau \]
其中 \(c\) 是 \(t\) 的最大值，\(\tau\ge 4\) 是某个正数
圆上测地距离（弧长）的核函数本身看起来像
\[ k_g(x, y) = W_\pi(\text{dist}_{\mathit{geo}}(x, y)) \]
简而言之，你可以认为
\(t\) 是时间，它从 \(0\) 运行到 \(24\)，然后返回到 \(0\)
\(c\) 是任何时间戳之间的最大距离，这里是 \(12\)
\(\tau\) 控制相关强度，更大的 \(\tau\) 导致函数更不平滑
period = 0.6
tau = 4
cov = pm.gp.cov.Circular(1, period=period, tau=tau)
K = cov(X).eval()
plt.plot(
X,
pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
for p in np.arange(0, 2, period):
plt.axvline(p, color="black")
plt.axhline(0, color="black")
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
我们可以看到 \(\tau\) 的效果，它添加了更多非平滑模式
period = 0.6
tau = 40
cov = pm.gp.cov.Circular(1, period=period, tau=tau)
K = cov(X).eval()
plt.plot(
X,
pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
for p in np.arange(0, 2, period):
plt.axvline(p, color="black")
plt.axhline(0, color="black")
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
Gibbs#
Gibbs 协方差函数将正定扭曲函数应用于长度尺度。与 WarpedInput 类似，长度尺度扭曲函数可以使用固定参数或随机变量参数来指定。
def tanh_func(x, ls1, ls2, w, x0):
"""
ls1: left saturation value
ls2: right saturation value
w: transition width
x0: transition location.
"""
return (ls1 + ls2) / 2.0 - (ls1 - ls2) / 2.0 * pt.tanh((x - x0) / w)
ls1 = 0.05
ls2 = 0.6
w = 0.3
x0 = 1.0
cov = pm.gp.cov.Gibbs(1, tanh_func, args=(ls1, ls2, w, x0))
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)
wf = tanh_func(X, ls1, ls2, w, x0).eval()
plt.plot(X, wf)
plt.ylabel("lengthscale")
plt.xlabel("X")
plt.title("Lengthscale as a function of X")
K = cov(X).eval()
plt.plot(
X,
pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
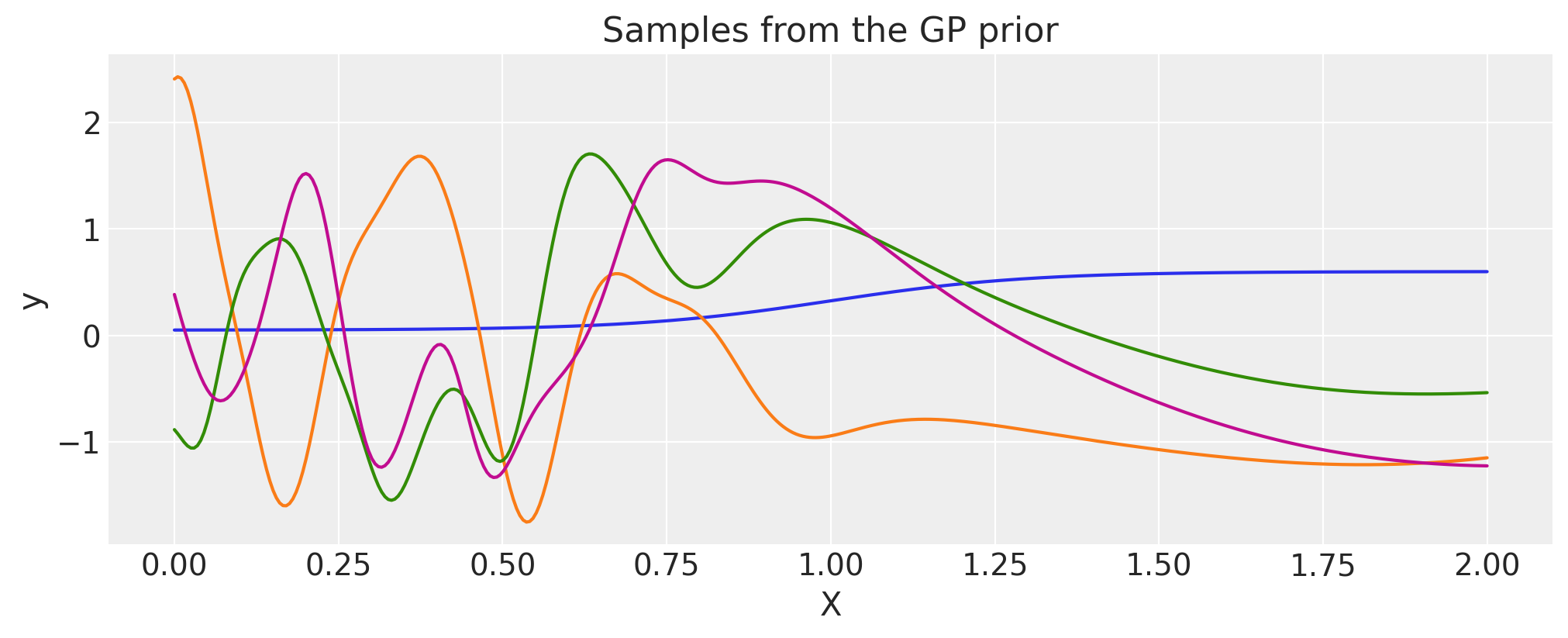
缩放协方差#
可以通过将某个基本核函数乘以非负函数 \(\phi(x)\) 来构造新的核函数或协方差函数，
\[ k_{\mathrm{scaled}}(x, x') = \phi(x) k_{\mathrm{base}}(x, x') \phi(x') \,. \]
这对于指定幅度在域内变化的协方差函数很有用。
def logistic(x, a, x0, c, d):
# a is the slope, x0 is the location
return d * pm.math.invlogit(a * (x - x0)) + c
a = 2.0
x0 = 5.0
c = 0.1
d = 2.0
cov_base = pm.gp.cov.ExpQuad(1, 0.2)
cov = pm.gp.cov.ScaledCov(1, scaling_func=logistic, args=(a, x0, c, d), cov_func=cov_base)
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-5)
X = np.linspace(0, 10, 400)[:, None]
lfunc = logistic(X.flatten(), a, b, c, d).eval()
plt.plot(X, lfunc)
plt.xlabel("X")
plt.ylabel(r"$\phi(x)$")
plt.title("The scaling function")
K = cov(X).eval()
plt.plot(
X,
pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
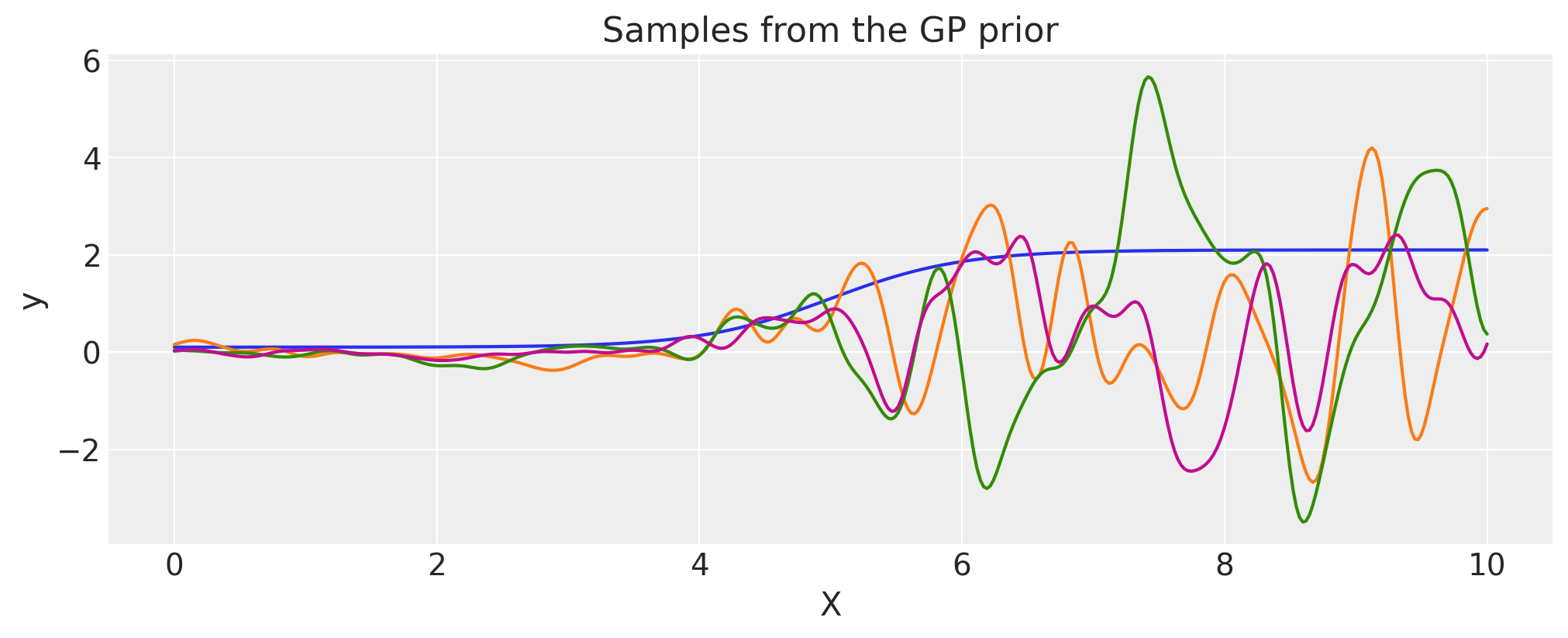
使用 ScaledCov 构建 Changepoint 核函数#
ScaledCov 核函数可用于创建 Changepoint 协方差。此协方差对从一种行为类型逐渐过渡到另一种行为类型的过程进行建模。
突变点核函数由下式给出
\[ k(x, x') = \phi(x)k_{1}(x, x')\phi(x) + (1 - \phi(x))k_{2}(x, x')(1 - \phi(x')) \]
其中 \(\phi(x)\) 是 logistic 函数。
def logistic(x, a, x0):
# a is the slope, x0 is the location
return pm.math.invlogit(a * (x - x0))
a = 2.0
x0 = 5.0
cov1 = pm.gp.cov.ScaledCov(
1, scaling_func=logistic, args=(-a, x0), cov_func=pm.gp.cov.ExpQuad(1, 0.2)
)
cov2 = pm.gp.cov.ScaledCov(
1, scaling_func=logistic, args=(a, x0), cov_func=pm.gp.cov.Cosine(1, 0.5)
)
cov = cov1 + cov2
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-5)
X = np.linspace(0, 10, 400)
plt.fill_between(
X,
np.zeros(400),
logistic(X, -a, x0).eval(),
label="ExpQuad region",
color="slateblue",
alpha=0.4,
)
plt.fill_between(
X, np.zeros(400), logistic(X, a, x0).eval(), label="Cosine region", color="firebrick", alpha=0.4
)
plt.legend()
plt.xlabel("X")
plt.ylabel(r"$\phi(x)$")
plt.title("The two scaling functions")
K = cov(X[:, None]).eval()
plt.plot(
X,
pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
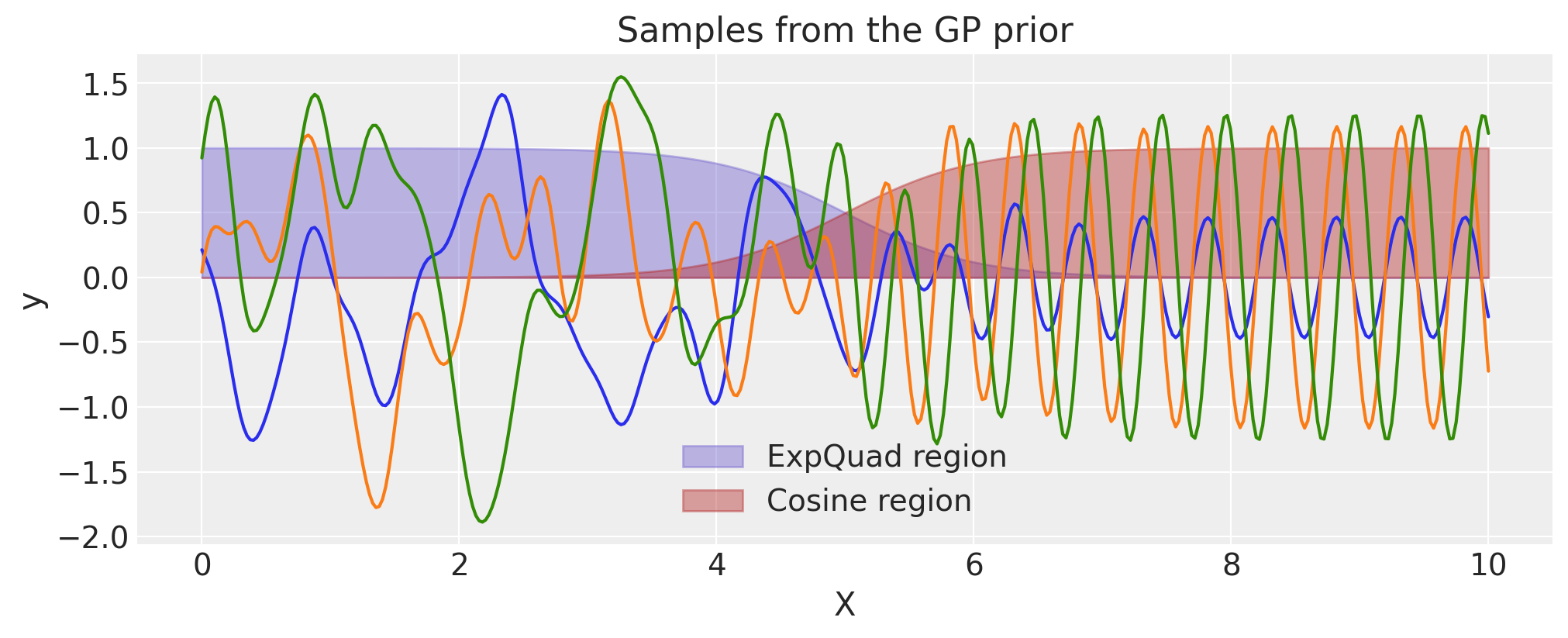
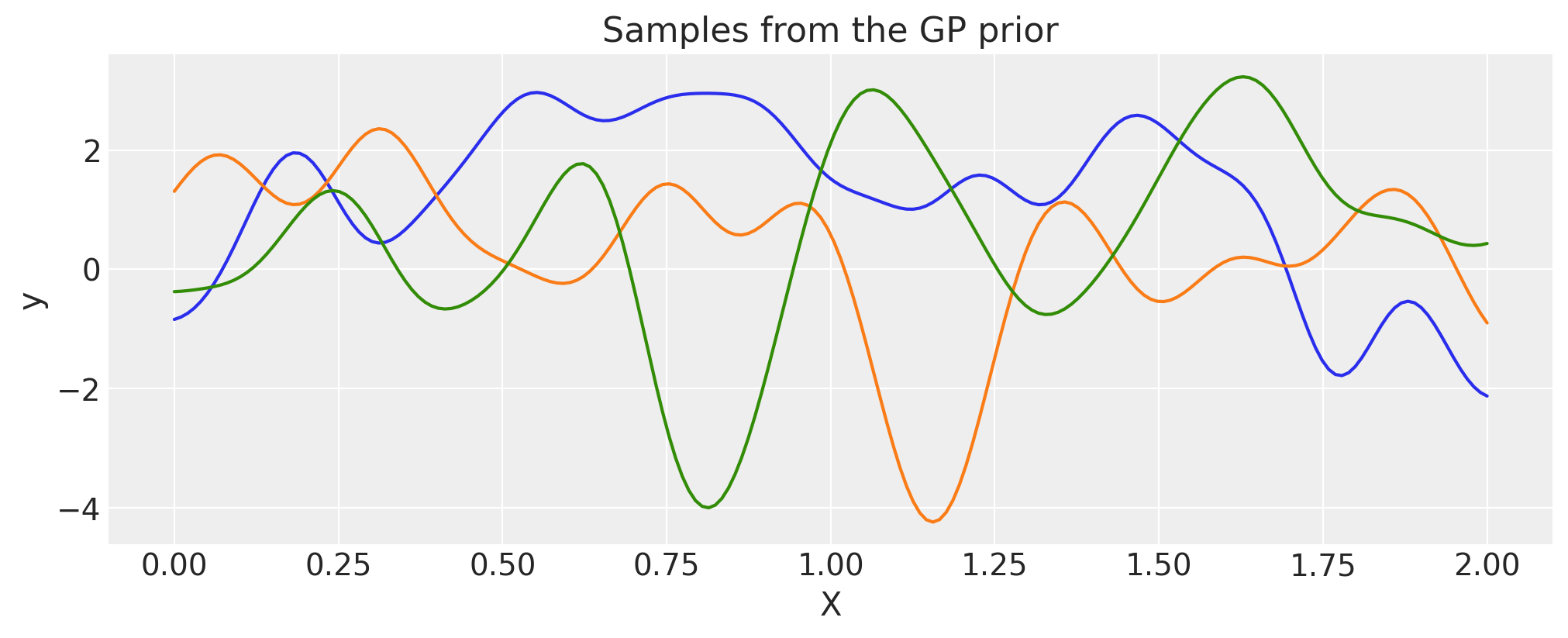
两个或多个协方差函数的组合#
你可以组合不同的协方差函数来建模复杂数据。
特别是，你可以对任何协方差函数执行以下操作
将其他协方差函数与第一个协方差函数相加，这些协方差函数具有相等或可广播的维度
将第一个协方差函数与标量或具有相等或可广播维度的协方差函数相乘
与标量求幂。
加法#
ls_1 = 0.1
tau_1 = 2.0
ls_2 = 0.5
tau_2 = 1.0
cov_1 = tau_1 * pm.gp.cov.ExpQuad(1, ls=ls_1)
cov_2 = tau_2 * pm.gp.cov.ExpQuad(1, ls=ls_2)
cov = cov_1 + cov_2
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)
X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()
plt.plot(
X,
pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
乘法#
ls_1 = 0.1
tau_1 = 2.0
ls_2 = 0.5
tau_2 = 1.0
cov_1 = tau_1 * pm.gp.cov.ExpQuad(1, ls=ls_1)
cov_2 = tau_2 * pm.gp.cov.ExpQuad(1, ls=ls_2)
cov = cov_1 * cov_2
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)
X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()
plt.plot(
X,
pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
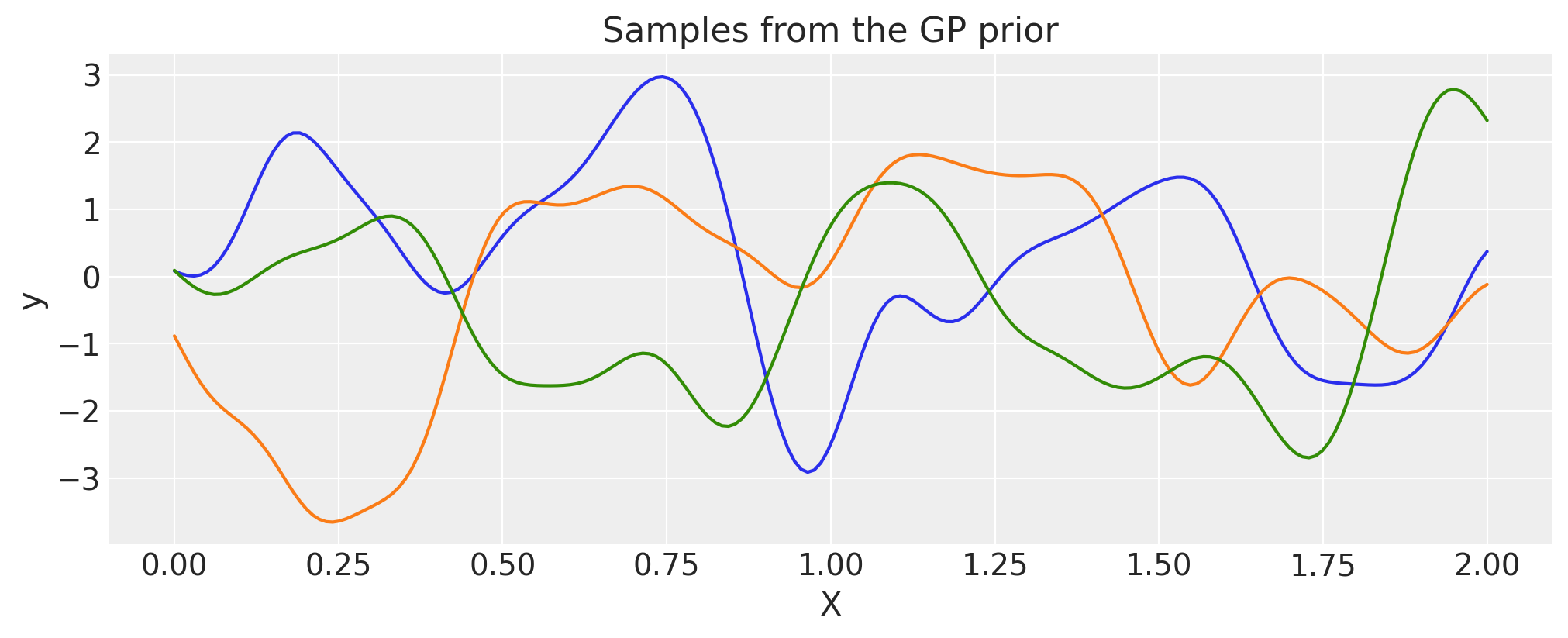
指数运算#
ls_1 = 0.1
tau_1 = 2.0
power = 2
cov_1 = tau_1 * pm.gp.cov.ExpQuad(1, ls=ls_1)
cov = cov_1**power
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)
X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()
plt.plot(
X,
pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
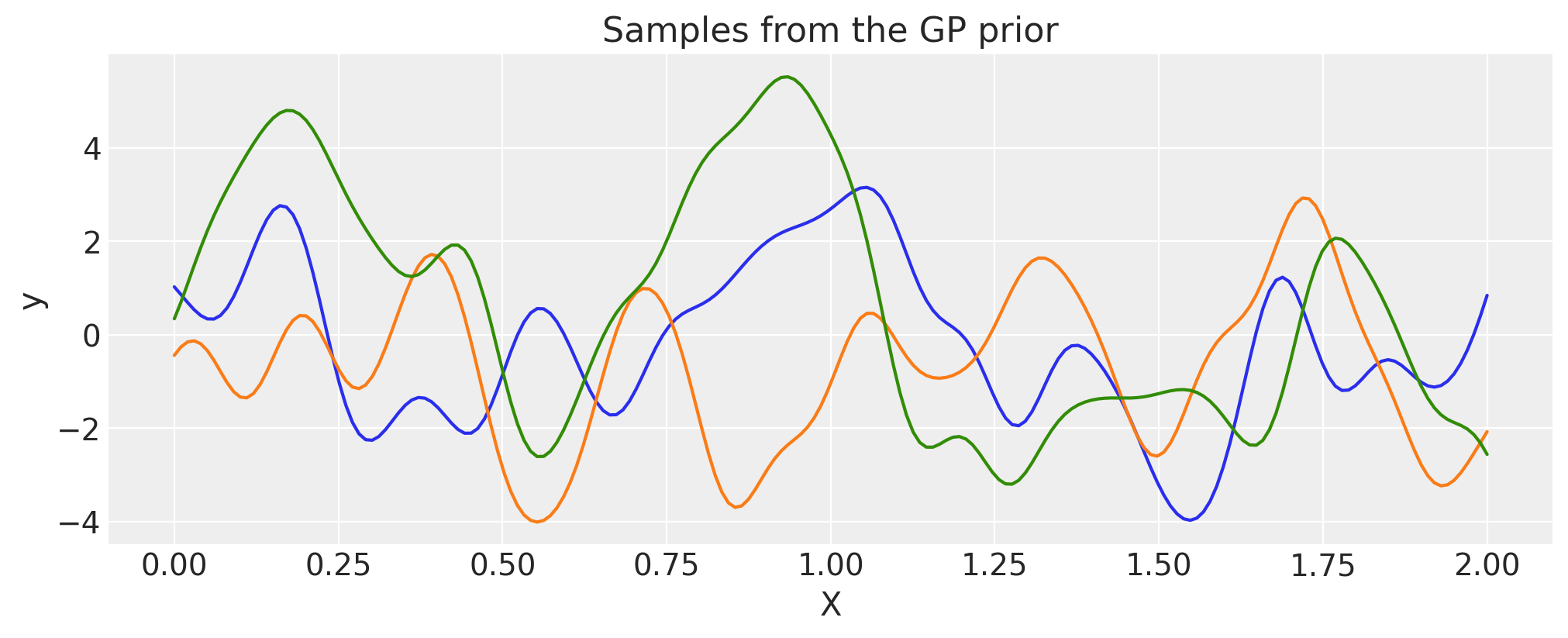
定义自定义协方差函数#
PyMC 中的协方差函数对象需要实现 __init__、diag 和 full 方法，并继承 gp.cov.Covariance。diag 仅返回协方差矩阵的对角线，而 full 返回完整的协方差矩阵。full 方法有两个输入 X 和 Xs。full(X) 返回平方协方差矩阵，full(X, Xs) 返回两组输入之间的交叉协方差。
例如，这是 WhiteNoise 协方差函数的实现
class WhiteNoise(pm.gp.cov.Covariance):
def __init__(self, sigma):
super(WhiteNoise, self).__init__(1, None)
self.sigma = sigma
def diag(self, X):
return tt.alloc(tt.square(self.sigma), X.shape[0])
def full(self, X, Xs=None):
if Xs is None:
return tt.diag(self.diag(X))
else:
return tt.alloc(0.0, X.shape[0], Xs.shape[0])
如果我们遗漏了重要的协方差或均值函数，请随时提交 pull 请求！
参考文献#
[1]
Carl Edward Rasmussen 和 Christopher K. I. Williams. 高斯过程用于机器学习. The MIT Press, 2006. ISBN 026218253X. URL: https://gaussianprocess.org/gpml/.
[2]
Espéran Padonou 和 O Roustant. 极坐标高斯过程用于在圆形域上进行预测. working paper or preprint, 2015 年 2 月. URL: https://hal.archives-ouvertes.fr/hal-01119942.
水印#
%load_ext watermark
%watermark -n -u -v -iv -w -p xarray
Last updated: Fri Nov 17 2023
Python implementation: CPython
Python version : 3.11.5
IPython version : 8.17.2
xarray: 2023.10.1
matplotlib: 3.8.1
arviz : 0.16.1
pymc : 5.9.2
pytensor : 2.17.4
numpy : 1.26.2
Watermark: 2.4.3
许可声明#
此示例库中的所有笔记本均根据 MIT 许可证提供，该许可证允许修改和重新分发以用于任何用途，前提是保留版权和许可声明。
引用 PyMC 示例#
要引用此笔记本，请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。
重要提示
许多笔记本改编自其他来源：博客、书籍…… 在这种情况下，你也应该引用原始来源。
还要记住引用你的代码使用的相关库。
这是一个 bibtex 格式的引用模板
@incollection{citekey,
author = "<notebook authors, see above>",
title = "<notebook title>",
editor = "PyMC Team",
booktitle = "PyMC examples",
doi = "10.5281/zenodo.5654871"
}
渲染后可能看起来像