高斯过程 (GP) 平滑#
此示例处理当我们想要平滑某些一维函数 \((x_i, y_i)\) 的观测数据点 \(y=f(x)\) 的情况,通过找到新的值 \((x_i, y'_i)\),使得新数据在沿 \(x\) 轴移动时更加“平滑”(请参阅下面的模型描述中关于通过方差分配来定义平滑度的更多信息)。
重要的是要注意,我们不是在处理在未知的 \(x\) 值处插值函数 \(y=f(x)\) 的问题。 这样的问题将被称为“回归”而不是“平滑”,将在其他示例中考虑。
如果我们假设 \(x\) 和 \(y\) 之间的函数依赖关系是线性的,那么通过对噪声进行独立性和正态性假设,我们可以推断出一条近似变量之间依赖关系的直线,即执行线性回归。 如果我们预先知道依赖关系的函数形式,我们也可以拟合更复杂的函数依赖关系(如二次、三次等)。
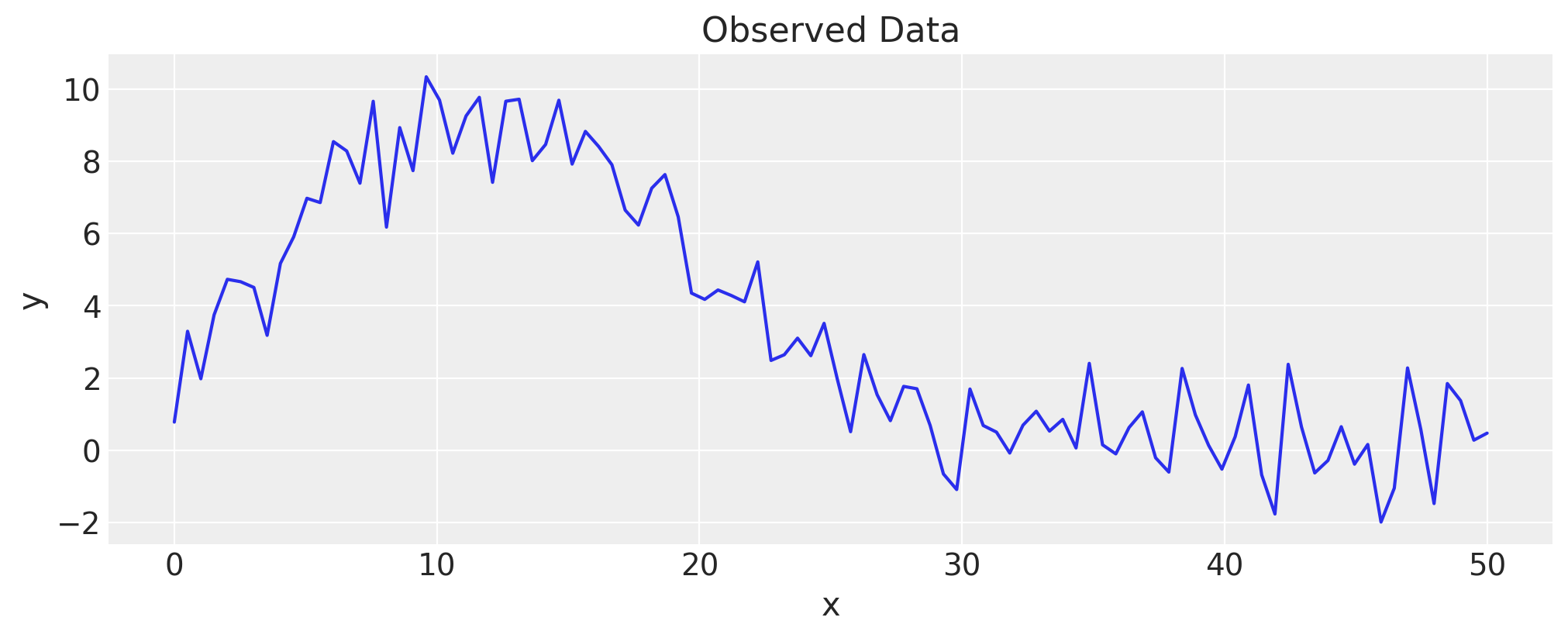
但是,\(y=f(x)\) 的函数形式并不总是预先知道的,并且给定数据,可能很难选择要拟合哪一个。 例如,给定以下观测数据,您不一定知道要使用哪个函数。 假设您没有看到生成它的公式
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import scipy.stats as stats
from pytensor import shared
%config InlineBackend.figure_format = "retina"
WARNING (pytensor.tensor.blas): Using NumPy C-API based implementation for BLAS functions.
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
plt.rcParams["figure.figsize"] = (10, 4)
x = np.linspace(0, 50, 100)
y = np.exp(1.0 + np.power(x, 0.5) - np.exp(x / 15.0)) + rng.normal(scale=1.0, size=x.shape)
fig, ax = plt.subplots()
ax.plot(x, y)
ax.set(title="Observed Data", xlabel="x", ylabel="y");
让我们首先尝试线性回归#
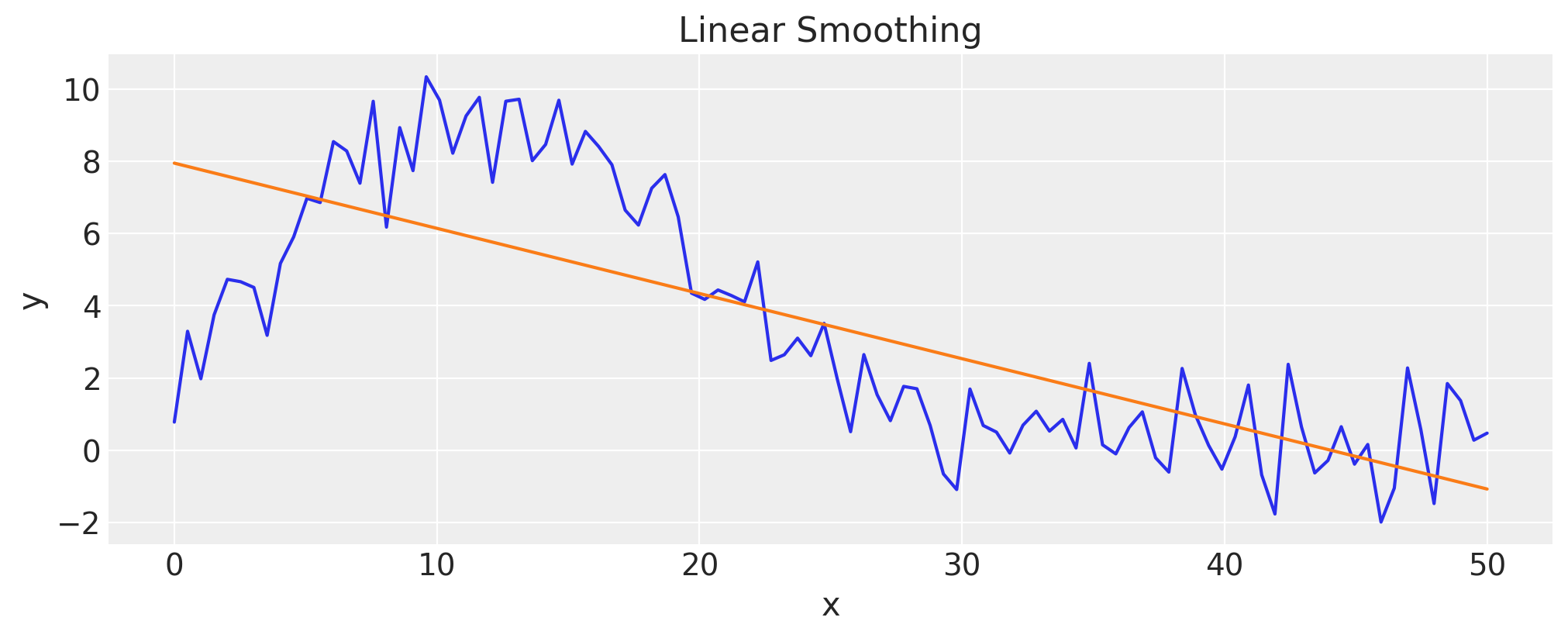
作为人类,我们看到存在一些噪声的非线性依赖关系,我们想要捕捉到这种依赖关系。 如果我们执行线性回归,我们看到“平滑”后的数据不太令人满意
lin = stats.linregress(x, y)
fig, ax = plt.subplots()
ax.plot(x, y)
lin = stats.linregress(x, y)
ax.plot(x, lin.intercept + lin.slope * x)
ax.set(title="Linear Smoothing", xlabel="x", ylabel="y");
线性回归模型回顾#
线性回归假设输入 \(x\) 和输出 \(y\) 之间存在线性依赖关系,并在其周围散布一些噪声,以便对于每个观测数据点,我们有
其中每个数据点的观测误差满足
具有相同的 \(\sigma\),并且误差是独立的
此模型的参数是 \(a\)、\(b\) 和 \(\sigma\)。 事实证明,在这些假设下,\(a\) 和 \(b\) 的最大似然估计不依赖于 \(\sigma\)。 然后可以在找到 \(a\) 和 \(b\) 的最可能值之后,单独估计 \(\sigma\)。
高斯过程平滑模型#
该模型允许通过假设 \(x\) 和 \(y\) 之间的依赖关系是 \(x\) 域上的布朗运动来偏离线性依赖关系。 这并没有像假设变量之间存在特定的函数依赖关系那样走得太远。 相反,通过控制未观测到的布朗运动的标准差,我们可以实现原始数据点处恢复的函数依赖关系的不同平滑度级别。
我们将要讨论的特定模型假设观测数据点在 \(x\) 域上是均匀分布的,因此可以由 \(i=1,\dots,N\) 索引,而不会失去一般性。 该模型描述如下
其中 \(z\) 是隐藏的布朗运动,\(y\) 是观测数据,并且每个观测的总方差 \(\sigma^2\) 在隐藏的布朗运动和噪声之间分配,比例分别为 \(1 - \alpha\) 和 \(\alpha\),参数 \(0 < \alpha < 1\) 指定平滑度。
当我们估计每个数据点 \(i=1,\dots,N\) 处隐藏过程 \(z_i\) 的最大似然值时,这些值提供了函数依赖关系 \(y=f(x)\) 的近似值,在原始数据点 \(x_i\) 处为 \(\mathrm{E}\,[f(x_i)] = z_i\)。 因此,再次强调,该方法称为平滑而不是回归。
让我们在 PyMC 中描述上述 GP 平滑模型#
让我们创建一个模型,其中包含一个共享参数,用于指定不同的平滑度级别。 我们为隐藏布朗运动的“mu”和“tau”参数使用非常宽的先验,您可以根据您的应用进行调整。
LARGE_NUMBER = 1e5
model = pm.Model()
with model:
smoothing_param = shared(0.9)
mu = pm.Normal("mu", sigma=LARGE_NUMBER)
tau = pm.Exponential("tau", 1.0 / LARGE_NUMBER)
z = pm.GaussianRandomWalk(
"z", mu=mu, sigma=pm.math.sqrt((1.0 - smoothing_param) / tau), shape=y.shape
)
obs = pm.Normal("obs", mu=z, tau=tau / smoothing_param, observed=y)
/Users/juanitorduz/anaconda3/envs/pymc-examples-env/lib/python3.11/site-packages/pymc/distributions/timeseries.py:293: UserWarning: Initial distribution not specified, defaulting to `Normal.dist(0, 100)`.You can specify an init_dist manually to suppress this warning.
warnings.warn(
让我们也创建一个辅助函数,用于推断 \(z\) 的最可能值
def infer_z(smoothing):
with model:
smoothing_param.set_value(smoothing)
res = pm.find_MAP(vars=[z], method="L-BFGS-B")
return res["z"]
请注意,在本示例中,我们仅关注未观测变量的 MAP 估计。 我们实际上对推断后验分布不感兴趣。 相反,我们有一个控制参数 \(\alpha\),它使我们能够在隐藏的布朗运动和噪声之间分配方差。 其他目标和/或不同的模型可能需要抽样以获得后验分布,但对于我们的目标,MAP 估计就足够了。
探索不同的平滑度级别#
让我们尝试将 50% 的方差分配给噪声,看看结果是否符合我们的预期。
smoothing = 0.5
z_val = infer_z(smoothing)
fig, ax = plt.subplots()
ax.plot(x, y)
ax.plot(x, z_val)
ax.set(title=f"Smoothing={smoothing}");
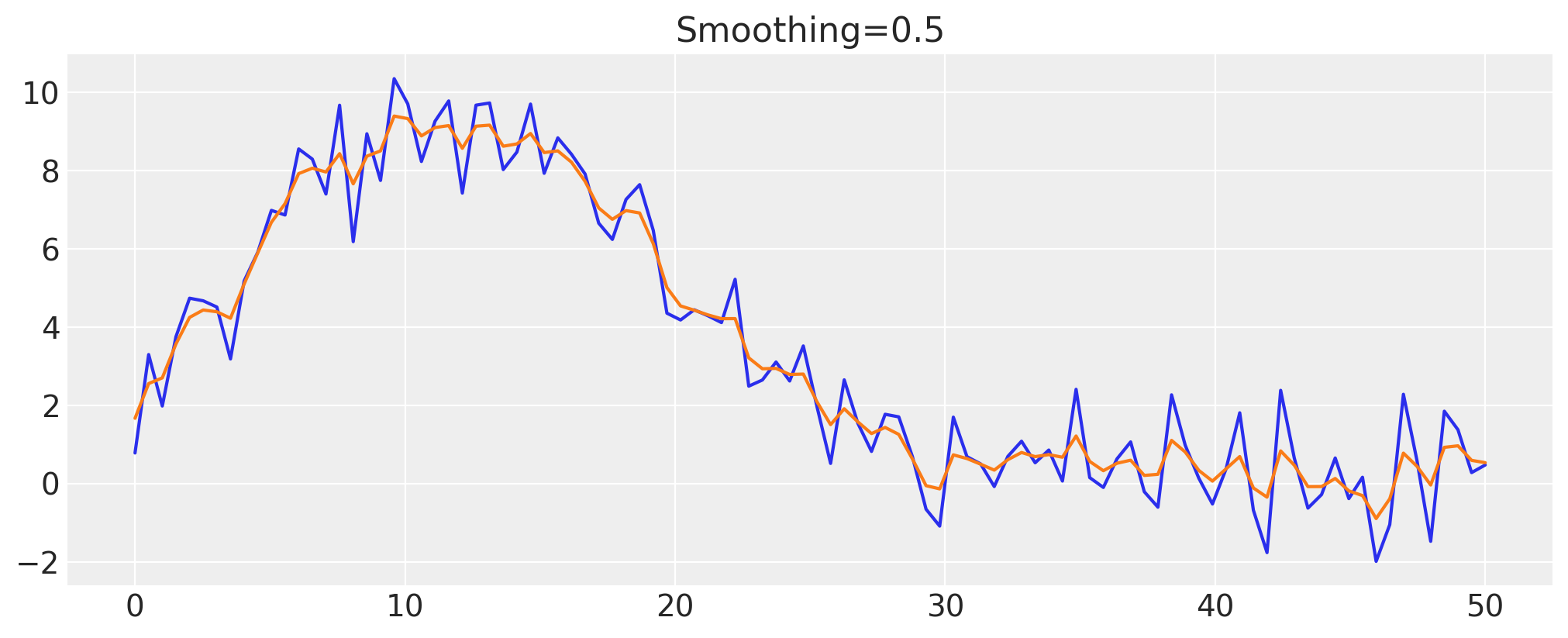
看来方差在噪声和隐藏过程之间均匀分配,正如预期的那样。
让我们尝试逐渐增加平滑度参数,看看我们是否可以获得更平滑的数据
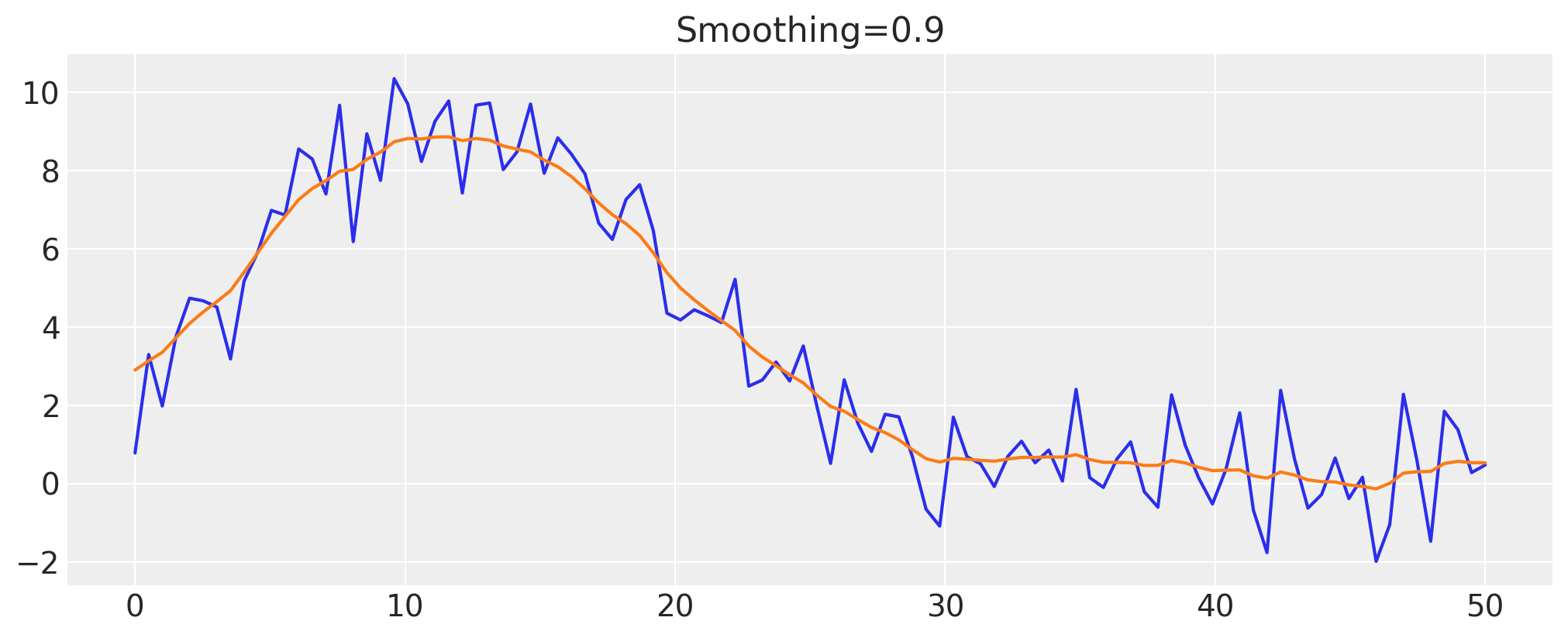
smoothing = 0.9
z_val = infer_z(smoothing)
fig, ax = plt.subplots()
ax.plot(x, y)
ax.plot(x, z_val)
ax.set(title=f"Smoothing={smoothing}");
“极限”平滑#
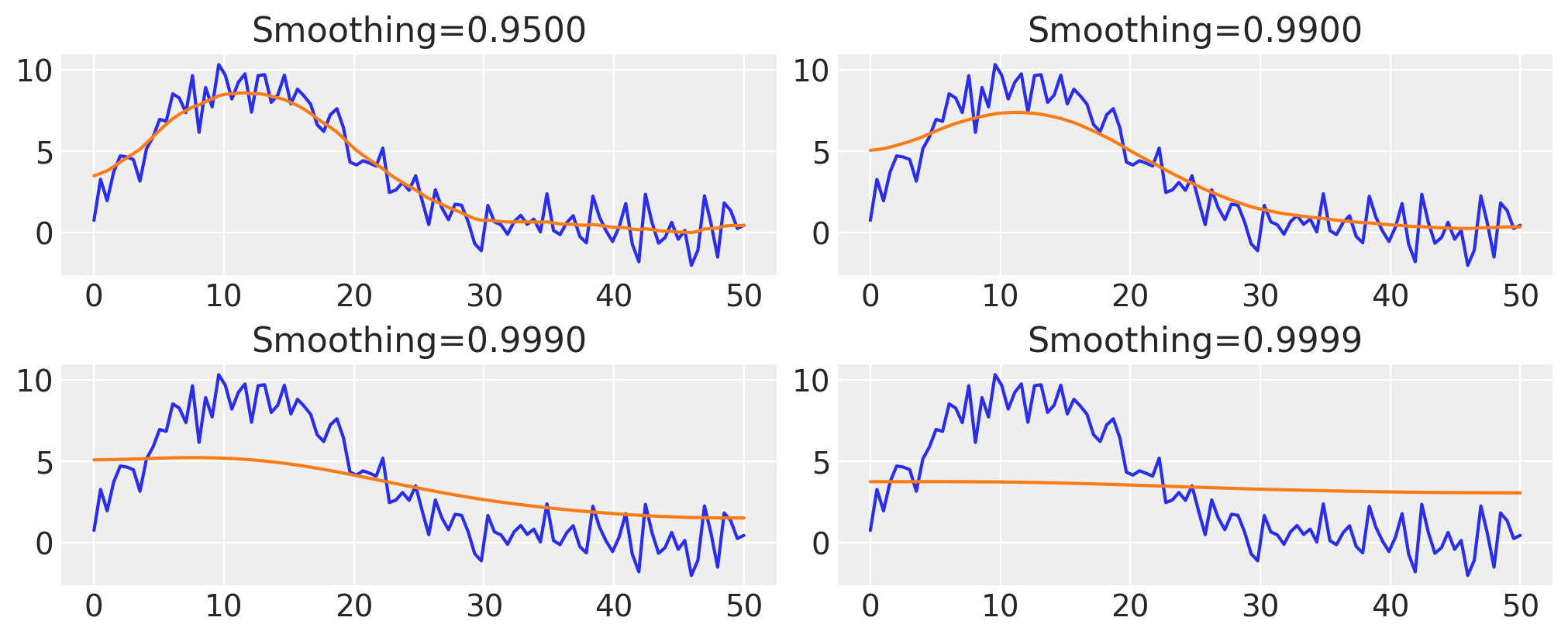
通过增加平滑度参数,我们可以逐步使隐藏布朗运动的推断值接近数据的平均值。 这是因为当我们增加平滑度参数时,我们允许越来越少的方差分配给布朗运动,因此最终它接近于在 \(x\) 域上几乎不变的过程
fig, axes = plt.subplots(nrows=2, ncols=2)
for ax, smoothing in zip(axes.ravel(), [0.95, 0.99, 0.999, 0.9999]):
z_val = infer_z(smoothing)
ax.plot(x, y)
ax.plot(x, z_val)
ax.set_title(f"Smoothing={smoothing:05.4f}")