多输出高斯过程：使用 Hadamard 乘积的互区域化模型#
本笔记本展示了如何使用 Coregion 核和输入核之间的 Hadamard 乘积来实现内在互区域化模型 (ICM) 和线性互区域化模型 (LCM)。这篇论文 by Bonilla et al. [2007] 讨论了多输出高斯过程。有关 ICM 和 LCM 的更多信息，请查看 Mauricio Alvarez 关于多输出高斯过程的演讲，以及他的幻灯片，最后一页有更多参考资料。
多输出高斯过程的优势在于它们能够同时学习和推断来自输入的具有相同不确定性来源的多个输出。在本例中，我们模拟了棒球数据集中几位投手在不同比赛日期中的平均旋转率。
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pytensor.tensor as pt
from pymc.gp.util import plot_gp_dist
%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
准备数据#
棒球数据集包含几位投手在不同比赛日期的平均旋转率。
# get data
try:
df = pd.read_csv("../data/fastball_spin_rates.csv")
except FileNotFoundError:
df = pd.read_csv(pm.get_data("fastball_spin_rates.csv"))
print(df.shape)
df.head()
(4845, 4)
| 投手姓名 | 比赛日期 | 平均旋转率 | 投球数 | |
|---|---|---|---|---|
| 0 | Wainwright, Adam | 2021-04-03 | 2127.415000 | 12 |
| 1 | Wainwright, Adam | 2021-04-08 | 2179.723000 | 11 |
| 2 | Wainwright, Adam | 2021-04-14 | 2297.968571 | 7 |
| 3 | Wainwright, Adam | 2021-04-20 | 2159.150000 | 13 |
| 4 | Wainwright, Adam | 2021-04-26 | 2314.515455 | 11 |
print(
f"There are {df['pitcher_name'].nunique()} pitchers, in {df['game_date'].nunique()} game dates"
)
There are 262 pitchers, in 182 game dates
# Standardise average spin rate
df["avg_spin_rate"] = (df["avg_spin_rate"] - df["avg_spin_rate"].mean()) / df["avg_spin_rate"].std()
df["avg_spin_rate"].describe()
count 4.838000e+03
mean 1.821151e-16
std 1.000000e+00
min -3.646438e+00
25% -6.803556e-01
50% 4.736011e-03
75% 6.837128e-01
max 3.752720e+00
Name: avg_spin_rate, dtype: float64
热门 N 位投手#
# Get top N popular pitchers by who attended most games
n_outputs = 5 # Top 5 popular pitchers
top_pitchers = df.groupby("pitcher_name")["game_date"].count().nlargest(n_outputs).reset_index()
top_pitchers = top_pitchers.reset_index().rename(columns={"index": "output_idx"})
top_pitchers
| 输出索引 | 投手姓名 | 比赛日期 | |
|---|---|---|---|
| 0 | 0 | Rodriguez, Richard | 64 |
| 1 | 1 | Taylor, Josh | 59 |
| 2 | 2 | Kopech, Michael | 43 |
| 3 | 3 | Wells, Tyler | 43 |
| 4 | 4 | Hearn, Taylor | 42 |
# Filter the data with only top N pitchers
adf = df.loc[df["pitcher_name"].isin(top_pitchers["pitcher_name"])].copy()
print(adf.shape)
adf.head()
(251, 4)
| 投手姓名 | 比赛日期 | 平均旋转率 | 投球数 | |
|---|---|---|---|---|
| 1631 | Rodriguez, Richard | 2021-04-01 | 1.245044 | 12 |
| 1632 | Rodriguez, Richard | 2021-04-06 | 2.032285 | 3 |
| 1633 | Rodriguez, Richard | 2021-04-08 | 1.868068 | 10 |
| 1634 | Rodriguez, Richard | 2021-04-12 | 1.801864 | 14 |
| 1635 | Rodriguez, Richard | 2021-04-13 | 1.916592 | 9 |
adf["avg_spin_rate"].describe()
count 251.000000
mean 0.774065
std 0.867510
min -1.050933
25% 0.102922
50% 0.559293
75% 1.517114
max 2.647740
Name: avg_spin_rate, dtype: float64
创建比赛日期索引#
# There are 142 game dates from 01 Apr 2021 to 03 Oct 2021.
adf.loc[:, "game_date"] = pd.to_datetime(adf.loc[:, "game_date"])
game_dates = adf.loc[:, "game_date"]
game_dates.min(), game_dates.max(), game_dates.nunique(), (game_dates.max() - game_dates.min())
(Timestamp('2021-04-01 00:00:00'),
Timestamp('2021-10-03 00:00:00'),
142,
Timedelta('185 days 00:00:00'))
# Create a game date index
dates_idx = pd.DataFrame(
{"game_date": pd.date_range(game_dates.min(), game_dates.max())}
).reset_index()
dates_idx = dates_idx.rename(columns={"index": "x"})
dates_idx.head()
| x | 比赛日期 | |
|---|---|---|
| 0 | 0 | 2021-04-01 |
| 1 | 1 | 2021-04-02 |
| 2 | 2 | 2021-04-03 |
| 3 | 3 | 2021-04-04 |
| 4 | 4 | 2021-04-05 |
创建训练数据#
adf = adf.merge(dates_idx, how="left", on="game_date")
adf = adf.merge(top_pitchers[["pitcher_name", "output_idx"]], how="left", on="pitcher_name")
adf.head()
| 投手姓名 | 比赛日期 | 平均旋转率 | 投球数 | x | 输出索引 | |
|---|---|---|---|---|---|---|
| 0 | Rodriguez, Richard | 2021-04-01 | 1.245044 | 12 | 0 | 0 |
| 1 | Rodriguez, Richard | 2021-04-06 | 2.032285 | 3 | 5 | 0 |
| 2 | Rodriguez, Richard | 2021-04-08 | 1.868068 | 10 | 7 | 0 |
| 3 | Rodriguez, Richard | 2021-04-12 | 1.801864 | 14 | 11 | 0 |
| 4 | Rodriguez, Richard | 2021-04-13 | 1.916592 | 9 | 12 | 0 |
adf = adf.sort_values(["output_idx", "x"])
X = adf[
["x", "output_idx"]
].values # Input data includes the index of game dates, and the index of pitchers
Y = adf["avg_spin_rate"].values # Output data includes the average spin rate of pitchers
X.shape, Y.shape
((251, 2), (251,))
可视化训练数据#
# Plot average spin rates of top pitchers
fig, ax = plt.subplots(1, 1, figsize=(14, 6))
legends = []
for pitcher in top_pitchers["pitcher_name"]:
cond = adf["pitcher_name"] == pitcher
ax.plot(adf.loc[cond, "x"], adf.loc[cond, "avg_spin_rate"], "-o")
legends.append(pitcher)
plt.title("Average spin rates of top 5 popular pitchers")
plt.xlabel("The index of game dates")
plt.ylim([-1.5, 4.0])
plt.legend(legends, loc="upper center");
内在互区域化模型 (ICM)#
内在互区域化模型 (ICM) 是线性互区域化模型 (LCM) 的一个特例，具有一个输入核，例如
\[ K_{ICM} = B \otimes K_{ExpQuad} \]
其中 \(B(o,o')\) 是输出核，\(K_{ExpQuad}(x,x')\) 是输入核。
\[ B = WW^T + diag(kappa) \]
def get_icm(input_dim, kernel, W=None, kappa=None, B=None, active_dims=None):
"""
This function generates an ICM kernel from an input kernel and a Coregion kernel.
"""
coreg = pm.gp.cov.Coregion(input_dim=input_dim, W=W, kappa=kappa, B=B, active_dims=active_dims)
icm_cov = kernel * coreg # Use Hadamard Product for separate inputs
return icm_cov
with pm.Model() as model:
# Priors
ell = pm.Gamma("ell", alpha=2, beta=0.5)
eta = pm.Gamma("eta", alpha=3, beta=1)
kernel = eta**2 * pm.gp.cov.ExpQuad(input_dim=2, ls=ell, active_dims=[0])
sigma = pm.HalfNormal("sigma", sigma=3)
# Get the ICM kernel
W = pm.Normal("W", mu=0, sigma=3, shape=(n_outputs, 2), initval=np.random.randn(n_outputs, 2))
kappa = pm.Gamma("kappa", alpha=1.5, beta=1, shape=n_outputs)
B = pm.Deterministic("B", pt.dot(W, W.T) + pt.diag(kappa))
cov_icm = get_icm(input_dim=2, kernel=kernel, B=B, active_dims=[1])
# Define a Multi-output GP
mogp = pm.gp.Marginal(cov_func=cov_icm)
y_ = mogp.marginal_likelihood("f", X, Y, sigma=sigma)
pm.model_to_graphviz(model)
%%time
with model:
gp_trace = pm.sample(2000, chains=1)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Sequential sampling (1 chains in 1 job)
NUTS: [ell, eta, sigma, W, kappa]
100.00% [3000/3000 21:17<00:00 Sampling chain 0, 0 divergences]
Sampling 1 chain for 1_000 tune and 2_000 draw iterations (1_000 + 2_000 draws total) took 1278 seconds.
CPU times: user 46min 50s, sys: 2h 2min 57s, total: 2h 49min 47s
Wall time: 21min 25s
预测#
# Prepare test data
M = 200 # number of data points
x_new = np.linspace(0, 200, M)[
:, None
] # Select 200 days (185 previous days, and add 15 days into the future).
X_new = np.vstack([x_new for idx in range(n_outputs)])
output_idx = np.vstack([np.repeat(idx, M)[:, None] for idx in range(n_outputs)])
X_new = np.hstack([X_new, output_idx])
%%time
with model:
preds = mogp.conditional("preds", X_new)
gp_samples = pm.sample_posterior_predictive(gp_trace, var_names=["preds"], random_seed=42)
Sampling: [preds]
100.00% [2000/2000 10:47<00:00]
CPU times: user 46min 13s, sys: 39min 48s, total: 1h 26min 2s
Wall time: 10min 50s
f_pred = gp_samples.posterior_predictive["preds"].sel(chain=0)
def plot_predictive_posteriors(f_pred, top_pitchers, M, X_new):
fig, axes = plt.subplots(n_outputs, 1, figsize=(12, 15))
for idx, pitcher in enumerate(top_pitchers["pitcher_name"]):
# Prediction
plot_gp_dist(
axes[idx],
f_pred[:, M * idx : M * (idx + 1)],
X_new[M * idx : M * (idx + 1), 0],
palette="Blues",
fill_alpha=0.1,
samples_alpha=0.1,
)
# Training data points
cond = adf["pitcher_name"] == pitcher
axes[idx].scatter(adf.loc[cond, "x"], adf.loc[cond, "avg_spin_rate"], color="r")
axes[idx].set_title(pitcher)
plt.tight_layout()
plot_predictive_posteriors(f_pred, top_pitchers, M, X_new)
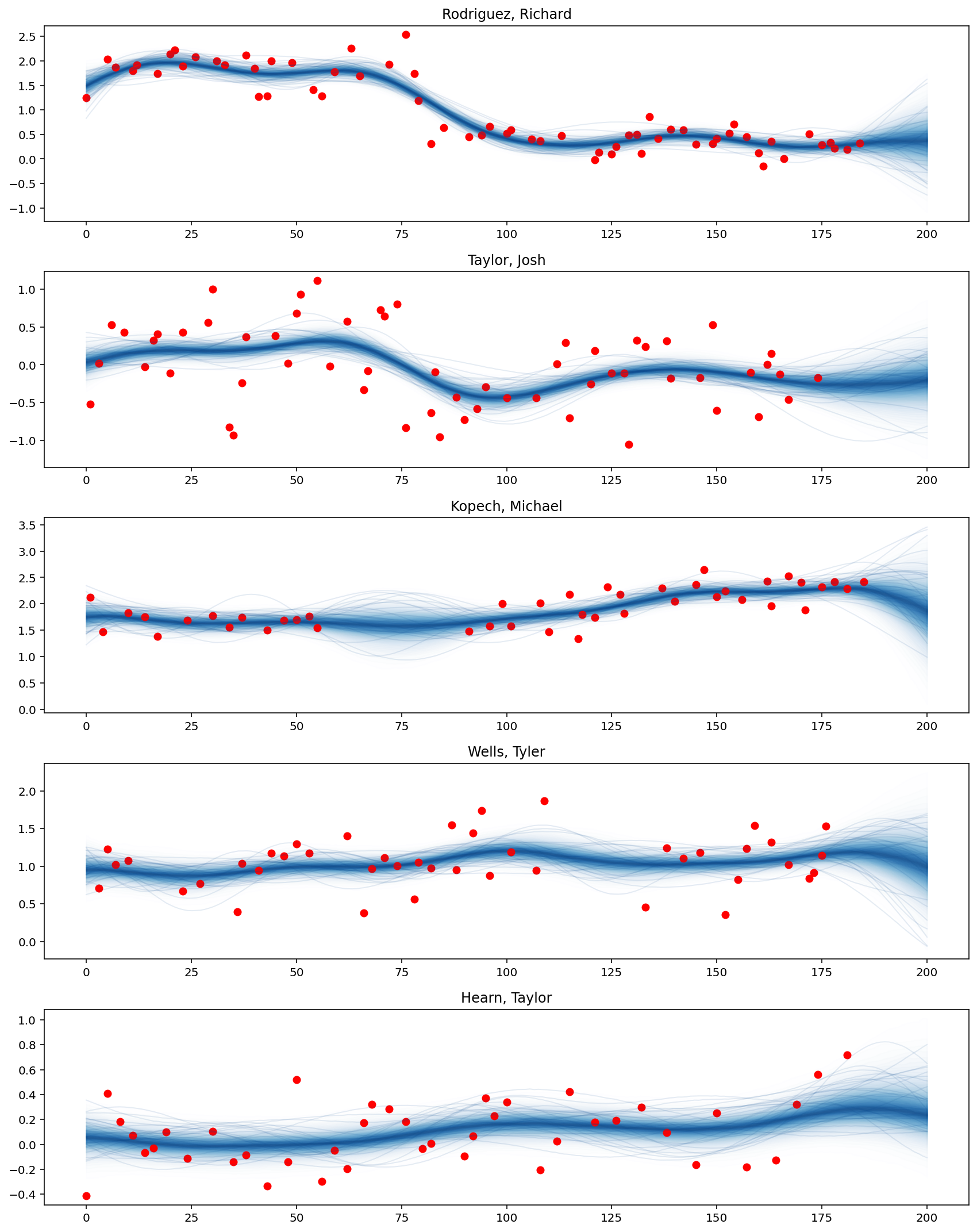
可以看出，Rodriguez Richard 的平均旋转率从第 75 场比赛日期开始显着下降。此外，Kopech Michael 的表现在中途休息几周后有所提高，而 Hearn Taylor 最近表现更好。
az.plot_trace(gp_trace)
plt.tight_layout()
线性互区域化模型 (LCM)#
LCM 是 ICM 的推广，具有两个或多个输入核，因此 LCM 核基本上是几个 ICM 核的总和。LMC 允许来自具有不同协方差（核）的 GP 的多个独立样本。
在本例中，除了 ExpQuad 核之外，我们还为输入数据添加了 Matern32 核。
\[ K_{LCM} = B \otimes K_{ExpQuad} + B \otimes K_{Matern32} \]
def get_lcm(input_dim, active_dims, num_outputs, kernels, W=None, B=None, name="ICM"):
"""
This function generates a LCM kernel from a list of input `kernels` and a Coregion kernel.
"""
if B is None:
kappa = pm.Gamma(f"{name}_kappa", alpha=5, beta=1, shape=num_outputs)
if W is None:
W = pm.Normal(
f"{name}_W",
mu=0,
sigma=5,
shape=(num_outputs, 1),
initval=np.random.randn(num_outputs, 1),
)
else:
kappa = None
cov_func = 0
for idx, kernel in enumerate(kernels):
icm = get_icm(input_dim, kernel, W, kappa, B, active_dims)
cov_func += icm
return cov_func
with pm.Model() as model:
# Priors
ell = pm.Gamma("ell", alpha=2, beta=0.5, shape=2)
eta = pm.Gamma("eta", alpha=3, beta=1, shape=2)
kernels = [pm.gp.cov.ExpQuad, pm.gp.cov.Matern32]
sigma = pm.HalfNormal("sigma", sigma=3)
# Define a list of covariance functions
cov_list = [
eta[idx] ** 2 * kernel(input_dim=2, ls=ell[idx], active_dims=[0])
for idx, kernel in enumerate(kernels)
]
# Get the LCM kernel
cov_lcm = get_lcm(input_dim=2, active_dims=[1], num_outputs=n_outputs, kernels=cov_list)
# Define a Multi-output GP
mogp = pm.gp.Marginal(cov_func=cov_lcm)
y_ = mogp.marginal_likelihood("f", X, Y, sigma=sigma)
pm.model_to_graphviz(model)
%%time
with model:
gp_trace = pm.sample(2000, chains=1)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Sequential sampling (1 chains in 1 job)
NUTS: [ell, eta, sigma, ICM_kappa, ICM_W]
100.00% [3000/3000 18:28<00:00 Sampling chain 0, 2 divergences]
Sampling 1 chain for 1_000 tune and 2_000 draw iterations (1_000 + 2_000 draws total) took 1109 seconds.
There were 2 divergences after tuning. Increase `target_accept` or reparameterize.
CPU times: user 40min 37s, sys: 1h 47min 9s, total: 2h 27min 46s
Wall time: 18min 39s
预测#
%%time
with model:
preds = mogp.conditional("preds", X_new)
gp_samples = pm.sample_posterior_predictive(gp_trace, var_names=["preds"], random_seed=42)
Sampling: [preds]
100.00% [2000/2000 12:50<00:00]
CPU times: user 51min 44s, sys: 50min 14s, total: 1h 41min 59s
Wall time: 12min 53s
plot_predictive_posteriors(f_pred, top_pitchers, M, X_new)
az.plot_trace(gp_trace)
plt.tight_layout()
致谢#
这项工作由 2022 年 Google 编程之夏 和 NUMFOCUS 支持。
参考文献#
[1]
Edwin V Bonilla, Kian Chai, and Christopher Williams. Multi-task gaussian process prediction. Advances in neural information processing systems, 2007. URL: https://papers.nips.cc/paper/2007/hash/66368270ffd51418ec58bd793f2d9b1b-Abstract.html.
水印#
%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,aeppl,xarray
The watermark extension is already loaded. To reload it, use:
%reload_ext watermark
Last updated: Sat Nov 12 2022
Python implementation: CPython
Python version : 3.9.12
IPython version : 8.3.0
pytensor: 2.8.6
aeppl : 0.0.36
xarray: 2022.3.0
pymc : 4.2.1
arviz : 0.13.0
pandas : 1.4.2
pytensor : 2.8.6
numpy : 1.22.4
matplotlib: 3.5.2
Watermark: 2.3.0
许可声明#
本示例库中的所有笔记本均根据 MIT 许可证 提供，该许可证允许修改和再分发用于任何用途，前提是保留版权和许可声明。
引用 PyMC 示例#
要引用此笔记本，请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。
重要提示
许多笔记本都改编自其他来源：博客、书籍等。在这种情况下，您也应该引用原始来源。
另请记住引用您的代码使用的相关库。
这是一个 bibtex 中的引用模板
@incollection{citekey,
author = "<notebook authors, see above>",
title = "<notebook title>",
editor = "PyMC Team",
booktitle = "PyMC examples",
doi = "10.5281/zenodo.5654871"
}
一旦渲染，它可能看起来像