使用 numpy 核的 Gaussian 过程

简单高斯过程拟合示例，改编自 Stan 的 example-models 存储库。

为了说明和普及的目的，此示例从头开始构建高斯过程。但是，PyMC 包括一个 module dedicated to Gaussian Processes 模块，建议使用该模块，而不是从头开始编写所有内容。

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import pytensor.tensor as pt
import seaborn as sns

from xarray_einstats.stats import multivariate_normal

print(f"Running on PyMC v{pm.__version__}")

Running on PyMC v4.1.3

RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")

# fmt: off
x = np.array([-5, -4.9, -4.8, -4.7, -4.6, -4.5, -4.4, -4.3, -4.2, -4.1, -4, 
-3.9, -3.8, -3.7, -3.6, -3.5, -3.4, -3.3, -3.2, -3.1, -3, -2.9, 
-2.8, -2.7, -2.6, -2.5, -2.4, -2.3, -2.2, -2.1, -2, -1.9, -1.8, 
-1.7, -1.6, -1.5, -1.4, -1.3, -1.2, -1.1, -1, -0.9, -0.8, -0.7, 
-0.6, -0.5, -0.4, -0.3, -0.2, -0.1, 0, 0.1, 0.2, 0.3, 0.4, 0.5, 
0.6, 0.7, 0.8, 0.9, 1, 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 
1.9, 2, 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9, 3, 3.1, 
3.2, 3.3, 3.4, 3.5, 3.6, 3.7, 3.8, 3.9, 4, 4.1, 4.2, 4.3, 4.4, 
4.5, 4.6, 4.7, 4.8, 4.9, 5])

y = np.array([1.04442478194401, 0.948306088493654, 0.357037759697332, 0.492336514646604, 
0.520651364364746, 0.112629866592809, 0.470995468454158, -0.168442254267804, 
0.0720344402575861, -0.188108980535916, -0.0160163306512027, 
-0.0388792158617705, -0.0600673630622568, 0.113568725264636, 
0.447160403837629, 0.664421188556779, -0.139510743820276, 0.458823971660986, 
0.141214654640904, -0.286957663528091, -0.466537724021695, -0.308185884317105, 
-1.57664872694079, -1.44463024170082, -1.51206214603847, -1.49393593601901, 
-2.02292464164487, -1.57047488853653, -1.22973445533419, -1.51502367058357, 
-1.41493587255224, -1.10140254663611, -0.591866485375275, -1.08781838696462, 
-0.800375653733931, -1.00764767602679, -0.0471028950122742, -0.536820626879737, 
-0.151688056391446, -0.176771681318393, -0.240094952335518, -1.16827876746502, 
-0.493597351974992, -0.831683011472805, -0.152347043914137, 0.0190364158178343, 
-1.09355955218051, -0.328157917911376, -0.585575679802941, -0.472837120425201, 
-0.503633622750049, -0.0124446353828312, -0.465529814250314, 
-0.101621725887347, -0.26988462590405, 0.398726664193302, 0.113805181040188, 
0.331353802465398, 0.383592361618461, 0.431647298655434, 0.580036473774238, 
0.830404669466897, 1.17919105883462, 0.871037583886711, 1.12290553424174, 
0.752564860804382, 0.76897960270623, 1.14738839410786, 0.773151715269892, 
0.700611498974798, 0.0412951045437818, 0.303526087747629, -0.139399513324585, 
-0.862987735433697, -1.23399179134008, -1.58924289116396, -1.35105117911049, 
-0.990144529089174, -1.91175364127672, -1.31836236129543, -1.65955735224704, 
-1.83516148300526, -2.03817062501248, -1.66764011409214, -0.552154350554687, 
-0.547807883952654, -0.905389222477036, -0.737156477425302, -0.40211249920415, 
0.129669958952991, 0.271142753510592, 0.176311762529962, 0.283580281859344, 
0.635808289696458, 1.69976647982837, 1.10748978734239, 0.365412229181044, 
0.788821368082444, 0.879731888124867, 1.02180766619069, 0.551526067300283])
# fmt: on
N = len(y)

我们将使用平方指数协方差函数，该函数依赖于数据中观察点之间的平方距离。

squared_distance = lambda x, y: (x[None, :] - y[:, None]) ** 2

with pm.Model() as gp_fit:
    mu = np.zeros(N)

    eta_sq = pm.HalfCauchy("eta_sq", 5)
    rho_sq = pm.HalfCauchy("rho_sq", 5)
    sigma_sq = pm.HalfCauchy("sigma_sq", 5)

    D = squared_distance(x, x)

    # Squared exponential
    sigma = pt.fill_diagonal(eta_sq * pt.exp(-rho_sq * D), eta_sq + sigma_sq)

    obs = pm.MvNormal("obs", mu, sigma, observed=y)

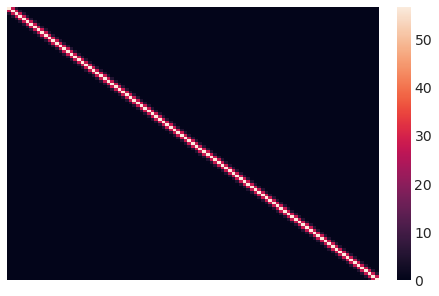
这是我们初始协方差矩阵的样子。直观地说，每个数据点的 Y 值都根据其平方距离与点相关。

sns.heatmap(sigma.eval(), xticklabels=False, yticklabels=False);

以下代码在值网格中生成来自高斯过程模型的预测

# Prediction over grid
xgrid = np.linspace(-6, 6)
D_pred = squared_distance(xgrid, xgrid)
D_off_diag = squared_distance(x, xgrid)

gp_fit.add_coords({"pred_id": xgrid, "pred_id2": xgrid})

with gp_fit as gp:
    # Covariance matrices for prediction
    sigma_pred = eta_sq * pt.exp(-rho_sq * D_pred)
    sigma_off_diag = eta_sq * pt.exp(-rho_sq * D_off_diag)

    # Posterior mean
    mu_post = pm.Deterministic(
        "mu_post", pt.dot(pt.dot(sigma_off_diag, pm.math.matrix_inverse(sigma)), y), dims="pred_id"
    )
    # Posterior covariance
    sigma_post = pm.Deterministic(
        "sigma_post",
        sigma_pred
        - pt.dot(pt.dot(sigma_off_diag, pm.math.matrix_inverse(sigma)), sigma_off_diag.T),
        dims=("pred_id", "pred_id2"),
    )

with gp_fit:
    svgd_approx = pm.fit(400, method="svgd", inf_kwargs=dict(n_particles=100))

100.00% [400/400 06:05<00:00]

gp_trace = svgd_approx.sample(1000)

az.plot_trace(gp_trace, var_names=["eta_sq", "rho_sq", "sigma_sq"]);

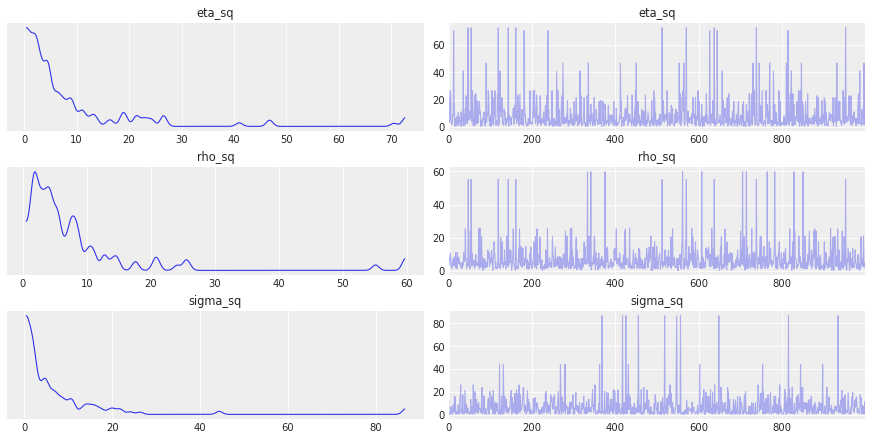
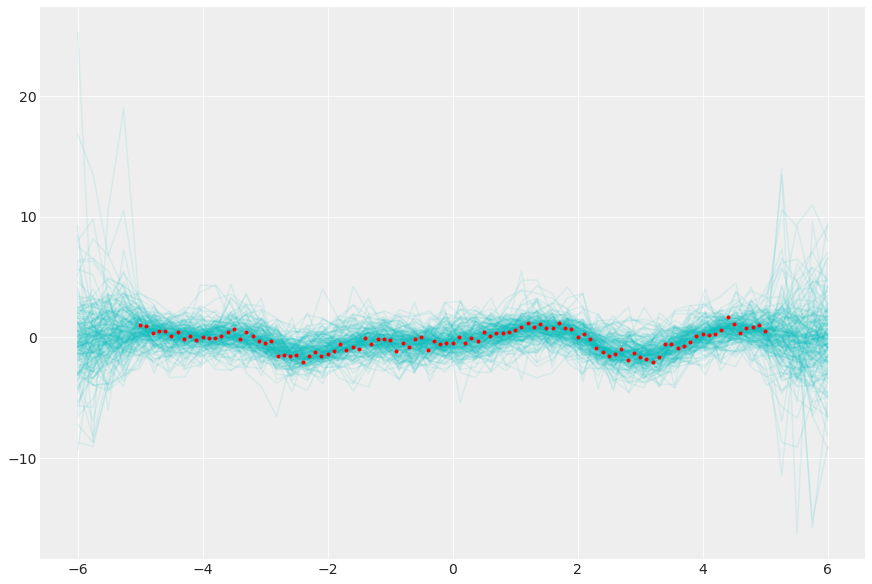
从后验高斯过程采样

post = az.extract(gp_trace, num_samples=200)

y_pred = multivariate_normal(
    post["mu_post"], post["sigma_post"], dims=("pred_id", "pred_id2")
).rvs()

_, ax = plt.subplots(figsize=(12, 8))
ax.plot(xgrid, y_pred.transpose(..., "sample"), "c-", alpha=0.1)
ax.plot(x, y, "r.");

作者

• 改编自 Stan 的 example-models 存储库，作者为 Chris Fonnesbeck，于 2016 年

• 由 Ana Rita Santos 和 Sandra Meneses 于 2022 年 7 月更新 (pymc#404)

水印

%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,aeppl,xarray,xarray_einstats

Last updated: Tue Aug 02 2022

Python implementation: CPython
Python version       : 3.10.5
IPython version      : 8.4.0

pytensor         : 2.7.7
aeppl          : 0.0.32
xarray         : 2022.6.0
xarray_einstats: 0.4.0.dev1

sys       : 3.10.5 | packaged by conda-forge | (main, Jun 14 2022, 07:07:06) [Clang 13.0.1 ]
pytensor    : 2.7.7
pymc      : 4.1.3
seaborn   : 0.11.2
matplotlib: 3.5.2
arviz     : 0.13.0.dev0
numpy     : 1.23.1

Watermark: 2.3.1

许可声明

本示例库中的所有笔记本均根据 MIT 许可证提供，该许可证允许修改和重新分发以用于任何用途，前提是保留版权和许可声明。

引用 PyMC 示例

要引用此笔记本，请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。

重要提示

许多笔记本都改编自其他来源：博客、书籍... 在这种情况下，您也应该引用原始来源。

另请记住引用您的代码使用的相关库。

这是一个 bibtex 中的引用模板

@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}

渲染后可能看起来像这样