有序分类结果的回归模型#
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pytensor.tensor as pt
import statsmodels.api as sm
from scipy.stats import bernoulli
from statsmodels.miscmodels.ordinal_model import OrderedModel
%config InlineBackend.figure_format = 'retina' # high resolution figures
az.style.use("arviz-darkgrid")
rng = np.random.default_rng(42)
序数尺度和调查数据#
与许多统计学领域一样,调查数据的语言也带有过载的词汇。在讨论调查设计时,您经常会听到基于设计的方法和基于模型的方法之间的对比,这些方法用于 (i) 抽样策略和 (ii) 对相关数据进行统计推断。我们不会深入研究不同抽样策略的细节,例如:简单随机抽样、整群随机抽样或使用人口权重方案的分层随机抽样。关于这些策略的文献浩如烟海,但在本笔记本中,我们将讨论何时以及为什么将模型驱动的统计推断应用于李克特量表调查响应数据和其他类型的有序分类数据是有用的。
有序类别:已知分布#
我们将从生成一些虚假数据开始。想象一下员工/经理的关系,其中年度流程的一部分包括进行 360 度评估。经理会收到其团队的评分(1 - 10),人力资源部会收集这些评分。人力资源经理想知道哪些因素会影响经理的评分,以及如何让获得 4 分的经理提升到 5 分,或让获得 7 分的经理提升到 8 分。他们有一种理论,即评分很大程度上是薪资的函数。
序数回归是一种旨在建模这些类型关系的统计技术,它可以与基于设计的方法形成对比,后者的重点是在调查设计的背景下提取简单的统计摘要,例如比例、计数或比率,并对这些导出的摘要中的误差容限提供强有力的保证。
def make_data():
np.random.seed(100)
salary = np.random.normal(40, 10, 500)
work_sat = np.random.beta(1, 0.4, 500)
work_from_home = bernoulli.rvs(0.7, size=500)
work_from_home_calc = np.where(work_from_home, 1.4 * work_from_home, work_from_home)
latent_rating = (
0.08423 * salary + 0.2 * work_sat + work_from_home_calc + np.random.normal(0, 1, 500)
)
explicit_rating = np.round(latent_rating, 0)
df = pd.DataFrame(
{
"salary": salary,
"work_sat": work_sat,
"work_from_home": work_from_home,
"latent_rating": latent_rating,
"explicit_rating": explicit_rating,
}
)
return df
try:
df = pd.read_csv("../data/fake_employee_manger_rating.csv")
df = df[["salary", "work_sat", "work_from_home", "latent_rating", "explicit_rating"]]
except FileNotFoundError:
df = make_data()
K = len(df["explicit_rating"].unique())
df.head()
| 薪资 | 工作满意度 | 居家办公 | 潜在评分 | 显式评分 | |
|---|---|---|---|---|---|
| 0 | 41.172474 | 0.632002 | 1 | 5.328188 | 5.0 |
| 1 | 40.984524 | 0.904452 | 0 | 3.198263 | 3.0 |
| 2 | 36.469472 | 0.911330 | 1 | 4.108042 | 4.0 |
| 3 | 6.453822 | 0.919106 | 0 | 1.496440 | 1.0 |
| 4 | 33.795497 | 0.894581 | 0 | 3.200672 | 3.0 |
我们指定数据的方式是,存在一个潜在的情感,它在尺度上是连续的,并且被粗略地离散化以表示序数评分尺度。我们指定数据的方式是,薪资驱动经理评分的相当线性的增长。
fig, axs = plt.subplots(1, 3, figsize=(15, 5))
axs = axs.flatten()
ax = axs[0]
ax.scatter(df["salary"], df["explicit_rating"], label="Explicit Rating", color="blue", alpha=0.3)
axs[1].scatter(
df["work_from_home"], df["latent_rating"], label="Latent Rating", color="red", alpha=0.3
)
axs[1].scatter(
df["work_from_home"], df["explicit_rating"], label="Explicit Rating", c="blue", alpha=0.3
)
axs[2].scatter(df["work_sat"], df["latent_rating"], label="Latent Rating", color="red", alpha=0.3)
axs[2].scatter(
df["work_sat"], df["explicit_rating"], label="Explicit Rating", color="blue", alpha=0.3
)
ax.scatter(df["salary"], df["latent_rating"], label="Latent Sentiment", color="red")
ax.set_title("Manager Ratings by Salary")
axs[1].set_title("Manager Ratings by WFH")
axs[2].set_title("Manager Ratings by Work Satisfaction")
ax.set_ylabel("Latent Sentiment")
ax.set_xlabel("Employee Salary")
axs[1].set_xlabel("Work From Home: Y/N")
axs[2].set_xlabel("Employee Work Satisfaction")
axs[1].legend();
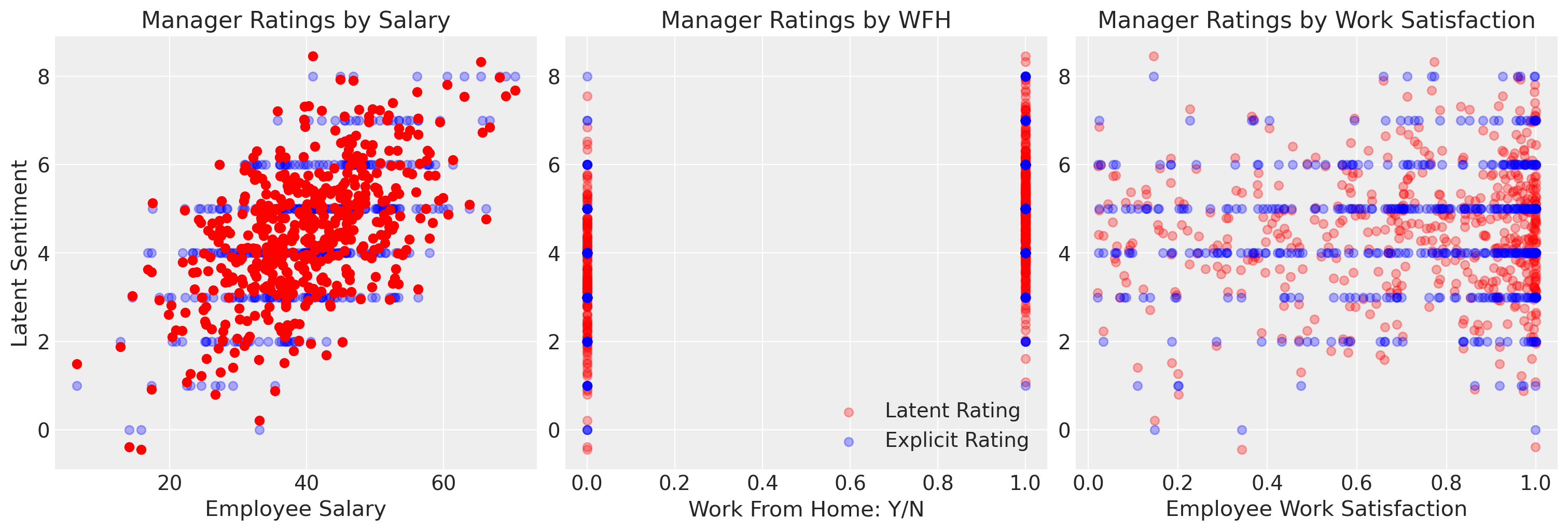
但是,我们可以在这里看到,如果我们使用简单的 OLS 拟合来拟合此模型,则它意味着超出分类尺度的值,这可能会促使过度热心的人力资源经理进行虚假的薪资增长。OLS 近似是有限的,因为它无法解释结果变量的适当性质。
exog = sm.add_constant(df[["salary", "work_from_home", "work_sat"]])
mod = sm.OLS(df["explicit_rating"], exog)
results = mod.fit()
results.summary()
results.predict([1, 200, 1, 0.6])
fig, axs = plt.subplots(1, 2, figsize=(20, 6))
axs = axs.flatten()
ax = axs[1]
salaries = np.linspace(10, 125, 20)
predictions = [results.predict([1, i, 1, 0.6])[0] for i in salaries]
ax.plot(salaries, predictions, label="Implied Linear function of Salaries on Outcome")
ax.set_title("Out of bound Prediction based on Salary")
ax.axhline(10, linestyle="--", color="black")
ax.set_xlabel("Hypothetical Salary")
ax.set_ylabel("Manager Rating Scale")
ax.axhline(0, linestyle="--", color="black")
axs[0].hist(results.resid, ec="white")
axs[0].set_title("Simple OLS Residuals on Training Data");
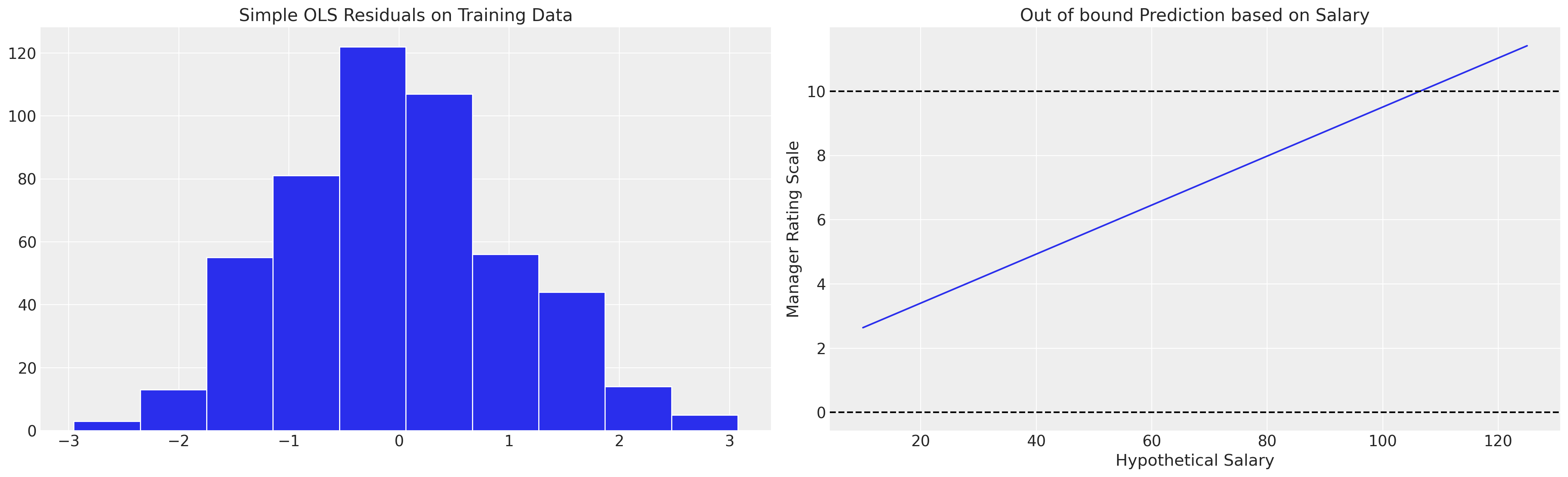
这暗示了在调查数据推断中设计方法和模型方法之间存在对比的原因。建模方法通常隐藏或掩盖了假设,这使得模型不可行,而保守方法倾向于在设计理念下进行推断,从而避免模型错误指定的风险。
序数回归模型:理念#
在本笔记本中,我们将展示如何将回归模型拟合到具有有序类别的结果,以避免一种类型的模型错误指定。这些类型的模型可以被视为逻辑回归模型在潜在连续尺度上具有多个阈值的应用。其理念是存在一个潜在的度量,可以通过度量的极端性进行划分,但我们只观察到个体居住的尺度分区的指标。这是一种非常自然的视角,例如,想象一下粗略的政治分类中隐藏的复杂性:自由主义者、温和派和保守派。您可能对任何数量的政治问题有各种各样的看法,但它们都在政治计算中被归纳为有限的一组(通常很差的)选择。过去 10 个政治选择中的哪一个将您从自由主义者推向温和派?
其理念是将结果变量(我们的分类)判断视为源自潜在的连续度量。我们看到的结果仅仅是在该连续度量上达到某个阈值时才会出现。序数回归的主要推断任务是推导出潜在连续空间中这些阈值的估计值。
在上面的数据集中,我们已经明确指定了关系,在接下来的步骤中,我们将估计各种序数回归模型。
拟合各种模型规范#
序数回归模型的模型规范通常使用 logit 变换和隐含的累积概率。对于具有概率 \(\pi_1, .... \pi_n\) 的 \(c\) 个结果类别,累积 logits 定义为
这被应用于回归上下文中,我们在其中以线性方式指定确定我们潜在结果的因素
这意味着
并且属于特定类别 \(j\) 的概率由属于以下定义的单元格的概率决定
以这种方式指定的序数回归的一个优点是,beta 项系数的解释在潜在空间中的每个区间都保持不变。模型参数的解释是典型的:\(x_{k}\) 单位增加对应于 \(Y_{latent}\) 增加 \(\beta_{k}\)。对于 probit 回归规范,也适用类似的解释。但是,我们必须注意比较具有不同变量的不同模型规范之间的系数解释。上述系数解释在模型中精确固定变量的情况下作为条件解释是有意义的。添加或删除变量会更改条件化,这会由于非可折叠现象而破坏模型的可比性。我们将在下面展示如何使用后验预测分布来比较模型的预测含义。
贝叶斯特性#
虽然序数回归通常在频率学范式中执行,但相同的技术可以应用于贝叶斯设置,并具有后验概率分布和后验预测模拟的所有优势。在 PyMC 中,至少有两种方法可以指定此模型上的先验。第一种方法使用约束狄利克雷分布来定义阈值的先验。第二种方法稍微宽松一些,允许指定具有合适数量切点的任何先验分布,并将排序变换应用于从先验分布生成的样本。
我们将在本笔记本中展示这两种方法,但正如我们将看到的,狄利克雷分布的定义确保了使其更适合约束结果空间的属性。在每种方法中,我们都可以像在更标准的回归模型中一样包含协变量。
PyMC 同时具有 OrderedLogistic 和 OrderedProbit 分布可用。
def constrainedUniform(N, min=0, max=1):
return pm.Deterministic(
"cutpoints",
pt.concatenate(
[
np.ones(1) * min,
pt.extra_ops.cumsum(pm.Dirichlet("cuts_unknown", a=np.ones(N - 2))) * (max - min)
+ min,
]
),
)
上面的函数(Ben Vincent 博士和 Adrian Seyboldt 的智慧结晶)看起来有点吓人,但这只是一个方便函数,用于指定我们 \(Y_{latent}\) 中切点的先验。狄利克雷分布的特殊之处在于,从该分布中抽取的样本之和必须为 1。上面的函数确保从先验分布中抽取的每个样本都是最大类别的累积份额,该份额大于我们序数分类的最小值。
def make_model(priors, model_spec=1, constrained_uniform=False, logit=True):
with pm.Model() as model:
if constrained_uniform:
cutpoints = constrainedUniform(K, 0, K)
else:
sigma = pm.Exponential("sigma", priors["sigma"])
cutpoints = pm.Normal(
"cutpoints",
mu=priors["mu"],
sigma=sigma,
transform=pm.distributions.transforms.univariate_ordered,
)
if model_spec == 1:
beta = pm.Normal("beta", priors["beta"][0], priors["beta"][1], size=1)
mu = pm.Deterministic("mu", beta[0] * df.salary)
elif model_spec == 2:
beta = pm.Normal("beta", priors["beta"][0], priors["beta"][1], size=2)
mu = pm.Deterministic("mu", beta[0] * df.salary + beta[1] * df.work_sat)
elif model_spec == 3:
beta = pm.Normal("beta", priors["beta"][0], priors["beta"][1], size=3)
mu = pm.Deterministic(
"mu", beta[0] * df.salary + beta[1] * df.work_sat + beta[2] * df.work_from_home
)
if logit:
y_ = pm.OrderedLogistic("y", cutpoints=cutpoints, eta=mu, observed=df.explicit_rating)
else:
y_ = pm.OrderedProbit("y", cutpoints=cutpoints, eta=mu, observed=df.explicit_rating)
idata = pm.sample(nuts_sampler="numpyro", idata_kwargs={"log_likelihood": True})
idata.extend(pm.sample_posterior_predictive(idata))
return idata, model
priors = {"sigma": 1, "beta": [0, 1], "mu": np.linspace(0, K, K - 1)}
idata1, model1 = make_model(priors, model_spec=1)
idata2, model2 = make_model(priors, model_spec=2)
idata3, model3 = make_model(priors, model_spec=3)
idata4, model4 = make_model(priors, model_spec=3, constrained_uniform=True)
idata5, model5 = make_model(priors, model_spec=3, constrained_uniform=True)
显示代码单元格输出
/Users/nathanielforde/mambaforge/envs/pymc_examples_new/lib/python3.9/site-packages/pymc/sampling/mcmc.py:243: UserWarning: Use of external NUTS sampler is still experimental
warnings.warn("Use of external NUTS sampler is still experimental", UserWarning)
Compiling...
Compilation time = 0:00:01.829062
Sampling...
Sampling time = 0:00:05.483080
Transforming variables...
Transformation time = 0:00:00.442042
Computing Log Likelihood...
/Users/nathanielforde/mambaforge/envs/pymc_examples_new/lib/python3.9/site-packages/pymc/sampling/mcmc.py:243: UserWarning: Use of external NUTS sampler is still experimental
warnings.warn("Use of external NUTS sampler is still experimental", UserWarning)
Compiling...
Compilation time = 0:00:02.785476
Sampling...
Sampling time = 0:00:05.161887
Transforming variables...
Transformation time = 0:00:00.215416
Computing Log Likelihood...
/Users/nathanielforde/mambaforge/envs/pymc_examples_new/lib/python3.9/site-packages/pymc/sampling/mcmc.py:243: UserWarning: Use of external NUTS sampler is still experimental
warnings.warn("Use of external NUTS sampler is still experimental", UserWarning)
Compiling...
Compilation time = 0:00:01.304173
Sampling...
Sampling time = 0:00:06.041616
Transforming variables...
Transformation time = 0:00:00.174980
Computing Log Likelihood...
/Users/nathanielforde/mambaforge/envs/pymc_examples_new/lib/python3.9/site-packages/pymc/sampling/mcmc.py:243: UserWarning: Use of external NUTS sampler is still experimental
warnings.warn("Use of external NUTS sampler is still experimental", UserWarning)
Compiling...
Compilation time = 0:00:02.029193
Sampling...
Sampling time = 0:00:04.205211
Transforming variables...
Transformation time = 0:00:00.332793
Computing Log Likelihood...
/Users/nathanielforde/mambaforge/envs/pymc_examples_new/lib/python3.9/site-packages/pymc/sampling/mcmc.py:243: UserWarning: Use of external NUTS sampler is still experimental
warnings.warn("Use of external NUTS sampler is still experimental", UserWarning)
Compiling...
Compilation time = 0:00:01.665197
Sampling...
Sampling time = 0:00:04.125931
Transforming variables...
Transformation time = 0:00:00.174673
Computing Log Likelihood...
az.summary(idata3, var_names=["sigma", "cutpoints", "beta"])
| 均值 | 标准差 | HDI_3% | HDI_97% | MCSE_均值 | MCSE_标准差 | ESS_批量 | ESS_尾部 | R_hat | |
|---|---|---|---|---|---|---|---|---|---|
| 西格玛 | 2.039 | 0.622 | 0.976 | 3.212 | 0.012 | 0.008 | 2782.0 | 2623.0 | 1.0 |
| 切点[0] | -1.639 | 0.793 | -3.173 | -0.239 | 0.015 | 0.011 | 2810.0 | 2564.0 | 1.0 |
| 切点[1] | 1.262 | 0.464 | 0.409 | 2.139 | 0.007 | 0.005 | 4086.0 | 3251.0 | 1.0 |
| 切点[2] | 3.389 | 0.441 | 2.598 | 4.249 | 0.008 | 0.005 | 3252.0 | 3280.0 | 1.0 |
| 切点[3] | 5.074 | 0.466 | 4.179 | 5.941 | 0.009 | 0.006 | 2850.0 | 2614.0 | 1.0 |
| 切点[4] | 6.886 | 0.508 | 5.964 | 7.875 | 0.010 | 0.007 | 2558.0 | 2924.0 | 1.0 |
| 切点[5] | 8.765 | 0.563 | 7.664 | 9.800 | 0.011 | 0.008 | 2440.0 | 3031.0 | 1.0 |
| 切点[6] | 10.338 | 0.614 | 9.183 | 11.505 | 0.012 | 0.009 | 2475.0 | 2949.0 | 1.0 |
| 切点[7] | 12.316 | 0.722 | 11.030 | 13.758 | 0.014 | 0.010 | 2633.0 | 3016.0 | 1.0 |
| 贝塔[0] | 0.130 | 0.010 | 0.111 | 0.149 | 0.000 | 0.000 | 3069.0 | 3306.0 | 1.0 |
| 贝塔[1] | -0.089 | 0.270 | -0.577 | 0.428 | 0.004 | 0.004 | 5076.0 | 2915.0 | 1.0 |
| 贝塔[2] | 2.498 | 0.201 | 2.126 | 2.871 | 0.004 | 0.003 | 3161.0 | 2944.0 | 1.0 |
pm.model_to_graphviz(model3)
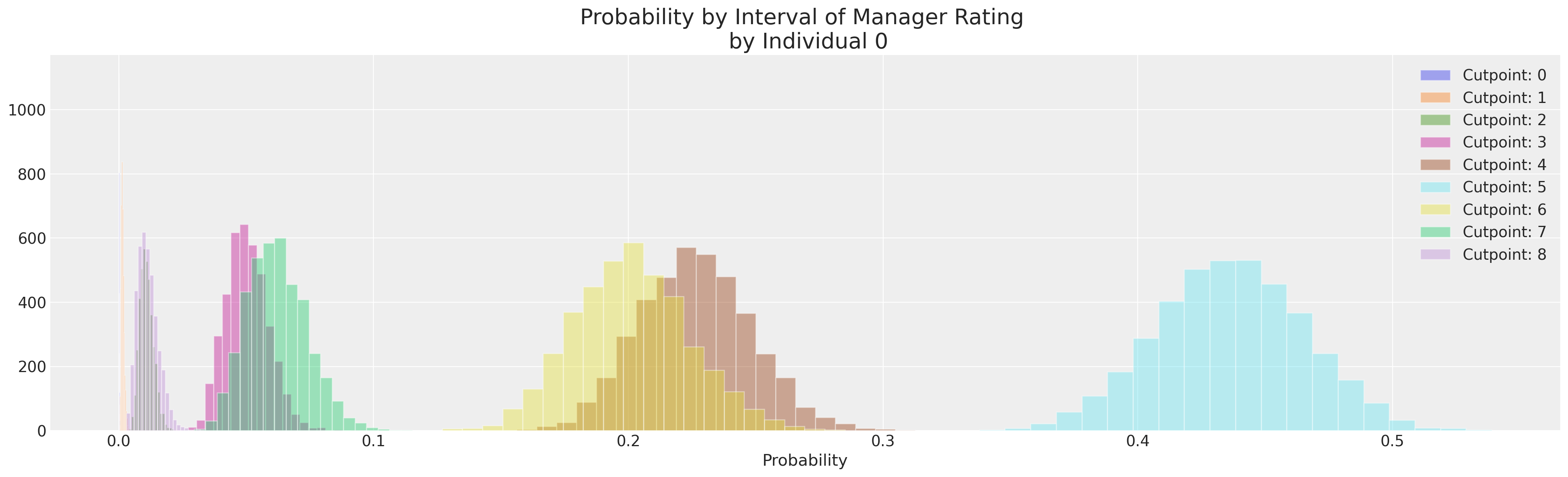
提取个体概率#
现在,对于每位经理的评分,我们可以查看与每个可用类别相关的概率。在我们的切点后验分布中,员工最有可能落入潜在连续度量的哪个部分。
implied_probs = az.extract(idata3, var_names=["y_probs"])
implied_probs.shape
(500, 9, 4000)
implied_probs[0].mean(axis=1)
<xarray.DataArray 'y_probs' (y_probs_dim_1: 9)>
array([1.11373333e-04, 1.47134815e-03, 1.08968413e-02, 5.03528852e-02,
2.26303020e-01, 4.36314380e-01, 2.00984249e-01, 6.21568993e-02,
1.14090037e-02])
Coordinates:
y_probs_dim_0 int64 0
* y_probs_dim_1 (y_probs_dim_1) int64 0 1 2 3 4 5 6 7 8fig, ax = plt.subplots(figsize=(20, 6))
for i in range(K):
ax.hist(implied_probs[0, i, :], label=f"Cutpoint: {i}", ec="white", bins=20, alpha=0.4)
ax.set_xlabel("Probability")
ax.set_title("Probability by Interval of Manager Rating \n by Individual 0", fontsize=20)
ax.legend();
implied_class = az.extract(idata3, var_names=["y"], group="posterior_predictive")
implied_class.shape
(500, 4000)
from scipy.stats import mode
mode(implied_class[0])
/var/folders/__/ng_3_9pn1f11ftyml_qr69vh0000gn/T/ipykernel_63059/3774112.py:3: FutureWarning: Unlike other reduction functions (e.g. `skew`, `kurtosis`), the default behavior of `mode` typically preserves the axis it acts along. In SciPy 1.11.0, this behavior will change: the default value of `keepdims` will become False, the `axis` over which the statistic is taken will be eliminated, and the value None will no longer be accepted. Set `keepdims` to True or False to avoid this warning.
mode(implied_class[0])
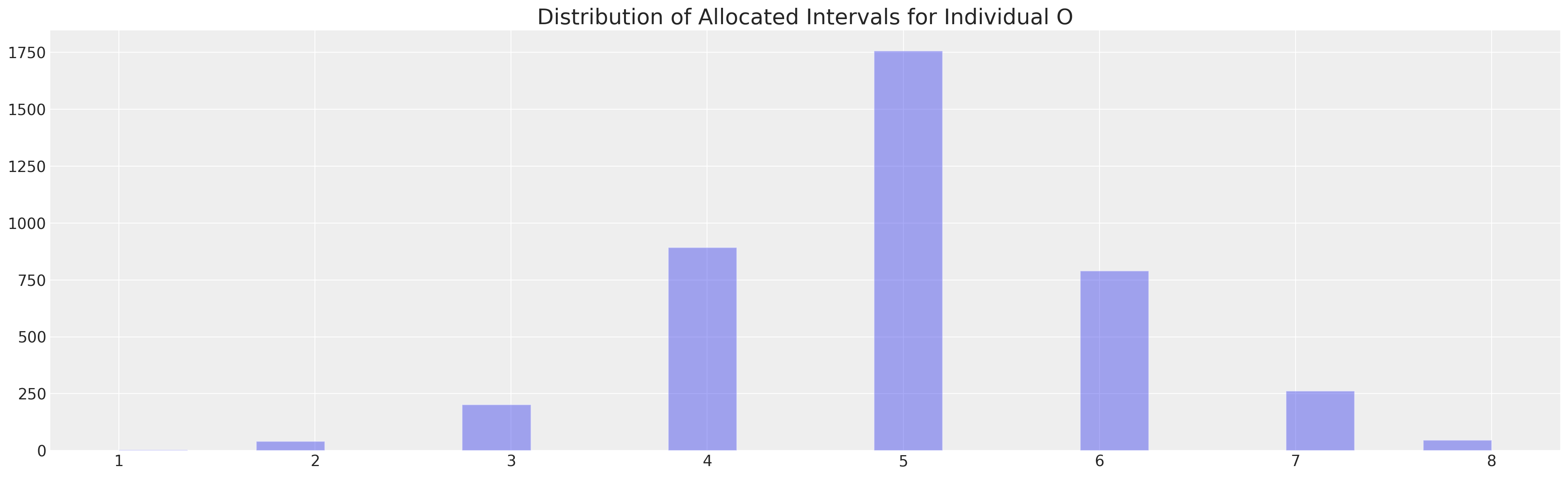
ModeResult(mode=array([5]), count=array([1758]))
fig, ax = plt.subplots(figsize=(20, 6))
ax.hist(implied_class[0], ec="white", bins=20, alpha=0.4)
ax.set_title("Distribution of Allocated Intervals for Individual O", fontsize=20);
比较模型:参数拟合和 LOO#
缓解模型错误指定风险的一种工具是在不同的候选模型之间进行比较,以检查预测准确性。
compare = az.compare(
{
"model_salary": idata1,
"model_salary_worksat": idata2,
"model_full": idata3,
"constrained_logit_full": idata4,
"constrained_probit_full": idata5,
}
)
az.plot_compare(compare)
compare
| 排名 | elpd_loo | p_loo | elpd_diff | 权重 | 标准误 | DSE | 警告 | 尺度 | |
|---|---|---|---|---|---|---|---|---|---|
| 模型_完整 | 0 | -738.115609 | 11.514954 | 0.000000 | 8.089471e-01 | 16.676300 | 0.000000 | 假 | 对数 |
| 约束_logit_完整 | 1 | -748.997150 | 7.502048 | 10.881541 | 1.910529e-01 | 12.737133 | 6.778651 | 假 | 对数 |
| 约束_probit_完整 | 2 | -749.078203 | 7.580680 | 10.962594 | 3.124925e-14 | 12.730696 | 6.776967 | 假 | 对数 |
| 模型_薪资 | 3 | -825.636071 | 8.339788 | 87.520462 | 1.785498e-14 | 15.967569 | 12.472026 | 假 | 对数 |
| 模型_薪资_工作满意度 | 4 | -826.443265 | 9.272995 | 88.327656 | 0.000000e+00 | 15.911693 | 12.464281 | 假 | 对数 |
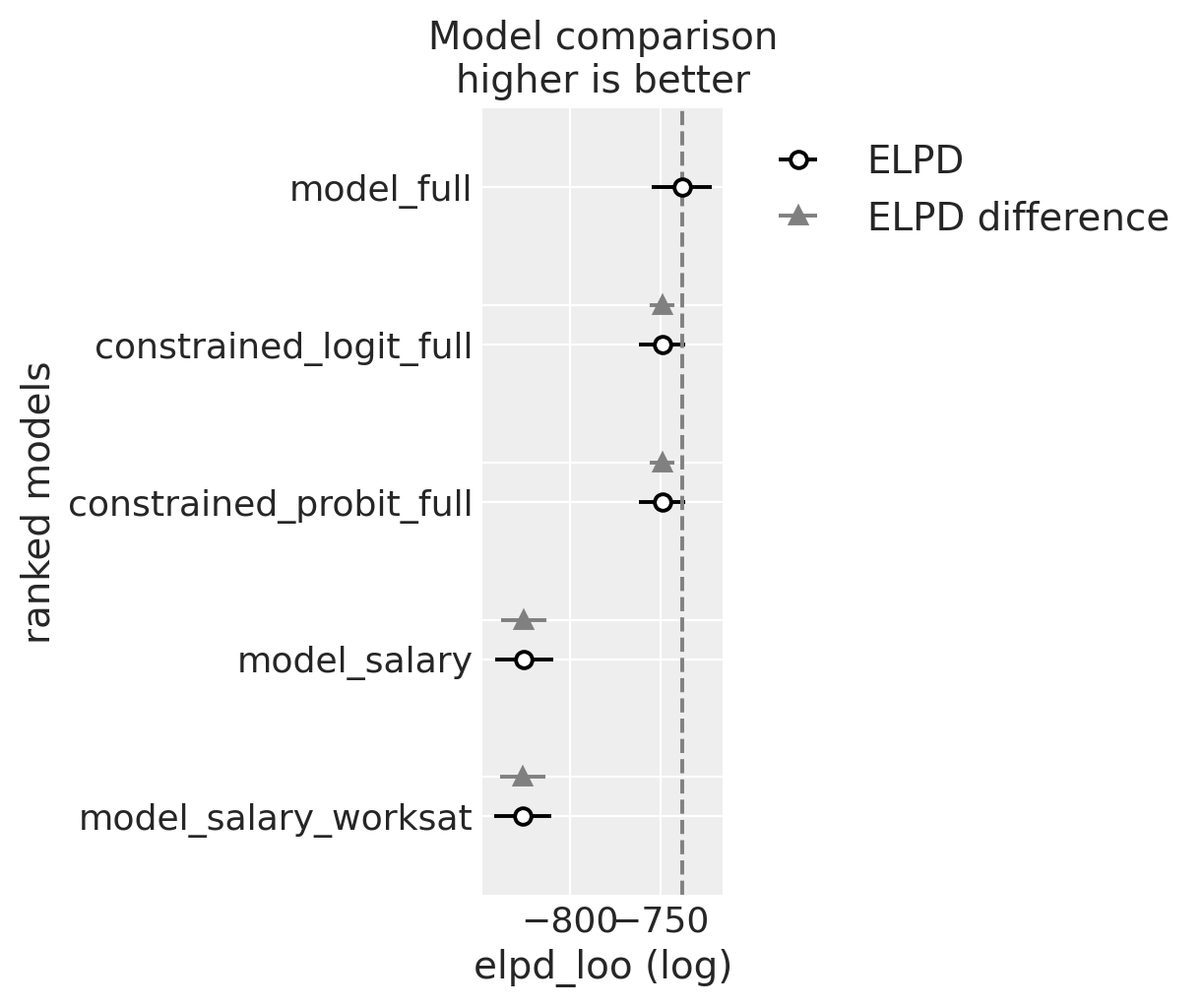
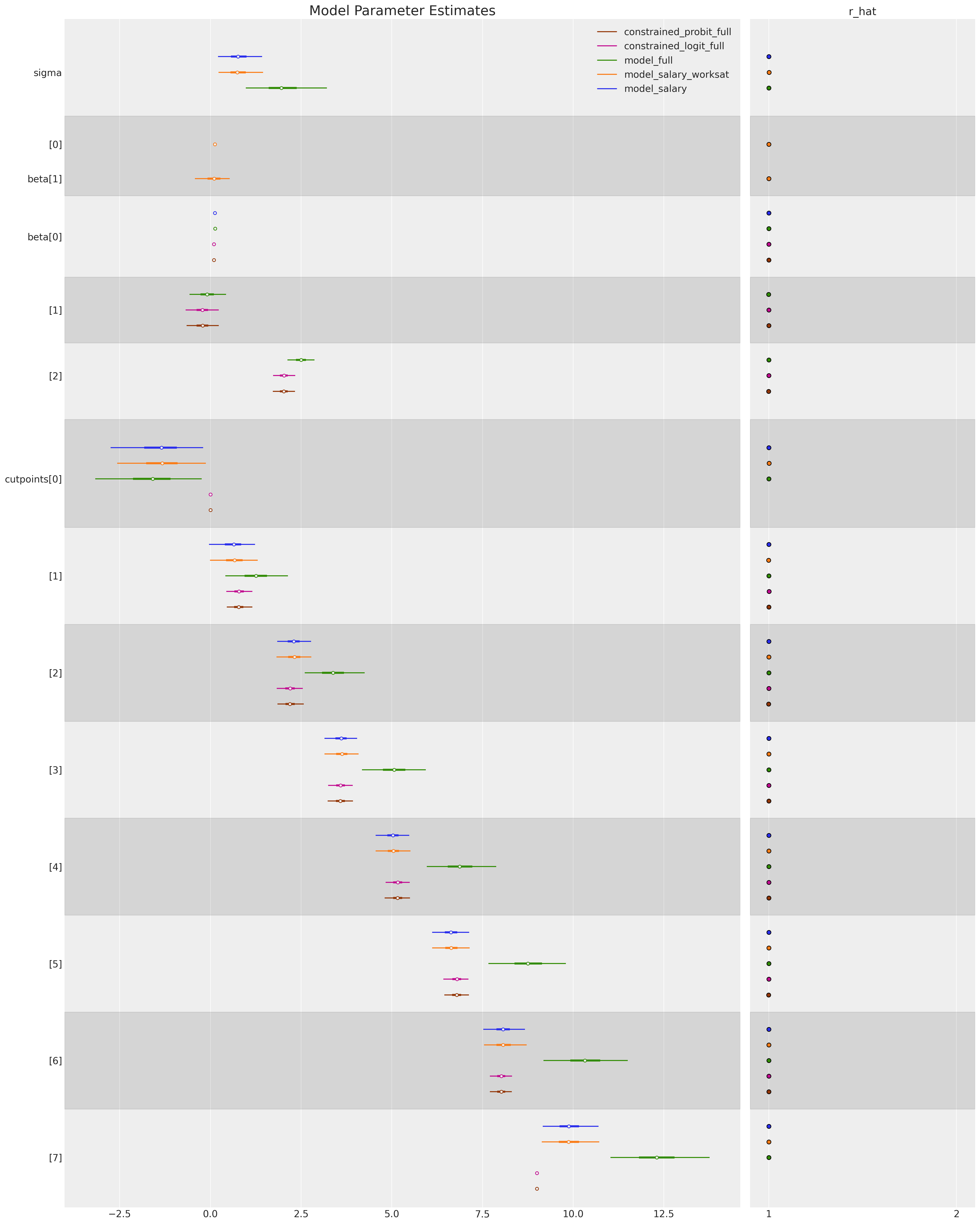
我们还可以比较控制每个回归模型的估计参数,以查看我们的模型拟合对替代参数化的稳健性如何。
ax = az.plot_forest(
[idata1, idata2, idata3, idata4, idata5],
var_names=["sigma", "beta", "cutpoints"],
combined=True,
ridgeplot_overlap=4,
figsize=(20, 25),
r_hat=True,
ridgeplot_alpha=0.3,
model_names=[
"model_salary",
"model_salary_worksat",
"model_full",
"constrained_logit_full",
"constrained_probit_full",
],
)
ax[0].set_title("Model Parameter Estimates", fontsize=20);
/Users/nathanielforde/mambaforge/envs/pymc_examples_new/lib/python3.9/site-packages/arviz/stats/diagnostics.py:592: RuntimeWarning: invalid value encountered in double_scalars
(between_chain_variance / within_chain_variance + num_samples - 1) / (num_samples)
az.summary(idata3, var_names=["cutpoints", "beta", "sigma"])
| 均值 | 标准差 | HDI_3% | HDI_97% | MCSE_均值 | MCSE_标准差 | ESS_批量 | ESS_尾部 | R_hat | |
|---|---|---|---|---|---|---|---|---|---|
| 切点[0] | -1.639 | 0.793 | -3.173 | -0.239 | 0.015 | 0.011 | 2810.0 | 2564.0 | 1.0 |
| 切点[1] | 1.262 | 0.464 | 0.409 | 2.139 | 0.007 | 0.005 | 4086.0 | 3251.0 | 1.0 |
| 切点[2] | 3.389 | 0.441 | 2.598 | 4.249 | 0.008 | 0.005 | 3252.0 | 3280.0 | 1.0 |
| 切点[3] | 5.074 | 0.466 | 4.179 | 5.941 | 0.009 | 0.006 | 2850.0 | 2614.0 | 1.0 |
| 切点[4] | 6.886 | 0.508 | 5.964 | 7.875 | 0.010 | 0.007 | 2558.0 | 2924.0 | 1.0 |
| 切点[5] | 8.765 | 0.563 | 7.664 | 9.800 | 0.011 | 0.008 | 2440.0 | 3031.0 | 1.0 |
| 切点[6] | 10.338 | 0.614 | 9.183 | 11.505 | 0.012 | 0.009 | 2475.0 | 2949.0 | 1.0 |
| 切点[7] | 12.316 | 0.722 | 11.030 | 13.758 | 0.014 | 0.010 | 2633.0 | 3016.0 | 1.0 |
| 贝塔[0] | 0.130 | 0.010 | 0.111 | 0.149 | 0.000 | 0.000 | 3069.0 | 3306.0 | 1.0 |
| 贝塔[1] | -0.089 | 0.270 | -0.577 | 0.428 | 0.004 | 0.004 | 5076.0 | 2915.0 | 1.0 |
| 贝塔[2] | 2.498 | 0.201 | 2.126 | 2.871 | 0.004 | 0.003 | 3161.0 | 2944.0 | 1.0 |
| 西格玛 | 2.039 | 0.622 | 0.976 | 3.212 | 0.012 | 0.008 | 2782.0 | 2623.0 | 1.0 |
比较切点:正态先验与均匀先验#
请注意,具有非约束切点的模型如何允许估计阈值低于零的情况发生。这在概念上没有多大意义,但可能会导致看似合理的后验预测分布。
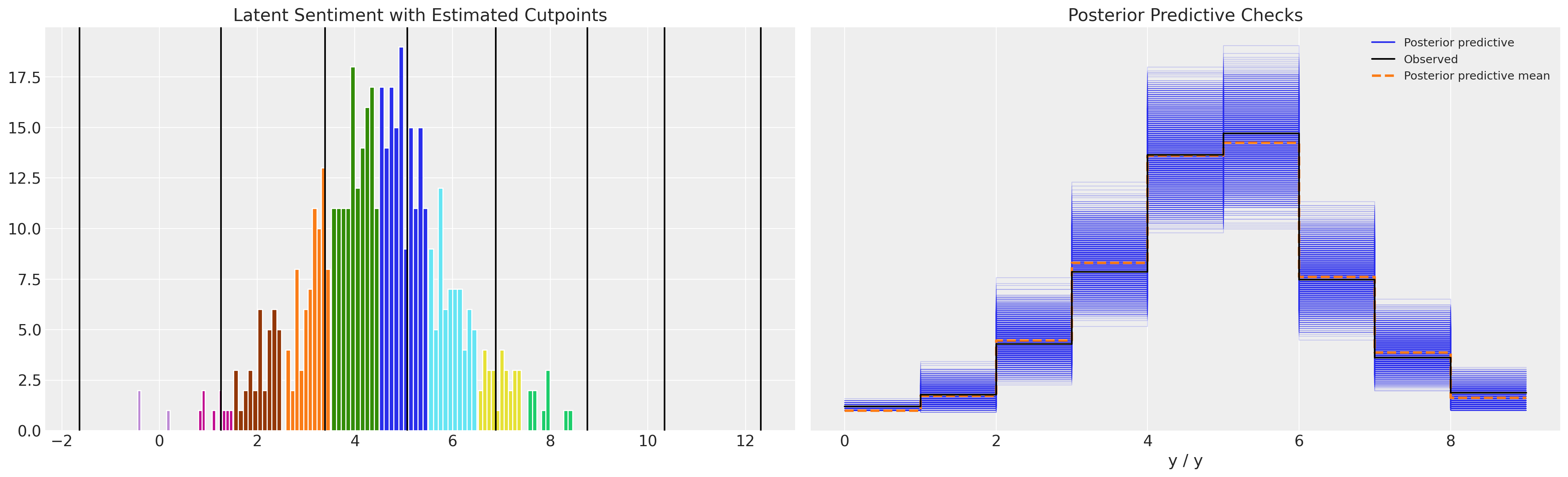
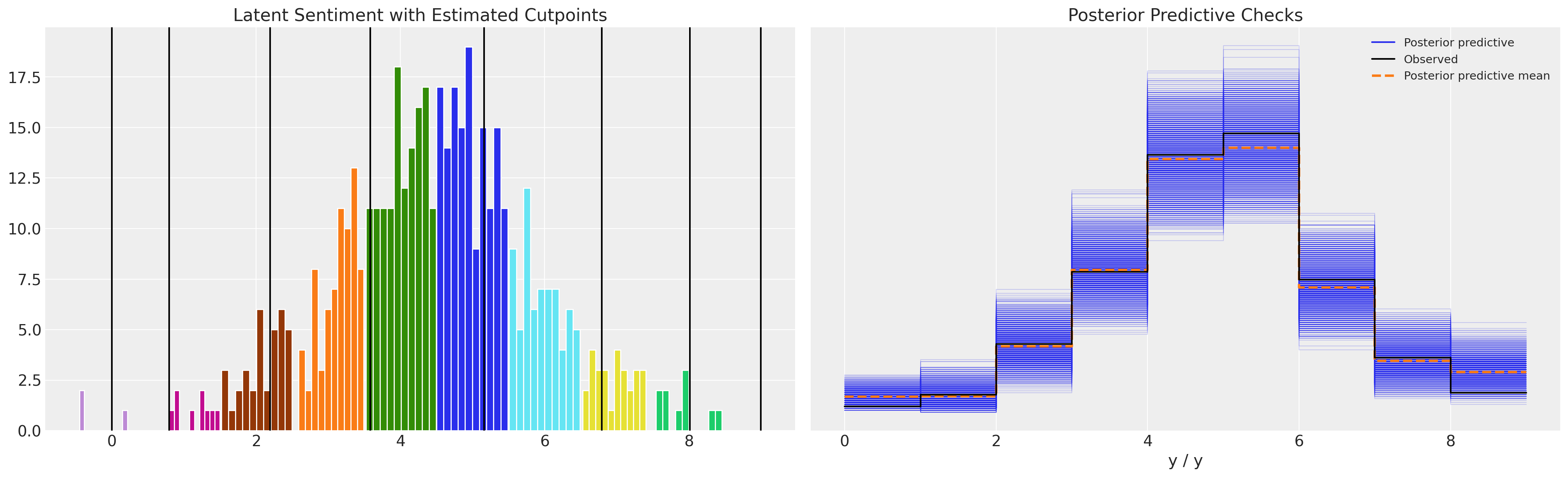
def plot_fit(idata):
posterior = idata.posterior.stack(sample=("chain", "draw"))
fig, axs = plt.subplots(1, 2, figsize=(20, 6))
axs = axs.flatten()
ax = axs[0]
for i in range(K - 1):
ax.axvline(posterior["cutpoints"][i].mean().values, color="k")
for r in df["explicit_rating"].unique():
temp = df[df["explicit_rating"] == r]
ax.hist(temp["latent_rating"], ec="white")
ax.set_title("Latent Sentiment with Estimated Cutpoints")
axs[1].set_title("Posterior Predictive Checks")
az.plot_ppc(idata, ax=axs[1])
plt.show()
plot_fit(idata3)
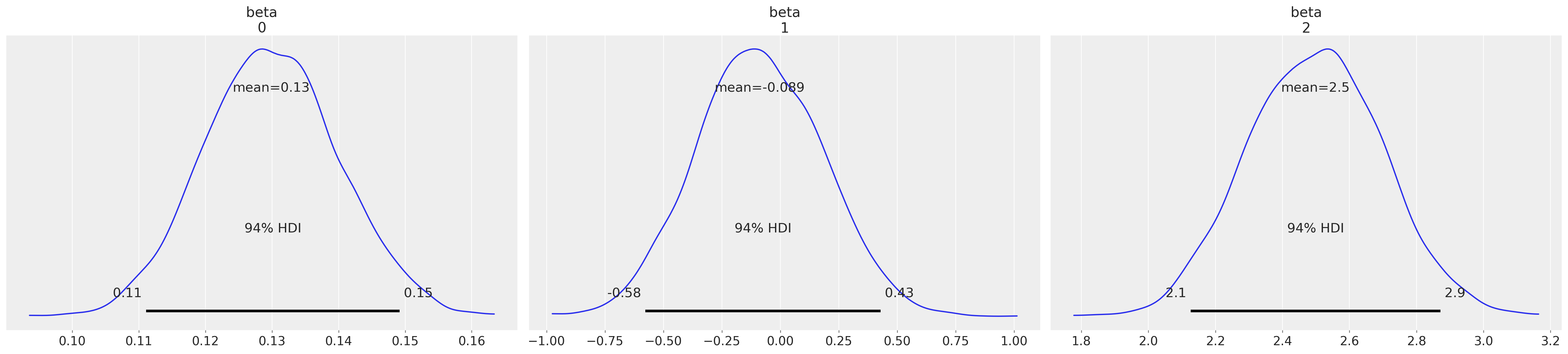
az.plot_posterior(idata3, var_names=["beta"]);
az.summary(idata3, var_names=["cutpoints"])
| 均值 | 标准差 | HDI_3% | HDI_97% | MCSE_均值 | MCSE_标准差 | ESS_批量 | ESS_尾部 | R_hat | |
|---|---|---|---|---|---|---|---|---|---|
| 切点[0] | -1.639 | 0.793 | -3.173 | -0.239 | 0.015 | 0.011 | 2810.0 | 2564.0 | 1.0 |
| 切点[1] | 1.262 | 0.464 | 0.409 | 2.139 | 0.007 | 0.005 | 4086.0 | 3251.0 | 1.0 |
| 切点[2] | 3.389 | 0.441 | 2.598 | 4.249 | 0.008 | 0.005 | 3252.0 | 3280.0 | 1.0 |
| 切点[3] | 5.074 | 0.466 | 4.179 | 5.941 | 0.009 | 0.006 | 2850.0 | 2614.0 | 1.0 |
| 切点[4] | 6.886 | 0.508 | 5.964 | 7.875 | 0.010 | 0.007 | 2558.0 | 2924.0 | 1.0 |
| 切点[5] | 8.765 | 0.563 | 7.664 | 9.800 | 0.011 | 0.008 | 2440.0 | 3031.0 | 1.0 |
| 切点[6] | 10.338 | 0.614 | 9.183 | 11.505 | 0.012 | 0.009 | 2475.0 | 2949.0 | 1.0 |
| 切点[7] | 12.316 | 0.722 | 11.030 | 13.758 | 0.014 | 0.010 | 2633.0 | 3016.0 | 1.0 |
虽然参数估计看起来合理,并且后验预测检查看起来也不错,但这里要看到的一点是,切点不受序数尺度定义的约束。在上面的模型中,它们在 0 以下变化。
但是,如果我们查看具有约束狄利克雷先验的模型
plot_fit(idata4)
az.plot_posterior(idata4, var_names=["beta"]);
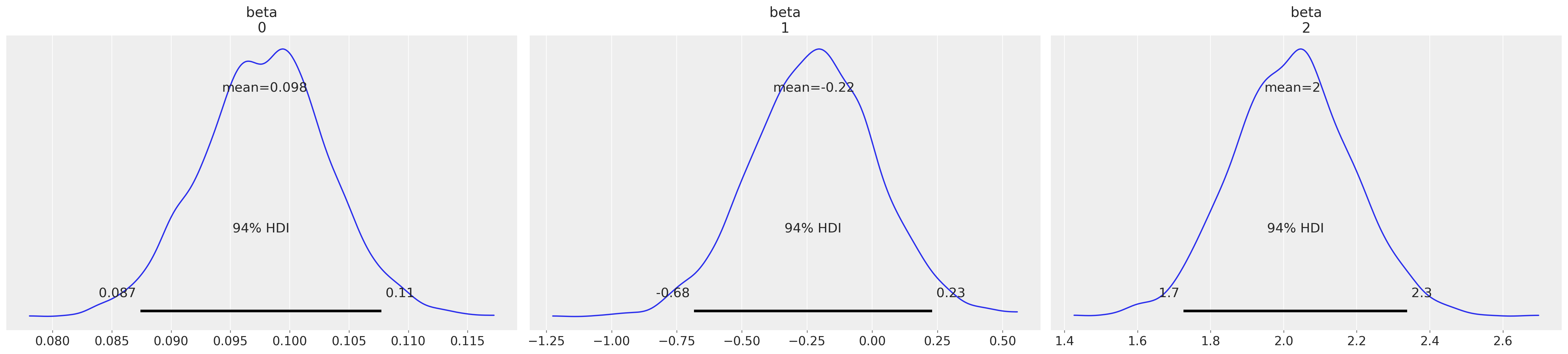
参数再次看起来合理,并且后验预测检查是合理的。但是现在,在使用约束均匀先验对切点进行约束后,我们估计的切点尊重序数尺度的定义。
az.summary(idata4, var_names=["cutpoints"])
/Users/nathanielforde/mambaforge/envs/pymc_examples_new/lib/python3.9/site-packages/arviz/stats/diagnostics.py:592: RuntimeWarning: invalid value encountered in double_scalars
(between_chain_variance / within_chain_variance + num_samples - 1) / (num_samples)
| 均值 | 标准差 | HDI_3% | HDI_97% | MCSE_均值 | MCSE_标准差 | ESS_批量 | ESS_尾部 | R_hat | |
|---|---|---|---|---|---|---|---|---|---|
| 切点[0] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 4000.0 | 4000.0 | NaN |
| 切点[1] | 0.794 | 0.192 | 0.438 | 1.159 | 0.003 | 0.002 | 3170.0 | 2907.0 | 1.0 |
| 切点[2] | 2.195 | 0.192 | 1.827 | 2.544 | 0.003 | 0.002 | 4133.0 | 3275.0 | 1.0 |
| 切点[3] | 3.584 | 0.180 | 3.242 | 3.924 | 0.003 | 0.002 | 4267.0 | 3214.0 | 1.0 |
| 切点[4] | 5.161 | 0.179 | 4.827 | 5.494 | 0.003 | 0.002 | 4725.0 | 3299.0 | 1.0 |
| 切点[5] | 6.790 | 0.182 | 6.424 | 7.110 | 0.003 | 0.002 | 4758.0 | 3417.0 | 1.0 |
| 切点[6] | 8.012 | 0.163 | 7.706 | 8.312 | 0.002 | 0.002 | 5549.0 | 2791.0 | 1.0 |
| 切点[7] | 9.000 | 0.000 | 9.000 | 9.000 | 0.000 | 0.000 | 3945.0 | 3960.0 | 1.0 |
与 Statsmodels 的比较#
这种类型的模型也可以使用最大似然法在频率学传统中进行估计。
modf_logit = OrderedModel.from_formula(
"explicit_rating ~ salary + work_sat + work_from_home", df, distr="logit"
)
resf_logit = modf_logit.fit(method="bfgs")
resf_logit.summary()
Optimization terminated successfully.
Current function value: 1.447704
Iterations: 59
Function evaluations: 65
Gradient evaluations: 65
| 因变量 | 显式评分 | 对数似然 | -723.85 |
|---|---|---|---|
| 模型 | OrderedModel | AIC | 1470. |
| 方法 | 最大似然 | BIC | 1516. |
| 日期 | 周四,2023 年 6 月 1 日 | ||
| 时间 | 21:32:42 | ||
| 观测数 | 500 | ||
| 残差自由度 | 489 | ||
| 模型自由度 | 11 |
| 系数 | 标准误 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| 薪资 | 0.1349 | 0.010 | 13.457 | 0.000 | 0.115 | 0.155 |
| 工作满意度 | 0.0564 | 0.286 | 0.197 | 0.844 | -0.504 | 0.617 |
| 居家办公 | 2.5985 | 0.206 | 12.590 | 0.000 | 2.194 | 3.003 |
| -0.0/1.0 | 0.2158 | 0.693 | 0.312 | 0.755 | -1.142 | 1.573 |
| 1.0/2.0 | 0.5127 | 0.332 | 1.543 | 0.123 | -0.138 | 1.164 |
| 2.0/3.0 | 0.6502 | 0.161 | 4.034 | 0.000 | 0.334 | 0.966 |
| 3.0/4.0 | 0.4962 | 0.108 | 4.598 | 0.000 | 0.285 | 0.708 |
| 4.0/5.0 | 0.6032 | 0.080 | 7.556 | 0.000 | 0.447 | 0.760 |
| 5.0/6.0 | 0.6399 | 0.076 | 8.474 | 0.000 | 0.492 | 0.788 |
| 6.0/7.0 | 0.4217 | 0.113 | 3.725 | 0.000 | 0.200 | 0.644 |
| 7.0/8.0 | 0.5054 | 0.186 | 2.712 | 0.007 | 0.140 | 0.871 |
我们还可以提取阈值或切点估计值,这与上面使用正态分布表示潜在经理评分的切点非常匹配。
num_of_thresholds = 8
modf_logit.transform_threshold_params(resf_logit.params[-num_of_thresholds:])
array([ -inf, 0.21579015, 1.88552907, 3.80152819, 5.44399832,
7.27200739, 9.16821716, 10.69274536, 12.35046331, inf])
探究模型的含义#
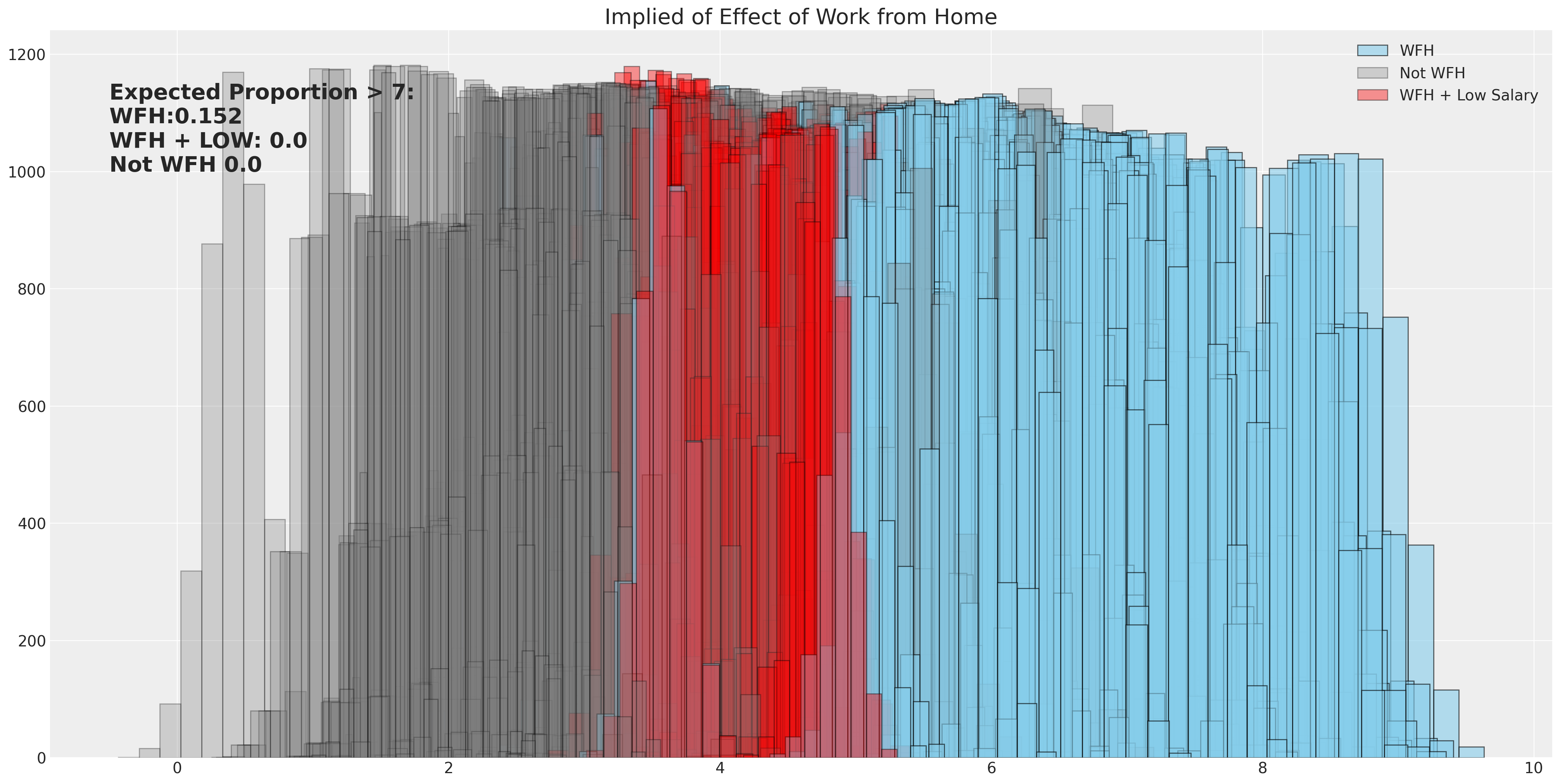
当我们想要评估模型的含义时,我们可以使用数据生成方程的已学习后验估计值,来模拟在特定阈值分数之上获得评分的调查结果的比例。在这里,我们允许在不同的工作条件下表示各种贝塔分布的完全不确定性,并衡量给经理评分高于 7 分的员工比例。
betas_posterior = az.extract(idata4)["beta"]
fig, ax = plt.subplots(figsize=(20, 10))
calc_wfh = [
df.iloc[i]["salary"] * betas_posterior[0, :]
+ df.iloc[i]["work_sat"] * betas_posterior[1, :]
+ 1 * betas_posterior[2, :]
for i in range(500)
]
calc_not_wfh = [
df.iloc[i]["salary"] * betas_posterior[0, :]
+ df.iloc[i]["work_sat"] * betas_posterior[1, :]
+ 0 * betas_posterior[2, :]
for i in range(500)
]
sal = np.random.normal(25, 5, 500)
calc_wfh_and_low_sal = [
sal[i] * betas_posterior[0, :]
+ df.iloc[i]["work_sat"] * betas_posterior[1, :]
+ 1 * betas_posterior[2, :]
for i in range(500)
]
### Use implied threshold on latent score to predict proportion of ratings above 7
prop_wfh = np.sum([np.mean(calc_wfh[i].values) > 6.78 for i in range(500)]) / 500
prop_not_wfh = np.sum([np.mean(calc_not_wfh[i].values) > 6.78 for i in range(500)]) / 500
prop_wfh_low = np.sum([np.mean(calc_wfh_and_low_sal[i].values) > 6.78 for i in range(500)]) / 500
for i in range(500):
if i == 499:
ax.hist(calc_wfh[i], alpha=0.6, color="skyblue", ec="black", label="WFH")
ax.hist(calc_not_wfh[i], alpha=0.3, color="grey", ec="black", label="Not WFH")
ax.hist(
calc_wfh_and_low_sal[i], alpha=0.4, color="red", ec="black", label="WFH + Low Salary"
)
else:
ax.hist(calc_wfh[i], alpha=0.6, color="skyblue", ec="black")
ax.hist(calc_wfh_and_low_sal[i], alpha=0.4, color="red", ec="black")
ax.hist(calc_not_wfh[i], alpha=0.3, color="grey", ec="black")
ax.set_title("Implied of Effect of Work from Home", fontsize=20)
ax.annotate(
f"Expected Proportion > 7: \nWFH:{prop_wfh} \nWFH + LOW: {prop_wfh_low} \nNot WFH {prop_not_wfh}",
xy=(-0.5, 1000),
fontsize=20,
fontweight="bold",
)
ax.legend();
Liddell 和 Kruschke 的 IMDB 电影评分数据#
使用序数回归模型而不是信任替代模型规范有充分的理由。例如,将有序类别视为连续度量的诱惑将导致错误的推断。Liddell 和 Kruschke 的论文 [Liddell 和 Kruschke,2018] 讨论了关于此主题的详细信息。我们将简要地复制他们关于这种现象如何在电影评分数据分析中出现的例子。
try:
movies = pd.read_csv("../data/MoviesData.csv")
except FileNotFoundError:
movies = pd.DataFrame(pm.get_data("MoviesData.csv"))
def pivot_movie(row):
row_ratings = row[["n1", "n2", "n3", "n4", "n5"]]
totals = []
for c, i in zip(row_ratings.index, range(5)):
totals.append(row_ratings[c] * [i])
totals = [item for sublist in totals for item in sublist]
movie = [row["Descrip"]] * len(totals)
id = [row["ID"]] * len(totals)
return pd.DataFrame({"rating": totals, "movie": movie, "movie_id": id})
movies_by_rating = pd.concat([pivot_movie(movies.iloc[i]) for i in range(len(movies))])
movies_by_rating.reset_index(inplace=True, drop=True)
movies_by_rating.shape
(284671, 3)
movies_by_rating.sample(100).head()
| 评分 | 电影 | 电影 ID | |
|---|---|---|---|
| 169636 | 4 | 高堡奇人第一季 | 23 |
| 218859 | 4 | 高堡奇人第一季 | 23 |
| 252960 | 4 | 亡命天涯第一季 | 26 |
| 8304 | 1 | 房间 | 6 |
| 99958 | 4 | 诈欺担保人第一季 | 19 |
def constrainedUniform(N, group, min=0, max=1):
return pm.Deterministic(
f"cutpoints_{group}",
pt.concatenate(
[
np.ones(1) * min,
pt.extra_ops.cumsum(pm.Dirichlet(f"cuts_unknown_{group}", a=np.ones(N - 2)))
* (max - min)
+ min,
]
),
)
我们将使用序数模型和度量模型来拟合此数据。这将显示序数拟合在多大程度上更具说服力。
K = 5
movies_by_rating = movies_by_rating[movies_by_rating["movie_id"].isin([1, 2, 3, 4, 5, 6])]
indx, unique = pd.factorize(movies_by_rating["movie_id"])
priors = {"sigma": 1, "mu": [0, 1], "cut_mu": np.linspace(0, K, K - 1)}
def make_movies_model(ordered=False):
with pm.Model() as model:
for g in movies_by_rating["movie_id"].unique():
if ordered:
cutpoints = constrainedUniform(K, g, 0, K - 1)
mu = pm.Normal(f"mu_{g}", 0, 1)
y_ = pm.OrderedLogistic(
f"y_{g}",
cutpoints=cutpoints,
eta=mu,
observed=movies_by_rating[movies_by_rating["movie_id"] == g].rating.values,
)
else:
mu = pm.Normal(f"mu_{g}", 0, 1)
sigma = pm.HalfNormal(f"sigma_{g}", 1)
y_ = pm.Normal(
f"y_{g}",
mu,
sigma,
observed=movies_by_rating[movies_by_rating["movie_id"] == g].rating.values,
)
idata = pm.sample_prior_predictive()
idata.extend(pm.sample(nuts_sampler="numpyro", idata_kwargs={"log_likelihood": True}))
idata.extend(pm.sample_posterior_predictive(idata))
return idata, model
idata_ordered, model_ordered = make_movies_model(ordered=True)
idata_normal_metric, model_normal_metric = make_movies_model(ordered=False)
显示代码单元格输出
Sampling: [cuts_unknown_1, cuts_unknown_2, cuts_unknown_3, cuts_unknown_4, cuts_unknown_5, cuts_unknown_6, mu_1, mu_2, mu_3, mu_4, mu_5, mu_6, y_1, y_2, y_3, y_4, y_5, y_6]
/Users/nathanielforde/mambaforge/envs/pymc_examples_new/lib/python3.9/site-packages/pymc/sampling/mcmc.py:243: UserWarning: Use of external NUTS sampler is still experimental
warnings.warn("Use of external NUTS sampler is still experimental", UserWarning)
Compiling...
Compilation time = 0:00:04.998186
Sampling...
Sampling time = 0:00:09.785681
Transforming variables...
Transformation time = 0:00:00.432907
Computing Log Likelihood...
Sampling: [mu_1, mu_2, mu_3, mu_4, mu_5, mu_6, sigma_1, sigma_2, sigma_3, sigma_4, sigma_5, sigma_6, y_1, y_2, y_3, y_4, y_5, y_6]
/Users/nathanielforde/mambaforge/envs/pymc_examples_new/lib/python3.9/site-packages/pymc/sampling/mcmc.py:243: UserWarning: Use of external NUTS sampler is still experimental
warnings.warn("Use of external NUTS sampler is still experimental", UserWarning)
Compiling...
Compilation time = 0:00:01.414912
Sampling...
Sampling time = 0:00:05.203627
Transforming variables...
Transformation time = 0:00:00.008429
Computing Log Likelihood...
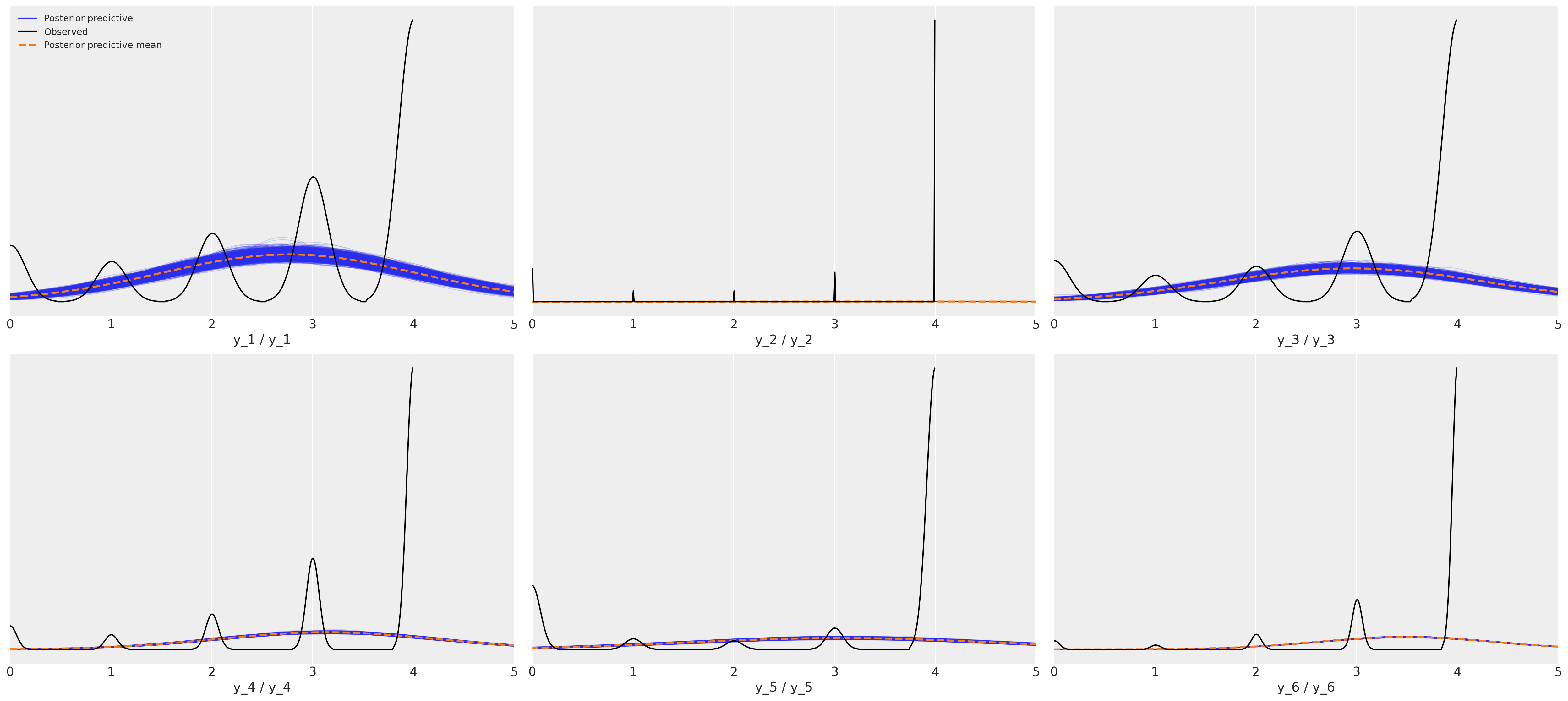
后验预测拟合:正态度量模型#
对于六部电影的电影评分数据来说,这是一个可怕的拟合。
axs = az.plot_ppc(idata_normal_metric)
axs = axs.flatten()
for ax in axs:
ax.set_xlim(0, 5);
后验预测拟合:有序响应模型#
这显示了六部电影中每部电影的更好的拟合。
az.plot_ppc(idata_ordered);
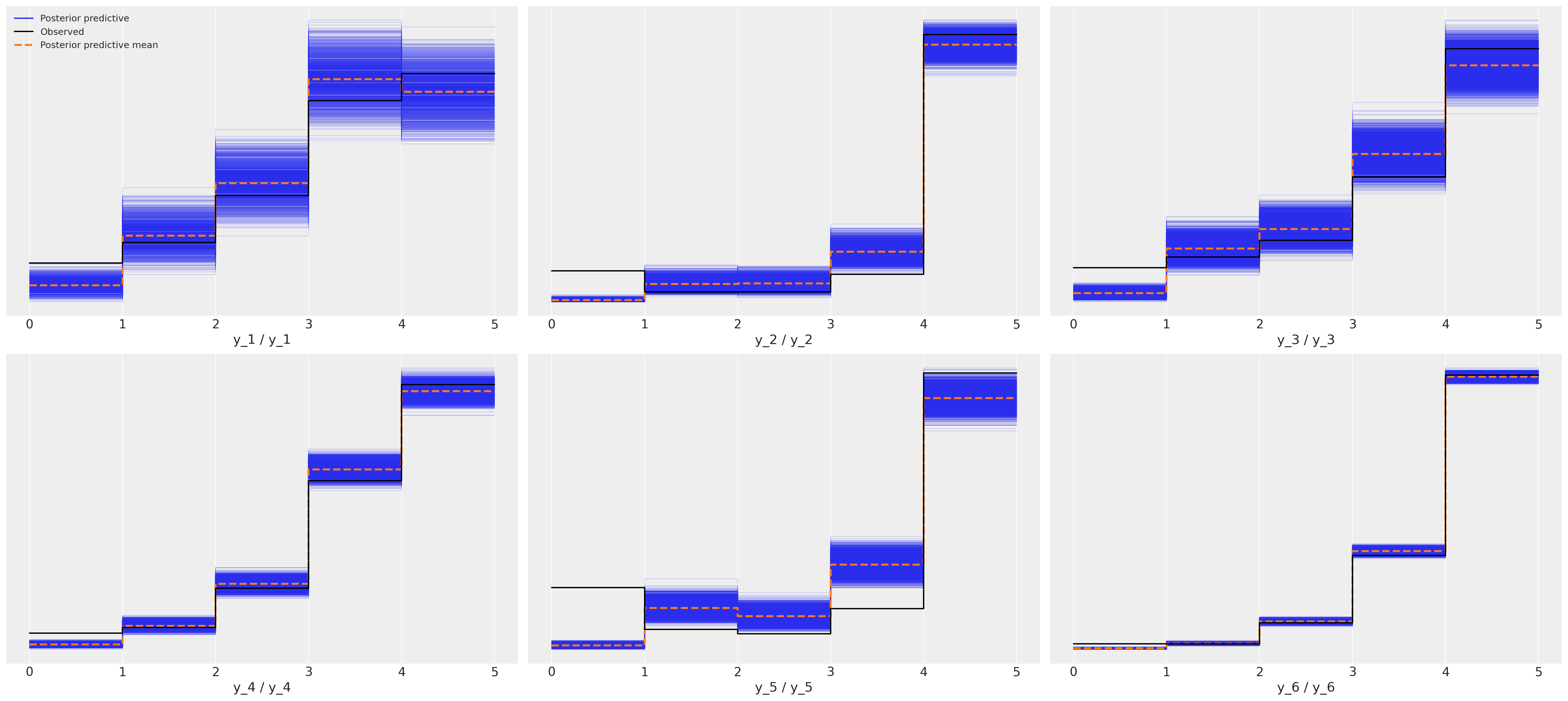
由于这是真实数据,我们不知道真实的数据生成过程,因此不可能说哪个模型是正确的,但我希望您会同意后验预测检查有力地支持了有序分类拟合是一个更有力的候选者的说法。这里要提出的更简单的一点是,度量模型的含义是错误的,如果我们希望对可能驱动良好电影评分的因素做出合理的推断,那么我们最好确保不要通过对似然函数的不良选择将噪声引入建模练习中。
比较模型拟合#
y_5_compare = az.compare({"ordered": idata_ordered, "metric": idata_normal_metric}, var_name="y_5")
y_5_compare
| 排名 | elpd_loo | p_loo | elpd_diff | 权重 | 标准误 | DSE | 警告 | 尺度 | |
|---|---|---|---|---|---|---|---|---|---|
| 有序 | 0 | -1651.276933 | 3.496302 | 0.000000 | 1.000000e+00 | 48.836869 | 0.000000 | 假 | 对数 |
| 度量 | 1 | -2191.541142 | 2.062035 | 540.264208 | 5.153936e-09 | 24.050997 | 28.196537 | 假 | 对数 |
y_6_compare = az.compare({"ordered": idata_ordered, "metric": idata_normal_metric}, var_name="y_6")
y_6_compare
| 排名 | elpd_loo | p_loo | elpd_diff | 权重 | 标准误 | DSE | 警告 | 尺度 | |
|---|---|---|---|---|---|---|---|---|---|
| 有序 | 0 | -13339.249536 | 3.100333 | 0.000000 | 1.0 | 110.330929 | 0.000000 | 假 | 对数 |
| 度量 | 1 | -17723.156659 | 4.154765 | 4383.907122 | 0.0 | 148.655963 | 85.797241 | 假 | 对数 |
az.plot_compare(y_5_compare)
<Axes: title={'center': 'Model comparison\nhigher is better'}, xlabel='elpd_loo (log)', ylabel='ranked models'>

az.plot_compare(y_6_compare)
<Axes: title={'center': 'Model comparison\nhigher is better'}, xlabel='elpd_loo (log)', ylabel='ranked models'>

比较模型之间的推断#
除了预测拟合之外,从不同建模选择中得出的推断也差异很大。想象一下,作为一名电影主管,试图决定是否继续制作续集,那么相对于竞争对手基准的电影表现评分可能是此决策的关键特征,而分析师的模型选择所引起的差异可能会对该选择产生过大的影响。
mosaic = """
AC
DE
BB
"""
fig, axs = plt.subplot_mosaic(mosaic, figsize=(15, 7))
axs = [axs[k] for k in axs.keys()]
axs
ordered_5 = az.extract(idata_ordered.posterior_predictive)["y_5"].mean(axis=0)
ordered_6 = az.extract(idata_ordered.posterior_predictive)["y_6"].mean(axis=0)
diff = ordered_5 - ordered_6
metric_5 = az.extract(idata_normal_metric.posterior_predictive)["y_5"].mean(axis=0)
metric_6 = az.extract(idata_normal_metric.posterior_predictive)["y_6"].mean(axis=0)
diff1 = metric_5 - metric_6
axs[0].hist(ordered_5, bins=30, ec="white", color="slateblue", label="Ordered Fit Movie 5")
axs[4].plot(
az.hdi(diff.unstack())["x"].values, [1, 1], "o-", color="slateblue", label="Ordered Fits"
)
axs[4].plot(
az.hdi(diff1.unstack())["x"].values, [1.2, 1.2], "o-", color="magenta", label="Metric Fits"
)
axs[2].hist(ordered_6, bins=30, ec="white", color="slateblue", label="Ordered Fit Movie 6")
axs[3].hist(metric_5, ec="white", label="Metric Fit Movie 5", bins=30, color="magenta")
axs[1].hist(metric_6, ec="white", label="Metric Fit Movie 6", bins=30, color="magenta")
axs[4].set_title("Implied Differences Between the \n Expected Rating")
axs[4].set_ylim(0.8, 1.4)
axs[4].set_yticks([])
axs[0].set_title("Expected Posterior Predictive Estimate \n for Movies Ordered Fits")
axs[1].set_title("Expected Posterior Predictive Estimate \n for Movie Metric Fits")
axs[4].set_xlabel("Difference between Movie 5 and 6")
axs[1].legend()
axs[0].legend()
axs[2].legend()
axs[3].legend()
axs[4].legend();
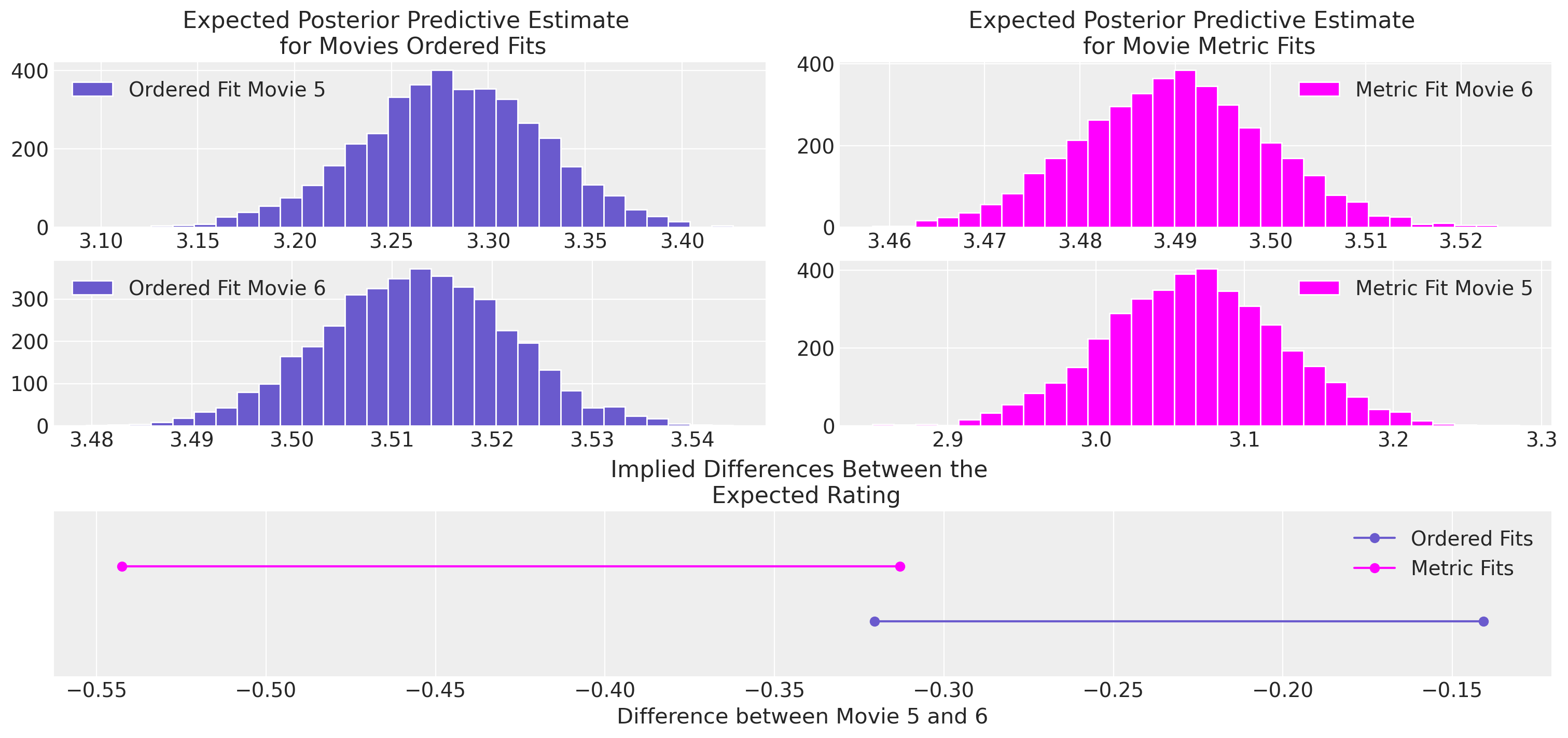
在决定是否投入制作电影时,有数百万美元的资金在线。该投资的回报至少部分是电影受欢迎程度的函数,电影的受欢迎程度既受到烂番茄和 IMDB 上的评分尺度的衡量,也受到其影响。因此,了解不同电影的相对受欢迎程度可能会在好莱坞转移大量资金,而此处看到的隐含差异确实很重要。对于考虑衡量幸福感和抑郁症的更重要的评分尺度,也遵循类似的考虑。
结论#
在本笔记本中,我们已经了解了如何使用 PyMC 构建序数回归模型,并使用将序数结果解释为潜在连续现象的离散结果来激发建模练习。我们已经看到了不同的模型规范如何生成或多或少可解释的模型基础参数估计值。我们还将序数回归方法与对序数数据进行更幼稚的回归方法进行了比较。结果有力地表明,序数回归避免了幼稚方法中出现的一些推断陷阱。此外,我们还表明,贝叶斯建模工作流程的灵活性可以为防范模型错误指定的风险提供保证,使其成为序数数据分析的可行且引人注目的方法。
参考文献#
Torrin M. Liddell 和 John K. Kruschke。《使用度量模型分析序数数据:可能出现什么问题?》。《实验社会心理学杂志》,2018 年。
水印#
%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor
Last updated: Thu Jun 01 2023
Python implementation: CPython
Python version : 3.9.16
IPython version : 8.11.0
pytensor: 2.11.1
numpy : 1.23.5
arviz : 0.15.1
pytensor : 2.11.1
statsmodels: 0.13.5
pandas : 1.5.3
pymc : 5.3.0
matplotlib : 3.7.1
Watermark: 2.3.1
许可证声明#
本示例库中的所有笔记本均根据 MIT 许可证提供,该许可证允许修改和再分发用于任何用途,前提是保留版权和许可证声明。
引用 PyMC 示例#
要引用此笔记本,请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。
重要提示
许多笔记本都改编自其他来源:博客、书籍...... 在这种情况下,您也应该引用原始来源。
另请记住引用您的代码使用的相关库。
这是一个 bibtex 中的引用模板
@incollection{citekey,
author = "<notebook authors, see above>",
title = "<notebook title>",
editor = "PyMC Team",
booktitle = "PyMC examples",
doi = "10.5281/zenodo.5654871"
}
渲染后可能看起来像