样本外预测#

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import seaborn as sns

from scipy.special import expit as inverse_logit
from sklearn.metrics import RocCurveDisplay, auc, roc_curve

RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")

生成示例数据#

我们想要拟合一个逻辑回归模型，其中两个数值特征之间存在乘法交互作用。

# Number of data points
n = 250
# Create features
x1 = rng.normal(loc=0.0, scale=2.0, size=n)
x2 = rng.normal(loc=0.0, scale=2.0, size=n)
# Define target variable
intercept = -0.5
beta_x1 = 1
beta_x2 = -1
beta_interaction = 2
z = intercept + beta_x1 * x1 + beta_x2 * x2 + beta_interaction * x1 * x2
p = inverse_logit(z)
# note binomial with n=1 is equal to a Bernoulli
y = rng.binomial(n=1, p=p, size=n)
df = pd.DataFrame(dict(x1=x1, x2=x2, y=y))
df.head()

	x1	x2	y
0	-0.445284	1.381325	0
1	2.651317	0.800736	1
2	-1.141940	-0.128204	0
3	1.336498	-0.931965	0
4	2.290762	3.400222	1

让我们对数据进行一些探索

sns.pairplot(data=df, kind="scatter");

/home/xian/mambaforge/envs/pymc/lib/python3.10/site-packages/seaborn/axisgrid.py:118: UserWarning: This figure was using constrained_layout, but that is incompatible with subplots_adjust and/or tight_layout; disabling constrained_layout.
  self._figure.tight_layout(*args, **kwargs)

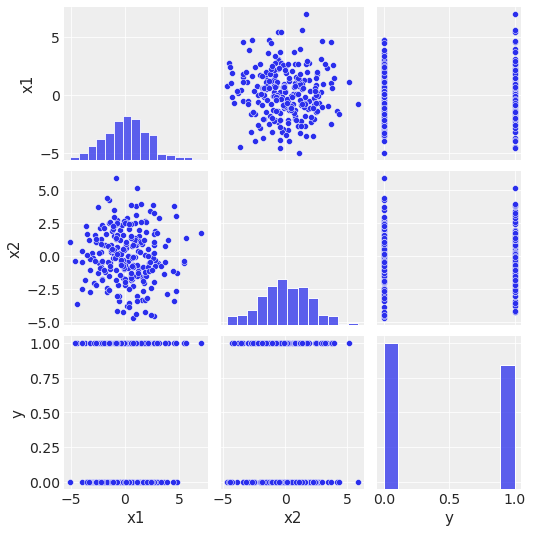
../_images/506205391b7910fb0cf250bf3397ddc842c5bb2f2650e089ebec9d542f49d3fa.png

\(x_1\) 和 \(x_2\) 不相关。
\(x_1\) 和 \(x_2\) 似乎不能独立地分离 \(y\) 类。
\(y\) 的分布不是高度不平衡的。

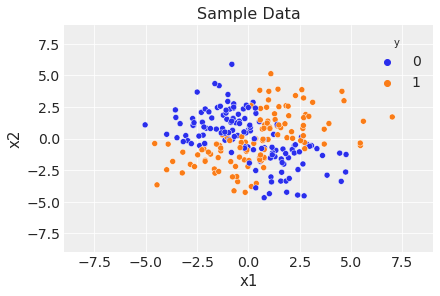
fig, ax = plt.subplots()
sns.scatterplot(x="x1", y="x2", data=df, hue="y")
ax.legend(title="y")
ax.set(title="Sample Data", xlim=(-9, 9), ylim=(-9, 9));

../_images/9101d5c4224baf8903f6f99c6d77f2758e5a6069d59d7782cf76b95c573f1049.png

准备建模数据#

labels = ["Intercept", "x1", "x2", "x1:x2"]
df["Intercept"] = np.ones(len(df))
df["x1:x2"] = df["x1"] * df["x2"]
# reorder columns to be in the same order as labels
df = df[labels]
x = df.to_numpy()

现在我们进行训练-测试拆分。

indices = rng.permutation(x.shape[0])
train_prop = 0.7
train_size = int(train_prop * x.shape[0])
training_idx, test_idx = indices[:train_size], indices[train_size:]
x_train, x_test = x[training_idx, :], x[test_idx, :]
y_train, y_test = y[training_idx], y[test_idx]

定义和拟合模型#

我们现在在 PyMC 中指定模型。

coords = {"coeffs": labels}

with pm.Model(coords=coords) as model:
    # data containers
    X = pm.MutableData("X", x_train)
    y = pm.MutableData("y", y_train)
    # priors
    b = pm.Normal("b", mu=0, sigma=1, dims="coeffs")
    # linear model
    mu = pm.math.dot(X, b)
    # link function
    p = pm.Deterministic("p", pm.math.invlogit(mu))
    # likelihood
    pm.Bernoulli("obs", p=p, observed=y)

pm.model_to_graphviz(model)

../_images/9c4259e66e923b8e4851430a0389ad05d9515c62b3aa2da1386dde2664a42848.svg

with model:
    idata = pm.sample()

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [b]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.

az.plot_trace(idata, var_names="b", compact=False);

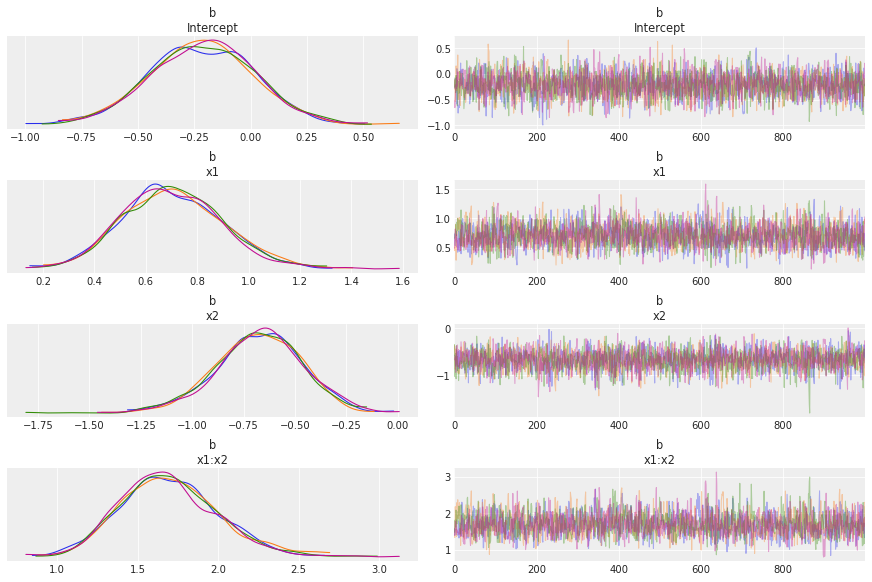
../_images/086d62ebe488d23b7bb23b691f89f6dc5f91549e8d545c4af5377fccc4d7023f.png

链看起来不错。

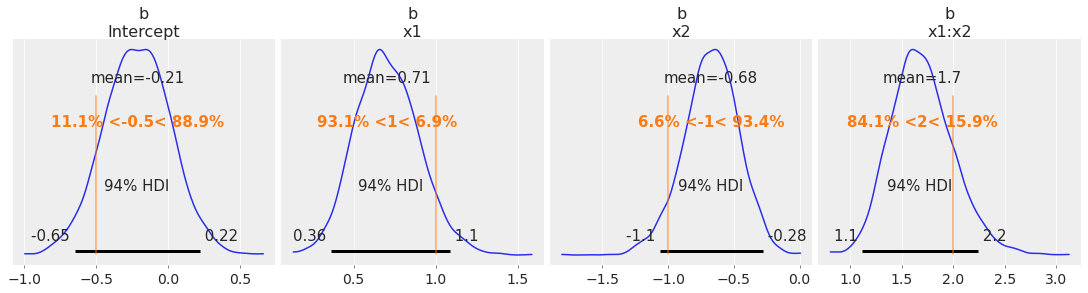
az.summary(idata, var_names="b")

	均值	标准差	hdi_3%	hdi_97%	mcse_均值	mcse_标准差	ess_bulk	ess_tail	r_hat
b[截距]	-0.215	0.231	-0.650	0.216	0.004	0.003	3037.0	2565.0	1.0
b[x1]	0.705	0.193	0.363	1.085	0.004	0.003	2296.0	2386.0	1.0
b[x2]	-0.675	0.209	-1.065	-0.281	0.004	0.003	2761.0	2419.0	1.0
b[x1:x2]	1.698	0.303	1.114	2.240	0.007	0.005	2079.0	2325.0	1.0

我们很好地恢复了这个模拟数据集的真实参数。

az.plot_posterior(
    idata, var_names=["b"], ref_val=[intercept, beta_x1, beta_x2, beta_interaction], figsize=(15, 4)
);

../_images/3d0d96bec3317ed7332e27d71e0f5c8670fe9e6b28126ecb61bda7b921b01b97.png

生成样本外预测#

现在我们在测试集上生成预测。

with model:
    pm.set_data({"X": x_test, "y": y_test})
    idata.extend(pm.sample_posterior_predictive(idata))

Sampling: [obs]

# Compute the point prediction by taking the mean and defining the category via a threshold.
p_test_pred = idata.posterior_predictive["obs"].mean(dim=["chain", "draw"])
y_test_pred = (p_test_pred >= 0.5).astype("int").to_numpy()

评估模型#

首先，让我们计算测试集上的准确率。

print(f"accuracy = {np.mean(y_test==y_test_pred): 0.3f}")

accuracy =  0.893

接下来，我们绘制 ROC 曲线并计算 AUC。

fpr, tpr, thresholds = roc_curve(
    y_true=y_test, y_score=p_test_pred, pos_label=1, drop_intermediate=False
)
roc_auc = auc(fpr, tpr)

fig, ax = plt.subplots()
roc_display = RocCurveDisplay(fpr=fpr, tpr=tpr, roc_auc=roc_auc)
roc_display = roc_display.plot(ax=ax, marker="o", markersize=4)
ax.set(title="ROC");

../_images/5fffe21f77484fe9be49fefe0ddcea41b0b4405197d6635e97884ed8f6020ef8.png

该模型表现如预期（我们当然知道数据生成过程，这在实际应用中几乎从未发生）。

模型决策边界#

最后，我们将描述和绘制模型决策边界，这是定义为以下内容的空间

\[\mathcal{B} = \{(x_1, x_2) \in \mathbb{R}^2 \: | \: p(x_1, x_2) = 0.5\}\]

其中 \(p\) 表示模型输出的属于 \(y=1\) 类的概率。为了使这个集合显式化，我们只需根据模型参数化写出条件

\[0.5 = \frac{1}{1 + \exp(-(\beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_{12} x_1x_2))}\]

这意味着

\[0 = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_{12} x_1x_2\]

求解 \(x_2\) 我们得到公式

\[x_2 = - \frac{\beta_0 + \beta_1 x_1}{\beta_2 + \beta_{12}x_1}\]

请注意，这条曲线是以奇点 \(x_1 = - \beta_2 / \beta_{12}\) 为中心的双曲线。

现在让我们使用网格绘制模型决策边界

def make_grid():
    x1_grid = np.linspace(start=-9, stop=9, num=300)
    x2_grid = x1_grid
    x1_mesh, x2_mesh = np.meshgrid(x1_grid, x2_grid)
    x_grid = np.stack(arrays=[x1_mesh.flatten(), x2_mesh.flatten()], axis=1)
    return x1_grid, x2_grid, x_grid


x1_grid, x2_grid, x_grid = make_grid()

with model:
    # Create features on the grid.
    x_grid_ext = np.hstack(
        (
            np.ones((x_grid.shape[0], 1)),
            x_grid,
            (x_grid[:, 0] * x_grid[:, 1]).reshape(-1, 1),
        )
    )
    # set the observed variables
    pm.set_data({"X": x_grid_ext})
    # calculate pushforward values of `p`
    ppc_grid = pm.sample_posterior_predictive(idata, var_names=["p"])

Sampling: []

# grid of predictions
grid_df = pd.DataFrame(x_grid, columns=["x1", "x2"])
grid_df["p"] = ppc_grid.posterior_predictive.p.mean(dim=["chain", "draw"])
p_grid = grid_df.pivot(index="x2", columns="x1", values="p").to_numpy()

现在我们在网格上计算模型决策边界以用于可视化目的。

def calc_decision_boundary(idata, x1_grid):
    # posterior mean of coefficients
    intercept = idata.posterior["b"].sel(coeffs="Intercept").mean().data
    b1 = idata.posterior["b"].sel(coeffs="x1").mean().data
    b2 = idata.posterior["b"].sel(coeffs="x2").mean().data
    b1b2 = idata.posterior["b"].sel(coeffs="x1:x2").mean().data
    # decision boundary equation
    return -(intercept + b1 * x1_grid) / (b2 + b1b2 * x1_grid)

我们最终得到了图和测试集上的预测

fig, ax = plt.subplots()

# data
sns.scatterplot(
    x=x_test[:, 1].flatten(),
    y=x_test[:, 2].flatten(),
    hue=y_test,
    ax=ax,
)

# decision boundary
ax.plot(x1_grid, calc_decision_boundary(idata, x1_grid), color="black", linestyle=":")

# grid of predictions
ax.contourf(x1_grid, x2_grid, p_grid, alpha=0.3)

ax.legend(title="y", loc="center left", bbox_to_anchor=(1, 0.5))
ax.set(title="Model Decision Boundary", xlim=(-9, 9), ylim=(-9, 9), xlabel="x1", ylabel="x2");

../_images/300d0cf80648831ccb0009c099225a7540f30c1fc7e80e3cd24f2dcaf375f6bd.png

请注意，我们已经通过使用后验样本的均值计算了模型决策边界。但是，如果我们使用完整分布，我们可以生成更好（且信息量更大！）的图（与其他指标（如准确率和 AUC）类似）。

参考文献#

作者#

由 Juan Orduz 创建。
由 Benjamin T. Vincent 于 2022 年 6 月更新至 PyMC v4
由 Benjamin T. Vincent 使用 PyMC v5 于 2022 年 12 月重新执行
由 Christian Luhmann 于 2023 年 12 月更新 (pymc-examples#616)

水印#

%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor

Last updated: Wed Dec 06 2023

Python implementation: CPython
Python version       : 3.10.8
IPython version      : 8.4.0

pytensor: 2.18.1

pymc      : 5.10.0
seaborn   : 0.12.2
pandas    : 1.4.3
matplotlib: 3.5.2
arviz     : 0.14.0
numpy     : 1.24.2

Watermark: 2.3.1

许可声明#

此示例库中的所有笔记本均在 MIT 许可证下提供，该许可证允许修改和再分发以用于任何用途，前提是保留版权和许可证声明。

引用 PyMC 示例#

要引用此笔记本，请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。

重要

许多笔记本都改编自其他来源：博客、书籍……在这种情况下，您也应该引用原始来源。

另请记住引用您的代码使用的相关库。

这是一个 bibtex 中的引用模板

@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}

一旦渲染，它可能看起来像

分类

标签