多层模型贝叶斯方法入门

分层或多层建模是回归建模的推广。

多层模型 是回归模型，其中构成模型参数被赋予概率模型。这意味着模型参数被允许按组变化。

观测单元通常自然地聚集。尽管集群是随机抽样的，并且集群内是随机抽样的，但集群会引起观测值之间的依赖性。

分层模型 是一种特殊的多层模型，其中参数彼此嵌套。

一些多层结构不是分层的。

• 例如，“国家”和“年份”不是嵌套的，但可能代表参数的独立但重叠的集群

我们将使用环境流行病学示例来阐述这个主题。

示例：氡污染 Gelman 和 Hill [2006]

氡是一种放射性气体，通过与地面的接触点进入房屋。它是一种致癌物，是非吸烟者肺癌的主要原因。氡水平在家庭之间差异很大。

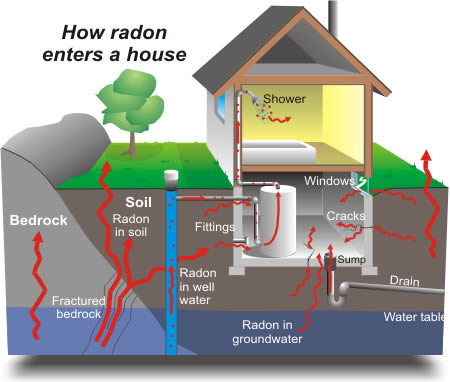
美国环保署对 80,000 户房屋的氡水平进行了研究。有两个重要的预测因子

• 地下室或一楼的测量值（地下室的氡含量较高）

• 县铀含量（与氡含量呈正相关）

我们将专注于明尼苏达州的氡水平建模。

此示例中的层次结构是县内的家庭。

数据组织

首先，我们从本地文件导入数据，并提取明尼苏达州的数据。

import os
import warnings

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pytensor.tensor as pt
import seaborn as sns
import xarray as xr

warnings.filterwarnings("ignore", module="scipy")

print(f"Running on PyMC v{pm.__version__}")

Running on PyMC v4.4.0

RANDOM_SEED = 8924
az.style.use("arviz-darkgrid")

原始数据以几个独立数据集的形式存在，我们将在此处导入、合并和处理这些数据集。首先是来自美国各地个别房屋的测量数据。我们将仅提取明尼苏达州的子集。

try:
    srrs2 = pd.read_csv(os.path.join("..", "data", "srrs2.dat"))
except FileNotFoundError:
    srrs2 = pd.read_csv(pm.get_data("srrs2.dat"))

srrs2.columns = srrs2.columns.map(str.strip)
srrs_mn = srrs2[srrs2.state == "MN"].copy()

接下来，通过组合两个变量获得县级预测因子铀。

try:
    cty = pd.read_csv(os.path.join("..", "data", "cty.dat"))
except FileNotFoundError:
    cty = pd.read_csv(pm.get_data("cty.dat"))

srrs_mn["fips"] = srrs_mn.stfips * 1000 + srrs_mn.cntyfips
cty_mn = cty[cty.st == "MN"].copy()
cty_mn["fips"] = 1000 * cty_mn.stfips + cty_mn.ctfips

使用 merge 方法将房屋和县级信息合并到单个 DataFrame 中。

srrs_mn = srrs_mn.merge(cty_mn[["fips", "Uppm"]], on="fips")
srrs_mn = srrs_mn.drop_duplicates(subset="idnum")
u = np.log(srrs_mn.Uppm).unique()

n = len(srrs_mn)

让我们编码县名并制作我们将使用的变量的本地副本。我们还需要每个唯一县的查找表 (dict) 以进行索引。

srrs_mn.county = srrs_mn.county.map(str.strip)
county, mn_counties = srrs_mn.county.factorize()
srrs_mn["county_code"] = county
radon = srrs_mn.activity
srrs_mn["log_radon"] = log_radon = np.log(radon + 0.1).values
floor_measure = srrs_mn.floor.values

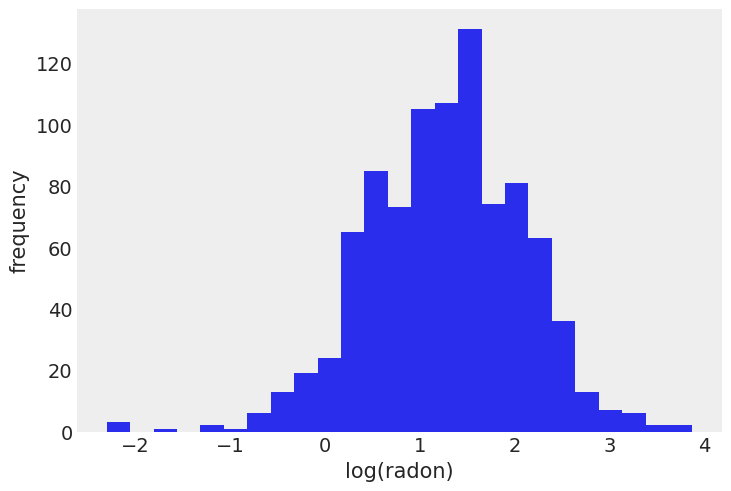
明尼苏达州氡水平分布（对数刻度）

srrs_mn.log_radon.hist(bins=25, grid=False)
plt.xlabel("log(radon)")
plt.ylabel("frequency");

传统方法

氡暴露建模的两种传统替代方法代表了偏差-方差权衡的两个极端

完全合并:

将所有县视为相同，并估计单个氡水平。

\[y_i = \alpha + \beta x_i + \epsilon_i\]

不合并:

独立地对每个县的氡进行建模。

\[y_i = \alpha_{j[i]} + \beta x_i + \epsilon_i\]

其中 \(j = 1,\ldots,85\)

误差 \(\epsilon_i\) 可能代表测量误差、房屋内的时间变化或房屋之间的变化。

以下是完全合并模型的斜率和截距的点估计

with pm.Model() as pooled_model:
    floor_ind = pm.MutableData("floor_ind", floor_measure, dims="obs_id")

    alpha = pm.Normal("alpha", 0, sigma=10)
    beta = pm.Normal("beta", mu=0, sigma=10)
    sigma = pm.Exponential("sigma", 5)

    theta = alpha + beta * floor_ind

    y = pm.Normal("y", theta, sigma=sigma, observed=log_radon, dims="obs_id")

pm.model_to_graphviz(pooled_model)

您可能想知道为什么我们甚至在变量 floor_ind 不是观测变量也不是模型的参数的情况下也使用上面的 pm.Data 容器。正如您将看到的，当我们绘制和诊断我们的模型时，这将使我们的生活轻松得多。ArviZ 将因此将 floor_ind 包含在结果 InferenceData 对象的 constant_data 组中。此外，在 InferenceData 对象中包含 floor_ind 使共享和重现分析变得更加容易，分析或重新运行模型所需的所有数据都存储在那里。

在运行模型之前，让我们做一些先验预测检查。

实际上，拥有合理的先验不仅是将科学知识纳入模型的一种方式，它还可以帮助并使 MCMC 机制更快——这里我们处理的是一个简单的线性回归，因此没有链接函数会来扭曲结果空间；但总有一天这会发生在你身上，你需要认真思考你的先验，以帮助你的 MCMC 采样器。因此，最好在比较容易的时候训练自己，而不是在非常困难的时候学习。

PyMC 中有一个方便的先验预测抽样函数

with pooled_model:
    prior_checks = pm.sample_prior_predictive(random_seed=RANDOM_SEED)

Sampling: [alpha, beta, sigma, y]

ArviZ InferenceData 在底层使用 xarray.Dataset，它可以使用 .plot 访问几个常用的绘图函数。在本例中，我们想要绘制平均对数氡水平的散点图（存储在变量 a 中），针对我们正在考虑的两个水平中的每一个。如果我们的期望图表受到 xarray 绘图功能的支持，我们可以利用 xarray 自动生成图表和标签。请注意一切是如何直接绘制和注释的，我们唯一需要做的更改是将 y 轴标签从 a 重命名为 平均对数氡水平。

prior = prior_checks.prior.squeeze(drop=True)

xr.concat((prior["alpha"], prior["alpha"] + prior["beta"]), dim="location").rename(
    "log_radon"
).assign_coords(location=["basement", "floor"]).plot.scatter(
    x="location", y="log_radon", edgecolors="none"
);

我不是氡专家，但在看到数据之前，这些先验似乎允许相当广泛的平均对数氡水平，无论是在地下室还是楼层测量的。但别担心，如果抽样给我们暗示它们可能不合适，我们可以随时更改这些先验——毕竟，先验是假设，而不是誓言；与大多数假设一样，它们可以被检验。

但是，我们已经可以想到一个改进：请记住，我们声明地下室的氡水平往往较高，因此我们可以通过强制楼层效应 (beta) 为负来将这种先验科学知识纳入我们的模型。目前，我们将保持模型不变，并相信数据中的信息将足够。

说到抽样，让我们启动贝叶斯机制！

with pooled_model:
    pooled_trace = pm.sample(random_seed=RANDOM_SEED)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [alpha, beta, sigma]

100.00% [8000/8000 00:03<00:00 采样 4 条链，0 个分歧]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 4 seconds.

没有分歧，采样只花了数秒！这里的链看起来非常好（良好的 R hat、良好的有效样本大小、小的 sd）。该模型还估计了预期的负楼层效应。

az.summary(pooled_trace, round_to=2)

	平均值	标准差	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
alpha	1.36	0.03	1.31	1.42	0.0	0.0	4200.11	3082.69	1.0
beta	-0.59	0.07	-0.73	-0.46	0.0	0.0	3944.89	3146.38	1.0
sigma	0.79	0.02	0.75	0.83	0.0	0.0	4816.78	3116.53	1.0

让我们绘制地下室 (alpha) 和楼层 (alpha + beta) 的预期氡水平与用于拟合模型的数据的关系

post_mean = pooled_trace.posterior.mean(dim=("chain", "draw"))

plt.scatter(srrs_mn.floor, np.log(srrs_mn.activity + 0.1))
xvals = xr.DataArray(np.linspace(-0.2, 1.2))
plt.plot(xvals, post_mean["beta"] * xvals + post_mean["alpha"], "r--");

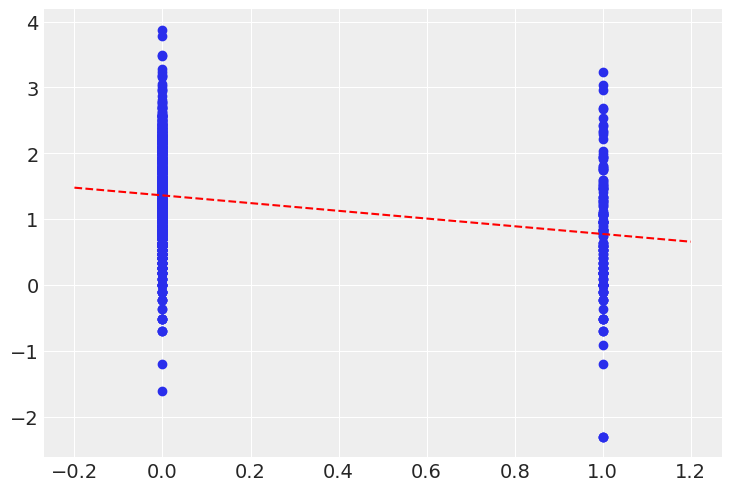
这看起来是合理的，但请注意，数据中存在大量的残差变异性。

现在让我们将注意力转向未合并模型，看看它与合并模型的比较结果。

coords = {"county": mn_counties}

with pm.Model(coords=coords) as unpooled_model:
    floor_ind = pm.MutableData("floor_ind", floor_measure, dims="obs_id")

    alpha = pm.Normal("alpha", 0, sigma=10, dims="county")
    beta = pm.Normal("beta", 0, sigma=10)
    sigma = pm.Exponential("sigma", 1)

    theta = alpha[county] + beta * floor_ind

    y = pm.Normal("y", theta, sigma=sigma, observed=log_radon, dims="obs_id")

pm.model_to_graphviz(unpooled_model)

with unpooled_model:
    unpooled_trace = pm.sample(random_seed=RANDOM_SEED)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [alpha, beta, sigma]

100.00% [8000/8000 00:06<00:00 采样 4 条链，0 个分歧]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 7 seconds.

这里的采样也很干净；让我们看看每个县的地下室（维度 0）和楼层（维度 1）的期望值

ax = az.plot_forest(
    unpooled_trace,
    var_names=["alpha"],
    r_hat=True,
    combined=True,
    figsize=(6, 18),
    labeller=az.labels.NoVarLabeller(),
)
ax[0].set_ylabel("alpha");

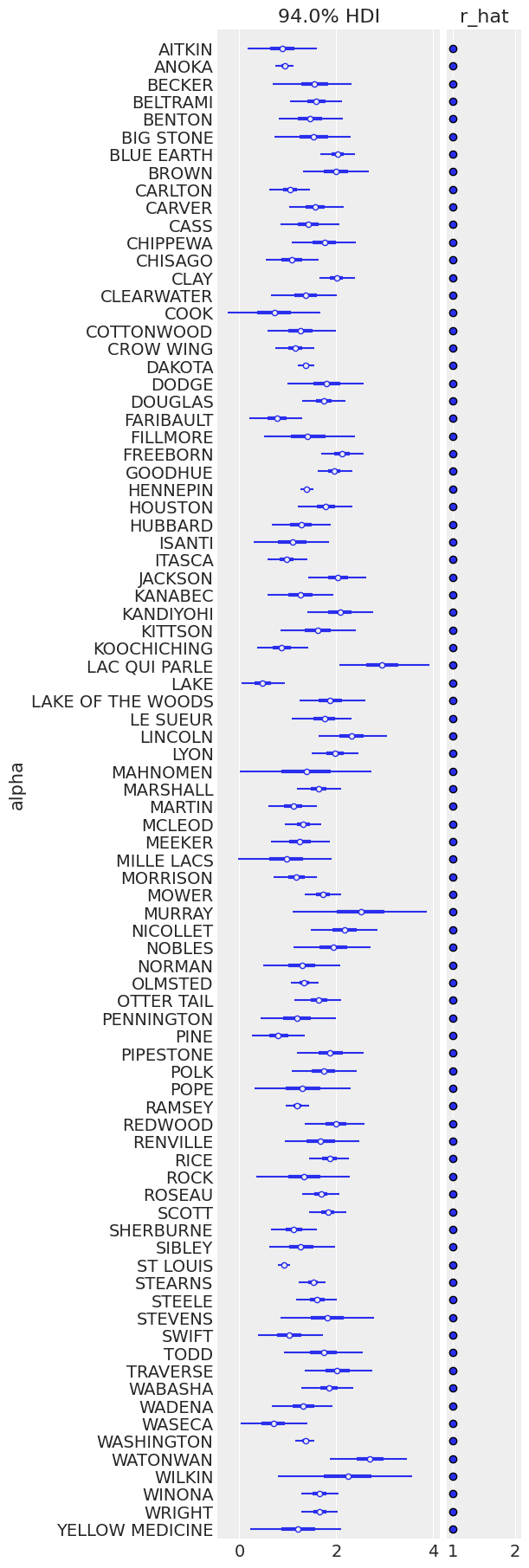
为了识别氡水平高的县，我们可以绘制有序的平均估计值及其 94% HPD

unpooled_means = unpooled_trace.posterior.mean(dim=("chain", "draw"))
unpooled_hdi = az.hdi(unpooled_trace)

unpooled_means_iter = unpooled_means.sortby("alpha")
unpooled_hdi_iter = unpooled_hdi.sortby(unpooled_means_iter.alpha)

_, ax = plt.subplots(figsize=(12, 5))
xticks = np.arange(0, 86, 6)
unpooled_means_iter.plot.scatter(x="county", y="alpha", ax=ax, alpha=0.8)
ax.vlines(
    np.arange(mn_counties.size),
    unpooled_hdi_iter.alpha.sel(hdi="lower"),
    unpooled_hdi_iter.alpha.sel(hdi="higher"),
    color="orange",
    alpha=0.6,
)
ax.set(ylabel="Radon estimate", ylim=(-2, 4.5))
ax.set_xticks(xticks)
ax.set_xticklabels(unpooled_means_iter.county.values[xticks])
ax.tick_params(rotation=90);

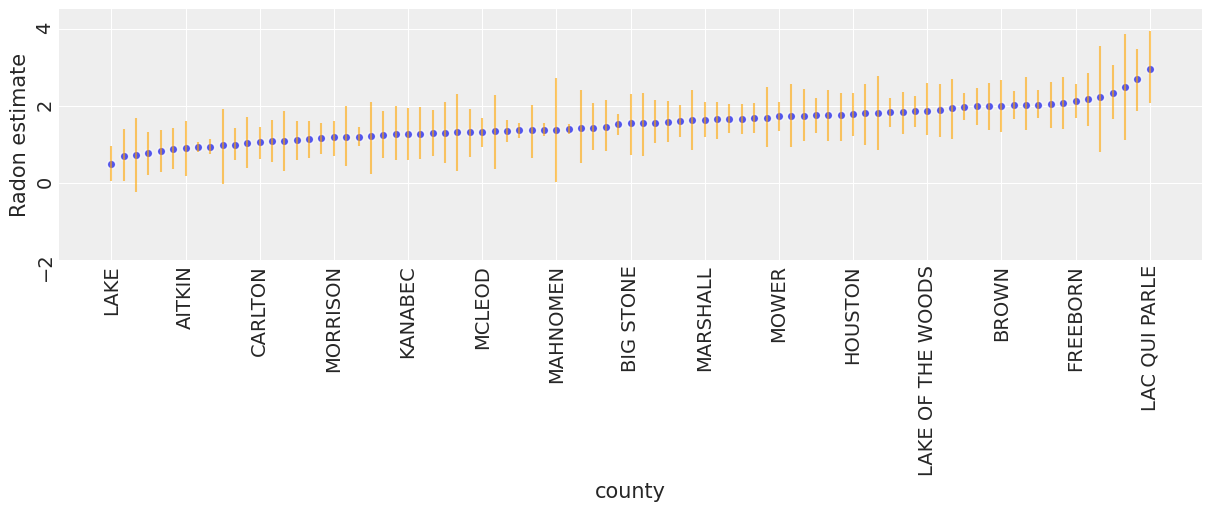
现在我们已经拟合了两种传统（即非分层）模型，让我们看看它们的推断有何不同。以下是代表一系列样本大小的县子集的合并和未合并估计值之间的可视化比较。

sample_counties = (
    "LAC QUI PARLE",
    "AITKIN",
    "KOOCHICHING",
    "DOUGLAS",
    "CLAY",
    "STEARNS",
    "RAMSEY",
    "ST LOUIS",
)

fig, axes = plt.subplots(2, 4, figsize=(12, 6), sharey=True, sharex=True)
axes = axes.ravel()
m = unpooled_means["beta"]
for i, c in enumerate(sample_counties):
    y = srrs_mn.log_radon[srrs_mn.county == c]
    x = srrs_mn.floor[srrs_mn.county == c]
    axes[i].scatter(x + np.random.randn(len(x)) * 0.01, y, alpha=0.4)

    # No pooling model
    b = unpooled_means["alpha"].sel(county=c)

    # Plot both models and data
    xvals = xr.DataArray(np.linspace(0, 1))
    axes[i].plot(xvals, m * xvals + b)
    axes[i].plot(xvals, post_mean["beta"] * xvals + post_mean["alpha"], "r--")
    axes[i].set_xticks([0, 1])
    axes[i].set_xticklabels(["basement", "floor"])
    axes[i].set_ylim(-1, 3)
    axes[i].set_title(c)
    if not i % 2:
        axes[i].set_ylabel("log radon level")

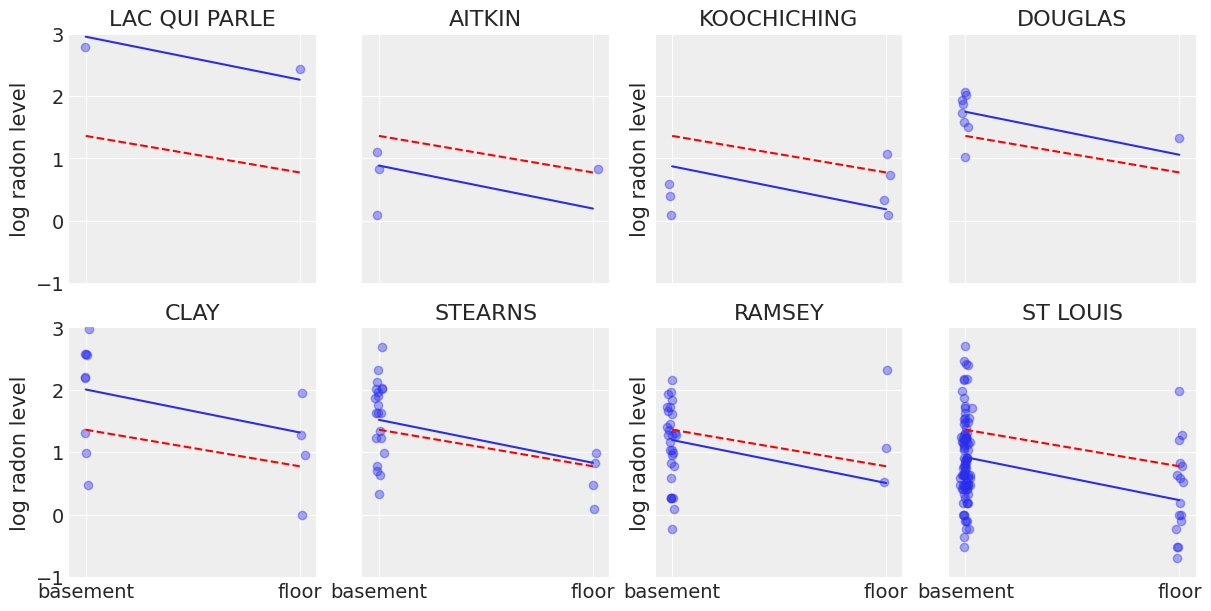
这些模型都不令人满意

• 如果我们试图识别高氡县，合并是无用的——因为，根据定义，合并模型估计的是州级别的氡。换句话说，合并导致最大程度的欠拟合：没有考虑到各县之间的差异，只估计了总体人口。

• 我们不信任使用少量观测值产生的极端未合并估计值。这导致最大程度的过拟合：仅考虑县内变化，而不估计总体人口（即州级别，它告诉我们各县之间的相似之处）。

对于小样本量，这个问题很严重，如上所示：在楼层测量数据很少的县中，如果这些数据点的氡水平高于地下室数据点（Aitkin、Koochiching、Ramsey），则该模型将估计这些县的楼层氡水平高于地下室。但我们不应该相信这个结论，因为科学知识和其他县的情况都告诉我们，通常情况恰恰相反（地下室氡 > 楼层氡）。因此，除非我们有很多观测值告诉我们特定县的情况并非如此，否则我们应该持怀疑态度，并将我们的县估计值缩小到州估计值——换句话说，我们应该在集群级别和人口级别信息之间取得平衡，并且缩小的程度将取决于每个集群中数据的极端程度和数量。

这就是分层模型发挥作用的地方。

多层和分层模型

当我们合并数据时，我们暗示它们是从同一模型中采样的。这忽略了抽样单元之间的任何变化（抽样方差除外）——我们假设所有县都是相同的

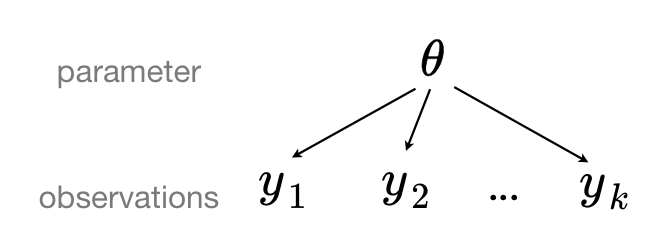
当我们分析未合并的数据时，我们暗示它们是从单独的模型中独立采样的。与合并情况的极端相反，这种方法声称抽样单元之间的差异太大而无法将它们组合起来——我们假设各县之间没有任何相似之处

在分层模型中，参数被视为来自参数的总体分布的样本。因此，我们认为它们既不是完全不同也不是完全相同。这就是部分合并

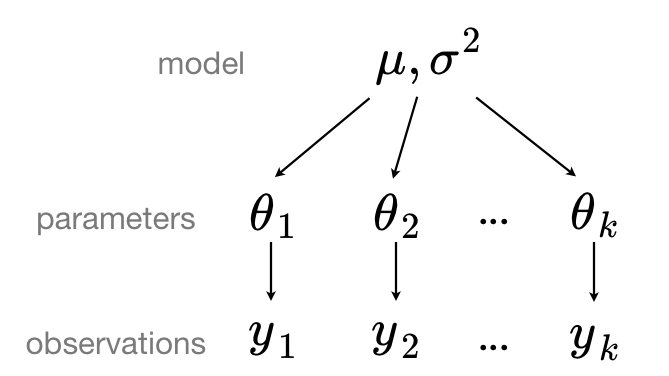
我们可以使用 PyMC 轻松指定多层模型，并使用马尔可夫链蒙特卡洛方法对其进行拟合。

部分合并模型

家庭氡数据集最简单的部分合并模型是仅估计氡水平的模型，没有任何级别的预测因子。部分合并模型代表了合并和未合并极端情况之间的折衷，近似于未合并县估计值和合并估计值的加权平均值（基于样本量）。

\[\hat{\alpha} \approx \frac{(n_j/\sigma_y^2)\bar{y}_j + (1/\sigma_{\alpha}^2)\bar{y}}{(n_j/\sigma_y^2) + (1/\sigma_{\alpha}^2)}\]

样本量较小的县的估计值将向全州平均值收缩，而样本量较大的县的估计值将更接近未合并的县估计值。

让我们从最简单的模型开始，该模型忽略了楼层与地下室测量值的影响。

with pm.Model(coords=coords) as partial_pooling:
    county_idx = pm.MutableData("county_idx", county, dims="obs_id")

    # Priors
    mu_a = pm.Normal("mu_a", mu=0.0, sigma=10)
    sigma_a = pm.Exponential("sigma_a", 1)

    # Random intercepts
    alpha = pm.Normal("alpha", mu=mu_a, sigma=sigma_a, dims="county")

    # Model error
    sigma_y = pm.Exponential("sigma_y", 1)

    # Expected value
    y_hat = alpha[county_idx]

    # Data likelihood
    y_like = pm.Normal("y_like", mu=y_hat, sigma=sigma_y, observed=log_radon, dims="obs_id")

pm.model_to_graphviz(partial_pooling)

with partial_pooling:
    partial_pooling_trace = pm.sample(tune=2000, random_seed=RANDOM_SEED)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [mu_a, sigma_a, alpha, sigma_y]

100.00% [12000/12000 00:09<00:00 采样 4 条链，0 个分歧]

Sampling 4 chains for 2_000 tune and 1_000 draw iterations (8_000 + 4_000 draws total) took 10 seconds.

N_county = srrs_mn.groupby("county")["idnum"].count().values

fig, axes = plt.subplots(1, 2, figsize=(10, 4), sharex=True, sharey=True)
for ax, trace, level in zip(
    axes,
    (unpooled_trace, partial_pooling_trace),
    ("no pooling", "partial pooling"),
):
    # add variable with x values to xarray dataset
    trace.posterior = trace.posterior.assign_coords({"N_county": ("county", N_county)})
    # plot means
    trace.posterior.mean(dim=("chain", "draw")).plot.scatter(
        x="N_county", y="alpha", ax=ax, alpha=0.9
    )
    ax.hlines(
        partial_pooling_trace.posterior.alpha.mean(),
        0.9,
        max(N_county) + 1,
        alpha=0.4,
        ls="--",
        label="Est. population mean",
    )

    # plot hdi
    hdi = az.hdi(trace).alpha
    ax.vlines(N_county, hdi.sel(hdi="lower"), hdi.sel(hdi="higher"), color="orange", alpha=0.5)

    ax.set(
        title=f"{level.title()} Estimates",
        xlabel="Nbr obs in county (log scale)",
        xscale="log",
        ylabel="Log radon",
    )
    ax.legend(fontsize=10)

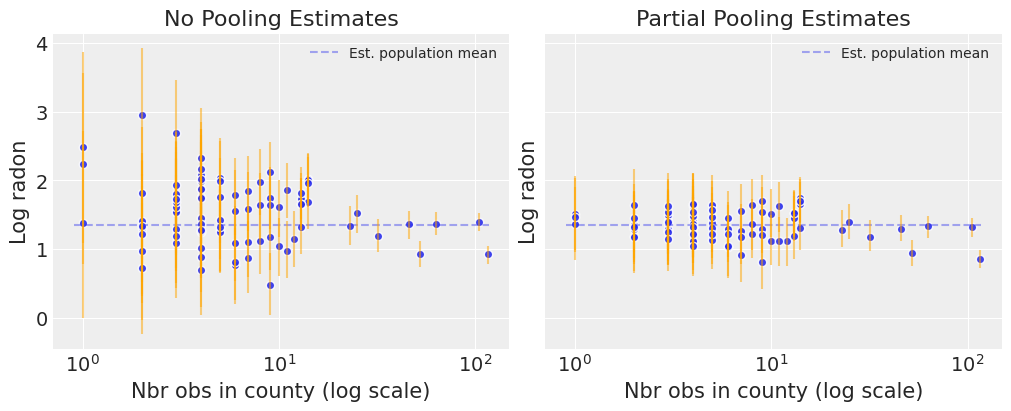
请注意未合并估计值和部分合并估计值之间的差异，尤其是在较小的样本量下：正如预期的那样，前者既更极端也更不精确。实际上，在部分合并模型中，小样本量县的估计值受到总体参数的影响——因此估计值更精确。此外，样本量越小，向总体平均值（灰色虚线）回归的程度就越大——因此估计值越不极端。换句话说，该模型对数据稀疏的县中与总体平均值的极端偏差持怀疑态度。这被称为 收缩。

现在让我们回到整合 floor 预测因子，但允许截距按县变化。

可变截距模型

此模型允许截距根据随机效应在县之间变化。

\[y_i = \alpha_{j[i]} + \beta x_{i} + \epsilon_i\]

其中

\[\epsilon_i \sim N(0, \sigma_y^2)\]

和截距随机效应

\[\alpha_{j[i]} \sim N(\mu_{\alpha}, \sigma_{\alpha}^2)\]

与“不合并”模型一样，我们为每个县设置一个单独的截距，但多层建模不是为每个县拟合单独的最小二乘回归模型，而是在县之间共享强度，从而允许在数据较少的县中进行更合理的推断。

with pm.Model(coords=coords) as varying_intercept:
    floor_idx = pm.MutableData("floor_idx", floor_measure, dims="obs_id")
    county_idx = pm.MutableData("county_idx", county, dims="obs_id")

    # Priors
    mu_a = pm.Normal("mu_a", mu=0.0, sigma=10.0)
    sigma_a = pm.Exponential("sigma_a", 1)

    # Random intercepts
    alpha = pm.Normal("alpha", mu=mu_a, sigma=sigma_a, dims="county")
    # Common slope
    beta = pm.Normal("beta", mu=0.0, sigma=10.0)

    # Model error
    sd_y = pm.Exponential("sd_y", 1)

    # Expected value
    y_hat = alpha[county_idx] + beta * floor_idx

    # Data likelihood
    y_like = pm.Normal("y_like", mu=y_hat, sigma=sd_y, observed=log_radon, dims="obs_id")

pm.model_to_graphviz(varying_intercept)

with varying_intercept:
    varying_intercept_trace = pm.sample(tune=2000, random_seed=RANDOM_SEED)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [mu_a, sigma_a, alpha, beta, sd_y]

100.00% [12000/12000 00:09<00:00 采样 4 条链，0 个分歧]

Sampling 4 chains for 2_000 tune and 1_000 draw iterations (8_000 + 4_000 draws total) took 10 seconds.

ax = pm.plot_forest(
    varying_intercept_trace,
    var_names=["alpha"],
    figsize=(6, 18),
    combined=True,
    r_hat=True,
    labeller=az.labels.NoVarLabeller(),
)
ax[0].set_ylabel("alpha")

Text(0, 0.5, 'alpha')

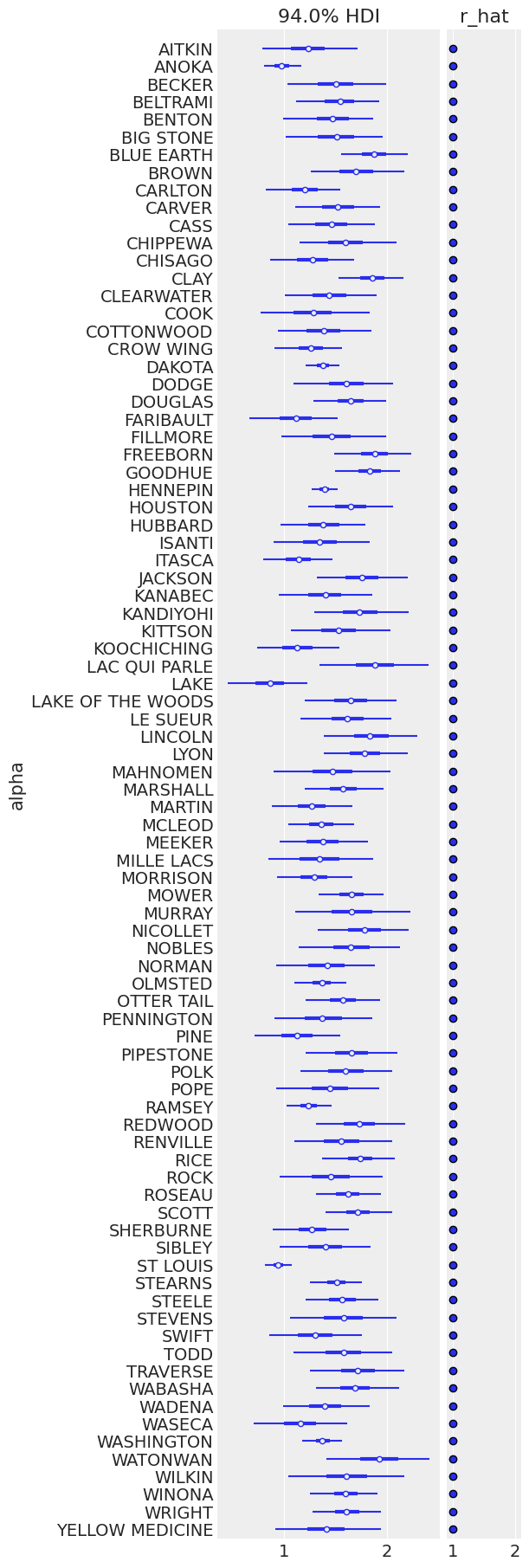
pm.plot_posterior(varying_intercept_trace, var_names=["sigma_a", "beta"]);

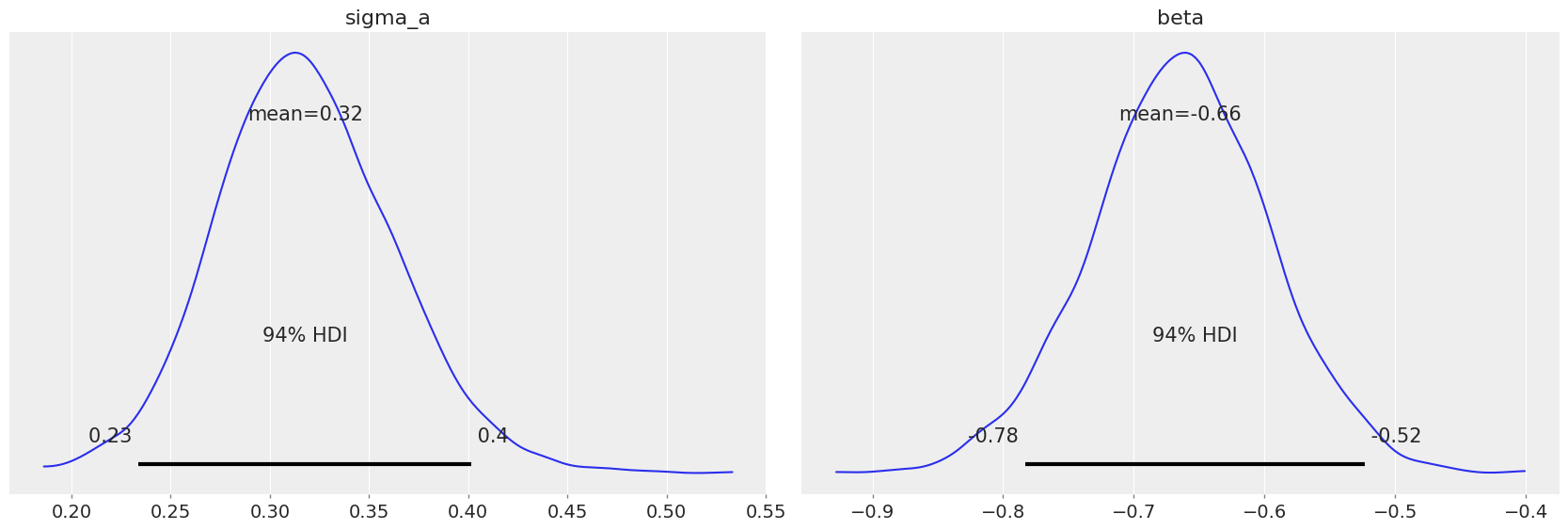
floor 系数的估计值约为 -0.66，可以解释为在考虑县因素后，没有地下室的房屋的氡水平约为有地下室的房屋的一半 (\(\exp(-0.66) = 0.52\))。

az.summary(varying_intercept_trace, var_names=["beta"])

	平均值	标准差	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
beta	-0.664	0.068	-0.783	-0.523	0.001	0.001	2624.0	2422.0	1.0

xvals = xr.DataArray([0, 1], dims="Level", coords={"Level": ["Basement", "Floor"]})
post = varying_intercept_trace.posterior  # alias for readability
theta = (
    (post.alpha + post.beta * xvals).mean(dim=("chain", "draw")).to_dataset(name="Mean log radon")
)

_, ax = plt.subplots()
theta.plot.scatter(x="Level", y="Mean log radon", alpha=0.2, color="k", ax=ax)  # scatter
ax.plot(xvals, theta["Mean log radon"].T, "k-", alpha=0.2)
# add lines too
ax.set_title("MEAN LOG RADON BY COUNTY");

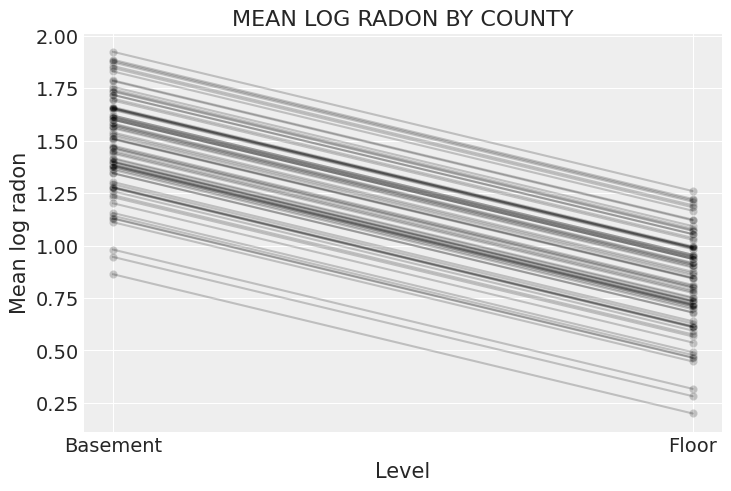
很容易证明，至少对于小样本量的县来说，部分合并模型比合并模型或未合并模型提供更客观合理的估计。

sample_counties = (
    "LAC QUI PARLE",
    "AITKIN",
    "KOOCHICHING",
    "DOUGLAS",
    "CLAY",
    "STEARNS",
    "RAMSEY",
    "ST LOUIS",
)

fig, axes = plt.subplots(2, 4, figsize=(12, 6), sharey=True, sharex=True)
axes = axes.ravel()
m = unpooled_means["beta"]
for i, c in enumerate(sample_counties):
    y = srrs_mn.log_radon[srrs_mn.county == c]
    x = srrs_mn.floor[srrs_mn.county == c]
    axes[i].scatter(x + np.random.randn(len(x)) * 0.01, y, alpha=0.4)

    # No pooling model
    b = unpooled_means["alpha"].sel(county=c)

    # Plot both models and data
    xvals = xr.DataArray(np.linspace(0, 1))
    axes[i].plot(xvals, m.values * xvals + b.values)
    axes[i].plot(xvals, post_mean["beta"] * xvals + post_mean["alpha"], "r--")

    varying_intercept_trace.posterior.sel(county=c).beta
    post = varying_intercept_trace.posterior.sel(county=c).mean(dim=("chain", "draw"))
    theta = post.alpha.values + post.beta.values * xvals
    axes[i].plot(xvals, theta, "k:")
    axes[i].set_xticks([0, 1])
    axes[i].set_xticklabels(["basement", "floor"])
    axes[i].set_ylim(-1, 3)
    axes[i].set_title(c)
    if not i % 2:
        axes[i].set_ylabel("log radon level")

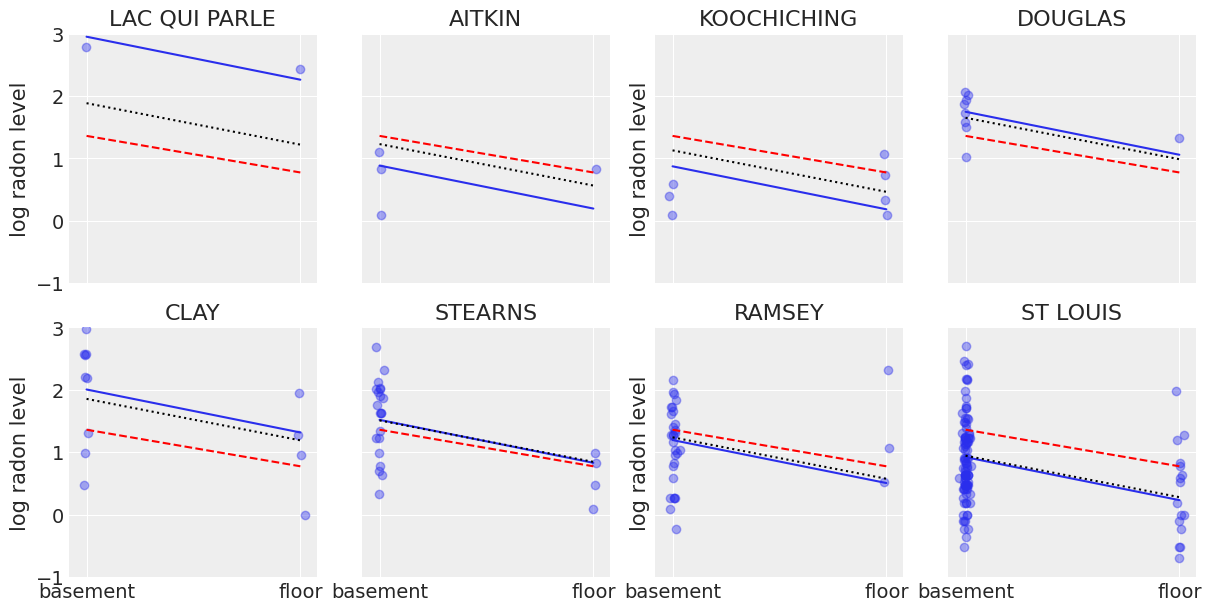
可变截距和斜率模型

最通用的模型允许截距和斜率都按县变化

\[y_i = \alpha_{j[i]} + \beta_{j[i]} x_{i} + \epsilon_i\]

with pm.Model(coords=coords) as varying_intercept_slope:
    floor_idx = pm.MutableData("floor_idx", floor_measure, dims="obs_id")
    county_idx = pm.MutableData("county_idx", county, dims="obs_id")

    # Priors
    mu_a = pm.Normal("mu_a", mu=0.0, sigma=10.0)
    sigma_a = pm.Exponential("sigma_a", 1)

    mu_b = pm.Normal("mu_b", mu=0.0, sigma=10.0)
    sigma_b = pm.Exponential("sigma_b", 1)

    # Random intercepts
    alpha = pm.Normal("alpha", mu=mu_a, sigma=sigma_a, dims="county")
    # Random slopes
    beta = pm.Normal("beta", mu=mu_b, sigma=sigma_b, dims="county")

    # Model error
    sigma_y = pm.Exponential("sigma_y", 1)

    # Expected value
    y_hat = alpha[county_idx] + beta[county_idx] * floor_idx

    # Data likelihood
    y_like = pm.Normal("y_like", mu=y_hat, sigma=sigma_y, observed=log_radon, dims="obs_id")

pm.model_to_graphviz(varying_intercept_slope)

with varying_intercept_slope:
    varying_intercept_slope_trace = pm.sample(tune=2000, random_seed=RANDOM_SEED)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [mu_a, sigma_a, mu_b, sigma_b, alpha, beta, sigma_y]

100.00% [12000/12000 00:37<00:00 采样 4 条链，7 个分歧]

Sampling 4 chains for 2_000 tune and 1_000 draw iterations (8_000 + 4_000 draws total) took 38 seconds.

请注意，此模型的轨迹包括分歧，这可能会在分歧发生的位置和频率方面存在问题。这些分歧可能发生在某些分层模型中，可以通过使用非中心参数化来避免。

非中心参数化

上面指定的部分合并模型使用斜率随机效应的中心化参数化。也就是说，各个县效应分布在县平均值附近，其散布由分层标准差参数控制。正如前面的图所示，此约束用于将县估计值收缩到总体平均值，收缩程度与县样本量成正比。这正是我们想要的，并且模型似乎非常适合——Gelman-Rubin 统计量正好为 1。

但是，仔细检查后，有一些麻烦的迹象。具体来说，让我们看一下随机效应的轨迹及其对应的标准差

fig, axs = plt.subplots(nrows=2)
axs[0].plot(varying_intercept_slope_trace.posterior.sel(chain=0)["sigma_b"], alpha=0.5)
axs[0].set(ylabel="sigma_b")
axs[1].plot(varying_intercept_slope_trace.posterior.sel(chain=0)["beta"], alpha=0.05)
axs[1].set(ylabel="beta");

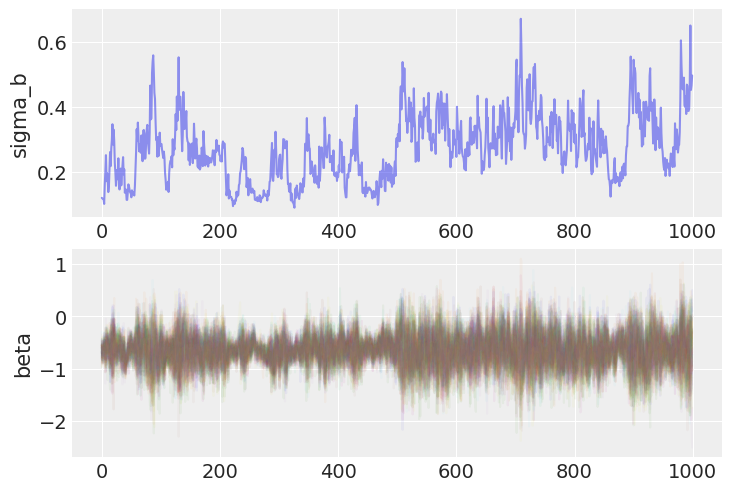
请注意，当链达到 \(\sigma_b\) 参数空间的下端时，它似乎“卡住”了，整个采样器，包括随机斜率 b，混合效果很差。

联合绘制随机效应方差和单个随机斜率之一，可以演示正在发生的事情。

ax = az.plot_pair(
    varying_intercept_slope_trace,
    var_names=["beta", "sigma_b"],
    coords=dict(county="AITKIN"),
    marginals=True,
    # marginal_kwargs={"kind": "hist"},
)
ax[1, 0].set_ylim(0, 0.7);

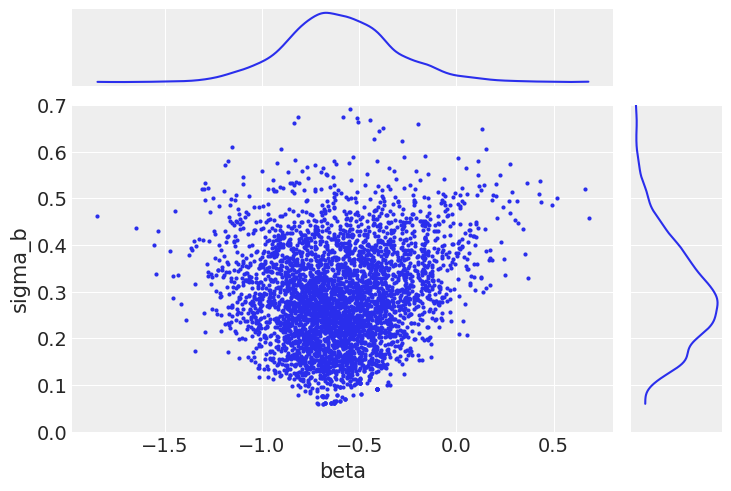
当组方差很小时，这意味着各个随机斜率本身接近组平均值。这导致组方差样本与任何斜率（尤其是样本量较小的斜率）之间呈漏斗状关系。

就其本身而言，这不是问题，因为这是我们期望的行为。但是，如果采样器针对参数空间中较宽（无约束）的部分进行调整，则在曲率较高的区域会遇到麻烦。这样做的结果是，\(\sigma_b\) 下限附近的邻域采样效果很差；实际上，在我们的链中，低于 0.1 的值根本没有被采样。这将导致有偏推断。

现在我们已经发现了问题，我们该如何解决它？解决此问题的最佳方法是重新参数化我们的模型。请注意此版本中的随机斜率

with pm.Model(coords=coords) as varying_intercept_slope_noncentered:
    floor_idx = pm.MutableData("floor_idx", floor_measure, dims="obs_id")
    county_idx = pm.MutableData("county_idx", county, dims="obs_id")

    # Priors
    mu_a = pm.Normal("mu_a", mu=0.0, sigma=10.0)
    sigma_a = pm.Exponential("sigma_a", 5)

    # Non-centered random intercepts
    # Centered: a = pm.Normal('a', mu_a, sigma=sigma_a, shape=counties)
    z_a = pm.Normal("z_a", mu=0, sigma=1, dims="county")
    alpha = pm.Deterministic("alpha", mu_a + z_a * sigma_a, dims="county")

    mu_b = pm.Normal("mu_b", mu=0.0, sigma=10.0)
    sigma_b = pm.Exponential("sigma_b", 5)

    # Non-centered random slopes
    z_b = pm.Normal("z_b", mu=0, sigma=1, dims="county")
    beta = pm.Deterministic("beta", mu_b + z_b * sigma_b, dims="county")

    # Model error
    sigma_y = pm.Exponential("sigma_y", 5)

    # Expected value
    y_hat = alpha[county_idx] + beta[county_idx] * floor_idx

    # Data likelihood
    y_like = pm.Normal("y_like", mu=y_hat, sigma=sigma_y, observed=log_radon, dims="obs_id")

pm.model_to_graphviz(varying_intercept_slope_noncentered)

这是一个 非中心化参数化。通过这种方式，我们的意思是随机偏差不再明确地建模为以 \(\mu_b\) 为中心。相反，它们是独立的标准正态分布 \(\upsilon\)，然后通过 \(\sigma_b\) 的适当值进行缩放，然后再通过均值进行位置变换。

此模型采样效果更好。

with varying_intercept_slope_noncentered:
    noncentered_trace = pm.sample(tune=3000, target_accept=0.95, random_seed=RANDOM_SEED)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [mu_a, sigma_a, z_a, mu_b, sigma_b, z_b, sigma_y]

100.00% [16000/16000 00:55<00:00 采样 4 条链，0 个分歧]

Sampling 4 chains for 3_000 tune and 1_000 draw iterations (12_000 + 4_000 draws total) took 56 seconds.

请注意，轨迹中的瓶颈已消失。

fig, axs = plt.subplots(nrows=2)
axs[0].plot(noncentered_trace.posterior.sel(chain=0)["sigma_b"], alpha=0.5)
axs[0].set(ylabel="sigma_b")
axs[1].plot(noncentered_trace.posterior.sel(chain=0)["beta"], alpha=0.05)
axs[1].set(ylabel="beta");

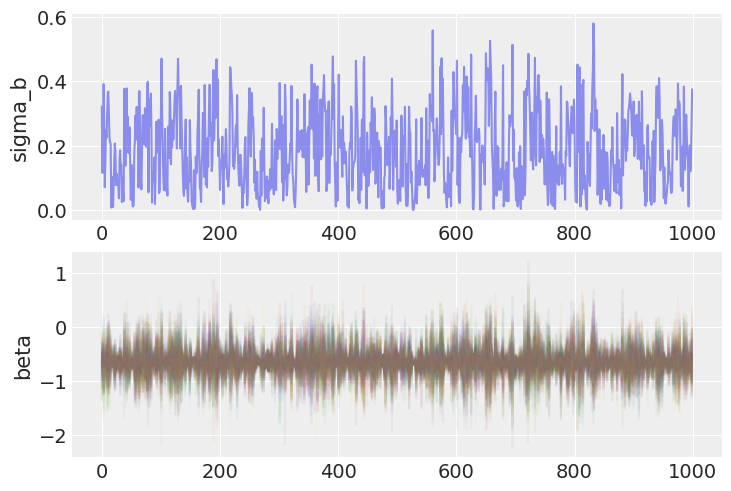
相应地，现在可以有效地采样斜率随机效应方差的后验分布的低端。

ax = az.plot_pair(
    noncentered_trace,
    var_names=["beta", "sigma_b"],
    coords=dict(county="AITKIN"),
    marginals=True,
    # marginal_kwargs={"kind": "hist"},
)
ax[1, 0].set_ylim(0, 0.7);

因此，我们现在完全探索了后验的支持。这减少了这些参数的偏差。

fig, (ax1, ax2) = plt.subplots(2, 1, sharex=True, constrained_layout=True)
az.plot_posterior(varying_intercept_slope_trace, var_names=["sigma_b"], ax=ax1)
az.plot_posterior(noncentered_trace, var_names=["sigma_b"], ax=ax2)
ax1.set_title("Centered (top) and non-centered (bottom)");

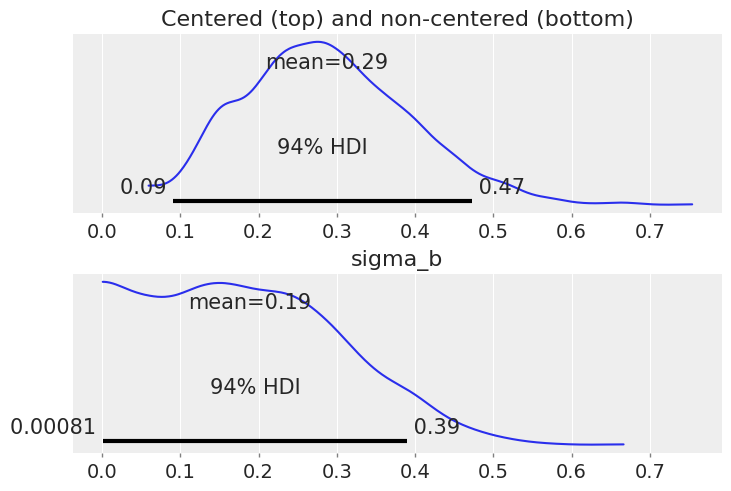
请注意，sigma_b 现在在零附近有很多密度，这表明县在对 floor “处理”的响应方面差异不大。

这就是原始参数化的问题：当斜率随机效应的值对于非常接近于零的标准差与正的标准差非常不同时，采样器很难处理后验分布的几何形状。但是，即使使用非中心模型，采样器对 sigma_b 也不是很舒适：实际上，如果您使用 az.summary 查看估计值，您会看到 sigma_b 的有效样本数量非常低。

另请注意，sigma_a 也不是很大——即各县的基线氡水平确实存在差异，但差异不大。但是，我们从这个分布中采样并没有太大的问题，因为它比 sigma_b 窄得多，并且不会危险地接近 0。

az.summary(varying_intercept_slope_trace, var_names=["sigma_a", "sigma_b"])

	平均值	标准差	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
sigma_a	0.323	0.045	0.241	0.408	0.001	0.001	1191.0	1807.0	1.01
sigma_b	0.287	0.106	0.090	0.473	0.010	0.007	105.0	155.0	1.05

为了总结此模型，让我们绘制每个县的氡与楼层之间的关系

xvals = xr.DataArray([0, 1], dims="Level", coords={"Level": ["Basement", "Floor"]})
post = noncentered_trace.posterior  # alias for readability
theta = (
    (post.alpha + post.beta * xvals).mean(dim=("chain", "draw")).to_dataset(name="Mean log radon")
)

_, ax = plt.subplots()
theta.plot.scatter(x="Level", y="Mean log radon", alpha=0.2, color="k", ax=ax)  # scatter
ax.plot(xvals, theta["Mean log radon"].T, "k-", alpha=0.2)
# add lines too
ax.set_title("MEAN LOG RADON BY COUNTY");

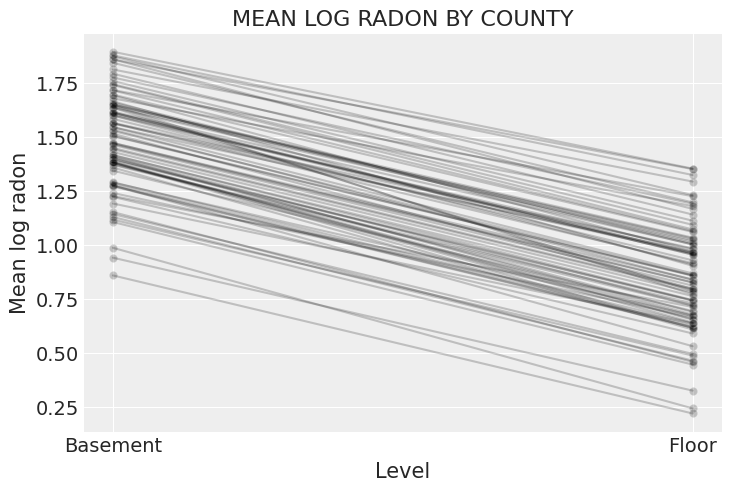
虽然截距和斜率都因县而异，但斜率的变化要小得多。

但是等等，还有更多！我们可以（也许应该）考虑截距和斜率之间的协变：当给定县的基线氡较低时，可能意味着楼层和地下室测量值之间的差异会减小——因为无论如何氡含量都不多。这将转化为 alpha 和 beta 之间的正相关，并且将此添加到我们的模型中将更有效地利用可用数据。

为了对这种相关性进行建模，我们将使用多元正态分布而不是 alpha 和 beta 的两个不同正态分布。这仅仅意味着每个县的参数都来自一个共同的分布，截距的均值为 mu_alpha，斜率的均值为 mu_beta，斜率和截距根据协方差矩阵 S 共同变化。用数学形式表示

\[y \sim Normal(\theta, \sigma)\]

\[\theta = \alpha + \beta \times floor\]

\[\begin{split}\begin{bmatrix} \alpha \\ \beta \end{bmatrix} \sim MvNormal(\begin{bmatrix} \mu_{\alpha} \\ \mu_{\beta} \end{bmatrix}, \Sigma)\end{split}\]

\[\begin{split}\Sigma = \begin{pmatrix} \sigma_{\alpha} & 0 \\ 0 & \sigma_{\beta} \end{pmatrix} P \begin{pmatrix} \sigma_{\alpha} & 0 \\ 0 & \sigma_{\beta} \end{pmatrix}\end{split}\]

其中 \(\alpha\) 和 \(\beta\) 分别是平均截距和斜率，\(\sigma_{\alpha}\) 和 \(\sigma_{\beta}\) 分别表示截距和斜率的变化，\(P\) 是截距和斜率的相关矩阵。在这种情况下，由于只有一个斜率，\(P\) 仅包含一个相关数字：\(\alpha\) 和 \(\beta\) 之间的相关性。

这很容易在 PyMC 中翻译

coords["param"] = ["alpha", "beta"]
coords["param_bis"] = ["alpha", "beta"]
with pm.Model(coords=coords) as covariation_intercept_slope:
    floor_idx = pm.MutableData("floor_idx", floor_measure, dims="obs_id")
    county_idx = pm.MutableData("county_idx", county, dims="obs_id")

    # prior stddev in intercepts & slopes (variation across counties):
    sd_dist = pm.Exponential.dist(0.5, shape=(2,))

    # get back standard deviations and rho:
    chol, corr, stds = pm.LKJCholeskyCov("chol", n=2, eta=2.0, sd_dist=sd_dist)

    # prior for average intercept:
    mu_alpha_beta = pm.Normal("mu_alpha", mu=0.0, sigma=5.0, shape=2)
    # prior for average slope:
    mu_beta = pm.Normal("mu_beta", mu=0.0, sigma=1.0)
    # population of varying effects:
    alpha_beta_county = pm.MvNormal(
        "alpha_beta_county", mu=mu_alpha_beta, chol=chol, dims=("county", "param")
    )

    # Expected value per county:
    theta = alpha_beta_county[county_idx, 0] + alpha_beta_county[county_idx, 1] * floor_idx
    # Model error:
    sigma = pm.Exponential("sigma", 1.0)

    y = pm.Normal("y", theta, sigma=sigma, observed=log_radon, dims="obs_id")

这是到目前为止我们完成的最复杂的模型，因此模型代码也相应复杂。主要的复杂性是协方差矩阵使用了 LKJCholeskyCov 分布。这是协方差矩阵的 Cholesky 分解，使其更容易采样。

正如您可能预期的那样，我们还希望在此处非中心化随机效应。这再次导致 Deterministic 操作，此处将协方差与独立的标准正态分布相乘。

coords["param"] = ["alpha", "beta"]
coords["param_bis"] = ["alpha", "beta"]
with pm.Model(coords=coords) as covariation_intercept_slope:
    floor_idx = pm.MutableData("floor_idx", floor_measure, dims="obs_id")
    county_idx = pm.MutableData("county_idx", county, dims="obs_id")

    # prior stddev in intercepts & slopes (variation across counties):
    sd_dist = pm.Exponential.dist(0.5, shape=(2,))

    # get back standard deviations and rho:
    chol, corr, stds = pm.LKJCholeskyCov("chol", n=2, eta=2.0, sd_dist=sd_dist)

    # priors for average intercept and slope:
    mu_alpha_beta = pm.Normal("mu_alpha_beta", mu=0.0, sigma=5.0, shape=2)

    # population of varying effects:
    z = pm.Normal("z", 0.0, 1.0, dims=("param", "county"))
    alpha_beta_county = pm.Deterministic(
        "alpha_beta_county", pt.dot(chol, z).T, dims=("county", "param")
    )

    # Expected value per county:
    theta = (
        mu_alpha_beta[0]
        + alpha_beta_county[county_idx, 0]
        + (mu_alpha_beta[1] + alpha_beta_county[county_idx, 1]) * floor_idx
    )

    # Model error:
    sigma = pm.Exponential("sigma", 1.0)

    y = pm.Normal("y", theta, sigma=sigma, observed=log_radon, dims="obs_id")

    covariation_intercept_slope_trace = pm.sample(
        1000,
        tune=3000,
        target_accept=0.95,
        idata_kwargs={"dims": {"chol_stds": ["param"], "chol_corr": ["param", "param_bis"]}},
    )

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [chol, mu_alpha_beta, z, sigma]

100.00% [16000/16000 01:50<00:00 采样 4 条链，0 个分歧]

Sampling 4 chains for 3_000 tune and 1_000 draw iterations (12_000 + 4_000 draws total) took 111 seconds.

az.plot_trace(
    covariation_intercept_slope_trace,
    var_names=["~z", "~chol", "~chol_corr"],
    compact=True,
    chain_prop={"ls": "-"},
);

az.plot_trace(
    covariation_intercept_slope_trace,
    var_names="chol_corr",
    lines=[("chol_corr", {}, 0.0)],
    compact=True,
    chain_prop={"ls": "-"},
    coords={
        "param": xr.DataArray(["alpha"], dims=["pointwise_sel"]),
        "param_bis": xr.DataArray(["beta"], dims=["pointwise_sel"]),
    },
);

因此，斜率和截距之间的相关性似乎是负的：当县截距增加时，县斜率往往会减小。换句话说，当一个县的地下室氡含量变大时，与楼层氡的差异往往也会变大（因为楼层读数变小而地下室读数变大）。但同样，不确定性范围很广，以至于相关性可能朝另一个方向发展，或者只是接近于零。

各县之间的变化有多大？上面不容易读取 sigma_ab，因此让我们做一个森林图，并将估计值与不包括斜率和截距之间协变的模型进行比较

az.plot_forest(
    [varying_intercept_slope_trace, covariation_intercept_slope_trace],
    model_names=["No covariation", "With covariation"],
    var_names=["mu_a", "mu_b", "mu_alpha_beta", "sigma_a", "sigma_b", "chol_stds", "chol_corr"],
    combined=True,
    figsize=(8, 6),
);

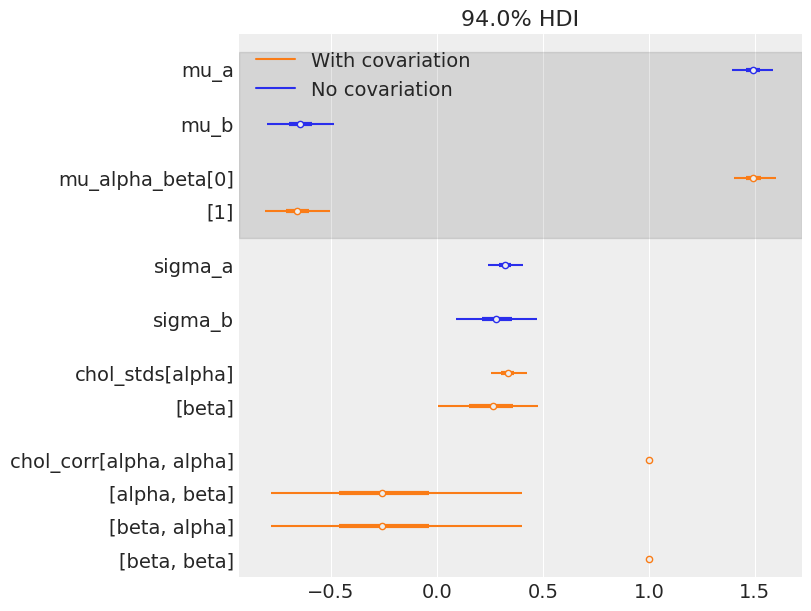
对于均值和标准差，估计值都非常接近。但请记住，相关性给出的信息仅在县级可见：从理论上讲，它使用来自数据的更多信息来获得对所有县参数更明智的信息合并。因此，让我们在视觉上比较两个模型在县级的估计值

# posterior means of covariation model:
a_county_cov = (
    covariation_intercept_slope_trace.posterior["mu_alpha_beta"][..., 0]
    + covariation_intercept_slope_trace.posterior["alpha_beta_county"].sel(param="alpha")
).mean(dim=("chain", "draw"))
b_county_cov = (
    covariation_intercept_slope_trace.posterior["mu_alpha_beta"][..., 1]
    + covariation_intercept_slope_trace.posterior["alpha_beta_county"].sel(param="beta")
).mean(dim=("chain", "draw"))

# plot both and connect with lines
avg_a_county = noncentered_trace.posterior["alpha"].mean(dim=("chain", "draw"))
avg_b_county = noncentered_trace.posterior["beta"].mean(dim=("chain", "draw"))
plt.scatter(avg_a_county, avg_b_county, label="No cov estimates", alpha=0.6)
plt.scatter(
    a_county_cov,
    b_county_cov,
    facecolors="none",
    edgecolors="k",
    lw=1,
    label="With cov estimates",
    alpha=0.8,
)
plt.plot([avg_a_county, a_county_cov], [avg_b_county, b_county_cov], "k-", alpha=0.5)
plt.xlabel("Intercept")
plt.ylabel("Slope")
plt.legend();

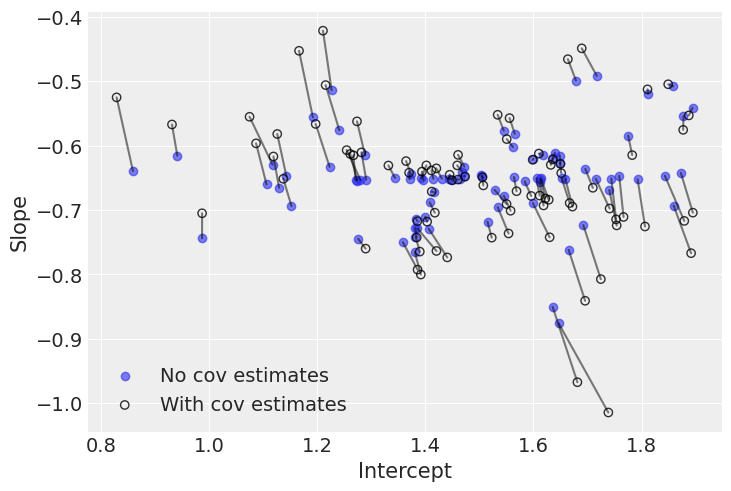
负相关在这里有点明显：当截距增加时，斜率减小。因此，我们理解了为什么模型将大部分后验权重放在相关项的负区域。然而，该模型为相关性实际上可能为零或正的可能性提供了重要的后验概率。

有趣的是，两种模型之间的差异发生在极端斜率和截距值处。这是因为第二个模型使用了截距和斜率之间略微的负相关性来调整它们的估计值：当截距大于（小于）平均值时，模型会向下（向上）推相关的斜率。

总的来说，这里有很多一致之处：对相关性进行建模并没有改变太多的推断。我们已经看到楼层的氡水平往往低于地下室，当我们检查平均效应（alpha 和 beta）和标准差的后验分布时，我们注意到它们几乎相同。但平均而言，具有协变的模型将更准确——因为它从数据中提取了额外的信息，以在两个维度上缩小估计值。

添加组级预测因子

多层模型的主要优势之一是能够同时处理多个级别的预测因子。如果我们考虑上面的可变截距模型

\[y_i = \alpha_{j[i]} + \beta x_{i} + \epsilon_i\]

我们可以使用县级协变量指定另一个回归模型，而不是使用简单的随机效应来描述预期氡值的变化。在这里，我们使用县铀读数 \(u_j\)，据认为它与氡水平有关

\[\alpha_j = \gamma_0 + \gamma_1 u_j + \zeta_j\]

\[\zeta_j \sim N(0, \sigma_{\alpha}^2)\]

因此，我们现在纳入了房屋级别预测因子（楼层或地下室）以及县级预测因子（铀）。

请注意，该模型既有每个县的指标变量，又有县级协变量。在经典回归中，这将导致共线性。在多层模型中，截距向组级线性模型的期望值的部分合并避免了这种情况。

组级预测因子还有助于减少组级变化，\(\sigma_{\alpha}\)（这里将是各县之间的变化，sigma_a）。一个重要的含义是组级估计导致更强的合并——根据定义，较小的 \(\sigma_{\alpha}\) 意味着县参数向总体州平均值更强地收缩。

这在 PyMC 中实现起来相当简单——我们只需添加另一个层级。

with pm.Model(coords=coords) as hierarchical_intercept:
    # Priors
    sigma_a = pm.HalfCauchy("sigma_a", 5)

    # County uranium model
    gamma_0 = pm.Normal("gamma_0", mu=0.0, sigma=10.0)
    gamma_1 = pm.Normal("gamma_1", mu=0.0, sigma=10.0)

    # Uranium model for intercept
    mu_a = pm.Deterministic("mu_a", gamma_0 + gamma_1 * u)
    # County variation not explained by uranium
    epsilon_a = pm.Normal("epsilon_a", mu=0, sigma=1, dims="county")
    alpha = pm.Deterministic("alpha", mu_a + sigma_a * epsilon_a, dims="county")

    # Common slope
    beta = pm.Normal("beta", mu=0.0, sigma=10.0)

    # Model error
    sigma_y = pm.Uniform("sigma_y", lower=0, upper=100)

    # Expected value
    y_hat = alpha[county] + beta * floor_measure

    # Data likelihood
    y_like = pm.Normal("y_like", mu=y_hat, sigma=sigma_y, observed=log_radon)

pm.model_to_graphviz(hierarchical_intercept)

你看到新的层级了吗？它包含 sigma_a 和 gamma，并且是二维的，因为它包含了 a_county 的线性模型。

with hierarchical_intercept:
    hierarchical_intercept_trace = pm.sample(tune=2000, random_seed=RANDOM_SEED)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [sigma_a, gamma_0, gamma_1, epsilon_a, beta, sigma_y]

100.00% [12000/12000 00:21<00:00 采样 4 条链，1 个偏差]

Sampling 4 chains for 2_000 tune and 1_000 draw iterations (8_000 + 4_000 draws total) took 22 seconds.

uranium = u
post = hierarchical_intercept_trace.posterior.assign_coords(uranium=uranium)
avg_a = post["mu_a"].mean(dim=("chain", "draw")).values[np.argsort(uranium)]
avg_a_county = post["alpha"].mean(dim=("chain", "draw"))
avg_a_county_hdi = az.hdi(post, var_names="alpha")["alpha"]

_, ax = plt.subplots()
ax.plot(uranium[np.argsort(uranium)], avg_a, "k--", alpha=0.6, label="Mean intercept")
az.plot_hdi(
    uranium,
    post["alpha"],
    fill_kwargs={"alpha": 0.1, "color": "k", "label": "Mean intercept HPD"},
    ax=ax,
)
ax.scatter(uranium, avg_a_county, alpha=0.8, label="Mean county-intercept")
ax.vlines(
    uranium,
    avg_a_county_hdi.sel(hdi="lower"),
    avg_a_county_hdi.sel(hdi="higher"),
    alpha=0.5,
    color="orange",
)
plt.xlabel("County-level uranium")
plt.ylabel("Intercept estimate")
plt.legend(fontsize=9);

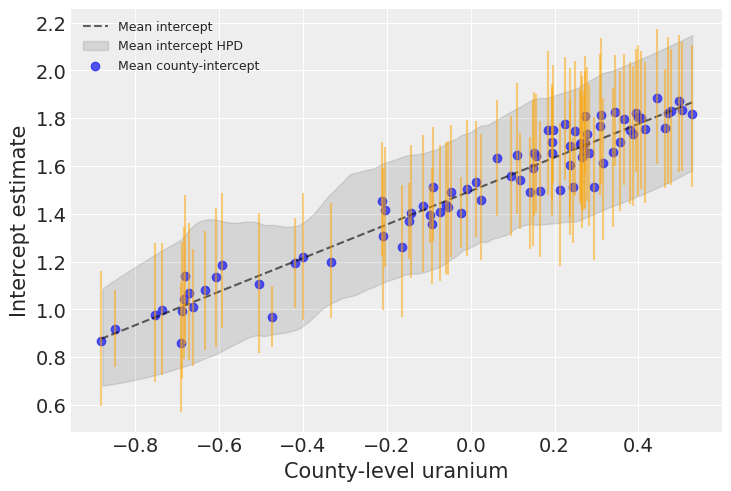
铀确实与每个县的基线氡水平密切相关。上面的图表显示了平均关系及其不确定性：一个普通县的基线氡水平作为铀的函数，以及该氡水平的 94% HPD（虚线和包络线）。蓝色点和橙色条表示基线氡和铀之间的关系，但现在是针对每个县。正如你所看到的，现在的不确定性更大，因为它是在平均不确定性的基础上增加的——毕竟每个县都有其特殊性。

如果我们将此模型的县级截距与没有县级协变量的部分汇集模型的县级截距进行比较：截距的标准误差比没有县级协变量的部分汇集模型的标准误差更窄。

labeller = az.labels.mix_labellers((az.labels.NoVarLabeller, az.labels.NoModelLabeller))
ax = az.plot_forest(
    [varying_intercept_trace, hierarchical_intercept_trace],
    model_names=["W/t. county pred.", "With county pred."],
    var_names=["alpha"],
    combined=True,
    figsize=(6, 40),
    textsize=9,
    labeller=labeller(),
)
ax[0].set_ylabel("alpha");

我们看到，对于包含县级协变量的模型，兼容区间更窄。这是预期的，因为协变量的作用是减少结果变量的变异性——前提是协变量具有预测价值。更重要的是，通过这个模型，我们能够从数据中挖掘出更多的信息。

层级之间的相关性

在某些情况下，在多个层级上拥有预测变量可以揭示个体层级变量和组残差之间的相关性。我们可以通过将个体预测变量的平均值作为协变量包含在组截距模型中来解决这个问题。

\[\alpha_j = \gamma_0 + \gamma_1 u_j + \gamma_2 \bar{x} + \zeta_j\]

这些通常被称为 情境效应。

为了将这些效应添加到我们的模型中，让我们创建一个新变量，其中包含每个县 floor 的平均值，并将其添加到我们之前的模型中。

# Create new variable for mean of floor across counties
avg_floor_data = srrs_mn.groupby("county")["floor"].mean().values

with pm.Model(coords=coords) as contextual_effect:
    floor_idx = pm.Data("floor_idx", floor_measure, mutable=True)
    county_idx = pm.Data("county_idx", county, mutable=True)
    y = pm.Data("y", log_radon, mutable=True)

    # Priors
    sigma_a = pm.HalfCauchy("sigma_a", 5)

    # County uranium model for slope
    gamma = pm.Normal("gamma", mu=0.0, sigma=10, shape=3)

    # Uranium model for intercept
    mu_a = pm.Deterministic("mu_a", gamma[0] + gamma[1] * u + gamma[2] * avg_floor_data)

    # County variation not explained by uranium
    epsilon_a = pm.Normal("epsilon_a", mu=0, sigma=1, dims="county")
    alpha = pm.Deterministic("alpha", mu_a + sigma_a * epsilon_a)

    # Common slope
    beta = pm.Normal("beta", mu=0.0, sigma=10)

    # Model error
    sigma_y = pm.Uniform("sigma_y", lower=0, upper=100)

    # Expected value
    y_hat = alpha[county_idx] + beta * floor_idx

    # Data likelihood
    y_like = pm.Normal("y_like", mu=y_hat, sigma=sigma_y, observed=y)

with contextual_effect:
    contextual_effect_trace = pm.sample(tune=2000, random_seed=RANDOM_SEED)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [sigma_a, gamma, epsilon_a, beta, sigma_y]

100.00% [12000/12000 00:22<00:00 采样 4 条链，5 个偏差]

Sampling 4 chains for 2_000 tune and 1_000 draw iterations (8_000 + 4_000 draws total) took 23 seconds.

az.summary(contextual_effect_trace, var_names="gamma", round_to=2)

	平均值	标准差	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
gamma[0]	1.43	0.05	1.33	1.51	0.0	0.0	2614.08	2072.20	1.0
gamma[1]	0.70	0.09	0.53	0.86	0.0	0.0	2935.94	1793.38	1.0
gamma[2]	0.39	0.19	0.04	0.77	0.0	0.0	3077.64	2550.77	1.0

因此，我们可能由此推断，地下室房屋比例较高的县往往具有较高的基线氡水平。这似乎是新的，因为到目前为止，我们看到 floor 与氡水平呈负相关。但请记住，这是在家庭层面上：氡往往在有地下室的房屋中较高。但在县级层面，似乎县内平均地下室越少，氡就越多。所以这并不矛盾。更重要的是，\(\gamma_2\) 的估计值非常不确定，并且与零重叠，因此这种关系可能不是很强。最后，请注意 \(\gamma_2\) 估计的是铀效应以外的其他东西，因为这已经由 \(\gamma_1\) 考虑在内——它回答了“一旦我们知道县内的铀水平，了解没有地下室的房屋比例是否有价值？”这个问题。

所有这一切都是为了说明我们不应该从因果关系的角度来解释这一点：没有可信的机制表明地下室（或其缺失）导致氡排放。更可能的是，我们的因果图遗漏了一些东西：一个混杂变量，一个既影响地下室建设又影响氡水平的变量，潜伏在某个黑暗的角落……也许是土壤类型，它可能会影响建造哪种类型的建筑物以及氡的水平？也许将此添加到我们的模型中将有助于因果推断。

预测

Gelman [2006] 使用交叉验证测试来检查未汇集、汇集和部分汇集模型的预测误差。

均方根交叉验证预测误差:

• 未汇集 = 0.86

• 汇集 = 0.84

• 多层级 = 0.79

在多层级模型中可以进行两种类型的预测。

1. 现有组内的新个体

2. 新组内的新个体

例如，如果我们想预测圣路易斯和卡纳贝克县一栋没有地下室的新房子的氡含量，我们只需要从具有适当截距的氡模型中采样。

也就是说，

\[\tilde{y}_i \sim N(\alpha_{69} + \beta (x_i=1), \sigma_y^2)\]

因为我们之前明智地将县索引和楼层值设置为共享变量，所以我们可以直接将它们修改为所需的值（分别为 69 和 1），并采样相应的后验预测，而无需重新定义和重新编译我们的模型。使用上面的模型

prediction_coords = {"obs_id": ["ST LOUIS", "KANABEC"]}
with contextual_effect:
    pm.set_data({"county_idx": np.array([69, 31]), "floor_idx": np.array([1, 1]), "y": np.ones(2)})
    stl_pred = pm.sample_posterior_predictive(contextual_effect_trace.posterior)

contextual_effect_trace.extend(stl_pred)

Sampling: [y_like]

100.00% [4000/4000 00:00<00:00]

az.plot_posterior(contextual_effect_trace, group="posterior_predictive");

多层级模型的优势

• 考虑观测数据的自然层级结构。

• 估计（代表性不足）组的系数。

• 在估计组级系数时，结合个体和组级信息。

• 允许个体层级系数在组之间变化。

作为解决此问题的层级建模的替代方法，请查看用于模拟氡水平的地理空间方法。

参考文献

[1]

Richard McElreath. Statistical rethinking: A Bayesian course with examples in R and Stan. Chapman and Hall/CRC, 2018.

[2]

Andrew Gelman and Jennifer Hill. Data analysis using regression and multilevel/hierarchical models. Cambridge university press, 2006.

[3]

Andrew Gelman. Multilevel (hierarchical) modeling: what it can and cannot do. Technometrics, 48(3):432–435, 2006.

作者

• Authored by Chris Fonnesbeck in May, 2017 (pymc#2124)

• Updated by Colin Carroll in June, 2018 (pymc#3049)

• Updated by Alex Andorra in January, 2020 (pymc#3765)

• Updated by Oriol Abril in June, 2020 (pymc#3963)

• Updated by Farhan Reynaldo in November 2021 (pymc-examples#246)

• Updated by Chris Fonnesbeck in Februry 2022 (pymc-examples#285)

• Updated by Chris Fonnesbeck in November 2022 (pymc-examples#468)

• Updated by Oriol Abril in November 2022 (pymc-examples#473)

Watermark

%load_ext watermark
%watermark -n -u -v -iv -w

Last updated: Wed Dec 07 2022

Python implementation: CPython
Python version       : 3.9.10
IPython version      : 8.7.0

arviz     : 0.14.0
xarray    : 2022.12.0
pymc      : 4.4.0
matplotlib: 3.6.2
pandas    : 1.5.2
seaborn   : 0.12.1
numpy     : 1.21.6
pytensor    : 2.8.7

Watermark: 2.3.0

许可声明

本示例库中的所有笔记本均根据 MIT 许可证 提供，该许可证允许修改和再分发以用于任何用途，前提是保留版权和许可声明。

引用 PyMC 示例

要引用此笔记本，请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。

重要

许多笔记本都改编自其他来源：博客、书籍…… 在这种情况下，您也应该引用原始来源。

还要记得引用您的代码使用的相关库。

这是一个 bibtex 中的引用模板

@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}

渲染后可能看起来像