离散变量的自动边缘化#

PyMC 非常适合对带有离散潜在变量的模型进行采样。但是，如果您坚持只使用 NUTS 采样器，您需要以某种方式去除您的离散变量。最好的方法是将它们边缘化，这样您就可以从 Rao-Blackwell 定理中受益，并获得参数的较低方差估计。

形式上，论证如下：采样器可以理解为近似期望 \(\mathbb{E}_{p(x, z)}[f(x, z)]\)，其中 \(f\) 是某个函数，而 \(p(x, z)\) 是一个分布。根据 全期望定律，我们知道：

\[ \mathbb{E}_{p(x, z)}[f(x, z)] = \mathbb{E}_{p(z)}\left[\mathbb{E}_{p(x \mid z)}\left[f(x, z)\right]\right] \]

令 \(g(z) = \mathbb{E}_{p(x \mid z)}\left[f(x, z)\right]\)，根据 全方差定律，我们知道：

\[ \mathbb{V}_{p(x, z)}[f(x, z)] = \mathbb{V}_{p(z)}[g(z)] + \mathbb{E}_{p(z)}\left[\mathbb{V}_{p(x \mid z)}\left[f(x, z)\right]\right] \]

因为期望是对方差求取的，所以它必须始终为正，因此我们知道

\[ \mathbb{V}_{p(x, z)}[f(x, z)] \geq \mathbb{V}_{p(z)}[g(z)] \]

直观地看，对模型中的变量进行边缘化处理使您可以使用 \(g\) 而不是 \(f\)。这种较低的方差最直接地体现在较低的蒙特卡洛标准误差 (mcse) 中，并间接体现在通常更高的有效样本量 (ESS) 中。

不幸的是，执行此计算通常很繁琐且不直观。幸运的是，pymc-experimental 现在支持一种自动执行此工作的方法！

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pytensor.tensor as pt

注意

此笔记本使用非 PyMC 依赖库，因此需要专门安装才能运行此笔记本。打开下面的下拉菜单以获取更多指导。

附加依赖库安装说明

为了运行此笔记本（在本地或 binder 上），您不仅需要安装可用的 PyMC 以及所有可选依赖项，还需要安装一些额外的依赖项。有关安装 PyMC 本身的建议，请参阅 安装

您可以使用您喜欢的包管理器安装这些依赖项，我们下面提供了 pip 和 conda 命令作为示例。

$ pip install pymc-experimental

请注意，如果您想（或需要）从笔记本内部而不是命令行安装软件包，您可以通过运行 pip 命令的变体来安装软件包

import sys

!{sys.executable} -m pip install pymc-experimental

您不应运行 !pip install，因为它可能会将软件包安装在不同的环境中，即使安装了，也可能无法从 Jupyter 笔记本中使用。

另一种选择是使用 conda

$ conda install pymc-experimental

当使用 conda 安装科学 python 软件包时，我们建议使用 conda forge

import pymc_extras as pmx

%config InlineBackend.figure_format = 'retina'  # high resolution figures
az.style.use("arviz-darkgrid")
rng = np.random.default_rng(32)

作为一个激励性的例子，考虑一个高斯混合模型

高斯混合模型#

有两种方法可以指定相同的模型。一种是明确指定混合的选择。

mu = pt.as_tensor([-2.0, 2.0])

with pm.Model() as explicit_mixture:
    idx = pm.Bernoulli("idx", 0.7)
    y = pm.Normal("y", mu=mu[idx], sigma=1.0)

plt.hist(pm.draw(y, draws=2000, random_seed=rng), bins=30, rwidth=0.9);
../_images/3575ef5cfcc8694380ccbedb0dabf1a6e320c6fa24e66910cb4e66b6c5f4caa4.png

另一种方法是我们使用内置的 NormalMixture 分布。在这里，混合分配不是我们模型中的显式变量。第一个模型没有什么特别之处，除了我们使用 pmx.MarginalModel 而不是 pm.Model 初始化它。这个不同的类将允许我们稍后边缘化变量。

with pm.Model() as prebuilt_mixture:
    y = pm.NormalMixture("y", w=[0.3, 0.7], mu=[-2, 2])

plt.hist(pm.draw(y, draws=2000, random_seed=rng), bins=30, rwidth=0.9);
../_images/47df6eb41fffc6c49b7c5df063d4a1157499ffd7804e2eb78b23f8c63165902c.png 
with prebuilt_mixture:
    idata = pm.sample(draws=2000, chains=4, random_seed=rng)

az.summary(idata)

Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 2 jobs)
NUTS: [y]
/home/zv/upstream/miniconda3/envs/pymc-dev/lib/python3.11/multiprocessing/popen_fork.py:66: RuntimeWarning: os.fork() was called. os.fork() is incompatible with multithreaded code, and JAX is multithreaded, so this will likely lead to a deadlock.
  self.pid = os.fork()

/home/zv/upstream/miniconda3/envs/pymc-dev/lib/python3.11/multiprocessing/popen_fork.py:66: RuntimeWarning: os.fork() was called. os.fork() is incompatible with multithreaded code, and JAX is multithreaded, so this will likely lead to a deadlock.
  self.pid = os.fork()





Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 14 seconds.
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details
The effective sample size per chain is smaller than 100 for some parameters.  A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details













mean
sd
hdi_3%
hdi_97%
mcse_mean
mcse_sd
ess_bulk
ess_tail
r_hat






y
0.854
2.059
-3.214
3.704
0.137
0.097
288.0
1919.0
1.02














with explicit_mixture:
    idata = pm.sample(draws=2000, chains=4, random_seed=rng)

az.summary(idata)









Multiprocess sampling (4 chains in 2 jobs)
CompoundStep
>BinaryGibbsMetropolis: [idx]
>NUTS: [y]
/home/zv/upstream/miniconda3/envs/pymc-dev/lib/python3.11/multiprocessing/popen_fork.py:66: RuntimeWarning: os.fork() was called. os.fork() is incompatible with multithreaded code, and JAX is multithreaded, so this will likely lead to a deadlock.
  self.pid = os.fork()





/home/zv/upstream/miniconda3/envs/pymc-dev/lib/python3.11/multiprocessing/popen_fork.py:66: RuntimeWarning: os.fork() was called. os.fork() is incompatible with multithreaded code, and JAX is multithreaded, so this will likely lead to a deadlock.
  self.pid = os.fork()









Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 19 seconds.
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details
The effective sample size per chain is smaller than 100 for some parameters.  A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details













mean
sd
hdi_3%
hdi_97%
mcse_mean
mcse_sd
ess_bulk
ess_tail
r_hat






idx
0.738
0.440
0.00
1.000
0.027
0.019
263.0
263.0
1.02




y
0.953
2.015
-3.18
3.714
0.116
0.082
404.0
1229.0
1.02










我们可以立即看到，边缘化模型的 ESS 更高。现在让我们边缘化选择，看看它在我们的模型中发生了什么变化。






explicit_mixture_marginalized = pmx.marginalize(explicit_mixture, ["idx"])

with explicit_mixture_marginalized:
    idata = pm.sample(draws=2000, chains=4, random_seed=rng)

az.summary(idata)









Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 2 jobs)
NUTS: [y]
/home/zv/upstream/miniconda3/envs/pymc-dev/lib/python3.11/multiprocessing/popen_fork.py:66: RuntimeWarning: os.fork() was called. os.fork() is incompatible with multithreaded code, and JAX is multithreaded, so this will likely lead to a deadlock.
  self.pid = os.fork()





/home/zv/upstream/miniconda3/envs/pymc-dev/lib/python3.11/multiprocessing/popen_fork.py:66: RuntimeWarning: os.fork() was called. os.fork() is incompatible with multithreaded code, and JAX is multithreaded, so this will likely lead to a deadlock.
  self.pid = os.fork()









Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 21 seconds.













mean
sd
hdi_3%
hdi_97%
mcse_mean
mcse_sd
ess_bulk
ess_tail
r_hat






y
0.837
2.062
-3.154
3.711
0.09
0.063
742.0
2676.0
1.0










正如我们所见，idx 变量现在消失了。我们也能够使用 NUTS 采样器，并且 ESS 有所提高。


但是 MarginalModel 有一个明显的优势。它仍然知道被边缘化的离散变量，并且我们可以获得给定其他变量的 idx 后验估计。我们使用 recover_marginals 方法来做到这一点。






idata = pmx.recover_marginals(explicit_mixture_marginalized, idata, random_seed=rng);













az.summary(idata)

















mean
sd
hdi_3%
hdi_97%
mcse_mean
mcse_sd
ess_bulk
ess_tail
r_hat






y
0.837
2.062
-3.154
3.711
0.090
0.063
742.0
2676.0
1.00




idx
0.706
0.456
0.000
1.000
0.021
0.015
457.0
457.0
1.01




lp_idx[0]
-6.303
5.195
-14.387
-0.000
0.201
0.142
742.0
2676.0
1.00




lp_idx[1]
-2.109
3.814
-10.204
-0.000
0.159
0.113
742.0
2676.0
1.00










这个 idx 变量使我们能够在运行 NUTS 采样器后恢复混合分配变量！我们可以通过从每个样本的关联 idx 中读取混合标签来分离出 y 的样本。






# fmt: off
post = idata.posterior
plt.hist(
    post.where(post.idx == 0).y.values.reshape(-1),
    bins=30,
    rwidth=0.9,
    alpha=0.75,
    label='idx = 0',
)
plt.hist(
    post.where(post.idx == 1).y.values.reshape(-1),
    bins=30,
    rwidth=0.9,
    alpha=0.75,
    label='idx = 1'
)
# fmt: on
plt.legend();








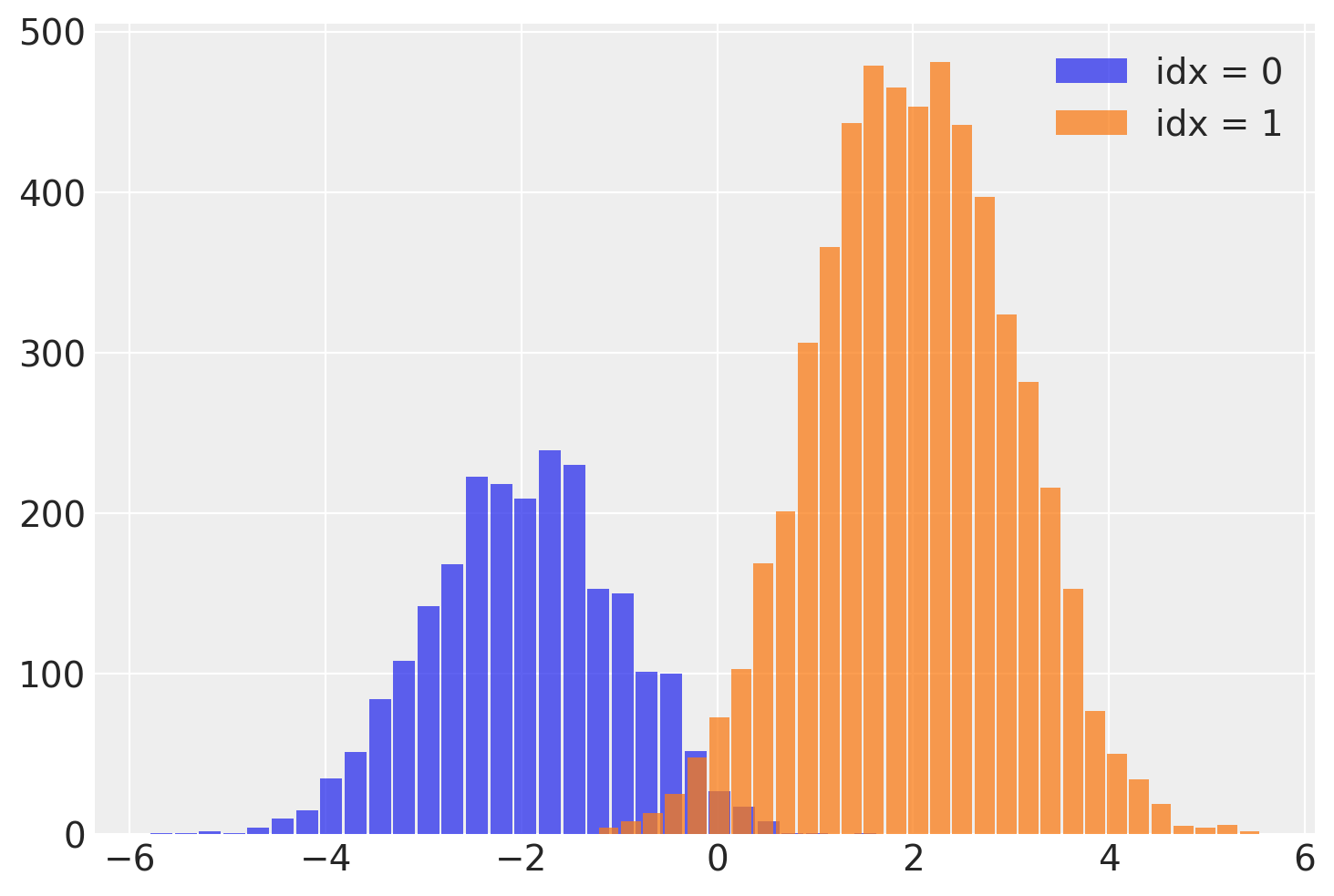
../_images/ea6a8032ad8ae2ce8117e55bbcf8e285d3d8732008abc169ec611fd642509806.png





需要注意的一个重要事项是，这个离散变量的 ESS 较低，尤其是尾部。这意味着 idx 可能无法很好地估计，特别是对于尾部。如果这很重要，我建议使用 lp_idx，它是给定每次迭代的样本值的 idx 的对数概率。在下一个示例中将进一步探讨使用 lp_idx 的好处。






煤矿模型#


相同的方法也适用于 煤矿 转换点模型。煤矿数据集记录了 1851 年至 1962 年间英国发生的煤矿灾难次数。时间序列数据集捕获了引入矿山安全法规的时间，我们尝试使用离散的 switchpoint 变量来估计发生的时间。






# fmt: off
disaster_data = pd.Series(
    [4, 5, 4, 0, 1, 4, 3, 4, 0, 6, 3, 3, 4, 0, 2, 6,
    3, 3, 5, 4, 5, 3, 1, 4, 4, 1, 5, 5, 3, 4, 2, 5,
    2, 2, 3, 4, 2, 1, 3, np.nan, 2, 1, 1, 1, 1, 3, 0, 0,
    1, 0, 1, 1, 0, 0, 3, 1, 0, 3, 2, 2, 0, 1, 1, 1,
    0, 1, 0, 1, 0, 0, 0, 2, 1, 0, 0, 0, 1, 1, 0, 2,
    3, 3, 1, np.nan, 2, 1, 1, 1, 1, 2, 4, 2, 0, 0, 1, 4,
    0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1]
)

# fmt: on
years = np.arange(1851, 1962)

with pm.Model() as disaster_model:
    switchpoint = pm.DiscreteUniform("switchpoint", lower=years.min(), upper=years.max())
    early_rate = pm.Exponential("early_rate", 1.0)
    late_rate = pm.Exponential("late_rate", 1.0)
    rate = pm.math.switch(switchpoint >= years, early_rate, late_rate)
    disasters = pm.Poisson("disasters", rate, observed=disaster_data)









/home/zv/upstream/miniconda3/envs/pymc-dev/lib/python3.11/site-packages/pymc/model/core.py:1288: RuntimeWarning: invalid value encountered in cast
  data = convert_observed_data(data).astype(rv_var.dtype)
/home/zv/upstream/miniconda3/envs/pymc-dev/lib/python3.11/site-packages/pymc/model/core.py:1302: ImputationWarning: Data in disasters contains missing values and will be automatically imputed from the sampling distribution.
  warnings.warn(impute_message, ImputationWarning)









我们将在边缘化 switchpoint 变量之前和之后对模型进行采样






with disaster_model:
    before_marg = pm.sample(chains=2, random_seed=rng)

disaster_model_marginalized = pmx.marginalize(disaster_model, ["switchpoint"])

with disaster_model_marginalized:
    after_marg = pm.sample(chains=2, random_seed=rng)









Multiprocess sampling (2 chains in 2 jobs)
CompoundStep
>CompoundStep
>>Metropolis: [switchpoint]
>>Metropolis: [disasters_unobserved]
>NUTS: [early_rate, late_rate]
/home/zv/upstream/miniconda3/envs/pymc-dev/lib/python3.11/multiprocessing/popen_fork.py:66: RuntimeWarning: os.fork() was called. os.fork() is incompatible with multithreaded code, and JAX is multithreaded, so this will likely lead to a deadlock.
  self.pid = os.fork()





/home/zv/upstream/miniconda3/envs/pymc-dev/lib/python3.11/multiprocessing/popen_fork.py:66: RuntimeWarning: os.fork() was called. os.fork() is incompatible with multithreaded code, and JAX is multithreaded, so this will likely lead to a deadlock.
  self.pid = os.fork()









Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 13 seconds.
We recommend running at least 4 chains for robust computation of convergence diagnostics
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details
The effective sample size per chain is smaller than 100 for some parameters.  A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details
/home/zv/upstream/pymc-extras/pymc_extras/model/marginal/distributions.py:297: NonSeparableLogpWarning: There are multiple dependent variables in a FiniteDiscreteMarginalRV. Their joint logp terms will be assigned to the first value: [4 5 4 0 1 ... 0 0 1 0 1].
  warn_non_separable_logp(values)
/home/zv/upstream/pymc-extras/pymc_extras/model/marginal/distributions.py:297: NonSeparableLogpWarning: There are multiple dependent variables in a FiniteDiscreteMarginalRV. Their joint logp terms will be assigned to the first value: [4 5 4 0 1 ... 0 0 1 0 1].
  warn_non_separable_logp(values)
/home/zv/upstream/pymc-extras/pymc_extras/model/marginal/distributions.py:297: NonSeparableLogpWarning: There are multiple dependent variables in a FiniteDiscreteMarginalRV. Their joint logp terms will be assigned to the first value: [4 5 4 0 1 ... 0 0 1 0 1].
  warn_non_separable_logp(values)
Multiprocess sampling (2 chains in 2 jobs)
CompoundStep
>NUTS: [late_rate, early_rate]
>Metropolis: [disasters_unobserved]
/home/zv/upstream/miniconda3/envs/pymc-dev/lib/python3.11/multiprocessing/popen_fork.py:66: RuntimeWarning: os.fork() was called. os.fork() is incompatible with multithreaded code, and JAX is multithreaded, so this will likely lead to a deadlock.
  self.pid = os.fork()





/home/zv/upstream/miniconda3/envs/pymc-dev/lib/python3.11/multiprocessing/popen_fork.py:66: RuntimeWarning: os.fork() was called. os.fork() is incompatible with multithreaded code, and JAX is multithreaded, so this will likely lead to a deadlock.
  self.pid = os.fork()









Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 36 seconds.
We recommend running at least 4 chains for robust computation of convergence diagnostics
The effective sample size per chain is smaller than 100 for some parameters.  A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details













az.summary(before_marg, var_names=["~disasters"], filter_vars="like")

















mean
sd
hdi_3%
hdi_97%
mcse_mean
mcse_sd
ess_bulk
ess_tail
r_hat






early_rate
3.090
0.278
2.594
3.630
0.009
0.006
1022.0
1049.0
1.0




late_rate
0.937
0.117
0.718
1.151
0.003
0.002
1239.0
1443.0
1.0




switchpoint
1889.785
2.581
1885.000
1894.000
0.204
0.145
164.0
275.0
1.0














az.summary(after_marg, var_names=["~disasters"], filter_vars="like")

















mean
sd
hdi_3%
hdi_97%
mcse_mean
mcse_sd
ess_bulk
ess_tail
r_hat






early_rate
3.078
0.284
2.577
3.653
0.006
0.005
2036.0
1344.0
1.0




late_rate
0.929
0.115
0.714
1.146
0.003
0.002
1303.0
1228.0
1.0










和以前一样，ESS 大幅提高


最后，让我们恢复 switchpoint 变量






after_marg = pmx.recover_marginals(disaster_model_marginalized, after_marg);













az.summary(after_marg, var_names=["~disasters", "~lp"], filter_vars="like")

















mean
sd
hdi_3%
hdi_97%
mcse_mean
mcse_sd
ess_bulk
ess_tail
r_hat






early_rate
3.078
0.284
2.577
3.653
0.006
0.005
2036.0
1344.0
1.0




late_rate
0.929
0.115
0.714
1.146
0.003
0.002
1303.0
1228.0
1.0




switchpoint
1889.812
2.434
1885.000
1893.000
0.108
0.077
494.0
1302.0
1.0










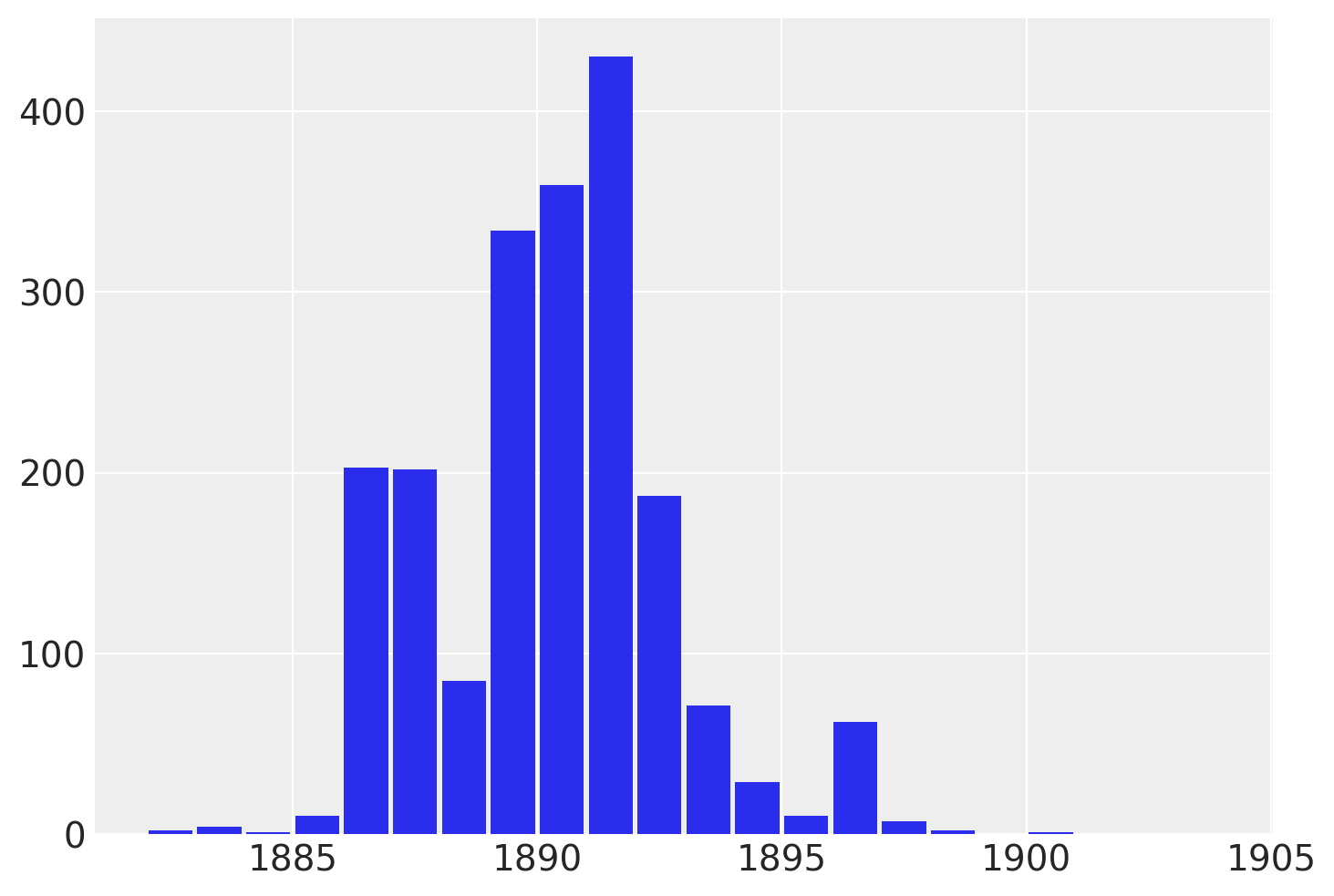
虽然 recover_marginals 能够对被边缘化的离散变量进行采样。但与每次抽取相关的概率通常可以提供更清晰的离散变量估计。特别是对于较低的概率值。通过比较采样值的直方图与对数概率图，可以最好地说明这一点。






post = after_marg.posterior.switchpoint.values.reshape(-1)
bins = np.arange(post.min(), post.max())
plt.hist(post, bins, rwidth=0.9);








../_images/11f33360da554e7af43050dc5ea222026e98c5c1be9866f402e57fb409e40d39.png









lp_switchpoint = after_marg.posterior.lp_switchpoint.mean(dim=["chain", "draw"])
x_max = years[lp_switchpoint.argmax()]

plt.scatter(years, lp_switchpoint)
plt.axvline(x=x_max, c="orange")
plt.xlabel(r"$\mathrm{year}$")
plt.ylabel(r"$\log p(\mathrm{switchpoint}=\mathrm{year})$");








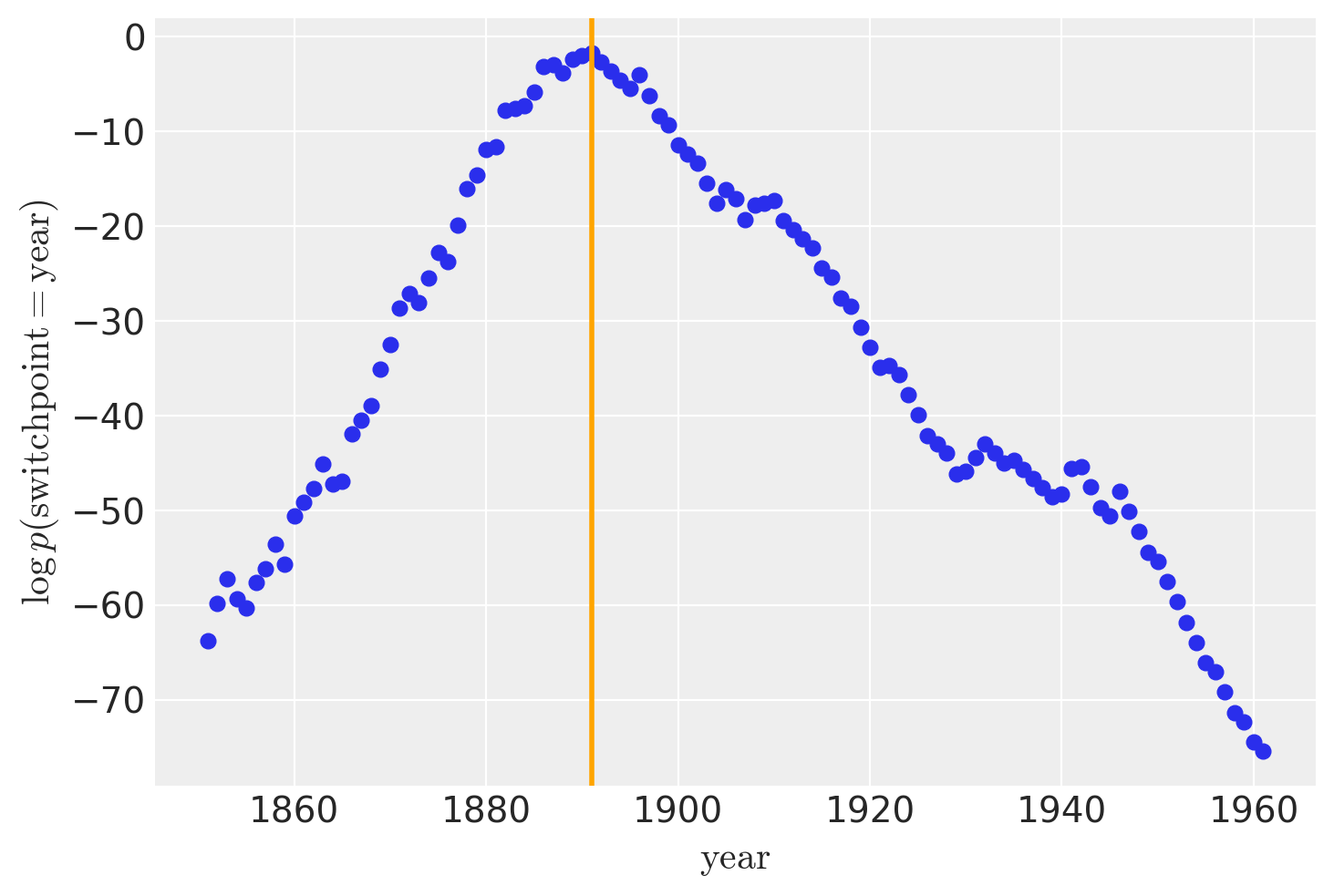
../_images/5ff3d37960b0637a2d71b63d954231646b2f2418bb89a9038e3c606ef44b06d5.png





通过绘制采样值的直方图而不是直接使用对数概率，我们对底层离散分布的探索变得更加嘈杂和不完整。






作者#







参考文献#







水印#






%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,xarray









Last updated: Sat Jan 04 2025

Python implementation: CPython
Python version       : 3.11.6
IPython version      : 8.22.2

pytensor: 2.26.4
xarray  : 2024.3.0

arviz      : 0.18.0
numpy      : 1.26.4
pymc_extras: 0.2.1
matplotlib : 3.8.4
pymc       : 5.19.1
pytensor   : 2.26.4
pandas     : 2.2.2

Watermark: 2.4.3













许可声明#


此示例库中的所有笔记本均根据 MIT 许可证 提供，该许可证允许修改和重新分发以用于任何用途，前提是保留版权和许可声明。






引用 PyMC 示例#


要引用此笔记本，请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。




重要


许多笔记本改编自其他来源：博客、书籍…… 在这种情况下，您也应该引用原始来源。


另请记住引用您的代码使用的相关库。




这是一个 bibtex 格式的引用模板


@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}





渲染后可能如下所示