import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc3 as pm
import theano

from scipy.integrate import odeint
from theano import *

THEANO_FLAGS = "optimizer=fast_compile"

print(f"PyMC3 Version: {pm.__version__}")

PyMC3 Version: 3.11.0

Lotka-Volterra 手动梯度法

作者：Sanmitra Ghosh

数学模型在各种科学和工程领域中被广泛用于模拟物理变量的时间演变。这些数学模型通常被描述为由模型结构（动力学变量的函数）和模型参数表征的 ODE。然而，对于绝大多数实际感兴趣的系统，有必要从实验观察中推断模型参数和适当的模型结构。这些实验数据通常显得稀缺且不完整。此外，大量被描述为动力系统的模型显示出草率的特征（参见 Gutenkunst 等人，2007 年），并且具有无法识别的参数组合。从实验数据中推断模型参数和结构的任务对于可靠地分析动力系统的行为并在考虑到其复杂性所带来的困难的情况下得出忠实的预测至关重要。此外，任何未来的模型预测都应包含和传播模型参数和/或结构中的可变性和不确定性。因此，推断方法也必须能够量化和传播从模型描述到模型预测的上述不确定性。作为处理不确定性的自然选择，至少在参数方面，贝叶斯推断越来越多地用于将 ODE 模型拟合到实验数据（Mark Girolami，2008 年）。然而，由于我上面指出的一些困难，使用贝叶斯推断拟合 ODE 模型是一项具有挑战性的任务。在本教程中，我将接受这一挑战，并将展示 PyMC3 如何潜在地用于此目的。

我必须指出，模型拟合（未知参数的推断）只是建模者为了更深入地了解物理过程而必须完成的众多关键任务之一。然而，这项任务的成功至关重要，而这正是 PyMC3 和概率编程 (ppl) 通常非常有用的地方。建模者可以充分利用 PyMC3 提供的各种采样器和分布来自动化推断。

在本教程中，我将重点关注拟合练习，即估计给定一些噪声实验时间序列的参数的后验分布。

ODE 参数的贝叶斯推断

我首先介绍耦合非线性 ODE 中推断的贝叶斯框架，定义如下

\[ \frac{d X(t)}{dt}=\boldsymbol{f}\big(X(t),\boldsymbol{\theta}\big), \]

其中 \(X(t)\in\mathbb{R}^K\) 是由 \(K\) 个耦合 ODE 组成的系统在每个时间点的解 - 状态向量 - 而 \(\boldsymbol{\theta}\in\mathbb{R}^D\) 是我们希望推断的参数向量。\(\boldsymbol{f}(\cdot)\) 是描述控制动力学的非线性函数。此外，在初值问题的情况下，令矩阵 \(\boldsymbol{X}(\boldsymbol{\theta}, \mathbf{x_0})\) 表示上述方程组在某些指定时间点对于参数 \(\boldsymbol{\theta}\) 和初始条件 \(\mathbf{x_0}\) 的解。

考虑一组噪声实验观测 \(\boldsymbol{Y} \in \mathbb{R}^{T\times K}\)，在 \(T\) 个实验时间点观察到 \(K\) 个状态。我们可以获得似然函数 \(p(\boldsymbol{Y}|\boldsymbol{X})\)，其中我使用符号 \(\boldsymbol{X}:=\boldsymbol{X}(\boldsymbol{\theta}, \mathbf{x_0})\)，并将其与参数的先验分布 \(p(\boldsymbol{\theta})\) 结合使用贝叶斯定理，以获得后验分布，如下所示

\[ p(\boldsymbol{\theta}|\boldsymbol{Y})=\frac{1}{Z}p(\boldsymbol{Y}|\boldsymbol{X})p(\boldsymbol{\theta}), \]

其中 \(Z=\int p(\boldsymbol{Y}|\boldsymbol{X})p(\boldsymbol{\theta}) d\boldsymbol{\theta} \) 是难以处理的边缘似然函数。由于这种难处理性，我们求助于近似推断并应用 MCMC。

对于本教程，我选择了两个 ODE

1. Lotka-Volterra 捕食者-猎物模型

2. Fitzhugh-Nagumo 动作电位模型

我将展示 PyMC3 支持的两种独特方法（NUTS 和 SMC 步进方法），用于估计这些模型中的未知参数。

Lotka-Volterra 捕食者-猎物模型

Lotka Volterra 模型描述了一个生态系统，用于描述捕食者和猎物物种之间的相互作用。这个 ODE 由下式给出

\[\begin{split} \begin{aligned} \frac{d x}{dt} &=\alpha x -\beta xy \\ \frac{d y}{dt} &=-\gamma y + \delta xy, \end{aligned} \end{split}\]

显示极限环行为，并且经常用于贝叶斯推断方法的基准测试。\(\boldsymbol{\theta}=(\alpha,\beta,\gamma,\delta, x(0),y(0))\) 是我们希望从状态向量 \(X(t)=(x(t),y(t))\) 的实验观察中推断出的未知参数集，状态向量包括猎物和捕食物种的浓度。\(x(0), y(0)\) 是求解 ODE 所需的状态的初始值，也被视为未知量。捕食者-猎物模型最近被用于演示 NUTS 采样器以及 Stan ppl 通常在 ODE 模型中推断的适用性。我将密切关注 这个 Stan 教程，因此我将完全按照 Stan 教程的方式设置此模型和相关的推断问题（包括数据）。首先让我写下代码，使用 SciPy 的 odeint 求解此 ODE。请注意，本教程中的方法不限于或绑定到 odeint。这里我选择 odeint 只是为了保持在 PyMC3 的依赖项（在本例中为 SciPy）内。

class LotkaVolterraModel:
    def __init__(self, y0=None):
        self._y0 = y0

    def simulate(self, parameters, times):
        alpha, beta, gamma, delta, Xt0, Yt0 = [x for x in parameters]

        def rhs(y, t, p):
            X, Y = y
            dX_dt = alpha * X - beta * X * Y
            dY_dt = -gamma * Y + delta * X * Y
            return dX_dt, dY_dt

        values = odeint(rhs, [Xt0, Yt0], times, (parameters,))
        return values


ode_model = LotkaVolterraModel()

处理 ODE 梯度

NUTS 需要目标密度相对于未知参数的对数梯度，\(\nabla_{\boldsymbol{\theta}}p(\boldsymbol{\theta}|\boldsymbol{Y})\)，可以使用微分的链式法则进行评估，如下所示

\[ \nabla_{\boldsymbol{\theta}}p(\boldsymbol{\theta}|\boldsymbol{Y}) = \frac{\partial p(\boldsymbol{\theta}|\boldsymbol{Y})}{\partial \boldsymbol{X}}^T \frac{\partial \boldsymbol{X}}{\partial \boldsymbol{\theta}}.\]

ODE 相对于其参数的梯度，项 \(\frac{\partial \boldsymbol{X}}{\partial \boldsymbol{\theta}}\)，可以使用局部敏感性分析获得，尽管这不是获得梯度的唯一方法。然而，就像求解 ODE（精确地说是非线性 ODE）一样，梯度的评估只能使用某种数值方法进行，例如著名的 Runge-Kutta 方法用于非刚性 ODE。PyMC3 使用 Theano 作为自动微分引擎，因此所有模型都是通过将 Theano 支持的可用原始操作 (Ops) 缝合在一起实现的。即使扩展 PyMC3，我们也需要组合可以表示为 Theano Ops 的符号组合的模型。然而，如果我们退一步思考 Theano，那么很明显，ODE 解及其相对于参数的梯度都不能符号化地表示为 Theano 原始 Ops 的组合。因此，从 Theano 的角度来看，ODE（以及就此而言的任何其他形式的非线性微分方程）是一个不可微分的黑盒函数。然而，有人可能会争辩说，如果在 Theano 中编码数值方法（例如使用 scan Op），那么可以符号化地表示评估 ODE 状态的数值方法，然后我们可以轻松地使用 Theano 的自动微分引擎，也可以通过微分数值求解器本身来获得梯度。我想指出的是，前者，获得解，确实可以通过这种方式实现，但获得的梯度将容易出错。此外，这需要完全“重新发明轮子”，因为人们必须从头开始在 Theano 中重新实现数十年前复杂的数值算法。

因此，在本教程中，我将介绍另一种方法，该方法包括定义新的 自定义 Theano Ops，扩展 Theano，它将包装数值解和向量-矩阵乘积，\( \frac{\partial p(\boldsymbol{\theta}|\boldsymbol{Y})}{\partial \boldsymbol{X}}^T \frac{\partial \boldsymbol{X}}{\partial \boldsymbol{\theta}}\)，在自动微分文献中通常称为向量-雅可比积 (VJP)。我想在此指出，在非线性 ODE 的上下文中，术语雅可比矩阵用于表示 ODE 动力学 \(\boldsymbol{f}\) 相对于 ODE 状态 \(X(t)\) 的梯度。因此，为了避免混淆，从现在开始我将使用术语向量-灵敏度积 (VSP) 来表示与术语 VJP 表示的相同量。

我将从介绍前向灵敏度分析开始。

ODE 灵敏度分析

对于耦合 ODE 系统 \(\frac{d X(t)}{dt} = \boldsymbol{f}(X(t),\boldsymbol{\theta})\)，解对参数的局部灵敏度由解随参数变化的变化量定义，即第 \(k\) 个状态的灵敏度简单来说就是其相对于第 \(d\) 个参数的梯度的时间演变。此量表示为 \(Z_{kd}(t)\)，由下式给出

\[Z_{kd}(t)=\frac{d }{d t} \left\{\frac{\partial X_k (t)}{\partial \theta_d}\right\} = \sum_{i=1}^K \frac{\partial f_k}{\partial X_i (t)}\frac{\partial X_i (t)}{\partial \theta_d} + \frac{\partial f_k}{\partial \theta_d}.\]

使用前向灵敏度分析，我们可以通过将原始 ODE 系统与灵敏度方程 \(Z_{kd}\) 扩充，获得每个时间点的状态 \(X(t)\) 及其相对于参数的导数，作为初值问题的解。然后可以使用选择的数值方法一起求解扩充的 ODE 系统 \(\big(X(t), Z(t)\big)\)。扩充的 ODE 系统需要灵敏度方程的初始值。所有这些都应设置为零，除了寻求状态相对于自身初始值的灵敏度的那些，即 \( \frac{\partial X_k(t)}{\partial X_k (0)} =1 \)。请注意，为了求解这个扩充系统，我们必须着手推导 \( \frac{\partial f_k}{\partial X_i (t)}\)（也称为 ODE 的雅可比矩阵）和 \(\frac{\partial f_k}{\partial \theta_d}\) 项的繁琐过程。值得庆幸的是，许多 ODE 求解器在用户要求时会计算这些项并求解扩充系统。一个例子是 SUNDIAL CVODES 求解器套件。CVODES 的 Python 包装器可以在 此处 找到。

但是，对于本教程，我将继续手动推导上述项，并在以下代码块中求解 Lotka-Volterra ODE 以及灵敏度。下面的函数 jac 和 dfdp 分别计算 Lotka-Volterra 模型的 \( \frac{\partial f_k}{\partial X_i (t)}\) 和 \(\frac{\partial f_k}{\partial \theta_d}\)。为了方便起见，我将灵敏度方程转换为矩阵形式。这里我扩展了上面的求解器代码片段，以在要求时包括灵敏度。

n_states = 2
n_odeparams = 4
n_ivs = 2


class LotkaVolterraModel:
    def __init__(self, n_states, n_odeparams, n_ivs, y0=None):
        self._n_states = n_states
        self._n_odeparams = n_odeparams
        self._n_ivs = n_ivs
        self._y0 = y0

    def simulate(self, parameters, times):
        return self._simulate(parameters, times, False)

    def simulate_with_sensitivities(self, parameters, times):
        return self._simulate(parameters, times, True)

    def _simulate(self, parameters, times, sensitivities):
        alpha, beta, gamma, delta, Xt0, Yt0 = [x for x in parameters]

        def r(y, t, p):
            X, Y = y
            dX_dt = alpha * X - beta * X * Y
            dY_dt = -gamma * Y + delta * X * Y
            return dX_dt, dY_dt

        if sensitivities:

            def jac(y):
                X, Y = y
                ret = np.zeros((self._n_states, self._n_states))
                ret[0, 0] = alpha - beta * Y
                ret[0, 1] = -beta * X
                ret[1, 0] = delta * Y
                ret[1, 1] = -gamma + delta * X
                return ret

            def dfdp(y):
                X, Y = y
                ret = np.zeros(
                    (self._n_states, self._n_odeparams + self._n_ivs)
                )  # except the following entries
                ret[0, 0] = (
                    X  # \frac{\partial  [\alpha X - \beta XY]}{\partial \alpha}, and so on...
                )
                ret[0, 1] = -X * Y
                ret[1, 2] = -Y
                ret[1, 3] = X * Y

                return ret

            def rhs(y_and_dydp, t, p):
                y = y_and_dydp[0 : self._n_states]
                dydp = y_and_dydp[self._n_states :].reshape(
                    (self._n_states, self._n_odeparams + self._n_ivs)
                )
                dydt = r(y, t, p)
                d_dydp_dt = np.matmul(jac(y), dydp) + dfdp(y)
                return np.concatenate((dydt, d_dydp_dt.reshape(-1)))

            y0 = np.zeros((2 * (n_odeparams + n_ivs)) + n_states)
            y0[6] = 1.0  # \frac{\partial  [X]}{\partial Xt0} at t==0, and same below for Y
            y0[13] = 1.0
            y0[0:n_states] = [Xt0, Yt0]
            result = odeint(rhs, y0, times, (parameters,), rtol=1e-6, atol=1e-5)
            values = result[:, 0 : self._n_states]
            dvalues_dp = result[:, self._n_states :].reshape(
                (len(times), self._n_states, self._n_odeparams + self._n_ivs)
            )
            return values, dvalues_dp
        else:
            values = odeint(r, [Xt0, Yt0], times, (parameters,), rtol=1e-6, atol=1e-5)
            return values


ode_model = LotkaVolterraModel(n_states, n_odeparams, n_ivs)

对于此模型，我已将相对和绝对公差分别设置为 \(10^{-6}\) 和 \(10^{-5}\)，正如 Stan 教程中建议的那样。这将产生足够精确的解。进一步降低公差将提高精度，但会增加计算时间。关于选择和使用数值方法求解 ODE 的全面讨论超出了本教程的范围。但是，我必须指出，ODE 求解器的不准确性确实会影响似然性，并因此影响推断。对于刚性系统更是如此。我建议感兴趣的读者阅读这篇精彩的博客文章，其中针对 心脏 ODE 模型 彻底讨论了这种影响。还有一个新兴的不确定性量化领域，它解决了数值算法不精确性引起的噪声问题，概率数值。这确实是一个优雅的框架，可以在考虑来自数值 ODE 求解器的误差的同时进行推断。

自定义 ODE Op

为了定义自定义 Op，我编写了两个 theano.Op 类 ODEGradop、ODEop。ODEop 本质上包装了 ODE 解，并将被 PyMC3 调用。ODEGradop 包装了数值 VSP，然后这个 op 又在 ODEop 中的 grad 方法中使用，以返回 VSP。请注意，我们传入两个函数：state、numpy_vsp 作为各自 Ops 的参数。稍后我将定义这些函数。这些函数充当垫片，我们使用它们将状态和 VSP 的数值解的 python 代码连接到 Theano，从而连接到 PyMC3。

class ODEGradop(theano.tensor.Op):
    def __init__(self, numpy_vsp):
        self._numpy_vsp = numpy_vsp

    def make_node(self, x, g):
        x = theano.tensor.as_tensor_variable(x)
        g = theano.tensor.as_tensor_variable(g)
        node = theano.Apply(self, [x, g], [g.type()])
        return node

    def perform(self, node, inputs_storage, output_storage):
        x = inputs_storage[0]

        g = inputs_storage[1]
        out = output_storage[0]
        out[0] = self._numpy_vsp(x, g)  # get the numerical VSP


class ODEop(theano.tensor.Op):
    def __init__(self, state, numpy_vsp):
        self._state = state
        self._numpy_vsp = numpy_vsp

    def make_node(self, x):
        x = theano.tensor.as_tensor_variable(x)

        return theano.tensor.Apply(self, [x], [x.type()])

    def perform(self, node, inputs_storage, output_storage):
        x = inputs_storage[0]
        out = output_storage[0]

        out[0] = self._state(x)  # get the numerical solution of ODE states

    def grad(self, inputs, output_grads):
        x = inputs[0]
        g = output_grads[0]

        grad_op = ODEGradop(self._numpy_vsp)  # pass the VSP when asked for gradient
        grad_op_apply = grad_op(x, g)

        return [grad_op_apply]

我必须指出，在我上面定义的自定义 ODE Ops 的方式中，ODE 可能针对相同的参数值求解两次，一次用于状态，另一次用于 VSP。为了避免这种行为，我编写了一个帮助类来阻止这种双重评估。

class solveCached:
    def __init__(self, times, n_params, n_outputs):
        self._times = times
        self._n_params = n_params
        self._n_outputs = n_outputs
        self._cachedParam = np.zeros(n_params)
        self._cachedSens = np.zeros((len(times), n_outputs, n_params))
        self._cachedState = np.zeros((len(times), n_outputs))

    def __call__(self, x):
        if np.all(x == self._cachedParam):
            state, sens = self._cachedState, self._cachedSens

        else:
            state, sens = ode_model.simulate_with_sensitivities(x, times)

        return state, sens


times = np.arange(0, 21)  # number of measurement points (see below)
cached_solver = solveCached(times, n_odeparams + n_ivs, n_states)

ODE 状态和 VSP 评估

大多数实际感兴趣的 ODE 系统将具有多个状态，因此求解器的输出（我到目前为止将其表示为 \(\boldsymbol{X}\)），对于在 \(T\) 个时间点求解的具有 \(K\) 个状态的系统，将是一个 \(T \times K\) 维矩阵。对于 Lotka-Volterra 模型，此矩阵的列表示各个物种浓度的时间演变。我将此矩阵展平为 \(TK\) 维向量 \(vec(\boldsymbol{X})\)，并相应地重新排列灵敏度以获得所需的向量-矩阵乘积。此时测试自定义 Op（如 此处 所述）是有益的。

def state(x):
    State, Sens = cached_solver(np.array(x, dtype=np.float64))
    cached_solver._cachedState, cached_solver._cachedSens, cached_solver._cachedParam = (
        State,
        Sens,
        x,
    )
    return State.reshape((2 * len(State),))


def numpy_vsp(x, g):
    numpy_sens = cached_solver(np.array(x, dtype=np.float64))[1].reshape(
        (n_states * len(times), len(x))
    )
    return numpy_sens.T.dot(g)

哈德逊湾公司数据

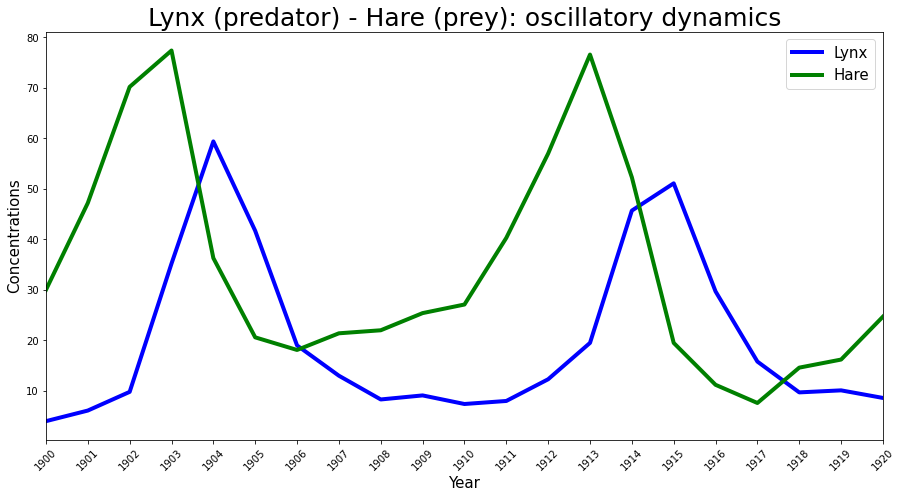
Lotka-Volterra 捕食者-猎物模型以前曾被成功用于解释捕食者和猎物自然种群的动态，例如哈德逊湾公司的猞猁和雪兔数据。这与 Stan 示例中使用的相同数据（此处 共享）相同，因此我将使用此数据集作为实验观测 \(\boldsymbol{Y}(t)\) 来推断参数。

Year = np.arange(1900, 1921, 1)
# fmt: off
Lynx = np.array([4.0, 6.1, 9.8, 35.2, 59.4, 41.7, 19.0, 13.0, 8.3, 9.1, 7.4,
                8.0, 12.3, 19.5, 45.7, 51.1, 29.7, 15.8, 9.7, 10.1, 8.6])
Hare = np.array([30.0, 47.2, 70.2, 77.4, 36.3, 20.6, 18.1, 21.4, 22.0, 25.4, 
                 27.1, 40.3, 57.0, 76.6, 52.3, 19.5, 11.2, 7.6, 14.6, 16.2, 24.7])
# fmt: on
plt.figure(figsize=(15, 7.5))
plt.plot(Year, Lynx, color="b", lw=4, label="Lynx")
plt.plot(Year, Hare, color="g", lw=4, label="Hare")
plt.legend(fontsize=15)
plt.xlim([1900, 1920])
plt.xlabel("Year", fontsize=15)
plt.ylabel("Concentrations", fontsize=15)
plt.xticks(Year, rotation=45)
plt.title("Lynx (predator) - Hare (prey): oscillatory dynamics", fontsize=25);

概率模型

我现在拥有定义 PyMC3 中概率模型所需的所有要素。正如我之前提到的，我将使用 Stan 示例中使用的完全相同的似然函数和先验来设置概率模型。观测数据定义如下

\[\log (\boldsymbol{Y(t)}) = \log (\boldsymbol{X(t)}) + \eta(t),\]

其中 \(\eta(t)\) 假设为均值为零的 i.i.d 高斯噪声，具有未知的标准差 \(\sigma\)，需要估计。上述乘法（在自然尺度上）噪声模型将对数正态分布编码为似然函数

\[\boldsymbol{Y(t)} \sim \mathcal{L}\mathcal{N}(\log (\boldsymbol{X(t)}), \sigma^2).\]

然后在参数上放置以下先验

\[\begin{split} \begin{aligned} x(0), y(0) &\sim \mathcal{L}\mathcal{N}(\log(10),1),\\ \alpha, \gamma &\sim \mathcal{N}(1,0.5),\\ \beta, \delta &\sim \mathcal{N}(0.05,0.05),\\ \sigma &\sim \mathcal{L}\mathcal{N}(-1,1). \end{aligned} \end{split}\]

对于关于先验和似然模型选择的直观解释（为了简洁起见，我省略了），我建议参考上面提到的 Stan 示例。上面的概率模型在下面的 PyMC3 中定义。请注意，展平的状态向量被重塑以匹配数据维度。

最后，我使用 pm.sample 方法默认运行 NUTS，并从后验获得 \(1500\) 个预热后样本。

theano.config.exception_verbosity = "high"
theano.config.floatX = "float64"


# Define the data matrix
Y = np.vstack((Hare, Lynx)).T

# Now instantiate the theano custom ODE op
my_ODEop = ODEop(state, numpy_vsp)

# The probabilistic model
with pm.Model() as LV_model:
    # Priors for unknown model parameters

    alpha = pm.Normal("alpha", mu=1, sigma=0.5)
    beta = pm.Normal("beta", mu=0.05, sigma=0.05)
    gamma = pm.Normal("gamma", mu=1, sigma=0.5)
    delta = pm.Normal("delta", mu=0.05, sigma=0.05)

    xt0 = pm.Lognormal("xto", mu=np.log(10), sigma=1)
    yt0 = pm.Lognormal("yto", mu=np.log(10), sigma=1)
    sigma = pm.Lognormal("sigma", mu=-1, sigma=1, shape=2)

    # Forward model
    all_params = pm.math.stack([alpha, beta, gamma, delta, xt0, yt0], axis=0)
    ode_sol = my_ODEop(all_params)
    forward = ode_sol.reshape(Y.shape)

    # Likelihood
    Y_obs = pm.Lognormal("Y_obs", mu=pm.math.log(forward), sigma=sigma, observed=Y)

    trace = pm.sample(1500, init="jitter+adapt_diag", cores=1)
trace["diverging"].sum()

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Initializing NUTS failed. Falling back to elementwise auto-assignment.
Sequential sampling (2 chains in 1 job)
CompoundStep
>CompoundStep
>>Slice: [yto]
>>Slice: [xto]
>>Slice: [delta]
>>Slice: [gamma]
>>Slice: [beta]
>>Slice: [alpha]
>NUTS: [sigma]

100.00% [2500/2500 10:54<00:00 链 0 采样，0 次发散]

/Users/CloudChaoszero/opt/anaconda3/envs/pymc3-dev-py38/lib/python3.8/site-packages/scipy/integrate/odepack.py:247: ODEintWarning: Excess work done on this call (perhaps wrong Dfun type). Run with full_output = 1 to get quantitative information.
  warnings.warn(warning_msg, ODEintWarning)

100.00% [2500/2500 11:12<00:00 链 1 采样，0 次发散]

Sampling 2 chains for 1_000 tune and 1_500 draw iterations (2_000 + 3_000 draws total) took 1327 seconds.
The rhat statistic is larger than 1.05 for some parameters. This indicates slight problems during sampling.
The estimated number of effective samples is smaller than 200 for some parameters.

0

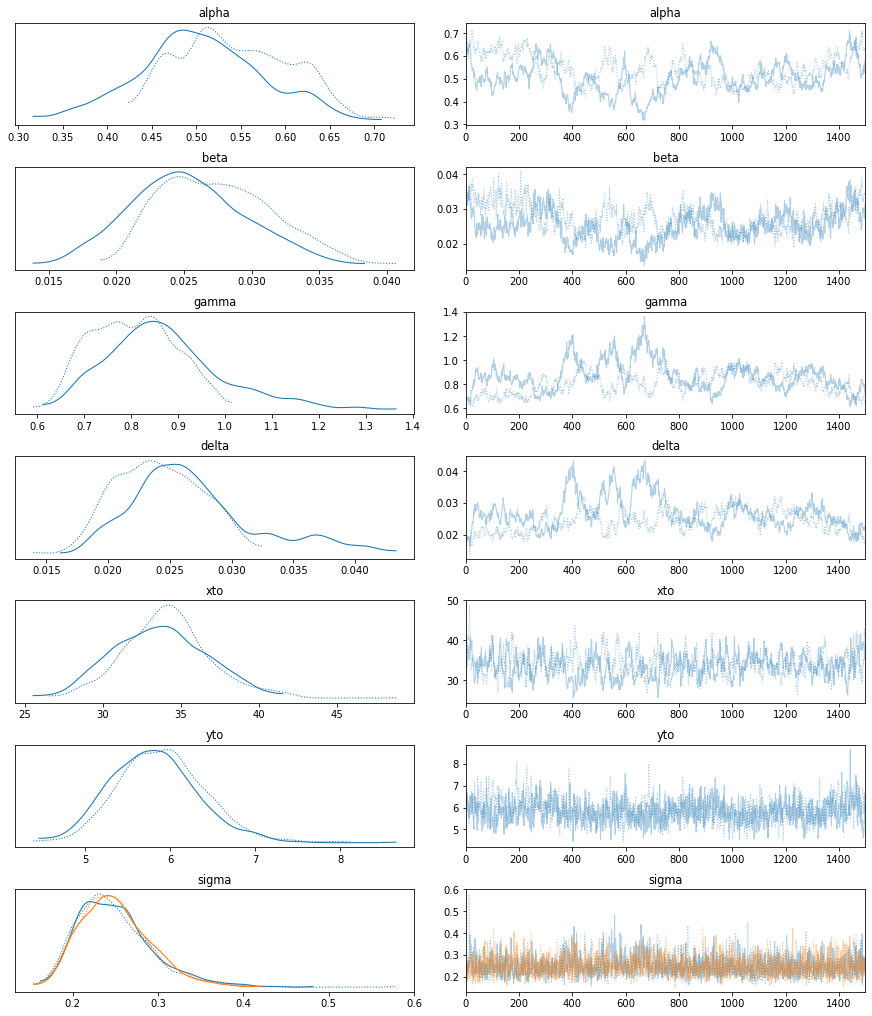
with LV_model:
    az.plot_trace(trace);

import pandas as pd

summary = az.summary(trace)
STAN_mus = [0.549, 0.028, 0.797, 0.024, 33.960, 5.949, 0.248, 0.252]
STAN_sds = [0.065, 0.004, 0.091, 0.004, 2.909, 0.533, 0.045, 0.044]
summary["STAN_mus"] = pd.Series(np.array(STAN_mus), index=summary.index)
summary["STAN_sds"] = pd.Series(np.array(STAN_sds), index=summary.index)
summary

	平均值	标准差	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_mean	ess_sd	ess_bulk	ess_tail	r_hat	STAN_mus	STAN_sds
alpha	0.524	0.069	0.403	0.653	0.017	0.012	16.0	16.0	16.0	15.0	1.12	0.549	0.065
beta	0.026	0.004	0.019	0.035	0.001	0.001	17.0	17.0	17.0	17.0	1.11	0.028	0.004
gamma	0.837	0.111	0.652	1.045	0.029	0.022	14.0	14.0	15.0	15.0	1.12	0.797	0.091
delta	0.026	0.005	0.017	0.034	0.001	0.001	12.0	11.0	16.0	17.0	1.12	0.024	0.004
xto	33.921	2.912	28.246	39.126	0.179	0.127	264.0	264.0	257.0	539.0	1.02	33.960	2.909
yto	5.857	0.515	4.873	6.783	0.039	0.028	174.0	174.0	175.0	1060.0	1.01	5.949	0.533
sigma[0]	0.249	0.044	0.173	0.330	0.002	0.001	683.0	661.0	789.0	896.0	1.00	0.248	0.045
sigma[1]	0.250	0.041	0.178	0.327	0.001	0.001	1793.0	1756.0	1864.0	1949.0	1.00	0.252	0.044

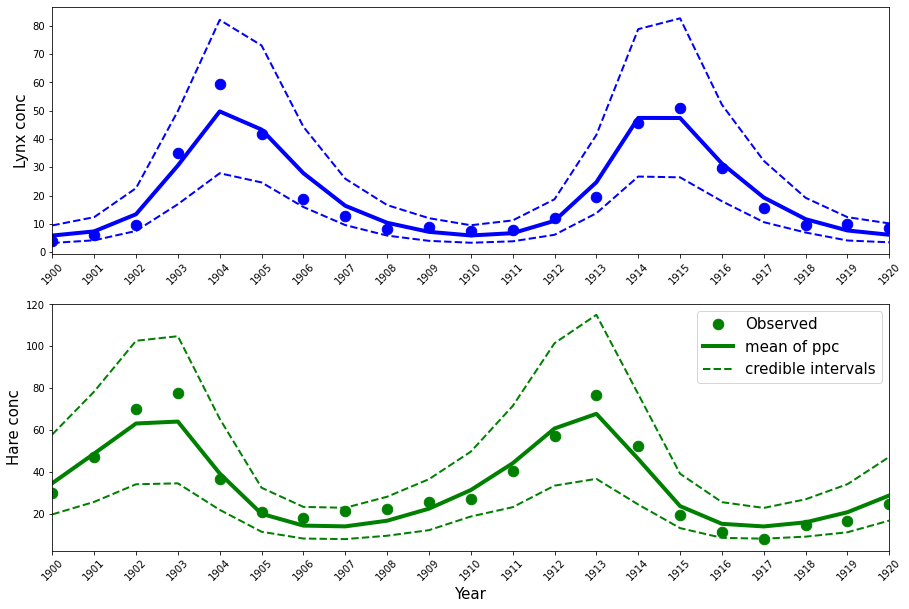
这些估计值与 Stan 教程中获得的估计值几乎相同（请参阅上面的最后两列），这是我们可以预期的。后验预测可以按如下方式绘制。

ppc_samples = pm.sample_posterior_predictive(trace, samples=1000, model=LV_model)["Y_obs"]
mean_ppc = ppc_samples.mean(axis=0)
CriL_ppc = np.percentile(ppc_samples, q=2.5, axis=0)
CriU_ppc = np.percentile(ppc_samples, q=97.5, axis=0)

/Users/CloudChaoszero/Documents/Projects-Dev/pymc3/pymc3/sampling.py:1687: UserWarning: samples parameter is smaller than nchains times ndraws, some draws and/or chains may not be represented in the returned posterior predictive sample
  warnings.warn(

100.00% [1000/1000 00:18<00:00]

plt.figure(figsize=(15, 2 * (5)))
plt.subplot(2, 1, 1)
plt.plot(Year, Lynx, "o", color="b", lw=4, ms=10.5)
plt.plot(Year, mean_ppc[:, 1], color="b", lw=4)
plt.plot(Year, CriL_ppc[:, 1], "--", color="b", lw=2)
plt.plot(Year, CriU_ppc[:, 1], "--", color="b", lw=2)
plt.xlim([1900, 1920])
plt.ylabel("Lynx conc", fontsize=15)
plt.xticks(Year, rotation=45)
plt.subplot(2, 1, 2)
plt.plot(Year, Hare, "o", color="g", lw=4, ms=10.5, label="Observed")
plt.plot(Year, mean_ppc[:, 0], color="g", lw=4, label="mean of ppc")
plt.plot(Year, CriL_ppc[:, 0], "--", color="g", lw=2, label="credible intervals")
plt.plot(Year, CriU_ppc[:, 0], "--", color="g", lw=2)
plt.legend(fontsize=15)
plt.xlim([1900, 1920])
plt.xlabel("Year", fontsize=15)
plt.ylabel("Hare conc", fontsize=15)
plt.xticks(Year, rotation=45);

使用 SMC 有效探索后验景观

多篇论文指出，ODE 的复杂非线性动力学导致后验景观极其难以被许多 MCMC 采样器有效地导航。因此，最近后验曲面的曲率信息已被用于构建强大的几何感知采样器（Mark Girolami 和 Ben Calderhead，2011 年），这些采样器在 ODE 推断问题中表现出色。另一组想法建议将复杂的推断任务分解为一系列更简单的任务。本质上，这个想法是使用顺序重要性采样从人为的、越来越复杂的分布序列中采样，其中序列中的第一个是从先验易于采样的分布，而序列中的最后一个是实际的复杂目标分布。相关的重要性分布是通过使用马尔可夫核（例如 MH 核）移动上一步采样的粒子集来构建的。

构建分布序列的一种简单方法是使用温度 \(\beta\)，该温度从 \(0\) 缓慢升高到 \(1\)。使用此温度变量 \(\beta\)，我们可以将退火中间分布写为

\[p_{\beta}(\boldsymbol{\theta}|\boldsymbol{y})\propto p(\boldsymbol{y}|\boldsymbol{\theta})^{\beta} p(\boldsymbol{\theta}).\]

从这些人为分布序列执行顺序重要性采样，以避免直接从 \(p(\boldsymbol{\theta}|\boldsymbol{y})\) 采样的困难任务的采样器，被称为顺序蒙特卡洛 (SMC) 采样器（P Del Moral 等人，2006 年）。这些采样器的性能对温度计划的选择很敏感，温度计划是用户定义的 \(\beta\) 在 \(0\) 和 \(1\) 之间的递增值集。幸运的是，PyMC3 提供了一个 SMC 采样器的版本（Jianye Ching 和 Yi-Chu Chen，2007 年），它可以自动计算出此温度计划。此外，PyMC3 的 SMC 采样器不需要对数目标密度的梯度。因此，将此采样器用于 ODE 模型中的推断非常容易。在下一个示例中，我将应用此 SMC 采样器来估计 Fitzhugh-Nagumo 模型的参数。

Fitzhugh-Nagumo 模型

Fitzhugh-Nagumo 模型由下式给出

\[\begin{split} \begin{aligned} \frac{dV}{dt}&=(V - \frac{V^3}{3} + R)c\\ \frac{dR}{dt}&=\frac{-(V-a+bR)}{c}, \end{aligned} \end{split}\]

由膜电压变量 \(V(t)\) 和恢复变量 \(R(t)\) 组成，是对鱿鱼巨轴突中尖峰（动作电位）生成的 Hodgkin-Huxley 模型的二维简化，其中 \(a\)、\(b\)、\(c\) 是模型参数。该模型产生丰富的动力学，因此后验曲面的几何形状复杂，这通常会导致许多 MCMC 采样器的性能不佳。因此，该模型被用于测试所讨论的几何 MCMC 方案的有效性，此后一直被用于基准测试其他新颖的 MCMC 方法。遵循 Mark Girolami 和 Ben Calderhead，2011 年，我也将使用从此模型人工生成的数据来设置用于估计 \(\boldsymbol{\theta}=(a,b,c)\) 的推断任务。

class FitzhughNagumoModel:
    def __init__(self, times, y0=None):
        self._y0 = np.array([-1, 1], dtype=np.float64)
        self._times = times

    def _simulate(self, parameters, times):
        a, b, c = [float(x) for x in parameters]

        def rhs(y, t, p):
            V, R = y
            dV_dt = (V - V**3 / 3 + R) * c
            dR_dt = (V - a + b * R) / -c
            return dV_dt, dR_dt

        values = odeint(rhs, self._y0, times, (parameters,), rtol=1e-6, atol=1e-6)
        return values

    def simulate(self, x):
        return self._simulate(x, self._times)

模拟数据

对于此示例，我将使用模拟数据，即我将从上面定义的正向模型生成噪声轨迹，参数 \(\theta\) 设置为 \((0.2,0.2,3)\)，并被标准差为 \(\sigma=0.5\) 的 i.i.d 高斯噪声破坏。初始值分别设置为 \(V(0)=-1\) 和 \(R(0)=1\)。同样，遵循 Mark Girolami 和 Ben Calderhead，2011 年，我将假设初始值是已知的。这些参数值将模型推入振荡状态。

n_states = 2
n_times = 200
true_params = [0.2, 0.2, 3.0]
noise_sigma = 0.5
FN_solver_times = np.linspace(0, 20, n_times)
ode_model = FitzhughNagumoModel(FN_solver_times)
sim_data = ode_model.simulate(true_params)
np.random.seed(42)
Y_sim = sim_data + np.random.randn(n_times, n_states) * noise_sigma
plt.figure(figsize=(15, 7.5))
plt.plot(FN_solver_times, sim_data[:, 0], color="darkblue", lw=4, label=r"$V(t)$")
plt.plot(FN_solver_times, sim_data[:, 1], color="darkgreen", lw=4, label=r"$R(t)$")
plt.plot(FN_solver_times, Y_sim[:, 0], "o", color="darkblue", ms=4.5, label="Noisy traces")
plt.plot(FN_solver_times, Y_sim[:, 1], "o", color="darkgreen", ms=4.5)
plt.legend(fontsize=15)
plt.xlabel("Time", fontsize=15)
plt.ylabel("Values", fontsize=15)
plt.title("Fitzhugh-Nagumo Action Potential Model", fontsize=25);

使用 Theano @as_op 定义不可微分的黑盒 op

请记住，我告诉过 SMC 采样器不需要梯度，顺便说一句，对于 PyMC3 也支持的其他采样器（例如 Metropolis-Hastings、Slice 采样器）也是如此。对于所有这些无梯度采样器，我将展示一种简单快速的方法来包装正向模型，即 Theano 中的 ODE 解。我们所要做的就是简单地使用装饰器 as_op，它将 python 函数转换为基本的 Theano Op。我们还使用 as_op 装饰器告诉 Theano，我们有三个参数，每个参数都是 Theano 标量。然后，输出是一个 Theano 矩阵，其列是状态向量。

import theano.tensor as tt

from theano.compile.ops import as_op


@as_op(itypes=[tt.dscalar, tt.dscalar, tt.dscalar], otypes=[tt.dmatrix])
def th_forward_model(param1, param2, param3):
    param = [param1, param2, param3]
    th_states = ode_model.simulate(param)

    return th_states

生成模型

由于我已经使用 i.i.d 高斯破坏了原始轨迹，因此似然函数由下式给出

\[\boldsymbol{Y} = \prod_{i=1}^T \mathcal{N}(\boldsymbol{X}(t_i)), \sigma^2\mathbb{I}),\]

其中 \(\mathbb{I}\in \mathbb{R}^{K \times K}\)。我们在 \((a,b,c)\) 上放置 Gamma、Normal、Uniform 先验，在 \(\sigma\) 上放置 HalfNormal 先验，如下所示

\[\begin{split} \begin{aligned} a & \sim \mathcal{Gamma}(2,1),\\ b & \sim \mathcal{N}(0,1),\\ c & \sim \mathcal{U}(0.1,1),\\ \sigma & \sim \mathcal{H}(1). \end{aligned} \end{split}\]

请注意我是如何在此示例中使用 start 参数的。就像 pm.sample 一样，pm.sample_smc 有许多设置，但我发现默认设置对于像这样的简单模型来说足够好。

draws = 1000
with pm.Model() as FN_model:
    a = pm.Gamma("a", alpha=2, beta=1)
    b = pm.Normal("b", mu=0, sigma=1)
    c = pm.Uniform("c", lower=0.1, upper=10)

    sigma = pm.HalfNormal("sigma", sigma=1)

    forward = th_forward_model(a, b, c)

    cov = np.eye(2) * sigma**2

    Y_obs = pm.MvNormal("Y_obs", mu=forward, cov=cov, observed=Y_sim)

    startsmc = {v.name: np.random.uniform(1e-3, 2, size=draws) for v in FN_model.free_RVs}

    trace_FN = pm.sample_smc(draws, start=startsmc)

Initializing SMC sampler...
Sampling 2 chains in 2 jobs
Stage:   0 Beta: 0.009
Stage:   1 Beta: 0.029
Stage:   2 Beta: 0.043
Stage:   3 Beta: 0.054
Stage:   4 Beta: 0.065
Stage:   5 Beta: 0.087
Stage:   6 Beta: 0.118
Stage:   7 Beta: 0.163
Stage:   8 Beta: 0.229
Stage:   9 Beta: 0.317
Stage:  10 Beta: 0.456
Stage:  11 Beta: 0.645
Stage:  12 Beta: 0.914
Stage:  13 Beta: 1.000
Stage:   0 Beta: 0.009
Stage:   1 Beta: 0.031
Stage:   2 Beta: 0.046
Stage:   3 Beta: 0.056
Stage:   4 Beta: 0.067
Stage:   5 Beta: 0.088
Stage:   6 Beta: 0.122
Stage:   7 Beta: 0.169
Stage:   8 Beta: 0.235
Stage:   9 Beta: 0.339
Stage:  10 Beta: 0.494
Stage:  11 Beta: 0.695
Stage:  12 Beta: 0.999
Stage:  13 Beta: 1.000

az.plot_posterior(trace_FN, kind="hist", bins=30, color="seagreen");

推断总结

使用 pm.SMC，我是否获得了与几何 MCMC 采样器相似的性能（参见 Mark Girolami 和 Ben Calderhead，2011 年）？我想是的！

results = [
    az.summary(trace_FN, ["a"]),
    az.summary(trace_FN, ["b"]),
    az.summary(trace_FN, ["c"]),
    az.summary(trace_FN, ["sigma"]),
]
results = pd.concat(results)
true_params.append(noise_sigma)
results["True values"] = pd.Series(np.array(true_params), index=results.index)
true_params.pop()
results

	平均值	标准差	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_mean	ess_sd	ess_bulk	ess_tail	r_hat	真值
a	0.261	0.020	0.223	0.298	0.007	0.005	8.0	8.0	8.0	108.0	1.18	0.2
b	0.149	0.084	-0.003	0.304	0.003	0.002	1014.0	654.0	1009.0	1772.0	1.01	0.2
c	2.895	0.041	2.815	2.968	0.016	0.012	7.0	7.0	7.0	98.0	1.22	3.0
sigma	0.609	0.010	0.591	0.628	0.005	0.004	4.0	4.0	4.0	75.0	1.38	0.5

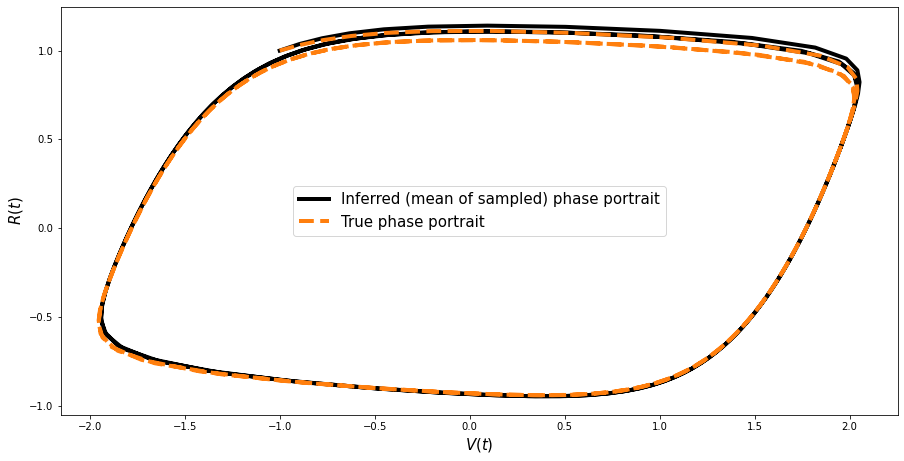
相位图的重建

很高兴检查我们是否可以基于获得的样本重建此模型的（著名）相位图。

params = np.array([trace_FN.get_values("a"), trace_FN.get_values("b"), trace_FN.get_values("c")]).T
params.shape
new_values = []
for ind in range(len(params)):
    ppc_sol = ode_model.simulate(params[ind])
    new_values.append(ppc_sol)
new_values = np.array(new_values)
mean_values = np.mean(new_values, axis=0)
plt.figure(figsize=(15, 7.5))

plt.plot(
    mean_values[:, 0],
    mean_values[:, 1],
    color="black",
    lw=4,
    label="Inferred (mean of sampled) phase portrait",
)
plt.plot(
    sim_data[:, 0], sim_data[:, 1], "--", color="#ff7f0e", lw=4, ms=6, label="True phase portrait"
)
plt.legend(fontsize=15)
plt.xlabel(r"$V(t)$", fontsize=15)
plt.ylabel(r"$R(t)$", fontsize=15);

展望

使用其他 ODE 模型

我试图使一切尽可能通用。因此，我的自定义 ODE Op、状态和 VSP 评估器以及缓存求解器不绑定到特定的 ODE 模型。因此，要使用任何其他 ODE 模型，只需根据您自己的特定 ODE 模型实现 simulate_with_sensitivities 方法即可。

其他形式的微分方程 (DDE、DAE、PDE)

我希望这两个例子已经阐明了 PyMC3 在拟合 ODE 模型方面的适用性。尽管 ODE 是数学模型最基本的组成部分，但实际上还存在其他形式的动力系统，例如时滞微分方程 (DDE)、微分代数方程 (DAE) 和偏微分方程 (PDE)，它们的参数估计同样重要。PyMC3 支持的 SMC 以及任何其他非梯度采样器都可以用于拟合所有这些形式的微分方程，当然要使用 as_op。然而，就像 ODE 一样，我们可以求解 DDE/DAE 的增广系统及其灵敏度方程。DDE 和 DAE 的灵敏度方程可以在这篇最新的论文中找到，C Rackauckas et al., 2018（公式 9 和 10）。因此，我们可以轻松地将 NUTS 采样器应用于这些模型。

Stan 已经支持 ODE

我相信在许多问题中，SMC 采样器比 NUTS 更适用，因此拥有这个选项是很好的。

模型选择

自 Vladislav Vyshemirsky 和 Mark Girolami, 2008 以来的大多数 ODE 推理文献都建议使用贝叶斯因子进行模型选择/比较。这涉及到边际似然的计算，这是一个更为细致的话题，我将避免对此进行任何讨论。幸运的是，SMC 采样器计算边际似然作为副产品，因此可以用于获得贝叶斯因子。请关注 PyMC3 的其他教程，以获取有关如何在运行 SMC 采样器后获得边际似然的更多信息。

由于我们通常将 ODE 推理构建为回归问题（在大多数情况下伴随 i.i.d 测量噪声假设），我们可以直接使用任何受支持的信息准则，例如广泛可用的信息准则 (WAIC)，而无需考虑使用哪种采样器进行推理。请参阅 PyMC3 的 API 以获取有关 WAIC 的更多信息。

其他 AD 包

虽然这是一个轻微的题外话，但我仍然想指出我对这个问题的观察。我在此提出的将 ODE（也扩展到 DDE/DAE）嵌入为自定义 Op 的方法可以轻松地推广到其他 AD 包，例如 TensorFlow 和 PyTorch。我曾能够使用 TensorFlow 的 py_func 构建自定义 TensorFlow ODE Op，然后在 Edward ppl 中使用它。我向那些有兴趣使用 Pyro ppl 的人推荐 本教程，以了解如何编写 PyTorch 扩展。

%load_ext watermark
%watermark -n -u -v -iv -w

Last updated: Sat Mar 13 2021

Python implementation: CPython
Python version       : 3.8.6
IPython version      : 7.20.0

logging   : 0.5.1.2
pandas    : 1.2.1
theano    : 1.1.2
numpy     : 1.20.0
sys       : 3.8.6 | packaged by conda-forge | (default, Jan 25 2021, 23:22:12) 
[Clang 11.0.1 ]
matplotlib: None
pymc3     : 3.11.0
arviz     : 0.11.0

Watermark: 2.1.0