近似贝叶斯计算

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm

print(f"Running on PyMC v{pm.__version__}")

Running on PyMC v5.9.1

%load_ext watermark
az.style.use("arviz-darkgrid")

序贯蒙特卡洛 - 近似贝叶斯计算

近似贝叶斯计算方法（也称为无似然推断方法）是一组用于在似然函数难以处理或评估成本高昂的情况下推断后验分布的技术。这并不意味着似然函数不是分析的一部分，只是我们正在近似似然，因此得名 ABC 方法。

当对某些研究领域（如系统生物学）中的复杂现象进行建模时，ABC 非常有用。此类模型通常包含无法观察到的随机量，这使得似然函数难以指定，但可以从模型中模拟数据。

这些方法遵循一般形式

1- 从先验/提议分布 \(\pi(\theta)\) 中抽取参数 \(\theta^*\)。

2- 使用一个函数模拟数据集 \(y^*\)，该函数接受 \(\theta\) 并返回与观测数据集 \(y_0\) 相同维度的数据集（模拟器）。

3- 使用距离函数 \(d\) 和容差阈值 \(\epsilon\) 比较模拟数据集 \(y^*\) 与实验数据集 \(y_0\)。

在某些情况下，在两个汇总统计量 \(d(S(y_0), S(y^*))\) 之间计算距离函数，避免了计算整个数据集距离的问题。

结果，我们从分布 \(\pi(\theta | d(y_0, y^*)) \leqslant \epsilon\) 中获得参数样本。

如果 \(\epsilon\) 足够小，则此分布将很好地近似后验分布 \(\pi(\theta | y_0)\)。

序贯蒙特卡洛 ABC 是一种通过一系列提议分布 \(\phi(\theta^{(i)})\) 传播采样参数，迭代地将先验变形为后验的方法，对接受的参数 \(\theta^{(i)}\) 进行加权，如下所示

\[ w^{(i)} \propto \frac{\pi(\theta^{(i)})}{\phi(\theta^{(i)})} \]

它结合了传统 SMC 的优点，即能够从具有多个峰值的分布中采样，但无需评估似然函数。

（Lintusaari，2016），（Toni，T.，2008），（Nuñez，Prangle，2015）

经典的高斯拟合

为了说明如何在 PyMC3 中使用 ABC，我们将从一个非常简单的示例开始，估计高斯数据的均值和标准差。

data = np.random.normal(loc=0, scale=1, size=1000)

显然，在正常情况下，使用高斯似然会做得很好。但这会违背本示例的目的，笔记本将在此处结束，一切都会非常无聊。因此，我们将定义一个模拟器。正态数据的非常简单的模拟器是伪随机数生成器，在现实生活中，我们的模拟器很可能更复杂。

def normal_sim(rng, a, b, size=1000):
    return rng.normal(a, b, size=size)

在 PyMC3 中定义 ABC 模型通常与定义其他 PyMC3 模型非常相似。两个重要的区别是：我们需要定义一个 Simulator分布，并且我们需要将 sample_smc 与 kernel="ABC" 一起使用。Simulator 用作通用接口，用于传递合成数据生成函数（在本例中为 normal_sim）、其参数、观测数据以及可选的距离函数和汇总统计量。在以下代码中，我们使用默认距离 gaussian_kernel 和 sort 汇总统计量。顾名思义，sort 在计算距离之前对数据进行排序。

最后，SMC-ABC 提供了存储模拟数据的选项。这可能很方便，因为模拟器可能评估成本很高，我们可能希望将模拟数据用于例如后验预测检查。

with pm.Model() as example:
    a = pm.Normal("a", mu=0, sigma=5)
    b = pm.HalfNormal("b", sigma=1)
    s = pm.Simulator("s", normal_sim, params=(a, b), sum_stat="sort", epsilon=1, observed=data)

    idata = pm.sample_smc()
    idata.extend(pm.sample_posterior_predictive(idata))

Initializing SMC sampler...
Sampling 6 chains in 6 jobs

100.00% [100/100 00:00<? 阶段：6 Beta：1.000]

Sampling: [s]

100.00% [12000/12000 00:00<00:00]

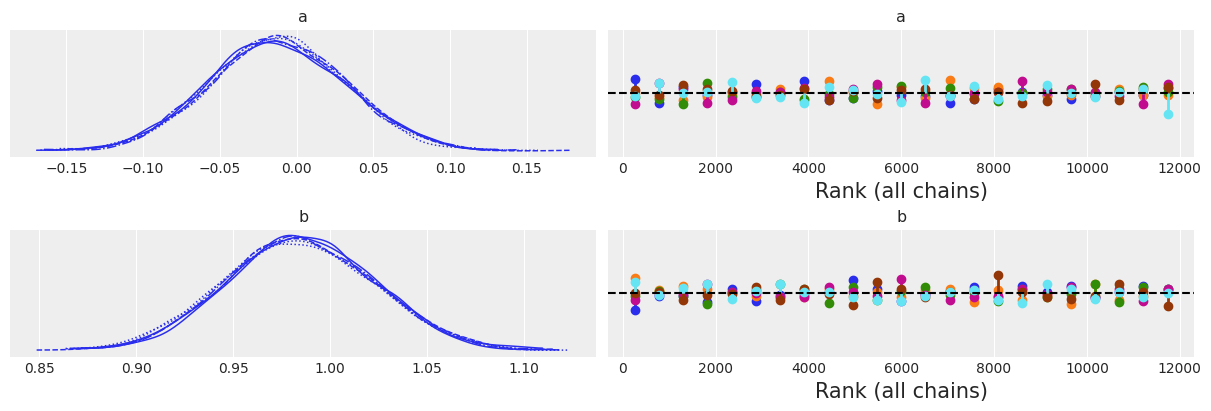
从 plot_trace 判断，采样器工作得很好，考虑到这是一个非常简单的模型，这并不奇怪。无论如何，看到平坦的秩图总是令人欣慰的 :-)

az.plot_trace(idata, kind="rank_vlines");

az.summary(idata, kind="stats")

	均值	标准差	hdi_3%	hdi_97%
a	-0.012	0.044	-0.093	0.072
b	0.985	0.039	0.914	1.059

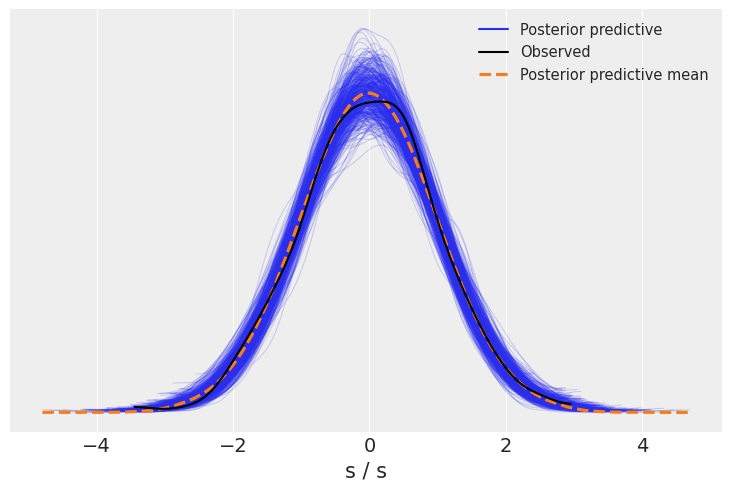
后验预测检查表明我们有一个总体良好的拟合，但合成数据比观测数据具有更重的尾部。您可能希望减小 epsilon 的值，看看是否可以获得更紧密的拟合。

az.plot_ppc(idata, num_pp_samples=500);

Lotka–Volterra 模型

Lotka-Volterra 模型是一个著名的生物学模型，描述了当存在捕食者/猎物相互作用时，两个物种的个体数量如何变化（《生态学和进化中的生物学家数学建模指南》，Otto 和 Day，2007 年）。例如，兔子和狐狸。给定每个物种的初始种群数量，此常微分方程 (ODE) 的积分描述了两个种群进展的曲线。此 ODE 采用四个参数

• a 是兔子在没有狐狸时的自然增长率。

• b 是兔子由于捕食造成的自然死亡率。

• c 是狐狸在没有兔子时的自然死亡率。

• d 是描述有多少被捕获的兔子可以创造一只新狐狸的因子。

请注意，SMC-ABC 和 ODE 之间没有什么本质上的特殊之处。原则上，模拟器可以是任何能够根据一组参数生成虚假数据的代码。

from scipy.integrate import odeint

# Definition of parameters
a = 1.0
b = 0.1
c = 1.5
d = 0.75

# initial population of rabbits and foxes
X0 = [10.0, 5.0]
# size of data
size = 100
# time lapse
time = 15
t = np.linspace(0, time, size)


# Lotka - Volterra equation
def dX_dt(X, t, a, b, c, d):
    """Return the growth rate of fox and rabbit populations."""

    return np.array([a * X[0] - b * X[0] * X[1], -c * X[1] + d * b * X[0] * X[1]])


# simulator function
def competition_model(rng, a, b, size=None):
    return odeint(dX_dt, y0=X0, t=t, rtol=0.01, args=(a, b, c, d))

使用模拟器函数，我们将获得添加了一些噪声的数据集，用于作为观测数据。

# function for generating noisy data to be used as observed data.
def add_noise(a, b):
    noise = np.random.normal(size=(size, 2))
    simulated = competition_model(None, a, b) + noise
    return simulated

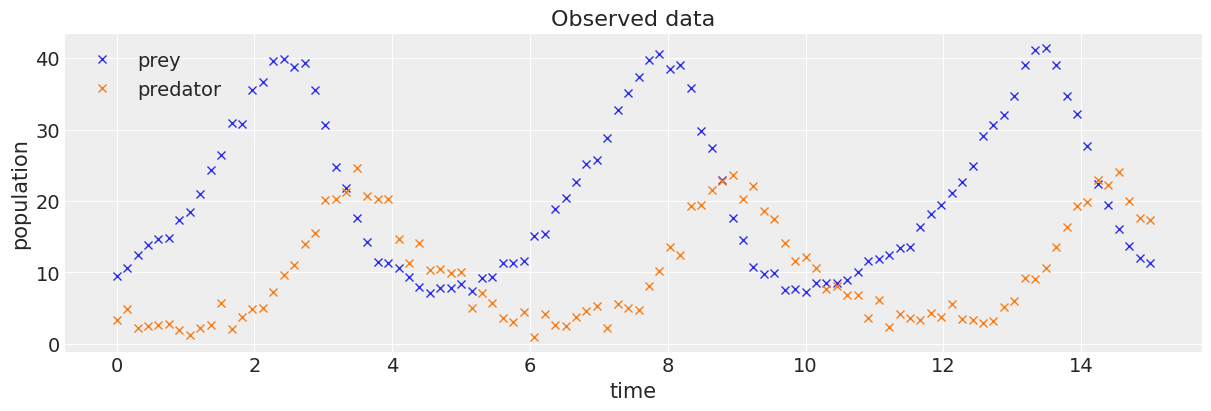
# plotting observed data.
observed = add_noise(a, b)
_, ax = plt.subplots(figsize=(12, 4))
ax.plot(t, observed[:, 0], "x", label="prey")
ax.plot(t, observed[:, 1], "x", label="predator")
ax.set_xlabel("time")
ax.set_ylabel("population")
ax.set_title("Observed data")
ax.legend();

与第一个示例一样，我们没有指定似然函数，而是使用了 pm.Simulator()。

with pm.Model() as model_lv:
    a = pm.HalfNormal("a", 1.0)
    b = pm.HalfNormal("b", 1.0)

    sim = pm.Simulator("sim", competition_model, params=(a, b), epsilon=10, observed=observed)

    idata_lv = pm.sample_smc()

Initializing SMC sampler...
Sampling 6 chains in 6 jobs

100.00% [100/100 00:00<? 阶段：6 Beta：1.000]

/tmp/ipykernel_8811/1881729530.py:22: RuntimeWarning: overflow encountered in multiply
  return np.array([a * X[0] - b * X[0] * X[1], -c * X[1] + d * b * X[0] * X[1]])
/home/dylan/.local/share/virtualenvs/project1-N1VmeQ3a/lib/python3.11/site-packages/scipy/integrate/_odepack_py.py:248: ODEintWarning: Illegal input detected (internal error). Run with full_output = 1 to get quantitative information.
  warnings.warn(warning_msg, ODEintWarning)

 intdy--  t (=r1) illegal            in above message,  r1 =  0.1075757575758D+02
      t not in interval tcur - hu (= r1) to tcur (=r2)       
      in above,  r1 =  0.1061791618969D+02   r2 =  0.1063479313299D+02
 intdy--  t (=r1) illegal            in above message,  r1 =  0.1090909090909D+02
      t not in interval tcur - hu (= r1) to tcur (=r2)       
      in above,  r1 =  0.1061791618969D+02   r2 =  0.1063479313299D+02
 lsoda--  trouble from intdy. itask = i1, tout = r1      in above message,  i1 =         1
      in above message,  r1 =  0.1090909090909D+02

/tmp/ipykernel_8811/1881729530.py:22: RuntimeWarning: overflow encountered in multiply
  return np.array([a * X[0] - b * X[0] * X[1], -c * X[1] + d * b * X[0] * X[1]])
/tmp/ipykernel_8811/1881729530.py:22: RuntimeWarning: invalid value encountered in scalar subtract
  return np.array([a * X[0] - b * X[0] * X[1], -c * X[1] + d * b * X[0] * X[1]])
/home/dylan/.local/share/virtualenvs/project1-N1VmeQ3a/lib/python3.11/site-packages/scipy/integrate/_odepack_py.py:248: ODEintWarning: Illegal input detected (internal error). Run with full_output = 1 to get quantitative information.
  warnings.warn(warning_msg, ODEintWarning)

 intdy--  t (=r1) illegal            in above message,  r1 =  0.1439393939394D+02
      t not in interval tcur - hu (= r1) to tcur (=r2)       
      in above,  r1 =  0.1431156096235D+02   r2 =  0.1431982016467D+02
 intdy--  t (=r1) illegal            in above message,  r1 =  0.1454545454545D+02
      t not in interval tcur - hu (= r1) to tcur (=r2)       
      in above,  r1 =  0.1431156096235D+02   r2 =  0.1431982016467D+02
 lsoda--  trouble from intdy. itask = i1, tout = r1      in above message,  i1 =         1
      in above message,  r1 =  0.1454545454545D+02

az.plot_trace(idata_lv, kind="rank_vlines");

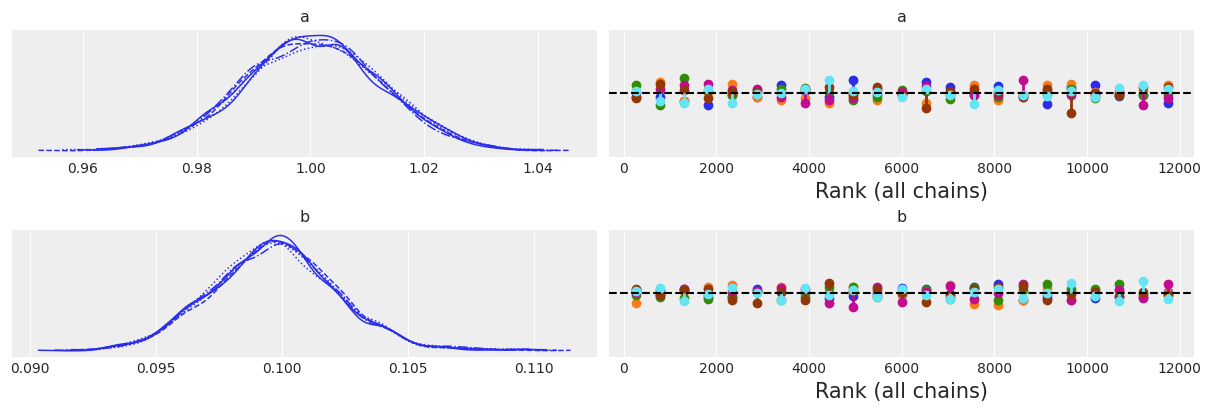
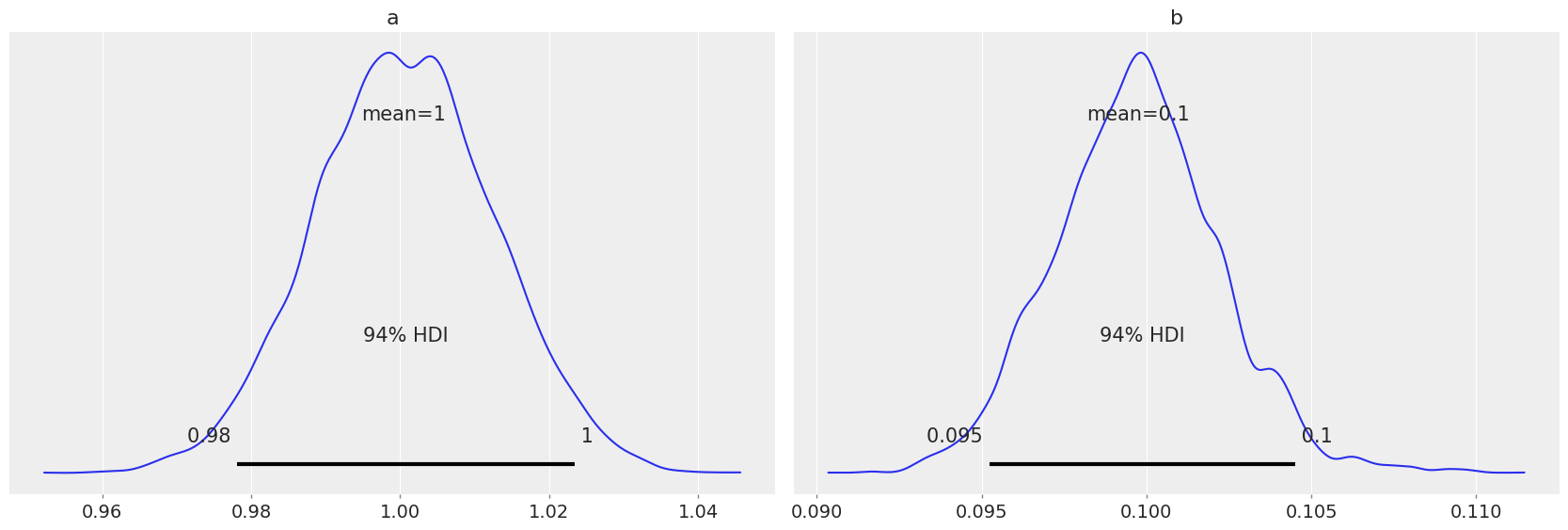
az.plot_posterior(idata_lv);

# plot results
_, ax = plt.subplots(figsize=(14, 6))
posterior = idata_lv.posterior.stack(samples=("draw", "chain"))
ax.plot(t, observed[:, 0], "o", label="prey", c="C0", mec="k")
ax.plot(t, observed[:, 1], "o", label="predator", c="C1", mec="k")
ax.plot(t, competition_model(None, posterior["a"].mean(), posterior["b"].mean()), linewidth=3)
for i in np.random.randint(0, size, 75):
    sim = competition_model(None, posterior["a"][i], posterior["b"][i])
    ax.plot(t, sim[:, 0], alpha=0.1, c="C0")
    ax.plot(t, sim[:, 1], alpha=0.1, c="C1")
ax.set_xlabel("time")
ax.set_ylabel("population")
ax.legend();

参考文献

[1]

Osvaldo A Martin、Ravin Kumar 和 Junpeng Lao。《Python 中的贝叶斯建模和计算》。 Chapman and Hall/CRC，2021 年。doi:10.1201/9781003019169。

%watermark -n -u -v -iv -w

Last updated: Fri Nov 17 2023

Python implementation: CPython
Python version       : 3.11.5
IPython version      : 8.17.1

numpy     : 1.25.2
pymc      : 5.9.1
matplotlib: 3.8.0
arviz     : 0.16.1

Watermark: 2.4.3

许可声明

本示例 галерея 中的所有笔记本均根据 MIT 许可证 提供，该许可证允许修改和再分发以用于任何用途，前提是保留版权和许可声明。

引用 PyMC 示例

要引用此笔记本，请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。

重要提示

许多笔记本都改编自其他来源：博客、书籍……在这种情况下，您也应该引用原始来源。

另请记住引用您的代码使用的相关库。

这是一个 bibtex 中的引用模板

@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}

渲染后可能看起来像