基本混淆因素

此笔记本是 Richard McElreath Statistical Rethinking 2023 系列讲座的 PyMC 移植版本的一部分。

视频 - 第 05 讲 - 基本混淆因素# 第 05 讲 - 基本混淆因素

# Ignore warnings
import warnings

import arviz as az
import numpy as np
import pandas as pd
import pymc as pm
import statsmodels.formula.api as smf
import utils as utils
import xarray as xr

from matplotlib import pyplot as plt
from matplotlib import style
from scipy import stats as stats

warnings.filterwarnings("ignore")

# Set matplotlib style
STYLE = "statistical-rethinking-2023.mplstyle"
style.use(STYLE)

因果关系与关联

华夫饼屋会导致离婚吗？

WAFFLEHOUSE_DIVORCE = utils.load_data("WaffleDivorce")
WAFFLEHOUSE_DIVORCE.head()

	地点	地点	人口	结婚年龄中位数	结婚率	结婚率标准误	离婚率	离婚率标准误	华夫饼屋数量	南方	1860 年奴隶数	1860 年人口	1860 年奴隶比例
0	阿拉巴马州	AL	4.78	25.3	20.2	1.27	12.7	0.79	128	1	435080	964201	0.45
1	阿拉斯加州	AK	0.71	25.2	26.0	2.93	12.5	2.05	0	0	0	0	0.00
2	亚利桑那州	AZ	6.33	25.8	20.3	0.98	10.8	0.74	18	0	0	0	0.00
3	阿肯色州	AR	2.92	24.3	26.4	1.70	13.5	1.22	41	1	111115	435450	0.26
4	加利福尼亚州	CA	37.25	26.8	19.1	0.39	8.0	0.24	0	0	0	379994	0.00

utils.plot_scatter(
    WAFFLEHOUSE_DIVORCE.WaffleHouses, WAFFLEHOUSE_DIVORCE.Divorce, zorder=60, alpha=1
)
for ii, row in WAFFLEHOUSE_DIVORCE.sort_values("Divorce", ascending=False).iloc[:25].iterrows():
    plt.annotate(row.Loc, (row.WaffleHouses + 5, row.Divorce), zorder=60)

ols_formula = "Divorce ~ WaffleHouses"
linear_divorce_ols = smf.ols("Divorce ~ WaffleHouses", data=WAFFLEHOUSE_DIVORCE).fit()
utils.plot_line(
    WAFFLEHOUSE_DIVORCE.WaffleHouses,
    linear_divorce_ols.predict(),
    color="C1",
    label=f"Linear Model\n{ols_formula}",
)

plt.xlabel("Waffle Houses per million")
plt.ylabel("divorce rate")
plt.legend();

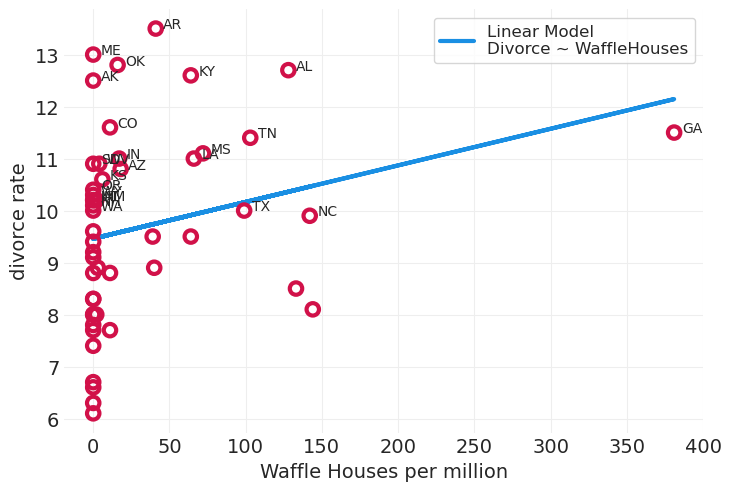
• 华夫饼屋倾向于位于美国南部

• 美国南部离婚率也更高

• 南方性在华夫饼屋和离婚率之间产生了很强的统计关联。

• 华夫饼屋导致离婚率是不可信的

关联在自然界中很常见 – 因果关系很少见

• 目标是解决一些 估计量 – 一个科学问题

  • 即我们想要创造的隐喻蛋糕

• 我们使用 估计器，这是一组组织代码和数据以创建估计量的估计的指令

  • 隐喻的食谱

• 结果 估计值 可能与您最初目标的估计量相同，也可能不同。 很多事情都可能导致这种情况

  • 糟糕的食谱（例如，估计器设计或混淆因素 – 本讲座的重点）

    • 正确的食谱将防御混淆因素

  • 食谱执行不佳（例如，代码错误或解释错误）

  • 糟糕的数据

混淆因素

• 样本的特征，以及我们如何使用它来误导我们

• 混淆因素是多样的

混淆因素周期表

• 叉形：\(X \leftarrow Z \rightarrow Y\)

• 管道：\(X \rightarrow Z \rightarrow Y\)

• 碰撞器：\(X \rightarrow Z \leftarrow Y\)

• 后代：\(X \rightarrow Z \rightarrow Y\)，\(Z \rightarrow A\)

"""Helper functions for displaying elemental confounds"""


def summarize_discrete_counfound_simulation(X, Y, Z):
    print(f"Correlation between X and Y: {np.corrcoef(X, Y)[0, 1]:1.2}")
    print("Cross tabulation:")
    print(utils.crosstab(X, Y, labels=["X", "Y"]))

    for z in [0, 1]:
        X_z = X[Z == z]
        Y_z = Y[Z == z]

        print(
            f"\nCorrelation between X and Y conditioned on Z={z}: {np.corrcoef(X_z, Y_z)[0, 1]:1.2f}"
        )
        print("Cross tabulation:")
        print(utils.crosstab(X_z, Y_z, labels=["X", "Y"]))


def fit_linear_models_to_simulated_data(data):
    models = {}
    models["unstratified"] = smf.ols("Y ~ X", data=data).fit()

    # Stratified Models
    for z in [0, 1]:
        models[f"Z={z}"] = smf.ols("Y ~ X", data=data[data.Z == z]).fit()
    return models


def plot_sms_linear_model_fit(model, xs, label, color):
    """Helper function to plot linear models"""
    params = model.params
    ys = params.Intercept + params.X * xs
    return utils.plot_line(xs, ys, label=label, color=color)


def plot_continuous_confound_simulation(data, title):
    """Helper function to plot simulations"""
    models = fit_linear_models_to_simulated_data(data)
    plt.subplots(figsize=(6, 6))

    xs = np.linspace(-4, 4, 20)
    for z in [0, 1]:
        color = f"C{np.abs(z - 1)}"  # Note: flip colormap
        utils.plot_scatter(data[data.Z == z].X, data[data.Z == z].Y, color=color)
        plot_sms_linear_model_fit(models[f"Z={z}"], xs, label=f"Z={z}", color=color)

    plot_sms_linear_model_fit(models["unstratified"], xs, label="total sample", color="black")

    plt.xlabel("X")
    plt.ylabel("Y")

    plt.xlim([-4, 4])
    plt.ylim([-4, 4])
    plt.legend()
    plt.title(title)

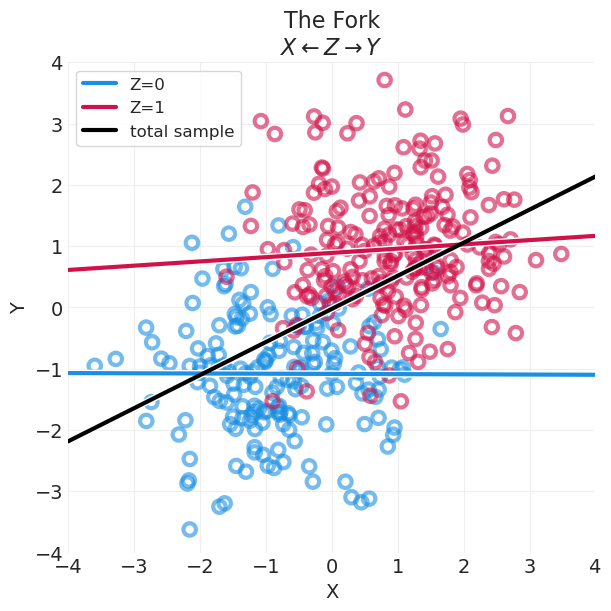
叉形 \(X \leftarrow Z \rightarrow Y\)

• \(Χ\) 和 \(Y\) 共享“共同原因” \(Z\)

• 共同原因 \(Z\) 导致 \(Χ\) 和 \(Y\) 之间产生关联

  • \(X \not \perp Y\)

• 一旦按 \(Z\) 分层，\(Χ\) 和 \(Y\) 之间在 \(Z\) 的每个水平 上都没有关联

  • \(X \perp Y | Z\)

utils.draw_causal_graph(
    edge_list=[("Z", "X"), ("Z", "Y")],
)

注意。 如果 \(Z\) 是唯一的共同原因，\(X\) 和 \(Y\) 将会是彼此的克隆。 \(X\) 和 \(Y\) 还有其他未建模/未观察到的影响因素 – 通常称为误差项 \(e_{X,Y}\)，它们未包含在上面的图中，但仍然导致 \(X\) 和 \(Y\) 之间的差异，并且应该被建模，通常作为任何生成模型中的噪声。

utils.draw_causal_graph(
    edge_list=[("Z", "X"), ("Z", "Y"), ("e_X", "X"), ("e_Y", "Y")],
    node_props={
        "e_X": {"style": "dashed"},
        "e_Y": {"style": "dashed"},
        "unobserved": {"style": "dashed"},
    },
)

叉形生成过程：离散示例

下面我们模拟一个叉形生成过程

\[\begin{split} \begin{align*} Z &\sim \text{Bernoulli}(0.5) \\ X &\sim \text{Bernoulli}(p*) \\ Y &\sim \text{Bernoulli}(p*) \\ p^* &= 0.9 \times Z + 0.1 \times (1 - Z) \\ \end{align*} \end{split}\]

utils.draw_causal_graph(
    edge_list=[("Z", "X"), ("Z", "Y")],
    edge_props={("Z", "X"): {"label": "p*"}, ("Z", "Y"): {"label": "p*"}},
    graph_direction="LR",
)

# Discrete Fork
np.random.seed(321)
n_samples = 1000
Z = stats.bernoulli.rvs(p=0.5, size=n_samples)
p_star = Z * 0.9 + (1 - Z) * 0.1
X = stats.bernoulli.rvs(p=p_star)
Y = stats.bernoulli.rvs(p=p_star)

证明

• \(X \not\!\perp Y\)

• \(X \perp Y | Z\)

summarize_discrete_counfound_simulation(X, Y, Z)

Correlation between X and Y: 0.63
Cross tabulation:
     X    Y
X  412  101
Y   86  401

Correlation between X and Y conditioned on Z=0: -0.02
Cross tabulation:
     X   Y
X  407  49
Y   41   4

Correlation between X and Y conditioned on Z=1: -0.01
Cross tabulation:
    X    Y
X   5   52
Y  45  397

叉形生成过程：连续示例

\[\begin{split} \begin{align*} Z &\sim \text{Bernoulli}(0.5) \\ X &\sim \text{Normal}(Z, 1) \\ Y &\sim \text{Normal}(Z, 1) \\ \mu^* &= 2Z -1 \\ \end{align*} \end{split}\]

# Continous Fork
np.random.seed(1234)
n_samples = 400

Z = stats.bernoulli.rvs(p=0.5, size=n_samples)

mu_star = 2 * Z - 1
X = stats.norm.rvs(loc=mu_star, size=n_samples)
Y = stats.norm.rvs(loc=mu_star, size=n_samples)

# Put simulated data into dataframe for statsmodels API
fork_data = pd.DataFrame(np.vstack([Z, X, Y]).T, columns=["Z", "X", "Y"])

plot_continuous_confound_simulation(fork_data, "The Fork\n$X \\leftarrow Z \\rightarrow Y$")

叉形示例：结婚率和离婚率（以及华夫饼屋！）

🧇 作为一个在南方长大的人，我喜欢华夫饼屋，并且由此及彼地喜欢这个例子。

import re


def plot_wafflehouse_pairwise(x_var, y_var, n_label=10, wafflehouse_divorce=WAFFLEHOUSE_DIVORCE):
    """Helper function for visualizing Wafflehouse data"""
    # Scatter by South
    for south, label in enumerate([None, "Southern\nStates"]):
        xs = wafflehouse_divorce[wafflehouse_divorce["South"] == south][x_var].values
        ys = wafflehouse_divorce[wafflehouse_divorce["South"] == south][y_var].values

        utils.plot_scatter(
            xs, ys, label=label, color=f"C{np.abs(south-1)}"  # Note: flip binary colorscale
        )

    # Annotate extreme values
    loc = wafflehouse_divorce["Loc"].tolist()

    xs = wafflehouse_divorce[x_var].values
    ys = wafflehouse_divorce[y_var].values
    xs_mean = np.mean(xs)
    ys_mean = np.mean(ys)

    def distance_from_center_of_mass(x, y):
        return (x - xs_mean) ** 2 + (y - ys_mean) ** 2

    sorted_xyl = sorted(zip(xs, ys, loc), key=lambda z: distance_from_center_of_mass(z[0], z[1]))[
        ::-1
    ]

    for li in range(n_label):
        x, y, label = sorted_xyl[li]
        plt.annotate(label, (x + 0.1, y + 0.1))

    def camelcase_to_label(string):
        return re.sub(r"(?<!^)(?=[A-Z])", " ", string).lower()

    plt.xlabel(camelcase_to_label(x_var))
    plt.ylabel(camelcase_to_label(y_var))

    plt.legend();

与猫头鹰结婚

1. 估计量

2. 科学模型

3. 统计模型

4. 分析

（1）估计量

结婚率 M 对 离婚率 D 的因果效应

utils.draw_causal_graph(
    edge_list=[("M", "D")],
    node_props={"M": {"label": "Marriage Rate, M"}, "D": {"label": "Divorce Rate, D"}},
    graph_direction="LR",
)

plot_wafflehouse_pairwise("Marriage", "Divorce", n_label=15)

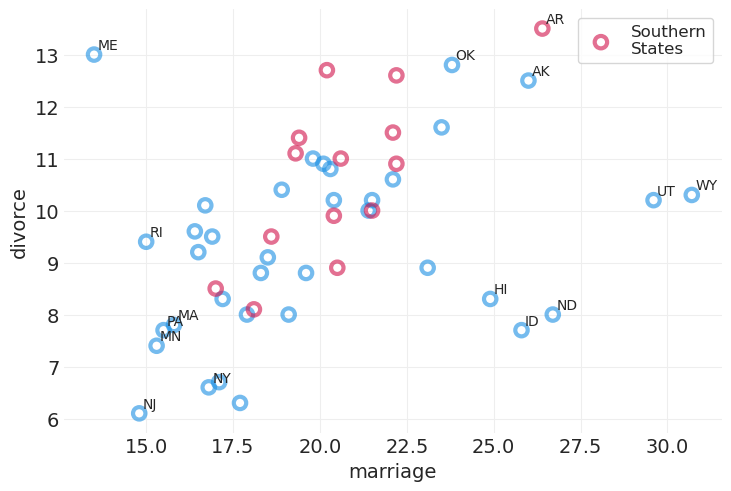
...另一个潜在的原因是 结婚年龄

utils.draw_causal_graph(
    edge_list=[("A", "D")],
    node_props={"A": {"label": "Median Marriage Age, A"}, "D": {"label": "Divorce Rate, D"}},
    graph_direction="LR",
)

plot_wafflehouse_pairwise("MedianAgeMarriage", "Divorce", n_label=15)

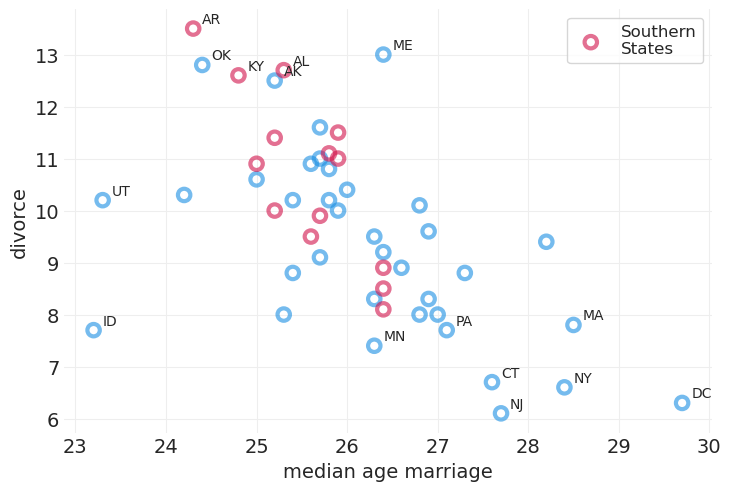
（2）科学模型

utils.draw_causal_graph(
    edge_list=[("M", "D"), ("A", "M"), ("A", "D")],
    edge_props={("A", "D"): {"label": " ?"}, ("M", "D"): {"label": " ?"}},
    graph_direction="LR",
)

_, axs = plt.subplots(1, 3, figsize=(12, 4))

plt.sca(axs[0])
plot_wafflehouse_pairwise("Marriage", "Divorce", n_label=15)

plt.sca(axs[1])
plot_wafflehouse_pairwise("MedianAgeMarriage", "Divorce", n_label=15)

plt.sca(axs[2])
plot_wafflehouse_pairwise("MedianAgeMarriage", "Marriage", n_label=15)

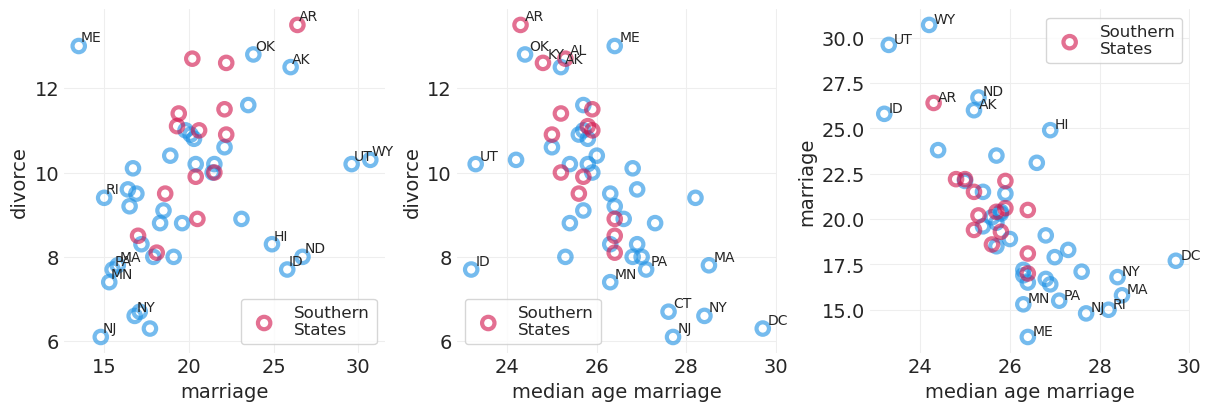
• 结婚率对离婚率的影响是否仅仅是它们共同原因年龄的结果——即叉形？

  • 仅从上面的散点图无法判断。

• 我们需要通过 按年龄分层来打破叉形

使用生成过程模型测试科学模型

注释

• McElreath 提到我们应该始终在标准分析流程中执行此测试步骤，但为了节省时间而跳过了，因此我们在此继续尝试一下。

• 此模拟将婚姻过程建模为年龄的函数，将离婚建模为年龄和婚姻的函数

• 此模拟是在标准化预测变量的空间中进行的

按连续变量分层

\[\begin{split} \begin{align*} D &= f(A, M) \\ D_i &\sim \text{Normal}(\mu_i, \sigma) \\ \mu_i &= \alpha + \beta_M M_i + \beta_A A_i \\ \mu_i &= (\alpha + \beta_A A_i) + \beta_M M_i \end{align*} \end{split}\]

其中 \((\alpha + \beta_A A_i)\) 可以被认为是 \(A\) 的每个连续值的有效截距

根据统计模型生成数据

统计叉形

\[\begin{split} \begin{align*} D &= f(A, M) \\ D_i &\sim \text{Normal}(\mu_i, \sigma) \\ \mu_i &= \alpha + \beta_M M_i + \beta_A A_i \\ \alpha &\sim \text{Normal}(\mu_?, \sigma_?) \\ \beta_{A, M} &\sim \text{Normal}(\mu_?, \sigma_?) \\ \sigma &\sim \text{Exponential}(\lambda_?) \end{align*} \end{split}\]

我们为先验使用什么参数 \(\theta_?\)？ 进入先验预测模拟

💡 当使用线性回归时，标准化 始终是一个好主意

• \(X_{standardized} = \frac{(X - \bar X)}{\bar \sigma}\)

• \(\bar X\) 和 \(\bar \sigma\) 是样本均值和标准差

• 导致均值为 0 和标准差为 1

• 简化先验定义

• 使推断运行更顺畅

• 始终可以反转标准化转换（使用 \(\bar X\) 和 \(\bar \sigma\)）以返回原始空间

先验预测模拟

使我们更好地了解模型在给定一组先验参数的情况下可以产生的线类型

def simulate_linear_model_priors(std=10, n_simulations=200):

    xs = np.linspace(-3, 3, 10)
    for ii in range(n_simulations):
        alpha = stats.norm.rvs(0, std)
        beta = stats.norm.rvs(0, std)
        ys = alpha + beta * xs
        plt.plot(xs, ys, color="C0", alpha=0.25)

    plt.xlim([-3, 3])
    plt.ylim([-3, 3])
    plt.xlabel("median age at marriage (standardized)")
    plt.ylabel("Divorce rate (standardized)")

过大的先验方差会导致不切实际的线性模型

simulate_linear_model_priors(std=10)

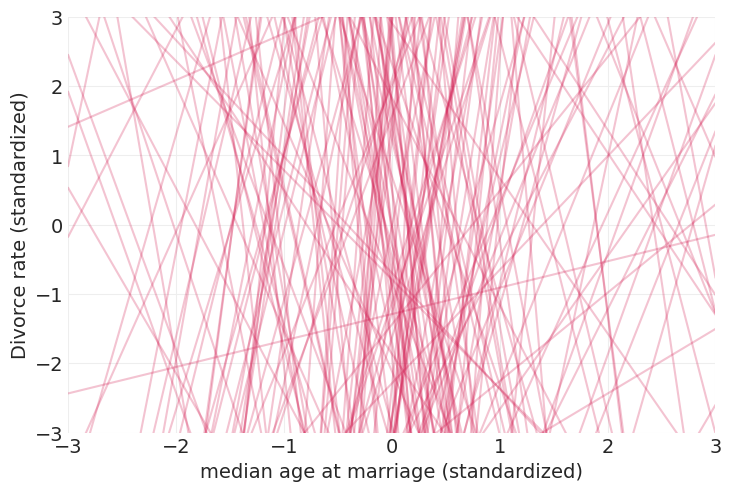
更合理的标准化变量的先验

simulate_linear_model_priors(std=0.5)

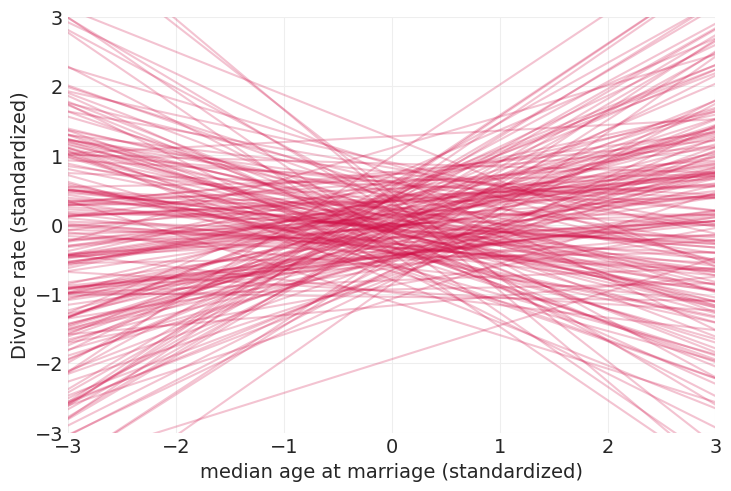
（3）婚姻对离婚的因果效应的统计模型

这是具有更合理先验的完整统计模型。

\[\begin{split} \begin{align*} D &= f(A, M) \\ D_i &\sim \text{Normal}(\mu_i, \sigma) \\ \mu_i &= \alpha + \beta_M M_i + \beta_A A_i \\ \alpha &\sim \text{Normal}(0, 0.2) \\ \beta_{A, M} &\sim \text{Normal}(0, 0.5) \\ \sigma &\sim \text{Exponential}(1) \end{align*} \end{split}\]

其中我们标准化了所有输入变量，以便我们可以对所有截距/斜率参数先验使用标准正态分布

在模拟数据上运行统计模型

验证我们可以从与统计模型匹配的生成过程中恢复参数

def simulate_divorce(
    beta_marriage_divorce=1,
    beta_age_divorce=-1,
    beta_age_marriage=0,
    alpha=0.0,
    sigma=0.5,
    random_seed=123,
):
    N_STATES = 50
    np.random.seed(random_seed)

    # Age (standardized)
    age = stats.norm.rvs(size=N_STATES)

    # Marriage rate
    marriage_rate = 0
    if beta_marriage_divorce != 0:
        marriage_rate = age * beta_age_marriage + stats.norm(0, sigma).rvs(size=N_STATES)

    # Divorce Rate
    mu = alpha + marriage_rate * beta_marriage_divorce + age * beta_age_divorce
    divorce_rate = stats.norm.rvs(mu, sigma)

    simulated_divorce = pd.DataFrame(
        {"MedianAgeMarriage": age, "Marriage": marriage_rate, "Divorce": divorce_rate}
    )

    # Shuffle actual labels to retain same proportion of Southern/Other states
    # i.e. Southern state has no effect on parameters in this simulation
    simulated_location = WAFFLEHOUSE_DIVORCE[["Loc", "South"]].sample(frac=1.0)
    simulated_divorce.loc[:, ["Loc", "South"]] = simulated_location
    return simulated_divorce

MARRIAGE_DIVORCE_SIMULATION_PARAMS = dict(
    beta_marriage_divorce=1, beta_age_divorce=-1, beta_age_marriage=0, alpha=0, sigma=0.5
)
SIMULATED_MARRIAGE_DIVORCE = simulate_divorce(**MARRIAGE_DIVORCE_SIMULATION_PARAMS, random_seed=1)

# Plot simulation
_, axs = plt.subplots(1, 3, figsize=(12, 4))

plt.sca(axs[0])
plot_wafflehouse_pairwise(
    "Marriage", "Divorce", n_label=15, wafflehouse_divorce=SIMULATED_MARRIAGE_DIVORCE
)

plt.sca(axs[1])
plot_wafflehouse_pairwise(
    "MedianAgeMarriage", "Divorce", n_label=15, wafflehouse_divorce=SIMULATED_MARRIAGE_DIVORCE
)

plt.sca(axs[2])
plot_wafflehouse_pairwise(
    "MedianAgeMarriage", "Marriage", n_label=15, wafflehouse_divorce=SIMULATED_MARRIAGE_DIVORCE
)

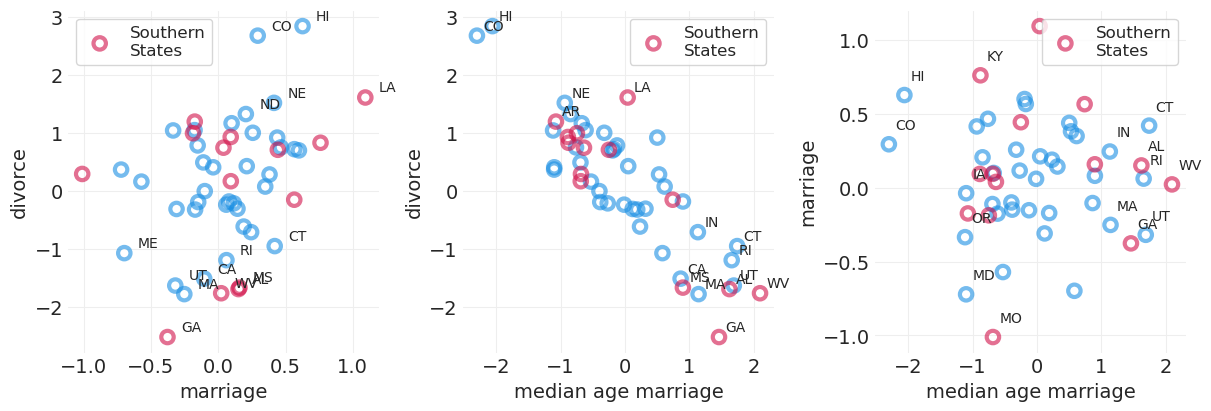
MARRIAGE_DIVORCE_MODEL_PARAMS = ["alpha", "beta_marriage", "beta_age", "sigma"]


def fit_marriage_divorce_model(data):
    with pm.Model() as divorce_model:

        # Observed Data
        age = pm.Data("age", data["MedianAgeMarriage"].values, dims="obs_ids")
        marriage_rate = pm.Data("marriage_rate", data["Marriage"].values, dims="obs_ids")
        divorce_rate = data["Divorce"].values

        sigma = pm.Exponential("sigma", 1)
        alpha = pm.Normal("alpha", 0, 0.2)
        beta_age = pm.Normal("beta_age", 0, 1)
        beta_marriage = pm.Normal("beta_marriage", 0, 1)

        ## Divorce process
        mu = alpha + beta_marriage * marriage_rate + beta_age * age
        pm.Normal("divorce_rate", mu, sigma, observed=divorce_rate, dims="obs_ids")
        divorce_inference = pm.sample(10000, target_accept=0.95)
    return divorce_model, divorce_inference


def plot_divorce_model_posterior(inference, model_params, actual_params=None, ax=None):
    if ax is None:
        _, ax = plt.subplots(figsize=(10, 2))

    plt.sca(ax)
    pm.plot_forest(inference, var_names=model_params, combined=True, ax=ax)
    title = "Posterior"
    if actual_params is not None:
        for param in actual_params:
            plt.axvline(param, color="k", linestyle="--")
        title += " and\nActual Parameter Values"
    plt.title(title)

simulated_marriage_divorce_model, simulated_marriage_divorce_inference = fit_marriage_divorce_model(
    SIMULATED_MARRIAGE_DIVORCE
)

Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [sigma, alpha, beta_age, beta_marriage]

Sampling 4 chains for 1_000 tune and 10_000 draw iterations (4_000 + 40_000 draws total) took 4 seconds.

pm.summary(simulated_marriage_divorce_inference, var_names=MARRIAGE_DIVORCE_MODEL_PARAMS)

	均值	标准差	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
alpha	0.044	0.063	-0.073	0.164	0.000	0.000	47976.0	29375.0	1.0
beta_marriage	0.928	0.164	0.605	1.224	0.001	0.001	45296.0	28420.0	1.0
beta_age	-0.980	0.067	-1.104	-0.852	0.000	0.000	47677.0	27826.0	1.0
sigma	0.458	0.049	0.368	0.548	0.000	0.000	42855.0	28475.0	1.0

plot_divorce_model_posterior(
    simulated_marriage_divorce_inference,
    model_params=MARRIAGE_DIVORCE_MODEL_PARAMS,
    actual_params=MARRIAGE_DIVORCE_SIMULATION_PARAMS.values(),
)

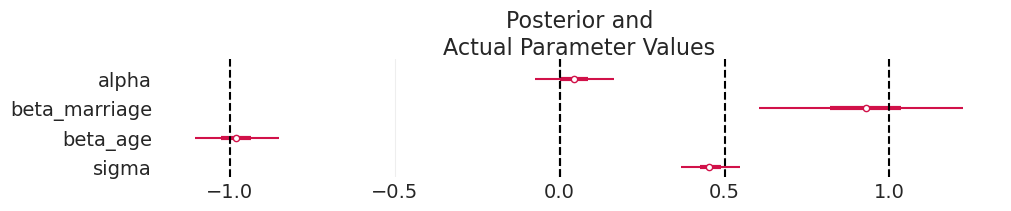
酷。 我们可以使用此模型恢复我们的参数。 让我们在真实数据上尝试一下。

# Generate a standardized version of the real data
WAFFLEHOUSE_DIVORCE_STD = WAFFLEHOUSE_DIVORCE.copy()

# standardize variables
for var in ["MedianAgeMarriage", "Marriage", "Divorce"]:
    WAFFLEHOUSE_DIVORCE_STD.loc[:, var] = utils.standardize(WAFFLEHOUSE_DIVORCE_STD[var])

marriage_divorce_model, marriage_divorce_inference = fit_marriage_divorce_model(
    WAFFLEHOUSE_DIVORCE_STD
)

Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [sigma, alpha, beta_age, beta_marriage]

Sampling 4 chains for 1_000 tune and 10_000 draw iterations (4_000 + 40_000 draws total) took 4 seconds.

plot_divorce_model_posterior(marriage_divorce_inference, model_params=MARRIAGE_DIVORCE_MODEL_PARAMS)

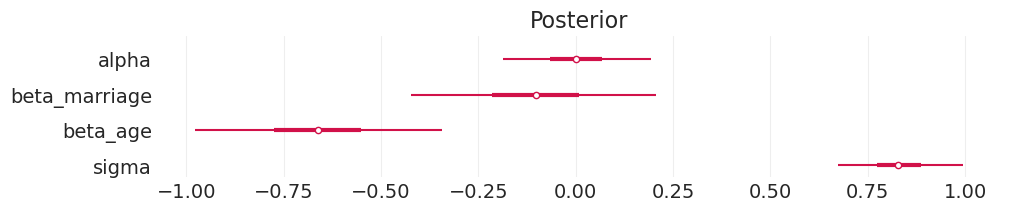
模拟干预

婚姻率对离婚率的因果效应

无干预

# Without Interventions
utils.draw_causal_graph(edge_list=[("M", "D"), ("A", "M"), ("A", "D")], graph_direction="LR")

\(do(M)\)

• 我们通过设置 \(M\) 的值来“扮演上帝”

• 删除进入 \(M\) 的箭头

  • 因此打破了 \(A\) 的关联

# With Interventions do(M)
utils.draw_causal_graph(edge_list=[("M", "D"), ("A", "D")], graph_direction="LR")

现在我们模拟两个世界，其中 \(M\) 取非常不同的值（例如 0 和 +1 标准差），以识别婚姻对年龄的可能因果效应范围。 原则上，我们可以对 \(M\) 连续范围内的任意数量的值执行此操作

np.random.seed(123)
n_simulations = int(1e3)
posterior = marriage_divorce_inference.posterior.sel(chain=0)

# Sample Ages
age_samples = stats.norm.rvs(0, 1, size=n_simulations)

# Sample parameters from posterior
alpha_samples = np.random.choice(posterior.alpha, size=n_simulations, replace=True)
sigma_samples = np.random.choice(posterior.sigma, size=n_simulations, replace=True)
beta_age_samples = np.random.choice(posterior.beta_age, size=n_simulations, replace=True)
beta_marriage_samples = np.random.choice(posterior.beta_marriage, size=n_simulations, replace=True)

marriage_contrast = {}
n_std_increase = 1
for do_marriage in [0, n_std_increase]:  # Playing God, setting the value of Marriage Rate
    mu = alpha_samples + beta_age_samples * age_samples + beta_marriage_samples * do_marriage
    marriage_contrast[do_marriage] = stats.norm.rvs(mu, sigma_samples)

marriage_contrast = marriage_contrast[n_std_increase] - marriage_contrast[0]
prob_lt_zero = (marriage_contrast < 0).mean()
az.plot_dist(marriage_contrast)
plt.axvline(0, color="k", linestyle="--")
plt.title(
    "Causal effect of increasing Marriage Rate\n"
    f"by {n_std_increase} standard deviations on Divorce Rate\n"
    f"$p(\delta < 0) = {prob_lt_zero:1.2}$"
);

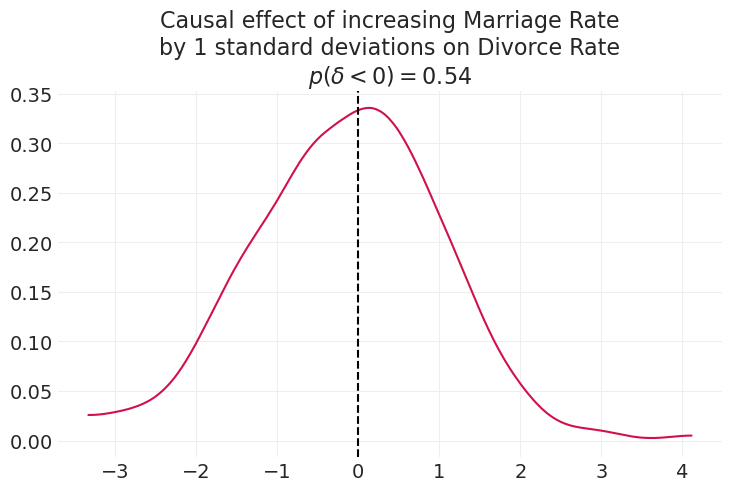
但这只是婚姻范围的一个切片。 我们可以使用 pymc 来查看在一定年龄范围内转移年龄的因果效应。

marriage_counterfactuals = xr.DataArray(np.linspace(-3, 3, 100))
age_counterfactuals = xr.DataArray(
    np.zeros_like(marriage_counterfactuals)
)  # set all to average age
with marriage_divorce_model:
    pm.set_data({"marriage_rate": marriage_counterfactuals, "age": age_counterfactuals})
    ppd_marriage_divorce = pm.sample_posterior_predictive(
        marriage_divorce_inference, extend_inferencedata=False
    )

Sampling: [divorce_rate]

az.plot_hdi(
    marriage_counterfactuals,
    ppd_marriage_divorce.posterior_predictive["divorce_rate"],
    color="C0",
    fill_kwargs={"alpha": 0.15},
)
plt.plot(
    marriage_counterfactuals,
    ppd_marriage_divorce.posterior_predictive["divorce_rate"].mean(dim=("chain", "draw")),
    color="C0",
)
plt.xlabel("marriage counterfactual (in standard deviations)")
plt.ylabel("causal effect (in std deviations)")
plt.title("Causal effect of Marriage Rate on\nDivorce Rate in standard deviations");

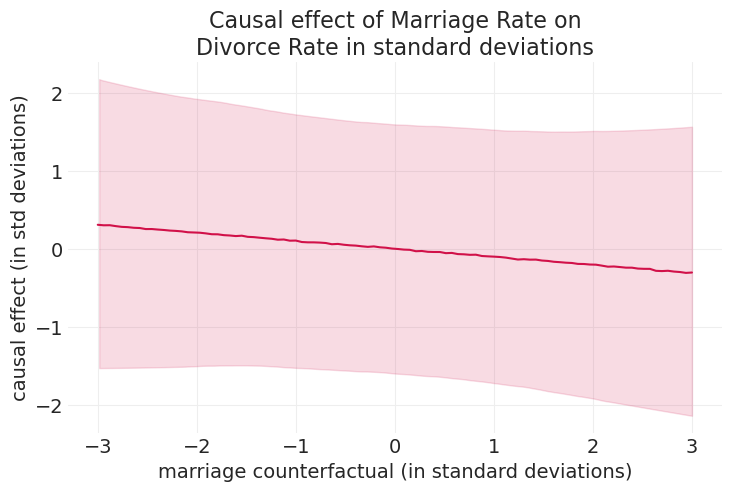
年龄对离婚率的因果效应？

• 我们如何实施 \(do(A)\)？

• 对于干预，我们不需要删除任何因果箭头

• 这需要一个忽略 \(M\) 的新模型

  • 然后我们可以模拟对 \(A\) 的任何干预

• 为什么我们可以忽略 \(M\)？

  • 因为 \(A \rightarrow M \rightarrow D\) 是 一个管道

管道 \(X \rightarrow Z \rightarrow Y\)

• \(Z\) 是 \(Χ\) 和 \(Y\) 的“中介”（\(Z\) 不影响 \(X\)）

• \(Χ\) 对 \(Y\) 的影响通过 \(Z\) 传递，因此 \(X\) 和 \(Y\) 是相关的

  • \(X \not \perp Y\)

• 一旦按 \(Z\) 分层，\(Χ\) 和 \(Y\) 之间在 \(Z\) 的每个水平 上都没有关联

  • \(X \perp Y | Z\)

• 统计上与叉形非常相似

• 因果关系上与叉形非常不同

utils.draw_causal_graph(edge_list=[("X", "Z"), ("Z", "Y")], graph_direction="LR")

离散示例

下面我们模拟一个“管道”生成过程

\[\begin{split} \begin{align*} X &\sim \text{Bernoulli}(0.5) \\ Z &\sim \text{Bernoulli}(p*) \\ Y &\sim \text{Bernoulli}(q*) \\ p^* &= 0.9 X + 0.1 (1 - X) \\ q^* &= 0.9 Z + 0.1 (1 - Z) \\ \end{align*} \end{split}\]

utils.draw_causal_graph(
    edge_list=[("X", "Z"), ("Z", "Y")],
    edge_props={("X", "Z"): {"label": "p*"}, ("Z", "Y"): {"label": "q*"}},
    graph_direction="LR",
)

np.random.seed(1234)
n_samples = 1000
X = stats.bernoulli.rvs(p=0.5, size=n_samples)

p_star = X * 0.9 + (1 - X) * 0.1
Z = stats.bernoulli.rvs(p=p_star, size=n_samples)

q_star = Z * 0.9 + (1 - Z) * 0.1
Y = stats.bernoulli.rvs(p=q_star, size=n_samples)

证明

• \(X \not \perp Y\)

• \(X \perp Y | Z\)

summarize_discrete_counfound_simulation(X, Y, Z)

Correlation between X and Y: 0.65
Cross tabulation:
     X    Y
X  396   84
Y   89  431

Correlation between X and Y conditioned on Z=0: -0.02
Cross tabulation:
     X   Y
X  392  46
Y   41   4

Correlation between X and Y conditioned on Z=1: -0.01
Cross tabulation:
    X    Y
X   4   38
Y  48  427

为什么会发生这种情况？

• \(X\) 了解的关于 \(Y\) 的所有信息，\(Z\) 都了解

• 一旦您了解了 \(Z\)，就无需再了解 \(X\) 和 \(Y\) 之间的关联

连续示例

\[\begin{split} \begin{align*} X &\sim \text{Normal}(0, 1) \\ Z &\sim \text{Bernoulli}(p^*) \\ Y &\sim \text{Normal}(\mu^*, 1) \\ p^* &= \frac{1}{1 + e^{-X}} \\ \mu^* &= 2Z - 1 \\ \end{align*} \end{split}\]

np.random.seed(1234)
n_samples = 1000

X = stats.norm.rvs(size=n_samples)
p_star = utils.invlogit(X)
Z = stats.bernoulli.rvs(p=p_star, size=n_samples)

mu_star = 2 * Z - 1
Y = stats.norm.rvs(loc=mu_star, size=n_samples)

pipe_data = pd.DataFrame(np.vstack([Z, X, Y]).T, columns=["Z", "X", "Y"])

plot_continuous_confound_simulation(pipe_data, "The Pipe\n$X \\rightarrow  Z \\rightarrow Y$")

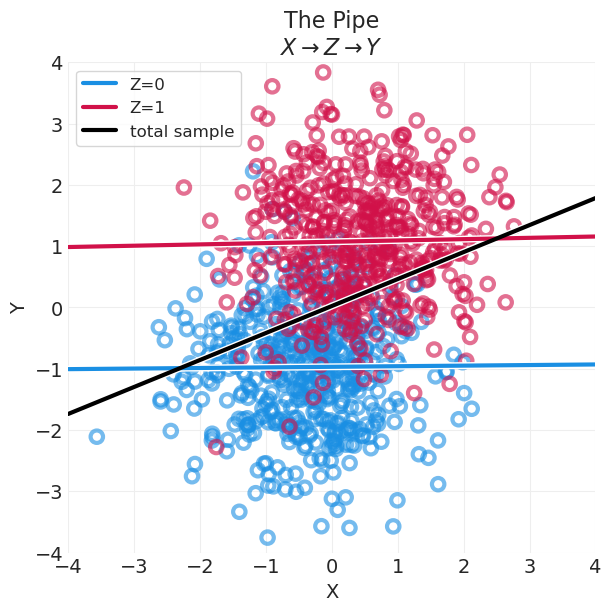
管道示例：植物生长

utils.draw_causal_graph(
    [("H0", "H1"), ("T", "H1"), ("T", "F"), ("F", "H1")],
    node_props={
        "T": {"color": "red", "label": "T, treatment"},
        "F": {"label": "F, fungus"},
        "H0": {"label": "H0, height at t0"},
        "H1": {"label": "H1, height at t1"},
    },
    edge_props={
        ("T", "H1"): {"color": "red"},
        ("T", "F"): {"color": "red"},
    },
    graph_direction="LR",
)

要估计治疗的 总因果效应，我们应该按 F 分层吗？

否

• 如果我们要估计 T 对 H1 的总因果效应，按 F 分层将是一个坏主意，因为图中存在 \(T \rightarrow F \rightarrow H1\) 管道。

• 按 F 分层会阻止有关 T 对 H1 的影响的信息通过 F 流动。

• 注意：按 \(F\) 分层将给出 \(T\) 对 \(H1\) 的 直接因果效应

这是一个 治疗后偏差 的示例。

经验法则：治疗的后果不应包含在估计器中。

年龄对离婚率的因果效应的统计模型

McElreath 提到了我们如何/应该构建和测试此模型，但在讲座中没有这样做，因此我们在此处进行！

年龄-离婚模型与婚姻-离婚模型相似，但我们不再需要按婚姻分层。

\[\begin{split} \begin{align*} D &= f(A, M) \\ D_i &\sim \text{Normal}(\mu_i, \sigma) \\ \mu_i &= \alpha + \beta_A A_i \\ \alpha &\sim \text{Normal}(0, 0.2) \\ \beta_A &\sim \text{Normal}(0, 1) \\ \sigma &\sim \text{Exponential}(1) \end{align*} \end{split}\]

AGE_DIVORCE_MODEL_PARAMS = ["sigma", "alpha", "beta_age"]


def fit_age_divorce_model(data):
    with pm.Model() as divorce_model:

        # Observed Data
        age = pm.Data("age", data["MedianAgeMarriage"].values, dims="obs_ids")

        alpha = pm.Normal("alpha", 0, 0.2)
        beta_age = pm.Normal("beta_age", 0, 1)
        sigma = pm.Exponential("sigma", 1)

        ## Divorce process
        mu = alpha + beta_age * age
        pm.Normal("divorce_rate", mu, sigma, observed=data["Divorce"].values, dims="obs_ids")
        divorce_inference = pm.sample(10000, target_accept=0.95)
    return divorce_model, divorce_inference

在模拟数据上测试年龄-离婚模型

AGE_DIVORCE_SIMULATION_PARAMS = dict(
    beta_age_divorce=-1.0, sigma=0.5, alpha=0.0, beta_marriage_divorce=0, beta_age_marriage=0
)
SIMULATED_AGE_DIVORCE = simulate_divorce(**AGE_DIVORCE_SIMULATION_PARAMS)

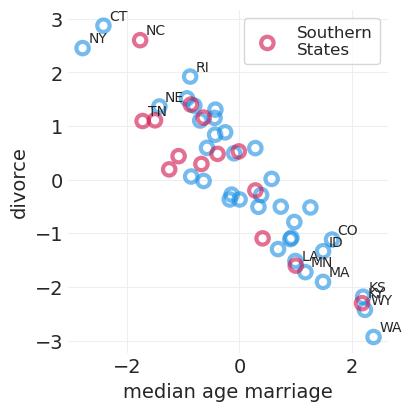
# Plot simulation
plt.subplots(figsize=(4, 4))
plot_wafflehouse_pairwise(
    "MedianAgeMarriage", "Divorce", n_label=15, wafflehouse_divorce=SIMULATED_AGE_DIVORCE
)

simulated_age_divorce_model, simulated_age_divorce_inference = fit_age_divorce_model(
    SIMULATED_AGE_DIVORCE
)

Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [alpha, beta_age, sigma]

Sampling 4 chains for 1_000 tune and 10_000 draw iterations (4_000 + 40_000 draws total) took 3 seconds.

plot_divorce_model_posterior(
    simulated_age_divorce_inference,
    model_params=AGE_DIVORCE_MODEL_PARAMS,
    actual_params=AGE_DIVORCE_SIMULATION_PARAMS.values(),
)

🤘

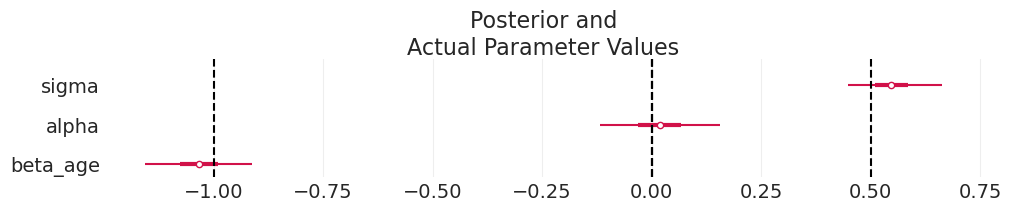
我们可以恢复模拟参数。

在真实数据上拟合年龄-离婚模型

age_divorce_model, age_divorce_inference = fit_age_divorce_model(WAFFLEHOUSE_DIVORCE_STD)

Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [alpha, beta_age, sigma]

Sampling 4 chains for 1_000 tune and 10_000 draw iterations (4_000 + 40_000 draws total) took 3 seconds.

plot_divorce_model_posterior(age_divorce_inference, model_params=AGE_DIVORCE_MODEL_PARAMS)

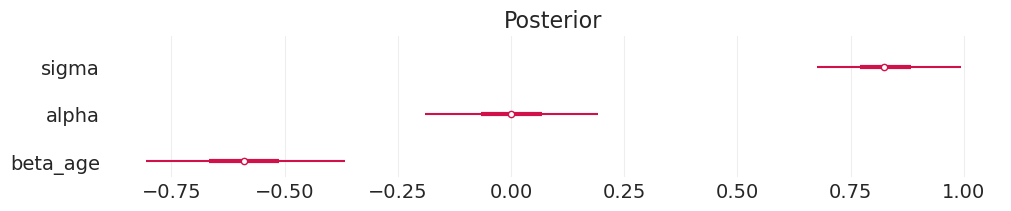
运行年龄反事实

age_counterfactuals = xr.DataArray(np.linspace(-3, 3, 100))

with age_divorce_model:
    pm.set_data({"age": age_counterfactuals})
    ppd_age = pm.sample_posterior_predictive(age_divorce_inference, extend_inferencedata=False)

Sampling: [divorce_rate]

az.plot_hdi(
    age_counterfactuals,
    ppd_age.posterior_predictive["divorce_rate"],
    color="C0",
    fill_kwargs={"alpha": 0.15},
)
plt.plot(
    age_counterfactuals,
    ppd_age.posterior_predictive["divorce_rate"].mean(dim=("chain", "draw")),
    color="C0",
)
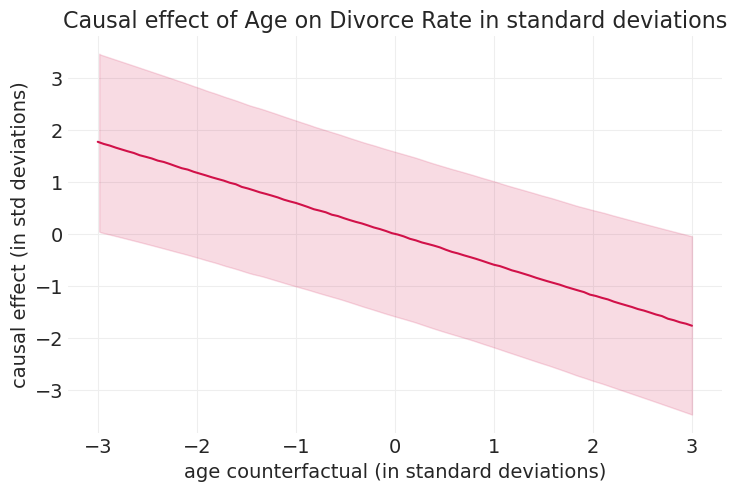
plt.xlabel("age counterfactual (in standard deviations)")
plt.ylabel("causal effect (in std deviations)")
plt.title("Causal effect of Age on Divorce Rate in standard deviations");

碰撞器 \(X \rightarrow Z \leftarrow Y\)

• \(Z\) 由 \(Χ\) 和 \(Y\) 共同导致

• \(X\) 和 \(Y\) 没有共同的原因，因此不相关联

  • \(X \perp Y\)

• 一旦按 \(Z\) 分层，\(Χ\) 和 \(Y\) 现在相关联

  • \(X \not \perp Y | Z\)

  • 按 \(Z\) 分层提供有关 \(X\) 和 \(Y\) 的信息

utils.draw_causal_graph(edge_list=[("X", "Z"), ("Y", "Z")])

离散示例

下面我们模拟一个“碰撞器”生成过程

\[\begin{split} \begin{align*} X &\sim \text{Bernoulli}(0.5) \\ Y &\sim \text{Bernoulli}(0.5) \\ Z &\sim \text{Bernoulli}(p*) \\ p^* &= \begin{cases} 0.9 ,& \text{if } X + Y \gt 0\\ 0.05, & \text{otherwise} \end{cases} \end{align*} \end{split}\]

utils.draw_causal_graph(
    edge_list=[("X", "p_star"), ("Y", "p_star"), ("p_star", "Z")],
    node_props={"p_star": {"label": "p*", "color": "green", "fontcolor": "green"}},
    edge_props={("p_star", "Z"): {"color": "green"}},
    graph_direction="LR",
)

注意：上面的结构不应与稍后讨论的“后代”混淆。 这里 \(p^*\) 是 \(X\) 和 \(Y\) 的确定性函数，它定义了 \(Z\) 的概率分布，而在后代中，下游变量（例如 \(A\)）“泄漏”有关碰撞器的信息。

np.random.seed(123)
n_samples = 1000

X = stats.bernoulli.rvs(p=0.5, size=n_samples)
Y = stats.bernoulli.rvs(p=0.5, size=n_samples)

# p(z | x, y)
p_star = np.where(X + Y > 0, 0.9, 0.05)
Z = stats.bernoulli.rvs(p=p_star, size=n_samples)

证明

• \(X \perp Y\)

• \(X \not \perp Y | Z\)

summarize_discrete_counfound_simulation(X, Y, Z)

Correlation between X and Y: -0.052
Cross tabulation:
     X    Y
X  240  268
Y  258  234

Correlation between X and Y conditioned on Z=0: 0.41
Cross tabulation:
     X   Y
X  229  21
Y   23  22

Correlation between X and Y conditioned on Z=1: -0.49
Cross tabulation:
     X    Y
X   11  247
Y  235  212

连续示例

\[\begin{split} \begin{align*} X &\sim \text{Normal}(0, 1) \\ Y &\sim \text{Normal}(0, 1) \\ Z &\sim \text{Bernoulli}(p*) \\ p^* &= \frac{1}{1 + e^{-(\alpha + \beta_{XZ}X + \beta_{YZ}Y)}} \\ \end{align*} \end{split}\]

np.random.seed(1234)

n_samples = 500
X = stats.norm.rvs(size=n_samples)
Y = stats.norm.rvs(size=n_samples)

beta_XZ = 2
beta_YZ = 2
alpha = -2

p_star = utils.invlogit(alpha + beta_XZ * X + beta_YZ * Y)
Z = stats.bernoulli.rvs(p=p_star)

collider_data = pd.DataFrame(np.vstack([Z, X, Y]).T, columns=["Z", "X", "Y"])

plot_continuous_confound_simulation(
    collider_data, "The Collider\n$X \\rightarrow  Z \\leftarrow Y$"
)

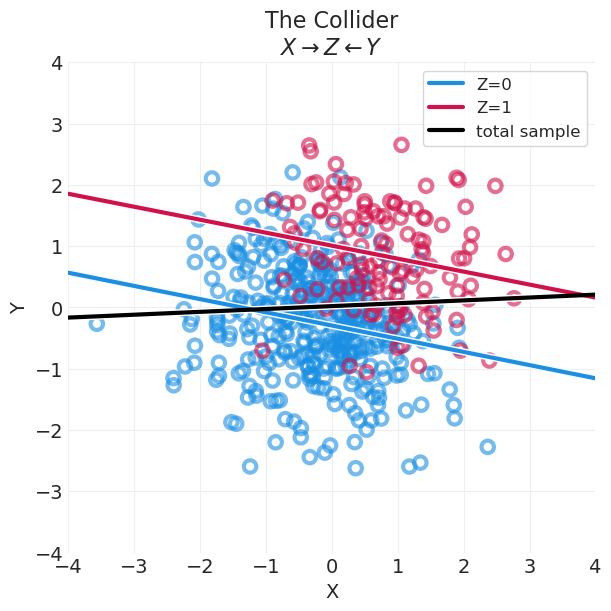
• 总样本显示没有关联

• 按 Z 分层显示负相关

为什么会发生这种情况？

阈值效应

• 如果 \(X\) 或 \(Y\) 中的任何一个足够大，它将导致一个条件值（上面的绿色确定性函数 \(p*\)），该值足够大，可以将样本与 \(Z=1\) 相关联。

• 类似地，如果 \(X\) 或 \(Y\) 中的任何一个足够小，它将使样本与 \(Z=0\) 相关联。

• 如果其中一个是足够高/低，而另一个是平均值或更低/更大，这将平均导致负相关。

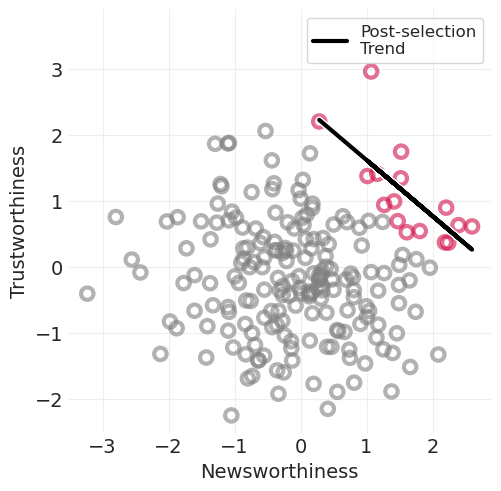
碰撞器示例： grants 奖励

\(N \rightarrow A \leftarrow T\)

• 要获得 \(A\) 奖励，grants 必须足够具有新闻价值 \(N\) 或值得信赖 \(T\)

• 很少有 grants 在两者上都很高

• 导致奖励 grants 出现负相关

• 后选择偏差

np.random.seed(123)
n_samples = 200

# N and T are independent
N = stats.norm.rvs(size=n_samples)
T = stats.norm.rvs(size=n_samples)

# Award criterion; either are large enough to threshold
A = np.where(N + T > 2, 1, 0)

for awarded in [0, 1]:
    color = "gray" if not awarded else "C0"
    N_A = N[A == awarded]
    T_A = T[A == awarded]
    utils.plot_scatter(N_A, T_A, color=color)

awarded_model = smf.ols("T ~ N", data=pd.DataFrame({"N": N_A, "T": T_A})).fit()
utils.plot_line(N_A, awarded_model.predict(), color="k", label="Post-selection\nTrend")
plt.xlabel("Newsworthiness")
plt.ylabel("Trustworthiness")
plt.axis("square")
plt.legend();

示例：年龄、幸福感和婚姻

\(A \rightarrow M \leftarrow H\)

• 你年龄越大，结婚的机会就越多

• 你越幸福，你就越和蔼可亲，因此更有可能与另一个人结婚

• 在这里，年龄不影响幸福感，它们是独立的

下面是讲座中模拟的粗略版本。 我们没有运行从 18 岁开始的时间模拟，也没有对每个时间点的每种幸福水平的婚姻状况进行抽样，而是仅在一个样本中进行了整个模拟，将结婚概率建模为年龄 \(A\) 和幸福感 \(H\) 的组合：\(p_{married} = \text{invlogit}(\beta_H (\bar H - 18) + \beta_A A)\)

age = np.arange(1, 71)
happiness = np.linspace(-2, 2, 40)
age_grid, happiness_grid = np.meshgrid(age, happiness)

# Arbitrary
beta_happiness = 20
beta_age = 1
min_marriage_age = 18

age_grid = age_grid.ravel()
happiness_grid = happiness_grid.ravel()
married_grid = []
for a, h in zip(age_grid, happiness_grid):
    p_marriage = utils.invlogit(h * beta_happiness + (a - 40 - 18) * beta_age)
    married_grid.append(stats.bernoulli(p=p_marriage).rvs())

married_grid = np.array(married_grid).astype(int)

utils.plot_scatter(
    age_grid[married_grid == 0],
    happiness_grid[married_grid == 0],
    s=20,
    alpha=1,
    color="lightgray",
    label="Unarried",
)
utils.plot_scatter(
    age_grid[married_grid == 1],
    happiness_grid[married_grid == 1],
    s=20,
    alpha=1,
    color="C0",
    label="Married",
)
plt.xlabel("Age")
plt.ylabel("Happiness (std)")
plt.legend();

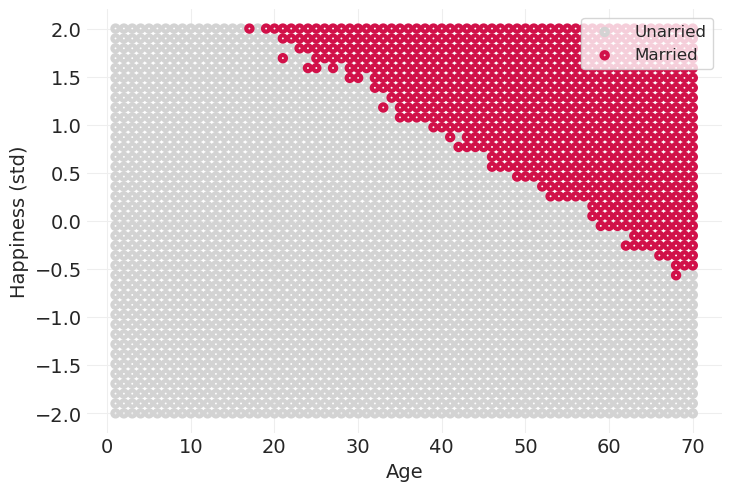
如果我们要仅按已婚人士（\(M=1\)）分层，我们将得出结论，年龄和幸福感呈负相关，尽管它们在此模拟中实际上是独立的。

碰撞器示例：餐厅成功

utils.draw_causal_graph(
    edge_list=[("F", "S"), ("L", "S")],
    node_props={
        "F": {"label": "Food Quality, F"},
        "L": {"label": "Location Quality, L"},
        "S": {"label": "Restaurant Successful, S"},
    },
)

模拟餐厅成功

\[\begin{split} \begin{align*} S &\sim \text{Bernoulli}(p_S) \\ p_S &= \text{invlogit}(\alpha+ \beta_Q Q + \beta_L L) \\ \end{align*} \end{split}\]

np.random.seed(123)
n_restaurants = 1000
food_quality = stats.norm.rvs(size=n_restaurants)  # standardized food quality
location_quality = stats.norm.rvs(size=n_restaurants)  # standardized quality of restaurant location

beta_food_quality = 20  # good food increases probability of success
beta_location_quality = 20  # good location also increases probability of success
intercept = -40  # the average restaurant will not succeed

p_success = utils.invlogit(
    food_quality * beta_food_quality + location_quality * beta_location_quality + intercept
)
stays_in_business = stats.bernoulli.rvs(p_success)

data = data = pd.DataFrame(
    np.vstack([location_quality, food_quality, stays_in_business]).T,
    columns=["location_quality", "food_quality", "stays_in_business"],
)

models = {}
models["unstratified"] = smf.ols("food_quality ~ location_quality", data=data).fit()

# Stratified Models (post-hoc selection based on successful business)
models["business_failed"] = smf.ols(
    "food_quality ~ location_quality", data=data[data.stays_in_business == 0]
).fit()
models["business_succeeded"] = smf.ols(
    "food_quality ~ location_quality", data=data[data.stays_in_business == 1]
).fit()

def plot_sms_restaurant_model_fit(model, xs, label, color):
    """Helper function to plot linear models"""
    params = model.params
    ys = params.Intercept + params.location_quality * xs
    return utils.plot_line(xs, ys, label=label, color=color)

xs = np.linspace(-4, 4, 20)

for sib, label in enumerate(["business_failed", "business_succeeded"]):
    scatter_data = data[data.stays_in_business == sib]
    utils.plot_scatter(
        scatter_data.location_quality,
        scatter_data.food_quality,
        color=f"C{sib}",
        label="successful" if sib else "failed",
    )

    plot_sms_restaurant_model_fit(models[label], xs, color=f"C{sib}", label=None)

plot_sms_restaurant_model_fit(models["unstratified"], xs, label="unstratified", color="black")

plt.xlabel("location quality (standardized)")
plt.ylabel("food quality (standardized)")

plt.xlim([-4, 4])
plt.ylim([-4, 4])
plt.legend();

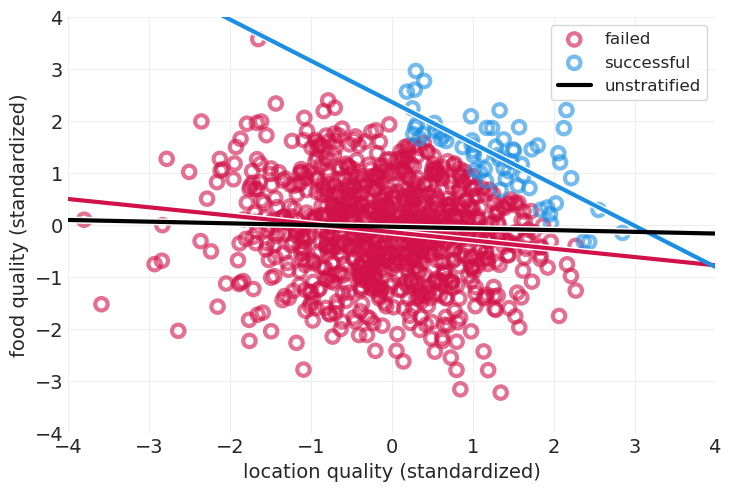
通过仅查看成功的餐厅，我们将误导自己并推断出位置质量较低的餐厅食物更好，而实际上位置和食物质量之间没有关系。

后代

呈现父级的稀释行为。

• 如果父级形成碰撞器，则后代充当弱碰撞器。 管道和叉形后代也是如此

离散示例：管道后代

在此示例中，后代从管道分支出来。 因此，我们应该观察到以下情况

• \(X \not \perp Y\)

• \(X \perp Y | Z\)

• \(X \not \perp Y | A\)，但 X 和 Y 之间的相关性应降低

utils.draw_causal_graph(edge_list=[("X", "Z"), ("Z", "A"), ("Z", "Y")], graph_direction="LR")

\[\begin{split} \begin{align*} X &\sim \text{Bernoulli}(0.5) \\ Z &\sim \text{Bernoulli}(p^*) \\ A &\sim \text{Bernoulli}(q^*) \\ Y &\sim \text{Bernoulli}(r^*) \\ p^* &= 0.9 X + 0.1 (1 - X) \\ q^* &= 0.9 Z + 0.1 (1 - Z) \\ r^* &= 0.9 Z + 0.1 (1 - Z) \\ \end{align*} \end{split}\]

utils.draw_causal_graph(
    edge_list=[("X", "Z"), ("Z", "A"), ("Z", "Y")],
    edge_props={
        ("X", "Z"): {"label": "p*"},
        ("Z", "A"): {"label": "q*"},
        ("Z", "Y"): {"label": "r*"},
    },
    graph_direction="LR",
)

n_samples = 1000

X = stats.bernoulli.rvs(p=0.5, size=n_samples)

p_star = 0.9 * X + 0.1 * (1 - X)
Z = stats.bernoulli.rvs(p=p_star, size=n_samples)

q_star = 0.9 * Z + 0.1 * (1 - Z)
A = stats.bernoulli.rvs(p=q_star, size=n_samples)

r_star = 0.9 * Z + 0.1 * (1 - Z)
Y = stats.bernoulli.rvs(p=r_star, size=n_samples)

证明

• \(X \not \perp Y\)

• \(X \perp Y | Z\)

summarize_discrete_counfound_simulation(X, Y, A)

Correlation between X and Y: 0.71
Cross tabulation:
     X    Y
X  425   66
Y   79  430

Correlation between X and Y conditioned on Z=0: 0.43
Cross tabulation:
     X   Y
X  378  40
Y   42  45

Correlation between X and Y conditioned on Z=1: 0.53
Cross tabulation:
    X    Y
X  47   26
Y  37  385

离散示例：碰撞器后代

在此示例中，后代从碰撞器分支出来。 因此，我们应该观察到以下情况

• \(X \perp Y\)

• \(X \not \perp Y | Z\)

• \(X \not \perp Y | A\)

utils.draw_causal_graph(edge_list=[("X", "Z"), ("Z", "A"), ("Y", "Z")], graph_direction="LR")

\[\begin{split} \begin{align*} X &\sim \text{Normal}(0, 1) \\ Y &\sim \text{Normal}(0, 1) \\ Z &\sim \text{Bernoulli}(p*) \\ A &\sim \text{Bernoulli}(q^*) \\ p^* &= \begin{cases} 0.9 ,& \text{if } X + Y \gt 2\\ 0.1, & \text{otherwise} \end{cases} \\ q^* &= 0.05 Z + 0.95 (1 - Z) \end{align*} \end{split}\]

n_samples = 1000

X = stats.norm.rvs(size=n_samples)
Y = stats.norm.rvs(size=n_samples)

p_star = np.where(X + Y > 2, 0.9, 0.1)
Z = stats.bernoulli.rvs(p=p_star, size=n_samples)

q_star = 0.95 * Z + 0.05 * (1 - Z)
A = stats.bernoulli.rvs(p=q_star, size=n_samples)

print(f"Correlation between X and Y: {np.corrcoef(X, Y)[0, 1]:1.2}")
for a in [0, 1]:
    print(
        f"Correlation between X and Y conditioned on A={a}: {np.corrcoef(X[A==a], Y[A==a])[0, 1]:1.2}"
    )

Correlation between X and Y: 0.035
Correlation between X and Y conditioned on A=0: -0.081
Correlation between X and Y conditioned on A=1: 0.21

后代无处不在

• 许多测量是我们要测量的对象的 代理

未观察到的混淆因素

• 混淆因素无处不在，并且会毁了你的一天

• 有些控制比其他控制更好

• 通常，尝试控制某些变量可能会打开通往未观察到的混淆因素的路径； 我们必须始终意识到这种可能性

作者

• 移植到 PyMC：Dustin Stansbury (2024)

• 基于 Richard McElreath 的 Statistical Rethinking (2023) 讲座

%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,aeppl,xarray

Last updated: Tue Dec 17 2024

Python implementation: CPython
Python version       : 3.12.5
IPython version      : 8.27.0

pytensor: 2.26.4
aeppl   : not installed
xarray  : 2024.7.0

numpy      : 1.26.4
arviz      : 0.19.0
pandas     : 2.2.2
pymc       : 5.19.1
scipy      : 1.14.1
re         : 2.2.1
statsmodels: 0.14.2
matplotlib : 3.9.2
xarray     : 2024.7.0

Watermark: 2.5.0

许可证声明

此示例库中的所有笔记本均根据 MIT 许可证 提供，该许可证允许修改和再分发以用于任何用途，前提是保留版权和许可证声明。

引用 PyMC 示例

要引用此笔记本，请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。

重要提示

许多笔记本改编自其他来源：博客、书籍... 在这种情况下，您也应该引用原始来源。

另请记住引用您的代码使用的相关库。

这是一个 bibtex 中的引用模板

@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}

一旦渲染，它可能看起来像