好的和坏的控制#

本笔记本是 Richard McElreath 的 Statistical Rethinking 2023 系列讲座的 PyMC 移植版本的一部分。

# Ignore warnings
import warnings

import arviz as az
import numpy as np
import pandas as pd
import pymc as pm
import statsmodels.formula.api as smf
import utils as utils
import xarray as xr

from matplotlib import pyplot as plt
from matplotlib import style
from scipy import stats as stats

warnings.filterwarnings("ignore")

# Set matplotlib style
STYLE = "statistical-rethinking-2023.mplstyle"
style.use(STYLE)

不惜一切代价避免耍小聪明#

耍小聪明是

不可靠的
不透明的

使用显式因果模型可以让人

使用逻辑推导含义
验证工作和假设
方便同行评审和验证

混杂因素#

回顾#

分叉 \(X \leftarrow Z \rightarrow Y\)
- \(X\) 和 \(Y\) 是相关的，除非我们按 \(Z\) 分层
管道 \(X \rightarrow Z \rightarrow Y\)
- \(X\) 和 \(Y\) 是相关的，除非我们按 \(Z\) 分层
碰撞 \(X \rightarrow Z \leftarrow Y\)
- \(X\) 和 \(Y\) 是不相关的，除非我们按 \(Z\) 分层
后代 \(Z \rightarrow A\)
- 后代 \(A\) 继承了父代 \(Z\) 的行为

utils.draw_causal_graph(
    edge_list=[("U", "X"), ("U", "Y"), ("X", "Y")],
    node_props={
        "X": {"label": "treatment, X"},
        "Y": {"label": "outcome, Y"},
        "U": {"label": "confound, U", "style": "dashed"},
        "unmeasured": {"style": "dashed"},
    },
    graph_direction="LR",
)

../_images/f076109de1e7d8ecc4abf08e618b077f79cbe23e0ff05f29247679a8ba778933.svg

utils.draw_causal_graph(
    edge_list=[("U", "X"), ("U", "Y"), ("X", "Y"), ("R", "X")],
    node_props={
        "X": {"label": "treatment, X"},
        "Y": {"label": "outcome, Y"},
        "U": {"label": "confound, U", "style": "dashed"},
        "R": {"label": "randomization, R"},
        "unmeasured": {"style": "dashed"},
    },
    edge_props={("U", "X"): {"color": "lightgray"}},
    graph_direction="LR",
)

../_images/457bd8644f1ebd5a73667d802ef2389e79dd3677db1a1675c7dbc6573bb71ddf.svg

黄金标准是 随机化。然而，随机化通常是不可能的

不可能的
实用主义
伦理考量
未测量的混杂因素

因果思考#

我们想要一个程序 \(do(X)\)，它以某种方式干预 \(X\)，使其可以“模仿”随机化的效果。
这样的程序将转换混杂图

没有随机化#

utils.draw_causal_graph(
    [
        ("U", "X"),
        ("U", "Y"),
        ("X", "Y"),
    ],
    graph_direction="LR",
)

../_images/cd456ec6c9461e3507147ef461166b1c220f29acc2eaf89c36e09318182380d0.svg

以这样一种方式，所有进入 X 的非因果箭头都已被移除

通过 \(do(X)\) 诱导的“随机化”#

utils.draw_causal_graph(
    [
        ("U", "Y"),
        ("X", "Y"),
    ],
    edge_props={("X", "Y"): {"label": "do(X)   "}},
    graph_direction="LR",
)

../_images/38473a03ba2091d24b3e083985fcff67e2242df46c419b674920b0b79fa49bcf.svg

事实证明，我们可以分析图结构来确定是否存在这样的程序

示例：简单混杂#

utils.draw_causal_graph(
    edge_list=[("U", "Y"), ("U", "X"), ("X", "Y")],
    node_props={
        "U": {"color": "red"},
    },
    edge_props={("U", "X"): {"color": "red"}, ("U", "Y"): {"color": "red"}},
    graph_direction="LR",
)

../_images/02abbf1328b44c29aecc81cc2b0959e3a2c4e78cafe3d173d15749984ccffa79.svg

在分叉示例中，我们已经表明，通过按混杂因素分层，我们通过对 U 进行条件化来“关闭”分叉，从而消除 U 对 X 的任何因果效应，从而使我们能够隔离治疗对 Y 的影响。

此过程是所谓的 Do 演算的一部分。运算符 do(X) 倾向于表示对 X 进行干预（即将其设置为独立于混杂因素的特定值）

\[ p(Y | do(X)) = \sum_U p(Y | X, U)p(U) = \mathbb{E}_U[p(Y | X, U)] \]

即，为我们提供 X 干预的程序等同于 Y 的分布，按治疗 X 和混杂因素 U 分层，并在混杂因素的分布上取平均值。

请注意，当我们对每个 X 使用线性回归估计器时，我们隐含地对我们的治疗和混杂因素进行边缘化和平均（例如，在模型形式 \(Y \sim \mathcal{N}(\alpha + \beta_X X + \beta_Z Z, \sigma^2)\) 中

通常，模型中将 X 与 Y 相关联的不是估计的系数
它是当我们更改 X 时 Y 的分布，在由控制/混杂变量（即 U）定义的分布上取平均值

Do 演算#

应用于 DAG，提供了一组用于识别 \(p(Y | do(X))\) 的规则
在选择函数或分布之前，告知什么是可能的
证明图形分析的合理性
如果 Do 演算声称推理是可能的，则不需要进一步的特殊假设来进行推理
- 通常，额外的假设可以使推理更强大

后门准则#

使用肉眼以图形方式应用 Do 演算的快捷方式。 用于查找要条件化的变量的最小充分调整集的一般规则。

识别连接治疗 X 和结果 Y 的所有路径，包括进入和退出 X 的路径（关联可以是直接/非直接的，因果关系是直接的）
那些进入 X 的路径中的任何一条都是后门（非因果）路径
找到变量的调整集，一旦条件化，它将“关闭/阻止”在其中识别出的所有后门路径

后门准则示例#

utils.draw_causal_graph(
    [("U", "Z"), ("Z", "X"), ("U", "Y"), ("X", "Y")],
    node_props={"Z": {"color": "red"}, "U": {"style": "dashed"}},
    edge_props={
        ("U", "Z"): {"color": "red"},
        ("Z", "X"): {"color": "red"},
        ("U", "Y"): {"color": "red"},
    },
    graph_direction="LR",
)

../_images/498111632055e1648c9cb65a17422b6ea33630a1dfc858e000f911fc1a85ff26.svg

后门路径以红色突出显示。

如果我们能够测量 \(U\)，我们可以只按 \(U\) 分层；但是，它是未观察到的。
但是，尽管无法测量 \(U\)，我们仍然可以通过对 \(Z\) 进行条件化来阻止后门路径。
这是可行的，因为 \(Z\) “知道”我们需要了解的关于 \(X\)、\(Y\) 之间关联的所有信息，这些信息是由于未测量的混杂因素 \(U\) 造成的。

按 \(Z\) 分层后的结果图#

\(U \rightarrow Z \rightarrow X\) 管道现在已被打破，将 \(X\) 与混杂因素 \(U\) 解除关联
注意：这不会消除混杂因素对 \(Y\) 的影响

utils.draw_causal_graph(
    [("U", "Z"), ("Z", "X"), ("U", "Y"), ("X", "Y")],
    node_props={"Z": {"color": "red"}, "U": {"style": "dashed"}},
    edge_props={
        ("U", "Z"): {"color": "red"},
        ("Z", "X"): {"color": "none"},
        ("U", "Y"): {"color": "red"},
    },
    graph_direction="LR",
)

../_images/64f0adfae4032a002ac4e36f769dbb8c9d5de5605380b84898ef9232d852b654.svg

通过模拟验证#

在这里，我们模拟了一种情况，其中 Y 是由 X 和未测量的混杂因素 U 引起的，U 也影响 Z 和 X。（我们也可以用数学方法证明，但模拟也相当有说服力——至少对我来说是这样）

\[\begin{split} \begin{align*} U &\sim \text{Bernoulli}(0.5) \\ Z &\sim \text{Normal}(\beta_{UZ}U, 1) \\ X &\sim \text{Normal}(\beta_{ZX}Z, 1) \\ Y &\sim \text{Normal}(\alpha + \beta_{XY}X + \beta_{UY}U, 1) \\ \end{align*} \end{split}\]

np.random.seed(123)
n_samples = 200

alpha = 0
beta_XY = 0
beta_UY = -1
beta_UZ = -1
beta_ZX = 1

U = stats.bernoulli.rvs(p=0.5, size=n_samples)
Z = stats.norm.rvs(loc=beta_UZ * U)
X = stats.norm.rvs(loc=beta_ZX * Z)
Y = stats.norm.rvs(loc=alpha + beta_XY * X + beta_UY * U)

未分层（混杂）模型#

\[\begin{split} \begin{align*} Y &\sim \text{Normal}(\mu_Y, \sigma_Y) \\ \mu_Y &= \alpha + \beta_{XY}X \\ \alpha &\sim \text{Normal}(0, 1) \\ \beta_{XY} &\sim \text{Normal}(0, 1) \\ \sigma_Y &\sim \text{Exponential}(1) \end{align*} \end{split}\]

拟合未分层模型，忽略 Z（和 U）#

with pm.Model() as unstratified_model:
    # Priors
    alpha_ = pm.Normal("alpha", 0, 1)
    beta_XY_ = pm.Normal("beta_XY", 0, 1)
    sigma_ = pm.Exponential("sigma", 1)

    # Likelihood
    mu_ = alpha_ + beta_XY_ * X
    Y_ = pm.Normal("Y", mu=mu_, sigma=sigma_, observed=Y)
    unstratified_model_inference = pm.sample()

Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [alpha, beta_XY, sigma]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.

az.summary(unstratified_model_inference)

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
alpha	-0.381	0.084	-0.535	-0.219	0.001	0.001	3503.0	3034.0	1.0
beta_XY	0.148	0.055	0.043	0.244	0.001	0.001	3763.0	3040.0	1.0
sigma	1.114	0.058	1.015	1.227	0.001	0.001	6091.0	3259.0	1.0

按 Z 分层（非混杂）#

\[\begin{split} \begin{align*} Y &\sim \text{Normal}(\mu_Y, \sigma_Y) \\ \mu_Y = &\alpha + \beta_{XY}X + \beta_{Z}Z \\ \alpha &\sim \text{Normal}(0, 1) \\ \beta_{*} &\sim \text{Normal}(0, 1) \\ \sigma_Y &\sim \text{Exponential}(1) \end{align*} \end{split}\]

# Fit the stratified Model
with pm.Model() as stratified_model:
    # Priors
    alpha_ = pm.Normal("alpha", 0, 1)
    beta_XY_ = pm.Normal("beta_XY", 0, 1)
    beta_Z_ = pm.Normal("beta_Z", 0, 1)
    sigma_ = pm.Exponential("sigma", 1)

    # Likelihood (includes Z)
    mu_ = alpha_ + beta_XY_ * X + beta_Z_ * Z
    Y_ = pm.Normal("Y", mu=mu_, sigma=sigma_, observed=Y)
    stratified_model_inference = pm.sample()

Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [alpha, beta_XY, beta_Z, sigma]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.

az.summary(stratified_model_inference)

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
alpha	-0.286	0.091	-0.450	-0.109	0.002	0.001	3570.0	2743.0	1.0
beta_XY	-0.026	0.078	-0.181	0.114	0.001	0.001	2989.0	2631.0	1.0
beta_Z	0.318	0.106	0.118	0.515	0.002	0.001	2650.0	2469.0	1.0
sigma	1.091	0.055	0.983	1.190	0.001	0.001	3813.0	2660.0	1.0

注意：模型系数 beta_Z 在 \(Z\) 对 \(Y\) 的因果效应方面没有任何意义。为了确定 \(Z\) 对 \(Y\) 的因果效应，您需要一个不同的估计器。一般来说，调整集中的变量是不可解释的。这与“表 2 谬误”有关

比较分层模型和未分层模型#

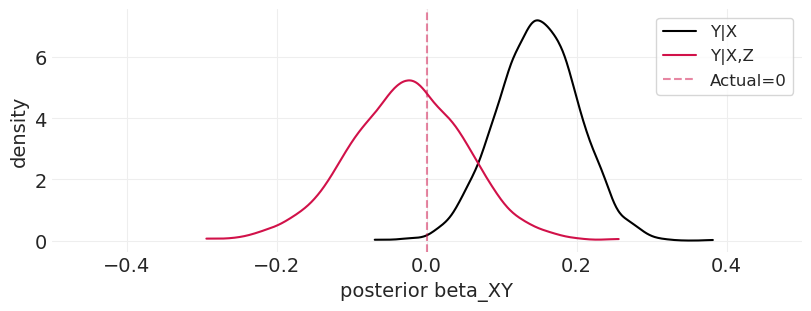
_, ax = plt.subplots(figsize=(8, 3))
az.plot_dist(unstratified_model_inference.posterior.beta_XY, color="k", label="Y|X", ax=ax)
az.plot_dist(stratified_model_inference.posterior.beta_XY, color="C0", label="Y|X,Z", ax=ax)
plt.axvline(beta_XY, color="C0", linestyle="--", alpha=0.5, label=f"Actual={beta_XY}")
plt.xlim([-0.5, 0.5])
plt.xlabel("posterior beta_XY")
plt.ylabel("density")
plt.legend();

../_images/d1a95b071b8657ccc42a02f43f9b770c06d19ae050808023c481ecf40f752bf6.png

更复杂的示例#

utils.draw_causal_graph(
    edge_list=[
        ("A", "Z"),
        ("A", "X"),
        ("Z", "X"),
        ("B", "Z"),
        ("B", "Y"),
        ("Z", "Y"),
        ("X", "Y"),
        ("C", "X"),
        ("C", "Y"),
    ],
    graph_direction="LR",
)

../_images/af4927adeee072c378aab5b8dea2a16f5eb87f5aacfb5937da373fe90a7e4362.svg

连接 X 到 Y 的所有路径#

utils.draw_causal_graph(
    edge_list=[
        ("A", "Z"),
        ("A", "X"),
        ("Z", "X"),
        ("B", "Z"),
        ("B", "Y"),
        ("Z", "Y"),
        ("X", "Y"),
        ("C", "X"),
        ("C", "Y"),
    ],
    edge_props={
        ("X", "Y"): {"color": "blue", "label": "Direct Causal Path", "fontcolor": "blue"},
    },
    graph_direction="LR",
)

../_images/b094c477304777b55982c7ee6b51120337600355eab53f997495ccc3a83a685b.svg

\(X \rightarrow Y\)#

直接的因果路径，保持开放

utils.draw_causal_graph(
    edge_list=[
        ("A", "Z"),
        ("A", "X"),
        ("Z", "X"),
        ("B", "Z"),
        ("B", "Y"),
        ("Z", "Y"),
        ("X", "Y"),
        ("C", "X"),
        ("C", "Y"),
    ],
    edge_props={
        ("C", "X"): {"color": "red", "label": "XCY", "fontcolor": "red"},
        ("C", "Y"): {"color": "red"},
    },
    graph_direction="LR",
)

../_images/f268703cdd869f3d0a74da1ebf0b4f25ebf122807530ad107a78e2a21145cc45.svg

\(X \leftarrow C \rightarrow Y\)#

后门非因果路径
通过按 \(C\) 分层来阻止

utils.draw_causal_graph(
    edge_list=[
        ("A", "Z"),
        ("A", "X"),
        ("Z", "X"),
        ("B", "Z"),
        ("B", "Y"),
        ("Z", "Y"),
        ("X", "Y"),
        ("C", "X"),
        ("C", "Y"),
    ],
    edge_props={
        ("Z", "X"): {"color": "red", "label": "XZY", "fontcolor": "red"},
        ("Z", "Y"): {"color": "red"},
    },
    graph_direction="LR",
)

../_images/b34cf65e46ca6d91ed70d0da88c72ec7e1dadb752c8bde0cc6157a6959228d90.svg

\(X \leftarrow Z \rightarrow Y\)#

后门非因果路径
通过按 \(Z\) 分层来阻止

utils.draw_causal_graph(
    edge_list=[
        ("A", "Z"),
        ("A", "X"),
        ("Z", "X"),
        ("B", "Z"),
        ("B", "Y"),
        ("Z", "Y"),
        ("X", "Y"),
        ("C", "X"),
        ("C", "Y"),
    ],
    edge_props={
        ("A", "X"): {"color": "red", "label": "XAZBY", "fontcolor": "red"},
        ("A", "Z"): {"color": "red"},
        ("B", "Z"): {"color": "red"},
        ("B", "Y"): {"color": "red"},
    },
    graph_direction="LR",
)

../_images/87028ee557d51cb7c21eab266d5b90f34b7e5b74644a189ede335a82ea29f7cb.svg

\(X \leftarrow A \rightarrow Z \leftarrow B \rightarrow Y\)#

后门非因果路径
通过按 \(A\) 或 \(B\) 分层来阻止；按 \(Z\) 分层会打开路径，因为它是一个碰撞变量
- 我们已经按 \(Z\) 分层，用于 \(X,Z,Y\) 后门路径

utils.draw_causal_graph(
    edge_list=[
        ("A", "Z"),
        ("A", "X"),
        ("Z", "X"),
        ("B", "Z"),
        ("B", "Y"),
        ("Z", "Y"),
        ("X", "Y"),
        ("C", "X"),
        ("C", "Y"),
    ],
    edge_props={
        ("A", "X"): {"color": "red", "label": "XAZY", "fontcolor": "red"},
        ("A", "Z"): {"color": "red"},
        ("Z", "Y"): {"color": "red"},
        ("Z", "Y"): {"color": "red"},
    },
    graph_direction="LR",
)

../_images/46887c03eeac571a3949cf9951a2b0777f1572e887d905db2aa9cef32e36130a.svg

\(X \leftarrow A \rightarrow Z \rightarrow Y\)#

后门非因果路径
通过按 \(A\) 分层来阻止；按 \(Z\) 分层会打开路径，因为它是一个碰撞变量
- 我们已经按 \(Z\) 分层，用于 \(X \leftarrow Z \rightarrow Y\) 后门路径

utils.draw_causal_graph(
    edge_list=[
        ("A", "Z"),
        ("A", "X"),
        ("Z", "X"),
        ("B", "Z"),
        ("B", "Y"),
        ("Z", "Y"),
        ("X", "Y"),
        ("C", "X"),
        ("C", "Y"),
    ],
    edge_props={
        ("Z", "X"): {"color": "red", "label": "XZBY", "fontcolor": "red"},
        ("B", "Z"): {"color": "red"},
        ("B", "Y"): {"color": "red"},
    },
    graph_direction="LR",
)

../_images/a91e8cfb9c3bf79e70418755a66d13a042fb846ddeb9523623996ee7a8032d26.svg

\(X \leftarrow Z \leftarrow B \rightarrow Y\)#

后门非因果路径
通过按 \(B\) 分层来阻止；按 \(Z\) 分层会打开路径，因为它是一个碰撞变量
- 我们已经按 \(Z\) 分层，用于 \(X \leftarrow Z \rightarrow Y\) 后门路径

结果最小调整集：Z、C、（A 或 B）#

选择 B 而不是 A 结果在统计上更有效率，尽管在因果关系上与选择 A 没有区别

具有未观察到的混杂因素的示例#

utils.draw_causal_graph(
    edge_list=[("G", "P"), ("P", "C"), ("G", "C"), ("u", "P"), ("u", "C")],
    node_props={
        "G": {"color": "blue"},
        "C": {"color": "blue"},
        "P": {"color": "red", "label": "collider, P"},
        "u": {"style": "dashed"},
        "unobserved": {"style": "dashed"},
    },
    edge_props={("G", "C"): {"color": "blue"}},
    graph_direction="LR",
)

../_images/a8ff8e554ddaec0d395dadffebdf01228279466f92309f17a162fd31b6cbcff4.svg

\(P\) 是 \(G\) 和 \(C\) 之间的调解变量
\(P\) 也是 \(G, u, C\) 之间的碰撞变量
如果我们想估计 \(G \rightarrow C\) 的直接效应，我们需要按 \(P\) 分层——关闭管道
但是，这将打开通往未观察到的混杂因素的碰撞变量路径。
无法准确估计 G 对 C 的直接因果效应
可以估计总因果效应

好的和坏的控制#

用于选择控制变量的常见不正确启发式方法：#

YOLO 方法 – 电子表格中的任何内容
忽略高度共线性的变量
- 错误，没有对此的支持
- 共线性可以通过许多不同的因果过程产生，这些过程可以被准确建模
添加治疗前变量是安全的
- 错误，治疗前变量，就像治疗后变量一样，可能导致混杂因素。

好的和坏的控制示例#

坏的控制#

utils.draw_causal_graph(
    edge_list=[("u", "Z"), ("v", "Z"), ("u", "X"), ("X", "Y"), ("v", "Y")],
    node_props={
        "u": {"style": "dashed"},
        "v": {"style": "dashed"},
        "X": {"color": "red"},
        "Y": {"color": "red"},
        "unobserved": {"style": "dashed"},
    },
    edge_props={("X", "Y"): {"color": "red"}},
    graph_direction="TD",
)

../_images/92e72073f2c098b0da1b824a6db62383614f4b2a7a4c476d5ab6af082e3287c6.svg

\(Z\) 是未观察到的变量 \(u\) 和 \(v\) 的碰撞变量，它们独立地影响 \(X\) 和 \(Y\)

列出路径#

\(X \rightarrow Y\)
- 因果，保持开放
\(X \leftarrow u \rightarrow Z \leftarrow v \rightarrow Y\)
- 后门，由于碰撞变量而关闭
- \(Z\) 是一个坏的控制：按 \(Z\) 分层会打开后门路径
- \(Z\) 可能是一个治疗前变量——并非总是适合按治疗前变量分层；绘制您的因果假设

坏的调解变量#

utils.draw_causal_graph(
    edge_list=[
        ("X", "Z"),
        ("Z", "Y"),
        ("u", "Z"),
        ("u", "Y"),
    ],
    node_props={
        "X": {"color": "red"},
        "Y": {"color": "red"},
        "u": {"style": "dashed"},
        "unobserved": {"style": "dashed"},
    },
    edge_props={("X", "Z"): {"color": "red"}, ("Z", "Y"): {"color": "red"}},
    graph_direction="LR",
)

../_images/1191f34e2efcf662e5d2f3970d081cf8ca3067f6a937c1e8d0eaae585322ae23.svg

列出路径#

\(X \rightarrow Z \rightarrow Y\)
- 因果，保持开放
\(X \rightarrow Z \leftarrow u \rightarrow Y\)
- 后门，但仅当按 Z 分层时
没有后门路径，因此无需按 Z 分层
可以测量 \(X\) 对 \(Y\) 的总效应，但不能测量直接效应，因为存在调解变量 \(Z\)

这里没有后门路径，因此无需控制任何混杂因素。事实上，按 Z（坏的调解变量）分层会引入估计偏差，因为它引入了 u 的因果效应，否则将被阻止。

Z 通常是一个治疗后变量，例如，在下面，“幸福感”受到“赢得彩票”治疗的影响

通过模拟验证坏的调解变量：#

utils.draw_causal_graph(
    edge_list=[
        ("X", "Z"),
        ("Z", "Y"),
        ("u", "Z"),
        ("u", "Y"),
    ],
    node_props={
        "X": {"color": "red"},
        "Y": {"color": "red"},
        "u": {"style": "dashed"},
        "unobserved": {"style": "dashed"},
    },
    edge_props={
        ("X", "Z"): {"color": "red", "label": "1"},
        ("Z", "Y"): {"color": "red", "label": "1"},
        ("u", "Z"): {"label": "1"},
        ("u", "Y"): {"label": "1"},
    },
    graph_direction="LR",
)

../_images/e179f8f5da9403c1b4a12461eb16d6c8b7870c82ac941247eb4ac6713bfddbbc.svg

def simulate_bad_mediator(beta_XZ, beta_ZY, n_samples=100):
    # independent variables
    u = stats.norm.rvs(size=n_samples)
    X = stats.norm.rvs(size=n_samples)

    # causal effect of X on Z
    mu_Z = X * beta_XZ + u
    Z = stats.norm.rvs(size=n_samples, loc=mu_Z)

    # Causal effect of Z on Y (including confound)
    mu_Y = Z * beta_ZY + u
    Y = stats.norm.rvs(size=n_samples, loc=mu_Y)

    # Put data into format for statsmodels
    data = pd.DataFrame(np.vstack([Y, X, Z, u]).T, columns=["Y", "X", "Z", "u"])

    unstratified_model = smf.ols("Y ~ X", data=data).fit()
    stratified_model = smf.ols("Y ~ X + Z", data=data).fit()

    return unstratified_model.params.X, stratified_model.params.X


def run_bad_mediator_simulation(
    beta_XZ=1, beta_ZY=1, n_simulations=500, n_samples_per_simualtion=100
):
    beta_X = beta_XZ * beta_ZY

    simulations = np.array(
        [
            simulate_bad_mediator(
                beta_XZ=beta_XZ, beta_ZY=beta_ZY, n_samples=n_samples_per_simualtion
            )
            for _ in range(n_simulations)
        ]
    )
    _, ax = plt.subplots(figsize=(8, 4))
    az.plot_dist(simulations[:, 0], label="Y ~ X\ncorrect", color="black", ax=ax)
    az.plot_dist(simulations[:, 1], label="Y ~ X + Z\nwrong", color="C0", ax=ax)
    plt.axvline(beta_X, color="k", linestyle="--", label=f"actual={beta_X}")
    plt.legend(loc="upper left")
    plt.xlabel("posterior mean")
    plt.ylabel("density");

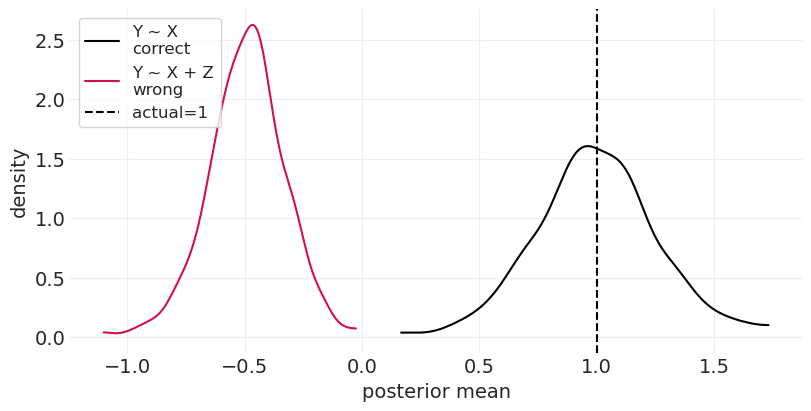
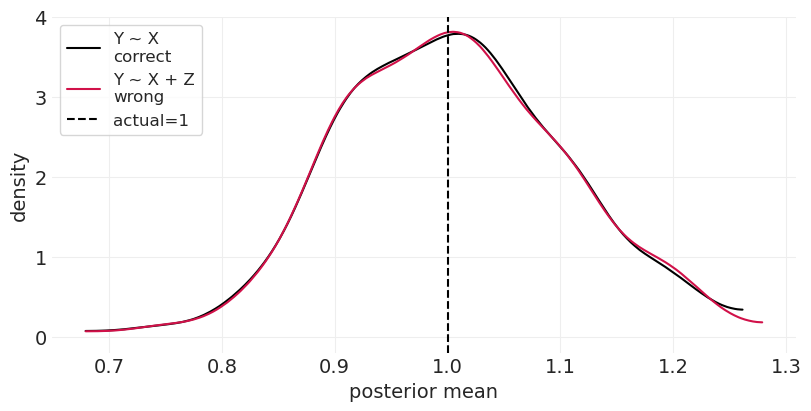
运行模拟，\(\beta_{XZ} = \beta_{ZY} = 1\)#

run_bad_mediator_simulation(beta_XZ=1, beta_ZY=1)

../_images/f4620695baa2336c0e1b99e5b0df0db82914fff9f798582005382b3cb48d5e1e.png

utils.draw_causal_graph(
    edge_list=[
        ("X", "Z"),
        ("Z", "Y"),
        ("u", "Z"),
        ("u", "Y"),
    ],
    node_props={
        "X": {"color": "red"},
        "Y": {"color": "red"},
        "u": {"style": "dashed"},
        "unobserved": {"style": "dashed"},
    },
    edge_props={
        ("X", "Z"): {"color": "red", "label": "1"},
        ("Z", "Y"): {"color": "red", "label": "0"},
        ("u", "Z"): {"label": "1"},
        ("u", "Y"): {"label": "1"},
    },
    graph_direction="LR",
)

../_images/3312adf469dc75c65907a4eaaefcee87216281978679a460cea13438368aca4b.svg

通过将 \(\beta_{ZY}\) 更改为 0 来关闭因果效应#

run_bad_mediator_simulation(beta_XZ=1, beta_ZY=0)

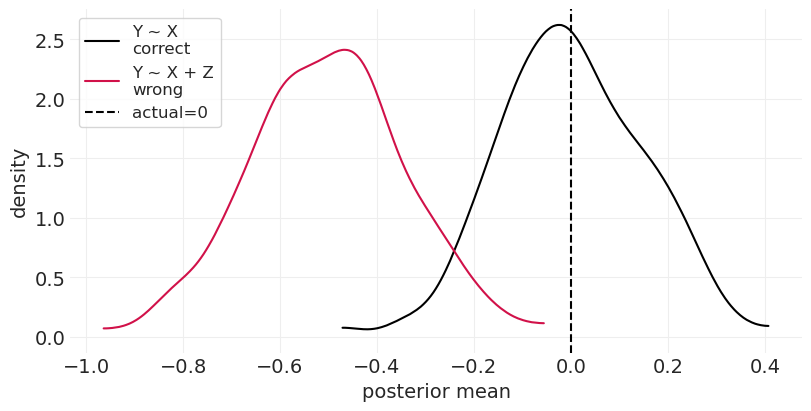
../_images/7a9942f183ddd63d0320ba79ebb360271be0c929057552d28038287de7c70d4c.png

尽管没有因果效应，但您最终得出了 X 对 Y 的负面效应的结论

碰撞变量和后代#

一般来说，避免碰撞变量！

添加目标变量的后代几乎总是一个糟糕的主意，因为您正在根据结果选择组。这被称为 病例对照偏差（根据结果选择）

utils.draw_causal_graph(
    edge_list=[("X", "Y"), ("X", "Z"), ("Y", "Z")],
    node_props={"X": {"color": "red"}, "Y": {"color": "red"}},
    edge_props={("X", "Y"): {"color": "red"}},
)

../_images/a2505a4cbe27021cef93c82acae294a4b596254e7f47ed7e61dd189cad439c66.svg

碰撞变量并不总是那么明显

utils.draw_causal_graph(
    edge_list=[
        ("X", "Y"),
        ("X", "Z"),
        ("u", "Y"),
        ("u", "Z"),
    ],
    node_props={
        "X": {"color": "red"},
        "Y": {"color": "red"},
        "u": {"style": "dashed"},
        "unobserved": {"style": "dashed"},
    },
    edge_props={("X", "Y"): {"color": "red"}},
)

../_images/dc1c7caa3bcaa6d9a1ac25acc9d57b7ba50a9e919a1dfe08ae6f537b892d47ce.svg

碰撞变量由未观察到的变量 u 形成

坏的后代：根据结果选择（病例对照偏差）#

在受结果影响的变量上分层是一种非常糟糕的做法。

减少了 \(Y\) 中可能由 \(X\) 解释的变异

utils.draw_causal_graph(
    edge_list=[
        ("X", "Y"),
        ("Y", "Z"),
    ],
    node_props={
        "X": {"color": "red", "label": "education, X"},
        "Y": {"color": "red", "label": "occupation, Y"},
        "Z": {"label": "income, Z"},
    },
    edge_props={("X", "Y"): {"color": "red"}},
    graph_direction="LR",
)

../_images/8413890dfd0c183df3461e0cc32900b667309566aa50e468085944e35c97b96e.svg

通过模拟验证：#

utils.draw_causal_graph(
    edge_list=[
        ("X", "Y"),
        ("Y", "Z"),
    ],
    node_props={
        "X": {"color": "red"},
        "Y": {"color": "red"},
    },
    edge_props={("X", "Y"): {"color": "red", "label": "1"}, ("Y", "Z"): {"label": "1"}},
    graph_direction="LR",
)

../_images/b794ee9f365a6c05a3038714bd5ac1889fa33d5319909571a0fc96abea79f067.svg

def simulate_case_control_bias(beta_XY=1, beta_YZ=1, n_samples=100):
    # independent variables
    X = stats.norm.rvs(size=n_samples)

    # Causal effect of Z on Y (including confound)
    mu_Y = X * beta_XY
    Y = stats.norm.rvs(size=n_samples, loc=mu_Y)

    # causal effect of X on Z
    mu_Z = Y * beta_YZ
    Z = stats.norm.rvs(size=n_samples, loc=mu_Z)

    # Put data into format for statsmodels
    data = pd.DataFrame(np.vstack([Y, X, Z]).T, columns=["Y", "X", "Z"])

    unstratified_model = smf.ols("Y ~ X", data=data).fit()
    stratified_model = smf.ols("Y ~ X + Z", data=data).fit()

    return unstratified_model.params.X, stratified_model.params.X


def run_case_control_simulation(
    beta_XY=1, beta_YZ=1, n_simulations=500, n_samples_per_simualtion=100
):
    beta_X = beta_XY

    simulations = np.array(
        [
            simulate_case_control_bias(
                beta_XY=beta_XY, beta_YZ=beta_YZ, n_samples=n_samples_per_simualtion
            )
            for _ in range(n_simulations)
        ]
    )
    _, ax = plt.subplots(figsize=(8, 4))
    az.plot_dist(simulations[:, 0], label="Y ~ X\ncorrect", color="black", ax=ax)
    az.plot_dist(simulations[:, 1], label="Y ~ X + Z\nwrong", color="C0", ax=ax)
    plt.axvline(beta_X, color="k", linestyle="--", label=f"actual={beta_X}")
    plt.legend(loc="upper left")
    plt.xlabel("posterior mean")
    plt.ylabel("density");

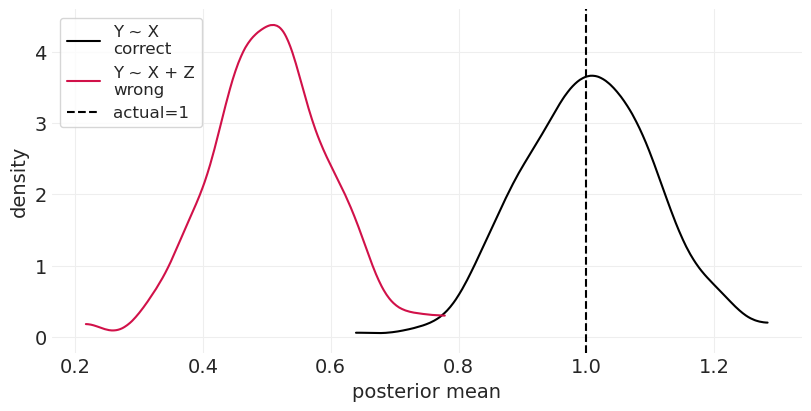
后代解释了 \(X\) 对 \(Y\) 的部分因果效应#

估计的因果效应已经减少，因为后代减少了 \(Y\) 中可以由 \(X\) 解释的变异

run_case_control_simulation(beta_XY=1, beta_YZ=1)

../_images/07ae40e305a694a3ee0bd6658e5e4b339ca3fe34e5caaaf9a12cf138f3db9d4b.png

通过设置 \(\beta_{YZ}=0\) 来消除后代效应#

后代在这里不再有任何影响，因此我们应该为分层模型和未分层模型恢复相同的（正确的）推理

run_case_control_simulation(beta_XY=1, beta_YZ=0)

../_images/6c6453597e8d9bf7152ec4b0c530e8877ad8a08eeb050d438aaf7544352da991.png

坏的祖先（又名精度寄生虫）#

现在 \(Z\) 是 \(X\) 的父代

没有后门路径，\(X\) 直接连接到 \(Y\)
当按 \(Z\) 分层时，您正在解释 \(X\) 中的变异，从而减少 \(X\) 和 \(Y\) 之间可以以其他方式解释的因果信息的量。
不会使您的估计产生偏差， 但它降低了精度，因此估计将具有更多不确定性

utils.draw_causal_graph(
    edge_list=[
        ("X", "Y"),
        ("Z", "X"),
    ],
    node_props={
        "X": {"color": "red"},
        "Y": {"color": "red"},
    },
    edge_props={("X", "Y"): {"color": "red", "label": "1"}, ("Z", "X"): {"label": "1"}},
    graph_direction="LR",
)

../_images/a0bf3b7889a585a0e6b5c4d5a5b7d3afdc2b81d0629e0460ebb4ebbf7a34df7f.svg

通过模拟验证#

utils.draw_causal_graph(
    edge_list=[
        ("X", "Y"),
        ("Z", "X"),
    ],
    node_props={
        "X": {"color": "red"},
        "Y": {"color": "red"},
    },
    edge_props={
        ("X", "Y"): {"color": "red", "label": "1"},
        ("Y", "Z"): {"color": "red", "label": "1"},
    },
    graph_direction="LR",
)

../_images/48f1f630d8946bb7a27f6ad5ebf2ab7d9a088ddb6459aebda0f8e835d66ce3b4.svg

np.random.seed(123)


def simulate_bad_ancestor(beta_ZX=1, beta_XY=1, unobserved_variance=None, n_samples=100):
    Z = stats.norm.rvs(size=n_samples)

    mu_X = Z * beta_ZX
    if unobserved_variance is not None:
        u = stats.norm.rvs(size=n_samples) * unobserved_variance
        mu_X += u

    X = stats.norm.rvs(size=n_samples, loc=mu_X)

    mu_Y = X * beta_XY
    if unobserved_variance is not None:
        mu_Y += u

    Y = stats.norm.rvs(size=n_samples, loc=mu_Y)

    data = pd.DataFrame(np.vstack([X, Y, Z]).T, columns=["X", "Y", "Z"])

    non_stratified_model = smf.ols("Y ~ X", data=data).fit()
    stratified_model = smf.ols("Y ~ X + Z", data=data).fit()

    return non_stratified_model.params.X, stratified_model.params.X


def run_bad_ancestor_simulation(
    beta_ZX=1, beta_XY=1, n_simulations=500, unobserved_variance=None, n_samples_per_simualtion=100
):
    beta_X = beta_XY

    simulations = np.array(
        [
            simulate_bad_ancestor(
                beta_ZX=beta_ZX,
                beta_XY=beta_XY,
                unobserved_variance=unobserved_variance,
                n_samples=n_samples_per_simualtion,
            )
            for _ in range(n_simulations)
        ]
    )
    _, ax = plt.subplots(figsize=(8, 4))
    az.plot_dist(simulations[:, 0], label="Y ~ X\ncorrect", color="black", ax=ax)
    az.plot_dist(simulations[:, 1], label="Y ~ X + Z\nwrong", color="C0", ax=ax)
    plt.axvline(beta_X, color="k", linestyle="--", label=f"actual={beta_X}")
    plt.legend(loc="upper left")
    plt.xlabel("posterior mean")
    plt.ylabel("density");

run_bad_ancestor_simulation()

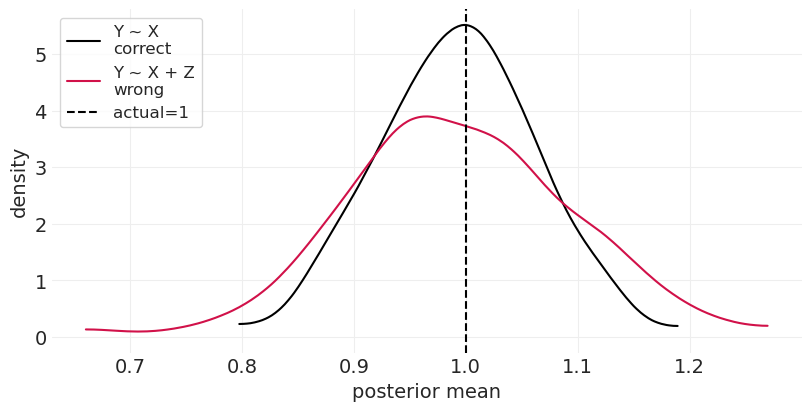
../_images/fd3d2e3f15437204e9986cc7c01816be6dd8fbab836474189057d83f61d7a9c5.png

按 Z 分层不会增加偏差（它以正确的值为中心），但它确实会增加估计器中的方差。这种精度降低与 Z 和 X 之间因果关系的大小成正比

增加 Z 和 X 之间的关系会进一步降低精度#

run_bad_ancestor_simulation(beta_ZX=3)

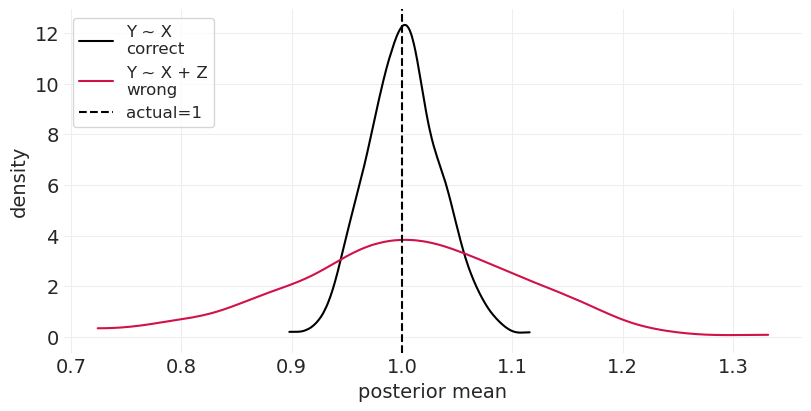
../_images/74e2fe26894cbfc8023c190930fe665b5ddd41b17eee93d002eaecc4b8944636.png

偏差放大#

当存在其他混杂因素（尤其是未观察到的分叉）时，在祖先上分层。 这就像偏差寄生虫场景，但它也增加了偏差。

utils.draw_causal_graph(
    edge_list=[("X", "Y"), ("Z", "X"), ("u", "X"), ("u", "Y")],
    node_props={
        "X": {"color": "red"},
        "Y": {"color": "red"},
        "u": {"style": "dashed"},
        "unobserved": {"style": "dashed"},
    },
    edge_props={("X", "Y"): {"color": "red"}, ("Y", "Z"): {"color": "red"}},
    graph_direction="LR",
)

../_images/d97e0c21d6c9deaf39338777eed6083cc62d225b5a6638965280c085192ce922.svg

通过模拟验证#

utils.draw_causal_graph(
    edge_list=[("X", "Y"), ("Z", "X"), ("u", "X"), ("u", "Y")],
    node_props={
        "X": {"color": "red"},
        "Y": {"color": "red"},
        "u": {"style": "dashed"},
        "unobserved": {"style": "dashed"},
    },
    edge_props={
        ("X", "Y"): {"color": "red", "label": "0"},
        ("Z", "X"): {"color": "red", "label": "1"},
    },
    graph_direction="LR",
)

../_images/5c6fbf999ec35457071576d0af0e7055e17f97b3211cb3d10f3205a8719a8165.svg

运行模拟，没有实际的因果效应，\(\beta_{XY} = 0\)#

run_bad_ancestor_simulation(beta_ZX=1, beta_XY=0, unobserved_variance=1)

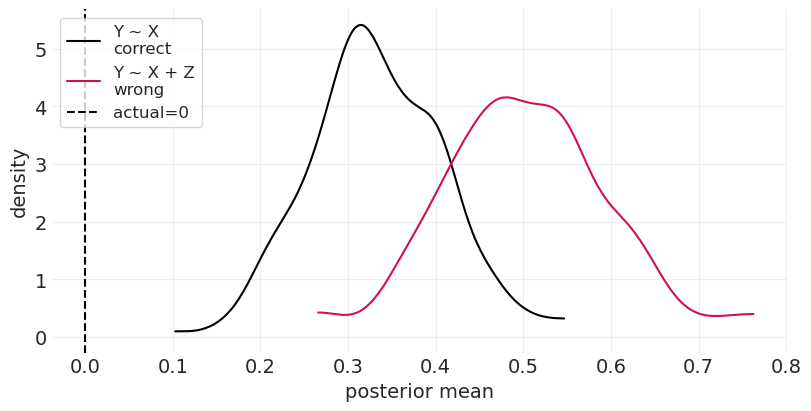
../_images/457b405be764b4d09502e55f5397233d9be0255d5fac606886478b77ada380e1.png

在上面我们看到，即使在最好的情况下，两个估计器都是有偏差的——我们无法观察到，因此也无法控制混杂因素 \(u\)。但是当按祖先分层时，情况会更糟。

粗略的解释

为了使 \(X\) 和 \(Y\) 相关联，它们的起因需要相关联
通过按 \(Z\) 分层，我们消除了 \(X\) 中由 \(Z\) 引起的变异量
这种 \(X\) 变异的减少使得混杂因素 \(u\) 相对而言更重要

偏差放大的离散示例#

def simulate_discrete_bias_amplifications(beta_ZX=1, beta_XY=1, n_samples=1000):
    Z = stats.bernoulli.rvs(p=0.5, size=n_samples)
    u = stats.norm.rvs(size=n_samples)

    mu_X = beta_ZX * Z + u
    X = stats.norm.rvs(loc=mu_X, size=n_samples)

    mu_Y = X * beta_XY + u
    Y = stats.norm.rvs(loc=mu_Y, size=n_samples)

    data = pd.DataFrame(np.vstack([u, Z, X, Y]).T, columns=["u", "Z", "X", "Y"])

    models = {}
    models["unstratified"] = smf.ols("Y ~ X", data=data).fit()
    models["z=0"] = smf.ols("Y ~ X", data=data[data.Z == 0]).fit()
    models["z=1"] = smf.ols("Y ~ X", data=data[data.Z == 1]).fit()

    return models, data

beta_ZX = 7
beta_ZY = 0
models, data = simulate_discrete_bias_amplifications(beta_ZX=beta_ZX, beta_XY=beta_XY)

fig, axs = plt.subplots(figsize=(5, 5))


def plot_linear_model(model, color, label):
    params = model.params
    xs = np.linspace(data.X.min(), data.X.max(), 10)
    ys = params.Intercept + params.X * xs
    utils.plot_line(xs, ys, color=color, label=label)


for z in [0, 1]:
    color = f"C{z}"
    utils.plot_scatter(data.X[data.Z == z], data.Y[data.Z == z], color=color)
    model = models[f"z={z}"]
    plot_linear_model(model, color=color, label=f"Z={z}")

model = models["unstratified"]
plot_linear_model(model, color="k", label=f"total sample")

plt.xlim([-5, 12])
plt.ylim([-5, 5])

plt.legend();

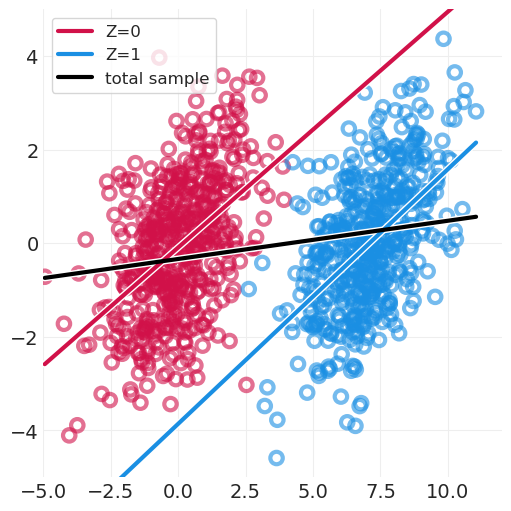
../_images/5a948df57d891f4567fc3d48ae4053e33229365b37badba860cbf6691989f9e2.png

当忽略 Z（祖先）时，估计仍然有些偏差（即，黑色斜率不是平坦的，因为它应该对于 \(\beta_{XY}=0\) 是平坦的）
但它远没有按 Z 分层时的各个斜率（蓝色/红色）那么糟糕。

回顾：好的和坏的控制#

混杂因素：使我们的因果估计“混淆”或“困惑”的估计器设计或样本
控制：添加到分析中的变量，以便因果估计成为可能
添加控制通常比省略它们更糟糕
使假设明确，并使用后门准则来验证这些假设

您必须进行科学建模才能进行科学分析

奖励：表 2 谬误#

并非所有系数都代表因果效应，特别是调整集中的系数
那些是因果效应的往往是部分效应，而不是总因果效应。
表 2 积极鼓励误解
如多次提到的：需要不同的估计器来解决不同的因果效应。

示例：吸烟、年龄、HIV 和中风#

utils.draw_causal_graph(
    edge_list=[
        ("X", "Y"),
        ("S", "Y"),
        ("S", "X"),
        ("A", "Y"),
        ("A", "X"),
        ("A", "S"),
    ],
    node_props={
        "X": {"label": "X, HIV", "color": "red"},
        "Y": {"label": "Y, Stroke", "color": "red"},
        "S": {"label": "S, Smoking"},
        "A": {"label": "A, Age"},
    },
    edge_props={("X", "Y"): {"color": "red"}},
    graph_direction="LR",
)

../_images/7ed58d248152d61597956ea87dd05959431f07cd007c042dea01994b313640fc.svg

通过后门准则识别路径#

\(X \rightarrow Y\) （前门）
\(X \leftarrow S \rightarrow Y\) （后门，分叉）
\(X \leftarrow A \rightarrow Y\) （后门，分叉）
\(X \leftarrow A \rightarrow S \rightarrow Y\) （后门，分叉和管道）

调整集是 \(\{S, A\}\)

条件统计模型#

\[\begin{split} \begin{align*} Y_i &\sim \mathcal{N}(\mu_i, \sigma) \\ \mu_i = &\alpha + \beta_X X_i + \beta_S S_i + \beta_A A_i \end{align*} \end{split}\]

“从各种变量的角度”看待模型#

从 X 的角度#

对 \(A\) 和 \(S\) 进行条件化实际上消除了进入 \(X\) 的箭头，\(\beta_X\) 给了我们 \(X\) 对 \(Y\) 的直接效应

我们通过按 \(S\) 和 \(A\) 分层，通过系数 \(\beta_S, \beta_A\) 消除了所有后门路径

utils.draw_causal_graph(
    edge_list=[
        ("X", "Y"),
        ("S", "Y"),
        ("S", "X"),
        ("A", "Y"),
        ("A", "X"),
        ("A", "S"),
    ],
    node_props={"X": {"color": "red"}, "Y": {"color": "red"}},
    edge_props={
        ("X", "Y"): {"color": "red"},
        ("A", "X"): {"color": "none"},
        ("S", "X"): {"color": "none"},
    },
    graph_direction="LR",
)

../_images/8cd290a50a5c17fce82138385183a4840fc2baee1b515ff5c36f78ffbdecc5e7.svg

从 S 的角度#

utils.draw_causal_graph(
    edge_list=[
        ("X", "Y"),
        ("S", "Y"),
        ("S", "X"),
        ("A", "Y"),
        ("A", "X"),
        ("A", "S"),
    ],
    node_props={"Y": {"color": "red"}, "S": {"color": "red"}},
    edge_props={
        ("X", "Y"): {"color": "red"},
        ("S", "X"): {"color": "red"},
        ("S", "Y"): {"color": "red"},
    },
    graph_direction="LR",
)

../_images/99b1ea190988cd775319a5e74aa0e7448a6e7755883ea33dfe18ab471646e3b0.svg

使用完整模型的调整图#

utils.draw_causal_graph(
    edge_list=[
        ("X", "Y"),
        ("S", "Y"),
        ("S", "X"),
        ("A", "Y"),
        ("A", "X"),
        ("A", "S"),
    ],
    node_props={"Y": {"color": "red"}, "S": {"color": "red"}},
    edge_props={
        ("S", "X"): {"color": "none"},
        ("A", "S"): {"color": "none"},
        ("S", "Y"): {"color": "red"},
    },
    graph_direction="LR",
)

../_images/f4d6e61c5356d3d437ad29e5e5149ee0c7c6ce22cd8e79138e2953293a42a798.svg

在无条件模型中，\(S\) 对 \(Y\) 的影响受到 \(A\) 的混淆，因为它是 \(S\) 和 \(Y\)（以及 \(X\)）的共同原因
对 \(A\) 和 \(X\) 进行条件化（通过上面的相同统计模型），\(\beta_{S}\) 给出了 \(S\) 对 \(Y\)/的直接效应
- 由于我们在线性回归中阻止了沿 \(X\) 的路径，因此我们不再获得总效应。

从 A 的角度#

在无条件模型中，\(A\) 对 \(Y\) 的总因果效应流经所有路径

utils.draw_causal_graph(
    edge_list=[
        ("X", "Y"),
        ("S", "Y"),
        ("S", "X"),
        ("A", "Y"),
        ("A", "X"),
        ("A", "S"),
    ],
    node_props={"Y": {"color": "red"}, "A": {"color": "red"}},
    edge_props={
        ("X", "Y"): {"color": "red"},
        ("A", "X"): {"color": "red"},
        ("A", "Y"): {"color": "red"},
        ("A", "S"): {"color": "red"},
        ("S", "X"): {"color": "red"},
        ("S", "Y"): {"color": "red"},
    },
    graph_direction="LR",
)

../_images/7447fb79d3e782924e0a0039fb0533fa382149121a8dad5cc392985174bbf896.svg

对 \(S\) 和 \(X\) 进行条件化（通过上面的相同统计模型），\(\beta_{A}\) 给出了 \(A\) 对 \(Y\)/的直接效应
- 由于我们在线性回归中阻止了沿 \(X\) 的路径，因此我们不再获得总效应。

utils.draw_causal_graph(
    edge_list=[
        ("X", "Y"),
        ("S", "Y"),
        ("S", "X"),
        ("A", "Y"),
        ("A", "X"),
        ("A", "S"),
    ],
    node_props={"Y": {"color": "red"}, "A": {"color": "red"}},
    edge_props={
        ("A", "X"): {"color": "none"},
        ("A", "S"): {"color": "none"},
        ("A", "Y"): {"color": "red"},
    },
    graph_direction="LR",
)

../_images/5dc9fb3952745c7e0c4a270ad9817a749ea00589ef9bdd36ca513095cc4c5bbf.svg

如果我们考虑变量上未观察到的混杂因素，这将变得更加棘手！

总结：表 2 谬误#

并非所有系数都具有相同的解释
- 不同的估计量需要不同的模型
不要将系数呈现为它们是相等的（即在表 2 中）
……或者，根本不要呈现系数，而是推出预测。
为每个提供明确的解释

作者#

由 Dustin Stansbury (2024) 移植到 PyMC
基于 Richard McElreath 的 Statistical Rethinking (2023) 讲座

%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,aeppl,xarray

Last updated: Tue Dec 17 2024

Python implementation: CPython
Python version       : 3.12.5
IPython version      : 8.27.0

pytensor: 2.26.4
aeppl   : not installed
xarray  : 2024.7.0

pymc       : 5.19.1
scipy      : 1.14.1
statsmodels: 0.14.2
xarray     : 2024.7.0
matplotlib : 3.9.2
pandas     : 2.2.2
numpy      : 1.26.4
arviz      : 0.19.0

Watermark: 2.5.0

许可声明#

本示例画廊中的所有笔记本均根据 MIT 许可证提供，该许可证允许修改和再分发以用于任何用途，前提是保留版权和许可证声明。

引用 PyMC 示例#

要引用此笔记本，请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。

重要

许多笔记本都是从其他来源改编而来的：博客、书籍…… 在这种情况下，您也应该引用原始来源。

另请记住引用您的代码使用的相关库。

这是一个 bibtex 中的引用模板

@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}

渲染后可能看起来像这样

分类

标签

好的和坏的控制#

不惜一切代价避免耍小聪明#

混杂因素#

回顾#

因果思考#

没有随机化#

通过 \(do(X)\) 诱导的“随机化”#

示例：简单混杂#

Do 演算#

后门准则#

后门准则示例#

按 \(Z\) 分层后的结果图#

通过模拟验证#

未分层（混杂）模型#

拟合未分层模型，忽略 Z（和 U）#

按 Z 分层（非混杂）#

比较分层模型和未分层模型#

更复杂的示例#

连接 X 到 Y 的所有路径#

\(X \rightarrow Y\)#

\(X \leftarrow C \rightarrow Y\)#

\(X \leftarrow Z \rightarrow Y\)#

\(X \leftarrow A \rightarrow Z \leftarrow B \rightarrow Y\)#

\(X \leftarrow A \rightarrow Z \rightarrow Y\)#

\(X \leftarrow Z \leftarrow B \rightarrow Y\)#

结果最小调整集：Z、C、（A 或 B）#

具有未观察到的混杂因素的示例#

好的和坏的控制#

用于选择控制变量的常见不正确启发式方法：#

好的和坏的控制示例#

坏的控制#

列出路径#

坏的调解变量#

列出路径#

通过模拟验证坏的调解变量：#

运行模拟，\(\beta_{XZ} = \beta_{ZY} = 1\)#

通过将 \(\beta_{ZY}\) 更改为 0 来关闭因果效应#

碰撞变量和后代#

坏的后代：根据结果选择（病例对照偏差）#

通过模拟验证：#

后代解释了 \(X\) 对 \(Y\) 的部分因果效应#

通过设置 \(\beta_{YZ}=0\) 来消除后代效应#

坏的祖先（又名精度寄生虫）#

通过模拟验证#

增加 Z 和 X 之间的关系会进一步降低精度#

偏差放大#

通过模拟验证#

运行模拟，没有实际的因果效应，\(\beta_{XY} = 0\)#

偏差放大的离散示例#

回顾：好的和坏的控制#

奖励：表 2 谬误#

示例：吸烟、年龄、HIV 和中风#

通过后门准则识别路径#

条件统计模型#

“从各种变量的角度”看待模型#

从 X 的角度#

从 S 的角度#

使用完整模型的调整图#

从 A 的角度#

总结：表 2 谬误#

作者#

许可声明#

引用 PyMC 示例#