多层模型#
本笔记本是 PyMC 对 Statistical Rethinking 2023 Richard McElreath 讲座系列的移植。
视频 - 第 12 讲 - 多层模型# 第 12 讲 - 多层模型
# Ignore warnings
import warnings
import arviz as az
import numpy as np
import pandas as pd
import pymc as pm
import statsmodels.formula.api as smf
import utils as utils
import xarray as xr
from matplotlib import pyplot as plt
from matplotlib import style
from scipy import stats as stats
warnings.filterwarnings("ignore")
# Set matplotlib style
STYLE = "statistical-rethinking-2023.mplstyle"
style.use(STYLE)
重复观测#
在 关于有序类别的第 11 讲 的结尾，McElreath 暗示可以利用 Trolley 数据集中故事和参与者的重复观察来改进估计。
使用重复观测可以得到更好的估计量
TROLLEY = utils.load_data("Trolley")
N_TROLLEY_RESPONSES = len(TROLLEY)
N_RESPONSE_CATEGORIES = TROLLEY.response.max()
TROLLEY.head()
| 案例 | 响应 | 顺序 | id | 年龄 | 男性 | 教育程度 | 行为 | 意图 | 接触 | 故事 | 行为2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | cfaqu | 4 | 2 | 96;434 | 14 | 0 | 中学 | 0 | 0 | 1 | aqu | 1 |
| 1 | cfbur | 3 | 31 | 96;434 | 14 | 0 | 中学 | 0 | 0 | 1 | bur | 1 |
| 2 | cfrub | 4 | 16 | 96;434 | 14 | 0 | 中学 | 0 | 0 | 1 | rub | 1 |
| 3 | cibox | 3 | 32 | 96;434 | 14 | 0 | 中学 | 0 | 1 | 1 | box | 1 |
| 4 | cibur | 3 | 4 | 96;434 | 14 | 0 | 中学 | 0 | 1 | 1 | bur | 1 |
def plot_trolly_response_distribution(variable, n_display=50, error_kwargs={}):
gb = TROLLEY[[variable, "response"]].groupby(variable)
plot_data = gb.mean()
plot_data.reset_index(inplace=True)
plot_data = plot_data.iloc[:n_display]
# IQR
plot_data.loc[:, "error_lower"] = (
plot_data["response"] - gb.quantile(0.25).reset_index()["response"]
)
plot_data.loc[:, "error_upper"] = (
gb.quantile(0.75).reset_index()["response"] - plot_data["response"]
)
utils.plot_scatter(plot_data.index, plot_data.response, color="C0")
utils.plot_errorbar(
plot_data.index,
plot_data.response,
plot_data.error_lower.abs(),
plot_data.error_upper.abs(),
colors="C0",
**error_kwargs,
)
plt.ylim(1, 7)
plt.xlabel(f"{variable} index")
plt.ylabel("response")
plt.title(f"{variable} response distribution")
故事响应的可变性#
故事重复#
12 个故事
TROLLEY.groupby("story").count()["case"]
story
aqu 662
boa 662
box 1324
bur 1324
car 662
che 662
pon 662
rub 662
sha 662
shi 662
spe 993
swi 993
Name: case, dtype: int64
plot_trolly_response_distribution("story")
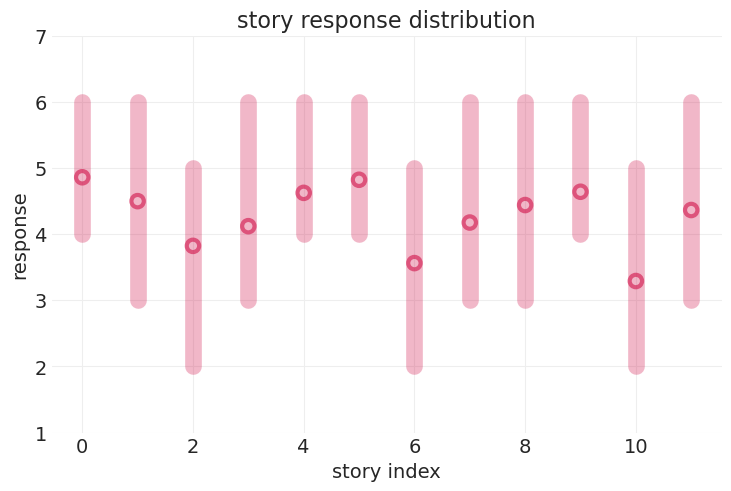
参与者响应的可变性#
331 位个体
TROLLEY.groupby("id").count()["case"]
id
96;434 30
96;445 30
96;451 30
96;456 30
96;458 30
..
98;225 30
98;227 30
98;245 30
98;257 30
98;299 30
Name: case, Length: 331, dtype: int64
plot_trolly_response_distribution("id", error_kwargs={"error_width": 6})
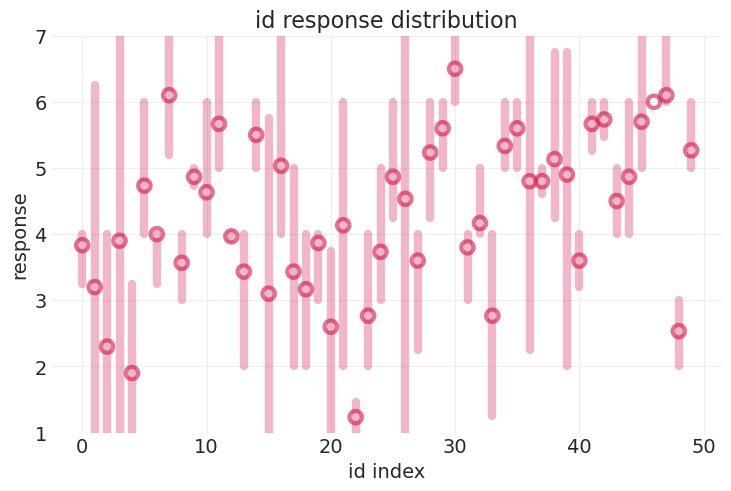
跨观测值建模可变性的方法#
完全合并#
\[\begin{split} \begin{align} R_i &\sim \text{OrderedLogit}(\phi_i, \alpha) \\ \phi_i &= \beta \end{align} \end{split}\]
全局 \(\beta\) 参数
将所有唯一类别（例如故事和/或参与者）视为相同
数据欠拟合，因为模型不够灵活
不合并#
\[\begin{split} \begin{align} R_i &\sim \text{OrderedLogit}(\phi_i, \alpha) \\ \phi_i &= \beta_{S[i]} \end{align} \end{split}\]
将所有唯一类别视为独立；每个类别都有自己的 \(\beta_{S}\)
模型具有“顺行性遗忘症”
不跨连续观测值共享信息
效率低下
数据过拟合，因为模型过于灵活，并且拟合到个体噪声
部分合并（多层模型）#
\[\begin{split} \begin{align} R_i &\sim \text{OrderedLogit}(\phi_i, \alpha) \\ \phi_i &= \beta_{S[i]} \\ \beta_i &\sim \text{Prior}_\beta(\eta) \\ \eta &\sim \text{PopulationPrior}(\theta) \end{align} \end{split}\]
参数从在总体中共享的全局分布中抽取
允许灵活性而不会过拟合
跨观测值共享信息
具有“记忆”
更有效率
学习更快
免费获得自适应正则化
抵抗过拟合
改进不平衡抽样的估计
案例研究：芦苇蛙生存#
48 个组；“水箱”
处理：密度、大小和捕食水平
结果：存活率
FROGS = utils.load_data("reedfrogs")
N_TANKS = len(FROGS)
FROGS.head()
| 密度 | pred | 大小 | surv | propsurv | |
|---|---|---|---|---|---|
| 0 | 10 | 否 | 大 | 9 | 0.9 |
| 1 | 10 | 否 | 大 | 10 | 1.0 |
| 2 | 10 | 否 | 大 | 7 | 0.7 |
| 3 | 10 | 否 | 大 | 10 | 1.0 |
| 4 | 10 | 否 | 小 | 9 | 0.9 |
utils.draw_causal_graph(
edge_list=[("T", "S"), ("D", "S"), ("G", "S"), ("P", "S")],
node_props={
"T": {"label": "tank, T"},
"S": {"label": "survivial, S", "color": "red"},
"D": {"label": "density, D"},
"G": {"label": "size, G"},
"P": {"label": "predators, P"},
},
)
\(T\)：水箱 ID
\(D\)：水箱密度 - 每个水箱中的蝌蚪数量 - 计数
\(G\)：水箱大小 - 分类（大/小）
\(P\)：捕食者的存在/不存在 - 分类
\(S\)：存活，存活的蝌蚪数量 - 计数
propsurv：存活率 \(\frac{S}{D}\)
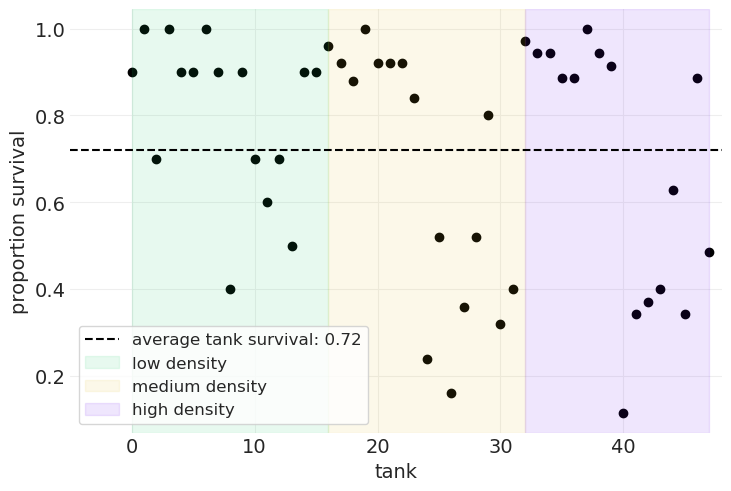
绘制所有水箱的平均存活率#
plt.scatter(FROGS.index, FROGS.propsurv, color="k")
# Plot average survival rate across tanks
global_mean = FROGS.propsurv.mean()
plt.axhline(
global_mean, color="k", linestyle="--", label=f"average tank survival: {global_mean:1.2}"
)
# Highlight different densities
density_change = FROGS[FROGS.density.diff() > 0].index.tolist()
density_change.append(N_TANKS - 1)
start = 0
density_labels = ["low", "medium", "high"]
for ii in range(3):
end = density_change[ii]
plt.axvspan(start, end, alpha=0.1, label=f"{density_labels[ii]} density", color=f"C{ii+2}")
start = end
plt.xlabel("tank")
plt.xlim([-5, N_TANKS])
plt.ylabel("proportion survival")
plt.legend();
让我们构建一个（多层）模型#
\[\begin{split} \begin{align*} S_i &\sim \text{Binomial}(D_i, p_i) \\ \text{logit}(p_i) &= \alpha_{T[i]} \\ \alpha_j &\sim \text{Normal}(\bar \alpha, \sigma_?) \\ \bar \alpha &\sim \text{Normal}(0, 1.5) \\ \end{align*} \end{split}\]
先验方差 \(\sigma\) 呢？#
现在，让我们尝试手动设置 \(\sigma\)，通过使用交叉验证来查看对多层模型的影响（我们稍后会估计它）
# Set up data / coords
N_SURVIVED = FROGS["surv"].astype(float)
N_TRIALS = FROGS["density"].values.astype(float)
PREDATOR_ID, PREDATORS = pd.factorize(FROGS["pred"], sort=True)
# Run grid search over sigmas
import logging
# Turn off logging for simulation
pmyc_logger = logging.getLogger("pymc")
pmyc_logger.setLevel(logging.CRITICAL)
n_sigmas = 20
sigmas = np.linspace(0.1, 5, n_sigmas)
inferences = []
print("Running grid search...")
for sigma in sigmas:
print("\r", f"sigma={sigma:1.2}")
with pm.Model() as m:
# Prior
alpha_bar = pm.Normal("alpha_bar", 0, 1.5)
alpha = pm.Normal("alpha", alpha_bar, sigma, shape=N_TANKS)
# Likelihood -- record p_survived for visualization
p_survived = pm.Deterministic("p_survived", pm.math.invlogit(alpha))
S = pm.Binomial("survived", n=N_TRIALS, p=p_survived, observed=N_SURVIVED)
inference = pm.sample(progressbar=False)
# log-likelihood for LOOCV scores and model comparison
inference = pm.compute_log_likelihood(inference, progressbar=False)
inferences.append(inference)
# Turn logging back on
pmyc_logger.setLevel(logging.INFO)
Running grid search...
sigma=0.1
sigma=0.36
sigma=0.62
sigma=0.87
sigma=1.1
sigma=1.4
sigma=1.6
sigma=1.9
sigma=2.2
sigma=2.4
sigma=2.7
sigma=2.9
sigma=3.2
sigma=3.5
sigma=3.7
sigma=4.0
sigma=4.2
sigma=4.5
sigma=4.7
sigma=5.0
def plot_survival_posterior(inference, sigma=None, color="C0", hdi_prob=0.89):
plt.figure()
# Plot observations
plt.scatter(x=FROGS.index, y=FROGS.propsurv, color="k", s=50, zorder=3)
# Posterior per-tank mean survival probability
posterior_mean = inference.posterior.mean(dim=("chain", "draw"))["p_survived"]
utils.plot_scatter(FROGS.index, posterior_mean, color=color, zorder=50, alpha=1)
# Posterior HDI error bars
hdis = az.hdi(inference.posterior, var_names="p_survived", hdi_prob=hdi_prob)[
"p_survived"
].values
error_upper = hdis[:, 1] - posterior_mean
error_lower = posterior_mean - hdis[:, 0]
xs = np.arange(len(posterior_mean))
utils.plot_errorbar(
xs=xs,
ys=posterior_mean,
error_lower=error_lower,
error_upper=error_upper,
colors=color,
error_width=8,
)
# Add mean indicators
empirical_mean = FROGS.propsurv.mean()
plt.axhline(y=empirical_mean, c="k", linestyle="--", label="Global Mean")
# Posterior mean
global_posterior_mean = utils.invlogit(
inference.posterior.mean(dim=("chain", "draw"))["alpha_bar"]
)
plt.axhline(global_posterior_mean, linestyle="--", label="Posterior Mean")
# Add tank density indicators
plt.axvline(15.5, color="k", alpha=0.25)
plt.axvline(31.5, color="k", alpha=0.25)
if sigma is not None:
plt.title(f"$\\sigma={sigma:1.2}$")
plt.ylim([0, 1.05])
plt.xlabel("tank #")
plt.ylabel("proportion survival")
plt.legend()
# Show extremes of parameter grid
for idx in [0, -1]:
plot_survival_posterior(inferences[idx], sigmas[idx])
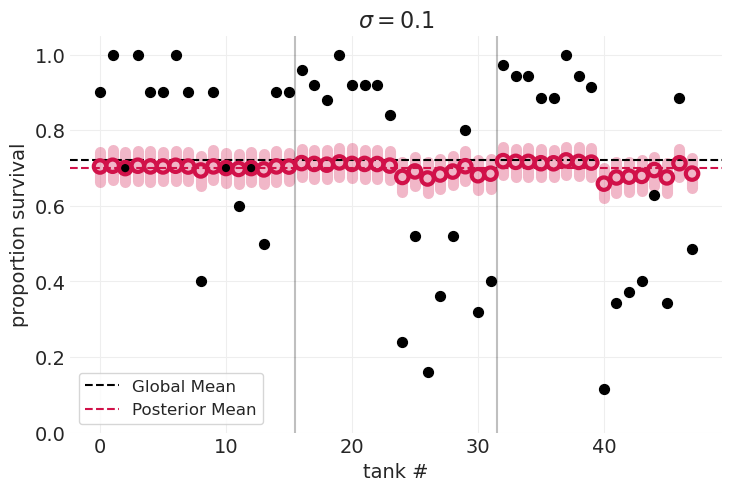
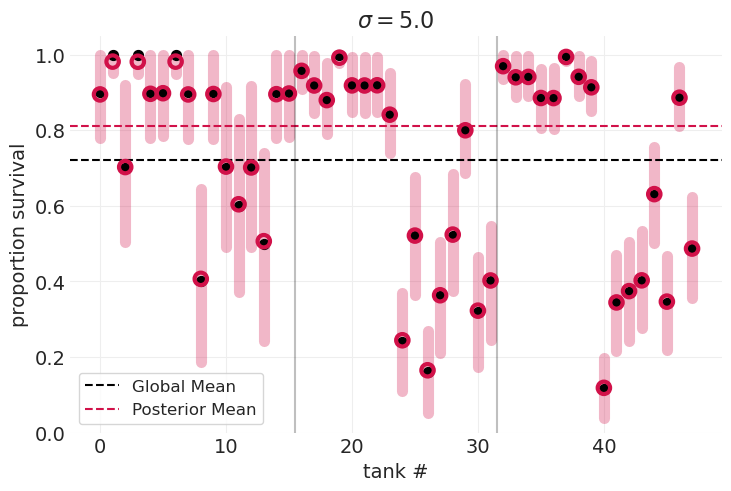
通过交叉验证识别最佳 \(\sigma\)#
\(\sigma=0.1\) 数据欠拟合，模型不够灵活，无法捕获不同水箱的可变性
\(\sigma=5.0\) 数据过拟合，模型过于灵活，后验分布集中在每个数据点周围
\(\sigma_{optimal}=?\) 我们可以比较在参数网格中为每个 \(\sigma\) 值拟合的模型的 LOOCV 分数，并识别得分最低的模型。
from collections import OrderedDict
def plot_model_comparisons(sigmas, inferences, multilevel_posterior=None):
plt.subplots(figsize=(10, 4))
comparisons = pm.compare(OrderedDict(zip(sigmas, inferences)), scale="deviance")
comparisons.sort_index(inplace=True)
utils.plot_scatter(
xs=sigmas, ys=comparisons["elpd_loo"], color="C0", label="Cross-validation score"
)
utils.plot_errorbar(
xs=sigmas,
ys=comparisons["elpd_loo"],
error_lower=comparisons["se"],
error_upper=comparisons["se"],
colors="C0",
)
# Highlight the optimal sigma
best = comparisons[comparisons["rank"] == 0]
plt.scatter(
x=best.index,
y=best["elpd_loo"],
s=300,
marker="*",
color="C1",
label="$\\sigma_{LOOCV}^*$:" + f" {best.index[0]:1.2}",
zorder=20,
)
# If provided, overlay the multilevel posterior (or, a scaled/offset version of it)
if multilevel_posterior is not None:
from scipy.stats import gaussian_kde
kde = gaussian_kde(multilevel_inference.posterior["sigma"][0])
sigma_grid = np.linspace(0.1, 5, 100)
sigma_posterior = kde(sigma_grid)
max_sigma_posterior = sigma_posterior.max()
multiplier = (0.7 * comparisons["elpd_loo"].max()) / max_sigma_posterior
offset = comparisons["elpd_loo"].min() * 0.95
plot_posterior = sigma_posterior * multiplier + offset
plt.plot(sigma_grid, plot_posterior, color="k", linewidth=3, label="Multi-level Posterior")
plt.xlim([0, 4])
plt.xlabel("$\\sigma$")
plt.ylabel("LOOCV Score (deviance)")
plt.legend()
# Output optimal parameters
optimal_sigma = best.index.values[0]
optimal_sigma_idx = sigmas.tolist().index(optimal_sigma)
return optimal_sigma_idx, optimal_sigma
optimal_sigma_idx, optimal_sigma = plot_model_comparisons(sigmas, inferences);
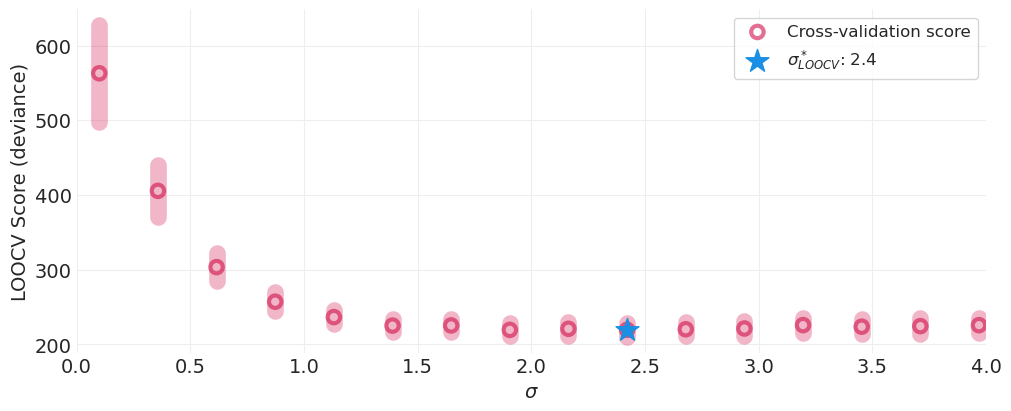
通过交叉验证识别的最佳 \(\sigma\) 模型#
plot_survival_posterior(inferences[optimal_sigma_idx], sigmas[optimal_sigma_idx])
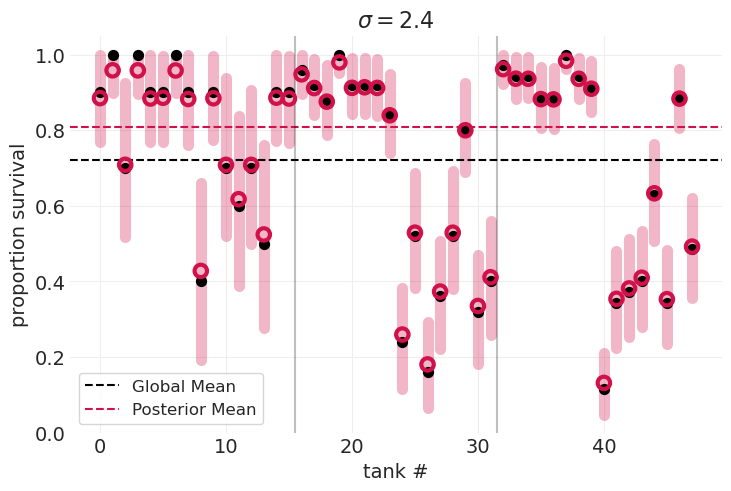
最佳模型
是正则化的，在偏差和方差之间进行权衡
演示了收缩:
后验均值不会悬停在数据点上方，而是“拉向”全局均值。
对于远离均值的数据点，“拉力”的量更大
构建多层（分层）模型#
自动正则化#
原则上，我们可以像上面那样使用交叉验证来估计最佳超参数值，但我们不需要这样做。我们可以通过使用分层模型结构，将先验分布放在该方差参数上来简单地学习最佳 \(\sigma\)。
婴儿的第一个多层模型#
\[\begin{split} \begin{align*} S_i &\sim \text{Binomial}(D_i, p_i)\\ \text{logit}(p_i) &= \alpha_{T[i]} \\ \alpha_j &\sim \text{Normal}(\bar \alpha, \sigma_?) \\ \bar \alpha &\sim \text{Normal}(0, 1.5) \\ \sigma &\sim \text{Exponential}(1) \end{align*} \end{split}\]
请注意，此先验在所有组之间共享，从而使其能够执行部分合并。
绘制婴儿的第一个多层模型的先验分布#
n_samples = 100_000
fig, axs = plt.subplots(1, 3, figsize=(10, 3))
sigmas_ = stats.expon(1).rvs(size=n_samples)
az.plot_dist(sigmas_, ax=axs[0])
axs[0].set_title("$\\sigma \\sim Exponential(1)$")
axs[0].set_xlim([0, 5])
axs[0].set_ylim([0, 1])
alpha_bars_ = stats.norm(0, 1.5).rvs(size=n_samples)
az.plot_dist(alpha_bars_, ax=axs[1])
axs[1].set_xlim([-6, 6])
axs[1].set_title("$\\bar \\alpha \\sim Normal(0, 1.5)$")
alphas_ = stats.norm.rvs(alpha_bars_, sigmas_)
az.plot_dist(alphas_, ax=axs[2])
axs[2].set_xlim([-6, 6])
axs[2].set_title("$\\alpha \\sim Normal(\\bar \\alpha, \\sigma)$")
plt.suptitle("Priors", fontsize=18);
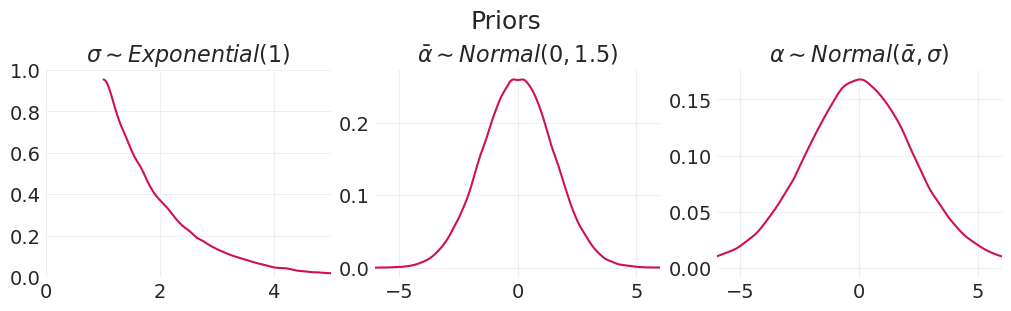
请注意，\(a_j\) 的先验分布（上方最右侧的图）是正态分布的混合，具有不同的均值（从 \(\bar a\) 先验分布中采样）和方差（从 \(\sigma\) 先验分布中采样）。因此，它不是正态分布，而是尾部更厚的分布，更类似于学生 t 分布
拟合多层模型#
with pm.Model() as multilevel_model:
# Priors
sigma = pm.Exponential("sigma", 1)
alpha_bar = pm.Normal("alpha_bar", 0, 1.5)
alpha = pm.Normal("alpha", alpha_bar, sigma, shape=N_TANKS)
# Likelihood (record log p_survived for visualization)
p_survived = pm.Deterministic("p_survived", pm.math.invlogit(alpha))
S = pm.Binomial("survived", n=N_TRIALS, p=p_survived, observed=N_SURVIVED)
multilevel_inference = pm.sample()
# Log-likelihood for model comparison
multilevel_inference = pm.compute_log_likelihood(multilevel_inference)
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [sigma, alpha_bar, alpha]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.
总结多层模型后验分布#
az.summary(multilevel_inference, var_names=["alpha_bar", "sigma"])
| 均值 | 标准差 | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| alpha_bar | 1.345 | 0.263 | 0.880 | 1.851 | 0.004 | 0.003 | 4341.0 | 2916.0 | 1.0 |
| sigma | 1.622 | 0.215 | 1.237 | 2.022 | 0.004 | 0.003 | 2726.0 | 3092.0 | 1.0 |
多层模型的后验 HDI 与通过交叉验证找到的最佳值重叠#
optimal_sigma_idx, optimal_sigma = plot_model_comparisons(
sigmas, inferences, multilevel_inference.posterior
);
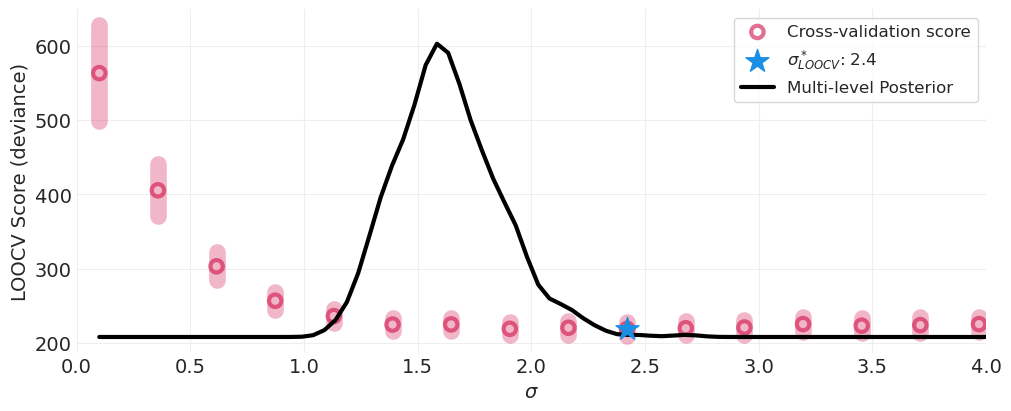
多层模型自动、高效地学习总体变异
免费获得正则化
比较多层模型和固定 sigma 模型#
固定 sigma 模型#
\[\begin{split} \begin{align*} S_i &\sim \text{Binomial}(D_i, p_i)\\ \text{logit}(p_i) &= \alpha_{T[i]} \\ \alpha_j &\sim \text{Normal}(\bar \alpha, 1) \\ \bar \alpha &\sim \text{Normal}(0, 1.5) \\ \end{align*} \end{split}\]
with pm.Model() as fixed_sigma_model:
# Sigma is fixed globally (no prior, and thus fewer defined params)
sigma = 1
# Prior
alpha_bar = pm.Normal("alpha_bar", 0, 1.5)
alpha = pm.Normal("alpha", alpha_bar, sigma, shape=N_TANKS)
# Likelihood -- record p_survived for visualization
p_survived = pm.Deterministic("p_survived", pm.math.invlogit(alpha))
S = pm.Binomial("survived", n=N_TRIALS, p=p_survived, observed=N_SURVIVED)
fixed_sigma_inference = pm.sample()
fixed_sigma_inference = pm.compute_log_likelihood(fixed_sigma_inference)
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [alpha_bar, alpha]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.
comparison = az.compare({"multi-level": multilevel_inference, "fixed-sigma": fixed_sigma_inference})
# Multi-level model has fewer effective parameters, despite having more defined parameters
assert comparison.loc["multi-level", "p_loo"] < comparison.loc["fixed-sigma", "p_loo"]
comparison
| 秩 | elpd_loo | p_loo | elpd_diff | 权重 | 标准误 | dse | 警告 | 尺度 | |
|---|---|---|---|---|---|---|---|---|---|
| 多层 | 0 | -111.620762 | 32.498049 | 0.000000 | 1.0 | 4.064596 | 0.000000 | 真 | 对数 |
| 固定 sigma | 1 | -122.344715 | 39.210856 | 10.723953 | 0.0 | 5.050636 | 3.077553 | 真 | 对数 |
多层模型在 LOO 分数方面表现更好（毫不意外）
多层模型具有更少的有效参数，尽管具有更多编程参数
这是因为模型更有效率，并在参数之间共享信息
演示由于样本大小导致的后验不确定性#
plot_survival_posterior(multilevel_inference)
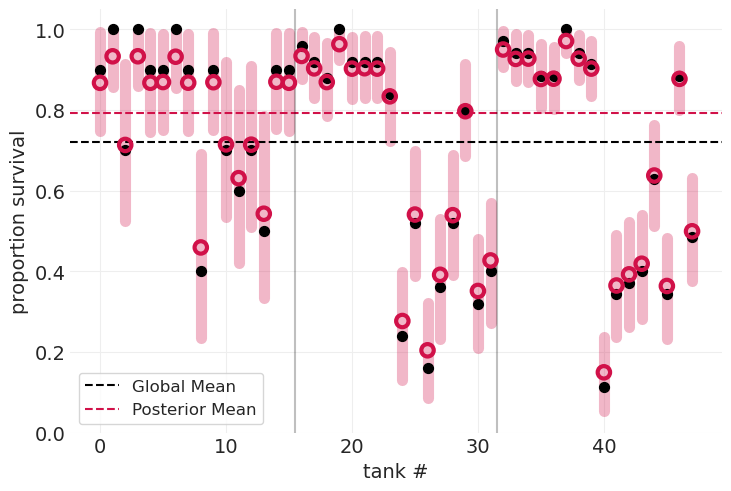
小水箱（在上图的最左侧）的观测值较少，因此
后验方差更宽
更多地收缩到全局均值
大水箱（在上图的最右侧）的观测值更多，因此
后验方差更紧
较少地收缩到全局均值
包括捕食者的存在#
PREDATOR_COLORS = ["C0" if p == 1 else "C1" for p in PREDATOR_ID]
# Multi-level model without predators (same plot as above, but with different color-coding)
plot_survival_posterior(multilevel_inference, color=PREDATOR_COLORS)
plt.title("Predators absent (blue) or present (red)");
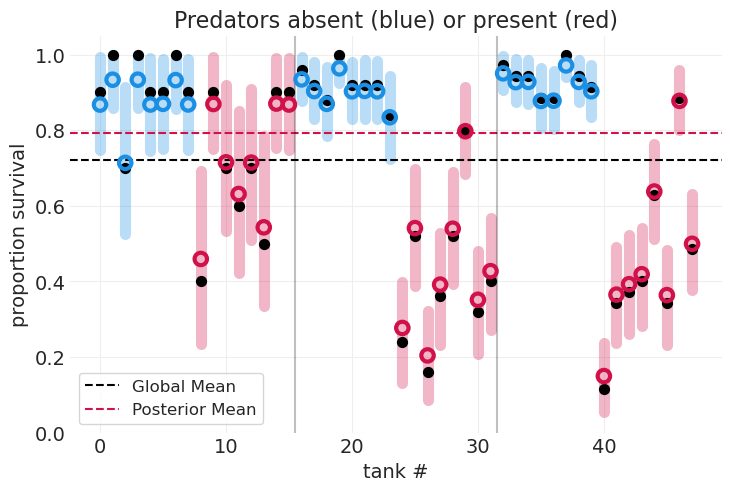
突出显示有捕食者的水箱表明，捕食者的存在（红色）降低了存活率
具有捕食者效应的多层模型#
utils.draw_causal_graph(
edge_list=[("T", "S"), ("D", "S"), ("G", "S"), ("P", "S")],
node_props={
"T": {"label": "tank, T"},
"S": {"label": "survivial, S", "color": "red"},
"D": {"label": "density, D"},
"G": {"label": "size, G"},
"P": {"label": "predators, P"},
},
edge_props={("T", "S"): {"color": "red"}, ("P", "S"): {"color": "red"}},
)
\[\begin{split} \begin{align*} S_i &\sim \text{Binomial}(D_i, p_i)\\ \text{logit}(p_i) &= \alpha_{T[i]} + \beta_P P_i\\ \beta_P &\sim \text{Normal}(0, .5) \\ \alpha_j &\sim \text{Normal}(\bar \alpha, \sigma) \\ \bar \alpha &\sim \text{Normal}(0, 1.5) \\ \sigma &\sim \text{Exponential}(1) \end{align*} \end{split}\]
TANK_ID = np.arange(N_TANKS)
with pm.Model() as predator_model:
# Global Priors
sigma = pm.Exponential("sigma", 1)
alpha_bar = pm.Normal("alpha_bar", 0, 1.5)
# Predator-specific prior
beta_predator = pm.Normal("beta_predator", 0, 0.5)
# Tank-specific prior
alpha = pm.Normal("alpha", alpha_bar, sigma, shape=N_TANKS)
# Record p_survived for visualization
p_survived = pm.math.invlogit(alpha[TANK_ID] + beta_predator * PREDATOR_ID)
p_survived = pm.Deterministic("p_survived", p_survived)
# Likelihood
S = pm.Binomial("survived", n=N_TRIALS, p=p_survived, observed=N_SURVIVED)
predator_inference = pm.sample()
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [sigma, alpha_bar, beta_predator, alpha]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 2 seconds.
# Predator model
plot_survival_posterior(predator_inference, color=PREDATOR_COLORS)
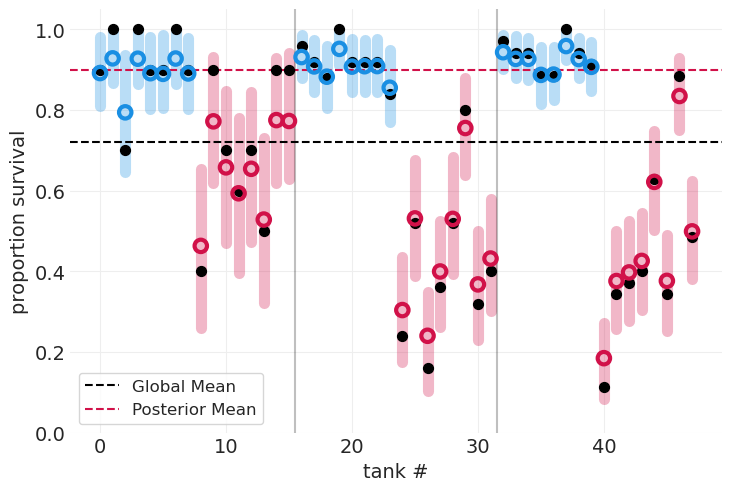
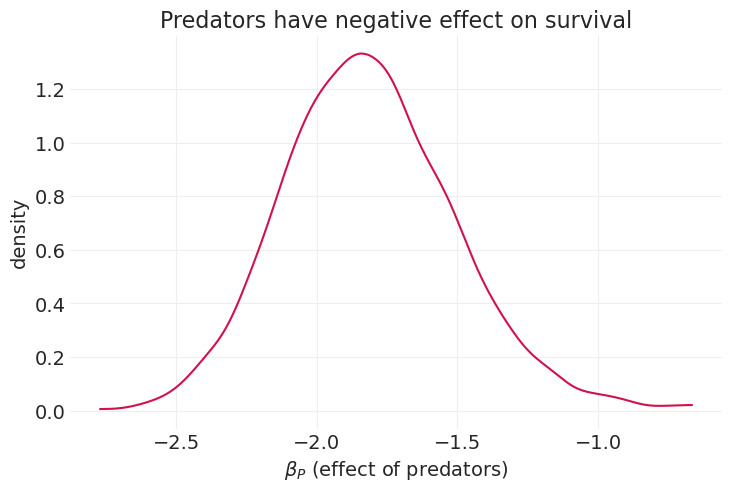
az.plot_dist(predator_inference.posterior["beta_predator"])
plt.xlabel("$\\beta_P$ (effect of predators)")
plt.ylabel("density")
plt.title("Predators have negative effect on survival");
预测与推断#
from matplotlib.lines import Line2D
from matplotlib.patches import Patch
# Should we probably be using the posterior predictive here, rather than the posterior?
multilevel_posterior_mean = multilevel_inference.posterior.mean(dim=("chain", "draw"))["p_survived"]
predator_posterior_mean = predator_inference.posterior.mean(dim=("chain", "draw"))["p_survived"]
fig, axs = plt.subplots(1, 2, figsize=(10, 5))
plt.sca(axs[0])
for x, y, c in zip(multilevel_posterior_mean, predator_posterior_mean, PREDATOR_COLORS):
utils.plot_scatter(xs=x, ys=y, color=c, alpha=0.8)
plt.plot((0, 1), (0, 1), "k--")
plt.xlabel("p(survive) - model without predators")
plt.ylabel("p(survive) - model with predators")
# Legend
legend_kwargs = dict(marker="o", color="none", markersize=8, alpha=0.8)
legend_elements = [
Line2D([0], [0], markerfacecolor="C0", label="Predators", **legend_kwargs),
Line2D([0], [0], markerfacecolor="C1", label="No Predators", **legend_kwargs),
]
plt.legend(handles=legend_elements, loc="lower right")
plt.title("extremely similar predictions")
plt.axis("square")
plt.sca(axs[1])
az.plot_dist(
multilevel_inference.posterior["sigma"],
ax=axs[1],
color="C1",
label="mST",
plot_kwargs={"lw": 3},
)
az.plot_dist(
predator_inference.posterior["sigma"],
ax=axs[1],
color="C0",
label="mSTP",
plot_kwargs={"lw": 3},
)
plt.xlim([0, 2.5])
plt.xlabel(r"$\sigma$")
plt.title(r"very different $\sigma$ values");
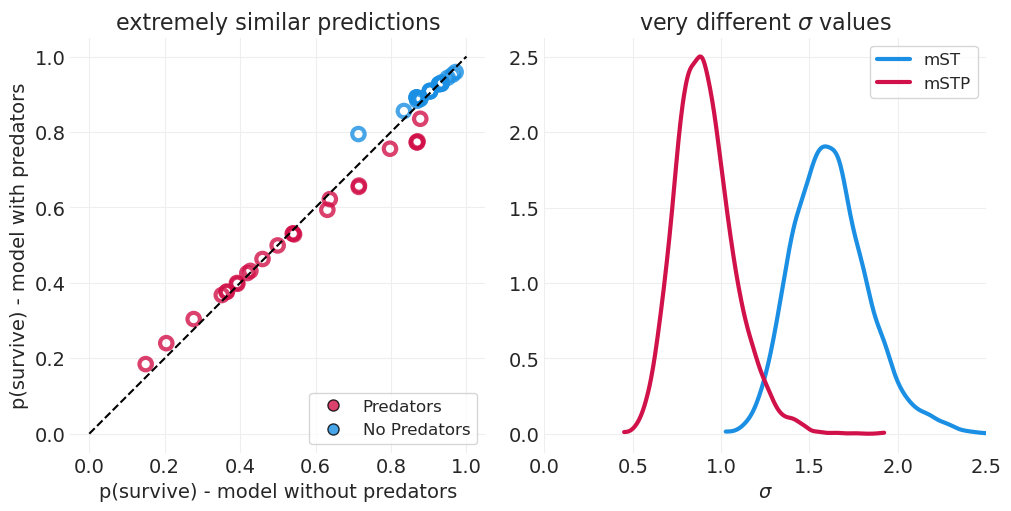
没有捕食者的模型可以像有捕食者的模型一样很好地预测存活率
这是因为多层模型仍然可以通过个体 \(\alpha_T\) 捕获水箱级别的可变性
然而，添加捕食者“解释了”更多的水箱级别方差。这通过捕食者模型中水箱级别可变性的 \(\sigma\) 值较小来证明。因此，捕食者模型必须考虑较少的水箱基础可变性才能捕获生存率的可变性。
变化效应的迷信#
~~部分合并需要从总体中随机抽样 ❌~~
~~类别/单位的数量必须很大 ❌~~
~~变异必须是高斯的 ❌~~
高斯先验可以学习非高斯分布
实际困难#
同时使用多个聚类（例如，参与者和故事）
抽样效率 – 重新编码（例如，中心/非中心先验）
其他参数（例如斜率）或未观察到的混杂因素的部分合并？
这些困难将在即将到来的关于多层模型的讲座中解决。 😅
奖励：固定效应、多层模型和蒙德拉克机器#
随机混杂因素#
utils.draw_causal_graph(
edge_list=[("G", "X"), ("G", "Y"), ("X", "Y"), ("Z", "Y")],
node_props={"G": {"style": "dashed"}, "unobserved": {"style": "dashed"}},
)
估计量：\(X\) 对 \(Y\) 的影响
结果 \(Y\)（例如，蝌蚪存活率）
个体级别特征 \(X\)
组级别特征 \(Z\)
未观察到的水箱效应 \(G\)
影响 \(X\) 和 \(Y\)
例如，水箱温度
创建从 \(X\) 到 \(Y\) 的后门路径（通过叉状结构）
我们无法直接测量 \(G\)。
但是，如果我们有重复观测，我们可以使用一些技巧。
估计量？
固定效应模型
多层模型
蒙德拉克机器
模拟一些数据#
# Generate data
np.random.seed(12)
N_GROUPS = 30
N_IDS = 200
ALPHA = -2 # p(Y) < .5 on average
BETA_ZY = -0.5
BETA_XY = 1
# Group-level data
GROUP = np.random.choice(np.arange(N_GROUPS).astype(int), size=N_IDS, replace=True)
Z = stats.norm.rvs(size=N_GROUPS) # Observed group traits
U = stats.norm(0, 1.5).rvs(size=N_GROUPS) # Unobserved group confound
# Individual-level data
X = stats.norm.rvs(U[GROUP]) # Observed individual traits
p = utils.invlogit(ALPHA + BETA_XY * X + U[GROUP] + BETA_ZY * Z[GROUP])
Y = stats.bernoulli.rvs(p=p)
在下面展示组不是随机抽样的#
朴素模型#
\[\begin{split} \begin{align*} Y &\sim \text{Bernoulli}(p) \\ \text{logit}(p_i) &= \alpha + \beta_{X}X + \beta_{Z} Z_{G[i]} \\ \alpha &\sim \text{Normal}(0, 10) \\ \beta_* &\sim \text{Normal}(0, 1) \end{align*} \end{split}\]
with pm.Model() as naive_model:
# Priors
fixed_sigma = 10 # no pooling
alpha = pm.Normal("alpha", 0, fixed_sigma) # no group effects
beta_XY = pm.Normal("beta_XY", 0, 1)
beta_ZY = pm.Normal("beta_ZY", 0, 1)
# Likelihood
p = pm.math.invlogit(alpha + beta_XY * X + beta_ZY * Z[GROUP])
pm.Bernoulli("Y_obs", p=p, observed=Y)
naive_inference = pm.sample()
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [alpha, beta_XY, beta_ZY]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.
固定效应模型#
\[\begin{split} \begin{align*} Y &\sim \text{Bernoulli}(p) \\ \text{logit}(p_i) &= \alpha_{G[i]} + \beta_{X}X_i + \beta_{Z} Z_{G[i]} \\ \alpha_j &\sim \text{Normal}(0, 10) \\ \beta_* &\sim \text{Normal}(0, 1) \end{align*} \end{split}\]
为每个组估计不同的平均率，不合并
\(\beta_Z\) 和 \(\beta_X\) 是全局参数
解释了 \(G\) 的组级别混杂效应（通过每个组的偏移量）
问题
无法识别任何组级别效应 \(Z\)
\(Z\) 是无法识别的，因为它是在全局添加的
存在无限数量的 \(\alpha_{G[i]} + \beta_Z Z_{G[i]}\) 等效组合
无法将 \(\beta_Z\) 的贡献与 \(\alpha\) 分离
无法在混合效应模型中包含组级别预测变量
效率低下
with pm.Model() as fixed_effects_model:
# Priors
fixed_sigma = 10 # no pooling
alpha = pm.Normal("alpha", 0, fixed_sigma, shape=N_GROUPS)
beta_XY = pm.Normal("beta_XY", 0, 1)
beta_ZY = pm.Normal("beta_ZY", 0, 1)
# Likelihood
p = pm.math.invlogit(alpha[GROUP] + beta_XY * X + beta_ZY * Z[GROUP])
pm.Bernoulli("Y_obs", p=p, observed=Y)
fixed_effect_inference = pm.sample()
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [alpha, beta_XY, beta_ZY]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 3 seconds.
There were 53 divergences after tuning. Increase `target_accept` or reparameterize.
多层模型#
\[\begin{split} \begin{align*} Y &\sim \text{Bernoulli}(p) \\ \text{logit}(p_i) &= \alpha_{G[i]} + \beta_{X}X + \beta_{Z} Z_{G[i]} \\ \beta_* &\sim \text{Normal}(0, 1) \\ \alpha_j &\sim \text{Normal}(\bar a, \tau) \\ \bar a &\sim \text{Normal}(0, 1) \\ \tau &\sim \text{Exponential}(10) \end{align*} \end{split}\]
为每个组估计不同的平均率，部分合并
更好的 \(G\) 效应估计
以估计 \(X\) 效应为代价
折衷估计混杂因素，以便它可以获得更好的组估计
可以识别 \(Z\) 效应
可以合并组级别预测变量
with pm.Model() as multilevel_model:
# Priors
alpha_bar = pm.Normal("alpha_bar", 0, 1)
tau = pm.Exponential("tau", 1)
# NOTE: non-centered prior reparameterization for numerical stability
z = pm.Normal("z", 0, 1, shape=N_GROUPS)
alpha = alpha_bar + z * tau
beta_XY = pm.Normal("beta_XY", 0, 1)
beta_ZY = pm.Normal("beta_ZY", 0, 1)
# Likelihood
p = pm.math.invlogit(alpha[GROUP] + beta_XY * X + beta_ZY * Z[GROUP])
pm.Bernoulli("Y_obs", p=p, observed=Y)
multilevel_inference = pm.sample(target_accept=0.95)
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [alpha_bar, tau, z, beta_XY, beta_ZY]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 3 seconds.
比较模型#
def compare_model_posteriors(inferences, labels, variable="beta_XY"):
"""Helper function to plot model posteriors"""
groundtruth = BETA_XY if variable == "beta_XY" else BETA_ZY
for ii, inference in enumerate(inferences):
az.plot_dist(inference.posterior[variable].values, color=f"C{ii}", label=labels[ii])
plt.axvline(groundtruth, label="actual", color="k", linestyle="--")
plt.title(f"posterior {variable}")
plt.legend();
compare_model_posteriors(
inferences=[naive_inference, fixed_effect_inference, multilevel_inference],
labels=["naive", "fixed", "multi-level"],
)
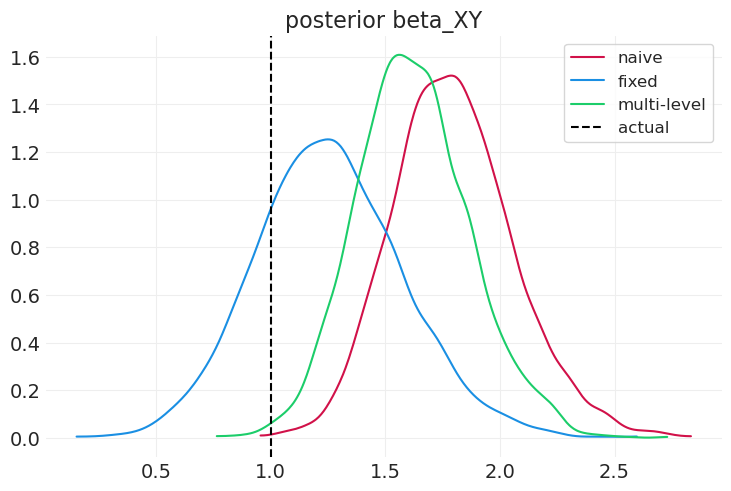
固定效应模型在识别个体级别组混杂因素方面比多层模型（和朴素模型）更好（尽管在此模拟中不是很好），但无法识别任何组效应。
compare_model_posteriors(
inferences=[naive_inference, fixed_effect_inference, multilevel_inference],
labels=["naive", "fixed", "multi-level"],
variable="beta_ZY",
)
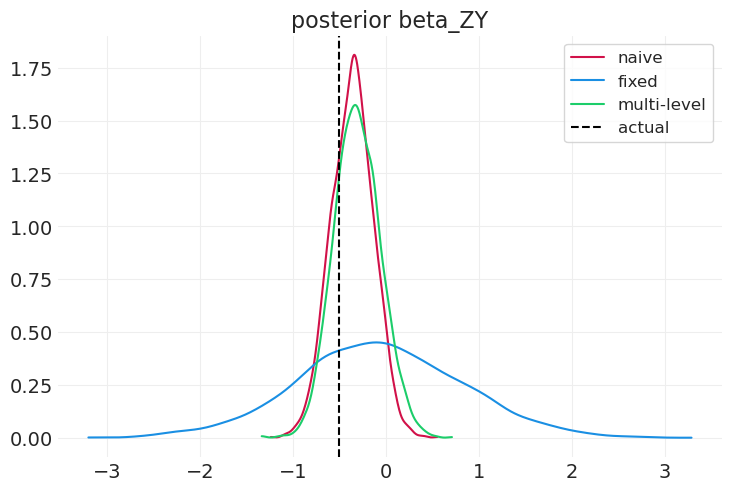
多层模型可以识别组效应，尽管它无法识别混杂因素。固定效应模型无法说明太多关于组级别效应的信息。
如果完全对预测感兴趣，则多层模型更好
如果对推断感兴趣（即通过 do 演算或反事实），您可能需要使用固定效应（尽管组级别预测准确性可能较差）
蒙德拉克机器#
utils.draw_causal_graph(
edge_list=[("G", "X"), ("G", "Y"), ("G", "X_bar"), ("X", "Y"), ("Z", "Y")],
node_props={"G": {"style": "dashed"}, "unobserved": {"style": "dashed"}},
)
统计模型#
\[\begin{split} \begin{align*} Y &\sim \text{Bernoulli}(p) \\ \text{logit}(p_i) &= \alpha_{G[i]} + \beta_{X}X + \beta_{Z} Z_{G[i]} + \beta_{\bar X} \bar X_{G[i]}\\ \beta_* &\sim \text{Normal}(0, 1) \\ \alpha_j &\sim \text{Normal}(\bar a, \tau) \\ \bar a &\sim \text{Normal}(0, 1) \\ \tau &\sim \text{Exponential}(10) \end{align*} \end{split}\]
为每个组估计不同的平均率，部分合并
利用图中的后代上的条件可以（至少部分地）消除父/祖先变量的混杂效应的思想。
使用组级别均值作为混杂变量的子项，以减少其混杂效应。
问题
有点效率低下
因为组的大小不同，我们还需要考虑组级别均值估计中的不确定性，蒙德拉克机器忽略了这一点
# Group-level average
Xbar = np.array([X[GROUP == g].mean() for g in range(N_GROUPS)])
with pm.Model() as mundlak_model:
# Priors
alpha_bar = pm.Normal("alpha_bar", 0, 1)
tau = pm.Exponential("tau", 1)
z = pm.Normal("z", 0, 1, shape=N_GROUPS)
# Note: uncentered reparameterization
alpha = alpha_bar + z * tau
beta_XY = pm.Normal("beta_XY", 0, 1)
beta_ZY = pm.Normal("beta_ZY", 0, 1)
beta_Xbar_Y = pm.Normal("beta_XbarY", 0, 1)
# Likelihood
p = pm.math.invlogit(
alpha[GROUP] + beta_XY * X + beta_ZY * Z[GROUP] + beta_Xbar_Y * Xbar[GROUP]
)
pm.Bernoulli("Y_obs", p=p, observed=Y)
mundlak_inference = pm.sample(target_accept=0.95)
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [alpha_bar, tau, z, beta_XY, beta_ZY, beta_XbarY]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 4 seconds.
compare_model_posteriors(
inferences=[naive_inference, fixed_effect_inference, multilevel_inference, mundlak_inference],
labels=["naive", "fixed", "multi-level", "Mundlak"],
)
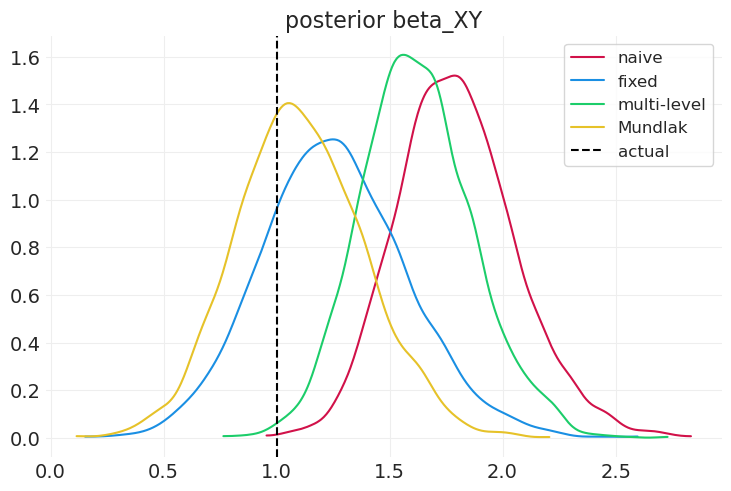
compare_model_posteriors(
inferences=[naive_inference, fixed_effect_inference, multilevel_inference, mundlak_inference],
labels=["naive", "fixed", "multi-level", "Mundlak"],
variable="beta_ZY",
)
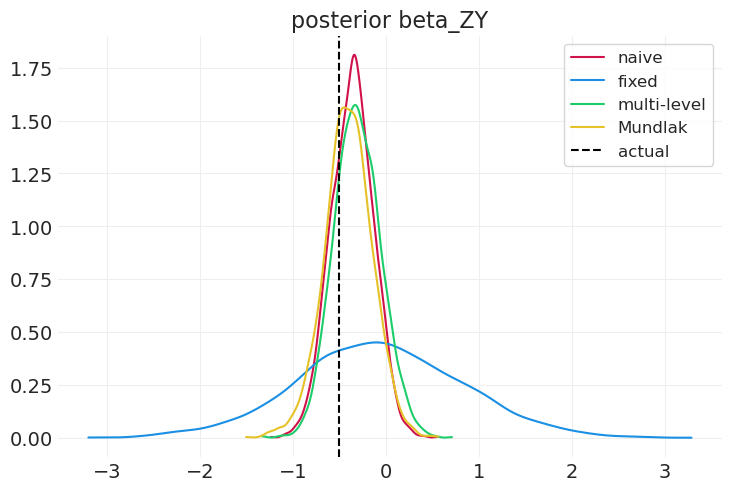
蒙德拉克机器能够捕获处理和组级别效应
潜在蒙德拉克机器（又名“完全豪华贝叶斯”）#
我们不仅对观察到的结果 \(Y\)（作为 \(X, G, Z\) 的函数）建模，还对处理 \(X\)（作为混杂因素 G 的函数）建模。
与蒙德拉克机器将 \(\bar X\) 折叠成点估计，从而忽略该均值估计中的不确定性不同，潜在蒙德拉克通过包含关于 \(X\) 的子模型来估计这种不确定性。
类似于测量误差模型
所以原始图
utils.draw_causal_graph(
edge_list=[("G", "X"), ("G", "Y"), ("X", "Y"), ("Z", "Y")],
node_props={"G": {"style": "dashed"}, "unobserved": {"style": "dashed"}},
)
1. \(X\) 子模型#
utils.draw_causal_graph(
edge_list=[
("G", "X"),
],
node_props={"G": {"style": "dashed"}, "unobserved": {"style": "dashed"}},
)
\[\begin{split} \begin{align*} X_i &\sim \text{Normal}(\mu_{X}, \sigma_X) \\ \mu_{X_i} &= \alpha_X + \beta_{GX} U_{G[i]} \\ U_G &\sim \text{Normal}(0, 1) \\ \alpha_X &\sim \text{Normal}(0, 1) \\ \sigma_X &\sim \text{Exponential}(1) \end{align*} \end{split}\]
2. \(Y\) 子模型#
utils.draw_causal_graph(
edge_list=[("G", "Y"), ("X", "Y"), ("Z", "Y")],
node_props={"G": {"style": "dashed"}, "unobserved": {"style": "dashed"}},
)
\[\begin{split} \begin{align*} Y_i &\sim \text{Bernoulli}(p_i) \\ \text{logit}(p_i) &= \alpha_{Y,G[i]} + \beta_{XY}X_i + \beta_{GY} U_{G[i]}\\ U_G &\sim \text{Normal}(0, 1) \\ \beta_* &\sim \text{Normal}(0, 1) \\ \alpha_{GY} &\sim \text{Normal}(\bar a, \tau) \\ \bar a &\sim \text{Normal}(0, 1) \\ \tau &\sim \text{Exponential}(1) \end{align*} \end{split}\]
with pm.Model() as latent_mundlak_model:
# Unobserved variable (could use various priors here)
G = pm.Normal("u_X", 0, 1, shape=N_GROUPS)
# ----------
# X sub-model
# X Priors
alpha_X = pm.Normal("alpha_X", 0, 1)
beta_GX = pm.Exponential("beta_GX", 1)
sigma_X = pm.Exponential("sigma_X", 1)
# X Likelihood
mu_X = alpha_X + beta_GX * G[GROUP]
X_ = pm.Normal("X", mu_X, sigma_X, observed=X)
# ----------
# Y sub-model
# Y priors
tau = pm.Exponential("tau", 1)
# Note: uncentered reparameterization
z = pm.Normal("z", 0, 1, size=N_GROUPS)
alpha_bar = pm.Normal("alph_bar", 0, 1)
alpha = alpha_bar + tau * z
beta_XY = pm.Normal("beta_XY", 0, 1)
beta_ZY = pm.Normal("beta_ZY", 0, 1)
beta_GY = pm.Normal("beta_GY", 0, 1)
# Y likelihood
p = pm.math.invlogit(alpha[GROUP] + beta_XY * X_ + beta_ZY * Z[GROUP] + beta_GY * G[GROUP])
pm.Bernoulli("Y", p=p, observed=Y)
latent_mundlak_inference = pm.sample(target_accept=0.95)
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [u_X, alpha_X, beta_GX, sigma_X, tau, z, alph_bar, beta_XY, beta_ZY, beta_GY]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 6 seconds.
compare_model_posteriors(
inferences=[
naive_inference,
fixed_effect_inference,
multilevel_inference,
mundlak_inference,
latent_mundlak_inference,
],
labels=["naive", "fixed", "multi-level", "Mundlak", "Luxury"],
)
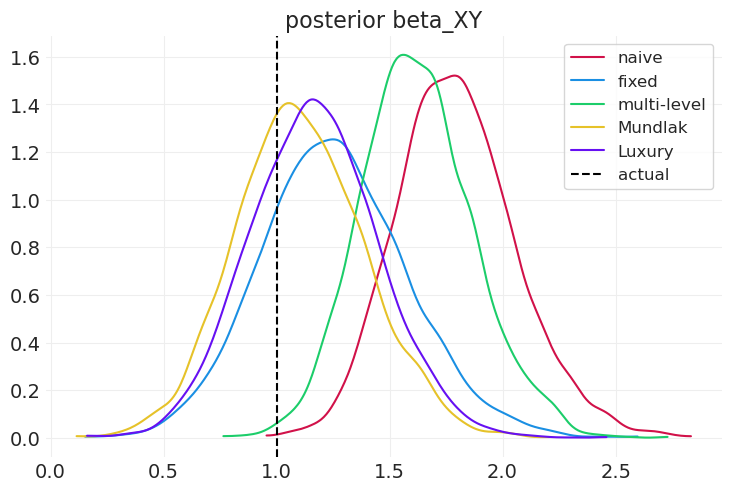
compare_model_posteriors(
inferences=[
naive_inference,
fixed_effect_inference,
multilevel_inference,
mundlak_inference,
latent_mundlak_inference,
],
labels=["naive", "fixed", "multi-level", "Mundlak", "Luxury"],
variable="beta_ZY",
)
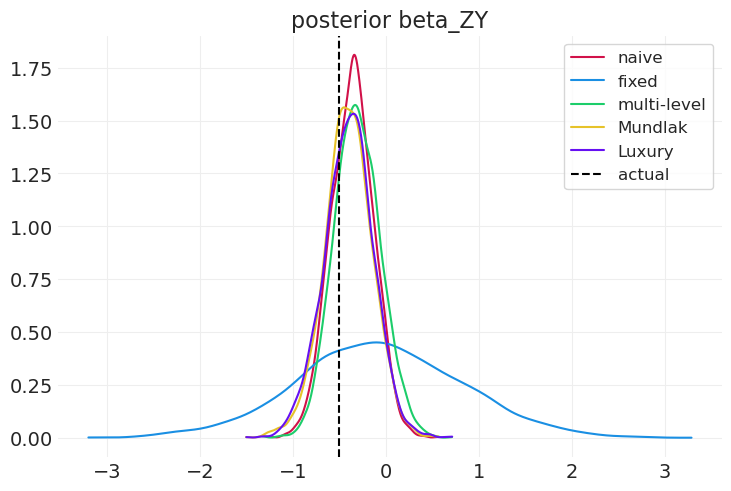
随机混杂因素：总结#
您应该使用固定效应吗？有时，但通常完全豪华贝叶斯是更好的选择
您应该使用蒙德拉克机器/平均 X 吗？
有时：它确实简化了数值计算，但以牺牲不确定性估计为代价。
通常无论如何都有计算能力，所以为什么不直接使用 FLB？
使用完整的生成模型
没有单一解决方案，所以只需明确说明模型
许可证声明#
本示例库中的所有笔记本均根据 MIT 许可证 提供，该许可证允许修改和再分发以用于任何用途，前提是保留版权和许可证声明。
引用 PyMC 示例#
要引用此笔记本，请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。
重要提示
许多笔记本改编自其他来源：博客、书籍... 在这种情况下，您也应该引用原始来源。
另请记住引用您的代码使用的相关库。
这是一个 bibtex 中的引用模板
@incollection{citekey,
author = "<notebook authors, see above>",
title = "<notebook title>",
editor = "PyMC Team",
booktitle = "PyMC examples",
doi = "10.5281/zenodo.5654871"
}
一旦呈现，可能看起来像