孟加拉国生育率再探#
utils.draw_causal_graph(
edge_list=[
("A", "C"),
("K", "C"),
("U", "C"),
("D", "C"),
("D", "U"),
("U", "K"),
("A", "K"),
("D", "K"),
]
)
估计量 1：每个地区 \(D\) 的避孕药具使用率 \(C\)
估计量 2：“城市化”的影响 \(U\)
估计量 3：孩子数量 \(K\) 和年龄 \(A\) 的影响
地区是聚类#
农村/城市细分#
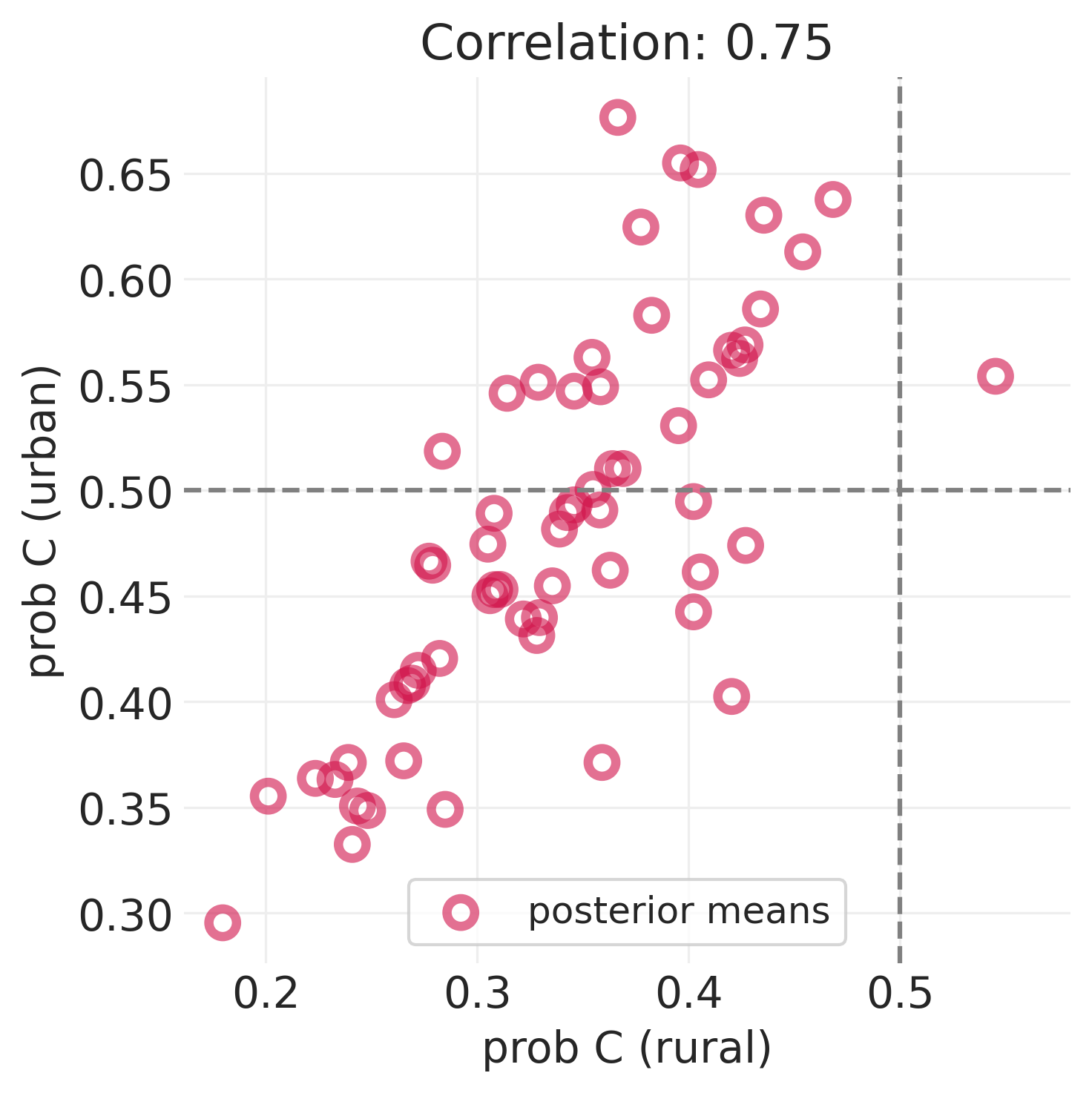
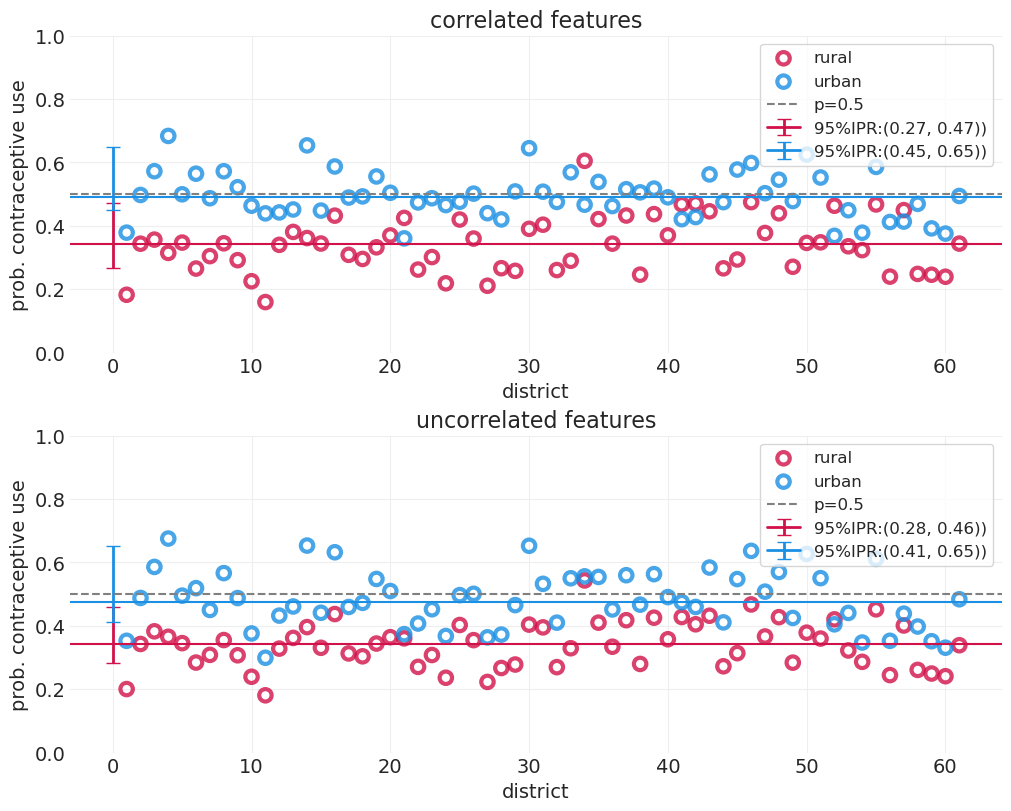
下面我们展示了农村地区（仅包括地区级截距 \(\alpha_{D[i]}\)）与城市地区（包括城市地区的额外截距 \(\beta_{D[i]}\)）组的避孕药具使用率。这些图是在 第 13 讲 - 多层冒险 中生成的。
utils.display_image("fertility_posterior_means_rural_urban.png", width=1000)
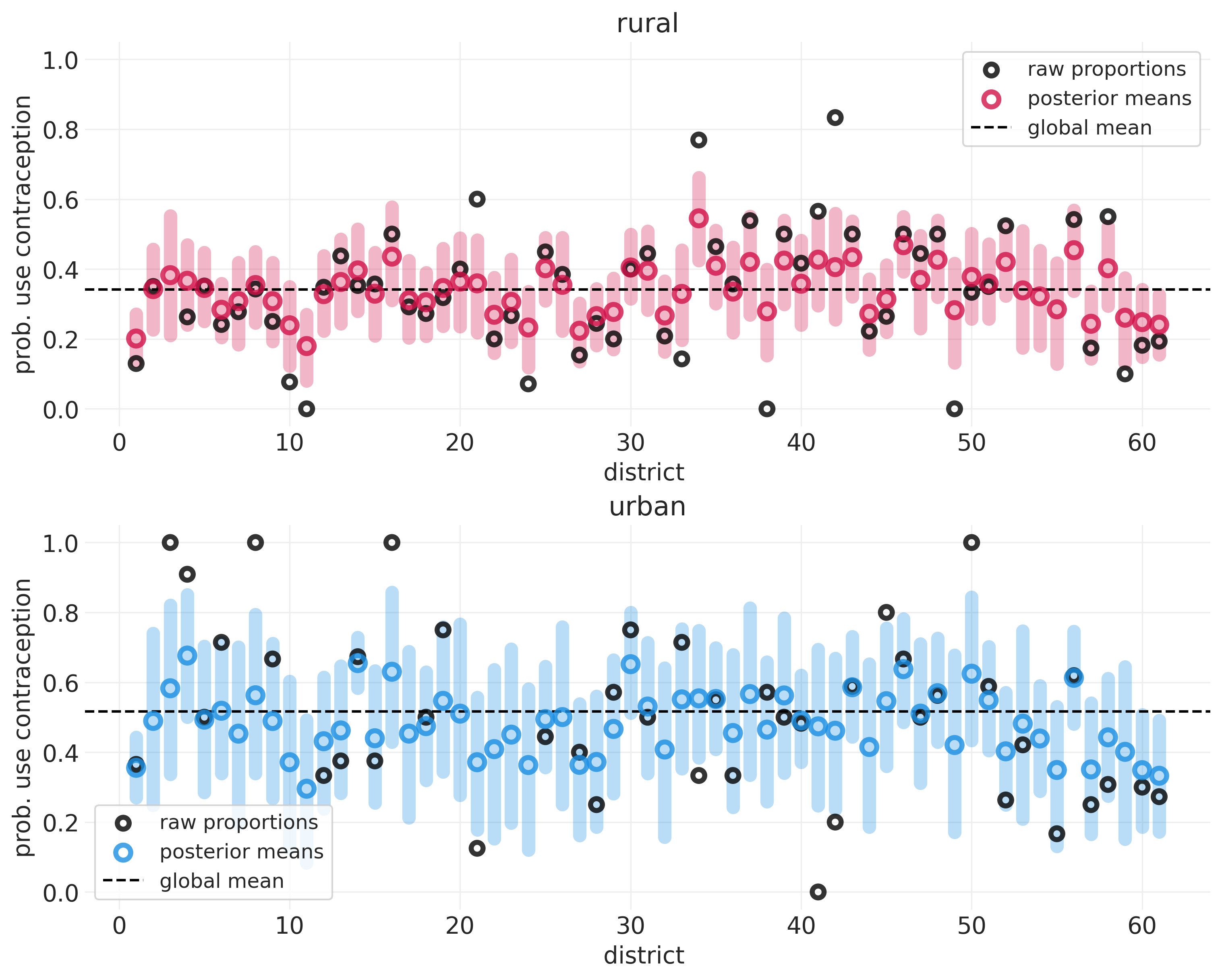
该图显示
平均而言，农村人口比城市地区人口更不可能使用避孕措施
顶部图中的虚线低于底部图中的虚线
城市样本较少，因此城市地区的不确定性范围较大
与农村地区相比，与城市人口相关的误差蓝色条更大，农村地区采样的民意调查更多。
城市化是一个相关特征#
下面我们绘制了城市地区 \(p(C | U=1)\) 与农村地区 \(p(C|U=0)\) 的避孕药具使用概率。这些图是在 第 13 讲 - 多层冒险 中生成的。
utils.display_image("fertility_p_C_rural_urban.png")
该图显示，城市/农村观察之间的避孕药具使用率是相关的 (cc>0.7)
🤔#
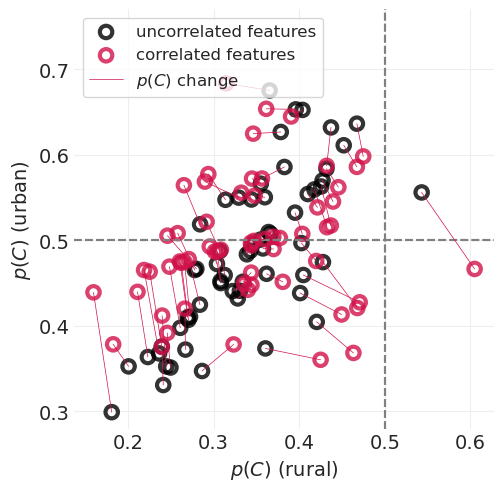
如果我们知道农村地区的避孕药具使用率，由于这种相关性，您可以更好地猜测城市地区的避孕药具使用率
我们没有让 Golem（即我们的统计模型）利用这种特征相关性，因此是在浪费信息
本讲座的重点是构建可以捕获特征之间相关信息的统计模型。
通过跨特征的部分合并，使推断更有效
估计相关性和部分合并演示
McElreath 继续展示了贝叶斯更新在具有相关特征的模型中的演示。它非常棒，我建议多次回顾该演示，但我太懒了，无法实现它（也没有聪明到在没有动画的情况下做到这一点，我正在尝试避免动画）。它将添加到 TODO 列表中。
添加相关特征#
每个聚类/子组的一个先验分布 \(\rightarrow a_j \sim \text{Normal}(\bar a , \sigma)\)；允许部分合并
如果一个特征，则一维先验
\(a_j \sim \text{Normal}(\bar a, \sigma)\)
N 个特征的 N 维分布
我们使用特征的联合分布，而不是独立的分布（就像我们在之前的讲座中所做的那样）
\(a_{j, 1..N} \sim \text{MVNormal}(A, \Sigma)\)
例如，\([\alpha_j, \beta_j] \sim \text{MVNormal}([\bar \alpha, \bar \beta], \Sigma_{\alpha, \beta})\)
难点：学习特征之间的关联/相关性
“估计均值很容易”
“估计标准差很难”
“估计相关性非常难”
也就是说，通常尝试学习相关性是个好主意
如果您没有足够的样本/信号，您将退回到先验
之前的模型 – 使用不相关的城市特征#
utils.draw_causal_graph(
edge_list=[
("A", "C"),
("K", "C"),
("U", "C"),
("D", "C"),
("D", "U"),
("U", "K"),
("A", "K"),
("D", "K"),
],
node_props={"U": {"color": "red"}, "D": {"color": "red"}, "C": {"color": "red"}},
edge_props={
("U", "K"): {"color": "red"},
("U", "C"): {"color": "red"},
("K", "C"): {"color": "red"},
},
)
这是未居中的实现，或多或少从之前的讲座中复制粘贴而来
FERTILITY = utils.load_data("bangladesh")
USES_CONTRACEPTION = FERTILITY["use.contraception"].values.astype(int)
DISTRICT_ID, _ = pd.factorize(FERTILITY.district)
DISTRICT = np.arange(1, 62).astype(
int
) # note: district 54 has no data so we create it's dim by hand
URBAN_ID, URBAN = pd.factorize(FERTILITY.urban, sort=True)
with pm.Model(coords={"district": DISTRICT}) as uncorrelated_model:
# Mutable data
urban = pm.Data("urban", URBAN_ID)
# Priors -- priors for $\alpha$ and $\beta$ are separate, independent Normal distributions
# District offset
alpha_bar = pm.Normal("alpha_bar", 0, 1) # the average district
sigma = pm.Exponential("sigma", 1) # variation amongst districts
# Uncentered parameterization
z_alpha = pm.Normal("z_alpha", 0, 1, dims="district")
alpha = pm.Deterministic("alpha", alpha_bar + z_alpha * sigma, dims="district")
# District / urban interaction
beta_bar = pm.Normal("beta_bar", 0, 1) # the average urban effect
tau = pm.Exponential("tau", 1) # variation amongst urban
# Uncentered parameterization
z_beta = pm.Normal("z_beta", 0, 1, dims="district")
beta = pm.Deterministic("beta", beta_bar + z_beta * tau, dims="district")
# Recored p(contraceptive)
p_C = pm.Deterministic("p_C", pm.math.invlogit(alpha + beta))
p_C_urban = pm.Deterministic("p_C_urban", pm.math.invlogit(alpha + beta))
p_C_rural = pm.Deterministic("p_C_rural", pm.math.invlogit(alpha))
# Likelihood
p = pm.math.invlogit(alpha[DISTRICT_ID] + beta[DISTRICT_ID] * urban)
C = pm.Bernoulli("C", p=p, observed=USES_CONTRACEPTION)
uncorrelated_inference = pm.sample(target_accept=0.95)
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [alpha_bar, sigma, z_alpha, beta_bar, tau, z_beta]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 10 seconds.
证明特征先验在不相关模型中是独立的#
下面我们从先验中采样，并表明所有地区的 \(\alpha\) 和 \(\beta\) 参数都与基轴对齐，表明没有相关性
def plot_2d_guassian_ci(R, mean=[0, 0], std=[1, 1], ci_prob=0.89, **plot_kwargs):
"""
Plot the `ci_prob`% confidence interval for a 2D Gaussian defined
by correlation matrix `R`, center `mean`, and standard deviations
`std` along the marginals.
"""
# Create a circle
angles = np.linspace(0, 2 * np.pi, 100)
radius = stats.norm.ppf(ci_prob)
circle = radius * np.vstack([np.cos(angles), np.sin(angles)])
# Warp circle using the covariance matrix
D = np.diag(std)
cov = D @ R @ D
ellipse = sqrtm(np.matrix(cov)) @ circle
plt.plot(ellipse[0] + mean[0], ellipse[1] + mean[1], linewidth=3, **plot_kwargs)
with uncorrelated_model:
prior_pred = pm.sample_prior_predictive()
districts = [1, 10, 30, 61]
n_districts = len(districts)
fig, axs = plt.subplots(n_districts, 1, figsize=(6, n_districts * 4))
for ii, district in enumerate(districts):
district_prior = prior_pred.prior.sel(district=district)
plt.sca(axs[ii])
az.plot_dist(
district_prior["alpha"],
district_prior["beta"],
ax=axs[ii],
contourf_kwargs={"cmap": "Reds"},
)
plt.xlim([-4, 4])
plt.ylim([-4, 4])
plt.xlabel("$\\alpha$")
plt.ylabel("$\\beta$")
plt.title(f"District {district} Prior")
Sampling: [C, alpha_bar, beta_bar, sigma, tau, z_alpha, z_beta]
上面我们可以看到不相关模型提供的先验。我们可以判断它们是不相关的，因为
分布的主轴垂直于参数值的轴。
即，PDF 轮廓没有“倾斜”
多元正态先验#
\[\begin{split} \begin{align*} [\alpha_j, \beta_j] &= \text{MVNormal}([\bar \alpha, \bar \beta], R, [\sigma, \tau]) \\ [\alpha_j, \beta_j]&:= \text{地区 } j \text{ 的特征} \\ R &:= \text{特征之间的相关矩阵} \\ [\sigma, \tau] &:= \text{每个参数 } j \text{ 的（独立）标准差} \\ \end{align*} \end{split}\]
来自多元先验的样本#
np.random.seed(123)
sigma = 1.0
tau = 2.0
R = np.array([[1, 0.8], [0.8, 1]]) # correlation matrix
stds = np.array([sigma, tau])
D = np.diag(stds)
Sigma = D @ R @ D # convert correlation matrix to covariance matrix
mvnorm = stats.multivariate_normal(cov=Sigma)
def mvn_norm_pdf(
xs,
ys,
):
return mvnorm.pdf(np.vstack([xs, ys]).T)
RESOLUTION = 100
xs = ys = np.linspace(-4, 4, RESOLUTION)
utils.plot_2d_function(xs, ys, mvn_norm_pdf, cmap="Reds")
n_samples = 50
samples = mvnorm.rvs(n_samples)
utils.plot_scatter(samples[:, 0], samples[:, 1], color="darkred", alpha=1, label="samples")
plt.xlabel("$\\alpha$")
plt.ylabel("$\\beta$")
plt.xlim([-4, 4])
plt.ylim([-4, 4])
plt.legend()
print(f"Standard deviations\n{stds}")
print(f"Correlation Matrix\n{R}")
print(f"Covariance Matrix\n{Sigma}")
print(f"Cholesky Matrix\n{np.linalg.cholesky(Sigma)}")
Standard deviations
[1. 2.]
Correlation Matrix
[[1. 0.8]
[0.8 1. ]]
Covariance Matrix
[[1. 1.6]
[1.6 4. ]]
Cholesky Matrix
[[1. 0. ]
[1.6 1.2]]
具有相关城市特征的模型#
\[\begin{split} \begin{align*} C_i &\sim \text{Bernouill}(p_i) \\ p_i &= \alpha_{D[i]} + \beta_{D[i]} U_i \\ [\alpha_j, \beta_j] &\sim \text{MVNormal}([\bar \alpha, \bar \beta], R, [\sigma, \tau]) \\ \sigma &\sim \text{Exponential}(1) \\ \tau &\sim \text{Exponential}(1) \\ R &\sim \text{LKJCorr}(4) \end{align*} \end{split}\]
关于 LKJCorr 先验#
以 Lewandowski-Kurowicka-Joe 命名，他们是关于该分布的原始论文的作者
相关矩阵的先验
采用形状参数 \(\eta>0\)
\(\eta=1\) 会导致相关矩阵上的均匀分布
\(\eta \rightarrow \infty\)，R 接近单位矩阵
更改相关矩阵的分布
etas = [1, 4, 10, 20, 100]
for ii, eta in enumerate(etas):
rv = pm.LKJCorr.dist(n=2, eta=eta)
samples = pm.draw(rv, 1000)
az.plot_dist(samples, color=f"C{ii}", label=f"LKJCorr$(\\eta={eta})$")
plt.legend()
plt.xlabel("correlation")
plt.ylabel("density")
plt.title("LKJCorr distribution of correlations");
从 LKJCorr 采样的相关矩阵#
import matplotlib.transforms as transforms
from matplotlib.patches import Ellipse
from scipy.linalg import sqrtm
def sample_correlation_matrix_LKJ(dim=2, eta=4, n_samples=1):
# Samples; LKJCorr returns correlations are returned as
# upper-triangular matrix entries
rv = pm.LKJCorr.dist(n=dim, eta=eta)
samples = pm.draw(rv, n_samples)
# Convert upper triangular entries to full correlation matrices
# (there's likely a way to vectorize this, but meh it's a demo)
covs = []
upper_idx = np.triu_indices(n=dim, k=1)
for sample in samples:
cov = np.eye(dim) * 0.5
cov[upper_idx[0], upper_idx[1]] = sample
cov += cov.T
covs.append(cov)
return np.array(covs)
def sample_LKJCorr_prior(eta=1, n_samples=20, ax=None):
plt.sca(ax)
for _ in range(n_samples):
R = sample_correlation_matrix_LKJ(eta=eta)
# Sample a random standard deviation along each dimension
std = stats.expon(0.1).rvs(2) # exponential
# std = np.random.rand(2) * 10 # uniform
# std = np.abs(np.random.randn(2)) # half-normal
plot_2d_guassian_ci(R, std=std, color="C0", alpha=0.25)
plt.xlim([-2, 2])
plt.ylim([-2, 2])
plt.xlabel("$\\alpha$")
plt.ylabel("$\\beta$")
plt.title(f"Random Correlations Sampled\nfrom LKJCorr({eta}) prior");
etas = [1, 4, 10, 1000]
n_etas = len(etas)
_, axs = plt.subplots(n_etas, 1, figsize=(6, 6 * n_etas))
for ii, eta in enumerate(etas):
sample_LKJCorr_prior(eta=eta, ax=axs[ii])
我们可以看到，随着 \(\eta\) 变得更大，相关矩阵的轴与参数空间的轴变得更加对齐，从而提供对角协方差样本
分析特征相关性#
correlated_posterior_mean = correlated_inference.posterior.mean(dim=("chain", "draw"))
print(f"Feature Covariance\n", correlated_posterior_mean["feature_cov"].values)
print(f"Feature Correlation\n", correlated_posterior_mean["feature_corr"].values)
print(f"Feature Std\n", correlated_posterior_mean["feature_std"].values)
Feature Covariance
[[ 0.32032104 -0.24587394]
[-0.24587394 0.60162453]]
Feature Correlation
[[ 1. -0.55103506]
[-0.55103506 1. ]]
Feature Std
[0.55748164 0.74948169]
与先验比较#
with correlated_model:
# Add prior samples
correlated_prior_predictive = pm.sample_prior_predictive()
Sampling: [C, Rho, alpha_bar, beta_bar, z]
def plot_posterior_mean_alpha_beta(posterior_mean, title=None):
alphas = posterior_mean["alpha"].values
betas = posterior_mean["beta"].values
alpha_mean = posterior_mean["alpha"].mean().values
beta_mean = posterior_mean["beta"].mean().values
# Correlated feature params
if "feature_corr" in posterior_mean:
posterior_R = posterior_mean["feature_corr"].values
posterior_std = posterior_mean["feature_std"].values
# Independent feature params
else:
cc = np.corrcoef(alphas, betas)[0][1]
posterior_R = np.array([[1, cc], [cc, 1]])
posterior_std = np.array([posterior_mean["sigma"], posterior_mean["tau"]])
plot_2d_guassian_ci(R=posterior_R, mean=(alpha_mean, beta_mean), std=posterior_std, color="C0")
utils.plot_scatter(
xs=posterior_mean["alpha"],
ys=posterior_mean["beta"],
color="k",
label="district param means",
)
plt.axvline(0, color="gray", linestyle="--")
plt.axhline(0, color="gray", linestyle="--")
plt.xlim([-2, 1])
plt.ylim([-2, 2])
plt.xlabel("$\\alpha$")
plt.ylabel("$\\beta$")
plt.legend()
plt.title(title)
_, axs = plt.subplots(1, 2, figsize=(10, 5))
# Plot correlation distribution for posterior and prior
plt.sca(axs[0])
plot_kwargs = {"linewidth": 3}
az.plot_dist(
correlated_inference.posterior["feature_corr"][:, :, 0, 1],
label="posterior",
plot_kwargs=plot_kwargs,
ax=axs[0],
)
az.plot_dist(
correlated_prior_predictive.prior["feature_corr"][:, :, 0, 1],
color="k",
label="prior",
plot_kwargs=plot_kwargs,
ax=axs[0],
)
plt.axvline(0, color="gray", linestyle="--")
plt.xlim([-1, 1])
plt.xlabel("correlation between $\\alpha$ and $\\beta$")
plt.ylabel("density")
plt.legend()
plt.sca(axs[1])
plot_posterior_mean_alpha_beta(correlated_posterior_mean)
plt.suptitle("Correlated Features", fontsize=18);
uncorrelated_posterior_mean = uncorrelated_inference.posterior.mean(dim=("chain", "draw"))
_, axs = plt.subplots(1, 2, figsize=(10, 5))
plt.sca(axs[0])
plot_posterior_mean_alpha_beta(uncorrelated_posterior_mean, title="uncorrelated features")
plt.sca(axs[1])
plot_posterior_mean_alpha_beta(correlated_posterior_mean, title="correlated features")
与不建模特征相关性的模型相比：具有不相关特征的模型表现出弱得多的负相关性（即，左侧的红色椭圆“向下倾斜”的程度较小）。
在结果尺度上比较模型。#
def plot_p_C_district_rural_urban(posterior_mean, title=None):
for ii, (label, p_C) in enumerate(zip(["rural", "urban"], ["p_C_rural", "p_C_urban"])):
color = f"C{ii}"
plot_data = posterior_mean[p_C]
utils.plot_scatter(DISTRICT, plot_data, label=label, color=color, alpha=0.8)
# Add quantile indicators
ql, median, qu = np.quantile(plot_data, [0.25, 0.5, 0.975])
error = np.array((median - ql, qu - median))[:, None]
plt.errorbar(
x=0,
y=median,
yerr=error,
color=color,
capsize=5,
linewidth=2,
label=f"95%IPR:({ql:0.2f}, {qu:0.2f}))",
)
plt.axhline(median, color=color)
plt.axhline(0.5, color="gray", linestyle="--", label="p=0.5")
plt.legend(loc="upper right")
plt.ylim([0, 1])
plt.xlabel("district")
plt.ylabel("prob. contraceptive use")
plt.title(title)
_, axs = plt.subplots(2, 1, figsize=(10, 8))
plt.sca(axs[0])
plot_p_C_district_rural_urban(correlated_posterior_mean, title="correlated features")
plt.sca(axs[1])
plot_p_C_district_rural_urban(uncorrelated_posterior_mean, title="uncorrelated features")
建模特征相关性允许城市地区以不同的方式捕获城市方差。虽然效果很微妙，但相关特征模型（顶部）表现出比不相关特征模型（0.41-0.65）更小的内百分位数范围 (IPR) (0.45-0.65)。
⚠️ 这实际上与讲座中报告的相反。我的直觉是，后验变异性会更小，因为我们正在跨特征共享信息，从而降低了我们的不确定性。但我很容易在这里做错或理解错误。
查看结果空间#
def plot_pC_rural_urban_xy(posterior_mean, label, color):
utils.plot_scatter(
xs=posterior_mean["p_C_rural"],
ys=posterior_mean["p_C_urban"],
label=label,
color=color,
alpha=0.8,
)
plt.axhline(0.5, color="gray", linestyle="--")
plt.axvline(0.5, color="gray", linestyle="--")
plt.xlabel("$p(C)$ (rural)")
plt.ylabel("$p(C)$ (urban)")
plt.legend()
plt.axis("square")
def plot_pC_xy_movement(posterior_mean_a, posterior_mean_b):
xs_a = posterior_mean_a["p_C_rural"]
xs_b = posterior_mean_b["p_C_rural"]
ys_a = posterior_mean_a["p_C_urban"]
ys_b = posterior_mean_b["p_C_urban"]
for ii, (xa, xb, ya, yb) in enumerate(zip(xs_a, xs_b, ys_a, ys_b)):
label = "$p(C) $ change" if not ii else None
plt.plot((xa, xb), (ya, yb), linewidth=0.5, color="C0", label=label)
plt.legend(loc="upper left")
plot_pC_rural_urban_xy(uncorrelated_posterior_mean, label="uncorrelated features", color="k")
plot_pC_rural_urban_xy(correlated_posterior_mean, label="correlated features", color="C0")
plot_pC_xy_movement(uncorrelated_posterior_mean, correlated_posterior_mean)
包括特征相关性#
点移动是因为跨特征的信息传递提供了更好的 \(p(C)\) 估计
农村地区与城市地区避孕药具使用率差异之间存在负相关关系
当一个地区的农村地区避孕药具使用率很高时，差异会更小（即城市地区也将具有较高的避孕药具使用率）
当农村地区避孕药具使用率较低时，城市地区将更加不同（即城市地区仍然倾向于具有较高的避孕药具使用率）
奖励：非居中（又名变换）先验#
不方便的后验#
由负对数似然中的陡峭曲率引起的不高效 MCMC
哈密顿蒙特卡洛在探索陡峭表面时遇到困难
导致“发散”跃迁
“冲破滑板公园的墙壁”
当哈密顿量在提议的开始/结束之间发生剧烈变化时检测到
变换先验以使其成为“更平滑的滑板公园”有所帮助
示例：魔鬼漏斗先验#
\[\begin{split} \begin{align*} v &\sim \text{Normal}(0, \sigma_v) \\ x &\sim \text{Normal}(0, \exp({v})) \end{align*} \end{split}\]
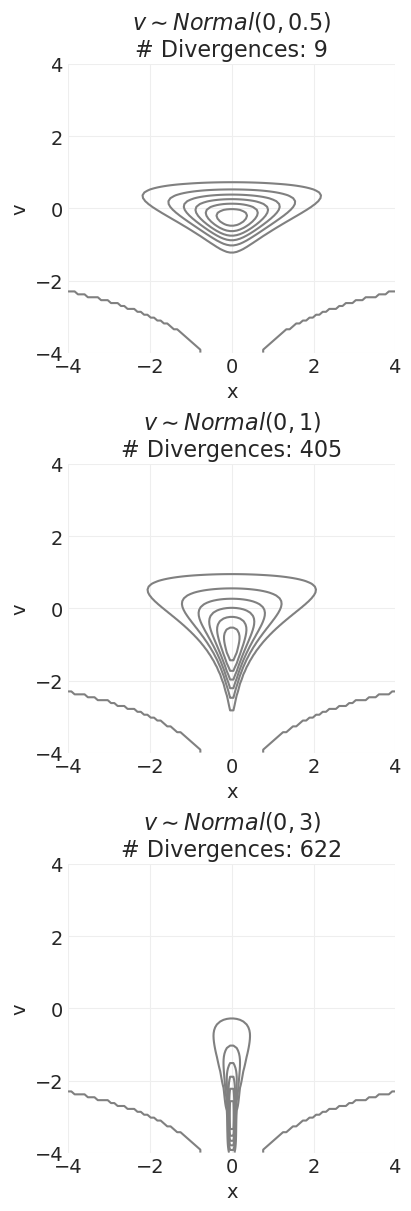
随着 \(\sigma_v\) 的增加，先验概率表面中会形成一个讨厌的槽，哈密顿动力学很难对其进行采样——即，滑板公园太陡峭和狭窄。
我太懒了，无法编写 McElreath 用来可视化每个发散路径的精美 HMC 动画。但是，我们仍然可以验证，当我们在魔鬼漏斗先验中增加 v 先验的 \(\sigma\) 时，发散的数量会增加。
居中先验模型#
from functools import partial
xs = vs = np.linspace(-4, 4, 100)
def prior_devils_funnel(xs, vs, sigma_v=0.5):
log_prior_v = stats.norm(0, sigma_v).logpdf(vs)
log_prior_x = stats.norm(0, np.exp(vs)).logpdf(xs)
log_prior = log_prior_v + log_prior_x
return np.exp(log_prior - log_prior.max())
# Loop over sigma_v, and show that divergences increase
# as the depth and narrowness of the trough increases
# for low values of v
sigma_vs = [0.5, 1, 3]
n_sigma_vs = len(sigma_vs)
fig, axs = plt.subplots(3, 1, figsize=(4, 4 * n_sigma_vs))
for ii, sigma_v in enumerate(sigma_vs):
with pm.Model() as centered_devils_funnel:
v = pm.Normal("v", 0, sigma_v)
x = pm.Normal("x", 0, pm.math.exp(v))
centered_devils_funnel_inference = pm.sample()
n_divergences = centered_devils_funnel_inference.sample_stats.diverging.sum().values
prior = partial(prior_devils_funnel, sigma_v=sigma_v)
plt.sca(axs[ii])
utils.plot_2d_function(xs, ys, prior, colors="gray", ax=axs[ii])
plt.xlabel("x")
plt.ylabel("v")
plt.title(f"$v \sim Normal(0, {sigma_v})$\n# Divergences: {n_divergences}")
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [v, x]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.
There were 9 divergences after tuning. Increase `target_accept` or reparameterize.
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [v, x]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.
There were 405 divergences after tuning. Increase `target_accept` or reparameterize.
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details
The effective sample size per chain is smaller than 100 for some parameters. A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [v, x]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.
There were 622 divergences after tuning. Increase `target_accept` or reparameterize.
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details
The effective sample size per chain is smaller than 100 for some parameters. A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details
怎么办？#
更小的步长：更好地处理陡峭度，但需要更长的时间来探索后验
重新参数化（变换）以使表面更平滑
非居中先验#
我们添加一个辅助变量 \(z\)，它具有平滑的概率表面。然后我们对该辅助变量进行采样，并对其进行变换以获得目标变量分布。对于魔鬼漏斗先验的情况
\[\begin{split} \begin{align*} v &\sim \text{Normal}(0, \sigma_v) \\ z &\sim \text{Normal}(0, 1) \\ x &= z \exp(v) \end{align*} \end{split}\]
sigma_vs = [0.5, 1, 3]
n_sigma_vs = len(sigma_vs)
fig, axs = plt.subplots(3, 1, figsize=(4, 4 * n_sigma_vs))
def prior_noncentered_devils_funnel(xs, vs, sigma_v=0.5):
"""Reparamterize into a smoother auxilary variable space"""
log_prior_v = stats.norm(0, sigma_v).logpdf(vs)
log_prior_z = stats.norm(0, 1).logpdf(xs)
log_prior = log_prior_v + log_prior_z
return np.exp(log_prior - log_prior.max())
for ii, sigma_v in enumerate(sigma_vs):
with pm.Model() as noncentered_devils_funnel:
v = pm.Normal("v", 0, sigma_v)
z = pm.Normal("z", 0, 1)
# Record x for reporting
x = pm.Deterministic("x", z * pm.math.exp(v))
noncentered_devils_funnel_inference = pm.sample()
n_divergences = noncentered_devils_funnel_inference.sample_stats.diverging.sum().values
prior = partial(prior_noncentered_devils_funnel, sigma_v=sigma_v)
plt.sca(axs[ii])
utils.plot_2d_function(xs, ys, prior, colors="gray", ax=axs[ii])
plt.xlabel("z")
plt.ylabel("v")
plt.title(f"$v \sim$ Normal(0, {sigma_v})\n# Divergences: {n_divergences}")
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [v, z]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [v, z]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [v, z]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.
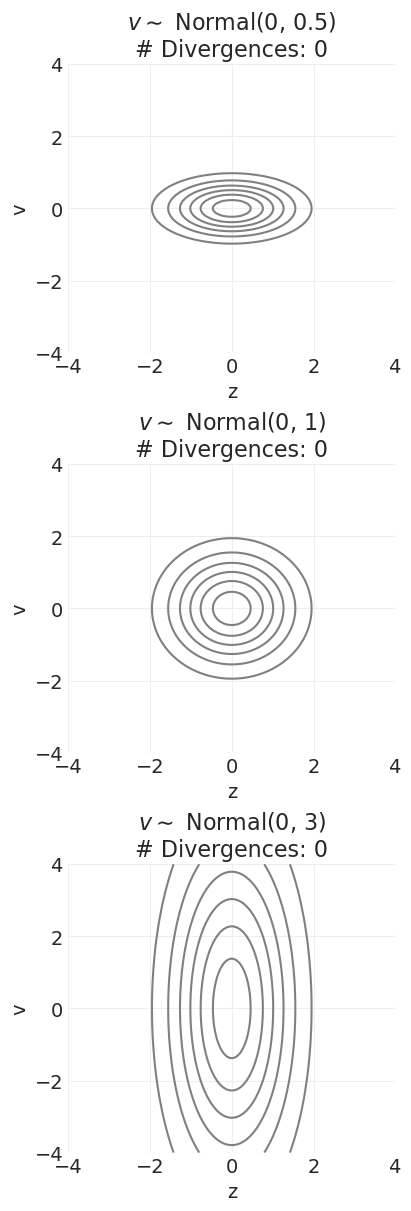
通过重新参数化，我们可以对多维正态分布进行采样，这些分布在对数空间中是更平滑的抛物线。
我们可以看到，对于所有先验方差值，发散的数量都持续减少。
检查 HMC 诊断#
az.summary(noncentered_devils_funnel_inference)["r_hat"]
v 1.0
x 1.0
z 1.0
Name: r_hat, dtype: float64
az.plot_trace(noncentered_devils_funnel_inference);
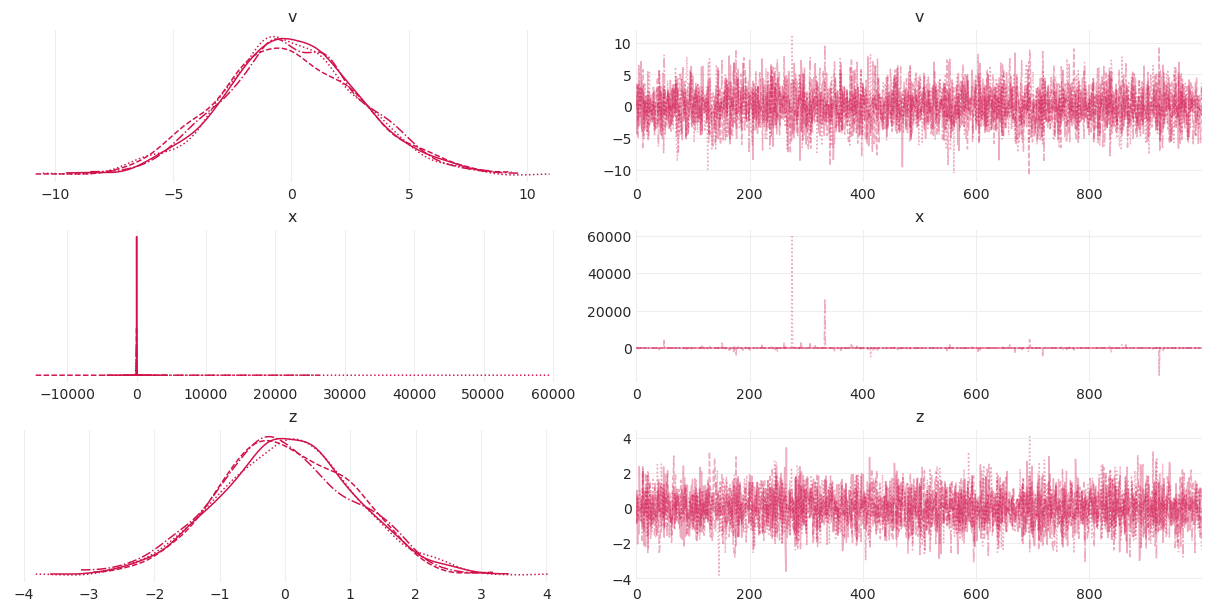
诊断看起来不错 👍
Rhats = 1\(v\) 和 \(z\) 链表现出“模糊毛毛虫”行为
Cholesky 因子和相关矩阵#
Cholesky 因子 \(\bf L\) 提供了一种有效的方法来编码相关矩阵 \(\Omega\)（比完整的相关矩阵需要更少的浮点数）
\(\Omega = \bf LL^T\)
\(\bf L\) 是一个下三角矩阵
我们可以使用 \(\Omega\) 的 Cholesky 分解 \(\bf L\) 对具有相关性 \(\Omega\) 和标准差 \(\sigma_i\) 的数据进行采样，如下所示
\[ X_\Omega \sim \text{diag}(\sigma_i)\bf{LZ}, \]
其中 \(\bf Z\) 是从标准正态分布中采样的 z 分数矩阵
演示从 Cholesky 因子重建相关矩阵#
orig_corr = np.array([[1, 0.6], [0.6, 1]])
print("Ground-truth Correlation Matrix\n", orig_corr)
L = np.linalg.cholesky(orig_corr)
print("\nCholesky Matrix of correlation matrix, L\n", L)
print("\nReconstructed correlation matrix from L\n", L @ L.T)
Ground-truth Correlation Matrix
[[1. 0.6]
[0.6 1. ]]
Cholesky Matrix of correlation matrix, L
[[1. 0. ]
[0.6 0.8]]
Reconstructed correlation matrix from L
[[1. 0.6]
[0.6 1. ]]
演示从 z 分数和 Cholesky 因子采样随机相关矩阵#
np.random.seed(12345)
N = 100_000
orig_sigmas = [2, 0.5]
# Matrix of z-score samples
Z = stats.norm().rvs(size=(2, N))
print("Raw z-score samples are indpendent\n", np.corrcoef(Z[0], Z[1]))
# Transform Z-scores using the Cholesky factorization of the correlation matrix
sLZ = np.diag(orig_sigmas) @ L @ Z
corr_sLZ = np.corrcoef(sLZ[0], sLZ[1])
print("\nCholesky-transformed z-scores have original correlation encoded\n", corr_sLZ)
assert np.isclose(orig_corr[0, 1], corr_sLZ[0, 1], atol=0.01)
std_sLZ = sLZ.std(axis=1)
print("\nOriginal std devs also encoded in transformed z-scores:\n", std_sLZ)
assert np.isclose(orig_sigmas[0], std_sLZ[0], atol=0.01)
assert np.isclose(orig_sigmas[1], std_sLZ[1], atol=0.01)
Raw z-score samples are indpendent
[[1. 0.00293945]
[0.00293945 1. ]]
Cholesky-transformed z-scores have original correlation encoded
[[1. 0.60268456]
[0.60268456 1. ]]
Original std devs also encoded in transformed z-scores:
[2.00212936 0.50024976]
何时使用变换先验#
取决于上下文
居中
每个聚类/子组中的大量数据
似然主导场景
非居中
许多聚类/子组，其中一些聚类中的数据稀疏
先验主导场景
许可证声明#
此示例库中的所有笔记本均根据 MIT 许可证 提供，该许可证允许修改和再分发用于任何用途，前提是保留版权和许可证声明。
引用 PyMC 示例#
要引用此笔记本，请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。
重要提示
许多笔记本都改编自其他来源：博客、书籍……在这种情况下，您也应该引用原始来源。
另请记住引用您的代码使用的相关库。
这是一个 bibtex 中的引用模板
@incollection{citekey,
author = "<notebook authors, see above>",
title = "<notebook title>",
editor = "PyMC Team",
booktitle = "PyMC examples",
doi = "10.5281/zenodo.5654871"
}
一旦呈现，它可能看起来像