贝叶斯生存分析#
生存分析 研究事件发生时间的分布。其应用领域涵盖医学、生物学、工程学和社会科学等诸多领域。本教程演示了如何在 Python 中使用 PyMC 拟合和分析贝叶斯生存模型。
我们通过分析来自 R 的 乳房切除术数据集 HSAUR 包中的数据集来说明这些概念。
import arviz as az
import numpy as np
import pandas as pd
import pymc as pm
import pytensor
from matplotlib import pyplot as plt
from pymc.distributions.timeseries import GaussianRandomWalk
from pytensor import tensor as T
print(f"Running on PyMC v{pm.__version__}")
Running on PyMC v5.0.1+42.g99dd7158
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
try:
df = pd.read_csv("../data/mastectomy.csv")
except FileNotFoundError:
df = pd.read_csv(pm.get_data("mastectomy.csv"))
df.event = df.event.astype(np.int64)
df.metastasized = (df.metastasized == "yes").astype(np.int64)
n_patients = df.shape[0]
patients = np.arange(n_patients)
df.head()
| 时间 | 事件 | 转移 | |
|---|---|---|---|
| 0 | 23 | 1 | 0 |
| 1 | 47 | 1 | 0 |
| 2 | 69 | 1 | 0 |
| 3 | 70 | 0 | 0 |
| 4 | 100 | 0 | 0 |
n_patients
44
每一行代表一位被诊断患有乳腺癌并接受乳房切除术的女性的观察结果。列 time 代表观察到的女性术后时间(以月为单位)。列 event 指示在观察期间该女性是否死亡。列 metastasized 代表癌症是否在手术前已转移。
本教程分析了乳房切除术后生存时间与癌症是否转移之间的关系。
生存分析速成课程#
首先,我们介绍一点(非常少的)理论。如果随机变量 \(T\) 是我们研究的事件发生的时间,则生存分析主要关注生存函数
其中 \(F\) 是 \(T\) 的 CDF。用 风险率 \(\lambda(t)\) 来表示生存函数在数学上很方便。风险率是在时间 \(t\) 事件发生的瞬时概率,前提是它尚未发生。也就是说,
求解生存函数的微分方程表明
生存函数的这种表示表明累积风险函数
是生存分析中的一个重要量,因为我们可以简洁地写成 \(S(t) = \exp(-\Lambda(t)).\)
生存分析中一个重要但微妙的点是删失。即使我们感兴趣的量是手术到死亡之间的时间,我们也没有观察到每个受试者的死亡。在我们进行分析的时间点,我们的一些受试者值得庆幸的是仍然活着。在我们的乳房切除术研究案例中,如果观察到受试者的死亡(观察未删失),则 df.event 为 1,如果未观察到死亡(观察已删失),则为零。
df.event.mean()
0.5909090909090909
我们略高于 40% 的观察结果被删失。我们在下面可视化观察到的持续时间,并指示哪些观察结果被删失。
fig, ax = plt.subplots(figsize=(8, 6))
ax.hlines(
patients[df.event.values == 0], 0, df[df.event.values == 0].time, color="C3", label="Censored"
)
ax.hlines(
patients[df.event.values == 1], 0, df[df.event.values == 1].time, color="C7", label="Uncensored"
)
ax.scatter(
df[df.metastasized.values == 1].time,
patients[df.metastasized.values == 1],
color="k",
zorder=10,
label="Metastasized",
)
ax.set_xlim(left=0)
ax.set_xlabel("Months since mastectomy")
ax.set_yticks([])
ax.set_ylabel("Subject")
ax.set_ylim(-0.25, n_patients + 0.25)
ax.legend(loc="center right");
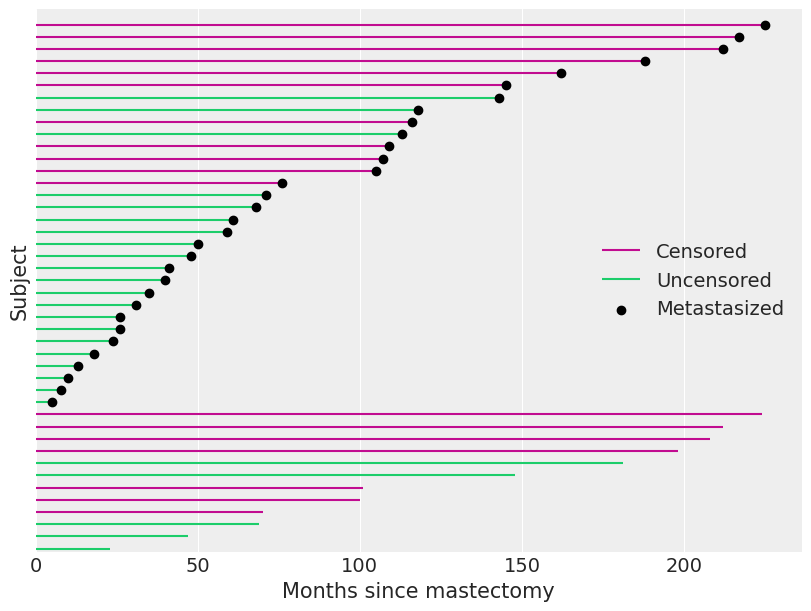
当观察结果被删失(df.event 为零)时,df.time 不是受试者的生存时间。我们从这种删失观察中可以得出的结论是,受试者的真实生存时间超过 df.time。
这对于本教程的目的来说已经足够了基本的生存分析理论;有关更广泛的介绍,请查阅 Aalen 等人^[Aalen, Odd, Ornulf Borgan, and Hakon Gjessing. Survival and event history analysis: a process point of view. Springer Science & Business Media, 2008.]
贝叶斯比例风险模型#
生存分析中最基本的两个估计量是生存函数的 Kaplan-Meier 估计量 和累积风险函数的 Nelson-Aalen 估计量。但是,由于我们想要了解转移对生存时间的影响,因此风险回归模型更合适。也许最常用的风险回归模型是 Cox 比例风险模型。在此模型中,如果我们有协变量 \(\mathbf{x}\) 和回归系数 \(\beta\),则风险率建模为
这里 \(\lambda_0(t)\) 是基线风险,它独立于协变量 \(\mathbf{x}\)。在本例中,协变量是一维向量 df.metastasized。
与许多回归情况不同,\(\mathbf{x}\) 不应包含对应于截距的常数项。如果 \(\mathbf{x}\) 包含对应于截距的常数项,则模型变为 不可识别。为了说明这种不可识别性,假设
如果 \(\tilde{\beta}_0 = \beta_0 + \delta\) 且 \(\tilde{\lambda}_0(t) = \lambda_0(t) \exp(-\delta)\),则 \(\lambda(t) = \tilde{\lambda}_0(t) \exp(\tilde{\beta}_0 + \mathbf{x} \beta)\) 也成立,使得具有 \(\beta_0\) 的模型不可识别。
为了使用 Cox 模型进行贝叶斯推断,我们必须指定 \(\beta\) 和 \(\lambda_0(t)\) 的先验。我们对 \(\beta\) 放置正态先验,\(\beta \sim N(\mu_{\beta}, \sigma_{\beta}^2),\) 其中 \(\mu_{\beta} \sim N(0, 10^2)\) 和 \(\sigma_{\beta} \sim U(0, 10)\)。
关于 \(\lambda_0(t)\) 的合适先验不太明显。我们选择半参数先验,其中 \(\lambda_0(t)\) 是分段常数函数。此先验要求我们将相关时间范围划分为端点为 \(0 \leq s_1 < s_2 < \cdots < s_N\) 的区间。使用此分区,如果 \(s_j \leq t < s_{j + 1}\),则 \(\lambda_0 (t) = \lambda_j\)。由于 \(\lambda_0(t)\) 被约束为具有此形式,我们所需要做的就是为 \(N - 1\) 个值 \(\lambda_j\) 选择先验。我们使用独立的模糊先验 \(\lambda_j \sim \operatorname{Gamma}(10^{-2}, 10^{-2}).\) 对于我们的乳房切除术示例,我们将每个间隔设为三个月。
我们看到死亡和删失观察结果在这些区间内的分布情况。
fig, ax = plt.subplots(figsize=(8, 6))
ax.hist(
df[df.event == 0].time.values,
bins=interval_bounds,
lw=0,
color="C3",
alpha=0.5,
label="Censored",
)
ax.hist(
df[df.event == 1].time.values,
bins=interval_bounds,
lw=0,
color="C7",
alpha=0.5,
label="Uncensored",
)
ax.set_xlim(0, interval_bounds[-1])
ax.set_xlabel("Months since mastectomy")
ax.set_yticks([0, 1, 2, 3])
ax.set_ylabel("Number of observations")
ax.legend();
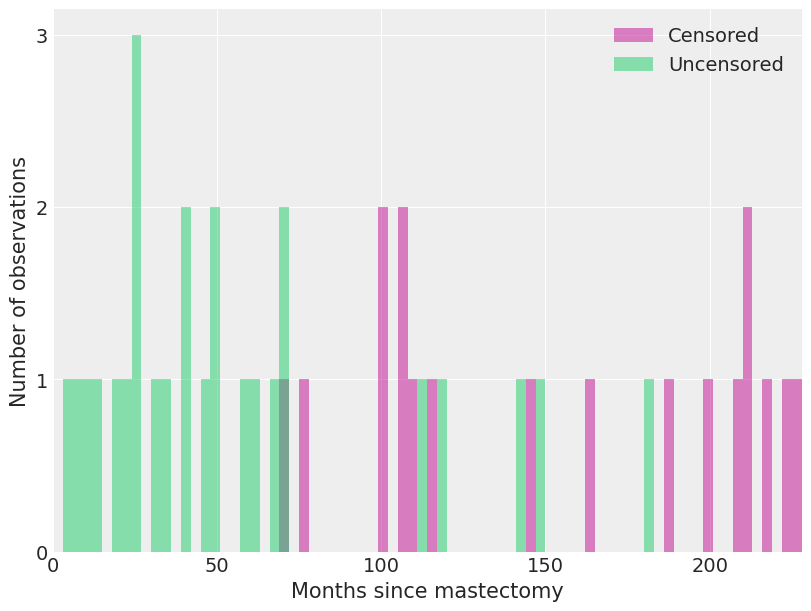
选择 \(\beta\) 和 \(\lambda_0(t)\) 的先验分布后,我们现在展示如何使用 MCMC 模拟和 pymc 拟合模型。关键的观察结果是,分段常数比例风险模型与泊松回归模型 密切相关。(这些模型并非完全相同,但它们的似然性相差一个仅取决于观察数据而不取决于参数 \(\beta\) 和 \(\lambda_j\) 的因子。有关详细信息,请参阅 Germán Rodríguez 的 WWS 509 课程笔记。)
我们根据第 \(i\) 个受试者是否在第 \(j\) 个区间内死亡来定义指示变量,
我们还将 \(t_{i, j}\) 定义为第 \(i\) 个受试者在第 \(j\) 个区间内处于风险中的时间量。
exposure = np.greater_equal.outer(df.time.to_numpy(), interval_bounds[:-1]) * interval_length
exposure[patients, last_period] = df.time - interval_bounds[last_period]
最后,将第 \(i\) 个受试者在第 \(j\) 个区间内承担的风险表示为 \(\lambda_{i, j} = \lambda_j \exp(\mathbf{x}_i \beta)\)。
我们可以使用均值为 \(t_{i, j}\ \lambda_{i, j}\) 的泊松随机变量来近似 \(d_{i, j}\)。此近似得出以下 pymc 模型。
coords = {"intervals": intervals}
with pm.Model(coords=coords) as model:
lambda0 = pm.Gamma("lambda0", 0.01, 0.01, dims="intervals")
beta = pm.Normal("beta", 0, sigma=1000)
lambda_ = pm.Deterministic("lambda_", T.outer(T.exp(beta * df.metastasized), lambda0))
mu = pm.Deterministic("mu", exposure * lambda_)
obs = pm.Poisson("obs", mu, observed=death)
我们现在从模型中抽样。
n_samples = 1000
n_tune = 1000
with model:
idata = pm.sample(
n_samples,
tune=n_tune,
target_accept=0.99,
random_seed=RANDOM_SEED,
)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [lambda0, beta]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 304 seconds.
我们看到,癌症已转移的受试者的风险率约为癌症未转移的受试者的 1.5 倍。
np.exp(idata.posterior["beta"]).mean()
<xarray.DataArray 'beta' ()> array(2.51161491)
az.plot_posterior(idata, var_names=["beta"]);
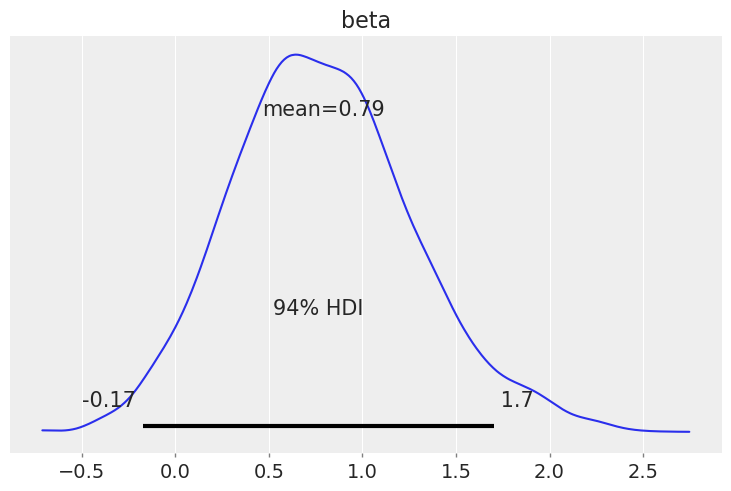
az.plot_autocorr(idata, var_names=["beta"]);

我们现在检查转移对累积风险和生存函数的影响。
base_hazard = idata.posterior["lambda0"]
met_hazard = idata.posterior["lambda0"] * np.exp(idata.posterior["beta"])
def cum_hazard(hazard):
return (interval_length * hazard).cumsum(axis=-1)
def survival(hazard):
return np.exp(-cum_hazard(hazard))
def get_mean(trace):
return trace.mean(("chain", "draw"))
fig, (hazard_ax, surv_ax) = plt.subplots(ncols=2, sharex=True, sharey=False, figsize=(16, 6))
az.plot_hdi(
interval_bounds[:-1],
cum_hazard(base_hazard),
ax=hazard_ax,
smooth=False,
color="C0",
fill_kwargs={"label": "Had not metastasized"},
)
az.plot_hdi(
interval_bounds[:-1],
cum_hazard(met_hazard),
ax=hazard_ax,
smooth=False,
color="C1",
fill_kwargs={"label": "Metastasized"},
)
hazard_ax.plot(interval_bounds[:-1], get_mean(cum_hazard(base_hazard)), color="darkblue")
hazard_ax.plot(interval_bounds[:-1], get_mean(cum_hazard(met_hazard)), color="maroon")
hazard_ax.set_xlim(0, df.time.max())
hazard_ax.set_xlabel("Months since mastectomy")
hazard_ax.set_ylabel(r"Cumulative hazard $\Lambda(t)$")
hazard_ax.legend(loc=2)
az.plot_hdi(interval_bounds[:-1], survival(base_hazard), ax=surv_ax, smooth=False, color="C0")
az.plot_hdi(interval_bounds[:-1], survival(met_hazard), ax=surv_ax, smooth=False, color="C1")
surv_ax.plot(interval_bounds[:-1], get_mean(survival(base_hazard)), color="darkblue")
surv_ax.plot(interval_bounds[:-1], get_mean(survival(met_hazard)), color="maroon")
surv_ax.set_xlim(0, df.time.max())
surv_ax.set_xlabel("Months since mastectomy")
surv_ax.set_ylabel("Survival function $S(t)$")
fig.suptitle("Bayesian survival model");
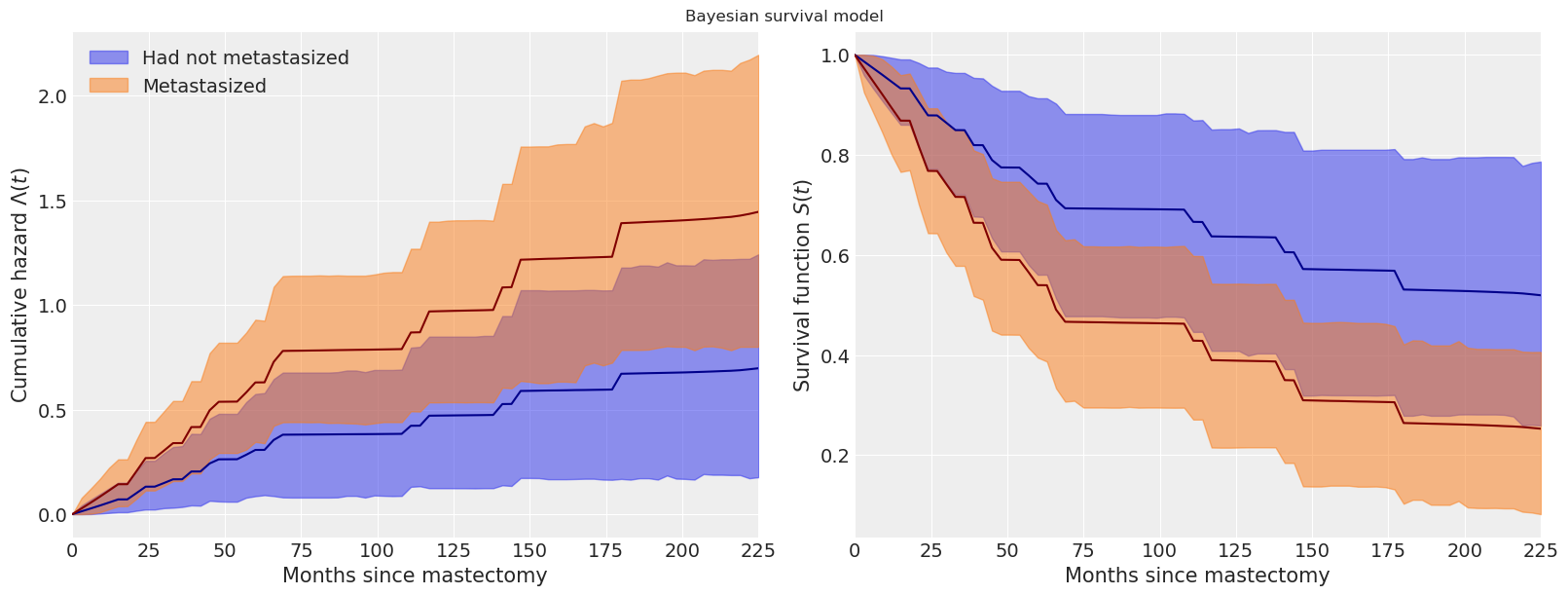
我们看到,转移受试者的累积风险最初增加得更快(大约 70 个月),之后它大致与基线累积风险平行增加。
这些图还显示了每个函数的逐点 95% 最高后验密度区间。使用 pymc 拟合的贝叶斯模型的明显优势之一是固有的不确定性量化在我们的估计中。
时变效应#
我们构建的模型的另一个优点是其灵活性。从上面的图中,我们可能合理地认为,由于转移而增加的额外风险随时间变化;癌症转移似乎会在乳房切除术后立即增加风险率,但由于转移引起的风险会随着时间的推移而降低。我们可以通过允许回归系数随时间变化来适应这种机制。在时变系数模型中,如果 \(s_j \leq t < s_{j + 1}\),我们令 \(\lambda(t) = \lambda_j \exp(\mathbf{x} \beta_j).\) 回归系数序列 \(\beta_1, \beta_2, \ldots, \beta_{N - 1}\) 形成一个正态随机游走,其中 \(\beta_1 \sim N(0, 1)\), \(\beta_j\ |\ \beta_{j - 1} \sim N(\beta_{j - 1}, 1)\)。
我们在 pymc 中实现此模型,如下所示。
coords = {"intervals": intervals}
with pm.Model(coords=coords) as time_varying_model:
lambda0 = pm.Gamma("lambda0", 0.01, 0.01, dims="intervals")
beta = GaussianRandomWalk("beta", init_dist=pm.Normal.dist(), sigma=1.0, dims="intervals")
lambda_ = pm.Deterministic("h", lambda0 * T.exp(T.outer(T.constant(df.metastasized), beta)))
mu = pm.Deterministic("mu", exposure * lambda_)
obs = pm.Poisson("obs", mu, observed=death)
我们继续从此模型中抽样。
with time_varying_model:
time_varying_idata = pm.sample(
n_samples,
tune=n_tune,
return_inferencedata=True,
target_accept=0.99,
random_seed=RANDOM_SEED,
)
/home/cfonnesbeck/GitHub/pymc/pymc/logprob/joint_logprob.py:167: UserWarning: Found a random variable that was neither among the observations nor the conditioned variables: [normal_rv{0, (0, 0), floatX, False}.0, normal_rv{0, (0, 0), floatX, False}.out]
warnings.warn(
/home/cfonnesbeck/GitHub/pymc/pymc/logprob/joint_logprob.py:167: UserWarning: Found a random variable that was neither among the observations nor the conditioned variables: [normal_rv{0, (0, 0), floatX, False}.0, normal_rv{0, (0, 0), floatX, False}.out]
warnings.warn(
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
/home/cfonnesbeck/GitHub/pymc/pymc/logprob/joint_logprob.py:167: UserWarning: Found a random variable that was neither among the observations nor the conditioned variables: [normal_rv{0, (0, 0), floatX, False}.0, normal_rv{0, (0, 0), floatX, False}.out]
warnings.warn(
/home/cfonnesbeck/GitHub/pymc/pymc/logprob/joint_logprob.py:167: UserWarning: Found a random variable that was neither among the observations nor the conditioned variables: [normal_rv{0, (0, 0), floatX, False}.0, normal_rv{0, (0, 0), floatX, False}.out]
warnings.warn(
/home/cfonnesbeck/GitHub/pymc/pymc/logprob/joint_logprob.py:167: UserWarning: Found a random variable that was neither among the observations nor the conditioned variables: [normal_rv{0, (0, 0), floatX, False}.0, normal_rv{0, (0, 0), floatX, False}.out]
warnings.warn(
/home/cfonnesbeck/GitHub/pymc/pymc/logprob/joint_logprob.py:167: UserWarning: Found a random variable that was neither among the observations nor the conditioned variables: [normal_rv{0, (0, 0), floatX, False}.0, normal_rv{0, (0, 0), floatX, False}.out]
warnings.warn(
/home/cfonnesbeck/GitHub/pymc/pymc/logprob/joint_logprob.py:167: UserWarning: Found a random variable that was neither among the observations nor the conditioned variables: [normal_rv{0, (0, 0), floatX, False}.0, normal_rv{0, (0, 0), floatX, False}.out]
warnings.warn(
/home/cfonnesbeck/GitHub/pymc/pymc/logprob/joint_logprob.py:167: UserWarning: Found a random variable that was neither among the observations nor the conditioned variables: [normal_rv{0, (0, 0), floatX, False}.0, normal_rv{0, (0, 0), floatX, False}.out]
warnings.warn(
/home/cfonnesbeck/GitHub/pymc/pymc/logprob/joint_logprob.py:167: UserWarning: Found a random variable that was neither among the observations nor the conditioned variables: [normal_rv{0, (0, 0), floatX, False}.0, normal_rv{0, (0, 0), floatX, False}.out]
warnings.warn(
/home/cfonnesbeck/GitHub/pymc/pymc/logprob/joint_logprob.py:167: UserWarning: Found a random variable that was neither among the observations nor the conditioned variables: [normal_rv{0, (0, 0), floatX, False}.0, normal_rv{0, (0, 0), floatX, False}.out]
warnings.warn(
/home/cfonnesbeck/GitHub/pymc/pymc/logprob/joint_logprob.py:167: UserWarning: Found a random variable that was neither among the observations nor the conditioned variables: [normal_rv{0, (0, 0), floatX, False}.0, normal_rv{0, (0, 0), floatX, False}.out]
warnings.warn(
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [lambda0, beta]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 536 seconds.
az.plot_forest(time_varying_idata, var_names=["beta"]);

我们从下面 \(\beta_j\) 随时间变化的图中看到,最初 \(\beta_j > 0\),表明由于转移而导致风险率升高,但随着 \(\beta_j < 0\) 最终,这种风险会降低。
fig, ax = plt.subplots(figsize=(8, 6))
beta_eti = time_varying_idata.posterior["beta"].quantile((0.025, 0.975), dim=("chain", "draw"))
beta_eti_low = beta_eti.sel(quantile=0.025)
beta_eti_high = beta_eti.sel(quantile=0.975)
ax.fill_between(interval_bounds[:-1], beta_eti_low, beta_eti_high, color="C0", alpha=0.25)
beta_hat = time_varying_idata.posterior["beta"].mean(("chain", "draw"))
ax.step(interval_bounds[:-1], beta_hat, color="C0")
ax.scatter(
interval_bounds[last_period[(df.event.values == 1) & (df.metastasized == 1)]],
beta_hat.isel(intervals=last_period[(df.event.values == 1) & (df.metastasized == 1)]),
color="C1",
zorder=10,
label="Died, cancer metastasized",
)
ax.scatter(
interval_bounds[last_period[(df.event.values == 0) & (df.metastasized == 1)]],
beta_hat.isel(intervals=last_period[(df.event.values == 0) & (df.metastasized == 1)]),
color="C0",
zorder=10,
label="Censored, cancer metastasized",
)
ax.set_xlim(0, df.time.max())
ax.set_xlabel("Months since mastectomy")
ax.set_ylabel(r"$\beta_j$")
ax.legend();
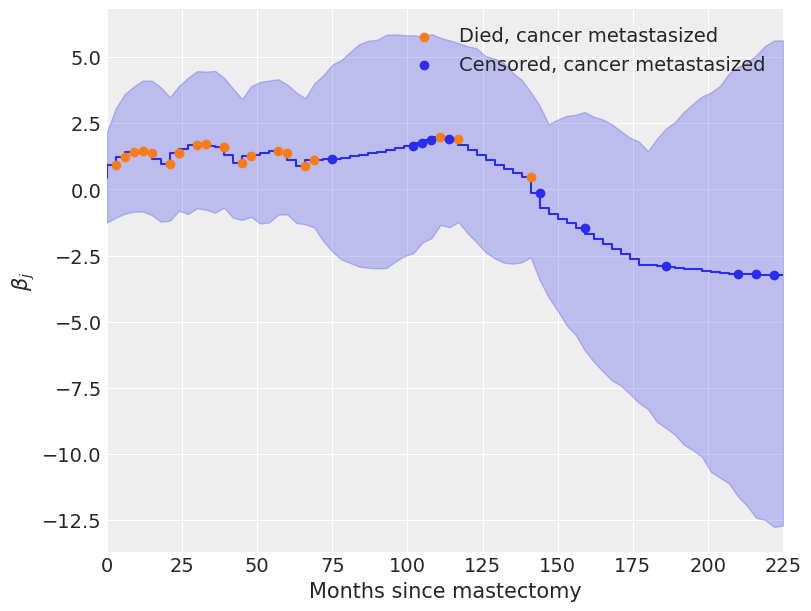
系数 \(\beta_j\) 在乳房切除术后约一百个月开始迅速下降,这似乎是合理的,因为在癌症已转移的十二名受试者中,只有三名活过这个时间点并在研究期间死亡。
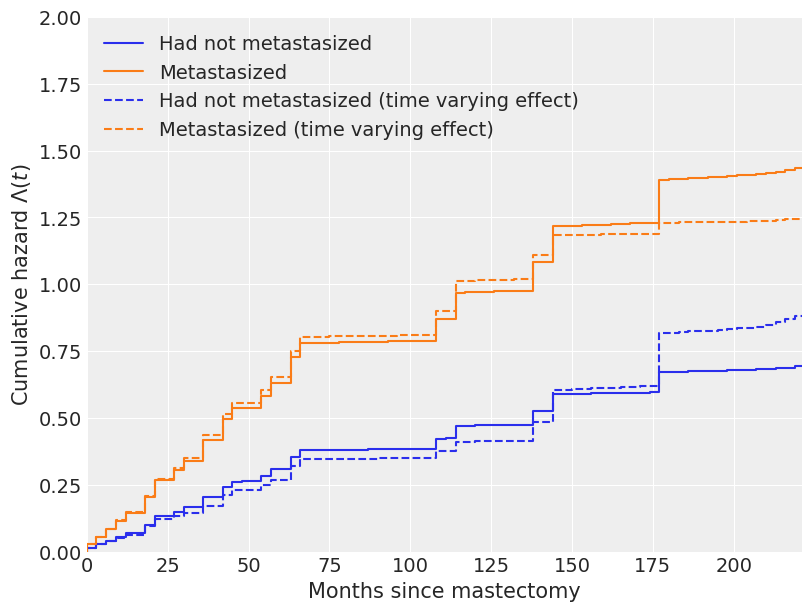
由于时变效应,我们对累积风险和生存函数的估计的变化在以下图中也很明显。
tv_base_hazard = time_varying_idata.posterior["lambda0"]
tv_met_hazard = time_varying_idata.posterior["lambda0"] * np.exp(
time_varying_idata.posterior["beta"]
)
fig, ax = plt.subplots(figsize=(8, 6))
ax.step(
interval_bounds[:-1],
cum_hazard(base_hazard.mean(("chain", "draw"))),
color="C0",
label="Had not metastasized",
)
ax.step(
interval_bounds[:-1],
cum_hazard(met_hazard.mean(("chain", "draw"))),
color="C1",
label="Metastasized",
)
ax.step(
interval_bounds[:-1],
cum_hazard(tv_base_hazard.mean(("chain", "draw"))),
color="C0",
linestyle="--",
label="Had not metastasized (time varying effect)",
)
ax.step(
interval_bounds[:-1],
cum_hazard(tv_met_hazard.mean(dim=("chain", "draw"))),
color="C1",
linestyle="--",
label="Metastasized (time varying effect)",
)
ax.set_xlim(0, df.time.max() - 4)
ax.set_xlabel("Months since mastectomy")
ax.set_ylim(0, 2)
ax.set_ylabel(r"Cumulative hazard $\Lambda(t)$")
ax.legend(loc=2);
fig, (hazard_ax, surv_ax) = plt.subplots(ncols=2, sharex=True, sharey=False, figsize=(16, 6))
az.plot_hdi(
interval_bounds[:-1],
cum_hazard(tv_base_hazard),
ax=hazard_ax,
color="C0",
smooth=False,
fill_kwargs={"label": "Had not metastasized"},
)
az.plot_hdi(
interval_bounds[:-1],
cum_hazard(tv_met_hazard),
ax=hazard_ax,
smooth=False,
color="C1",
fill_kwargs={"label": "Metastasized"},
)
hazard_ax.plot(interval_bounds[:-1], get_mean(cum_hazard(tv_base_hazard)), color="darkblue")
hazard_ax.plot(interval_bounds[:-1], get_mean(cum_hazard(tv_met_hazard)), color="maroon")
hazard_ax.set_xlim(0, df.time.max())
hazard_ax.set_xlabel("Months since mastectomy")
hazard_ax.set_ylim(0, 2)
hazard_ax.set_ylabel(r"Cumulative hazard $\Lambda(t)$")
hazard_ax.legend(loc=2)
az.plot_hdi(interval_bounds[:-1], survival(tv_base_hazard), ax=surv_ax, smooth=False, color="C0")
az.plot_hdi(interval_bounds[:-1], survival(tv_met_hazard), ax=surv_ax, smooth=False, color="C1")
surv_ax.plot(interval_bounds[:-1], get_mean(survival(tv_base_hazard)), color="darkblue")
surv_ax.plot(interval_bounds[:-1], get_mean(survival(tv_met_hazard)), color="maroon")
surv_ax.set_xlim(0, df.time.max())
surv_ax.set_xlabel("Months since mastectomy")
surv_ax.set_ylabel("Survival function $S(t)$")
fig.suptitle("Bayesian survival model with time varying effects");
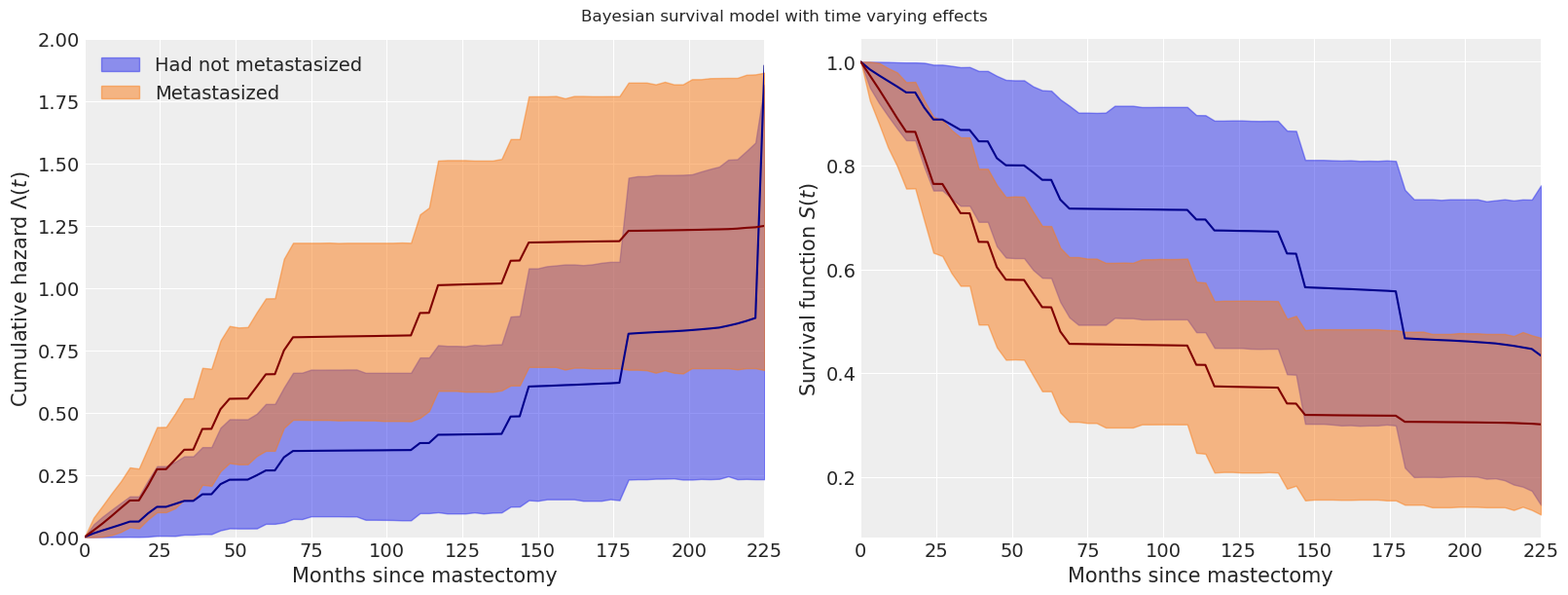
我们实际上只触及了生存分析和贝叶斯生存分析方法的表面。有关贝叶斯生存分析的更多信息,请参见 Ibrahim 等人 (2005)。 (例如,我们可能希望在我们原始模型或时变模型中考虑个体脆弱性。)
本教程以 IPython 笔记本 的形式提供,点击此处。它改编自一篇最初发表在此处的博客文章。
许可证声明#
本示例 галерея 中的所有笔记本均根据 MIT 许可证 提供,该许可证允许修改和重新分发以用于任何用途,前提是保留版权和许可证声明。
引用 PyMC 示例#
要引用此笔记本,请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。
重要提示
许多笔记本都改编自其他来源:博客、书籍……在这种情况下,您也应该引用原始来源。
另请记住引用您的代码使用的相关库。
这是一个 bibtex 中的引用模板
@incollection{citekey,
author = "<notebook authors, see above>",
title = "<notebook title>",
editor = "PyMC Team",
booktitle = "PyMC examples",
doi = "10.5281/zenodo.5654871"
}
一旦渲染,它可能看起来像