Weibull 加速失效时间模型重新参数化#

import arviz as az
import numpy as np
import pymc as pm
import pytensor.tensor as pt

print(f"Running on PyMC v{pm.__version__}")

Running on PyMC v5.18.2

注意

此 notebook 使用的库不是 PyMC 的依赖项，因此需要专门安装才能运行此 notebook。打开下面的下拉菜单以获取更多指导。

额外的依赖项安装说明

为了运行此 notebook（在本地或 Binder 上），您不仅需要安装可用的 PyMC 以及所有可选依赖项，还需要安装一些额外的依赖项。有关安装 PyMC 本身的建议，请参阅 安装

您可以使用首选的包管理器安装这些依赖项，我们以 pip 和 conda 命令为例提供如下。

$ pip install statsmodels

请注意，如果您想（或需要）从 notebook 内部而不是命令行安装软件包，您可以通过运行 pip 命令的变体来安装软件包

import sys

!{sys.executable} -m pip install statsmodels

您不应运行 !pip install，因为它可能会将软件包安装在不同的环境中，即使已安装，也无法从 Jupyter notebook 中使用。

另一种选择是使用 conda

$ conda install statsmodels

当使用 conda 安装科学 Python 包时，我们建议使用 conda-forge

# These dependencies need to be installed separately from PyMC
import statsmodels.api as sm

%config InlineBackend.figure_format = 'retina'
# These seeds are for sampling data observations
RANDOM_SEED = 8927
np.random.seed(RANDOM_SEED)
# Set a seed for reproducibility of posterior results
seed: int = sum(map(ord, "aft_weibull"))
rng: np.random.Generator = np.random.default_rng(seed=seed)
az.style.use("arviz-darkgrid")

数据集#

之前的关于贝叶斯参数生存分析的示例 notebook 介绍了两种不同的加速失效时间 (AFT) 模型：Weibull 和对数线性模型。在本 notebook 中，我们介绍了 Weibull AFT 模型的三个不同的参数化。

我们将使用的数据集是 flchain R 数据集，它来自一项医学研究，该研究调查了血清游离轻链 (FLC) 对寿命的影响。通过运行以下代码阅读数据的完整文档

print(sm.datasets.get_rdataset(package='survival', dataname='flchain').__doc__).

# Fetch and clean data
data = (
    sm.datasets.get_rdataset(package="survival", dataname="flchain")
    .data.sample(500)  # Limit ourselves to 500 observations
    .reset_index(drop=True)
)

y = data.futime.values
censored = ~data["death"].values.astype(bool)

y[:5]

array([ 975, 2272,  138, 4262, 4928])

censored[:5]

array([False,  True, False,  True,  True])

使用 pm.Potential#

在建模删失数据时，我们遇到了一个独特的问题。严格来说，对于删失值，我们没有任何数据：我们只知道删失值的数量。我们如何将此信息包含在我们的模型中？

一种方法是使用 pm.Potential。PyMC2 文档 非常好地解释了它的用法。本质上，声明 pm.Potential('x', logp) 将把 logp 添加到模型的对数似然中。

但是，pm.Potential 仅影响基于概率的抽样，这排除了使用 pm.sample_prior_predictice 和 pm.sample_posterior_predictive。我们可以通过使用 pm.Censored 来克服这些限制。我们可以通过定义 pm.Censored 的 upper 参数来建模我们的右删失数据。

参数化 1#

此参数化是 Weibull 生存函数的直观、直接的参数化。这可能是人们首先想到的参数化。

# normalize the event time between 0 and 1
y_norm = y / np.max(y)

# If censored then observed event time else maximum time
right_censored = [x if x > 0 else np.max(y_norm) for x in y_norm * censored]

with pm.Model() as model_1:
    alpha_sd = 1.0

    mu = pm.Normal("mu", mu=0, sigma=1)
    alpha_raw = pm.Normal("a0", mu=0, sigma=0.1)
    alpha = pm.Deterministic("alpha", pt.exp(alpha_sd * alpha_raw))
    beta = pm.Deterministic("beta", pt.exp(mu / alpha))
    beta_backtransformed = pm.Deterministic("beta_backtransformed", beta * np.max(y))

    latent = pm.Weibull.dist(alpha=alpha, beta=beta)
    y_obs = pm.Censored("Censored_likelihood", latent, upper=right_censored, observed=y_norm)

with model_1:
    idata_param1 = pm.sample(nuts_sampler="numpyro", random_seed=rng)

az.plot_trace(idata_param1, var_names=["alpha", "beta"])

array([[<Axes: title={'center': 'alpha'}>,
        <Axes: title={'center': 'alpha'}>],
       [<Axes: title={'center': 'beta'}>,
        <Axes: title={'center': 'beta'}>]], dtype=object)
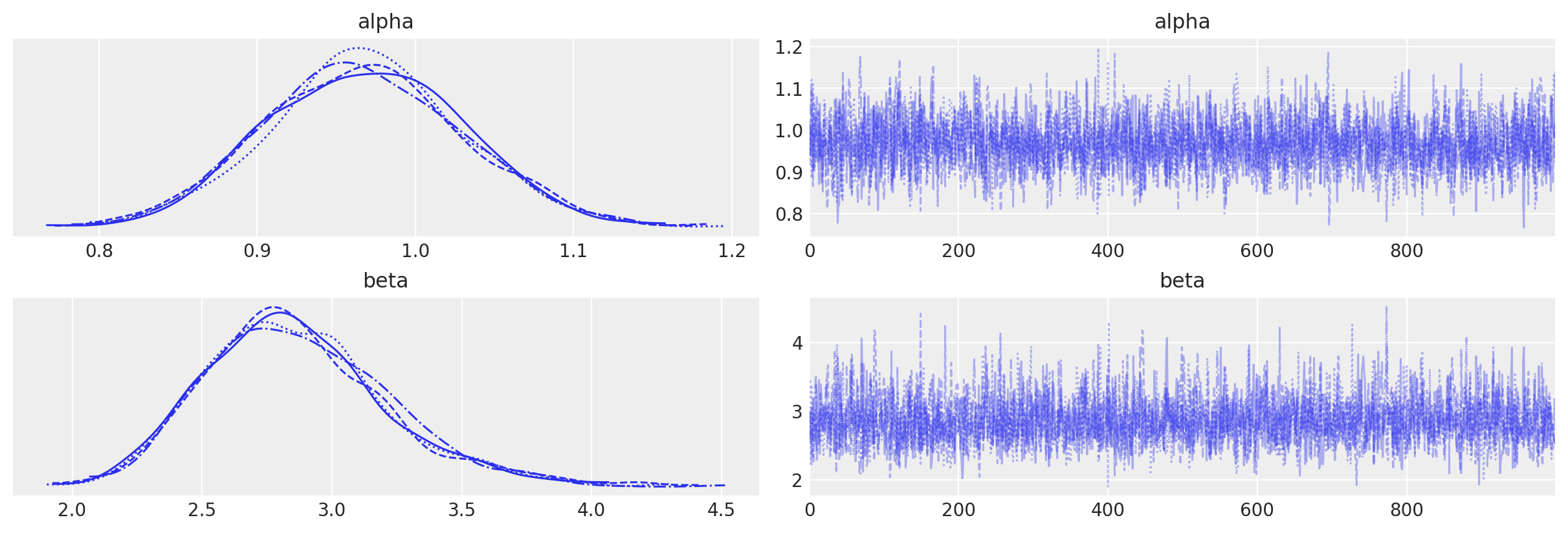
../_images/5c3c37d792d4ae704ccf9731de2baa51f798257852aef9b91dcb5d1befddadc9.png 
az.summary(idata_param1, var_names=["alpha", "beta", "beta_backtransformed"], round_to=2)
平均值 标准差 hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
alpha 0.97 0.06 0.85 1.08 0.00 0.0 2752.10 2282.64 1.0
beta 2.86 0.35 2.23 3.54 0.01 0.0 2677.53 2519.18 1.0
beta_backtransformed 14694.41 1806.79 11450.50 18165.12 34.64 24.5 2677.53 2519.18 1.0

参数化 2#

请注意，令人困惑的是，alpha 现在称为 r，而 alpha 表示先验；我们保留此符号是为了忠实于 Stan 中的原始实现。在此参数化中，我们仍然对相同的参数 alpha（现在是 r）和 beta 进行建模。

有关更多信息，请参阅 此 Stan 示例模型 和 相应的文档。

with pm.Model() as model_2:
    alpha = pm.Normal("alpha", mu=0, sigma=1)
    r = pm.Gamma("r", alpha=2, beta=1)
    beta = pm.Deterministic("beta", pt.exp(-alpha / r))
    beta_backtransformed = pm.Deterministic("beta_backtransformed", beta * np.max(y))

    latent = pm.Weibull.dist(alpha=r, beta=beta)
    y_obs = pm.Censored("Censored_likelihood", latent, upper=right_censored, observed=y_norm)

with model_2:
    idata_param2 = pm.sample(nuts_sampler="numpyro", random_seed=rng)

az.plot_trace(idata_param2, var_names=["r", "beta"])

array([[<Axes: title={'center': 'r'}>, <Axes: title={'center': 'r'}>],
       [<Axes: title={'center': 'beta'}>,
        <Axes: title={'center': 'beta'}>]], dtype=object)
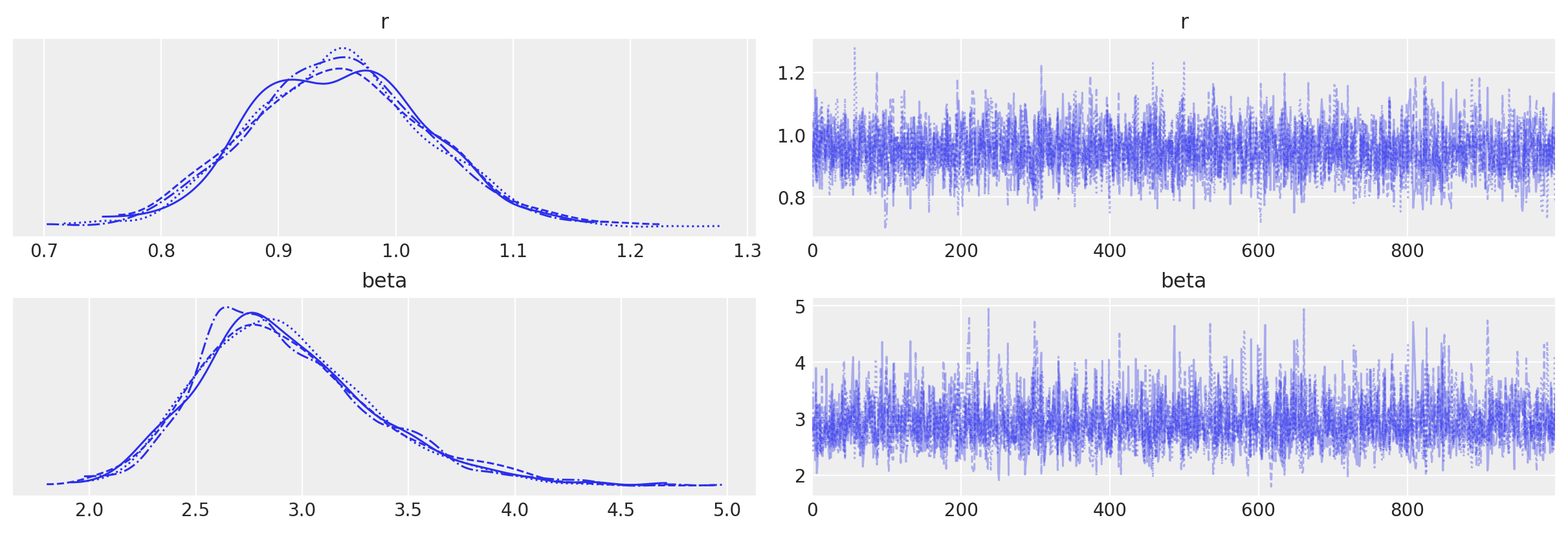
../_images/56c22e18df74d52bb75350fb86f6f9dc0bef577572b4dcf3936d1aa39a307afe.png 
az.summary(idata_param2, var_names=["r", "beta", "beta_backtransformed"], round_to=2)
平均值 标准差 hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
r 0.95 0.08 0.80 1.09 0.00 0.00 2907.17 2504.73 1.0
beta 2.93 0.43 2.23 3.81 0.01 0.01 2661.47 2456.59 1.0
beta_backtransformed 15060.96 2201.68 11442.10 19549.83 42.35 29.96 2661.47 2456.59 1.0

参数化 3#

在此参数化中，我们使用 Gumbel 分布对数线性误差分布进行建模，而不是直接对生存函数进行建模。有关更多信息，请参阅 此博客文章。

logtime = np.log(y)

# If censored then observed event time else maximum time
right_censored = [x if x > 0 else np.max(logtime) for x in logtime * censored]

with pm.Model() as model_3:
    s = pm.HalfNormal("s", tau=3.0)
    gamma = pm.Normal("gamma", mu=0, sigma=5)

    latent = pm.Gumbel.dist(mu=gamma, beta=s)
    y_obs = pm.Censored("Censored_likelihood", latent, upper=right_censored, observed=logtime)

with model_3:
    idata_param3 = pm.sample(tune=4000, draws=2000, nuts_sampler="numpyro", random_seed=rng)

az.plot_trace(idata_param3)

array([[<Axes: title={'center': 'gamma'}>,
        <Axes: title={'center': 'gamma'}>],
       [<Axes: title={'center': 's'}>, <Axes: title={'center': 's'}>]],
      dtype=object)
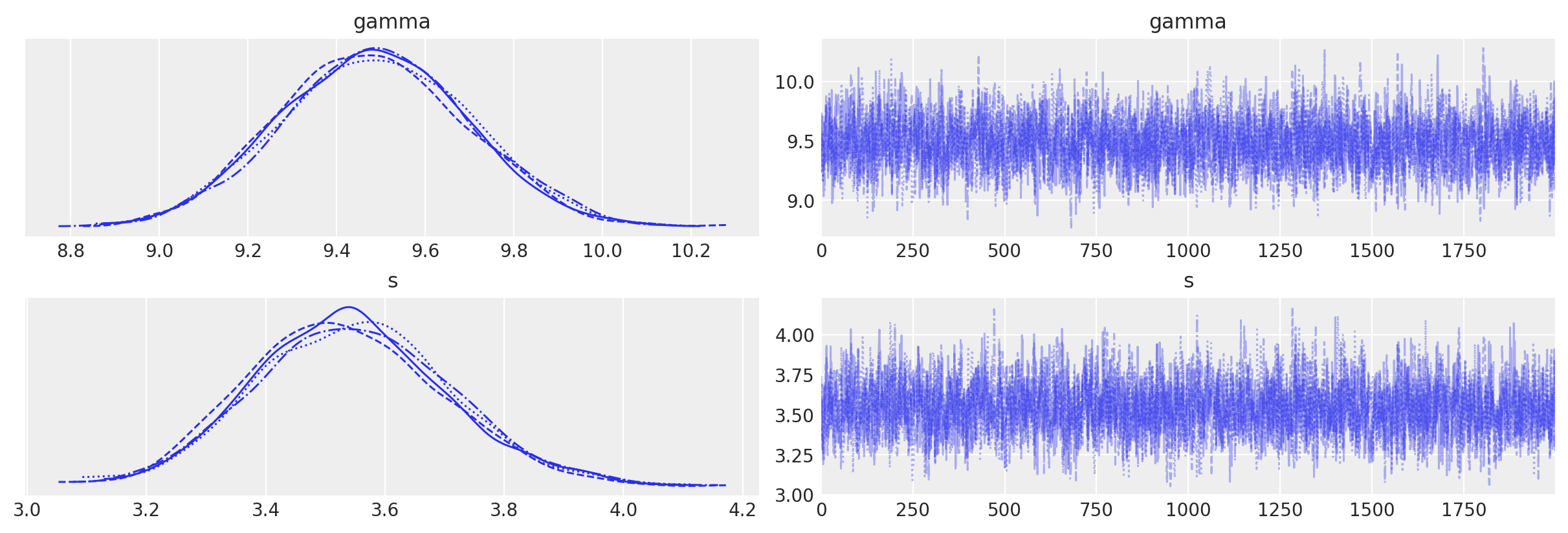
../_images/7e062de9dac35861a87f76119ab3ed3a249f19ef978160a757f05f50db6e6996.png 
az.summary(idata_param3, round_to=2)
平均值 标准差 hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
gamma 9.49 0.21 9.10 9.89 0.0 0.0 2727.89 3337.16 1.0
s 3.54 0.16 3.24 3.85 0.0 0.0 2701.50 4170.84 1.0

作者#

  • 最初由 Junpeng Lao 于 2018 年 4 月 21 日整理。请参阅原始代码此处。

  • 由 George Ho 于 2018 年 7 月 15 日创作并移植到 Jupyter notebook。

  • 由 Chris Fonnesbeck 于 2023 年 1 月 16 日更新，以兼容 PyMC v5。

  • 由 Jonathan Dekermanjian 于 2024 年 11 月 25 日更新，以将 pm.Potential 替换为 pm.Censored。

%load_ext watermark
%watermark -n -u -v -iv -w

Last updated: Tue Nov 26 2024

Python implementation: CPython
Python version       : 3.12.7
IPython version      : 8.27.0

numpy      : 1.26.4
statsmodels: 0.14.4
pymc       : 5.18.2
arviz      : 0.20.0
pytensor   : 2.26.3

Watermark: 2.5.0

许可声明#

此示例库中的所有 notebook 均根据 MIT 许可证 提供，该许可证允许修改和再分发用于任何用途，前提是版权和许可声明得到保留。

引用 PyMC 示例#

要引用此 notebook，请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。

重要提示

许多 notebook 都改编自其他来源：博客、书籍... 在这种情况下，您也应该引用原始来源。

另请记住引用您的代码使用的相关库。

这是一个 bibtex 中的引用模板

@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}

渲染后可能如下所示