PyMC 中 AR(1) 模型的分析#

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm

%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 8927
np.random.seed(RANDOM_SEED)
az.style.use("arviz-darkgrid")

考虑以下 AR(2) 过程，在无限过去初始化

\[ y_t = \rho_0 + \rho_1 y_{t-1} + \rho_2 y_{t-2} + \epsilon_t, \]

其中 \(\epsilon_t \overset{iid}{\sim} {\cal N}(0,1)\)。假设你想从观测样本 \(Y^T = \{ y_0, y_1,\ldots, y_T \}\) 中学习关于 \(\rho\) 的信息。

首先，让我们生成一些合成样本数据。我们通过从 AR(2) 过程生成 10,000 个样本，然后丢弃前 5,000 个样本来模拟“无限过去”

T = 10000

# true stationarity:
true_rho = 0.7, -0.3
# true standard deviation of the innovation:
true_sigma = 2.0
# true process mean:
true_center = -1.0

y = np.random.normal(loc=true_center, scale=true_sigma, size=T)
y[1] += true_rho[0] * y[0]
for t in range(2, T - 100):
    y[t] += true_rho[0] * y[t - 1] + true_rho[1] * y[t - 2]

y = y[-5000:]
plt.plot(y, alpha=0.8)
plt.xlabel("Timestep")
plt.ylabel("$y$");

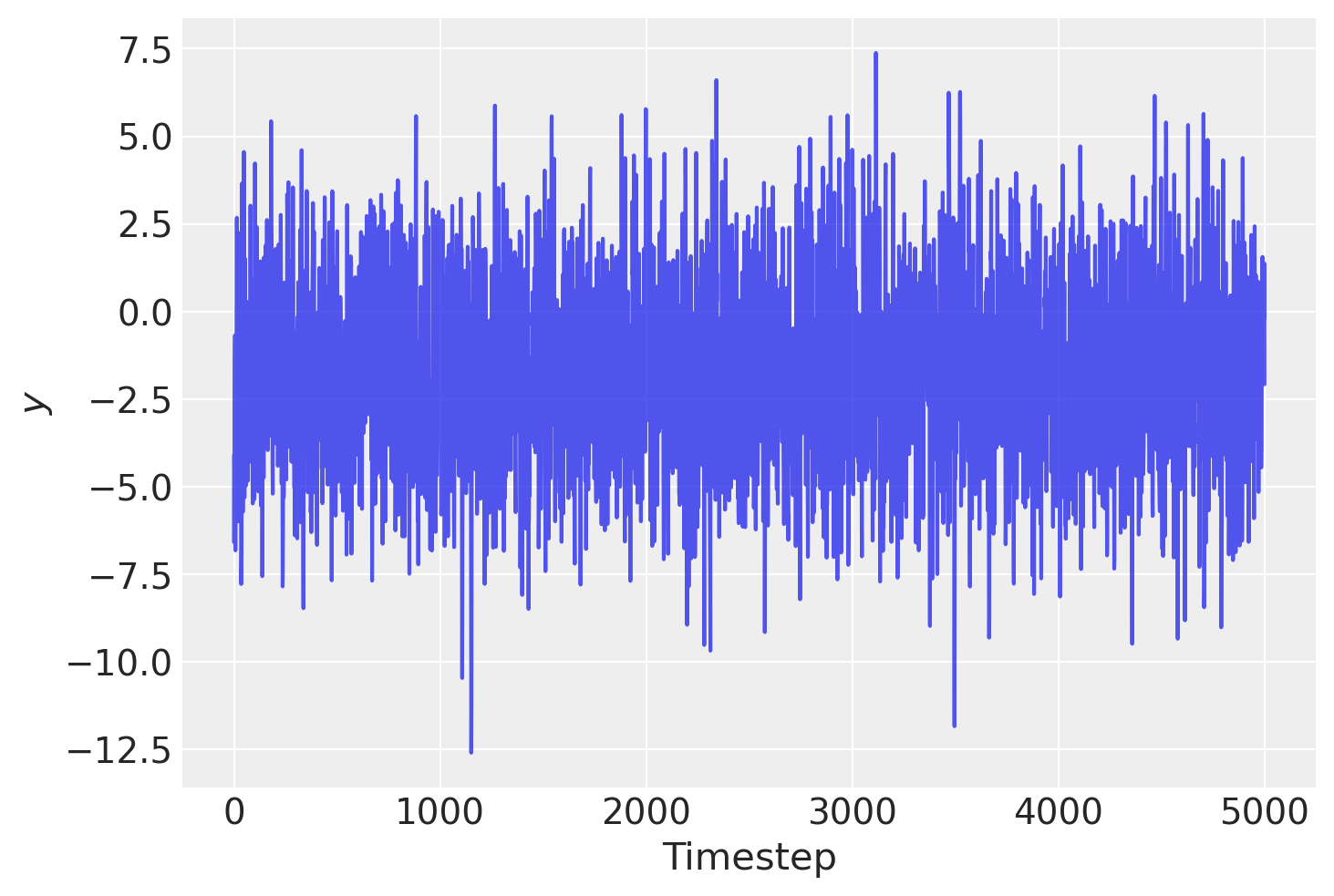
../_images/58d7f2f82cfb880f1711815ffa168839d405b5c9e380a1eeafe1ba3f5995746c.png

让我们首先尝试拟合错误的模型！假设我们不知道生成模型，因此为了简单起见，仅拟合 AR(1) 模型。

此生成过程在 PyMC 中非常容易实现。由于我们希望在 AR 过程中包含截距项，因此我们必须设置 constant=True，否则当 rho 的大小为 2 时，PyMC 会假定我们想要一个 AR2 过程。此外，默认情况下，\(N(0, 100)\) 分布将用作初始值的先验。我们可以通过将分布（不是完整的 RV）传递给 init_dist 参数来覆盖此设置。

with pm.Model() as ar1:
    # assumes 95% of prob mass is between -2 and 2
    rho = pm.Normal("rho", mu=0.0, sigma=1.0, shape=2)
    # precision of the innovation term
    tau = pm.Exponential("tau", lam=0.5)

    likelihood = pm.AR(
        "y", rho=rho, tau=tau, constant=True, init_dist=pm.Normal.dist(0, 10), observed=y
    )

    idata = pm.sample(1000, tune=2000, random_seed=RANDOM_SEED)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [rho, tau]

100.00% [12000/12000 00:04<00:00 Sampling 4 chains, 0 divergences]

Sampling 4 chains for 2_000 tune and 1_000 draw iterations (8_000 + 4_000 draws total) took 5 seconds.

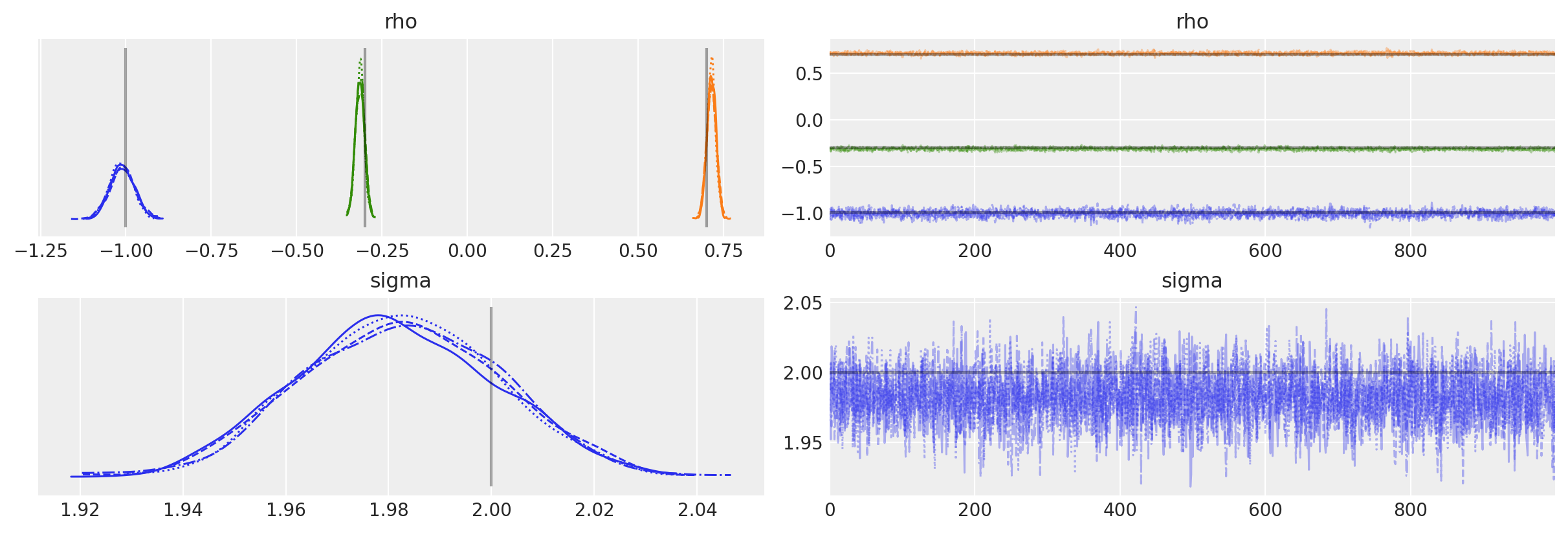
我们可以看到，即使我们假设了错误的模型，参数估计实际上也离真实值不远。

az.plot_trace(
    idata,
    lines=[
        ("rho", {}, [true_center, true_rho[0]]),
        ("tau", {}, true_sigma**-2),
    ],
);

../_images/f156ee9ab7d2c0c2d5f4f9681e8f29e423d83b0b859e6edb9359b18e92b85543.png

扩展到 AR(p)#

现在让我们拟合正确的底层模型，AR(2)

\[ y_t = \rho_0 + \rho_1 y_{t-1} + \rho_2 y_{t-2} + \epsilon_t. \]

AR 分布通过传递给 AR 的 rho 参数的大小（包括均值）推断过程的阶数。

我们还将使用创新的标准差（而不是精度）来参数化分布。

with pm.Model() as ar2:
    rho = pm.Normal("rho", 0.0, 1.0, shape=3)
    sigma = pm.HalfNormal("sigma", 3)
    likelihood = pm.AR(
        "y", rho=rho, sigma=sigma, constant=True, init_dist=pm.Normal.dist(0, 10), observed=y
    )

    idata = pm.sample(
        1000,
        tune=2000,
        random_seed=RANDOM_SEED,
    )

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [rho, sigma]

100.00% [12000/12000 00:09<00:00 Sampling 4 chains, 0 divergences]

Sampling 4 chains for 2_000 tune and 1_000 draw iterations (8_000 + 4_000 draws total) took 9 seconds.

后验图显示我们已正确推断出生成模型参数。

az.plot_trace(
    idata,
    lines=[
        ("rho", {}, (true_center,) + true_rho),
        ("sigma", {}, true_sigma),
    ],
);

../_images/b28650d1ac573d2e837360f4b32bca44ffc6587e19ebd94a00fecd9c8f24b6bb.png

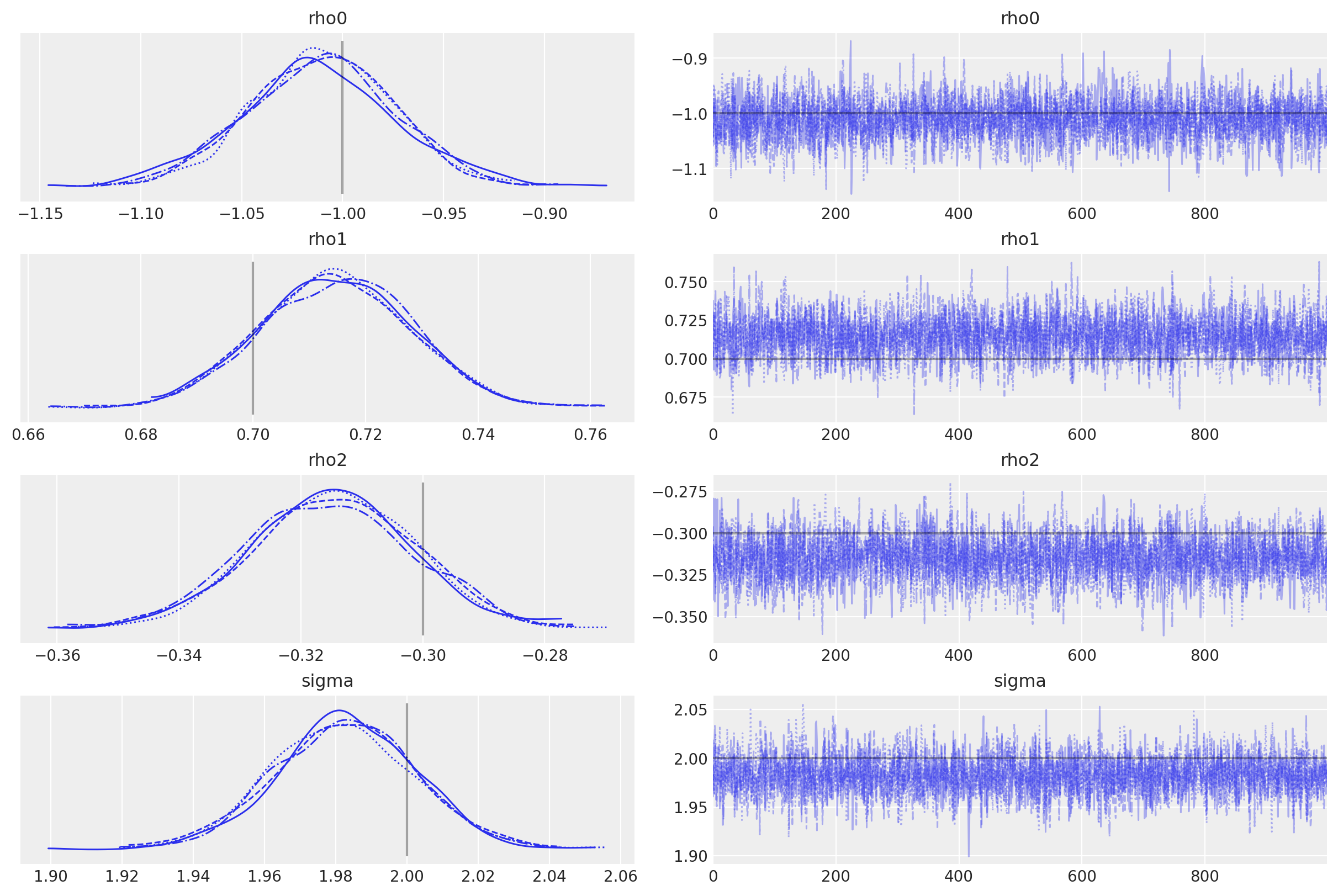
如果 AR 参数不是同分布的，您也可以将 AR 参数集作为列表传递。

import pytensor.tensor as pt

with pm.Model() as ar2_bis:
    rho0 = pm.Normal("rho0", mu=0.0, sigma=5.0)
    rho1 = pm.Uniform("rho1", -1, 1)
    rho2 = pm.Uniform("rho2", -1, 1)
    sigma = pm.HalfNormal("sigma", 3)
    likelihood = pm.AR(
        "y",
        rho=pt.stack([rho0, rho1, rho2]),
        sigma=sigma,
        constant=True,
        init_dist=pm.Normal.dist(0, 10),
        observed=y,
    )

    idata = pm.sample(
        1000,
        tune=2000,
        target_accept=0.9,
        random_seed=RANDOM_SEED,
    )

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [rho0, rho1, rho2, sigma]

100.00% [12000/12000 00:09<00:00 Sampling 4 chains, 0 divergences]

Sampling 4 chains for 2_000 tune and 1_000 draw iterations (8_000 + 4_000 draws total) took 10 seconds.

az.plot_trace(
    idata,
    lines=[
        ("rho0", {}, true_center),
        ("rho1", {}, true_rho[0]),
        ("rho2", {}, true_rho[1]),
        ("sigma", {}, true_sigma),
    ],
);

../_images/8ffec071c306f08310f08a22789f799907d98c0dc5c9696c71c5acb1cbe95e53.png

作者#

由 Ed Herbst 于 2016 年 8 月撰写 (pymc#1546)
由 Chris Fonnesbeck 于 2023 年 1 月更新 (pymc-examples#493)

%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,aeppl,xarray

Last updated: Sat Jan 07 2023

Python implementation: CPython
Python version       : 3.9.0
IPython version      : 8.7.0

pytensor: 2.8.11
aeppl   : not installed
xarray  : 2022.12.0

sys       : 3.9.0 | packaged by conda-forge | (default, Nov 26 2020, 07:57:39) 
[GCC 9.3.0]
pymc      : 5.0.1
arviz     : 0.14.0
pytensor  : 2.8.11
numpy     : 1.23.5
matplotlib: 3.6.2

Watermark: 2.3.1

许可声明#

此示例库中的所有笔记本均根据 MIT 许可证提供，该许可证允许修改和再分发用于任何用途，前提是保留版权和许可声明。

引用 PyMC 示例#

要引用此笔记本，请使用 Zenodo 为 pymc-examples 仓库提供的 DOI。

重要提示

许多笔记本改编自其他来源：博客、书籍…… 在这种情况下，您也应该引用原始来源。

另请记住引用您的代码使用的相关库。

这是一个 BibTeX 引用模板

@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}

渲染后可能如下所示

分类

标签

PyMC 中 AR(1) 模型的分析#

扩展到 AR(p)#

作者#

许可声明#

引用 PyMC 示例#