GLM：分批 ADVI 在分层回归模型上的应用#

与高斯混合模型不同，（分层）回归模型具有自变量。这些变量影响似然函数，但不是随机变量。当使用小批量时，我们应该注意这一点。

%env PYTENSOR_FLAGS=device=cpu, floatX=float32, warn_float64=ignore

import os

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pytensor
import pytensor.tensor as pt
import seaborn as sns

from scipy import stats

print(f"Running on PyMC v{pm.__version__}")

env: PYTENSOR_FLAGS=device=cpu, floatX=float32, warn_float64=ignore
Running on PyMC v5.0.1

%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")

try:
    data = pd.read_csv(os.path.join("..", "data", "radon.csv"))
except FileNotFoundError:
    data = pd.read_csv(pm.get_data("radon.csv"))

data

	未命名：0	idnum	州	州2	stfips	邮编	区域	typebldg	楼层	房间	...	pcterr	adjwt	dupflag	zipflag	cntyfips	县	fips	Uppm	县代码	log_radon
0	0	5081.0	MN	MN	27.0	55735	5.0	1.0	1.0	3.0	...	9.7	1146.499190	1.0	0.0	1.0	AITKIN	27001.0	0.502054	0	0.832909
1	1	5082.0	MN	MN	27.0	55748	5.0	1.0	0.0	4.0	...	14.5	471.366223	0.0	0.0	1.0	AITKIN	27001.0	0.502054	0	0.832909
2	2	5083.0	MN	MN	27.0	55748	5.0	1.0	0.0	4.0	...	9.6	433.316718	0.0	0.0	1.0	AITKIN	27001.0	0.502054	0	1.098612
3	3	5084.0	MN	MN	27.0	56469	5.0	1.0	0.0	4.0	...	24.3	461.623670	0.0	0.0	1.0	AITKIN	27001.0	0.502054	0	0.095310
4	4	5085.0	MN	MN	27.0	55011	3.0	1.0	0.0	4.0	...	13.8	433.316718	0.0	0.0	3.0	ANOKA	27003.0	0.428565	1	1.163151
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
914	914	5995.0	MN	MN	27.0	55363	5.0	1.0	0.0	4.0	...	4.5	1146.499190	0.0	0.0	171.0	WRIGHT	27171.0	0.913909	83	1.871802
915	915	5996.0	MN	MN	27.0	55376	5.0	1.0	0.0	7.0	...	8.3	1105.956867	0.0	0.0	171.0	WRIGHT	27171.0	0.913909	83	1.526056
916	916	5997.0	MN	MN	27.0	55376	5.0	1.0	0.0	4.0	...	5.2	1214.922779	0.0	0.0	171.0	WRIGHT	27171.0	0.913909	83	1.629241
917	917	5998.0	MN	MN	27.0	56297	5.0	1.0	0.0	4.0	...	9.6	1177.377355	0.0	0.0	173.0	YELLOW MEDICINE	27173.0	1.426590	84	1.335001
918	918	5999.0	MN	MN	27.0	56297	5.0	1.0	0.0	4.0	...	8.0	1214.922779	0.0	0.0	173.0	YELLOW MEDICINE	27173.0	1.426590	84	1.098612

919 行 × 30 列

county_idx = data["county_code"].values
floor_idx = data["floor"].values
log_radon_idx = data["log_radon"].values

coords = {"counties": data.county.unique()}

在这里，log_radon_idx_t 是因变量，而 floor_idx_t 和 county_idx_t 决定了自变量。

log_radon_idx_t = pm.Minibatch(log_radon_idx, batch_size=100)
floor_idx_t = pm.Minibatch(floor_idx, batch_size=100)
county_idx_t = pm.Minibatch(county_idx, batch_size=100)

with pm.Model(coords=coords) as hierarchical_model:
    # Hyperpriors for group nodes
    mu_a = pm.Normal("mu_alpha", mu=0.0, sigma=100**2)
    sigma_a = pm.Uniform("sigma_alpha", lower=0, upper=100)
    mu_b = pm.Normal("mu_beta", mu=0.0, sigma=100**2)
    sigma_b = pm.Uniform("sigma_beta", lower=0, upper=100)

每个县的截距，围绕组均值 mu_a 分布。上面我们只是将 mu 和 sd 设置为固定值，而这里我们为所有 a 和 b 插入一个公共组分布（它们是与示例中唯一县的数量相同长度的向量）。

with hierarchical_model:
    a = pm.Normal("alpha", mu=mu_a, sigma=sigma_a, dims="counties")
    # Intercept for each county, distributed around group mean mu_a
    b = pm.Normal("beta", mu=mu_b, sigma=sigma_b, dims="counties")

氡水平的模型预测 a[county_idx] 转换为 a[0, 0, 0, 1, 1, ...]，因此我们将一个县的多个家庭测量值与其系数关联起来。

with hierarchical_model:
    radon_est = a[county_idx_t] + b[county_idx_t] * floor_idx_t

最后，我们指定似然函数

with hierarchical_model:
    # Model error
    eps = pm.Uniform("eps", lower=0, upper=100)

    # Data likelihood
    radon_like = pm.Normal(
        "radon_like", mu=radon_est, sigma=eps, observed=log_radon_idx_t, total_size=len(data)
    )

与 log_radon_idx_t 相关的随机变量 radon_like 应提供给 ADVI 函数，以表示其为似然项中的观测值。

另一方面，minibatches 应包括以上三个变量。

然后，使用小批量运行 ADVI。

with hierarchical_model:
    approx = pm.fit(100_000, callbacks=[pm.callbacks.CheckParametersConvergence(tolerance=1e-4)])

idata_advi = approx.sample(500)

/home/fonnesbeck/mambaforge/envs/pie/lib/python3.9/site-packages/pymc/logprob/joint_logprob.py:167: UserWarning: Found a random variable that was neither among the observations nor the conditioned variables: [integers_rv{0, (0, 0), int64, False}.0, integers_rv{0, (0, 0), int64, False}.out]
  warnings.warn(
/home/fonnesbeck/mambaforge/envs/pie/lib/python3.9/site-packages/pymc/logprob/joint_logprob.py:167: UserWarning: Found a random variable that was neither among the observations nor the conditioned variables: [integers_rv{0, (0, 0), int64, False}.0, integers_rv{0, (0, 0), int64, False}.out]
  warnings.warn(
/home/fonnesbeck/mambaforge/envs/pie/lib/python3.9/site-packages/pymc/logprob/joint_logprob.py:167: UserWarning: Found a random variable that was neither among the observations nor the conditioned variables: [integers_rv{0, (0, 0), int64, False}.0, integers_rv{0, (0, 0), int64, False}.out]
  warnings.warn(
/home/fonnesbeck/mambaforge/envs/pie/lib/python3.9/site-packages/pymc/logprob/joint_logprob.py:167: UserWarning: Found a random variable that was neither among the observations nor the conditioned variables: [integers_rv{0, (0, 0), int64, False}.0, integers_rv{0, (0, 0), int64, False}.out]
  warnings.warn(

11.50% [11499/100000 00:03<00:27 平均损失 = 263.87]

检查 ELBO 的轨迹，并将结果与 MCMC 进行比较。

plt.plot(approx.hist);

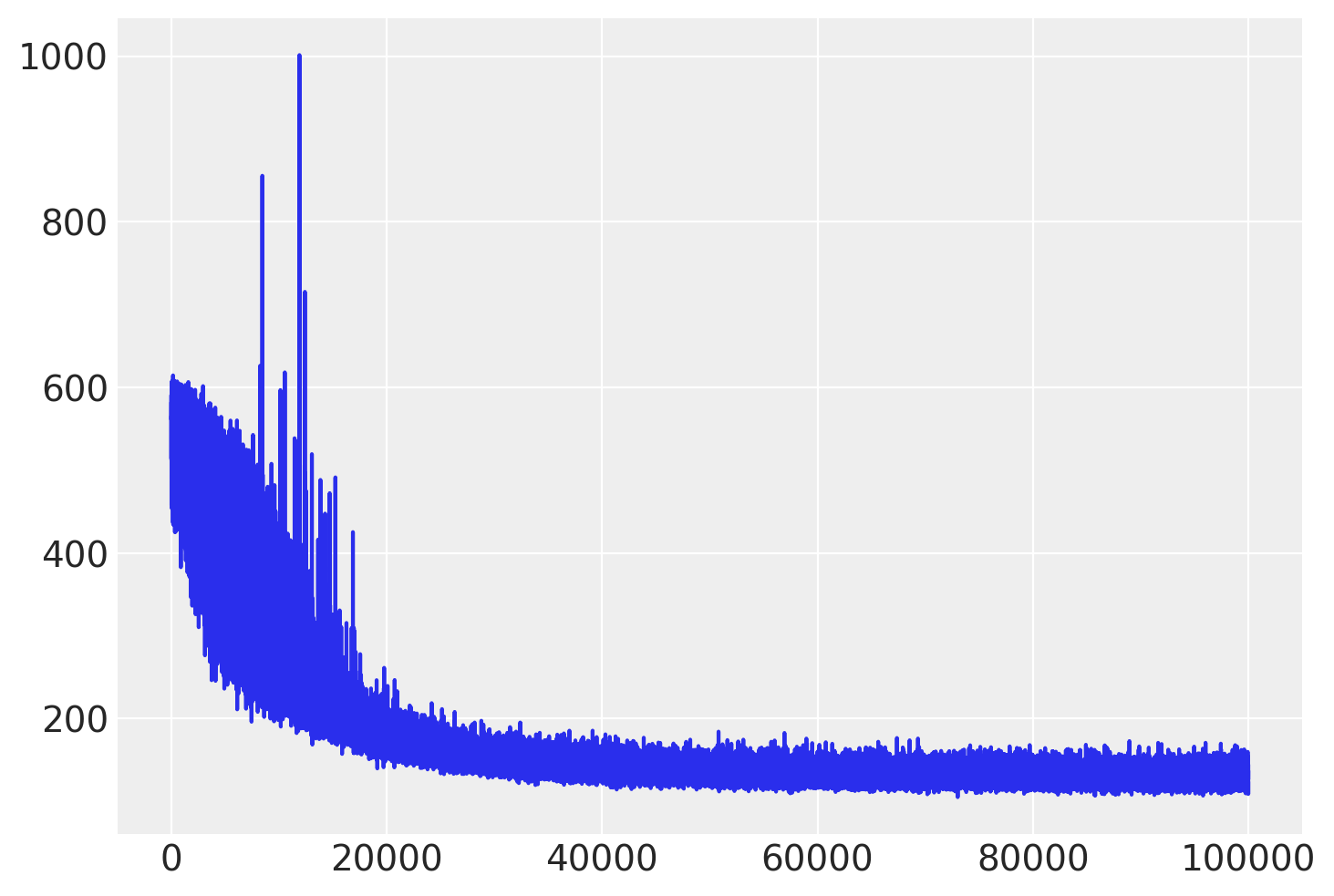
../_images/af9b90617fc072dcb41643f8d1228130d436ae7589248a7adcc8582793cf8ce3.png

我们可以从平均场近似中提取协方差矩阵，并将其用作 NUTS 算法的缩放矩阵。

scaling = approx.cov.eval()

此外，我们可以生成样本（每个链一个），用作采样器的起点。

n_chains = 4
sample = approx.sample(return_inferencedata=False, size=n_chains)
start_dict = list(sample[i] for i in range(n_chains))

# Inference button (TM)!
with pm.Model(coords=coords):
    mu_a = pm.Normal("mu_alpha", mu=0.0, sigma=100**2)
    sigma_a = pm.Uniform("sigma_alpha", lower=0, upper=100)
    mu_b = pm.Normal("mu_beta", mu=0.0, sigma=100**2)
    sigma_b = pm.Uniform("sigma_beta", lower=0, upper=100)

    a = pm.Normal("alpha", mu=mu_a, sigma=sigma_a, dims="counties")
    b = pm.Normal("beta", mu=mu_b, sigma=sigma_b, dims="counties")

    # Model error
    eps = pm.Uniform("eps", lower=0, upper=100)

    radon_est = a[county_idx] + b[county_idx] * floor_idx

    radon_like = pm.Normal("radon_like", mu=radon_est, sigma=eps, observed=log_radon_idx)

    # essentially, this is what init='advi' does
    step = pm.NUTS(scaling=scaling, is_cov=True)
    hierarchical_trace = pm.sample(draws=2000, step=step, chains=n_chains, initvals=start_dict)

Multiprocess sampling (4 chains in 4 jobs)
NUTS: [mu_alpha, sigma_alpha, mu_beta, sigma_beta, alpha, beta, eps]

100.00% [8000/8000 08:57<00:00 采样 4 个链，0 个发散]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 538 seconds.

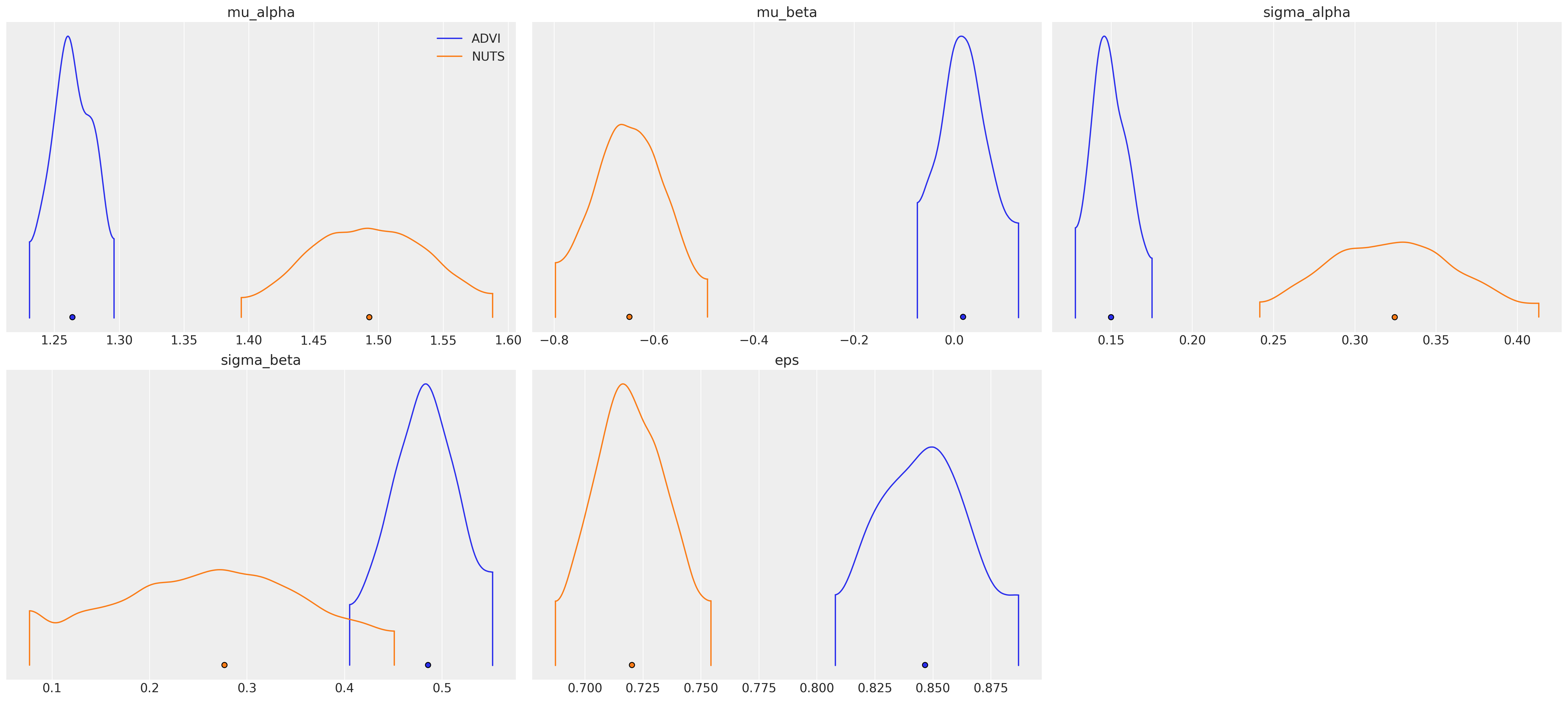
az.plot_density(
    data=[idata_advi, hierarchical_trace],
    var_names=["~alpha", "~beta"],
    data_labels=["ADVI", "NUTS"],
);

../_images/18875cd5cae6a7bbdb3a6f263a7ced96e137b1c84fa7648cda85b425255a7d6c.png

水印#

%load_ext watermark
%watermark -n -u -v -iv -w -p xarray

Last updated: Thu Sep 23 2021

Python implementation: CPython
Python version       : 3.8.10
IPython version      : 7.25.0

xarray: 0.17.0

numpy     : 1.21.0
seaborn   : 0.11.1
pandas    : 1.2.1
matplotlib: 3.3.4
theano    : 1.1.2
pymc3     : 3.11.2
scipy     : 1.7.1
arviz     : 0.11.2

Watermark: 2.2.0

许可声明#

此示例库中的所有笔记本均根据 MIT 许可证提供，该许可证允许修改和再分发用于任何用途，前提是保留版权和许可声明。

引用 PyMC 示例#

要引用此笔记本，请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。

重要提示

许多笔记本都改编自其他来源：博客、书籍…… 在这种情况下，您也应该引用原始来源。

另请记住引用您的代码使用的相关库。

这是一个 BibTeX 格式的引用模板

@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}

渲染后可能如下所示

分类

标签

GLM：分批 ADVI 在分层回归模型上的应用#

水印#

许可声明#

引用 PyMC 示例#