使用 BART 建模异方差性#

在本笔记本中，我们展示了如何使用 BART 建模异方差性，如 pymc-bart 的论文第 4.1 节 [Quiroga et al., 2022] 中所述。我们使用 R 包 datarium [Kassambara, 2019] 提供的 marketing 数据集。我们的想法是将营销渠道对销售额的贡献建模为预算的函数。

import os

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pymc_bart as pmb

%config InlineBackend.figure_format = "retina"
az.style.use("arviz-darkgrid")
plt.rcParams["figure.figsize"] = [10, 6]
rng = np.random.default_rng(42)

读取数据#

try:
    df = pd.read_csv(os.path.join("..", "data", "marketing.csv"), sep=";", decimal=",")
except FileNotFoundError:
    df = pd.read_csv(pm.get_data("marketing.csv"), sep=";", decimal=",")

n_obs = df.shape[0]

df.head()

	youtube	facebook	newspaper	sales
0	276.12	45.36	83.04	26.52
1	53.40	47.16	54.12	12.48
2	20.64	55.08	83.16	11.16
3	181.80	49.56	70.20	22.20
4	216.96	12.96	70.08	15.48

EDA#

我们首先查看数据。我们将重点关注 Youtube。

fig, ax = plt.subplots()
ax.plot(df["youtube"], df["sales"], "o", c="C0")
ax.set(title="Sales as a function of Youtube budget", xlabel="budget", ylabel="sales");

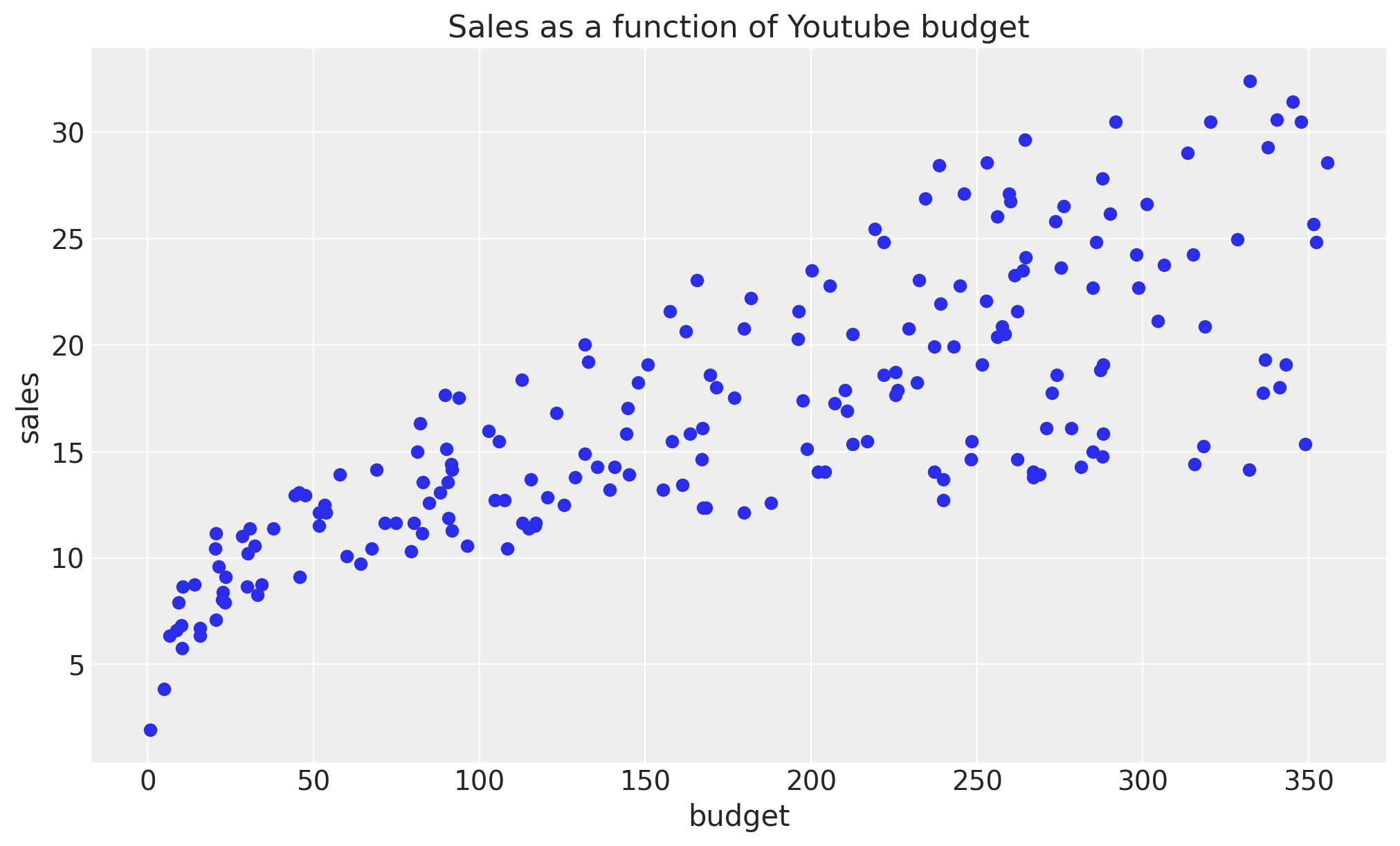
../_images/2a70660877b52a1474f190519f6d49f2a352f6ee88cc7578c0df40439f737732.png

我们清楚地看到均值和方差都随着预算的增加而增加。一种可能性是手动选择这些函数的显式参数化，例如平方根或对数。但是，在本例中，我们希望使用 BART 模型从数据中学习这些函数。

模型规范#

我们继续准备用于建模的数据。我们将使用 budget 作为预测变量，sales 作为响应变量。

X = df["youtube"].to_numpy().reshape(-1, 1)
Y = df["sales"].to_numpy()

接下来，我们指定模型。请注意，我们只需要一个 BART 分布，它可以向量化以同时建模均值和方差。我们使用 Gamma 分布作为似然函数，因为我们期望销售额为正。

with pm.Model() as model_marketing_full:
    w = pmb.BART("w", X=X, Y=np.log(Y), m=100, shape=(2, n_obs))
    y = pm.Gamma("y", mu=pm.math.exp(w[0]), sigma=pm.math.exp(w[1]), observed=Y)

pm.model_to_graphviz(model=model_marketing_full)

../_images/586d3a55d5a7f8b7074d3d1ebc80b746bb7b7c58861e742c85e5bd1d14689064.svg

我们现在拟合模型。

with model_marketing_full:
    idata_marketing_full = pm.sample(2000, random_seed=rng, compute_convergence_checks=False)
    posterior_predictive_marketing_full = pm.sample_posterior_predictive(
        trace=idata_marketing_full, random_seed=rng
    )

Multiprocess sampling (4 chains in 4 jobs)
PGBART: [w]

Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 156 seconds.
Sampling: [y]

结果#

我们现在可以可视化均值和似然函数的后验预测分布。

posterior_mean = idata_marketing_full.posterior["w"].mean(dim=("chain", "draw"))[0]

w_hdi = az.hdi(ary=idata_marketing_full, group="posterior", var_names=["w"], hdi_prob=0.5)

pps = az.extract(
    posterior_predictive_marketing_full, group="posterior_predictive", var_names=["y"]
).T

idx = np.argsort(X[:, 0])


fig, ax = plt.subplots()
az.plot_hdi(
    x=X[:, 0],
    y=pps,
    ax=ax,
    hdi_prob=0.90,
    fill_kwargs={"alpha": 0.3, "label": r"Observations $90\%$ HDI"},
)
az.plot_hdi(
    x=X[:, 0],
    hdi_data=np.exp(w_hdi["w"].sel(w_dim_0=0)),
    ax=ax,
    fill_kwargs={"alpha": 0.6, "label": r"Mean $50\%$ HDI"},
)
ax.plot(df["youtube"], df["sales"], "o", c="C0", label="Raw Data")
ax.legend(loc="upper left")
ax.set(
    title="Sales as a function of Youtube budget - Posterior Predictive",
    xlabel="budget",
    ylabel="sales",
);

/home/osvaldo/proyectos/00_BM/arviz-devs/arviz/arviz/plots/hdiplot.py:161: FutureWarning: hdi currently interprets 2d data as (draw, shape) but this will change in a future release to (chain, draw) for coherence with other functions
  hdi_data = hdi(y, hdi_prob=hdi_prob, circular=circular, multimodal=False, **hdi_kwargs)

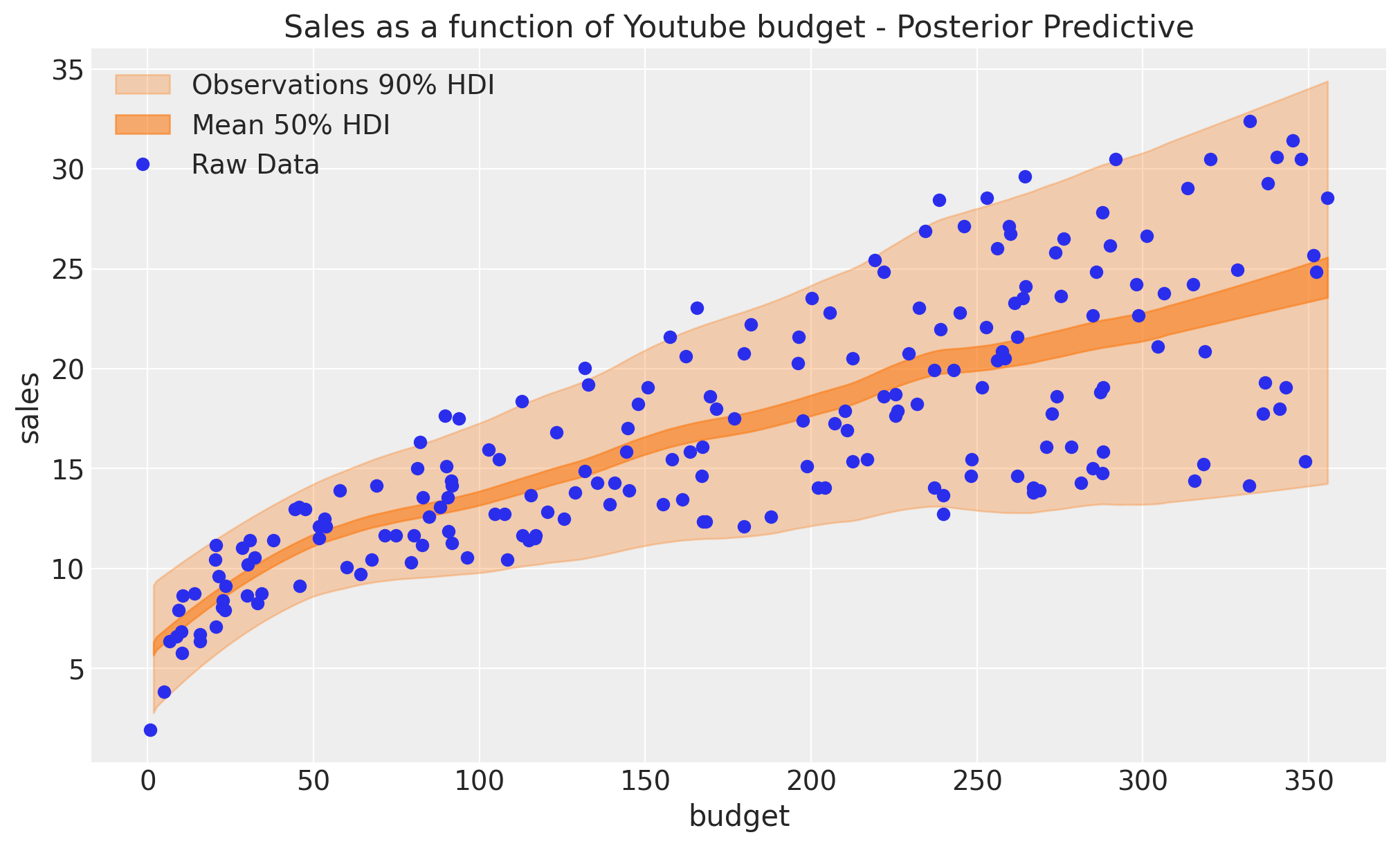
../_images/c7af179be280454fac44e14ae0e2816e1c557090f0962095e05429437c886652.png

拟合效果看起来不错！事实上，我们看到均值和方差都随着预算的增加而增加。

作者#

由 Juan Orduz 于 2023 年 2 月撰写
由 Osvaldo Martin 于 2023 年 3 月重新运行
由 Osvaldo Martin 于 2023 年 11 月重新运行
由 Osvaldo Martin 于 2024 年 12 月重新运行

参考文献#

[1]

Miriana Quiroga, Pablo G Garay, Juan M. Alonso, Juan Martin Loyola, 和 Osvaldo A Martin. Bayesian additive regression trees for probabilistic programming. 2022. URL: https://arxiv.org/abs/2206.03619, doi:10.48550/ARXIV.2206.03619.

[2]

Alboukadel Kassambara. datarium: Data Bank for Statistical Analysis and Visualization. 2019. R package version 0.1.0. URL: https://cran.r-project.cn/package=datarium.

水印#

%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor

Last updated: Mon Dec 23 2024

Python implementation: CPython
Python version       : 3.11.5
IPython version      : 8.16.1

pytensor: 2.26.4

pymc_bart : 0.6.0
arviz     : 0.20.0.dev0
pymc      : 5.19.1
matplotlib: 3.8.4
pandas    : 2.1.2
numpy     : 1.26.4

Watermark: 2.4.3

许可声明#

本示例库中的所有笔记本均根据 MIT 许可证提供，该许可证允许修改和再分发用于任何用途，前提是保留版权和许可声明。

引用 PyMC 示例#

要引用此笔记本，请使用 Zenodo 为 pymc-examples 仓库提供的 DOI。

重要提示

许多笔记本改编自其他来源：博客、书籍……在这种情况下，您也应该引用原始来源。

另请记住引用您的代码使用的相关库。

这是一个 bibtex 格式的引用模板

@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}

渲染后可能如下所示

分类

标签