NBA 犯规分析与项目反应理论#
import os
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
%matplotlib inline
print(f"Running on PyMC v{pm.__version__}")
Running on PyMC v4.0.0b6
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
简介#
本教程展示了贝叶斯项目反应理论的应用 [Fox, 2010],使用 PyMC 分析 NBA 篮球犯规数据。 基于 Austin Rochford 的博客文章 NBA 犯规和贝叶斯项目反应理论。
动机#
我们的场景是,我们观察到一个二元结果(是否判罚犯规),来自两个具有不同角色的主体(涉嫌犯规的球员和在比赛中处于不利地位的球员)的互动(一次篮球比赛)。此外,每个犯规或处于不利地位的主体都是一个个体,可能会被观察到多次(例如,勒布朗·詹姆斯在多场比赛中被观察到犯规)。那么,可能不仅主体的角色,而且单个球员的能力也对观察到的结果有所贡献。因此,我们希望估计每个个体(潜在)能力作为犯规或处于不利地位的主体对观察到的结果的贡献。 例如,这将使我们能够对球员进行从更有效到效率较低的排名,量化此排名中的不确定性,并发现犯规判罚中涉及的额外分层结构。所有这些都非常有用!
那么,我们如何研究这种常见且复杂的多主体互动场景,以及一千多个个体之间的分层结构?
尽管场景非常复杂,但贝叶斯项目反应理论与现代强大的统计软件相结合,提供了相当优雅且有效的建模选项。 其中一个选项采用了称为 Rasch 模型 的 广义线性模型,我们现在将更详细地讨论它。
Rasch 模型#
我们的数据来源于官方的 NBA 最后两分钟报告,包含 2015 年至 2021 年之间的比赛数据。在此数据集中,每一行 k 都是一次涉及两名球员(犯规者和处于不利地位者)的比赛,其中犯规已被判罚或未被判罚。 因此,我们将裁判在比赛 k 中判罚犯规的概率 p_k 建模为所涉及球员的函数。 因此,我们为每位球员定义两个潜在变量,即
theta:估计球员在处于不利地位时被判罚犯规的能力,以及b:估计球员在犯规时未被判罚犯规的能力。
请注意,这些球员的参数越高,对球员的球队来说结果就越好。 然后,使用标准 Rasch 模型估计这两个参数,假设比赛 k 中所涉及的相应球员的 p_k 的对数优势比等于 theta-b。 此外,我们在所有 theta 和所有 b 上放置分层超先验,以考虑球员之间的共享能力以及不同球员的大量不同观察次数。
讨论#
我们的分析给出了每个球员的潜在技能 theta 和 b 的估计,以后验分布的形式呈现。 我们通过三种方式分析此结果。
我们首先展示共享超先验的作用,通过展示观察次数较少的球员的后验如何被拉向联盟平均水平。
其次,我们按均值对后验进行排名,以查看最佳和最差的犯规和处于不利地位的球员,并观察到一些球员仍然在 Austin Rochford 博客文章 中针对不同数据估计的相同模型中排名前 10。
第三,我们展示了我们如何发现按位置对球员进行分组很可能是在我们的模型中引入信息量更大的额外分层层,并将此作为感兴趣的读者的练习。 最后,让我们总结一下,轻松地向模型添加知情分层结构的机会是使贝叶斯建模非常灵活和强大的一种特性,可用于量化在引入(或发现)特定问题知识至关重要的场景中的不确定性。
此笔记本中的分析分四个主要步骤执行
数据收集和处理。
Rasch 模型的定义和实例化。
后验抽样和收敛性检查。
后验结果分析。
数据收集和处理#
我们首先从原始数据集导入数据,该数据集可以在 此 URL 找到。 每行对应于 2015-16 赛季和 2020-21 赛季之间的 NBA 比赛。 我们仅导入了五列,即
committing:比赛中犯规球员的姓名。disadvantaged:比赛中处于不利地位的球员的姓名。decision:比赛的复审判决,可以取四个值,即CNC:正确未判罚,INC:错误未判罚,IC:错误判罚,CC:正确判罚。
committing_position:犯规球员的位置,可以取值G:后卫,F:前锋,C:中锋,G-F,F-G,F-C,C-F。
disadvantaged_position:处于不利地位的球员的位置,可能的值与上述相同。
我们注意到,我们已经从原始数据集中删除了涉及少于两名球员的比赛(例如走步犯规或违例)。 此外,原始数据集不包含有关球员位置的信息,这是我们自己添加的。
try:
df_orig = pd.read_csv(os.path.join("..", "data", "item_response_nba.csv"), index_col=0)
except FileNotFoundError:
df_orig = pd.read_csv(pm.get_data("item_response_nba.csv"), index_col=0)
df_orig.head()
| 犯规 | 不利 | 判决 | 犯规位置 | 不利位置 | |
|---|---|---|---|---|---|
| 比赛 ID | |||||
| 1 | 埃弗里·布拉德利 | 斯蒂芬·库里 | CNC | G | G |
| 3 | 以赛亚·托马斯 | 安德烈·伊戈达拉 | CNC | G | G-F |
| 4 | 杰·克劳德 | 哈里森·巴恩斯 | INC | F | F |
| 6 | 德雷蒙德·格林 | 以赛亚·托马斯 | CC | F | G |
| 7 | 埃弗里·布拉德利 | 斯蒂芬·库里 | CC | G | G |
我们现在分三个步骤处理数据
我们通过从
df_orig中删除位置信息来创建数据帧df,并创建一个数据帧df_position,收集所有具有相应位置的球员。 (最后一个数据帧将在笔记本的最后才使用。)我们向
df添加一个名为foul_called的列,如果比赛被判罚犯规,则赋值为 1,否则赋值为 0。我们为犯规和处于不利地位的球员分配 ID,并使用此索引来识别每次观察到的比赛中的相应球员。
最后,我们显示主数据帧 df 的头部以及一些基本统计信息。
# 1. Construct df and df_position
df = df_orig[["committing", "disadvantaged", "decision"]]
df_position = pd.concat(
[
df_orig.groupby("committing").committing_position.first(),
df_orig.groupby("disadvantaged").disadvantaged_position.first(),
]
).to_frame()
df_position = df_position[~df_position.index.duplicated(keep="first")]
df_position.index.name = "player"
df_position.columns = ["position"]
# 2. Create the binary foul_called variable
def foul_called(decision):
"""Correct and incorrect noncalls (CNC and INC) take value 0.
Correct and incorrect calls (CC and IC) take value 1.
"""
out = 0
if (decision == "CC") | (decision == "IC"):
out = 1
return out
df = df.assign(foul_called=lambda df: df["decision"].apply(foul_called))
# 3 We index observed calls by committing and disadvantaged players
committing_observed, committing = pd.factorize(df.committing, sort=True)
disadvantaged_observed, disadvantaged = pd.factorize(df.disadvantaged, sort=True)
df.index.name = "play_id"
# Display of main dataframe with some statistics
print(f"Number of observed plays: {len(df)}")
print(f"Number of disadvantaged players: {len(disadvantaged)}")
print(f"Number of committing players: {len(committing)}")
print(f"Global probability of a foul being called: " f"{100*round(df.foul_called.mean(),3)}%\n\n")
df.head()
Number of observed plays: 46861
Number of disadvantaged players: 770
Number of committing players: 789
Global probability of a foul being called: 23.3%
| 犯规 | 不利 | 判决 | foul_called | |
|---|---|---|---|---|
| 比赛 ID | ||||
| 1 | 埃弗里·布拉德利 | 斯蒂芬·库里 | CNC | 0 |
| 3 | 以赛亚·托马斯 | 安德烈·伊戈达拉 | CNC | 0 |
| 4 | 杰·克劳德 | 哈里森·巴恩斯 | INC | 0 |
| 6 | 德雷蒙德·格林 | 以赛亚·托马斯 | CC | 1 |
| 7 | 埃弗里·布拉德利 | 斯蒂芬·库里 | CC | 1 |
项目反应模型#
模型定义#
我们用以下符号表示:
\(N_d\) 和 \(N_c\) 分别为处于不利地位和犯规球员的数量,
\(K\) 为比赛次数,
\(k\) 为一场比赛,
\(y_k\) 为比赛 \(k\) 中观察到的判罚/未判罚,
\(p_k\) 为比赛 \(k\) 中判罚犯规的概率,
\(i(k)\) 为比赛 \(k\) 中处于不利地位的球员,以及
\(j(k)\) 为比赛 \(k\) 中犯规的球员。
我们假设每个处于不利地位的球员都由潜在变量描述
\(\theta_i\),其中 \(i=1,2,...,N_d\),
每个犯规球员都由潜在变量描述
\(b_j\),其中 \(j=1,2,...,N_c\)。
然后,我们将每次观察 \(y_k\) 建模为概率为 \(p_k\) 的独立伯努利试验的结果,其中
对于 \(k=1,2,...,K\),通过定义(通过 非中心参数化)
具有先验/超先验
请注意,\(p_k\) 始终依赖于 \(\mu_\theta,\,\sigma_\theta\) 和 \(\sigma_b\)(“合并先验”),并且由于 \(\Delta_{\theta,i}\) 和 \(\Delta_{b,j}\)(“未合并先验”),也依赖于比赛中涉及的实际球员。 这意味着我们的模型具有部分合并功能。 此外,请注意,我们不将 \(\theta\) 和 \(b\) 合并,因此即使对于同一球员,也假设这些技能是独立的。 另外,请注意,我们将 \(b_{j}\) 的均值归一化为零。
最后,请注意我们如何从数据反向构建此模型。 这是一种非常自然的构建模型的方式,使我们能够快速了解每个变量如何与其他变量及其直觉联系起来。 同时,当在下面实例化模型时,构建方向相反,即从先验开始,向上移动到观察结果。
PyMC 实现#
我们现在在 PyMC 中实现上述模型。 请注意,为了轻松跟踪球员(因为我们有数百名球员既是犯规者又是处于不利地位者),我们使用了 coords 参数用于 pymc.Model。 (有关此功能的教程,请参阅笔记本 使用数据容器 或 此博客文章。) 我们选择的先验与 Austin Rochford 的文章 中的相同,以使比较保持一致。
coords = {"disadvantaged": disadvantaged, "committing": committing}
with pm.Model(coords=coords) as model:
# Data
foul_called_observed = pm.Data("foul_called_observed", df.foul_called, mutable=False)
# Hyperpriors
mu_theta = pm.Normal("mu_theta", 0.0, 100.0)
sigma_theta = pm.HalfCauchy("sigma_theta", 2.5)
sigma_b = pm.HalfCauchy("sigma_b", 2.5)
# Priors
Delta_theta = pm.Normal("Delta_theta", 0.0, 1.0, dims="disadvantaged")
Delta_b = pm.Normal("Delta_b", 0.0, 1.0, dims="committing")
# Deterministic
theta = pm.Deterministic("theta", Delta_theta * sigma_theta + mu_theta, dims="disadvantaged")
b = pm.Deterministic("b", Delta_b * sigma_b, dims="committing")
eta = pm.Deterministic("eta", theta[disadvantaged_observed] - b[committing_observed])
# Likelihood
y = pm.Bernoulli("y", logit_p=eta, observed=foul_called_observed)
我们现在绘制我们的模型,以显示变量 theta 和 b 上的分层结构(和非中心参数化)。
pm.model_to_graphviz(model)
抽样和收敛性#
我们现在从我们的 Rasch 模型中抽样。
with model:
trace = pm.sample(1000, tune=1500, random_seed=RANDOM_SEED)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [mu_theta, sigma_theta, sigma_b, Delta_theta, Delta_b]
Sampling 4 chains for 1_500 tune and 1_000 draw iterations (6_000 + 4_000 draws total) took 431 seconds.
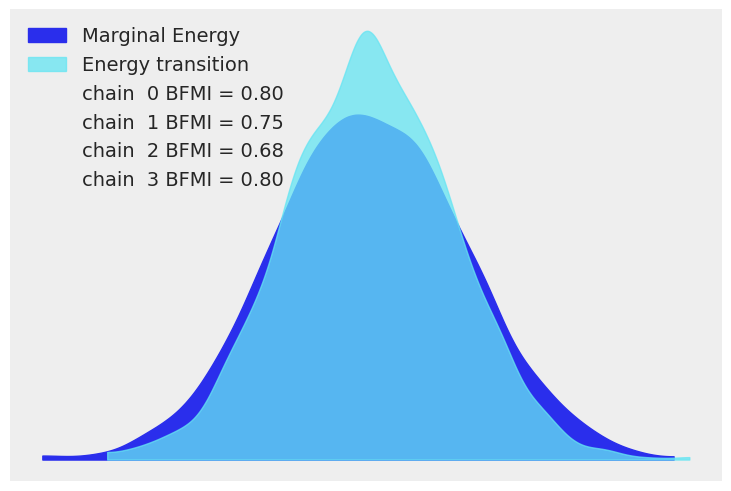
我们在下面绘制了获得的迹的能量差。 此外,我们假设我们的采样器已收敛,因为它通过了所有自动 PyMC 收敛性检查。
az.plot_energy(trace);
后验分析#
部分合并的可视化#
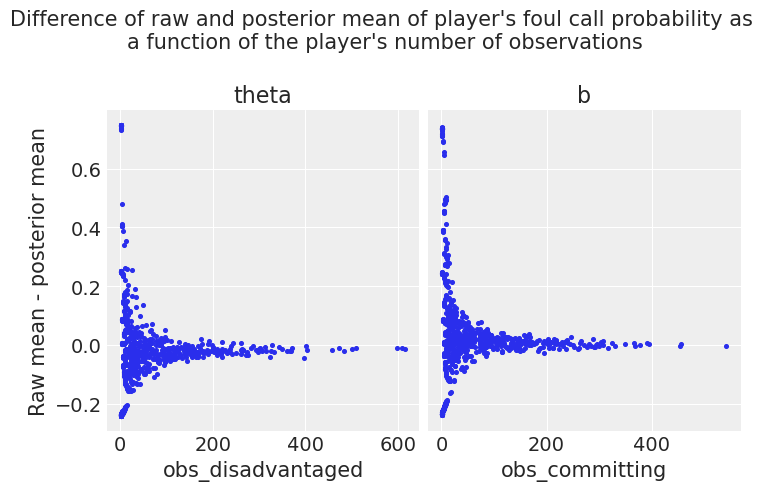
我们的第一个检查是绘制
y:每个处于不利地位和犯规球员的原始平均概率(来自数据)与后验平均概率之间的差值
x:作为每个处于不利地位和犯规球员的观察次数的函数。
正如预期的那样,这些图显示,我们模型的分层结构倾向于估计观察次数较少的球员的后验接近全局平均值。
# Global posterior means of μ_theta and μ_b
mu_theta_mean, mu_b_mean = trace.posterior["mu_theta"].mean(), 0
# Raw mean from data of each disadvantaged player
disadvantaged_raw_mean = df.groupby("disadvantaged")["foul_called"].mean()
# Raw mean from data of each committing player
committing_raw_mean = df.groupby("committing")["foul_called"].mean()
# Posterior mean of each disadvantaged player
disadvantaged_posterior_mean = (
1 / (1 + np.exp(-trace.posterior["theta"].mean(dim=["chain", "draw"]))).to_pandas()
)
# Posterior mean of each committing player
committing_posterior_mean = (
1
/ (1 + np.exp(-(mu_theta_mean - trace.posterior["b"].mean(dim=["chain", "draw"])))).to_pandas()
)
# Compute difference of raw and posterior mean for each
# disadvantaged and committing player
def diff(a, b):
return a - b
df_disadvantaged = pd.DataFrame(
disadvantaged_raw_mean.combine(disadvantaged_posterior_mean, diff),
columns=["Raw - posterior mean"],
)
df_committing = pd.DataFrame(
committing_raw_mean.combine(committing_posterior_mean, diff), columns=["Raw - posterior mean"]
)
# Add the number of observations for each disadvantaged and committing player
df_disadvantaged = df_disadvantaged.assign(obs_disadvantaged=df["disadvantaged"].value_counts())
df_committing = df_committing.assign(obs_committing=df["committing"].value_counts())
# Plot the difference between raw and posterior means as a function of
# the number of observations
fig, (ax1, ax2) = plt.subplots(1, 2, sharey=True)
fig.suptitle(
"Difference of raw and posterior mean of player's foul call probability as "
"\na function of the player's number of observations\n",
fontsize=15,
)
ax1.scatter(data=df_disadvantaged, x="obs_disadvantaged", y="Raw - posterior mean", s=7, marker="o")
ax1.set_title("theta")
ax1.set_ylabel("Raw mean - posterior mean")
ax1.set_xlabel("obs_disadvantaged")
ax2.scatter(data=df_committing, x="obs_committing", y="Raw - posterior mean", s=7)
ax2.set_title("b")
ax2.set_xlabel("obs_committing")
plt.show()
顶部和底部犯规和处于不利地位的球员#
由于我们成功估计了处于不利地位(theta)和犯规(b)球员的技能,我们终于可以检查哪些球员在我们的模型中表现更好和更差。 因此,我们现在使用森林图绘制我们的后验。 我们绘制了根据潜在技能 theta 和 b 分别排名的前 10 名和后 10 名球员。
def order_posterior(inferencedata, var, bottom_bool):
xarray_ = inferencedata.posterior[var].mean(dim=["chain", "draw"])
return xarray_.sortby(xarray_, ascending=bottom_bool)
top_theta, bottom_theta = (
order_posterior(trace, "theta", False),
order_posterior(trace, "theta", True),
)
top_b, bottom_b = (order_posterior(trace, "b", False), order_posterior(trace, "b", True))
amount = 10 # How many top players we want to display in each cathegory
fig = plt.figure(figsize=(17, 14))
fig.suptitle(
"\nPosterior estimates for top and bottom disadvantaged (theta) and "
"committing (b) players \n(94% HDI)\n",
fontsize=25,
)
theta_top_ax = fig.add_subplot(221)
b_top_ax = fig.add_subplot(222)
theta_bottom_ax = fig.add_subplot(223, sharex=theta_top_ax)
b_bottom_ax = fig.add_subplot(224, sharex=b_top_ax)
# theta: plot top
az.plot_forest(
trace,
var_names=["theta"],
combined=True,
coords={"disadvantaged": top_theta["disadvantaged"][:amount]},
ax=theta_top_ax,
labeller=az.labels.NoVarLabeller(),
)
theta_top_ax.set_title(f"theta: top {amount}")
theta_top_ax.set_xlabel("theta\n")
theta_top_ax.set_xlim(xmin=-2.5, xmax=0.1)
theta_top_ax.vlines(mu_theta_mean, -1, amount, "k", "--", label=("League average"))
theta_top_ax.legend(loc=2)
# theta: plot bottom
az.plot_forest(
trace,
var_names=["theta"],
colors="blue",
combined=True,
coords={"disadvantaged": bottom_theta["disadvantaged"][:amount]},
ax=theta_bottom_ax,
labeller=az.labels.NoVarLabeller(),
)
theta_bottom_ax.set_title(f"theta: bottom {amount}")
theta_bottom_ax.set_xlabel("theta")
theta_bottom_ax.vlines(mu_theta_mean, -1, amount, "k", "--", label=("League average"))
theta_bottom_ax.legend(loc=2)
# b: plot top
az.plot_forest(
trace,
var_names=["b"],
colors="blue",
combined=True,
coords={"committing": top_b["committing"][:amount]},
ax=b_top_ax,
labeller=az.labels.NoVarLabeller(),
)
b_top_ax.set_title(f"b: top {amount}")
b_top_ax.set_xlabel("b\n")
b_top_ax.set_xlim(xmin=-1.5, xmax=1.5)
b_top_ax.vlines(0, -1, amount, "k", "--", label="League average")
b_top_ax.legend(loc=2)
# b: plot bottom
az.plot_forest(
trace,
var_names=["b"],
colors="blue",
combined=True,
coords={"committing": bottom_b["committing"][:amount]},
ax=b_bottom_ax,
labeller=az.labels.NoVarLabeller(),
)
b_bottom_ax.set_title(f"b: bottom {amount}")
b_bottom_ax.set_xlabel("b")
b_bottom_ax.vlines(0, -1, amount, "k", "--", label="League average")
b_bottom_ax.legend(loc=2)
plt.show();
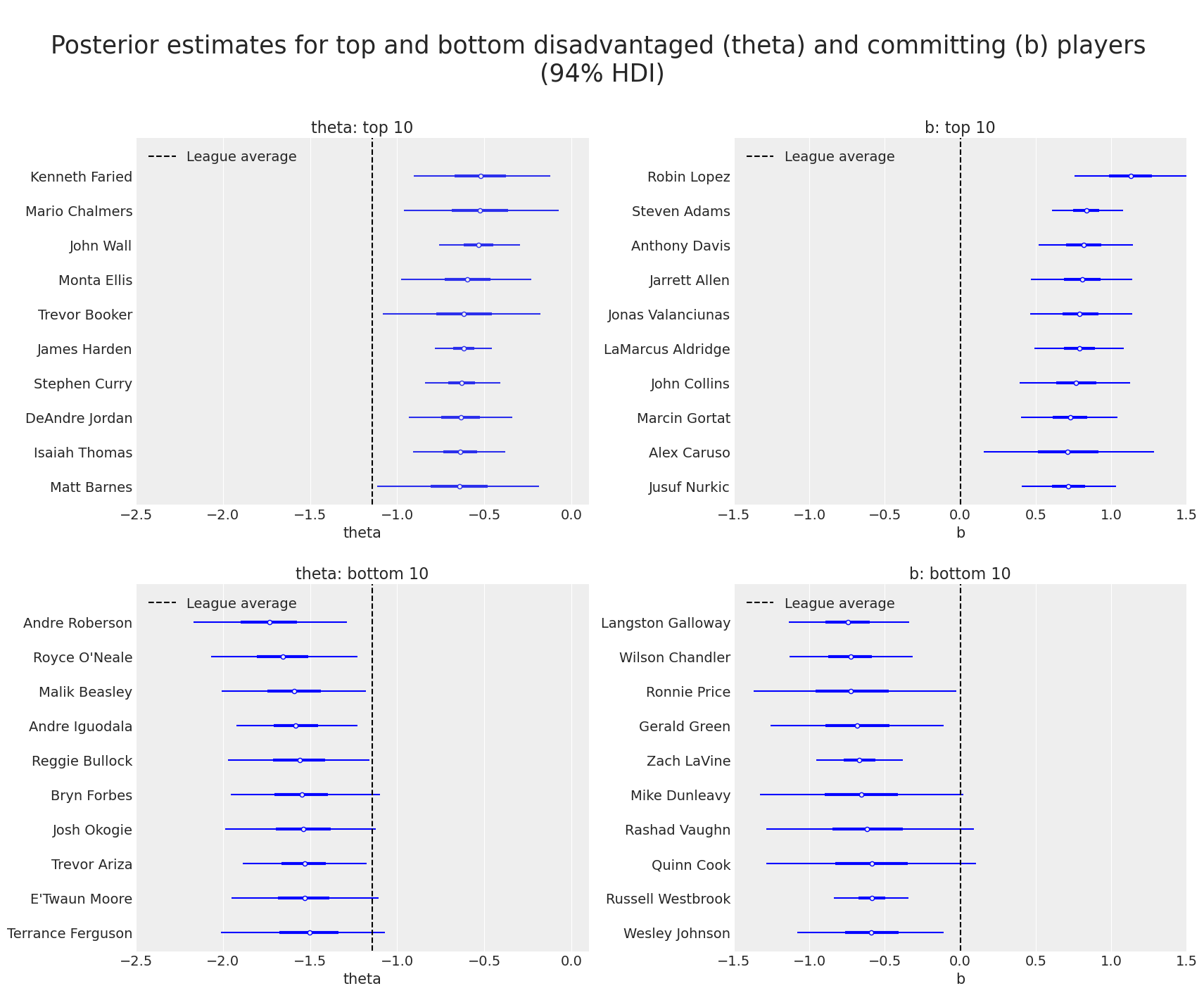
通过访问 Austin Rochford 文章 并检查那里的 Rasch 模型的类似表格(使用 2016-17 赛季的数据),读者可以看到,在我们更大的数据集(涵盖 2015-16 至 2020-21 赛季)中,两种技能中的几位顶级球员仍然排在前 10 名。
发现额外的分层结构#
一个自然要问的问题是,作为处于不利地位的球员(即 theta 较高的球员)是否也可能擅长作为犯规球员(即 b 较高的球员),反之亦然。 因此,接下来的两个图显示了相对于 b (resp.theta)的顶级球员的 theta (resp. b)得分。
amount = 20 # How many top players we want to display
top_theta_players = top_theta["disadvantaged"][:amount].values
top_b_players = top_b["committing"][:amount].values
top_theta_in_committing = set(committing).intersection(set(top_theta_players))
top_b_in_disadvantaged = set(disadvantaged).intersection(set(top_b_players))
if (len(top_theta_in_committing) < amount) | (len(top_b_in_disadvantaged) < amount):
print(
f"Some players in the top {amount} for theta (or b) do not have observations for b (or theta).\n",
"Plot not shown",
)
else:
fig = plt.figure(figsize=(17, 14))
fig.suptitle(
"\nScores as committing (b) for best disadvantaged (theta) players"
" and vice versa"
"\n(94% HDI)\n",
fontsize=25,
)
b_top_theta = fig.add_subplot(121)
theta_top_b = fig.add_subplot(122)
az.plot_forest(
trace,
var_names=["b"],
colors="blue",
combined=True,
coords={"committing": top_theta_players},
figsize=(7, 7),
ax=b_top_theta,
labeller=az.labels.NoVarLabeller(),
)
b_top_theta.set_title(f"\nb score for top {amount} in theta\n (94% HDI)\n\n", fontsize=17)
b_top_theta.set_xlabel("b")
b_top_theta.vlines(mu_b_mean, -1, amount, color="k", ls="--", label="League average")
b_top_theta.legend(loc="upper right", bbox_to_anchor=(0.46, 1.05))
az.plot_forest(
trace,
var_names=["theta"],
colors="blue",
combined=True,
coords={"disadvantaged": top_b_players},
figsize=(7, 7),
ax=theta_top_b,
labeller=az.labels.NoVarLabeller(),
)
theta_top_b.set_title(f"\ntheta score for top {amount} in b\n (94% HDI)\n\n", fontsize=17)
theta_top_b.set_xlabel("theta")
theta_top_b.vlines(mu_theta_mean, -1, amount, color="k", ls="--", label="League average")
theta_top_b.legend(loc="upper right", bbox_to_anchor=(0.46, 1.05));
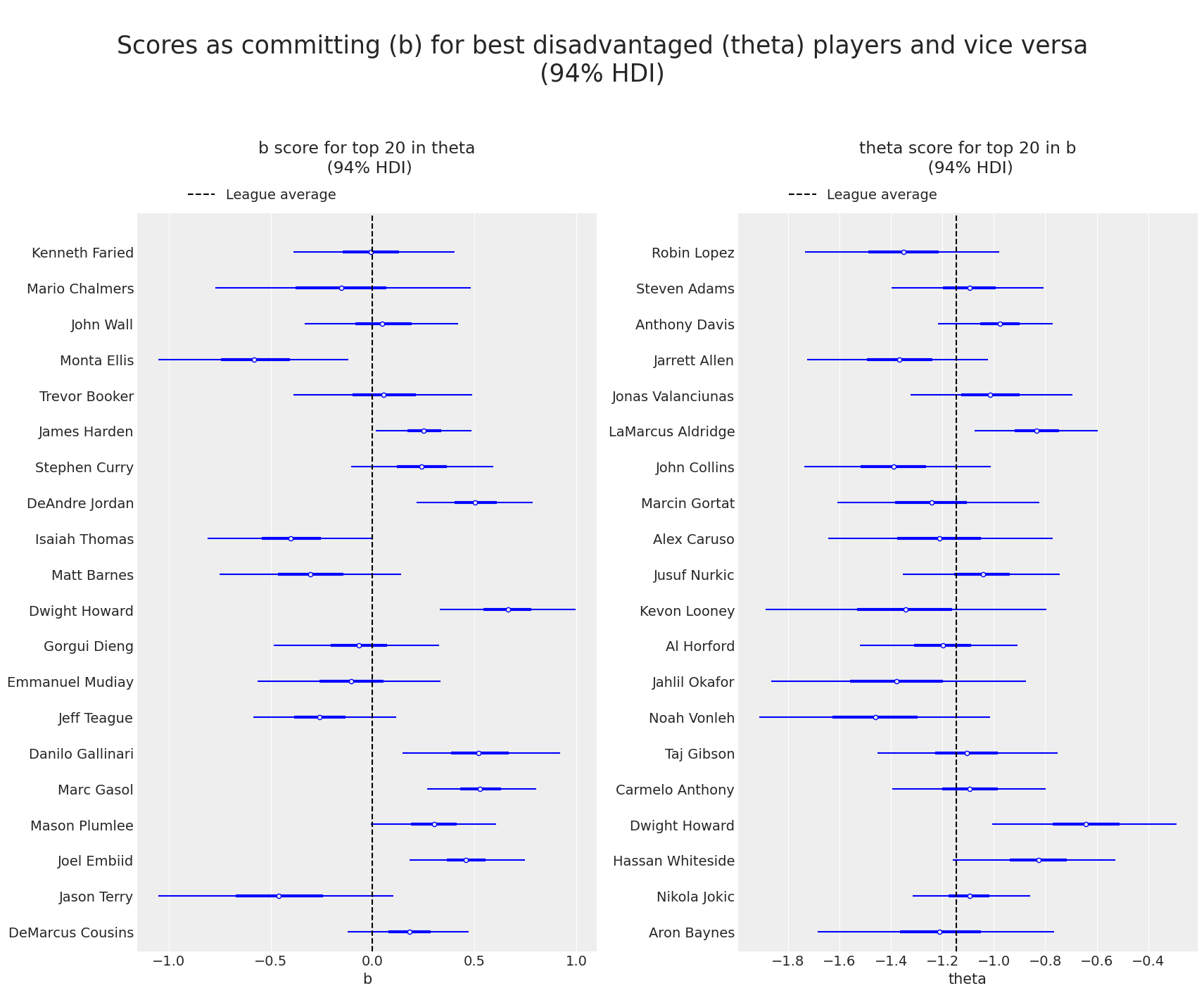
这些图表明,在 theta 中获得高分与在 b 中获得高分或低分无关。 此外,凭借一点 NBA 篮球知识,人们可以直观地注意到,中锋或前锋球员比后卫或控球后卫更有可能获得更高的 b 分数。 鉴于最后的观察,我们决定绘制直方图,以显示顶级不利(theta)和犯规(b)球员的不同位置的出现情况。 有趣的是,我们在下面看到,最好的不利球员中最大一部分是后卫,同时,最好的犯规球员中最大一部分是中锋(同时后卫的比例非常小)。
amount = 50 # How many top players we want to display
top_theta_players = top_theta["disadvantaged"][:amount].values
top_b_players = top_b["committing"][:amount].values
positions = ["C", "C-F", "F-C", "F", "G-F", "G"]
# Histogram of positions of top disadvantaged players
fig = plt.figure(figsize=(8, 6))
top_theta_position = fig.add_subplot(121)
df_position.loc[df_position.index.isin(top_theta_players)].position.value_counts().loc[
positions
].plot.bar(ax=top_theta_position, color="orange", label="theta")
top_theta_position.set_title(f"Positions of top {amount} disadvantaged (theta)\n", fontsize=12)
top_theta_position.legend(loc="upper left")
# Histogram of positions of top committing players
top_b_position = fig.add_subplot(122, sharey=top_theta_position)
df_position.loc[df_position.index.isin(top_b_players)].position.value_counts().loc[
positions
].plot.bar(ax=top_b_position, label="b")
top_b_position.set_title(f"Positions of top {amount} committing (b)\n", fontsize=12)
top_b_position.legend(loc="upper right");
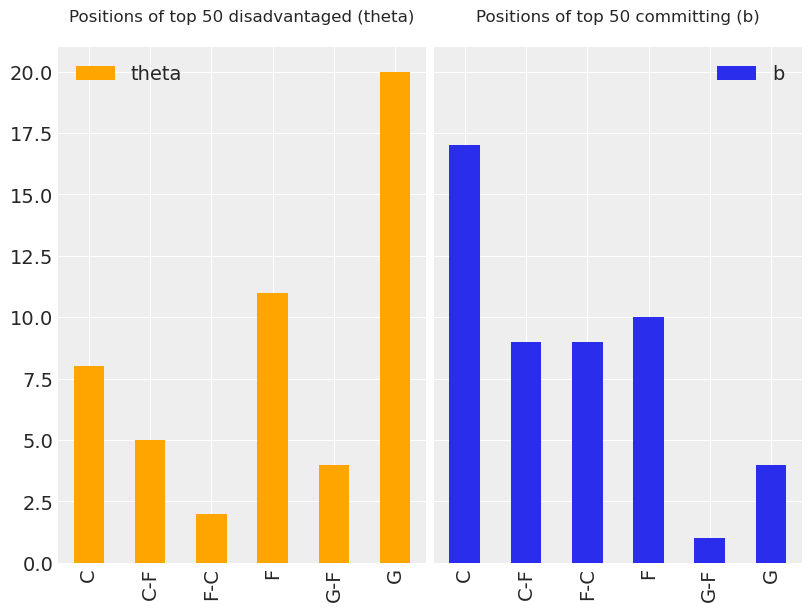
上面的直方图表明,在我们的模型中添加分层层可能是合适的。 也就是说,按各自的位置对处于不利地位和犯规的球员进行分组,以考虑位置在评估潜在技能 theta 和 b 中的作用。 这可以在我们的 Rasch 模型中通过为按位置分组的每个球员施加均值和方差超先验来完成,这留给读者作为练习。 为此,请注意,数据帧 df_orig 的设置正是为了添加这种分层结构。 玩得开心!
衷心感谢 Eric Ma 提出的许多有用的评论,这些评论改进了本笔记本。
参考文献#
Jean-Paul Fox. 贝叶斯项目反应建模:理论与应用。 Springer, 2010.
水印#
%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,aeppl,xarray
Last updated: Sat Apr 23 2022
Python implementation: CPython
Python version : 3.9.12
IPython version : 8.2.0
pytensor: 2.6.2
aeppl : 0.0.28
xarray: 2022.3.0
matplotlib: 3.5.1
numpy : 1.22.3
pymc : 4.0.0b6
arviz : 0.13.0.dev0
pandas : 1.4.2
Watermark: 2.3.0
许可声明#
此示例库中的所有笔记本均根据 MIT 许可证 提供,该许可证允许修改和重新分发用于任何用途,前提是保留版权和许可声明。
引用 PyMC 示例#
要引用此笔记本,请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。
重要提示
许多笔记本改编自其他来源:博客、书籍... 在这种情况下,您也应该引用原始来源。
另请记住引用您的代码使用的相关库。
这是一个 bibtex 中的引用模板
@incollection{citekey,
author = "<notebook authors, see above>",
title = "<notebook title>",
editor = "PyMC Team",
booktitle = "PyMC examples",
doi = "10.5281/zenodo.5654871"
}
一旦呈现,它可能看起来像