贝叶斯 A/B 测试简介

from dataclasses import dataclass
from typing import Dict, List, Union

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm

from scipy.stats import bernoulli, expon

RANDOM_SEED = 4000
rng = np.random.default_rng(RANDOM_SEED)

%config InlineBackend.figure_format = 'retina'
az.style.use("arviz-darkgrid")

plotting_defaults = dict(
    bins=50,
    kind="hist",
    textsize=10,
)

本笔记本演示了如何实现贝叶斯 A/B 测试分析。我们实现了 VWO 的贝叶斯 A/B 测试白皮书 ([Stucchio, 2015]) 中讨论的模型，并讨论了这些模型不同先验选择的影响。本笔记本不讨论其他相关主题，例如如何选择先验、提前停止和功效分析。

什么是 A/B 测试？

来自 https://vwo.com/ab-testing/

A/B 测试（也称为拆分测试）是一种将同一网页的两个变体同时展示给网站访问者的不同部分，并比较哪个变体驱动更多转化的过程。

具体来说，A/B 测试通常用于软件行业，以确定是否应向用户发布新功能或对现有功能的更改，以及更改对核心产品指标（“转化”）的影响。此外

• 我们可以同时测试两个以上的变体。我们将在本笔记本中讨论如何分析这些测试。

• “转化”的具体含义可能因测试而异，但我们将重点关注两类转化：

  • 伯努利转化 - 访问者是否执行目标操作的标志（例如，至少完成一次购买）。

  • 价值转化 - 每个访问者的实际价值（例如，美元收入，也可能为 0）。

如果您之前在生物学、心理学和其他科学的背景下研究过受控实验，那么 A/B 测试听起来很像受控实验 - 事实也确实如此！对照组和处理组的概念，以及实验设计原则，是 A/B 测试的基石。主要区别在于运行实验的背景：A/B 测试通常由在线软件公司运行，其中受试者是网站/应用程序的访问者，感兴趣的结果是可以跟踪的行为，例如注册、购买产品和返回网站。

A/B 测试通常使用传统的假设检验（参见t 检验）进行分析，但另一种方法是使用贝叶斯统计。这使我们能够纳入先验分布，并为“是否存在获胜变体？”和“差距有多大？”等问题产生一系列结果。

伯努利转化

让我们首先处理一个简单的双变体 A/B 测试，其中感兴趣的指标是执行操作的用户比例（例如，至少购买一件商品），即伯努利转化。我们的变体称为 A 和 B，其中 A 指的是现有着陆页，B 指的是我们要测试的新页面。我们想要对其进行统计推断的结果是 B 是否比 A“更好”，这取决于每个变体的潜在“真实”转化率。我们可以将此公式化如下

设 \(\theta_A, \theta_B\) 分别为变体 A 和 B 的真实转化率。那么变体 A 中访问者是否转化的结果是随机变量 \(\mathrm{Bernoulli}(\theta_A)\)，变体 B 中是 \(\mathrm{Bernoulli}(\theta_B)\)。如果我们假设访问者在着陆页上的行为与其他访问者无关（一个合理的假设），那么变体的总转化次数 \(y\) 服从二项分布

\[y \sim \sum^N\mathrm{Bernoulli}(\theta) = \mathrm{Binomial}(N, \theta)\]

在贝叶斯框架下，我们假设真实的转化率 \(\theta_A, \theta_B\) 是未知的，而是它们各自服从 Beta 分布。假设潜在的转化率是独立的（我们会随机分配每个变体的流量，因此一个变体不会影响另一个变体）

\[\theta_A \sim \theta_B \sim \mathrm{Beta}(\alpha, \beta)\]

A/B 测试期间的观察数据（似然分布）是：登陆页面的访问者数量 N，以及至少购买一件商品的访问者数量 y

\[y_A \sim \mathrm{Binomial}(n = N_A, p = \theta_A), y_B \sim \mathrm{Binomial}(n = N_B, p = \theta_B)\]

有了这个，我们可以从 \(\theta_A, \theta_B\) 的联合后验中抽样。

您可能已经注意到，Beta 分布是二项分布的共轭先验，因此我们不需要 MCMC 抽样来估计后验（确切的解决方案可以在 VWO 论文中找到）。我们仍然会演示如何使用 PyMC 进行抽样，这样做可以更轻松地使用不同的先验、依赖性假设等来扩展模型。

最后，请记住，我们感兴趣的结果是 B 是否比 A 更好。实践中衡量 B 是否更好的常用指标是转化率的相对提升，即 \(\theta_B\) 相对于 \(\theta_A\) 的百分比差异

\[\mathrm{reluplift}_B = \theta_B / \theta_A - 1\]

我们将在下面的 PyMC 中实现此模型设置。

@dataclass
class BetaPrior:
    alpha: float
    beta: float

@dataclass
class BinomialData:
    trials: int
    successes: int

class ConversionModelTwoVariant:
    def __init__(self, priors: BetaPrior):
        self.priors = priors

    def create_model(self, data: List[BinomialData]) -> pm.Model:
        trials = [d.trials for d in data]
        successes = [d.successes for d in data]
        with pm.Model() as model:
            p = pm.Beta("p", alpha=self.priors.alpha, beta=self.priors.beta, shape=2)
            obs = pm.Binomial("y", n=trials, p=p, shape=2, observed=successes)
            reluplift = pm.Deterministic("reluplift_b", p[1] / p[0] - 1)
        return model

现在我们已经定义了一个可以接受先验和我们的合成数据作为输入的类，我们的第一步是选择合适的先验。在实践中执行此操作时，需要考虑一些事项，但就本笔记本而言，我们将重点关注以下内容

• 我们假设为每个变体设置相同的 Beta 先验。

• 当我们为 alpha 和 beta 设置低值时，会出现无信息或弱信息先验。例如，alpha = 1, beta = 1 导致均匀分布作为先验。如果我们孤立地考虑一个分布，则设置此先验表明我们对参数的值一无所知，也不了解我们对其的置信度。然而，在 A/B 测试的上下文中，我们有兴趣比较一个变体相对于另一个变体的相对提升。使用弱信息 Beta 先验，这种相对提升分布非常宽，因此我们隐含地表明变体之间可能差异很大。

• 当我们为 alpha 和 beta 设置高值时，会出现强先验。与上述相反，强先验意味着相对提升分布很窄，即我们的先验信念是变体之间差异不大。

我们通过先验预测检查来说明这些要点。

先验预测检查

请注意，我们可以在这些先验预测检查中传入观察数据的任意值。从先验预测分布中抽样时，PyMC 不会使用该数据。

weak_prior = ConversionModelTwoVariant(BetaPrior(alpha=100, beta=100))

strong_prior = ConversionModelTwoVariant(BetaPrior(alpha=10000, beta=10000))

with weak_prior.create_model(data=[BinomialData(1, 1), BinomialData(1, 1)]):
    weak_prior_predictive = pm.sample_prior_predictive(samples=10000, return_inferencedata=False)

with strong_prior.create_model(data=[BinomialData(1, 1), BinomialData(1, 1)]):
    strong_prior_predictive = pm.sample_prior_predictive(samples=10000, return_inferencedata=False)

fig, axs = plt.subplots(2, 1, figsize=(7, 7), sharex=True)
az.plot_posterior(weak_prior_predictive["reluplift_b"], ax=axs[0], **plotting_defaults)
axs[0].set_title(f"B vs. A Rel Uplift Prior Predictive, {weak_prior.priors}", fontsize=10)
axs[0].axvline(x=0, color="red")
az.plot_posterior(strong_prior_predictive["reluplift_b"], ax=axs[1], **plotting_defaults)
axs[1].set_title(f"B vs. A Rel Uplift Prior Predictive, {strong_prior.priors}", fontsize=10)
axs[1].axvline(x=0, color="red");

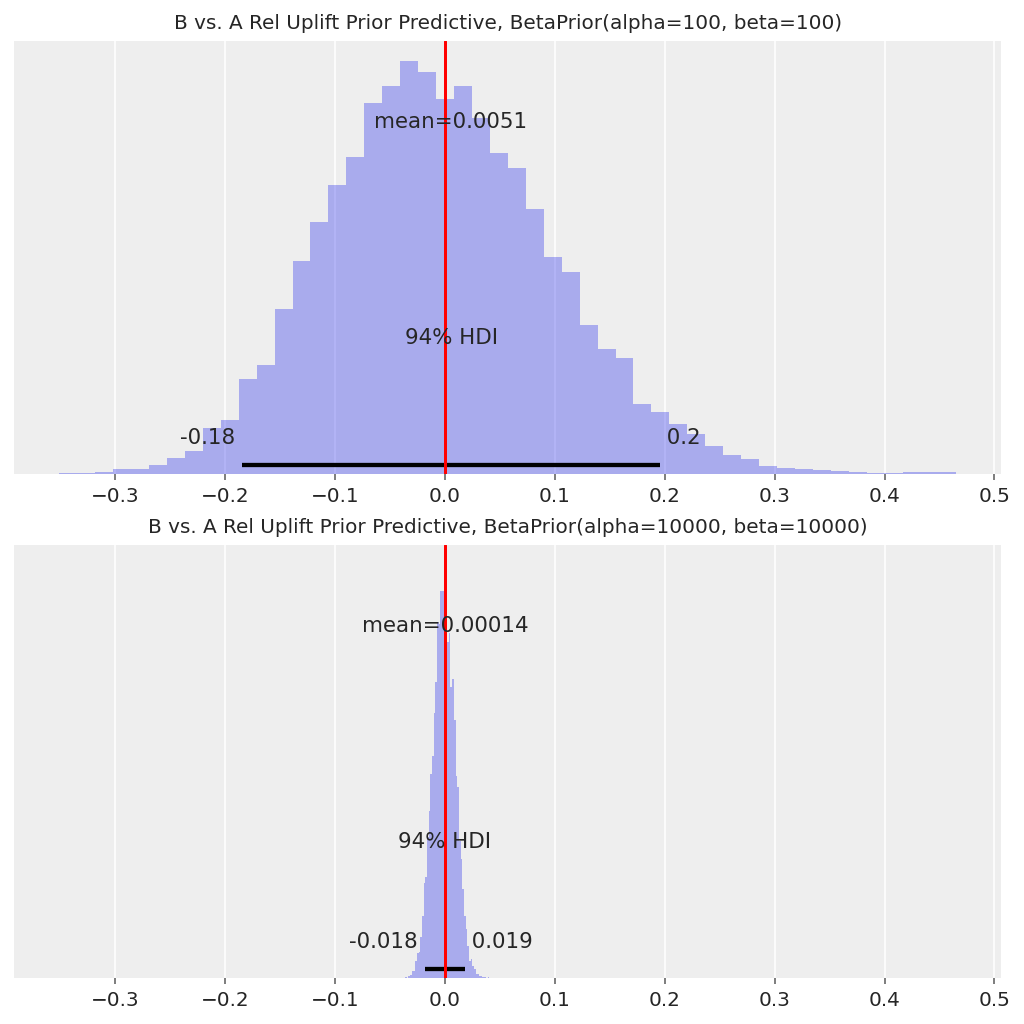
使用弱先验，我们 B 相对于 A 的相对提升的 94% HDI 大约为 [-20%, +20%]，而使用强先验，则大约为 [-2%, +2%]。这实际上是相对提升分布的“起点”，并将影响观察到的转化如何转化为后验分布。

我们在实践中如何选择这些先验取决于运行 A/B 测试的公司的更广泛背景。强先验可以帮助防范虚假发现，但可能需要更多数据来检测获胜变体（如果存在），而更多数据 = 需要更多时间运行测试。弱先验更重视观察到的数据，但也可能由于提前停止问题而导致更多虚假发现。

下面我们将逐步介绍两种不同先验选择的推断结果。

数据

我们生成两个数据集：一个数据集在其中每个变体的“真实”转化率相同，另一个数据集在其中变体 B 具有更高的真实转化率。

def generate_binomial_data(
    variants: List[str], true_rates: List[str], samples_per_variant: int = 100000
) -> pd.DataFrame:
    data = {}
    for variant, p in zip(variants, true_rates):
        data[variant] = bernoulli.rvs(p, size=samples_per_variant)
    agg = (
        pd.DataFrame(data)
        .aggregate(["count", "sum"])
        .rename(index={"count": "trials", "sum": "successes"})
    )
    return agg

# Example generated data
generate_binomial_data(["A", "B"], [0.23, 0.23])

	A	B
试验次数	100000	100000
成功次数	22979	22970

我们还将编写一个函数来包装数据生成、抽样和后验图，以便我们可以轻松比较两种情况（相同真实率与不同真实率）下两种模型（强先验和弱先验）的结果。

def run_scenario_twovariant(
    variants: List[str],
    true_rates: List[float],
    samples_per_variant: int,
    weak_prior: BetaPrior,
    strong_prior: BetaPrior,
) -> None:
    generated = generate_binomial_data(variants, true_rates, samples_per_variant)
    data = [BinomialData(**generated[v].to_dict()) for v in variants]
    with ConversionModelTwoVariant(priors=weak_prior).create_model(data):
        trace_weak = pm.sample(draws=5000)
    with ConversionModelTwoVariant(priors=strong_prior).create_model(data):
        trace_strong = pm.sample(draws=5000)

    true_rel_uplift = true_rates[1] / true_rates[0] - 1

    fig, axs = plt.subplots(2, 1, figsize=(7, 7), sharex=True)
    az.plot_posterior(trace_weak.posterior["reluplift_b"], ax=axs[0], **plotting_defaults)
    axs[0].set_title(f"True Rel Uplift = {true_rel_uplift:.1%}, {weak_prior}", fontsize=10)
    axs[0].axvline(x=0, color="red")
    az.plot_posterior(trace_strong.posterior["reluplift_b"], ax=axs[1], **plotting_defaults)
    axs[1].set_title(f"True Rel Uplift = {true_rel_uplift:.1%}, {strong_prior}", fontsize=10)
    axs[1].axvline(x=0, color="red")
    fig.suptitle("B vs. A Rel Uplift")
    return trace_weak, trace_strong

情景 1 - 相同的潜在转化率

trace_weak, trace_strong = run_scenario_twovariant(
    variants=["A", "B"],
    true_rates=[0.23, 0.23],
    samples_per_variant=100000,
    weak_prior=BetaPrior(alpha=100, beta=100),
    strong_prior=BetaPrior(alpha=10000, beta=10000),
)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [p]

100.00% [24000/24000 00:09<00:00 抽样 4 条链，0 次发散]

Sampling 4 chains for 1_000 tune and 5_000 draw iterations (4_000 + 20_000 draws total) took 21 seconds.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [p]

100.00% [24000/24000 00:09<00:00 抽样 4 条链，0 次发散]

Sampling 4 chains for 1_000 tune and 5_000 draw iterations (4_000 + 20_000 draws total) took 20 seconds.

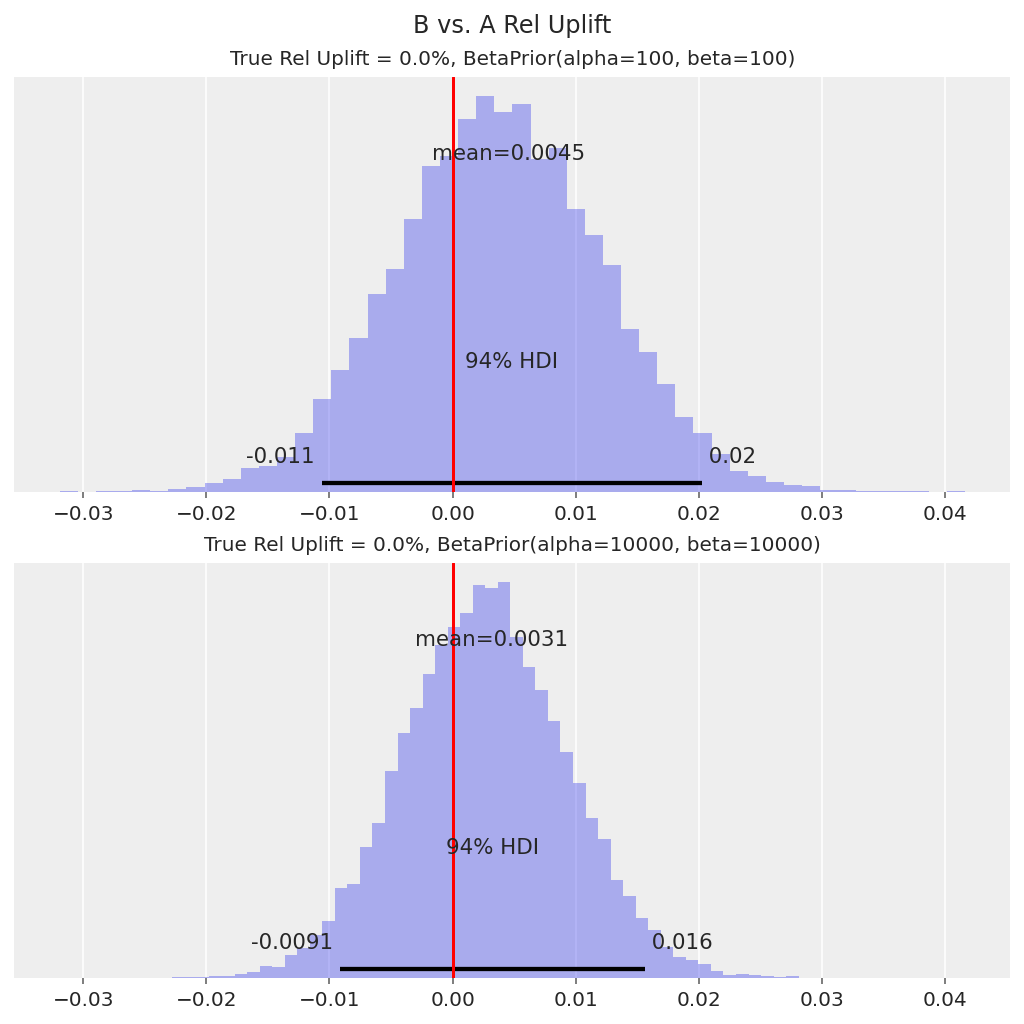
• 在这两种情况下，真实提升 0% 都位于 94% HDI 范围内。

• 然后，我们可以使用此相对提升分布来决定是否将变体 B 中的新着陆页/功能应用为默认设置。例如，我们可以决定，如果 94% HDI 高于 0，我们将推出变体 B。在这种情况下，0 在 HDI 中，因此决定是不推出变体 B。

情景 2 - 不同的潜在转化率

run_scenario_twovariant(
    variants=["A", "B"],
    true_rates=[0.21, 0.23],
    samples_per_variant=100000,
    weak_prior=BetaPrior(alpha=100, beta=100),
    strong_prior=BetaPrior(alpha=10000, beta=10000),
)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [p]

100.00% [24000/24000 00:09<00:00 抽样 4 条链，0 次发散]

Sampling 4 chains for 1_000 tune and 5_000 draw iterations (4_000 + 20_000 draws total) took 21 seconds.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [p]

100.00% [24000/24000 00:09<00:00 抽样 4 条链，0 次发散]

Sampling 4 chains for 1_000 tune and 5_000 draw iterations (4_000 + 20_000 draws total) took 20 seconds.

(Inference data with groups:
 	> posterior
 	> log_likelihood
 	> sample_stats
 	> observed_data,
 Inference data with groups:
 	> posterior
 	> log_likelihood
 	> sample_stats
 	> observed_data)

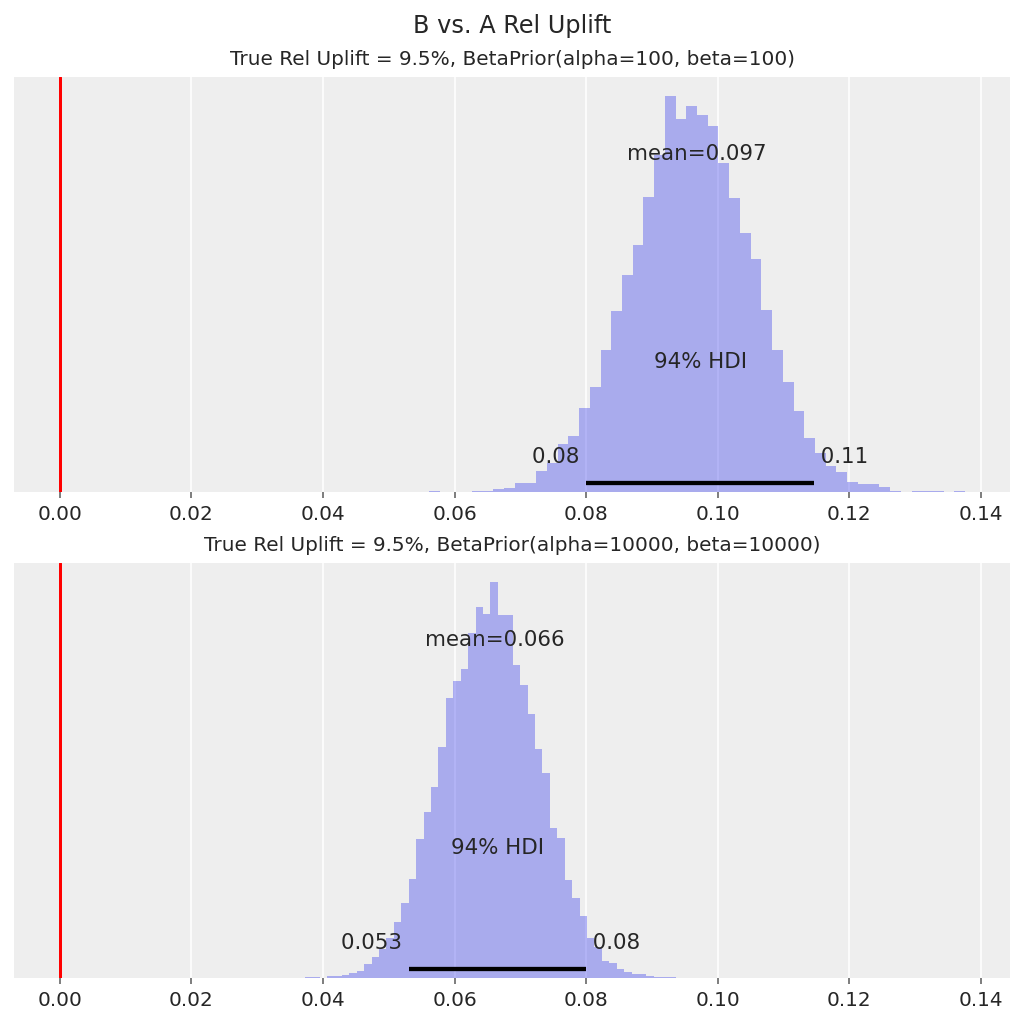
• 在这两种情况下，后验相对提升分布都表明 B 比 A 具有更高的转化率，因为 94% HDI 远高于 0。在这种情况下，决定是将变体 B 推广给所有用户，这种结果称为“真实发现”。

• 也就是说，在实践中，我们通常也对变体 B 好多少感兴趣。对于具有强先验的模型，先验有效地将相对提升分布拉近 0，因此我们对相对提升的中心估计是保守的（即低估的）。我们需要更多数据才能使我们的推断更接近 9.5% 的真实相对提升。

以上示例演示了如何使用简单的 Beta-二项式模型执行双变体测试的 A/B 测试分析，以及选择弱先验与强先验的优点和缺点。在下一节中，我们将提供处理多变体（“A/B/n”）测试的指南。

推广到多变体测试

在本节中，为了简单起见，我们将继续使用伯努利转化和 Beta-二项式模型。重点是如何分析具有 3 个或更多变体的测试 - 例如，我们不仅有一个不同的着陆页要测试，而且有多个我们想要一次测试的想法。我们如何判断它们中是否存在获胜者？

这里我们可以采取两种主要方法

1. 将 A 作为“对照组”。将其他变体（B、C 等）与 A 一一比较。

2. 对于每个变体，与其他变体的 max() 进行比较。

方法 1 对大多数人来说很直观，并且很容易解释。但是，如果有两个变体都优于对照组，并且我们想知道哪个更好怎么办？我们无法通过单独的提升分布进行推断。方法 2 确实处理了这种情况 - 它有效地尝试找出所有变体中是否存在明显的赢家或明显的输家。

我们将在下面实现两种方法的模型设置，清理我们之前的代码，使其推广到 n 变体情况。请注意，我们也可以将此模型重新用于 2 变体情况。

class ConversionModel:
    def __init__(self, priors: BetaPrior):
        self.priors = priors

    def create_model(self, data: List[BinomialData], comparison_method) -> pm.Model:
        num_variants = len(data)
        trials = [d.trials for d in data]
        successes = [d.successes for d in data]
        with pm.Model() as model:
            p = pm.Beta("p", alpha=self.priors.alpha, beta=self.priors.beta, shape=num_variants)
            y = pm.Binomial("y", n=trials, p=p, observed=successes, shape=num_variants)
            reluplift = []
            for i in range(num_variants):
                if comparison_method == "compare_to_control":
                    comparison = p[0]
                elif comparison_method == "best_of_rest":
                    others = [p[j] for j in range(num_variants) if j != i]
                    if len(others) > 1:
                        comparison = pm.math.maximum(*others)
                    else:
                        comparison = others[0]
                else:
                    raise ValueError(f"comparison method {comparison_method} not recognised.")
                reluplift.append(pm.Deterministic(f"reluplift_{i}", p[i] / comparison - 1))
        return model

def run_scenario_bernoulli(
    variants: List[str],
    true_rates: List[float],
    samples_per_variant: int,
    priors: BetaPrior,
    comparison_method: str,
) -> az.InferenceData:
    generated = generate_binomial_data(variants, true_rates, samples_per_variant)
    data = [BinomialData(**generated[v].to_dict()) for v in variants]
    with ConversionModel(priors).create_model(data=data, comparison_method=comparison_method):
        trace = pm.sample(draws=5000)

    n_plots = len(variants)
    fig, axs = plt.subplots(nrows=n_plots, ncols=1, figsize=(3 * n_plots, 7), sharex=True)
    for i, variant in enumerate(variants):
        if i == 0 and comparison_method == "compare_to_control":
            axs[i].set_yticks([])
        else:
            az.plot_posterior(trace.posterior[f"reluplift_{i}"], ax=axs[i], **plotting_defaults)
        axs[i].set_title(f"Rel Uplift {variant}, True Rate = {true_rates[i]:.2%}", fontsize=10)
        axs[i].axvline(x=0, color="red")
    fig.suptitle(f"Method {comparison_method}, {priors}")

    return trace

我们生成数据，其中变体 B 和 C 远高于 A，但彼此非常接近

_ = run_scenario_bernoulli(
    variants=["A", "B", "C"],
    true_rates=[0.21, 0.23, 0.228],
    samples_per_variant=100000,
    priors=BetaPrior(alpha=5000, beta=5000),
    comparison_method="compare_to_control",
)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [p]

100.00% [24000/24000 00:09<00:00 抽样 4 条链，0 次发散]

Sampling 4 chains for 1_000 tune and 5_000 draw iterations (4_000 + 20_000 draws total) took 22 seconds.

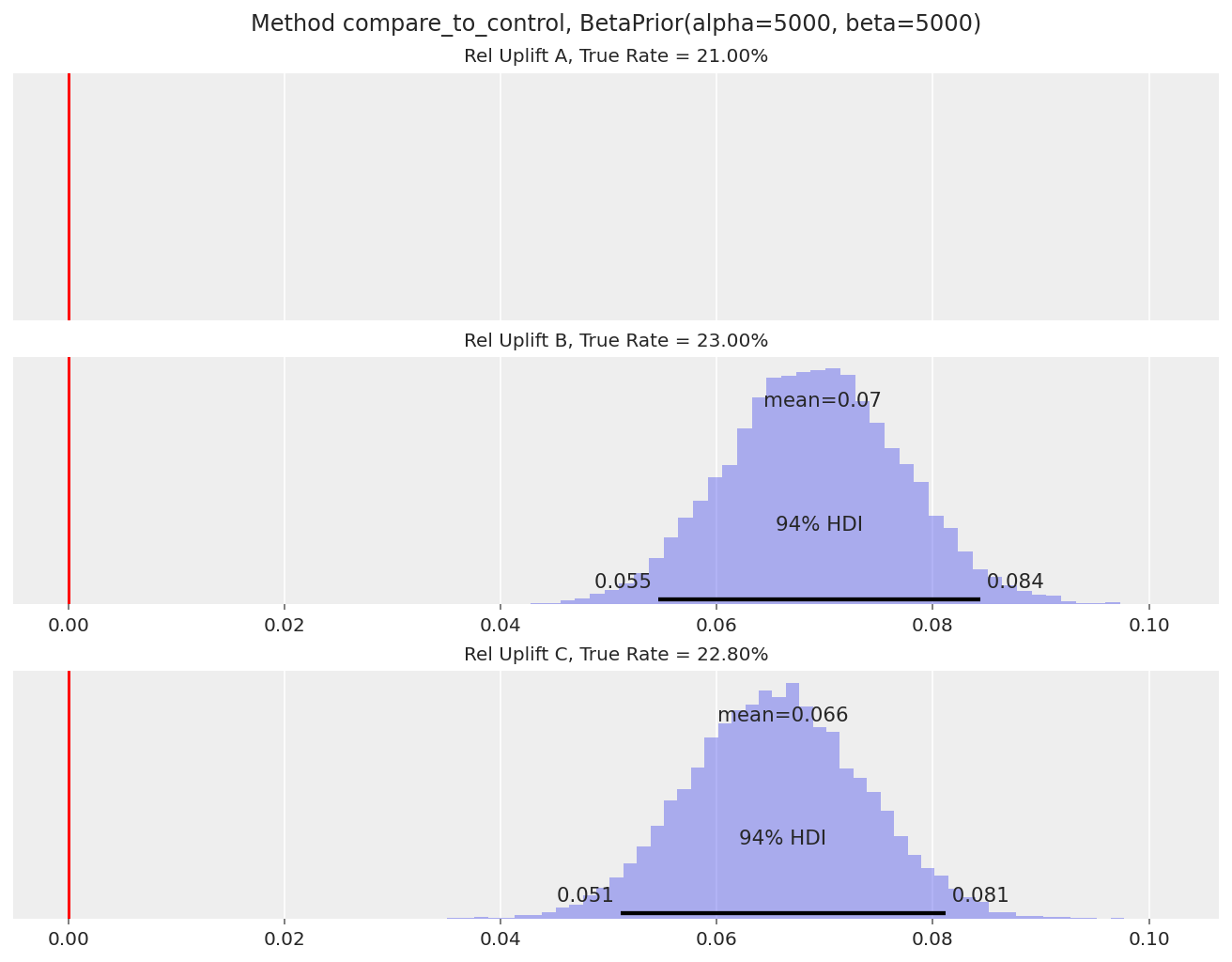
• B 和 C 的相对提升后验都表明它们明显优于 A（94% HDI 远高于 0），相对提升大约为 7-8%。

• 但是，我们无法推断 B 和 C 之间是否存在赢家。

_ = run_scenario_bernoulli(
    variants=["A", "B", "C"],
    true_rates=[0.21, 0.23, 0.228],
    samples_per_variant=100000,
    priors=BetaPrior(alpha=5000, beta=5000),
    comparison_method="best_of_rest",
)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [p]

100.00% [24000/24000 00:10<00:00 抽样 4 条链，0 次发散]

Sampling 4 chains for 1_000 tune and 5_000 draw iterations (4_000 + 20_000 draws total) took 22 seconds.

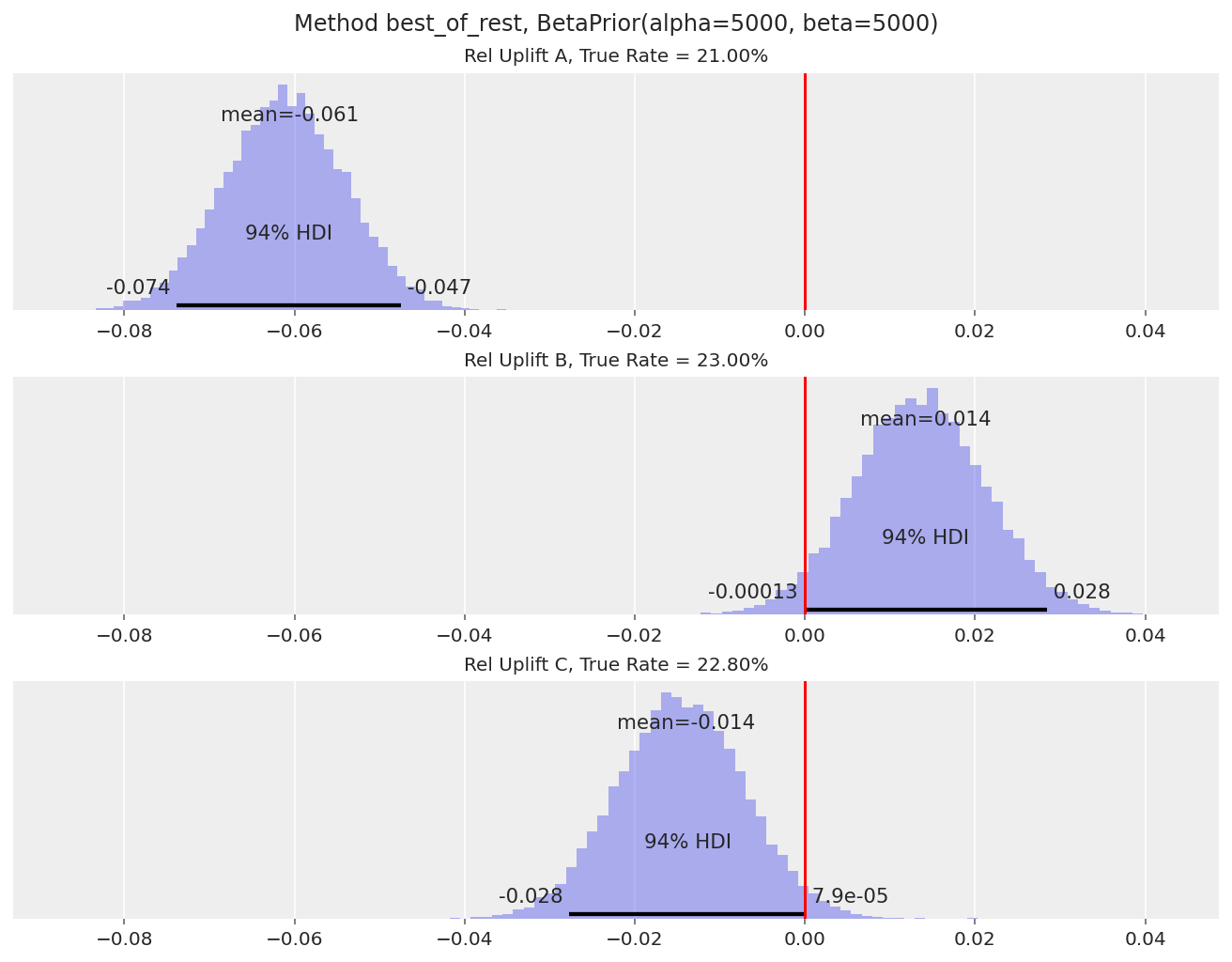
• A 的提升图告诉我们，与变体 B 和 C 相比，它显然是失败者（A 的相对提升的 94% HDI 远低于 0）。

• 请注意，B 和 C 的相对提升计算有效地忽略了变体 A。这是因为，例如，当我们计算 B 的 reluplift 时，其他变体的最大值很可能是变体 C。类似地，当我们计算 C 的 reluplift 时，它很可能与 B 进行比较。

• B 和 C 的提升图告诉我们，我们还不能确定这两个变体之间是否存在明显的赢家，因为 94% HDI 仍然与 0 重叠。我们需要更大的样本量才能检测到 23% 与 22.8% 的转化率差异。

• 这种方法的一个缺点是我们无法直接说明这些变体相对于变体 A（对照组）的提升是多少。这个数字在实践中通常很重要，因为它使我们能够估计如果将 A/B 测试更改推广到所有访问者，总体影响是什么。但是，我们可以通过将问题重新定义为“与其他两个变体相比，A 差多少”（这在变体 A 的相对提升分布中显示）来近似获得此数字。

价值转化

现在，如果我们想在变体产生的收入方面比较 A/B 测试变体，和/或估计获胜变体带来多少额外收入，该怎么办？我们不能为此使用 Beta-二项式模型，因为现在每个访问者的可能值都在 [0, Inf) 范围内。VWO 论文中提出的模型如下

单个访问者产生的收入为 收入 = 付费概率 * 付费时的平均花费金额

\[\mathrm{Revenue}_i = \mathrm{Bernoulli}(\theta)_i * \mathrm{Exponential}(\lambda)_i I(\mathrm{Bernoulli}(\theta)_i = 1)\]

我们假设付费概率与付费时的平均花费金额无关。这是一个实践中的典型假设，除非我们有理由相信这两个参数具有依赖性。有了这个，我们可以为付费的访问者总数和购买访问者中花费的总金额创建单独的模型（假设每个访问者的行为之间是独立的）

\[c \sim \sum^N\mathrm{Bernoulli}(\theta) = \mathrm{Binomial}(N, \theta)\]

\[r \sim \sum^K\mathrm{Exponential}(\lambda) = \mathrm{Gamma}(K, \lambda)\]

其中 \(N\) 是访问者总数，\(K\) 是至少购买一次的访问者总数。

我们可以重用之前的 Beta-二项式模型来对伯努利转化进行建模。对于平均购买金额，我们使用 Gamma 先验（这也是 Gamma 似然的共轭先验）。因此，在双变体测试中，设置如下

\[\theta_A \sim \theta_B \sim \mathrm{Beta}(\alpha_1, \beta_1)\]

\[\lambda_A \sim \lambda_B \sim \mathrm{Gamma}(\alpha_2, \beta_2)\]

\[c_A \sim \mathrm{Binomial}(N_A, \theta_A), c_B \sim \mathrm{Binomial}(N_B, \theta_B)\]

\[r_A \sim \mathrm{Gamma}(c_A, \lambda_A), r_B \sim \mathrm{Gamma}(c_B, \lambda_B)\]

\[\mu_A = \theta_A * \dfrac{1}{\lambda_A}, \mu_B = \theta_B * \dfrac{1}{\lambda_B}\]

\[\mathrm{reluplift}_B = \mu_B / \mu_A - 1\]

\(\mu\) 这里表示每个访问者的平均收入，包括那些未进行购买的访问者。这是捕获总体收入影响的最佳方法 - 某些变体可能会提高平均销售价值，但会降低付费访问者的比例（例如，如果我们在着陆页上推广更昂贵的商品）。

下面我们将模型设置放入代码中并执行先验预测检查。

@dataclass
class GammaPrior:
    alpha: float
    beta: float

@dataclass
class RevenueData:
    visitors: int
    purchased: int
    total_revenue: float

class RevenueModel:
    def __init__(self, conversion_rate_prior: BetaPrior, mean_purchase_prior: GammaPrior):
        self.conversion_rate_prior = conversion_rate_prior
        self.mean_purchase_prior = mean_purchase_prior

    def create_model(self, data: List[RevenueData], comparison_method: str) -> pm.Model:
        num_variants = len(data)
        visitors = [d.visitors for d in data]
        purchased = [d.purchased for d in data]
        total_revenue = [d.total_revenue for d in data]

        with pm.Model() as model:
            theta = pm.Beta(
                "theta",
                alpha=self.conversion_rate_prior.alpha,
                beta=self.conversion_rate_prior.beta,
                shape=num_variants,
            )
            lam = pm.Gamma(
                "lam",
                alpha=self.mean_purchase_prior.alpha,
                beta=self.mean_purchase_prior.beta,
                shape=num_variants,
            )
            converted = pm.Binomial(
                "converted", n=visitors, p=theta, observed=purchased, shape=num_variants
            )
            revenue = pm.Gamma(
                "revenue", alpha=purchased, beta=lam, observed=total_revenue, shape=num_variants
            )
            revenue_per_visitor = pm.Deterministic("revenue_per_visitor", theta * (1 / lam))
            theta_reluplift = []
            reciprocal_lam_reluplift = []
            reluplift = []
            for i in range(num_variants):
                if comparison_method == "compare_to_control":
                    comparison_theta = theta[0]
                    comparison_lam = 1 / lam[0]
                    comparison_rpv = revenue_per_visitor[0]
                elif comparison_method == "best_of_rest":
                    others_theta = [theta[j] for j in range(num_variants) if j != i]
                    others_lam = [1 / lam[j] for j in range(num_variants) if j != i]
                    others_rpv = [revenue_per_visitor[j] for j in range(num_variants) if j != i]
                    if len(others_rpv) > 1:
                        comparison_theta = pm.math.maximum(*others_theta)
                        comparison_lam = pm.math.maximum(*others_lam)
                        comparison_rpv = pm.math.maximum(*others_rpv)
                    else:
                        comparison_theta = others_theta[0]
                        comparison_lam = others_lam[0]
                        comparison_rpv = others_rpv[0]
                else:
                    raise ValueError(f"comparison method {comparison_method} not recognised.")
                theta_reluplift.append(
                    pm.Deterministic(f"theta_reluplift_{i}", theta[i] / comparison_theta - 1)
                )
                reciprocal_lam_reluplift.append(
                    pm.Deterministic(
                        f"reciprocal_lam_reluplift_{i}", (1 / lam[i]) / comparison_lam - 1
                    )
                )
                reluplift.append(
                    pm.Deterministic(f"reluplift_{i}", revenue_per_visitor[i] / comparison_rpv - 1)
                )
        return model

对于 Beta 先验，我们可以设置与之前类似的先验 - 以 0.5 为中心，alpha 和 beta 的大小决定分布的“薄厚”。

我们需要更加注意 Gamma 先验。Gamma 先验的均值为 \(\dfrac{\alpha_G}{\beta_G}\)，并且需要设置为给定现有平均购买值的合理值。例如，如果 alpha 和 beta 的设置使得均值为 1 美元，但网站的每个访问者的平均收入要高得多，为 100 美元，则这可能会影响我们的推断。

c_prior = BetaPrior(alpha=5000, beta=5000)
mp_prior = GammaPrior(alpha=9000, beta=900)

data = [
    RevenueData(visitors=1, purchased=1, total_revenue=1),
    RevenueData(visitors=1, purchased=1, total_revenue=1),
]

with RevenueModel(c_prior, mp_prior).create_model(data, "best_of_rest"):
    revenue_prior_predictive = pm.sample_prior_predictive(samples=10000, return_inferencedata=False)

fig, ax = plt.subplots()
az.plot_posterior(revenue_prior_predictive["reluplift_1"], ax=ax, **plotting_defaults)
ax.set_title(f"Revenue Rel Uplift Prior Predictive, {c_prior}, {mp_prior}", fontsize=10)
ax.axvline(x=0, color="red");

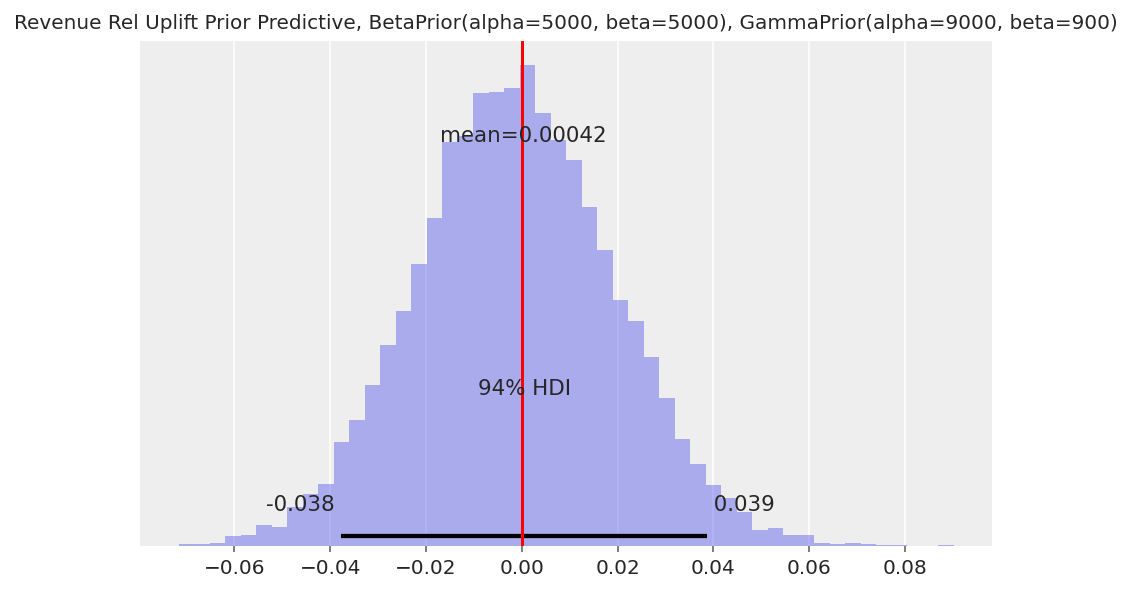
与伯努利转化的模型类似，先验预测提升分布的宽度将取决于我们先验的强度。有关使用弱先验与强先验的优点和缺点的讨论，请参阅伯努利转化部分。

接下来，我们为模型生成合成数据。我们将生成以下情景

• 相同的购买倾向和相同的平均购买价值。

• 较低的购买倾向和较高的平均购买价值，但每个访问者的总体收入相同。

• 较高的购买倾向和较高的平均购买价值，以及每个访问者的总体收入较高。

def generate_revenue_data(
    variants: List[str],
    true_conversion_rates: List[float],
    true_mean_purchase: List[float],
    samples_per_variant: int,
) -> pd.DataFrame:
    converted = {}
    mean_purchase = {}
    for variant, p, mp in zip(variants, true_conversion_rates, true_mean_purchase):
        converted[variant] = bernoulli.rvs(p, size=samples_per_variant)
        mean_purchase[variant] = expon.rvs(scale=mp, size=samples_per_variant)
    converted = pd.DataFrame(converted)
    mean_purchase = pd.DataFrame(mean_purchase)
    revenue = converted * mean_purchase
    agg = pd.concat(
        [
            converted.aggregate(["count", "sum"]).rename(
                index={"count": "visitors", "sum": "purchased"}
            ),
            revenue.aggregate(["sum"]).rename(index={"sum": "total_revenue"}),
        ]
    )
    return agg

def run_scenario_value(
    variants: List[str],
    true_conversion_rates: List[float],
    true_mean_purchase: List[float],
    samples_per_variant: int,
    conversion_rate_prior: BetaPrior,
    mean_purchase_prior: GammaPrior,
    comparison_method: str,
) -> az.InferenceData:
    generated = generate_revenue_data(
        variants, true_conversion_rates, true_mean_purchase, samples_per_variant
    )
    data = [RevenueData(**generated[v].to_dict()) for v in variants]
    with RevenueModel(conversion_rate_prior, mean_purchase_prior).create_model(
        data, comparison_method
    ):
        trace = pm.sample(draws=5000, chains=2, cores=1)

    n_plots = len(variants)
    fig, axs = plt.subplots(nrows=n_plots, ncols=1, figsize=(3 * n_plots, 7), sharex=True)
    for i, variant in enumerate(variants):
        if i == 0 and comparison_method == "compare_to_control":
            axs[i].set_yticks([])
        else:
            az.plot_posterior(trace.posterior[f"reluplift_{i}"], ax=axs[i], **plotting_defaults)
        true_rpv = true_conversion_rates[i] * true_mean_purchase[i]
        axs[i].set_title(f"Rel Uplift {variant}, True RPV = {true_rpv:.2f}", fontsize=10)
        axs[i].axvline(x=0, color="red")
    fig.suptitle(f"Method {comparison_method}, {conversion_rate_prior}, {mean_purchase_prior}")

    return trace

情景 1 - 相同的潜在购买率和平均购买价值

_ = run_scenario_value(
    variants=["A", "B"],
    true_conversion_rates=[0.1, 0.1],
    true_mean_purchase=[10, 10],
    samples_per_variant=100000,
    conversion_rate_prior=BetaPrior(alpha=5000, beta=5000),
    mean_purchase_prior=GammaPrior(alpha=9000, beta=900),
    comparison_method="best_of_rest",
)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Sequential sampling (2 chains in 1 job)
NUTS: [theta, lam]

100.00% [6000/6000 00:14<00:00 链 0 抽样，0 次发散]

100.00% [6000/6000 00:13<00:00 链 1 抽样，0 次发散]

Sampling 2 chains for 1_000 tune and 5_000 draw iterations (2_000 + 10_000 draws total) took 28 seconds.

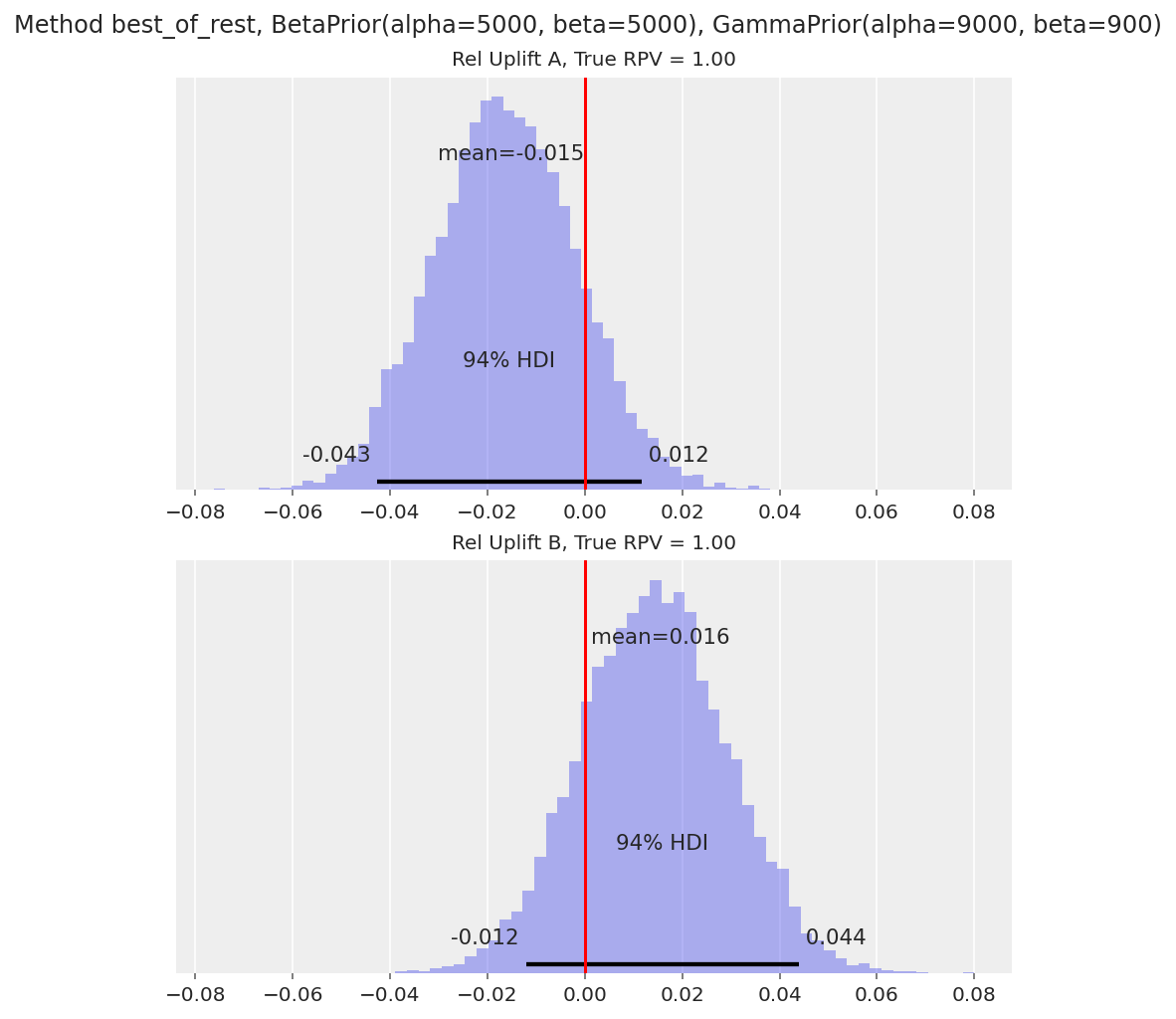
• 94% HDI 包含预期的 0。

情景 2 - 较低的购买率、较高的平均购买额、相同的每个访问者的总体收入

scenario_value_2 = run_scenario_value(
    variants=["A", "B"],
    true_conversion_rates=[0.1, 0.08],
    true_mean_purchase=[10, 12.5],
    samples_per_variant=100000,
    conversion_rate_prior=BetaPrior(alpha=5000, beta=5000),
    mean_purchase_prior=GammaPrior(alpha=9000, beta=900),
    comparison_method="best_of_rest",
)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Sequential sampling (2 chains in 1 job)
NUTS: [theta, lam]

100.00% [6000/6000 00:13<00:00 链 0 抽样，0 次发散]

100.00% [6000/6000 00:14<00:00 链 1 抽样，0 次发散]

Sampling 2 chains for 1_000 tune and 5_000 draw iterations (2_000 + 10_000 draws total) took 28 seconds.

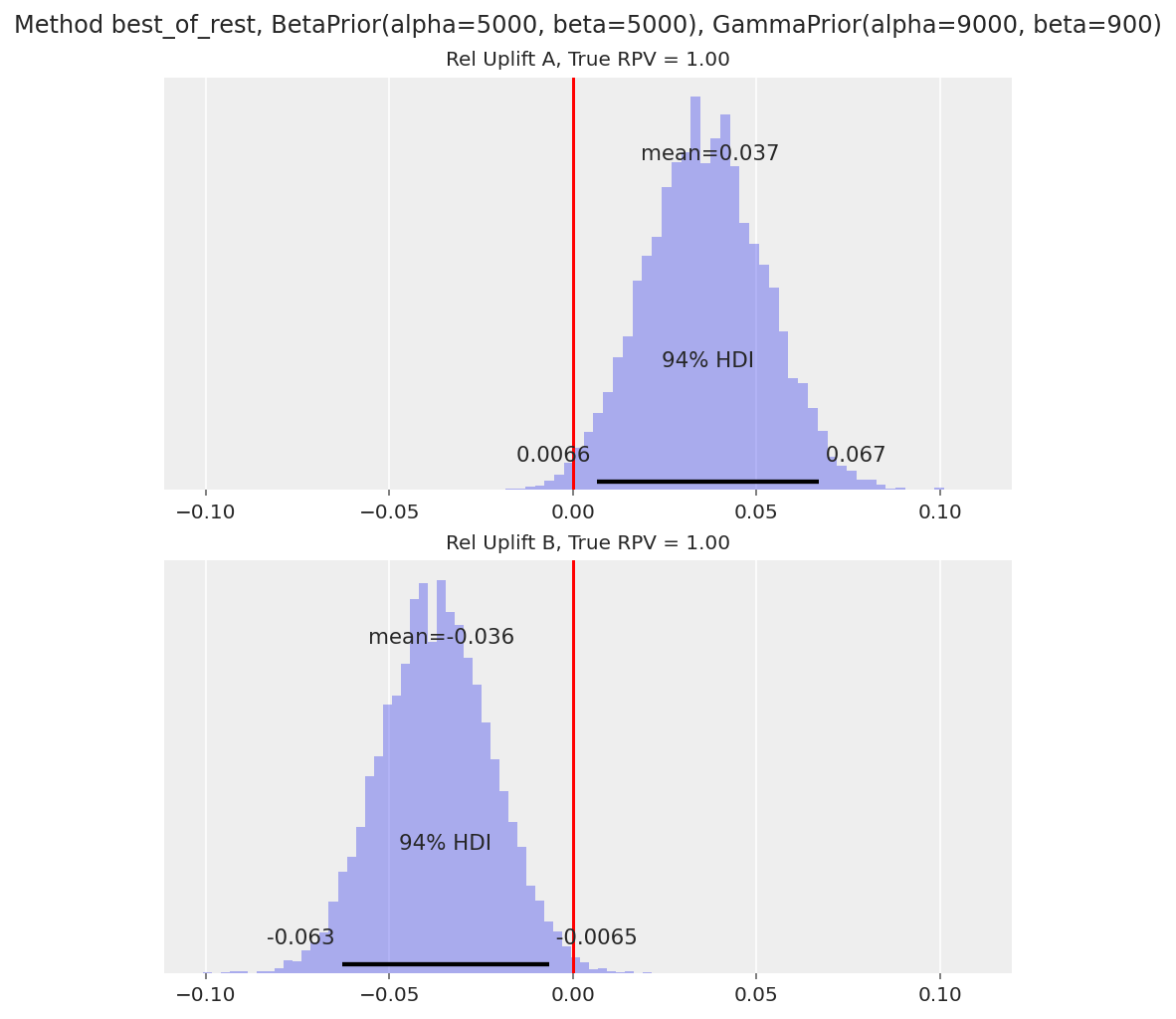
• 每个访问者平均收入 (RPV) 的 94% HDI 包含预期的 0。

• 在这些情况下，绘制 theta（购买任何东西的概率）和 1 / lam（平均购买价值）的相对提升分布也很有用，以了解 A/B 测试如何影响访问者行为。我们在下面展示这一点

axs = az.plot_posterior(
    scenario_value_2,
    var_names=["theta_reluplift_1", "reciprocal_lam_reluplift_1"],
    **plotting_defaults,
)
axs[0].set_title(f"Conversion Rate Uplift B, True Uplift = {(0.04 / 0.05 - 1):.2%}", fontsize=10)
axs[0].axvline(x=0, color="red")
axs[1].set_title(
    f"Revenue per Converting Visitor Uplift B, True Uplift = {(25 / 20 - 1):.2%}", fontsize=10
)
axs[1].axvline(x=0, color="red");

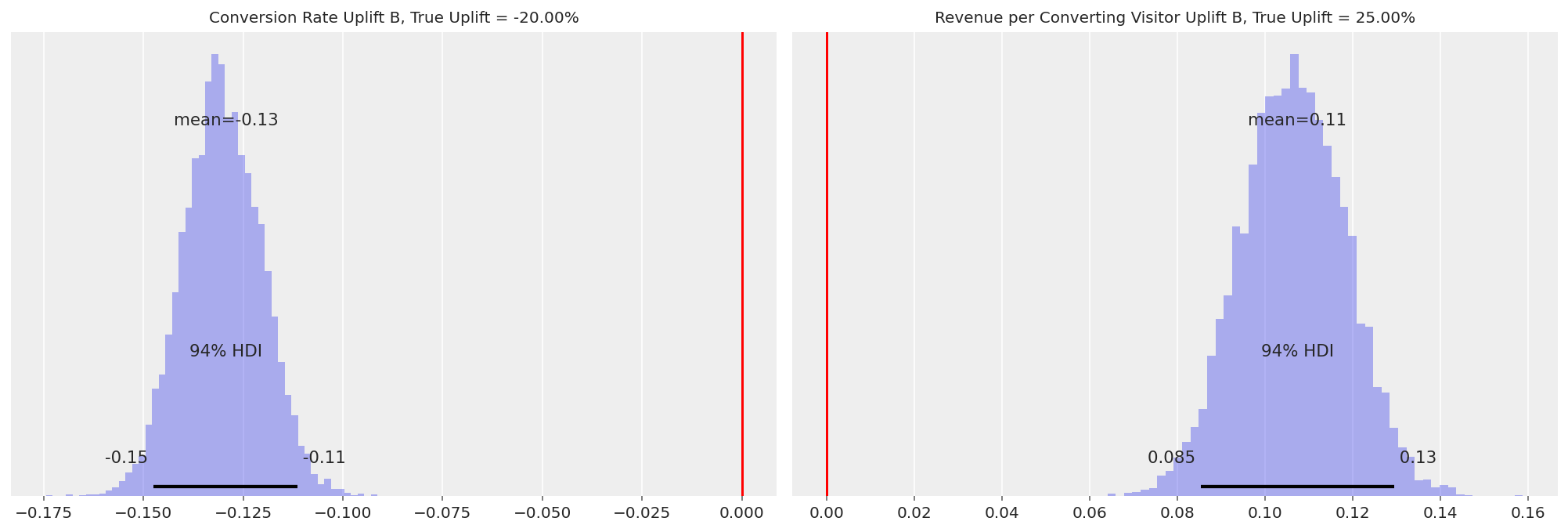
• 变体 B 的转化率提升的 HDI 远低于 0，而每个转化访问者的收入的 HDI 远高于 0。因此，该模型能够捕获购买访问者的减少以及平均购买金额的增加。

情景 3 - 更高的购买倾向和平均购买价值

_ = run_scenario_value(
    variants=["A", "B"],
    true_conversion_rates=[0.1, 0.11],
    true_mean_purchase=[10, 10.5],
    samples_per_variant=100000,
    conversion_rate_prior=BetaPrior(alpha=5000, beta=5000),
    mean_purchase_prior=GammaPrior(alpha=9000, beta=900),
    comparison_method="best_of_rest",
)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Sequential sampling (2 chains in 1 job)
NUTS: [theta, lam]

100.00% [6000/6000 00:15<00:00 链 0 抽样，0 次发散]

100.00% [6000/6000 00:13<00:00 链 1 抽样，0 次发散]

Sampling 2 chains for 1_000 tune and 5_000 draw iterations (2_000 + 10_000 draws total) took 30 seconds.

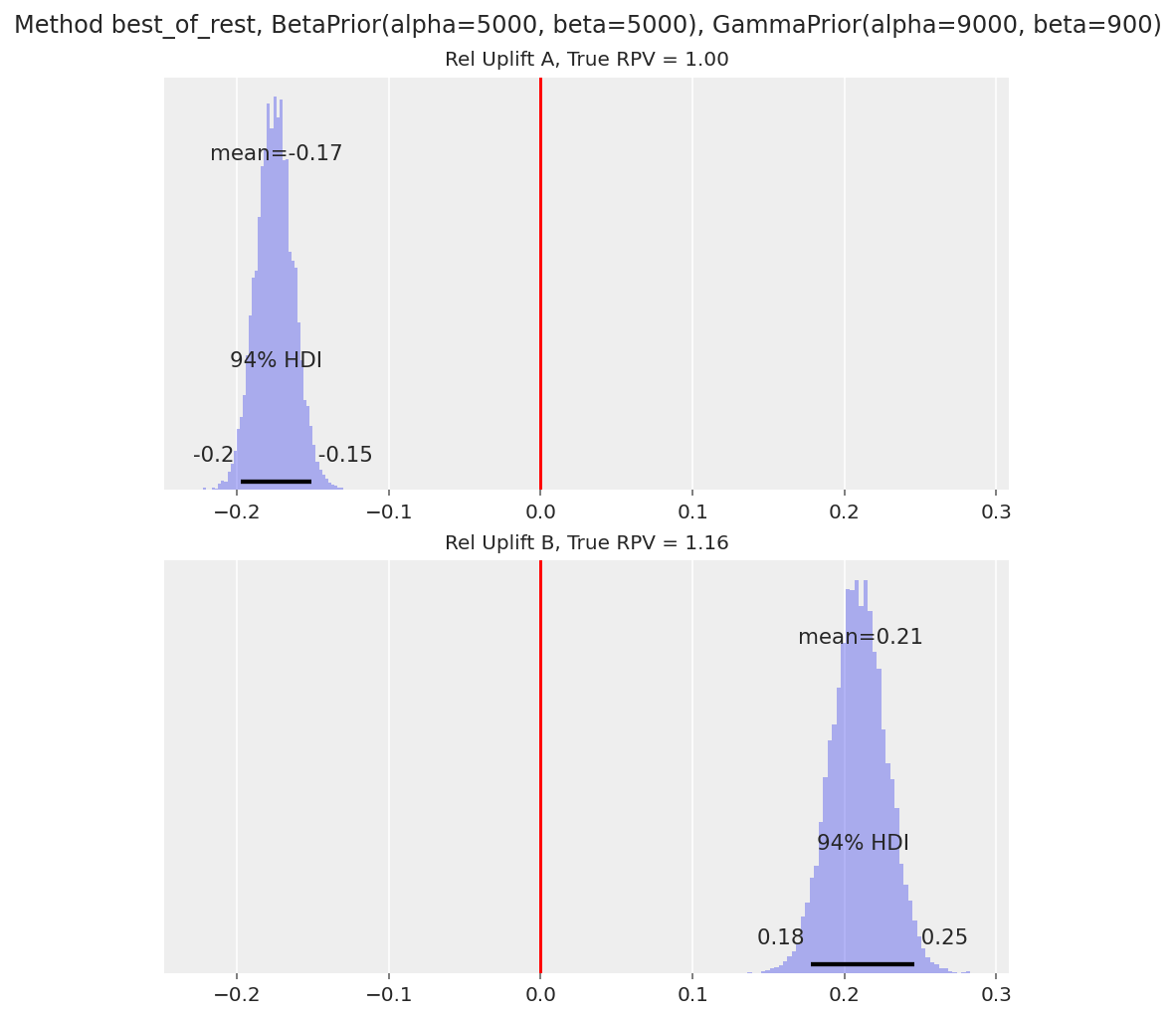
• 变体 B 的 94% HDI 高于预期值 0。

请注意，在实践中使用价值转化时的一个担忧（在我们仅模拟合成数据时不会出现）是异常值的存在。例如，一个变体中的访问者可能花费数千美元，并且观察到的收入数据不再遵循像 Gamma 这样的“好”分布。通常在运行统计分析之前估算这些异常值（我们必须小心完全删除它们，因为这可能会使推断产生偏差），或者退回到伯努利转化以进行决策。

延伸阅读

在实践中实施贝叶斯框架来分析 A/B 测试还有许多其他注意事项。其中包括

• 我们如何选择先验分布？

• 在实践中，人们每天都会查看 A/B 测试结果，而不仅仅是在测试结束时查看一次。我们如何在更快地发现真实差异与最大限度地减少虚假发现（“提前停止”问题）之间取得平衡？

• 如果我们使用贝叶斯模型来分析结果，我们如何使用功效分析来计划 A/B 测试的长度和规模？

• 除了转化率（每个访问者的伯努利随机变量）之外，在线软件中的许多价值分布都无法用正态分布、Gamma 分布等“好”密度来拟合。我们如何对这些进行建模？

各种教科书和在线资源更详细地深入探讨了这些领域。《Doing Bayesian Data Analysis》([Kruschke, 2014]) 作者 John Kruschke 是一本很棒的资源，并且已翻译成 PyMC 此处。

我们还计划创建更多关于这些主题的 PyMC 教程，敬请期待！

作者

• 由 Cuong Duong 于 2021 年 5 月创作 (pymc-examples#164)

• 由 percevalve 于 2022 年 5 月重新执行 (pymc-examples#351)

参考文献

[1]

Chris Stucchio。贝叶斯 a/b 测试在 vwo 中的应用。2015 年。URL: https://vwo.com/downloads/VWO_SmartStats_technical_whitepaper.pdf。

[2]

John Kruschke。《Doing Bayesian data analysis: A tutorial with R, JAGS, and Stan》。Academic Press，2014 年。

水印

%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,xarray

Last updated: Thu Sep 22 2022

Python implementation: CPython
Python version       : 3.8.10
IPython version      : 8.4.0

pytensor: 2.7.3
xarray: 2022.3.0

matplotlib: 3.5.2
sys       : 3.8.10 (default, Mar 25 2022, 22:18:25) 
[Clang 12.0.5 (clang-1205.0.22.11)]
numpy     : 1.22.1
pymc      : 4.0.1
arviz     : 0.12.1
pandas    : 1.4.3

Watermark: 2.3.1

许可声明

本示例库中的所有笔记本均根据 MIT 许可证 提供，该许可证允许修改和重新分发以用于任何用途，前提是保留版权和许可声明。

引用 PyMC 示例

要引用本笔记本，请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。

重要提示

许多笔记本改编自其他来源：博客、书籍……在这种情况下，您也应该引用原始来源。

另请记住引用您的代码使用的相关库。

这是一个 bibtex 中的引用模板

@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}

渲染后可能如下所示