反事实推断：计算 COVID-19 导致的超额死亡人数

因果推理和反事实思维是非常有趣但复杂的话题！尽管如此，我们可以通过相对简单的例子来深入理解这些概念。本笔记本重点介绍使用 PyMC 进行贝叶斯因果推理的概念和实际应用。

我们使用因 COVID-19 导致的超额死亡人数这一令人警醒但重要的例子来进行说明。因此，本笔记本中的思想与 Google 的 CausalImpact 高度重叠（参见 Brodersen等. [2015]）。实际上，我们将尝试使用英格兰和威尔士的数据来估计自 COVID-19 爆发以来“超额死亡”的人数。超额死亡的定义为

\[ \text{超额死亡} = \underbrace{\text{报告死亡人数}}_{\text{实际死亡人数的噪声度量}} - \underbrace{\text{预期死亡人数}}_{\text{不可测量的反事实}} \]

对超额死亡人数提出主张需要因果/反事实推理。虽然报告的死亡人数只不过是世界上真实可观察事实的（可能是嘈杂和/或滞后的）度量，但预期死亡人数是不可测量的，因为这些死亡人数永远不会在我们的时间线中实现。也就是说，预期死亡人数是一个反事实的思想实验，我们可以在其中问“如果……会发生什么？”

总体策略

我们实际上该如何进行呢？我们将遵循以下策略

1. 导入关于各种原因导致的报告死亡人数（我们的结果变量）以及一些合理的预测变量的数据

   • 月平均温度

   • 年份中的月份，我们用它来模拟季节性影响

   • 以及时间，用于模拟任何潜在的线性趋势。

2. 拆分为 pre 和 post covid 数据集。这是一个重要的步骤。我们希望根据我们在 COVID-19 之前所了解的内容来建立模型，以便我们可以根据 COVID-19 产生任何影响之前的数据来构建我们的反事实预测。

3. 基于 pre 数据集估计模型参数。

4. 回溯预测 模型在 COVID-19 之前的时期预期的死亡人数。这不是反事实，但可以告诉我们模型在解释已观察到的数据方面的能力。

5. 反事实推断 - 我们使用我们的模型来构建反事实预测。如果没有 COVID-19，我们预计未来会看到什么？这可以通过著名的 do-算子 来实现。实际上，我们通过对样本外数据进行后验预测来实现这一点。

6. 通过将报告的死亡人数与我们的反事实（预期死亡人数）进行比较来计算超额死亡人数。

建模策略

我们可以采用许多不同的方法进行建模。因为我们处理的是时间序列数据，那么使用时间序列建模方法将非常明智。例如，Google 的 CausalImpact 使用 贝叶斯结构时间序列 模型，但我们可以选择许多其他时间序列模型。

但由于本案例研究的重点是反事实推理，而不是时间序列建模的具体细节，我选择了更简单的时间序列模型线性回归方法（有关更多信息，请参见 Martin 等. [2021]）。

因果推断免责声明

读者应该意识到，我们在此处可以提出的因果主张当然是有限制的。如果我们处理的是营销示例，我们在一段时间内进行了促销活动，并希望推断超额销售额，那么只有当我们尽职尽责地考虑了在促销期间可能发生的其他因素时，我们才能提出强有力的因果主张。

同样，自 2020 年 1 月以来，英国也发生了 许多其他变化（有据可查的首批 COVID-19 病例时间）在英格兰和威尔士。因此，如果我们想做到非常可靠，那么我们应该考虑其他可能相关的因素。

最后，我们不是声称有 \(x\) 人直接死于 COVID-19 病毒。超额死亡概念的美妙之处在于，它涵盖了所有原因导致的死亡人数，这些死亡人数超过了我们的预期。因此，它不仅涵盖了直接死于 COVID-19 病毒的人，还涵盖了病毒和医疗可及性的所有下游影响，例如。

import calendar
import os

import arviz as az
import matplotlib.dates as mdates
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pytensor.tensor as pt
import seaborn as sns
import xarray as xr

%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")

现在让我们定义一些辅助函数

显示代码单元格内容 隐藏代码单元格内容

def ZeroSumNormal(name, *, sigma=None, active_dims=None, dims, model=None):
    model = pm.modelcontext(model=model)

    if isinstance(dims, str):
        dims = [dims]

    if isinstance(active_dims, str):
        active_dims = [active_dims]

    if active_dims is None:
        active_dims = dims[-1]

    def extend_axis(value, axis):
        n_out = value.shape[axis] + 1
        sum_vals = value.sum(axis, keepdims=True)
        norm = sum_vals / (pt.sqrt(n_out) + n_out)
        fill_val = norm - sum_vals / pt.sqrt(n_out)
        out = pt.concatenate([value, fill_val], axis=axis)
        return out - norm

    dims_reduced = []
    active_axes = []
    for i, dim in enumerate(dims):
        if dim in active_dims:
            active_axes.append(i)
            dim_name = f"{dim}_reduced"
            if name not in model.coords:
                model.add_coord(dim_name, length=len(model.coords[dim]) - 1, mutable=False)
            dims_reduced.append(dim_name)
        else:
            dims_reduced.append(dim)

    raw = pm.Normal(f"{name}_raw", sigma=sigma, dims=dims_reduced)
    for axis in active_axes:
        raw = extend_axis(raw, axis)
    return pm.Deterministic(name, raw, dims=dims)


def format_x_axis(ax, minor=False):
    # major ticks
    ax.xaxis.set_major_formatter(mdates.DateFormatter("%Y %b"))
    ax.xaxis.set_major_locator(mdates.YearLocator())
    ax.grid(which="major", linestyle="-", axis="x")
    # minor ticks
    if minor:
        ax.xaxis.set_minor_formatter(mdates.DateFormatter("%Y %b"))
        ax.xaxis.set_minor_locator(mdates.MonthLocator())
        ax.grid(which="minor", linestyle=":", axis="x")
    # rotate labels
    for label in ax.get_xticklabels(which="both"):
        label.set(rotation=70, horizontalalignment="right")


def plot_xY(x, Y, ax):
    quantiles = Y.quantile((0.025, 0.25, 0.5, 0.75, 0.975), dim=("chain", "draw")).transpose()

    az.plot_hdi(
        x,
        hdi_data=quantiles.sel(quantile=[0.025, 0.975]),
        fill_kwargs={"alpha": 0.25},
        smooth=False,
        ax=ax,
    )
    az.plot_hdi(
        x,
        hdi_data=quantiles.sel(quantile=[0.25, 0.75]),
        fill_kwargs={"alpha": 0.5},
        smooth=False,
        ax=ax,
    )
    ax.plot(x, quantiles.sel(quantile=0.5), color="C1", lw=3)


# default figure sizes
figsize = (10, 5)

# create a list of month strings, for plotting purposes
month_strings = calendar.month_name[1:]

导入数据

为了我们的目的，我们将获取英格兰和威尔士报告的死亡人数（每月）。此数据可从国家统计局数据集 英格兰和威尔士每月登记的死亡人数 中获得。我手动下载了 2006-2022 年的此数据，并将其汇总到一个 .csv 文件中。我还添加了英国月平均温度数据作为预测变量，该数据从 英国气象局的英国平均温度 数据集中获得。

try:
    df = pd.read_csv(os.path.join("..", "data", "deaths_and_temps_england_wales.csv"))
except FileNotFoundError:
    df = pd.read_csv(pm.get_data("deaths_and_temps_england_wales.csv"))

df["date"] = pd.to_datetime(df["date"])
df = df.set_index("date")

# split into separate dataframes for pre and post onset of COVID-19
pre = df[df.index < "2020"]
post = df[df.index >= "2020"]

可视化数据

报告的死亡人数随时间变化

绘制时间序列图显示，死亡人数存在明显的季节性，我们还可以猜测，每年的平均死亡人数可能会增加。

ax = sns.lineplot(data=df, x="date", y="deaths", hue="pre")
format_x_axis(ax)

季节性

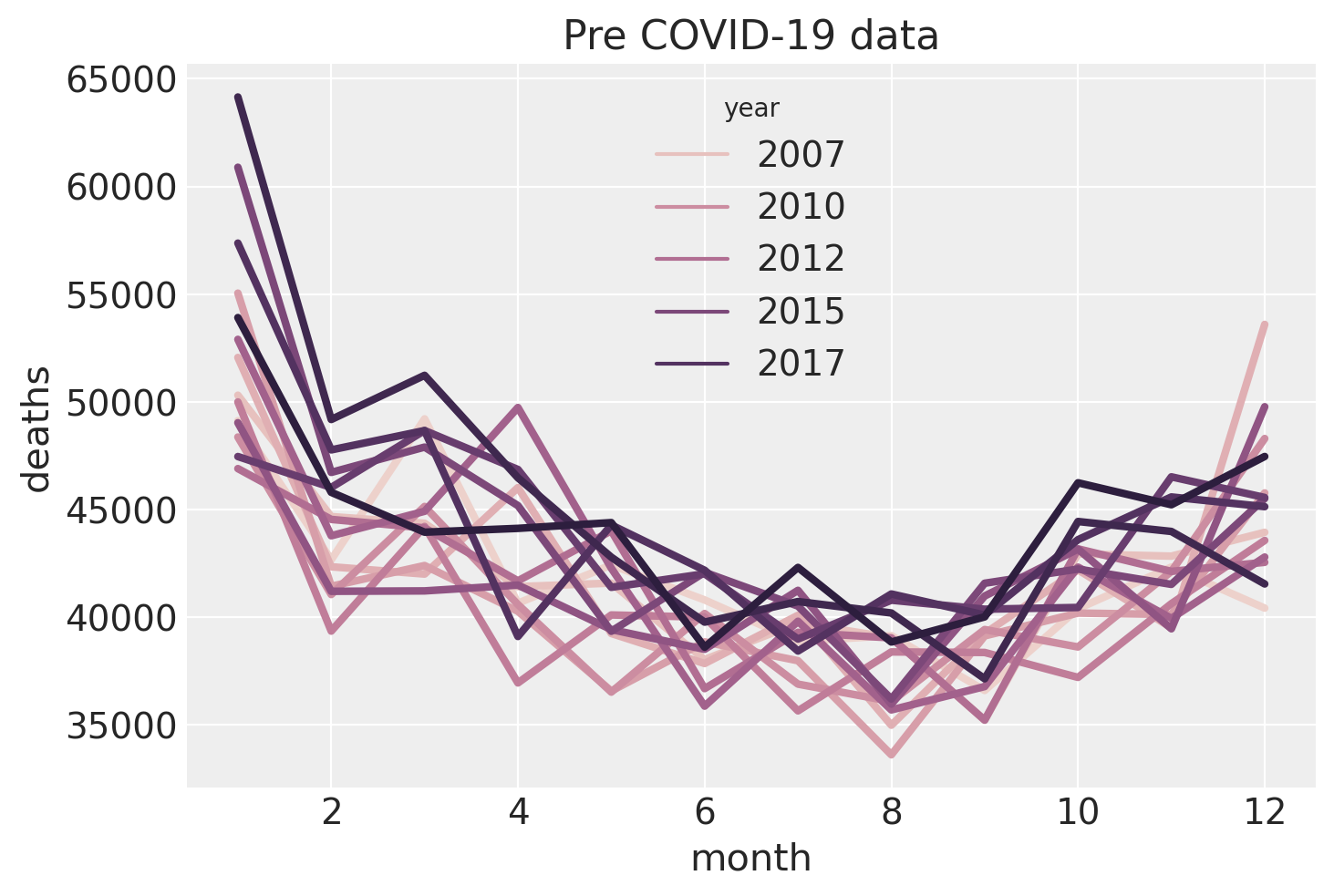
让我们更仔细地看一下季节性模式（仅限 covid 前数据），方法是绘制死亡人数随月份变化的函数图，我们将对年份进行颜色编码。这证实了我们对死亡人数季节性趋势的怀疑，冬季的死亡人数多于夏季。我们还可以看到 1 月份的死亡人数很多，其次是 2 月份略有下降，然后在 3 月份反弹。这可能是以下因素的组合造成的

• 12 月实际发生的死亡人数 push-back 到 1 月份登记

• 或 pull-forward，许多本应在 2 月份死亡的弱势群体最终在 1 月份死亡，这可能是由于寒冷的天气条件。

颜色编码支持了我们对年份存在积极主要影响的怀疑——即每年的基线死亡人数正在增加。

ax = sns.lineplot(data=pre, x="month", y="deaths", hue="year", lw=3)
ax.set(title="Pre COVID-19 data");

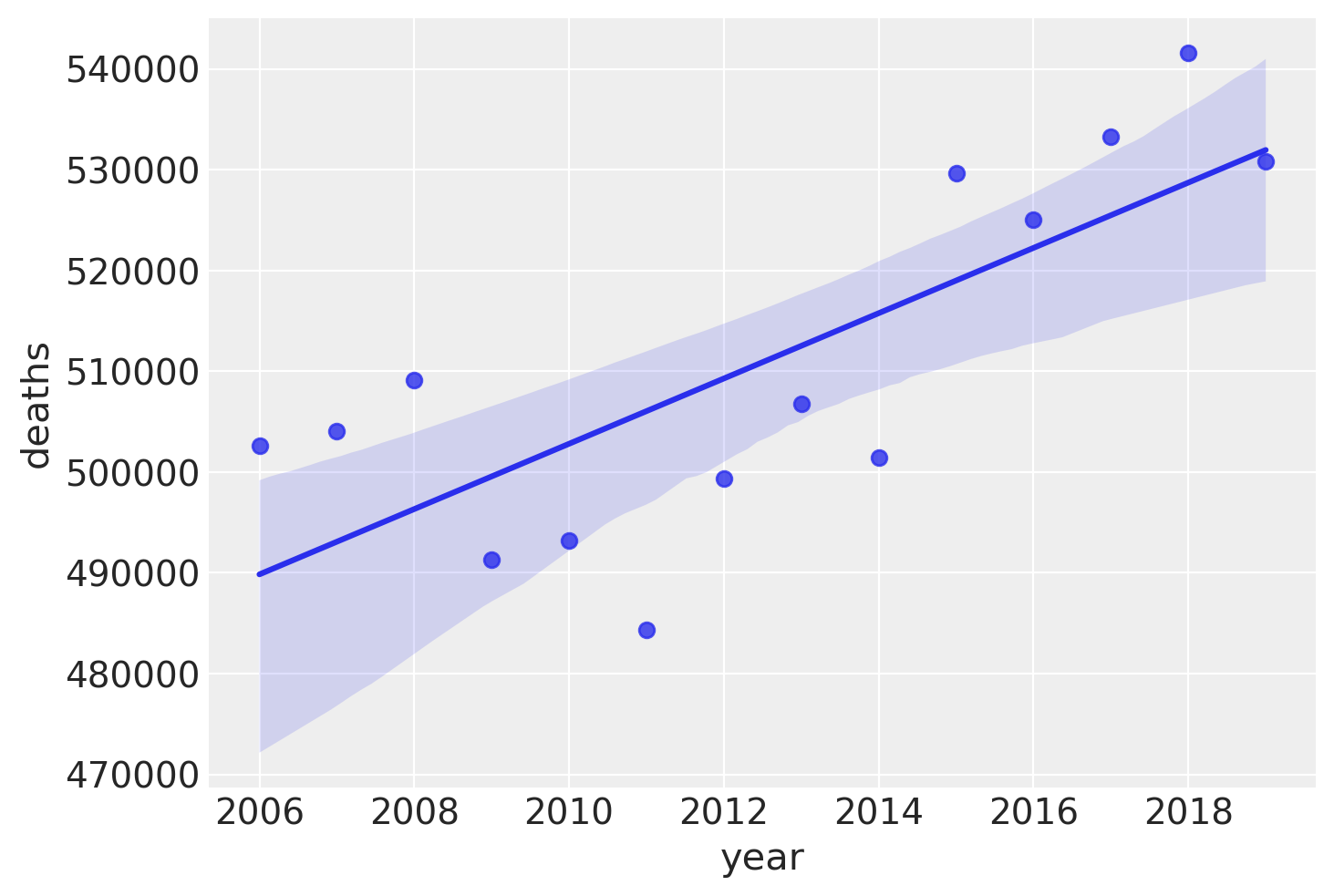
线性趋势

让我们更仔细地看一下这一点，方法是绘制 COVID-19 之前随时间变化的死亡总人数。虽然这里存在一些变异性，但似乎添加线性趋势作为预测变量将捕获报告死亡人数中的一些方差，因此可以更好地建立报告死亡人数的模型。

annual_deaths = pd.DataFrame(pre.groupby("year")["deaths"].sum()).reset_index()
sns.regplot(x="year", y="deaths", data=annual_deaths);

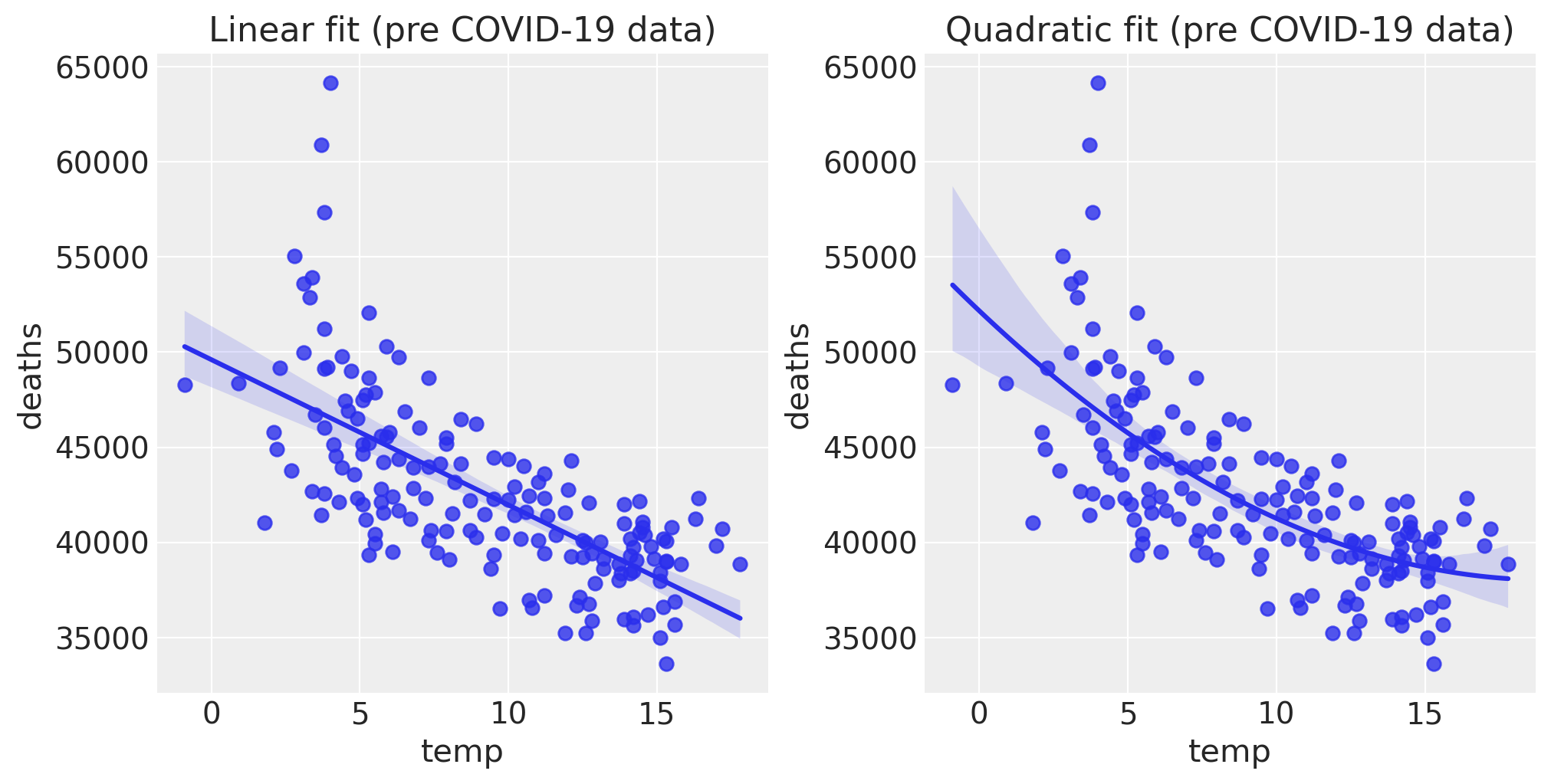
温度对死亡人数的影响

仅查看 pre 数据，月平均温度与死亡人数之间存在明显的负相关关系。在更广泛的温度范围内，很明显死亡人数与温度之间将呈 U 形关系。但在英格兰和威尔士的气候中，我们只看到了这条曲线的下侧。尽管如此，这种关系可能近似为二次关系，但就我们的目的而言，线性关系似乎是一个合理的起点。

fig, ax = plt.subplots(1, 2, figsize=figsize)
sns.regplot(x="temp", y="deaths", data=pre, scatter_kws={"s": 40}, order=1, ax=ax[0])
ax[0].set(title="Linear fit (pre COVID-19 data)")
sns.regplot(x="temp", y="deaths", data=pre, scatter_kws={"s": 40}, order=2, ax=ax[1])
ax[1].set(title="Quadratic fit (pre COVID-19 data)");

让我们检查一下这种关系的斜率，这将有助于为我们模型中的温度系数定义先验。

# NOTE: results are returned from higher to lower polynomial powers
slope, intercept = np.polyfit(pre["temp"], pre["deaths"], 1)
print(f"{slope:.0f} deaths/degree")

-764 deaths/degree

基于此，如果我们仅关注温度与死亡人数之间的关系，我们预计平均月温度每升高 \(1^\circ C\)，死亡人数将减少 764 人。因此，在为温度效应系数定义先验时，我们可以使用此数字。

建模

我们将使用截距、线性趋势、季节性偏差（每个月）和平均月温度来估计随时间变化的报告死亡人数。因此，这是一个非常简单的线性模型。唯一值得注意的是，我们转换了正态分布的月度偏差，使其均值为零，以将模型的自由度减少一个，这应该有助于参数的可识别性。

with pm.Model(coords={"month": month_strings}) as model:
    # observed predictors and outcome
    month = pm.MutableData("month", pre["month"].to_numpy(), dims="t")
    time = pm.MutableData("time", pre["t"].to_numpy(), dims="t")
    temp = pm.MutableData("temp", pre["temp"].to_numpy(), dims="t")
    deaths = pm.MutableData("deaths", pre["deaths"].to_numpy(), dims="t")

    # priors
    intercept = pm.Normal("intercept", 40_000, 10_000)
    month_mu = ZeroSumNormal("month mu", sigma=3000, dims="month")
    linear_trend = pm.TruncatedNormal("linear trend", 0, 50, lower=0)
    temp_coeff = pm.Normal("temp coeff", 0, 200)

    # the actual linear model
    mu = pm.Deterministic(
        "mu",
        intercept + (linear_trend * time) + month_mu[month - 1] + (temp_coeff * temp),
        dims="t",
    )
    sigma = pm.HalfNormal("sigma", 2_000)
    # likelihood
    pm.TruncatedNormal("obs", mu=mu, sigma=sigma, lower=0, observed=deaths, dims="t")

pm.model_to_graphviz(model)

先验预测检查

作为贝叶斯工作流程的一部分，我们将绘制先验预测，以查看模型在观察到任何数据之前找到的结果。

with model:
    idata = pm.sample_prior_predictive(random_seed=RANDOM_SEED)


fig, ax = plt.subplots(figsize=figsize)

plot_xY(pre.index, idata.prior_predictive["obs"], ax)
format_x_axis(ax)
ax.plot(pre.index, pre["deaths"], label="observed")
ax.set(title="Prior predictive distribution in the pre COVID-19 era")
plt.legend();

Sampling: [intercept, linear trend, month mu_raw, obs, sigma, temp coeff]

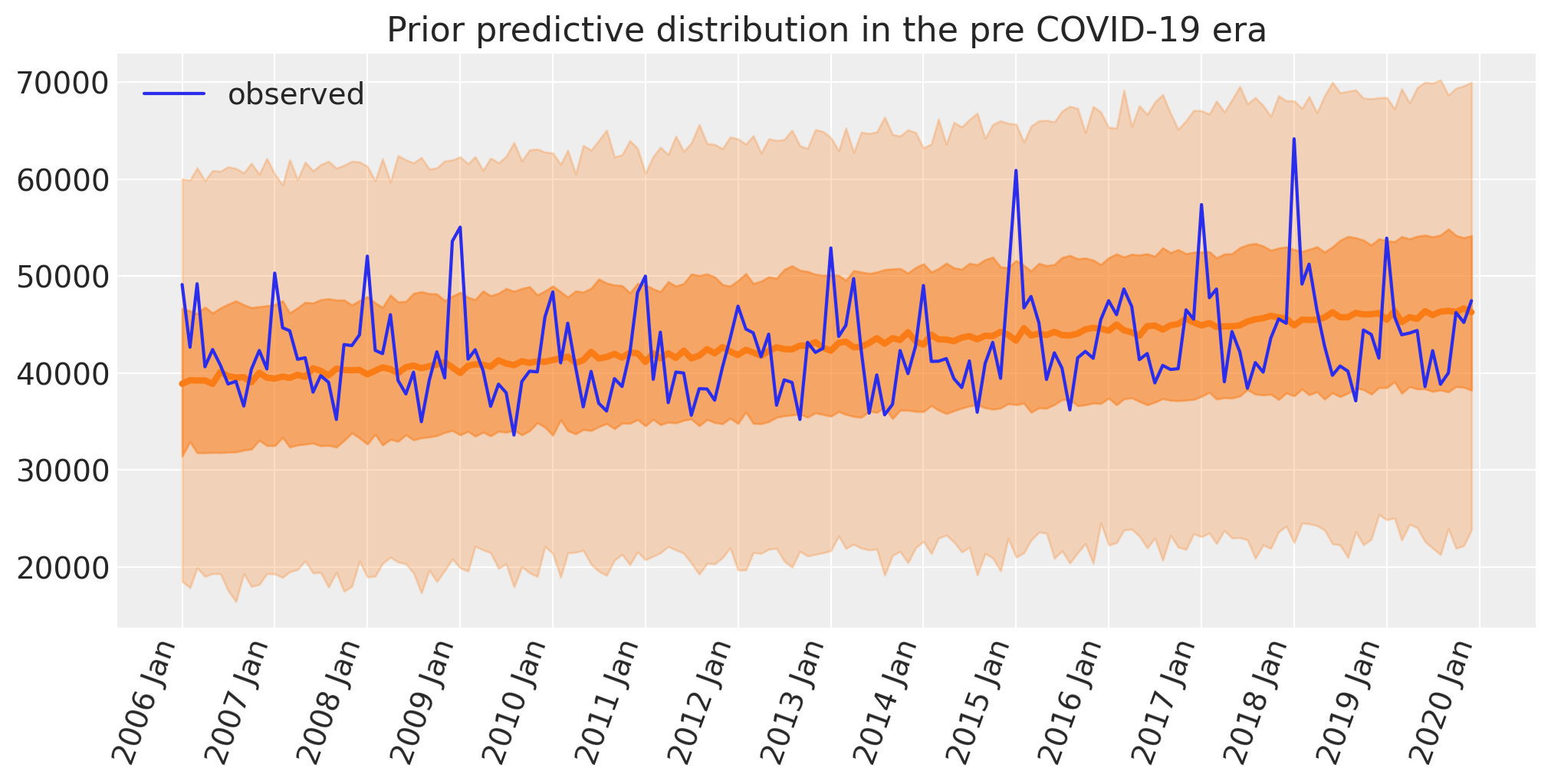
这似乎是合理的

• 先验死亡人数看起来以观察到的数字为中心。

• 鉴于先验，预测的死亡人数范围非常广，因此不太可能过度约束模型。

• 该模型不会预测每月的死亡人数为负数。

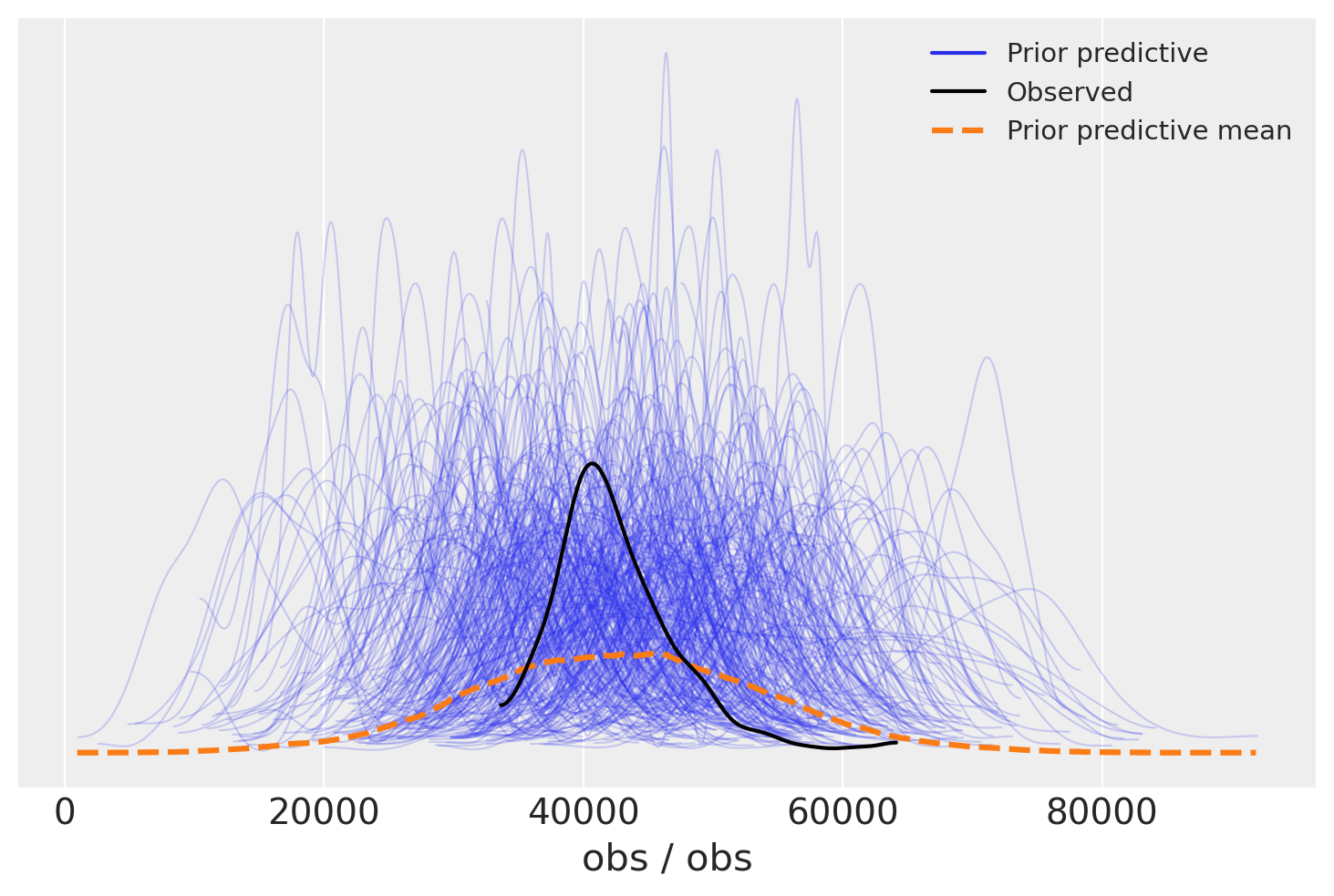
我们可以使用 Arviz 先验预测检查 (ppc) 图更详细地查看这一点。我们再次看到，观测值的分布以实际观测值为中心，但分布更广。这很有用，因为我们知道先验条件不是太严格，不太可能系统地向上或向下影响我们的后验预测。

az.plot_ppc(idata, group="prior");

推断

为后验分布抽取样本，请记住我们仅对 COVID-19 之前的数据执行此操作。

with model:
    idata.extend(pm.sample(random_seed=RANDOM_SEED))

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [intercept, month mu_raw, linear trend, temp coeff, sigma]

100.00% [8000/8000 00:06<00:00 采样 4 个链，0 个偏差]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 6 seconds.

az.plot_trace(idata, var_names=["~mu", "~month mu_raw"]);

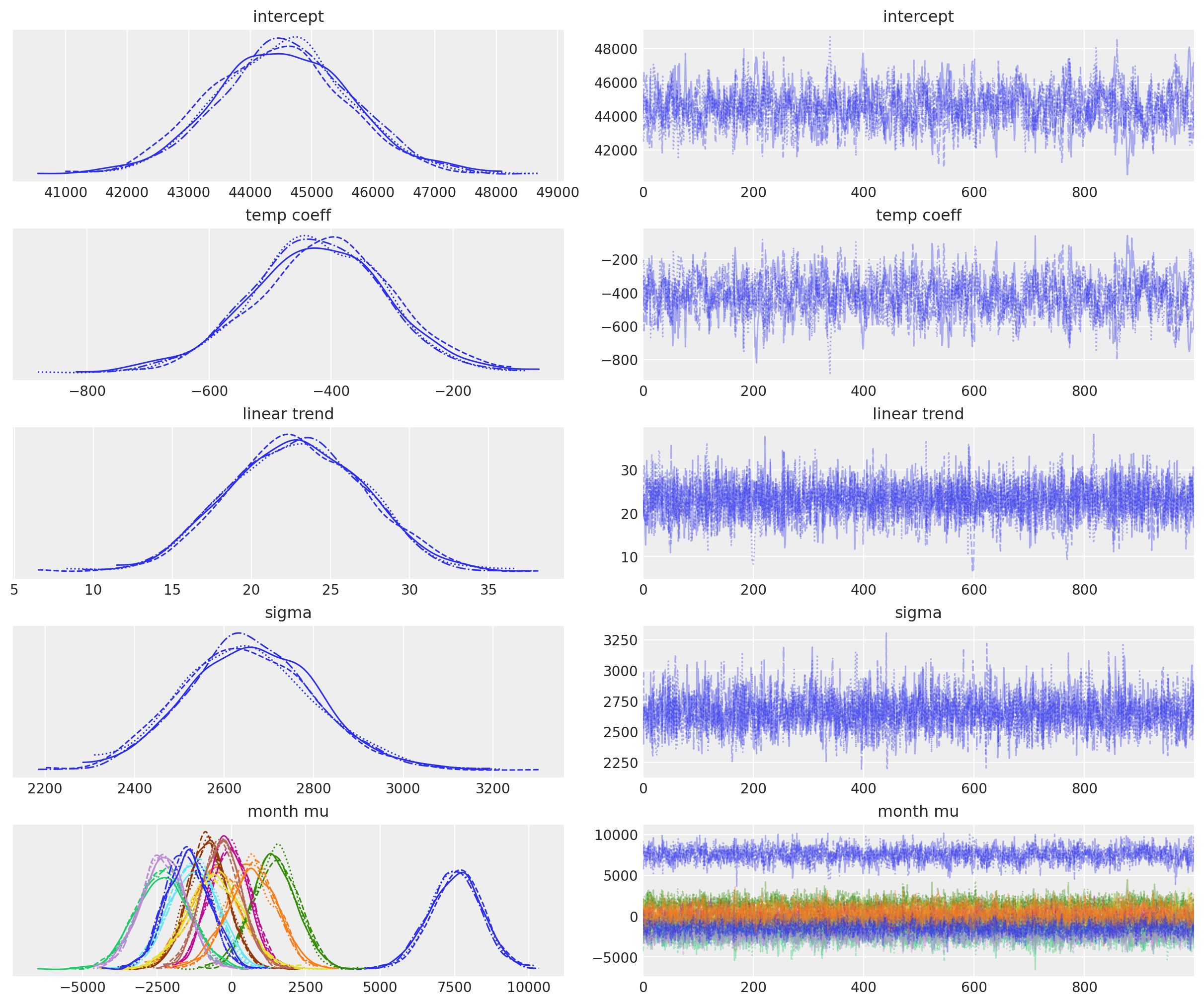
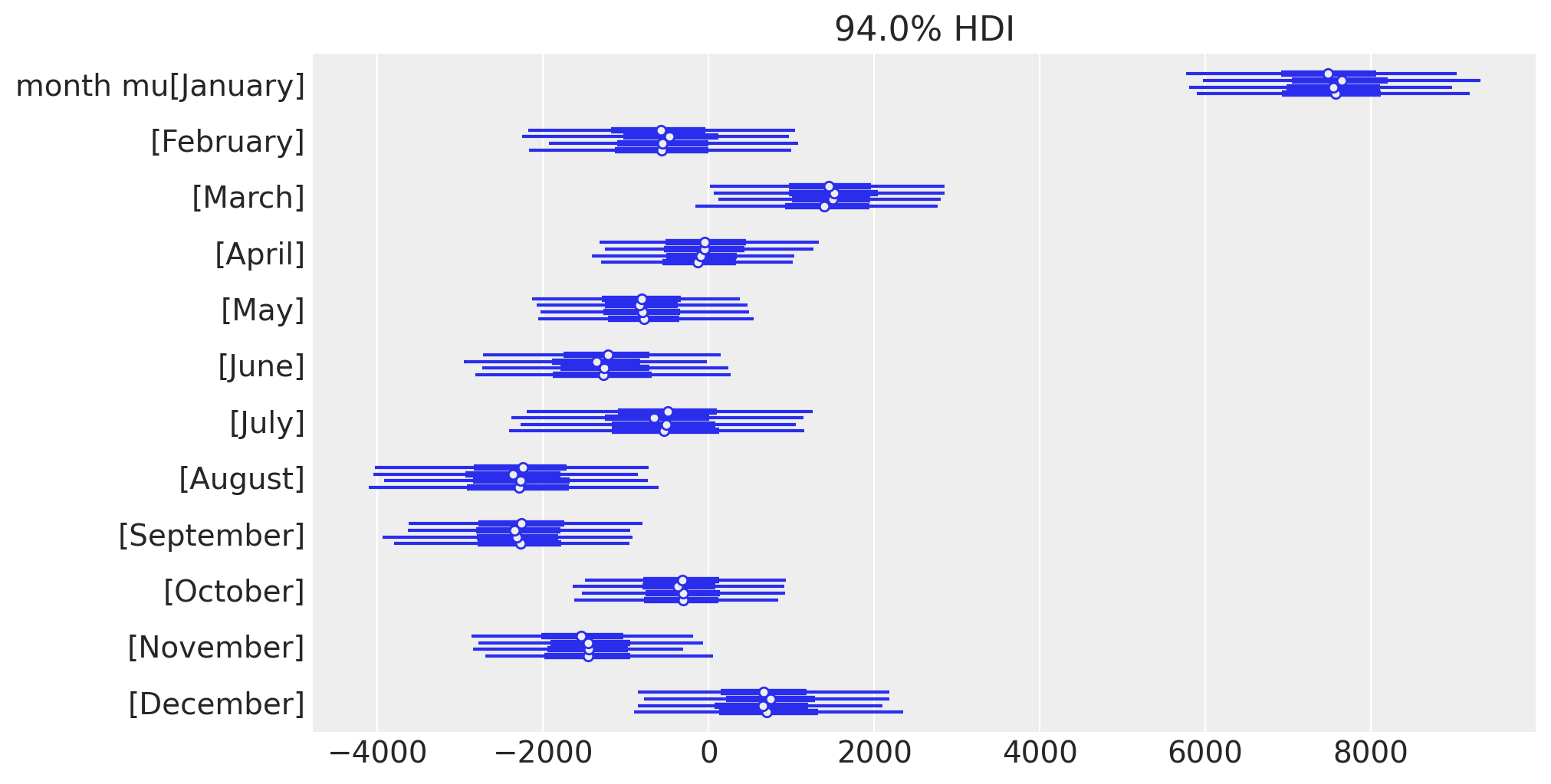
让我们也以不同的方式查看每月偏差的后验估计，以关注季节性影响。

az.plot_forest(idata.posterior, var_names="month mu", figsize=figsize);

后验预测检查

贝叶斯工作流程的另一个重要方面是绘制模型的后验预测，这使我们能够了解模型回溯预测已观察到的数据的效果如何。正是在此时，我们可以决定模型是否过于简单（那么我们将在模型中构建更多的复杂性）或者是否可以。

with model:
    idata.extend(pm.sample_posterior_predictive(idata, random_seed=RANDOM_SEED))


fig, ax = plt.subplots(figsize=figsize)

az.plot_hdi(pre.index, idata.posterior_predictive["obs"], hdi_prob=0.5, smooth=False)
az.plot_hdi(pre.index, idata.posterior_predictive["obs"], hdi_prob=0.95, smooth=False)
ax.plot(pre.index, pre["deaths"], label="observed")
format_x_axis(ax)
ax.set(title="Posterior predictive distribution in the pre COVID-19 era")
plt.legend();

Sampling: [obs]

100.00% [4000/4000 00:00<00:00]

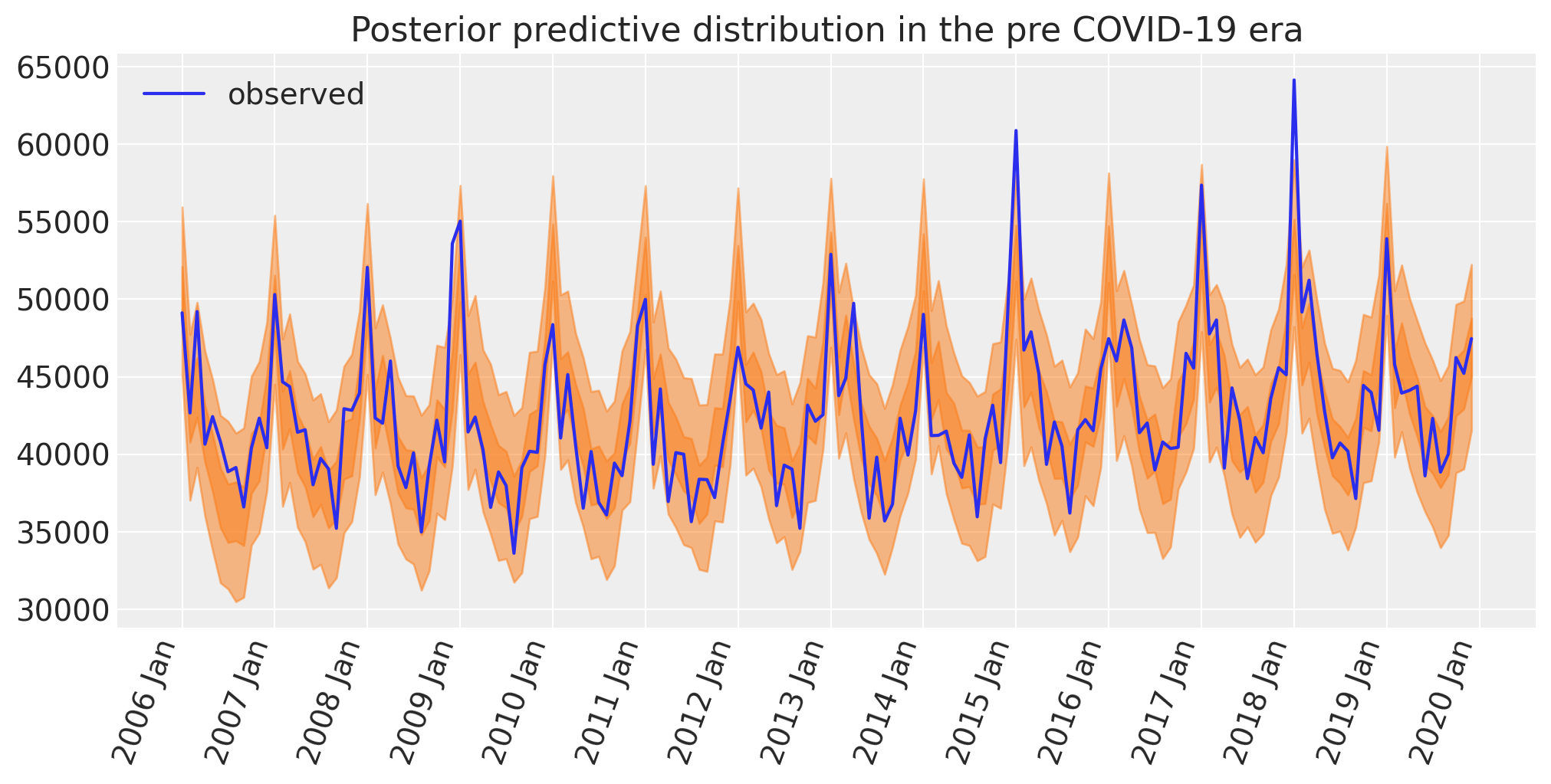
现在让我们再进行一次检查，但重点关注季节性影响。我们将复制我们在上面绘制的死亡人数随年份月份变化的图。为了防止绘图完全混乱，我们将仅绘制后验均值。因此，这不是后验预测检查，而是后验检查。

temp = idata.posterior["mu"].mean(dim=["chain", "draw"]).to_dataframe()
pre = pre.assign(deaths_predicted=temp["mu"].values)

fig, ax = plt.subplots(1, 2, figsize=figsize, sharey=True)
sns.lineplot(data=pre, x="month", y="deaths", hue="year", ax=ax[0], lw=3)
ax[0].set(title="Observed")
sns.lineplot(data=pre, x="month", y="deaths_predicted", hue="year", ax=ax[1], lw=3)
ax[1].set(title="Model predicted mean");

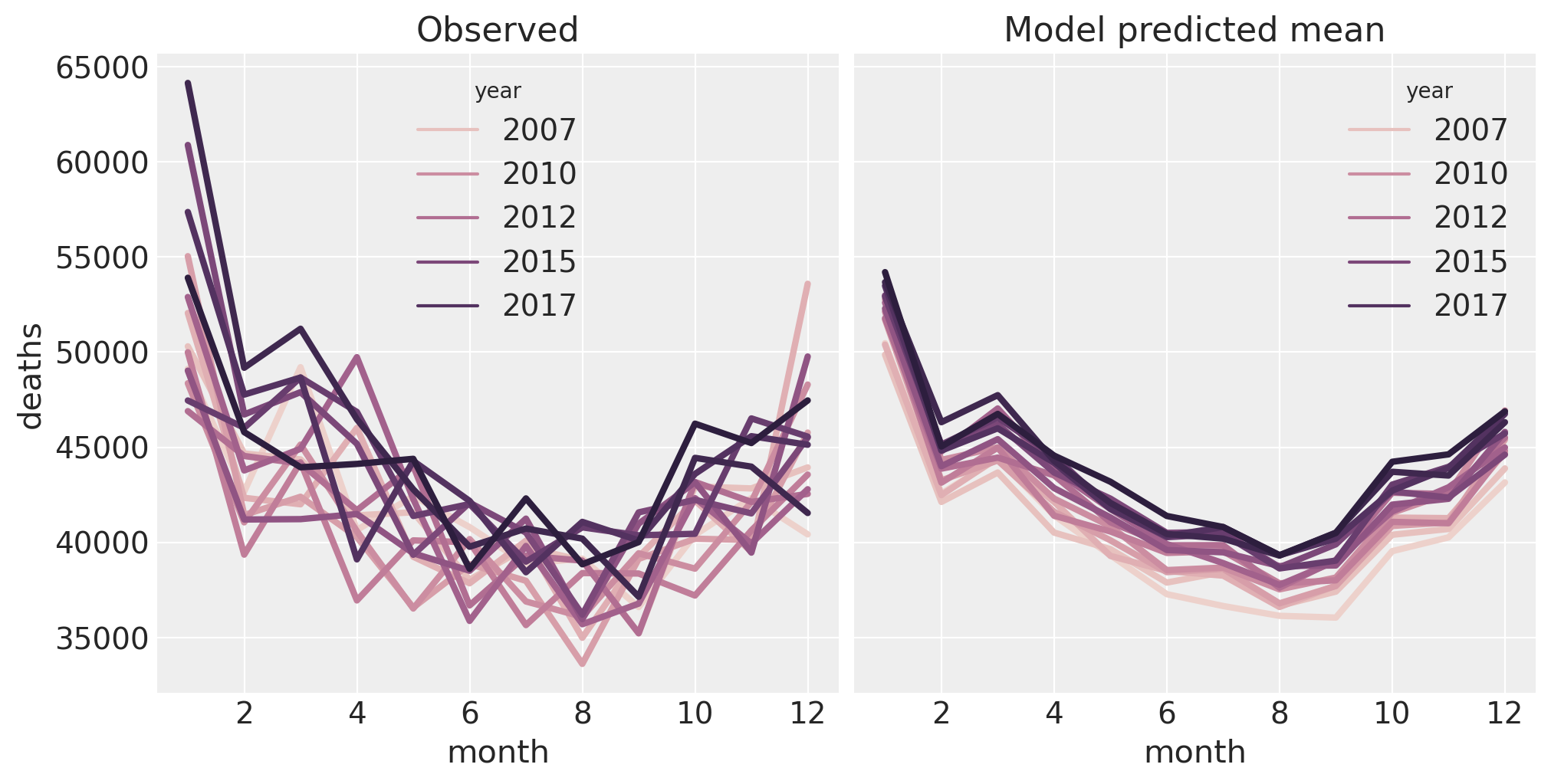
该模型在捕获数据属性方面做得相当好。在右侧，我们可以清楚地看到 month 和 year 的主要影响。但是，我们可以看到在 1 月份的数据（左侧）中发生了一些有趣的事情，而模型没有捕获到。这可能可以通过在 month 和 year 之间添加交互作用来捕获在模型中，但这留给读者作为练习。

超额死亡人数：Covid 前

此步骤不是严格必要的，但我们可以将超额死亡人数公式应用于模型对 pre 期间的回溯预测。这很有用，因为我们可以检查模型的优劣。

显示代码单元格来源 隐藏代码单元格来源

# convert deaths into an XArray object with a labelled dimension to help in the next step
deaths = xr.DataArray(pre["deaths"].to_numpy(), dims=["t"])

# do the calculation by taking the difference
excess_deaths = deaths - idata.posterior_predictive["obs"]

fig, ax = plt.subplots(figsize=figsize)
# the transpose is to keep arviz happy, ordering the dimensions as (chain, draw, t)
az.plot_hdi(pre.index, excess_deaths.transpose(..., "t"), hdi_prob=0.5, smooth=False)
az.plot_hdi(pre.index, excess_deaths.transpose(..., "t"), hdi_prob=0.95, smooth=False)
format_x_axis(ax)
ax.axhline(y=0, color="k")
ax.set(title="Excess deaths, pre COVID-19");

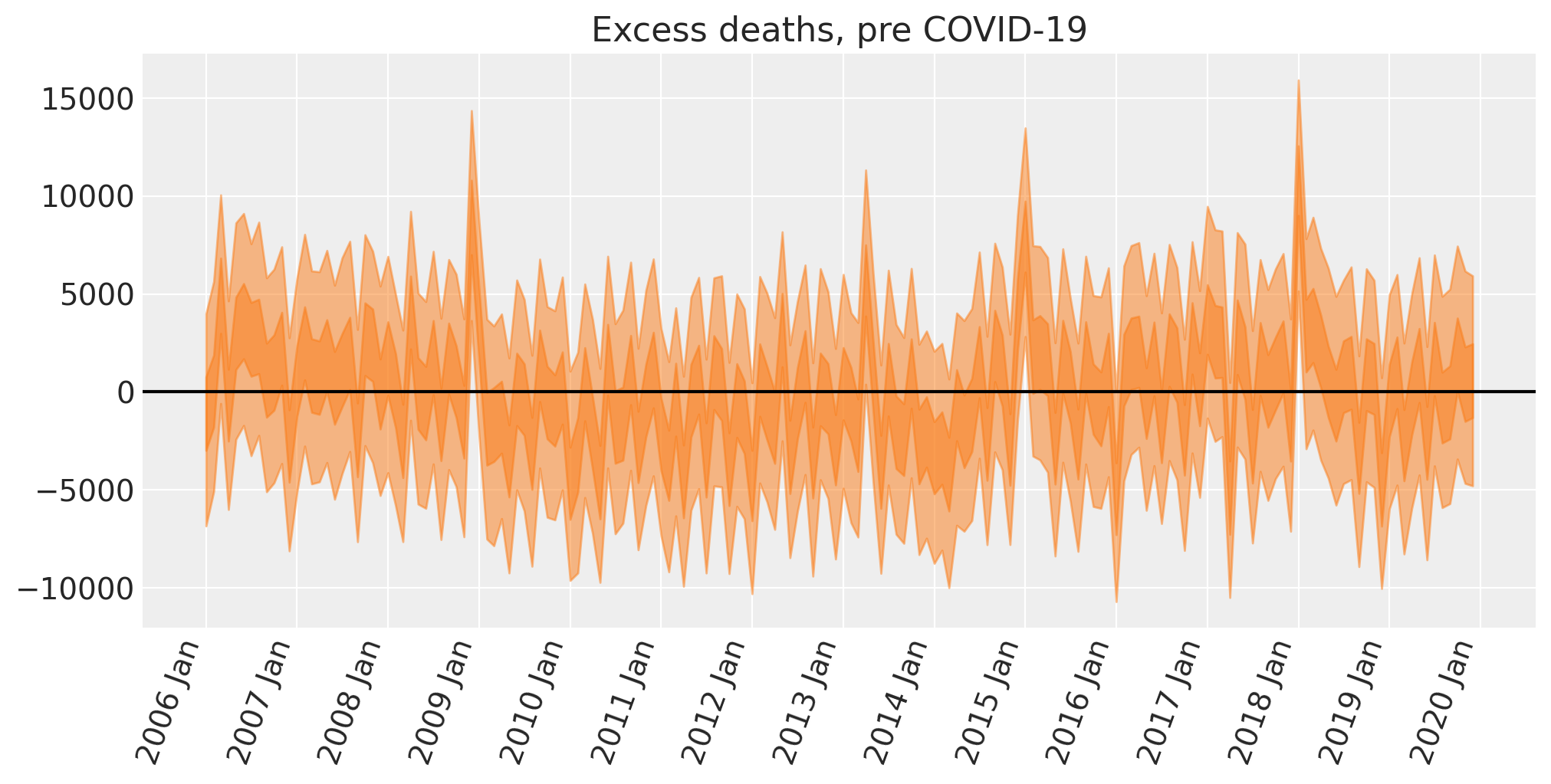
我们可以看到这里有一些峰值，其中超额死亡人数可能大于零。这种情况超出了我们可以从以下方面预期的范围：a) 季节性影响，b) 线性增加趋势，c) 寒冷冬季的影响。

如果我们感兴趣，那么我们可以开始生成关于哪些额外的预测变量可能解释这种情况的假设。一些想法可能包括普通感冒的流行程度，或最低月平均温度，这可能会增加平均温度未捕获的额外预测信息。

我们还可以看到，模型没有完全捕获到一些额外的时间趋势。后验均值与零之间存在一些系统的低频漂移。也就是说，数据中存在额外的方差，而我们的预测变量没有完全捕获到，这可能是由弱势群体规模随时间变化引起的。

但我们已接近计算 COVID-19 期间超额死亡人数的目标，因此我们将继续前进，因为此处的主要目的是反事实思维，而不是构建有史以来最全面的报告死亡人数模型。

反事实推断

现在我们将使用我们的模型来预测“一切照旧”情景中报告的死亡人数。

因此，我们使用来自 post 数据帧的 month 和时间 (t) 以及 temp 数据更新模型，并运行后验预测抽样以预测在这种反事实情景中我们将观察到的报告死亡人数。我们也可以称之为“预测”。

with model:
    pm.set_data(
        {
            "month": post["month"].to_numpy(),
            "time": post["t"].to_numpy(),
            "temp": post["temp"].to_numpy(),
        }
    )
    counterfactual = pm.sample_posterior_predictive(
        idata, var_names=["obs"], random_seed=RANDOM_SEED
    )

Sampling: [obs]

100.00% [4000/4000 00:00<00:00]

显示代码单元格来源 隐藏代码单元格来源

fig, ax = plt.subplots(figsize=figsize)

plot_xY(post.index, counterfactual.posterior_predictive["obs"], ax)
format_x_axis(ax, minor=True)
ax.plot(post.index, post["deaths"], label="reported deaths")
ax.set(title="Counterfactual: Posterior predictive forecast of deaths if COVID-19 had not appeared")
plt.legend();

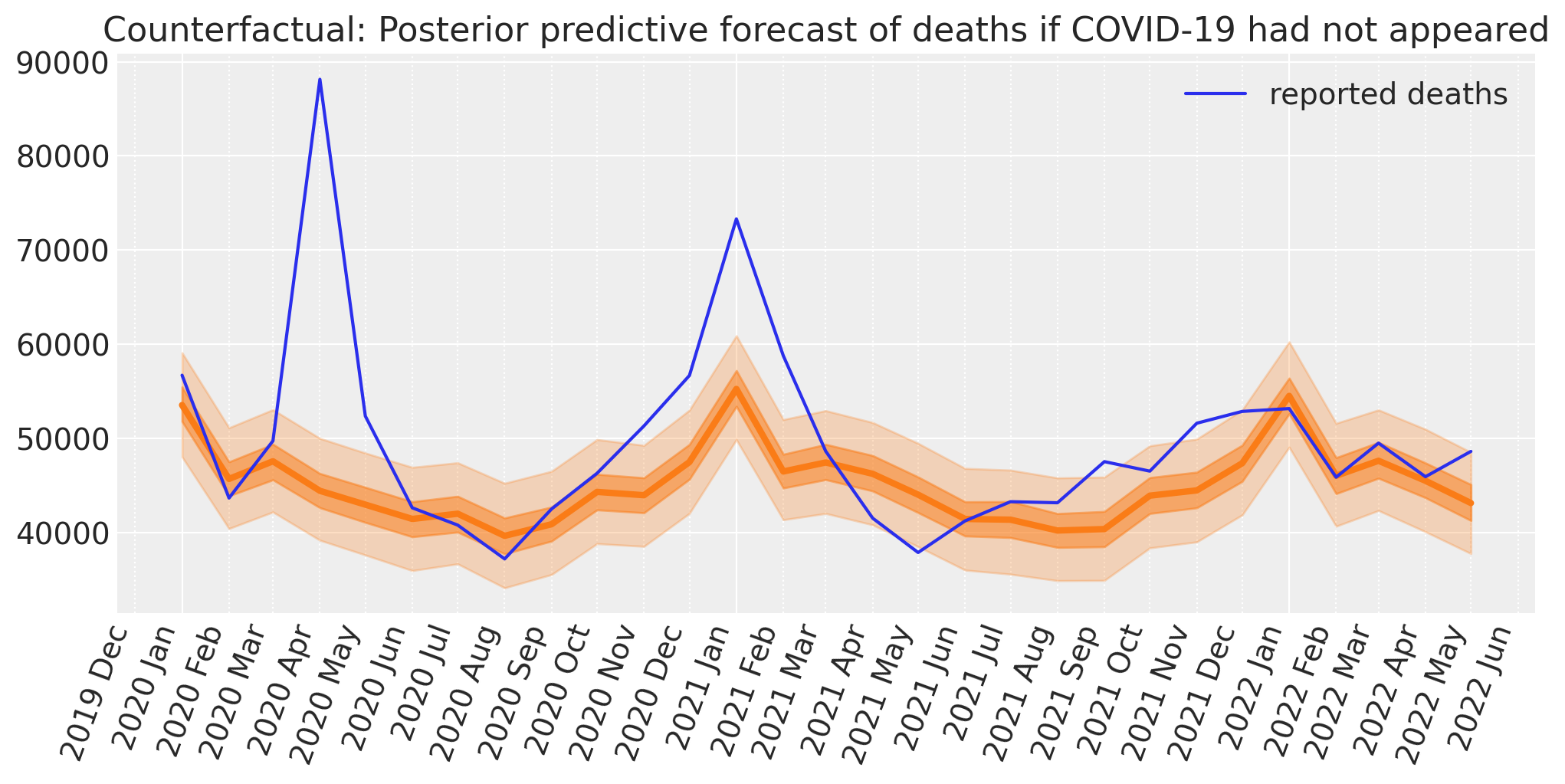
我们现在拥有计算超额死亡人数所需的要素。即，报告的死亡人数，以及在从 covid 前到 covid 后时代没有发生任何变化的情况下，贝叶斯反事实预测的死亡人数。

超额死亡人数：自 Covid 爆发以来

现在我们将使用反事实情景下预测的死亡人数，并将其与报告的死亡人数进行比较，从而得出我们对超额死亡人数的反事实估计。

# convert deaths into an XArray object with a labelled dimension to help in the next step
deaths = xr.DataArray(post["deaths"].to_numpy(), dims=["t"])

# do the calculation by taking the difference
excess_deaths = deaths - counterfactual.posterior_predictive["obs"]

我们可以轻松地计算累积超额死亡人数

# calculate the cumulative excess deaths
cumsum = excess_deaths.cumsum(dim="t")

显示代码单元格来源 隐藏代码单元格来源

fig, ax = plt.subplots(2, 1, figsize=(figsize[0], 9), sharex=True)

# Plot the excess deaths
# The transpose is to keep arviz happy, ordering the dimensions as (chain, draw, t)
plot_xY(post.index, excess_deaths.transpose(..., "t"), ax[0])
format_x_axis(ax[0], minor=True)
ax[0].axhline(y=0, color="k")
ax[0].set(title="Excess deaths, since COVID-19 onset")

# Plot the cumulative excess deaths
plot_xY(post.index, cumsum.transpose(..., "t"), ax[1])
format_x_axis(ax[1], minor=True)
ax[1].axhline(y=0, color="k")
ax[1].set(title="Cumulative excess deaths, since COVID-19 onset");

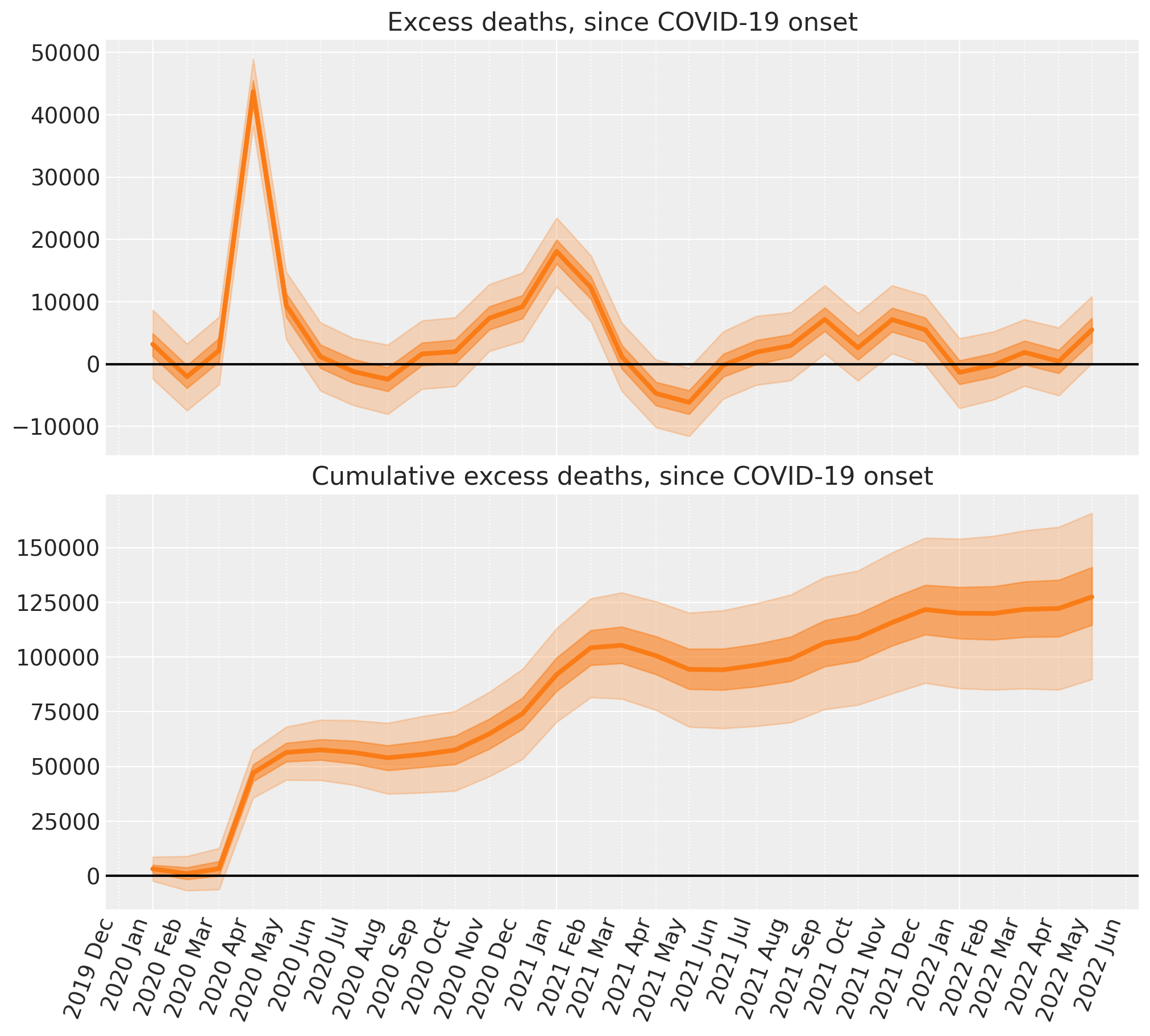
就这样，我们已经在 PyMC 中完成了一些贝叶斯反事实推断！仅需几个步骤，我们就完成了

• 构建了一个简单的线性回归模型。

• 基于 COVID-19 之前的数据推断了模型参数，运行了先验和后验预测检查。我们注意到该模型相当不错，但与往常一样，将来可能还有改进模型的方法。

• 使用该模型创建了如果没有任何改变，未来（COVID-19 时代）将会发生什么的反事实预测。

• 通过将报告的死亡人数与我们的反事实预期死亡人数进行比较，计算了超额死亡人数（和累积超额死亡人数）。

当然，坏消息是，截至最后一个数据点（2022 年 5 月），英格兰和威尔士的超额死亡人数已开始再次上升。

参考文献

[1]

Kay H. Brodersen, Fabian Gallusser, Jim Koehler, Nicolas Remy, 和 Steven L. Scott. Inferring causal impact using bayesian structural time-series models. Annals of Applied Statistics, 9:247–274, 2015.

[2]

Osvaldo A Martin, Ravin Kumar, 和 Junpeng Lao. Bayesian Modeling and Computation in Python. Chapman and Hall/CRC, 2021. doi:10.1201/9781003019169.

作者

• 由 Benjamin T. Vincent 于 2022 年 7 月编写。

• 由 Benjamin T. Vincent 于 2023 年 2 月更新，以在 PyMC v5 上运行

水印

%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,aeppl,xarray

Last updated: Wed Feb 01 2023

Python implementation: CPython
Python version       : 3.11.0
IPython version      : 8.9.0

pytensor: 2.8.11
aeppl   : not installed
xarray  : 2023.1.0

pymc      : 5.0.1
arviz     : 0.14.0
matplotlib: 3.6.3
pandas    : 1.5.3
numpy     : 1.24.1
xarray    : 2023.1.0
seaborn   : 0.12.2
pytensor  : 2.8.11

Watermark: 2.3.1

许可声明

此示例库中的所有笔记本均根据 MIT 许可证 提供，该许可证允许修改和再分发以用于任何用途，前提是保留版权和许可声明。

引用 PyMC 示例

要引用此笔记本，请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。

重要提示

许多笔记本都改编自其他来源：博客、书籍……在这种情况下，您也应该引用原始来源。

另请记住引用您的代码使用的相关库。

这是一个 bibtex 中的引用模板

@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}

渲染后可能看起来像