贝叶斯中介分析#
本笔记本涵盖了贝叶斯中介分析。当我们想要探索预测变量和结果变量之间可能的中介路径时,这非常有用。
重要的是要注意,中介分析的方法随着时间的推移而发展。本笔记本深受 Hayes [2017] 的方法的影响,该方法在他的教科书《中介、调节和条件过程分析导论》中阐述。
读者应该意识到,中介分析通常与调节分析相混淆,对此我们有单独的示例 (贝叶斯调节分析)。
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import seaborn as sns
from pandas import DataFrame
%config InlineBackend.figure_format = 'retina'
plt.rcParams.update({"font.size": 14})
seed = 42
rng = np.random.default_rng(seed);
中介模型#
简单的中介模型非常简单,其中 \(m\) 是 \(x\) 的线性函数,\(y\) 是 \(x\) 和 \(m\) 的线性函数
其中 \(i\) 索引每个观察值(数据集中的行),\(i_M\) 和 \(i_Y\) 是截距参数。请注意,\(x_i\)、\(m_i\) 和 \(y_i\) 是观测数据。
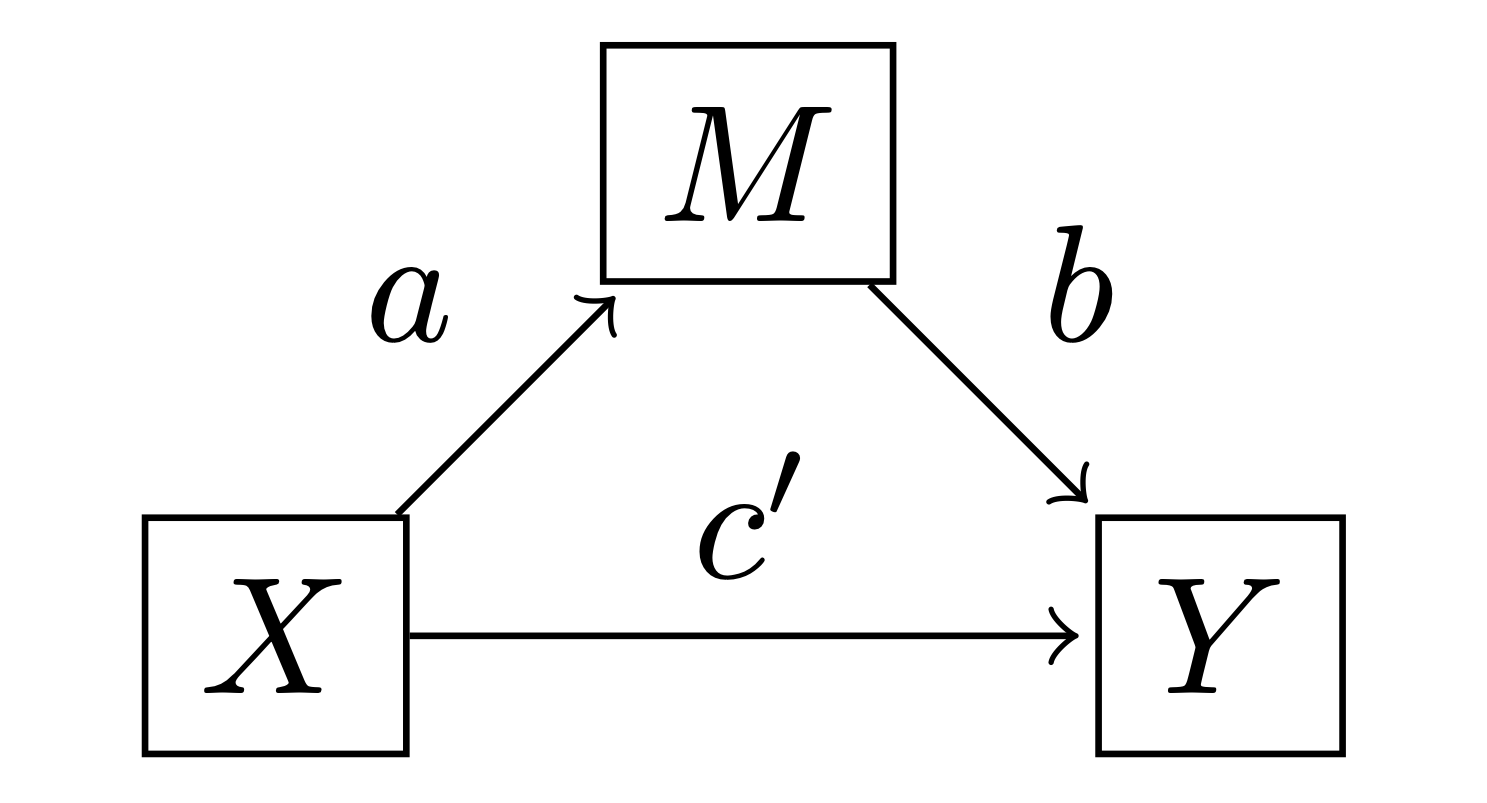
使用 Hayes [2017] 的定义,我们可以定义一些感兴趣的效应
直接效应: 由 \(c'\) 给出。在 \(x\) 上相差一个单位但在 \(m\) 上相等的两个案例,估计在 \(y\) 上相差 \(c'\) 个单位。
间接效应: 由 \(a \cdot b\) 给出。在 \(x\) 上相差一个单位的两个案例,由于 \(x \rightarrow m\) 和 \(m \rightarrow y\) 的效应,估计在 \(y\) 上相差 \(a \cdot b\) 个单位。
总效应: 是 \(c = c' + a \cdot b\),它只是直接效应和间接效应的总和。这可以理解为:在 \(x\) 上相差一个单位的两个案例,由于间接路径 \(x \rightarrow m \rightarrow y\),估计在 \(y\) 上相差 \(a \cdot b\) 个单位,由于直接路径 \(x \rightarrow y\),估计相差 \(c'\) 个单位。总效应也可以通过评估替代模型 \(y_i \sim \mathrm{Normal}(i_{Y*} + c \cdot x_i, \sigma_{Y*})\) 来估计。
生成模拟数据#
def make_data():
N = 75
a, b, cprime = 0.5, 0.6, 0.3
im, iy, σm, σy = 2.0, 0.0, 0.5, 0.5
x = rng.normal(loc=0, scale=1, size=N)
m = im + rng.normal(loc=a * x, scale=σm, size=N)
y = iy + (cprime * x) + rng.normal(loc=b * m, scale=σy, size=N)
print(f"True direct effect = {cprime}")
print(f"True indirect effect = {a*b}")
print(f"True total effect = {cprime+a*b}")
return x, m, y
x, m, y = make_data()
sns.pairplot(DataFrame({"x": x, "m": m, "y": y}));
True direct effect = 0.3
True indirect effect = 0.3
True total effect = 0.6
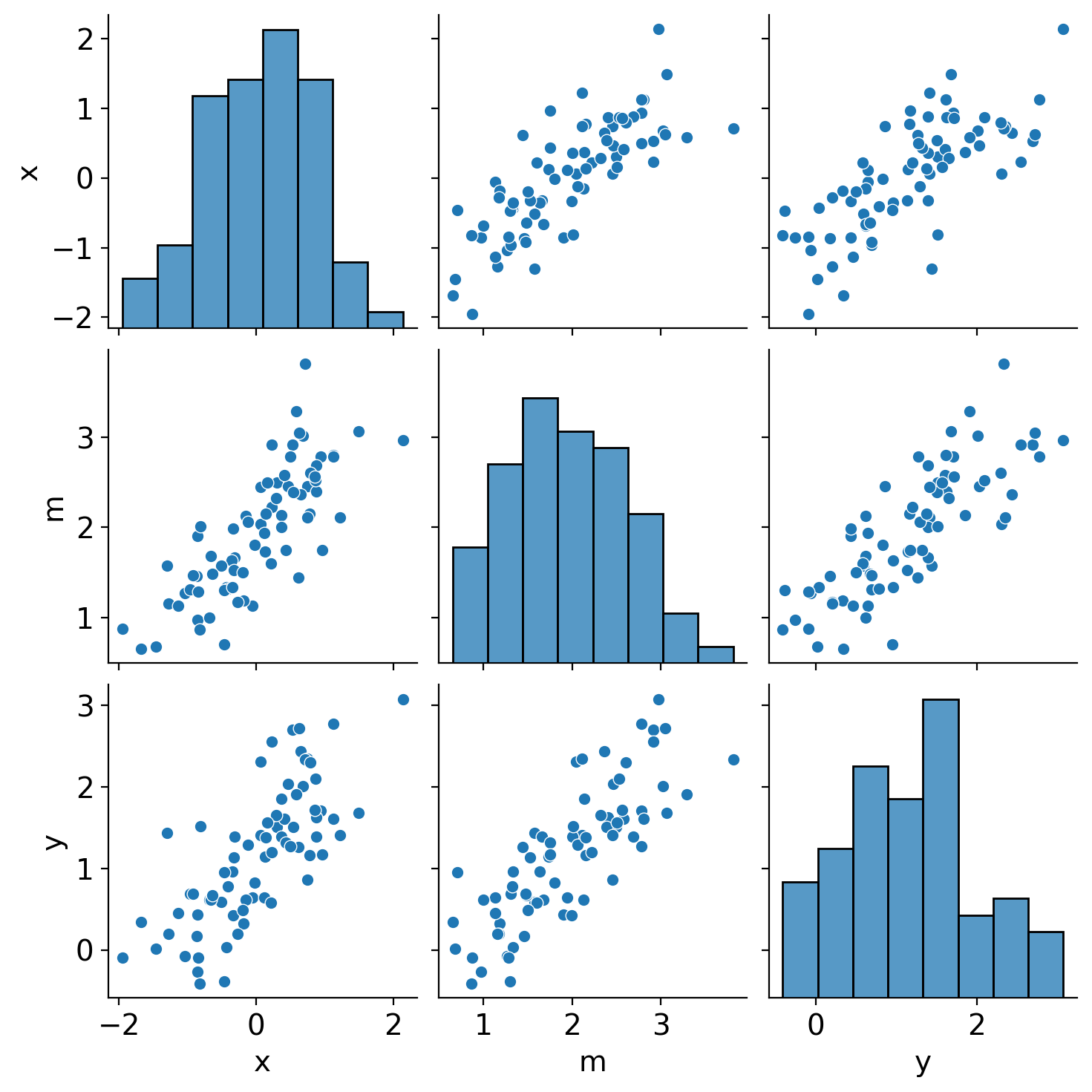
定义 PyMC 模型并进行推断#
def mediation_model(x, m, y):
with pm.Model() as model:
x = pm.ConstantData("x", x, dims="obs_id")
y = pm.ConstantData("y", y, dims="obs_id")
m = pm.ConstantData("m", m, dims="obs_id")
# intercept priors
im = pm.Normal("im", mu=0, sigma=10)
iy = pm.Normal("iy", mu=0, sigma=10)
# slope priors
a = pm.Normal("a", mu=0, sigma=10)
b = pm.Normal("b", mu=0, sigma=10)
cprime = pm.Normal("cprime", mu=0, sigma=10)
# noise priors
σm = pm.HalfCauchy("σm", 1)
σy = pm.HalfCauchy("σy", 1)
# likelihood
pm.Normal("m_likelihood", mu=im + a * x, sigma=σm, observed=m, dims="obs_id")
pm.Normal("y_likelihood", mu=iy + b * m + cprime * x, sigma=σy, observed=y, dims="obs_id")
# calculate quantities of interest
indirect_effect = pm.Deterministic("indirect effect", a * b)
total_effect = pm.Deterministic("total effect", a * b + cprime)
return model
model = mediation_model(x, m, y)
pm.model_to_graphviz(model)
with model:
result = pm.sample(tune=4000, target_accept=0.9, random_seed=42)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [im, iy, a, b, cprime, σm, σy]
Sampling 4 chains for 4_000 tune and 1_000 draw iterations (16_000 + 4_000 draws total) took 9 seconds.
可视化迹图以检查收敛性。
az.plot_trace(result)
plt.tight_layout()
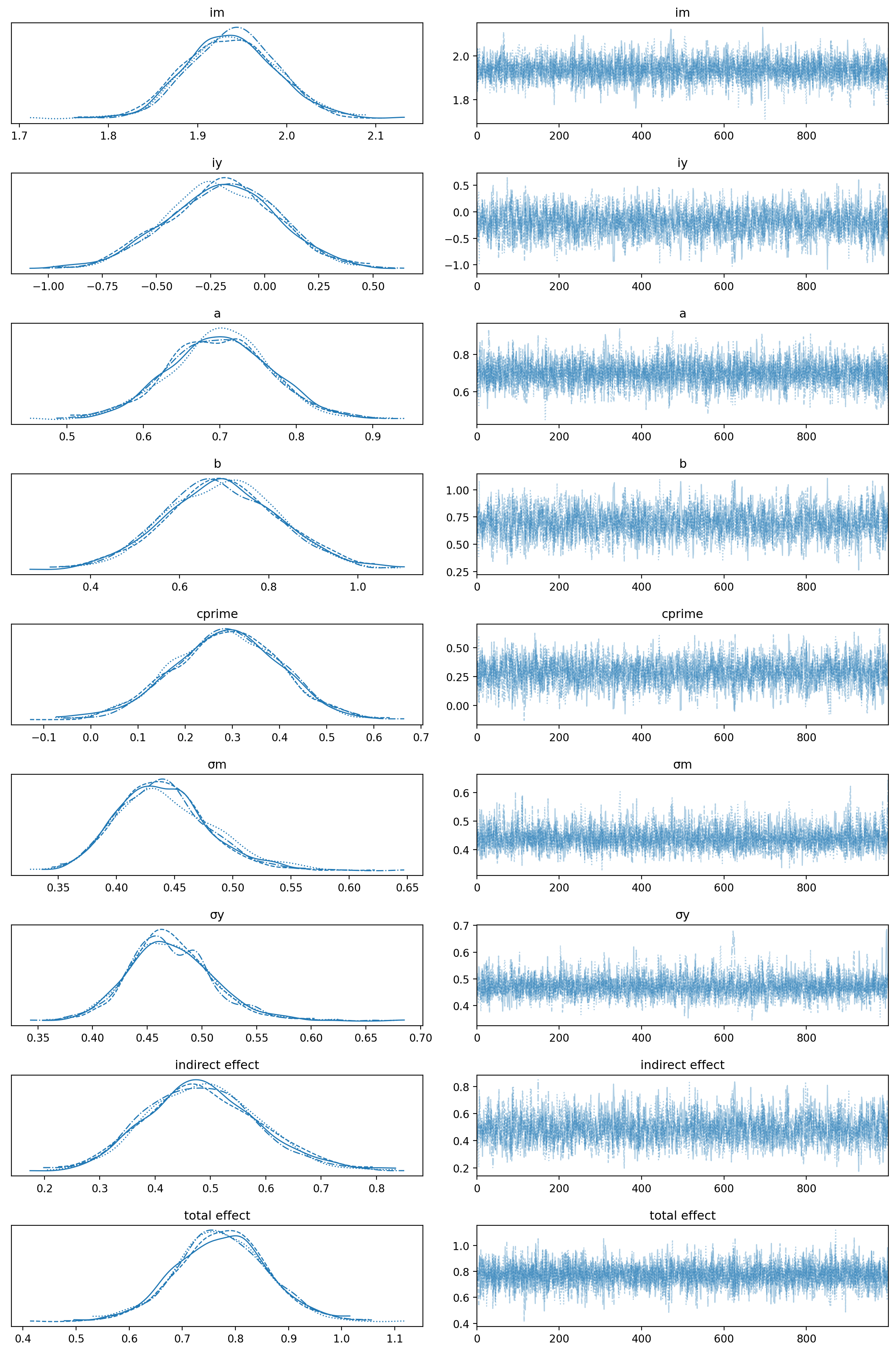
我们有良好的链混合,并且每个链的后验分布看起来非常相似,因此在这方面没有问题。
可视化重要参数#
首先,我们将使用配对图来查看联合后验分布。
az.plot_pair(
result,
marginals=True,
point_estimate="median",
figsize=(12, 12),
scatter_kwargs={"alpha": 0.05},
var_names=["a", "b", "cprime", "indirect effect", "total effect"],
);
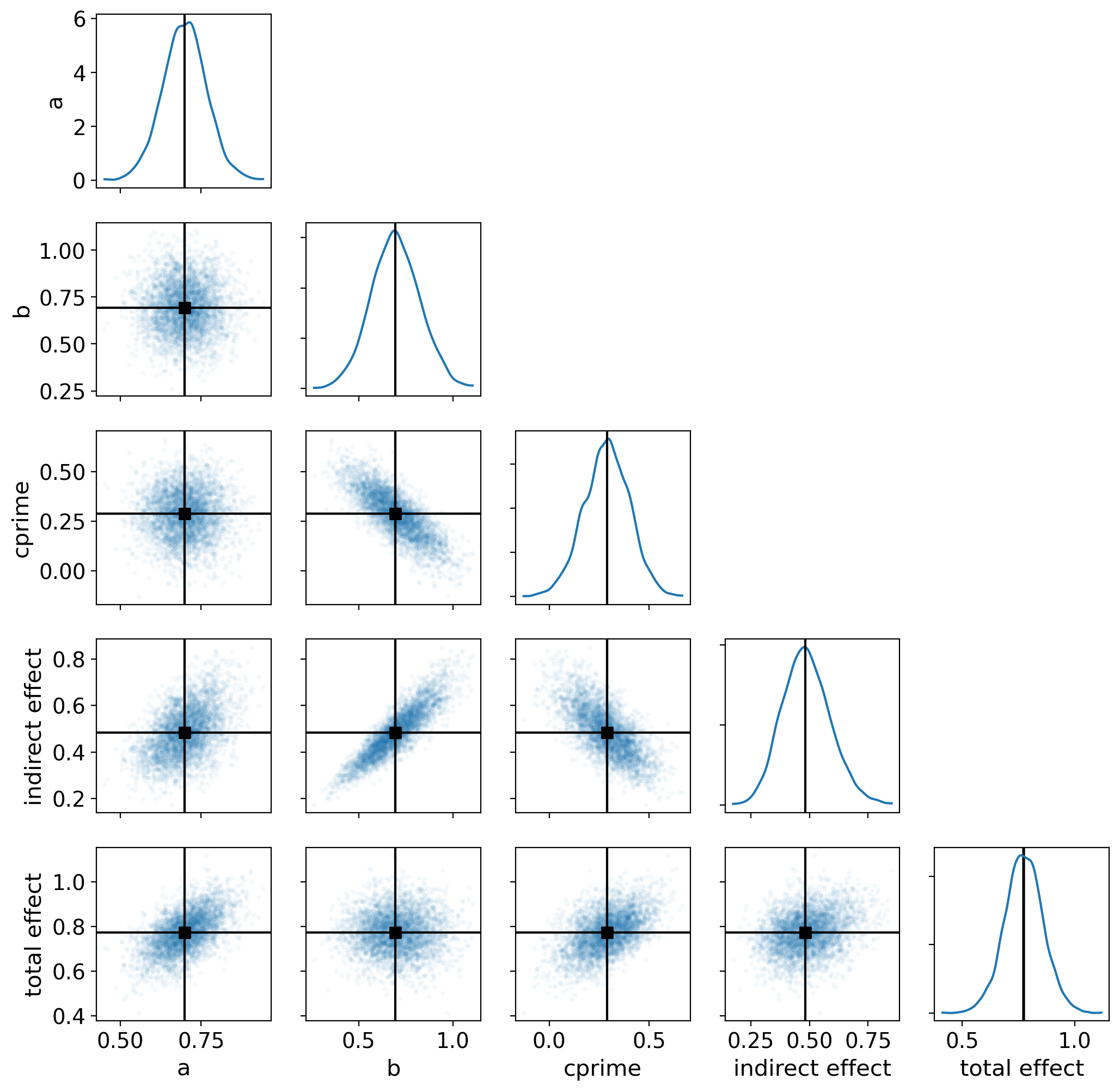
解释结果#
我们可以仔细看看间接效应、总效应和直接效应
ax = az.plot_posterior(
result,
var_names=["cprime", "indirect effect", "total effect"],
ref_val=0,
hdi_prob=0.95,
figsize=(14, 4),
)
ax[0].set(title="direct effect");

后验均值直接效应为 0.29,这意味着 x 每增加 1 个单位,y 会因直接效应 \(x \rightarrow y\) 而增加 0.29。
后验均值间接效应为 0.49,这意味着 x 每增加 1 个单位,y 会通过路径 \(x \rightarrow m \rightarrow y\) 增加 0.49。间接效应为零的概率非常小。
后验均值总效应为 0.77,这意味着 x 每增加 1 个单位,y 会通过直接和间接路径增加 0.77。
使用仅总效应模型进行双重检查#
上面,我们提到总效应也可以通过评估替代模型 \(y_i \sim \mathrm{Normal}(i_{Y*} + c \cdot x_i, \sigma_{Y*})\) 来估计。在这里,我们将通过比较中介模型中 \(c'\) 的后验分布和此替代模型中 \(c\) 的后验分布来检查这一点。
with pm.Model() as total_effect_model:
_x = pm.ConstantData("_x", x, dims="obs_id")
iy = pm.Normal("iy", mu=0, sigma=1)
c = pm.Normal("c", mu=0, sigma=1)
σy = pm.HalfCauchy("σy", 1)
μy = iy + c * _x
pm.Normal("yy", mu=μy, sigma=σy, observed=y, dims="obs_id")
with total_effect_model:
total_effect_result = pm.sample(tune=4000, target_accept=0.9, random_seed=42)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [iy, c, σy]
Sampling 4 chains for 4_000 tune and 1_000 draw iterations (16_000 + 4_000 draws total) took 2 seconds.
fig, ax = plt.subplots(figsize=(14, 4))
az.plot_posterior(
total_effect_result, var_names=["c"], point_estimate=None, hdi_prob="hide", c="r", lw=4, ax=ax
)
az.plot_posterior(
result, var_names=["total effect"], point_estimate=None, hdi_prob="hide", c="k", lw=4, ax=ax
);
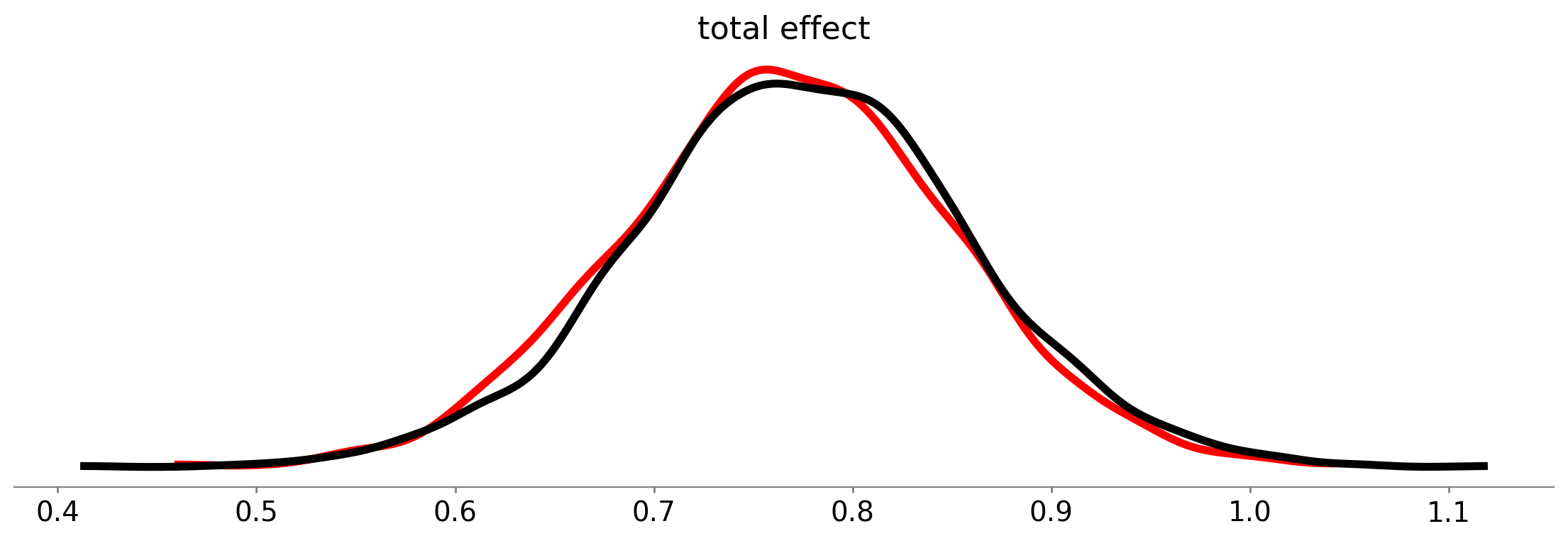
正如我们所见,中介模型(黑曲线)和直接模型(红曲线)的直接效应的后验分布几乎相同。
参数估计与假设检验#
本笔记本侧重于贝叶斯参数估计的方法。在许多情况下,这完全足够了,更多信息可以在 Yuan 和 MacKinnon [2009] 中找到。它将告诉我们,除其他外,我们对直接效应、间接效应和总效应的后验信念是什么。我们可以使用这些后验信念进行后验预测检查,以直观地检查模型对数据的解释程度。
然而,根据用例的不同,最好检验关于是否存在间接效应 (\(x \rightarrow m \rightarrow y\)) 的假设。在这种情况下,采取更明确的假设检验方法来检查中介模型相对于简单直接效应模型(即 \(y_i = \mathrm{Normal}(i_{Y*} + c \cdot x_i, \sigma_{Y*})\))的相对可信度可能更合适。读者可以参考 Nuijten 等人 et al. [2015] 了解贝叶斯中介模型的假设检验方法,并参考 Kruschke [2011] 了解更多关于参数估计与假设检验的信息。
总结#
正如一开始所说,中介分析中使用的程序随着时间的推移而发展。因此,有很多人不一定跟上现代最佳实践的步伐。本笔记本中的方法坚持 Hayes [2017] 概述的方法,但了解一些这段历史以避免混淆是相关的 - 如果在同行评审中为你的方法辩护,这一点尤其重要。
参考文献#
水印#
%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,aeppl,xarray
Last updated: Wed Feb 01 2023
Python implementation: CPython
Python version : 3.11.0
IPython version : 8.9.0
pytensor: 2.8.11
aeppl : not installed
xarray : 2023.1.0
arviz : 0.14.0
pymc : 5.0.1
matplotlib: 3.6.3
numpy : 1.24.1
seaborn : 0.12.2
Watermark: 2.3.1
许可声明#
本示例库中的所有笔记本均根据 MIT 许可证 提供,该许可证允许修改和再分发以用于任何用途,前提是保留版权和许可声明。
引用 PyMC 示例#
要引用此笔记本,请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。
重要提示
许多笔记本改编自其他来源:博客、书籍…… 在这种情况下,您也应该引用原始来源。
另请记住引用您的代码使用的相关库。
这是一个 bibtex 格式的引用模板
@incollection{citekey,
author = "<notebook authors, see above>",
title = "<notebook title>",
editor = "PyMC Team",
booktitle = "PyMC examples",
doi = "10.5281/zenodo.5654871"
}
渲染后可能看起来像