分层二项模型:大鼠肿瘤示例#
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pytensor.tensor as pt
from scipy.special import gammaln
%config InlineBackend.figure_format = 'retina'
az.style.use("arviz-darkgrid")
本简短教程演示了如何使用 PyMC 对贝叶斯数据分析第 3 版第 5 章中的大鼠肿瘤示例进行推断 [Gelman et al., 2013]。读者应已熟悉 PyMC API。
假设我们对实验大鼠发生子宫内膜间质息肉的概率感兴趣。我们有来自先前进行的 71 项试验的数据,并希望使用这些数据进行推断。
BDA3 的作者选择以分层方式对这个问题建模。设 \(y_i\) 为在 \(n_i\) 只实验大鼠中,发生子宫内膜间质息肉的大鼠数量。我们将发生子宫内膜间质息肉的啮齿动物数量建模为二项分布
允许发生子宫内膜间质息肉的概率(即 \(\theta_i\))从某些总体分布中抽取。为了便于分析,我们假设 \(\theta_i\) 服从 Beta 分布
我们可以自由指定 \(\alpha, \beta\) 的先验分布。我们选择一个弱信息先验分布,以反映我们对 \(\alpha, \beta\) 真值的无知。BDA3 的作者选择 \(\alpha, \beta\) 的联合超先验为
更多信息,请参阅贝叶斯数据分析第 3 版第 110 页。
直接计算的解法#
我们的联合后验分布是
可以将其重写为以下形式,以获得 \(\alpha\) 和 \(\beta\) 的边际后验分布,即
有关推导边际后验分布的更多信息,请参阅 BDA3 第 110 页。稍加努力,我们可以绘制边际后验,并估计 \(\alpha\) 和 \(\beta\) 的均值,而无需诉诸 MCMC。然而,我们将看到这需要相当大的努力。
BDA3 的作者选择绘制参数化 \((\log(\alpha/\beta), \log(\alpha+\beta))\) 下的曲面。我们也这样做。在示例的其余部分,令 \(x = \log(\alpha/\beta)\) 和 \(z = \log(\alpha+\beta)\)。
# rat data (BDA3, p. 102)
# fmt: off
y = np.array([
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1,
1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 5, 2,
5, 3, 2, 7, 7, 3, 3, 2, 9, 10, 4, 4, 4, 4, 4, 4, 4,
10, 4, 4, 4, 5, 11, 12, 5, 5, 6, 5, 6, 6, 6, 6, 16, 15,
15, 9, 4
])
n = np.array([
20, 20, 20, 20, 20, 20, 20, 19, 19, 19, 19, 18, 18, 17, 20, 20, 20,
20, 19, 19, 18, 18, 25, 24, 23, 20, 20, 20, 20, 20, 20, 10, 49, 19,
46, 27, 17, 49, 47, 20, 20, 13, 48, 50, 20, 20, 20, 20, 20, 20, 20,
48, 19, 19, 19, 22, 46, 49, 20, 20, 23, 19, 22, 20, 20, 20, 52, 46,
47, 24, 14
])
# fmt: on
N = len(n)
# Compute on log scale because products turn to sums
def log_likelihood(alpha, beta, y, n):
LL = 0
# Summing over data
for Y, N in zip(y, n):
LL += (
gammaln(alpha + beta)
- gammaln(alpha)
- gammaln(beta)
+ gammaln(alpha + Y)
+ gammaln(beta + N - Y)
- gammaln(alpha + beta + N)
)
return LL
def log_prior(A, B):
return -5 / 2 * np.log(A + B)
def trans_to_beta(x, y):
return np.exp(y) / (np.exp(x) + 1)
def trans_to_alpha(x, y):
return np.exp(x) * trans_to_beta(x, y)
# Create space for the parameterization in which we wish to plot
X, Z = np.meshgrid(np.arange(-2.3, -1.3, 0.01), np.arange(1, 5, 0.01))
param_space = np.c_[X.ravel(), Z.ravel()]
df = pd.DataFrame(param_space, columns=["X", "Z"])
# Transform the space back to alpha beta to compute the log-posterior
df["alpha"] = trans_to_alpha(df.X, df.Z)
df["beta"] = trans_to_beta(df.X, df.Z)
df["log_posterior"] = log_prior(df.alpha, df.beta) + log_likelihood(df.alpha, df.beta, y, n)
df["log_jacobian"] = np.log(df.alpha) + np.log(df.beta)
df["transformed"] = df.log_posterior + df.log_jacobian
df["exp_trans"] = np.exp(df.transformed - df.transformed.max())
# This will ensure the density is normalized
df["normed_exp_trans"] = df.exp_trans / df.exp_trans.sum()
surface = df.set_index(["X", "Z"]).exp_trans.unstack().values.T
fig, ax = plt.subplots(figsize=(8, 8))
ax.contourf(X, Z, surface)
ax.set_xlabel(r"$\log(\alpha/\beta)$", fontsize=16)
ax.set_ylabel(r"$\log(\alpha+\beta)$", fontsize=16)
ix_z, ix_x = np.unravel_index(np.argmax(surface, axis=None), surface.shape)
ax.scatter([X[0, ix_x]], [Z[ix_z, 0]], color="red")
text = r"$({a},{b})$".format(a=np.round(X[0, ix_x], 2), b=np.round(Z[ix_z, 0], 2))
ax.annotate(
text,
xy=(X[0, ix_x], Z[ix_z, 0]),
xytext=(-1.6, 3.5),
ha="center",
fontsize=16,
color="white",
arrowprops={"facecolor": "white"},
);
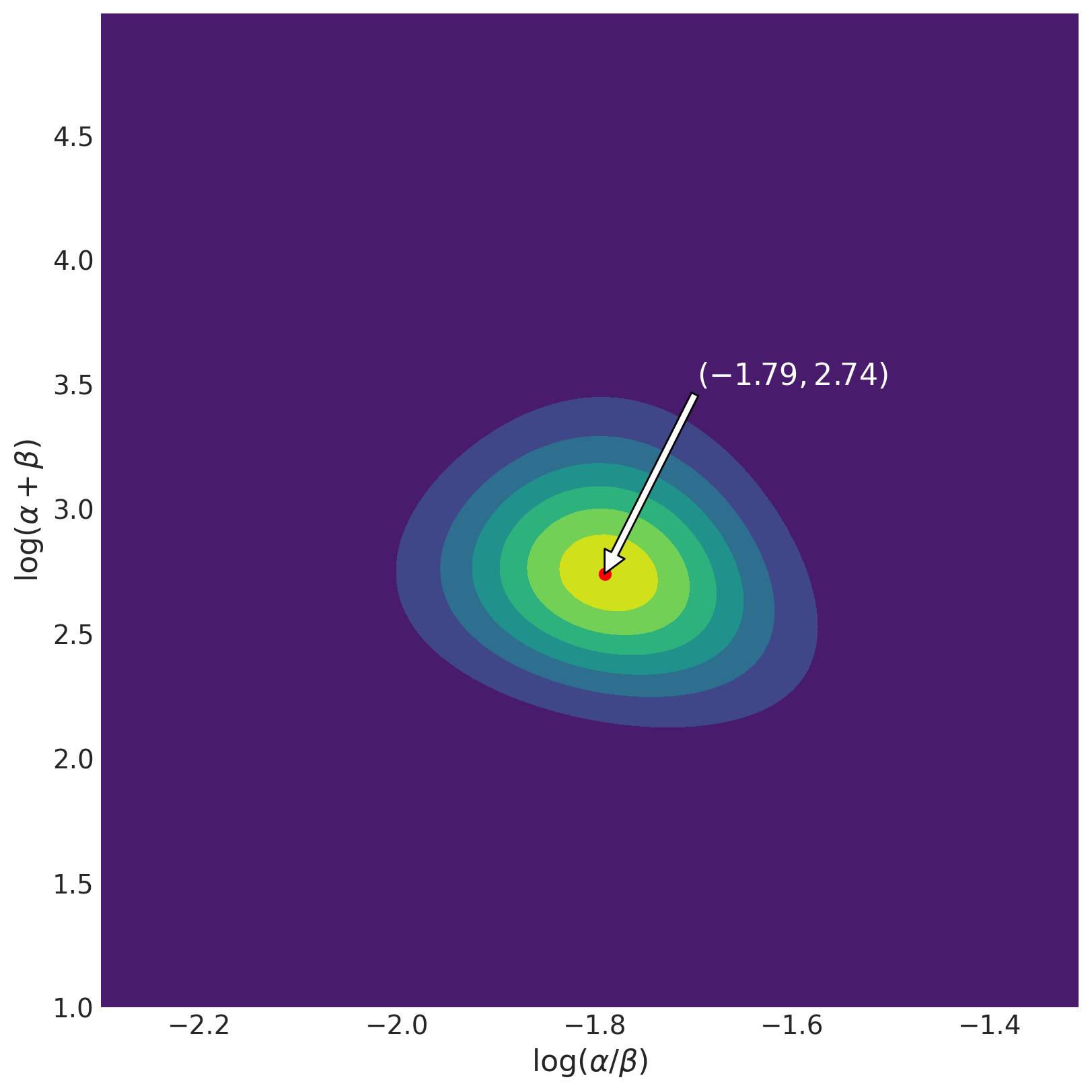
该图显示后验分布在众数 (-1.79, 2.74) 附近大致对称。这对应于 \(\alpha = 2.21\) 和 \(\beta = 13.27\)。我们可以像 BDA3 的作者那样计算边际均值,使用
# Estimated mean of alpha
(df.alpha * df.normed_exp_trans).sum().round(3)
2.403
# Estimated mean of beta
(df.beta * df.normed_exp_trans).sum().round(3)
14.319
使用 PyMC 计算后验分布#
直接计算边际后验分布工作量很大,对于足够复杂的模型,并非总是可行。
另一方面,在 PyMC 中创建分层模型很简单。我们可以使用从后验分布获得的样本来估计 \(\alpha\) 和 \(\beta\) 的均值。
coords = {
"obs_id": np.arange(N),
"param": ["alpha", "beta"],
}
def logp_ab(value):
"""prior density"""
return pt.log(pt.pow(pt.sum(value), -5 / 2))
with pm.Model(coords=coords) as model:
# Uninformative prior for alpha and beta
n_val = pm.ConstantData("n_val", n)
ab = pm.HalfNormal("ab", sigma=10, dims="param")
pm.Potential("p(a, b)", logp_ab(ab))
X = pm.Deterministic("X", pt.log(ab[0] / ab[1]))
Z = pm.Deterministic("Z", pt.log(pt.sum(ab)))
theta = pm.Beta("theta", alpha=ab[0], beta=ab[1], dims="obs_id")
p = pm.Binomial("y", p=theta, observed=y, n=n_val)
trace = pm.sample(draws=2000, tune=2000, target_accept=0.95)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [ab, theta]
Sampling 2 chains for 2_000 tune and 2_000 draw iterations (4_000 + 4_000 draws total) took 52 seconds.
# Check the trace. Looks good!
az.plot_trace(trace, var_names=["ab", "X", "Z"], compact=False);
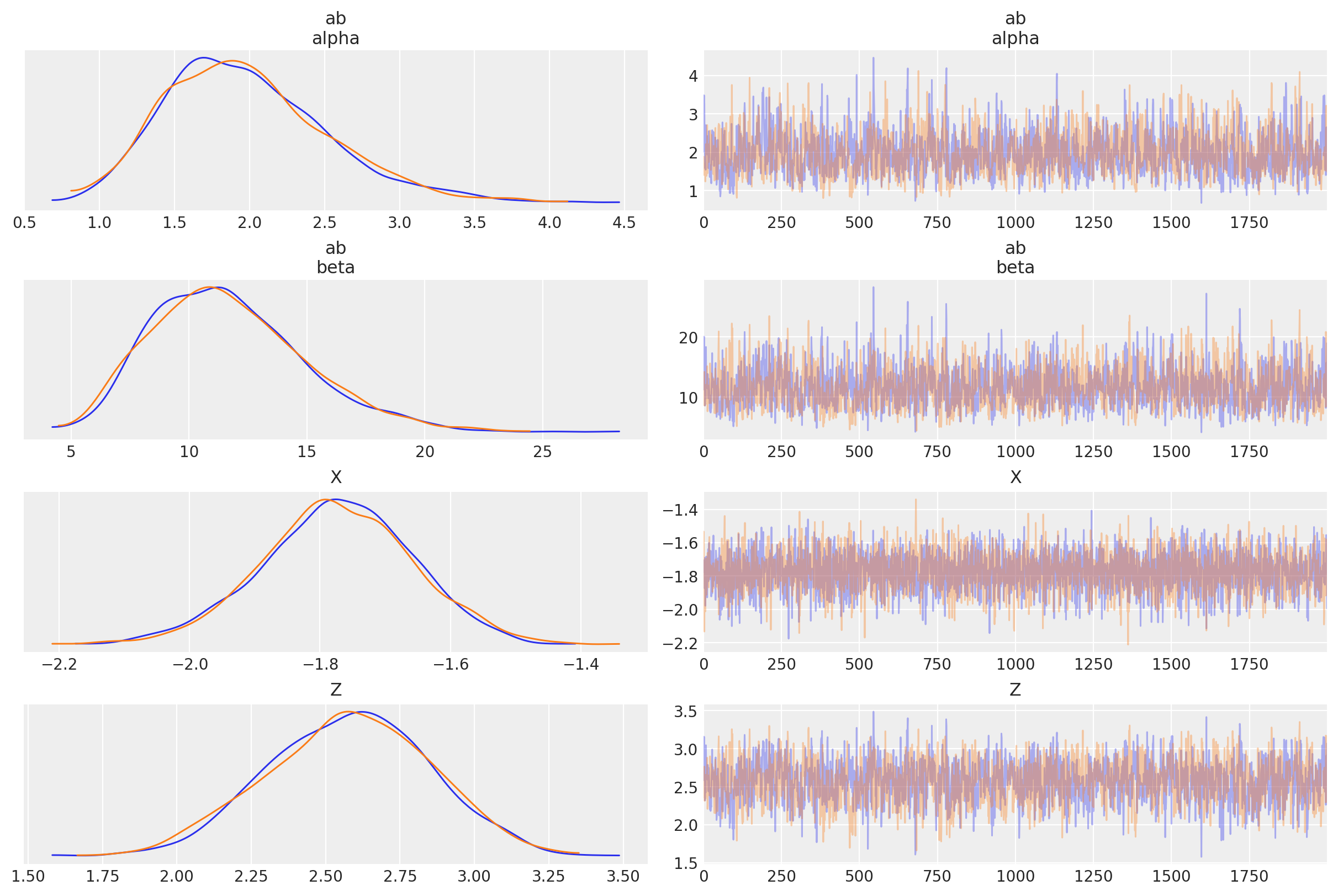
我们可以绘制 \(x\) 和 \(z\) 的核密度估计图。它看起来与我们从解析边际后验密度绘制的等高线图非常相似。这是一个好兆头,并且需要更少的努力。
az.plot_pair(trace, var_names=["X", "Z"], kind="kde");
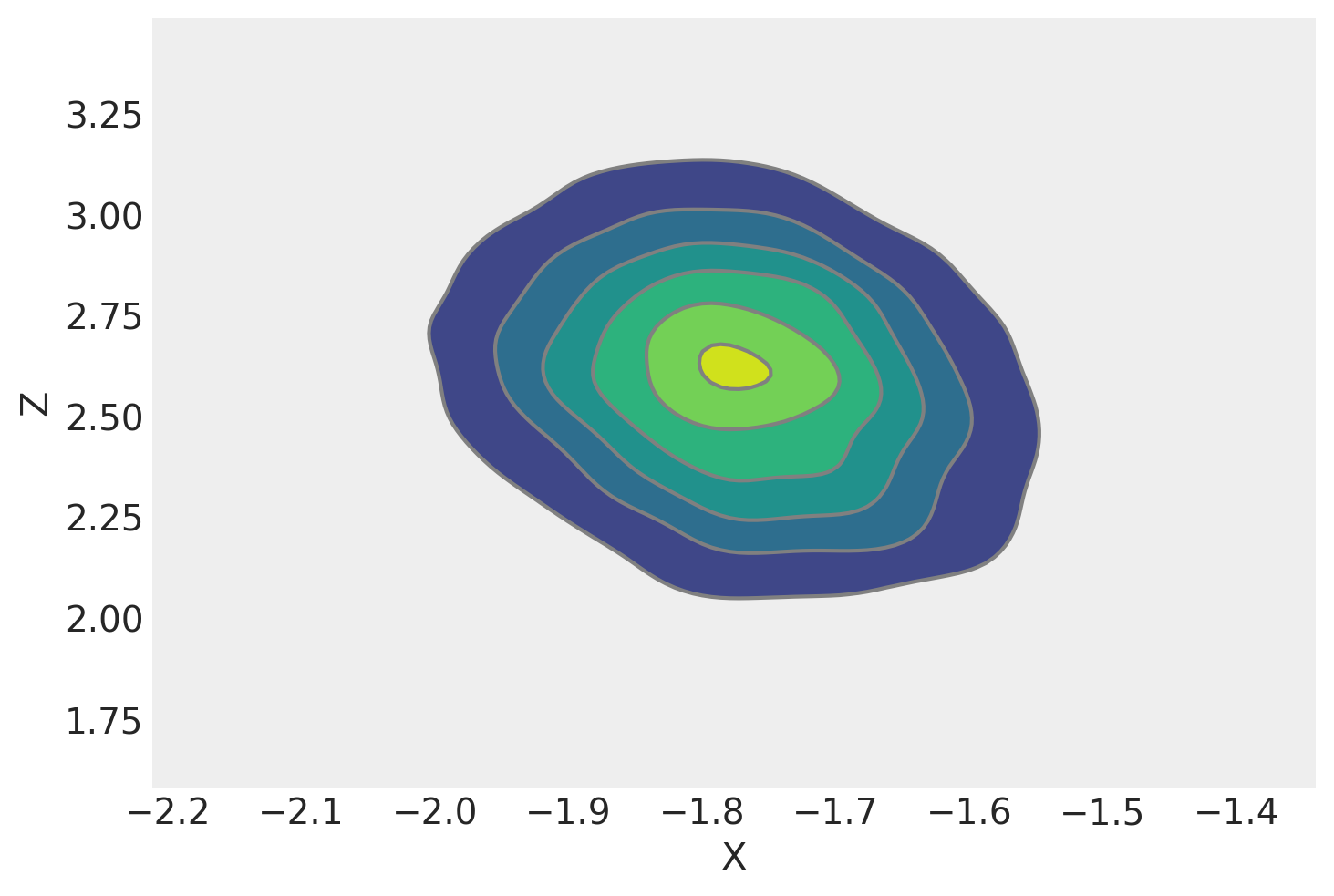
从这里,我们可以使用迹来计算分布的均值。
az.plot_posterior(trace, var_names=["ab"]);
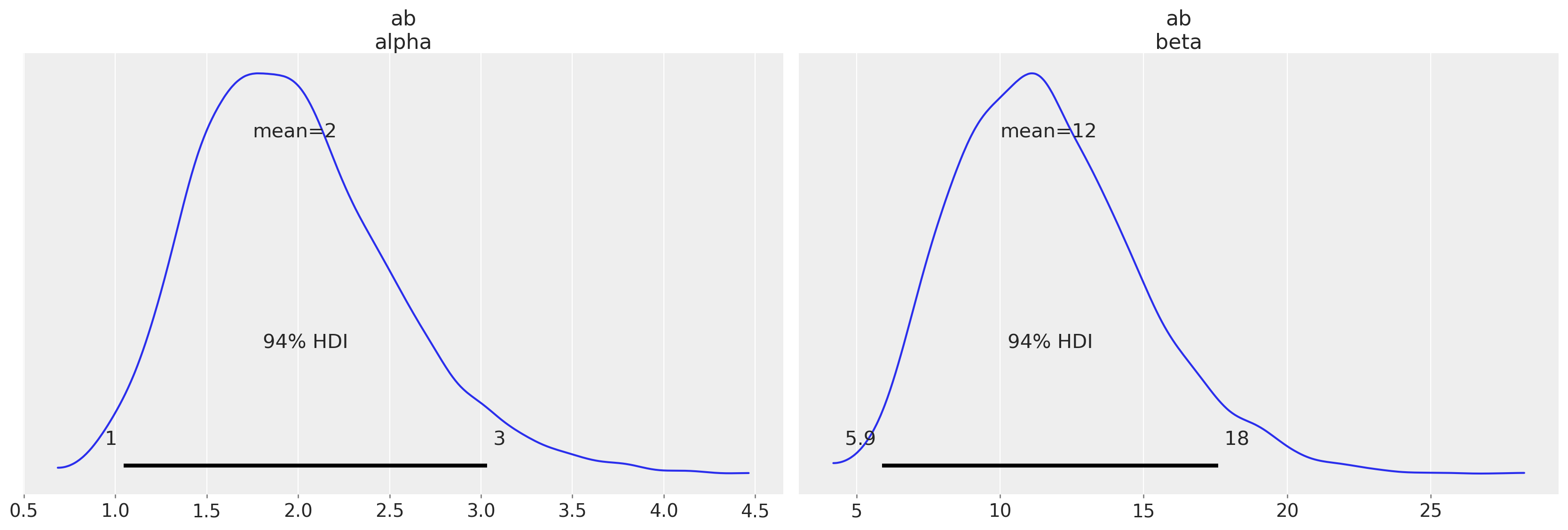
# estimate the means from the samples
trace.posterior["ab"].mean(("chain", "draw"))
<xarray.DataArray 'ab' (param: 2)> array([ 1.98032415, 11.68417729]) Coordinates: * param (param) <U5 'alpha' 'beta'
结论#
对于某些模型,解析计算后验分布的统计量非常困难,甚至不可能。PyMC 提供了一种简单的方法,只需几行代码即可从模型的后验分布中抽取样本。在这里,我们使用 PyMC 获取了 BDA3 第 5 章中大鼠肿瘤示例的后验均值估计值。从 PyMC 获得的估计值与从解析后验密度获得的估计值非常接近,令人鼓舞。
参考文献#
水印#
%load_ext watermark
%watermark -n -u -v -iv -w
Last updated: Tue Jan 10 2023
Python implementation: CPython
Python version : 3.11.0
IPython version : 8.8.0
matplotlib: 3.6.2
pymc : 5.0.1
arviz : 0.14.0
pytensor : 2.8.11
numpy : 1.24.1
pandas : 1.5.2
Watermark: 2.3.1
许可声明#
本示例库中的所有 Notebook 均根据 MIT 许可证提供,该许可证允许修改和再分发用于任何用途,前提是保留版权和许可声明。
引用 PyMC 示例#
要引用此 Notebook,请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。
重要提示
许多 Notebook 改编自其他来源:博客、书籍…… 在这种情况下,您也应引用原始来源。
另请记住引用代码中使用的相关库。
这是一个 bibtex 格式的引用模板
@incollection{citekey,
author = "<notebook authors, see above>",
title = "<notebook title>",
editor = "PyMC Team",
booktitle = "PyMC examples",
doi = "10.5281/zenodo.5654871"
}
渲染后可能如下所示