GLM-序数特征#

序数外生特征：贝叶斯工作流程的实践示例#

在此示例中，我们在模型中使用**序数外生预测特征**

y ~ x + e
y: Numeric
x: Ordinal Category

… 这与估计**序数内生目标特征**形成对比，我们在另一个 notebook 中展示了这一点

免责声明

  • 此 Notebook 仅为实践示例，并非旨在作为学术参考

  • 理论和数学可能不正确、符号错误或使用不当

  • 代码可能包含错误、低效、过时的方法，文本可能存在拼写错误

  • 使用风险自负！

目录#

讨论#

问题陈述#

人类行为和经济学都关乎表达我们在现实世界中有限选项之间的序数偏好。

我们经常遇到现实情况和数据集，其中预测特征是序数类别，记录偏好或总结指标值，这在保险和健康领域尤为常见。例如：

  • 作为完全主观的意见，在不同观察之间可能有所不同（例如 ["差", "中", "好", "更好", "好得多", "最好", "实际上最好"]）- 这些很难处理，并且是糟糕数据设计的症状

  • 在主观但标准化的量表上（例如 ["非常不同意", "不同意", "同意", "非常同意"]），这是熟悉的 李克特量表 的方法

  • 作为指标量表上真实客观值的汇总分箱（例如，将年龄分箱为年龄组 ["<30", "30 至 60", "60+"]），或已映射到指标量表的主观值（例如，医疗健康自评分 ["0-10%", ..., "90-100%"]） - 这些通常是对指标的误用，因为数据已被压缩（丢失信息），并且分箱的原因和箱边缘的选择通常是未知的

在所有这些情况下，关键问题是分类值及其序数等级不一定与目标变量线性相关。例如，在 4 值李克特量表（如上所示）中，"非常同意"（等级 4）的相对效应可能不是 "同意"（等级 3）加 1：3+1 != 4。

另一种说法是，序数类别之间的指标距离是未知的，并且可能是不相等的。例如，在 4 值李克特量表（如上所示）中，"不同意" vs "同意" 之间的差异可能与 "同意" vs "非常同意" 之间的差异不同。

不幸的是，这些属性可能会鼓励建模者将序数特征合并为分类特征（具有无限自由度 - 因此我们丢失了排序/等级信息），或者作为数值系数（忽略了不相等的间距、非线性响应）。两者都是糟糕的选择，并且对模型性能产生微妙的负面影响。

最后一个细微之处是，我们可能在训练数据集中看不到所有有效的分类序数级别。例如，我们可能知道范围是 ["c0", "c1", "c2", "c3"]，但只看到 ["c0", "c1", "c3"]。这是一个缺失数据问题，可能会进一步鼓励误用数值系数来平均或“插值”值。我们应该做的是将我们对数据领域的了解融入到模型结构中，以自动插补系数的值。这实际上是此处数据集中的情况（参见第 0 节）！

演示的数据和模型#

我们的问题陈述是，当面对这样的序数特征时，我们希望

  1. 推断一系列先验分配器，将序数类别转换为线性（多项式）量表

  2. 预测内生特征，像往常一样，捕获来自序数的信息

此 notebook 提供了一个机会来

  • 演示使用约束 Dirichlet 先验的通用方法，基于 [Bürkner P, 2018]，并在 Austin Rochford 的 pymc 特定示例中进行了演示 [Rochford, n.d.]

  • 通过结构性地纠正序数特征中缺失的级别值来改进这两种方法

  • 演示一个相当完整的贝叶斯工作流程 [Gelman et al., 2020]，包括数据整理和从 RDataset 获取数据

此 notebook 是另一个 notebook (TBD) 的伙伴，我们在其中估计**序数内生目标特征**。

设置#

注意

此 notebook 使用的库不是 PyMC 依赖项，因此需要专门安装才能运行此 notebook。打开下面的下拉菜单以获取更多指导。

额外依赖项安装说明

为了运行此 notebook（本地或在 binder 上），您不仅需要安装可用的 PyMC 以及所有可选依赖项，还需要安装一些额外的依赖项。有关安装 PyMC 本身的建议，请参阅 安装

您可以使用首选的软件包管理器安装这些依赖项，我们提供以下 pip 和 conda 命令作为示例。

$ pip install

请注意，如果您想（或需要）从 notebook 内部而不是命令行安装软件包，您可以通过运行 pip 命令的变体来安装软件包

import sys

!{sys.executable} -m pip install

您不应运行 !pip install，因为它可能会将软件包安装在不同的环境中，即使安装了也无法从 Jupyter notebook 中使用。

另一种选择是使用 conda 代替

$ conda install

当使用 conda 安装科学 python 软件包时，我们建议使用 conda forge

# uncomment to install in a Google Colab environment
# !pip install pyreadr watermark

from copy import deepcopy

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pyreadr
import pytensor.tensor as pt

from matplotlib import gridspec
from pymc.testing import assert_no_rvs

import warnings  # isort:skip # suppress seaborn, it's far too chatty

warnings.simplefilter(action="ignore", category=FutureWarning)  # isort:skip
import seaborn as sns

%matplotlib inline
%config InlineBackend.figure_format = 'retina'

sns.set_theme(
    style="darkgrid",
    palette="muted",
    context="notebook",
    rc={"figure.dpi": 72, "savefig.dpi": 144, "figure.figsize": (12, 4)},
)

# set target_accept quite high to minimise divergences in mdlb
SAMPLE_KWS = dict(
    progressbar=True,
    draws=500,
    tune=2000,
    chains=4,
    idata_kwargs=dict(log_likelihood=True),
)

USE_LOCAL_DATASET = False

0. 整理数据集#

我们使用与 [Bürkner P, 2018] 中相同的健康数据集，名为 ICFCoreSetCWP.RData，可在 R 软件包 ordPens 中找到

根据 Bürkner 论文（第 4 节：案例研究），此数据集来自一项关于**慢性广泛性疼痛 (CWP)** 的研究，其中 420 名患者对 67 个健康特征（每个特征都是主观序数类别）进行了自我调查，并被分配了一个不同生成的（也是主观的）身体健康指标。在数据集中，这 67 个特征被命名为，例如：
b1602, b102, … d450, d455, … s770 等，目标特征名为 phcs。

根据 Bürkner 论文，我们将子选择 2 个特征 d450, d455（衡量患者步行能力障碍的指标，量表为 [0 到 4] ["没有问题" 到 "完全有问题"]）并使用它们来预测 phcs。

非常有趣的是，对于特征 d450，最高序数级别值 4 在数据集中没有出现，因此我们遇到了缺失数据问题，这可能会进一步鼓励误用数值系数来平均或“插值”值。我们应该做的是将我们对数据领域的了解融入到模型结构中，以自动插补系数的值。这意味着我们的模型可以对可能出现 d450=4 值的新数据进行预测。

** *仅为了完整性（但此 notebook 不需要），该研究报告在 Gertheiss, J., Hogger, S., Oberhauser, C., & Tutz, G. (2011). Selection of ordinally 784 scaled independent variables with applications to international classification of functioning 785 core sets. Journal of the Royal Statistical Society: Series C (Applied Statistics), 60 (3), 786 377–395. *

注意，包含了一些样板步骤，但用 ~~删除线~~ 划掉了，并附有解释性注释，例如“在此简单示例中不需要”。这是为了保留逻辑工作流程，该工作流程通常更有用

0.1 提取#

令人恼火但不足为奇的是，对于 R 项目，尽管数据集是一个小的、简单的表格，但它仅以晦涩的 R 二进制格式提供，并且已压缩，因此我们将下载、解压并本地存储为普通的 CSV 文件。这使用了非常有用的 pyreadr 软件包。

if USE_LOCAL_DATASET:
    dfr = pd.read_csv("icf_core_set_cwp.csv", index_col="rownames")
else:
    import os
    import tarfile
    import urllib.request

    url = "https://cran.r-project.org.cn/src/contrib/ordPens_1.1.0.tar.gz"
    filehandle, _ = urllib.request.urlretrieve(url)
    rbytes = tarfile.open(filehandle).extractfile(member="ordPens/data/ICFCoreSetCWP.RData").read()
    fn = "ICFCoreSetCWP.RData"
    with open(fn, "wb") as f:
        f.write(rbytes)
    dfr = pyreadr.read_r(fn)["ICFCoreSetCWP"]
    os.remove(fn)
    dfr.to_csv("icf_core_set_cwp.csv")

print(dfr.shape)
display(pd.concat((dfr.describe(include="all").T, dfr.isnull().sum(), dfr.dtypes), axis=1))
display(dfr.head())

(420, 68)
计数 均值 标准差 最小值 25% 50% 75% 最大值 0 1
b1602 420.0 0.542857 0.901111 0.00 0.00 0.000 1.0000 3.00 0 int32
b122 420.0 0.533333 0.871908 0.00 0.00 0.000 1.0000 4.00 0 int32
b126 420.0 0.866667 0.982585 0.00 0.00 1.000 2.0000 3.00 0 int32
b130 420.0 1.180952 1.075045 0.00 0.00 1.000 2.0000 4.00 0 int32
b134 420.0 1.352381 1.147632 0.00 0.00 1.000 2.0000 4.00 0 int32
... ... ... ... ... ... ... ... ... ... ...
e575 420.0 0.350000 1.466857 -4.00 0.00 0.000 1.0000 4.00 0 int32
e580 420.0 1.080952 1.648929 -4.00 0.00 1.000 2.0000 4.00 0 int32
e590 420.0 0.190476 1.391040 -4.00 0.00 0.000 0.0000 4.00 0 int32
s770 420.0 0.890476 1.023544 0.00 0.00 1.000 2.0000 4.00 0 int32
phcs 420.0 32.407548 8.167084 10.08 26.58 31.865 37.5475 53.17 0 float64

68 行 × 10 列

b1602 b122 b126 b130 b134 b140 b147 b152 b164 b180 ... e450 e455 e460 e465 e570 e575 e580 e590 s770 phcs
rownames
1 0 1 2 1 1 0 0 2 0 0 ... 4 0 0 0 3 3 4 3 0 44.33
2 3 2 2 3 3 2 3 3 3 1 ... 3 3 2 2 2 2 2 2 2 21.09
3 0 1 2 1 1 0 1 2 0 0 ... 4 0 0 0 3 3 4 0 0 41.74
4 0 0 0 2 1 0 0 0 0 0 ... 2 2 -1 0 0 2 2 1 1 33.96
5 0 0 0 0 0 0 0 0 0 0 ... 1 0 0 0 0 0 0 0 0 46.29

5 行 × 68 列

观察

  • 看起来不错 - 如果这是一个合适的项目，我们想知道这些神秘的列标题实际上是什么意思

  • 为此目的，我们将仅使用几个特征 [d450, d455]，并将继续进行

0.2 清理#

fts_austin = ["d450", "d455", "phcs"]
df = dfr[fts_austin].copy()
display(pd.concat((df.describe(include="all").T, df.isnull().sum(), df.dtypes), axis=1))
df.head()
计数 均值 标准差 最小值 25% 50% 75% 最大值 0 1
d450 420.0 0.940476 0.998223 0.00 0.00 1.000 2.0000 3.00 0 int32
d455 420.0 1.585714 1.224174 0.00 1.00 2.000 2.0000 4.00 0 int32
phcs 420.0 32.407548 8.167084 10.08 26.58 31.865 37.5475 53.17 0 float64
d450 d455 phcs
rownames
1 0 2 44.33
2 3 3 21.09
3 0 2 41.74
4 3 2 33.96
5 0 0 46.29

~~0.2.1 清理观测值~~#

在此简单示例中不需要

0.2.2 清理特征#

~~0.2.2.1 重命名特征~~#

实际上不需要任何操作，当我们强制 dtype 并设置索引时，将重命名索引

~~0.2.2.2 更正特征~~#

在此简单示例中不需要

0.2.2.3 强制数据类型#

强制 d450 为字符串表示形式和有序分类 dtype（以 int 形式提供，这没有帮助）#

ft = "d450"
idx = df[ft].notnull()
df.loc[idx, ft] = df.loc[idx, ft].apply(lambda x: f"c{x}")
df[ft].unique()

array(['c0', 'c3', 'c1', 'c2'], dtype=object)

注意，强制分类级别包括 c4，这在数据领域中是有效的，但未观察到

lvls = ["c0", "c1", "c2", "c3", "c4"]
df[ft] = pd.Categorical(df[ft].values, categories=lvls, ordered=True)
df[ft].cat.categories

Index(['c0', 'c1', 'c2', 'c3', 'c4'], dtype='object')

强制 d455 为字符串表示形式和有序分类 dtype（以 int 形式提供，这没有帮助）#

ft = "d455"
idx = df[ft].notnull()
df.loc[idx, ft] = df.loc[idx, ft].apply(lambda x: f"c{x}")
df[ft].unique()

array(['c2', 'c3', 'c0', 'c1', 'c4'], dtype=object)

lvls = ["c0", "c1", "c2", "c3", "c4"]
df[ft] = pd.Categorical(df[ft].values, categories=lvls, ordered=True)
df[ft].cat.categories

Index(['c0', 'c1', 'c2', 'c3', 'c4'], dtype='object')

0.2.2.4 创建并设置索引#

df0 = df.reset_index()
df0["oid"] = df0["rownames"].apply(lambda n: f"o{str(n).zfill(3)}")
df = df0.drop("rownames", axis=1).set_index("oid").sort_index()
assert df.index.is_unique

0.3 非常有限的快速 EDA#

print(df.shape)
display(pd.concat((df.describe(include="all").T, df.isnull().sum(), df.dtypes), axis=1))
display(df.head())

(420, 3)
计数 唯一值 顶部 频率 均值 标准差 最小值 25% 50% 75% 最大值 0 1
d450 420 4 c0 189 NaN NaN NaN NaN NaN NaN NaN 0 category
d455 420 5 c2 113 NaN NaN NaN NaN NaN NaN NaN 0 category
phcs 420.0 NaN NaN NaN 32.407548 8.167084 10.08 26.58 31.865 37.5475 53.17 0 float64
d450 d455 phcs
oid
o001 c0 c2 44.33
o002 c3 c3 21.09
o003 c0 c2 41.74
o004 c3 c2 33.96
o005 c0 c0 46.29

0.3.1 单变量目标 phcs#

fts = ["phcs"]
v_kws = dict(data=df, cut=0)
cs = sns.color_palette(n_colors=len(fts))
f, axs = plt.subplots(len(fts), 1, figsize=(12, 1 + 1.4 * len(fts)), squeeze=False)
for i, ft in enumerate(fts):
    ax = sns.violinplot(x=ft, **v_kws, ax=axs[0][i], color=cs[i])
    _ = ax.set_title(ft)
_ = f.suptitle("Univariate numerics")
_ = f.tight_layout()
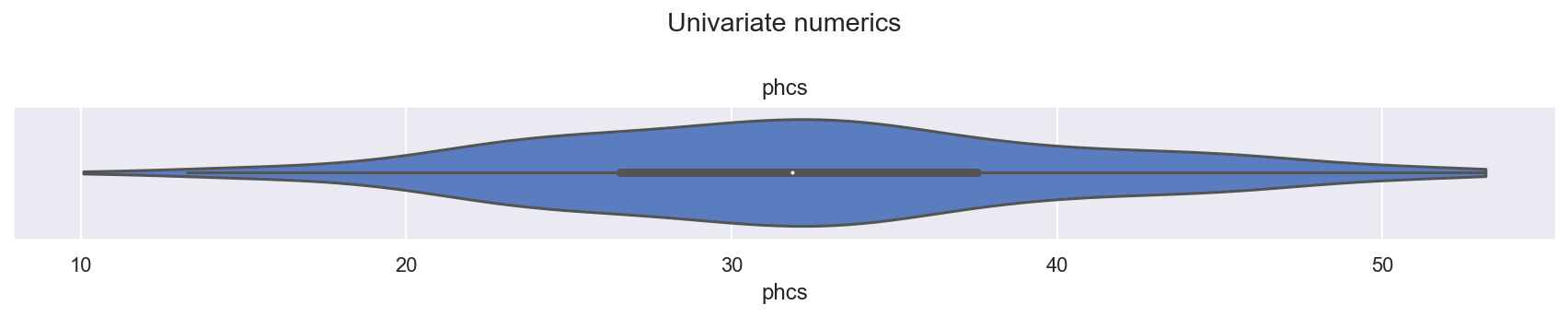
../_images/6ef5afd4f6618d3c0ed365a070e3a9ddea28b7ef7be11e7e131885f831f4ea37.png

观察

  • phcs 是身体健康的主观评分指标，有关详细信息，请参见 [Bürkner P, 2018]

  • 看起来表现良好，单峰，平滑

0.3.2 目标 phcs vs ['d450', 'd455']#

def plot_numeric_vs_cat(df, ftnum="phcs", ftcat="d450") -> plt.figure:
    f = plt.figure(figsize=(12, 3))
    gs = gridspec.GridSpec(1, 2, width_ratios=[4, 1], figure=f)
    ax0 = f.add_subplot(gs[0])
    ax1 = f.add_subplot(gs[1], sharey=ax0)
    _ = ax0.set(title=f"Distribution of `{ftnum}` wihin each `{ftcat}` category")
    _ = ax1.set(title=f"Count obs per `{ftcat}` category", ylabel=False)

    kws_box = dict(
        orient="h",
        showmeans=True,
        whis=(3, 97),
        meanprops=dict(markerfacecolor="w", markeredgecolor="#333333", marker="d", markersize=12),
    )

    _ = sns.boxplot(x=ftnum, y=ftcat, data=df, **kws_box, ax=ax0)  # hue=ftcat,
    _ = sns.countplot(y=ftcat, data=df, ax=ax1)  # hue=ftcat, seaborn >= 0.13
    _ = ax0.invert_yaxis()
    _ = ax1.yaxis.label.set_visible(False)
    _ = plt.setp(ax1.get_yticklabels(), visible=False)
    _ = f.suptitle(f"Summary stats for {len(df)} obs in dataset")
    _ = f.tight_layout()


f = plot_numeric_vs_cat(df, ftnum="phcs", ftcat="d450")
f = plot_numeric_vs_cat(df, ftnum="phcs", ftcat="d455")
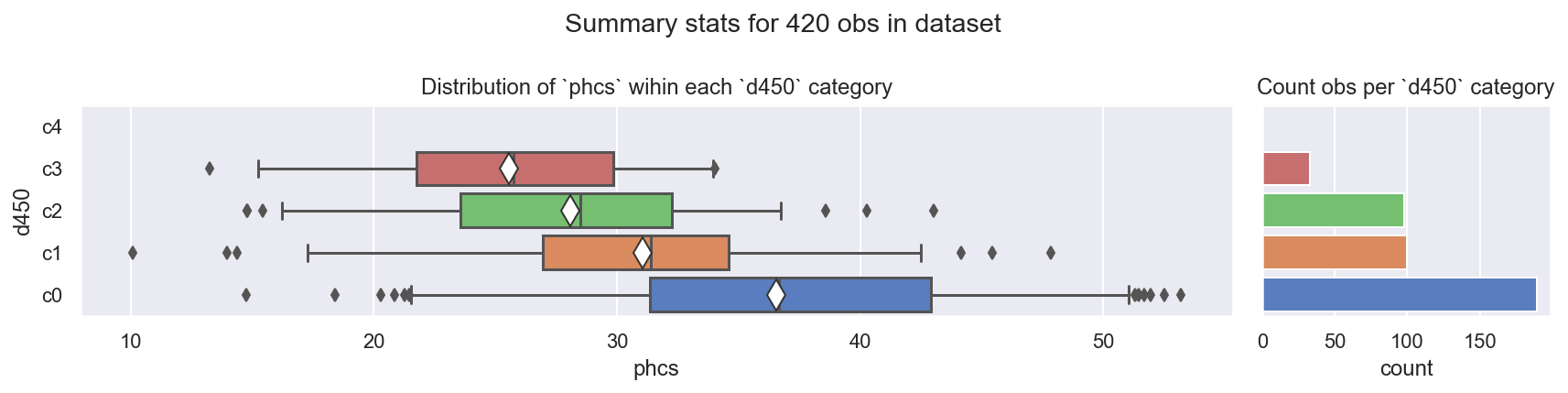
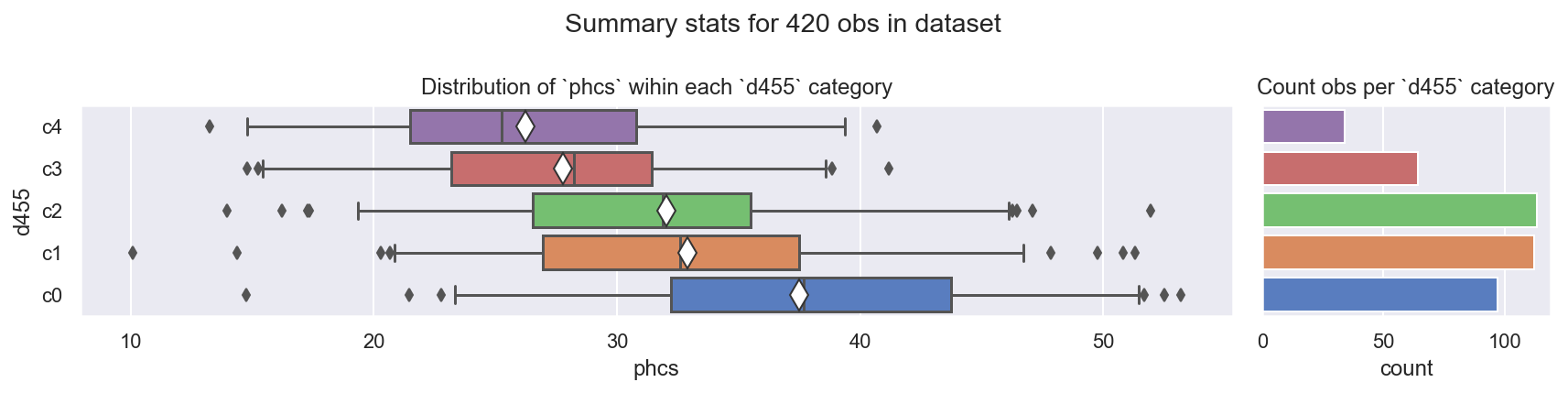
../_images/0f445f9b032e3e7693732b2051d3340186c4db3eec9ea8a6d29b2b59b4512af7.png ../_images/a2ebaab5ad80818b83df814fb6301e97b197054bb847e8dda7c3dc4967ec36ee.png

观察

phcs vs d450:

  • c0 更宽更高：可能是一个包罗万象的类别，因为它也被大量观察到

  • c3 计数较少

  • c4 未观察到：它在数据中缺失，尽管在数据领域中是有效的

phcs vs d455:

  • c1 和 c2 看起来非常相似

  • c4 计数较少

0.4 将数据集转换为模型输入的 dfx#

重要提示

  • 提醒一下，贝叶斯推断方法**不需要** test 数据集（也不需要 k 折交叉验证）来拟合参数。我们也不需要 holdout（样本外）数据集来评估模型性能，因为我们可以使用样本内 PPC、LOO-PIT 和 ELPD 评估

  • 因此，我们将整个数据集 df 用作模型输入

  • 根据真实世界的模型实现，我们可能会

    • 分离出一个 holdout 集（即使我们不需要它）来目视检查预测输出，但这里我们有一个汇总数据集，因此这既不可能也不合适

    • 创建一个 forecast 集来演示我们如何在生产中使用模型及其预测输出。

注意

  • 这是一个简化的/缩减的转换过程，仍然允许将来添加更多特征的可能性

基于其预先存在的分类顺序，将序数分类映射到序数数值（int）

df["d450_idx"] = df["d450"].cat.codes.astype(int)
df["d450_num"] = df["d450_idx"].copy()

df["d455_idx"] = df["d455"].cat.codes.astype(int)
df["d455_num"] = df["d455_idx"].copy()

转换（zscore 和缩放）数值

fts_num = ["d450_num", "d455_num"]
fts_non_num = ["d450_idx", "d455_idx"]
fts_y = ["phcs"]

MNS = np.nanmean(df[fts_num], axis=0)
SDEVS = np.nanstd(df[fts_num], axis=0)
dfx_num = (df[fts_num] - MNS) / SDEVS

icpt = pd.Series(np.ones(len(df)), name="intercept", index=dfx_num.index)

# concat including y_idx which will be used as observed
dfx = pd.concat((df[fts_y], icpt, df[fts_non_num], dfx_num), axis=1)
dfx.sample(5, random_state=42)
phcs 截距 d450_idx d455_idx d450_num d455_num
oid
o152 33.40 1.0 0 0 -0.943274 -1.296879
o351 45.42 1.0 1 1 0.059701 -0.479027
o185 31.40 1.0 2 3 1.062676 1.156676
o395 29.01 1.0 2 2 1.062676 0.338824
o449 23.32 1.0 2 0 1.062676 -1.296879

0.5 创建 forecast 集并转换为模型输入的 dffx#

注意： 我们偏离了 [Rochford, n.d.] 和 [Bürkner P, 2018] 中使用的数据集，以确保我们的 forecast 数据集包含 d450 和 d455 的所有有效级别。具体而言，观察到的数据集不包含域有效的 d450 = 4，因此我们将确保我们的预测集包含它。

LVLS_D450_D455 = ["c0", "c1", "c2", "c3", "c4"]
dff = pd.merge(
    pd.Series(LVLS_D450_D455, name="d450"), pd.Series(LVLS_D450_D455, name="d455"), how="cross"
)
dff["d450"] = pd.Categorical(dff["d450"].values, categories=LVLS_D450_D455, ordered=True)
dff["d455"] = pd.Categorical(dff["d455"].values, categories=LVLS_D450_D455, ordered=True)
dff["phcs"] = 0.0
dff["oid"] = [f"o{str(n).zfill(3)}" for n in range(len(dff))]
dff.set_index("oid", inplace=True)
dff.head()
d450 d455 phcs
oid
o000 c0 c0 0.0
o001 c0 c1 0.0
o002 c0 c2 0.0
o003 c0 c3 0.0
o004 c0 c4 0.0

转换为模型输入的 dffx

dff["d450_idx"] = dff["d450"].cat.codes.astype(int)
dff["d455_idx"] = dff["d455"].cat.codes.astype(int)
dff["d450_num"] = dff["d450_idx"].copy()
dff["d455_num"] = dff["d455_idx"].copy()

dffx_num = (dff[fts_num] - MNS) / SDEVS
icptf = pd.Series(np.ones(len(dff)), name="intercept", index=dffx_num.index)

# # concat including y_idx which will be used as observed
dffx = pd.concat((dff[fts_y], icptf, dff[fts_non_num], dffx_num), axis=1)
dffx.sample(5, random_state=42)
phcs 截距 d450_idx d455_idx d450_num d455_num
oid
o008 0.0 1.0 1 3 0.059701 1.156676
o016 0.0 1.0 3 1 2.065651 -0.479027
o000 0.0 1.0 0 0 -0.943274 -1.296879
o023 0.0 1.0 4 3 3.068627 1.156676
o011 0.0 1.0 2 1 1.062676 -0.479027

1. 模型 A：错误的方法 - 简单线性系数#

这是一个简单的线性模型，我们承认分类特征是有序的，但忽略了因子值对系数的影响可能不是等距的，而是假设等距

\[\begin{split} \begin{align} \sigma_{\beta} &\sim \text{InverseGamma}(11, 10) \\ \beta &\sim \text{Normal}(0, \sigma_{\beta}, \text{shape}=j) \\ \\ \text{lm} &= \beta^{T}\mathbb{x}_{i,j} \\ \epsilon &\sim \text{InverseGamma}(11, 10) \\ \hat{y_{i}} &\sim \text{Normal}(\mu=\text{lm}, \epsilon) \\ \end{align} \end{split}\]

其中

  • 观测值 \(i\) 包含数值特征 \(j\)，\(\hat{y_{i}}\) 是我们的估计值，此处为 phcs

  • 线性子模型 \(\beta^{T}\mathbb{x}_{ij}\) 让我们回归到这些特征上

  • 值得注意的是

    • \(\mathbb{x}_{i,d450}\) 被视为数值特征

    • \(\mathbb{x}_{i,d455}\) 被视为数值特征

1.1 构建模型对象#

ft_y = "phcs"
fts_x = ["intercept", "d450_num", "d455_num"]

COORDS = dict(oid=dfx.index.values, y_nm=ft_y, x_nm=fts_x)

with pm.Model(coords=COORDS) as mdla:
    # 0. create (Mutable)Data containers for obs (Y, X)
    y = pm.Data("y", dfx[ft_y].values, dims="oid")  # (i, )
    x = pm.Data("x", dfx[fts_x].values, dims=("oid", "x_nm"))  # (i, x)

    # 1. define priors for numeric exogs
    b_s = pm.InverseGamma("beta_sigma", alpha=11, beta=10)  # (1, )
    b = pm.Normal("beta", mu=0, sigma=b_s, dims="x_nm")  # (x, )

    # 2. define likelihood
    epsilon = pm.InverseGamma("epsilon", alpha=11, beta=10)
    _ = pm.Normal("phcs_hat", mu=pt.dot(x, b.T), sigma=epsilon, observed=y, dims="oid")

RVS_PPC = ["phcs_hat"]
RVS_SIMPLE_COMMON = ["beta_sigma", "beta", "epsilon"]

验证构建的模型结构是否符合我们的意图，并验证参数化#

display(pm.model_to_graphviz(mdla, formatting="plain"))
display(dict(unobserved=mdla.unobserved_RVs, observed=mdla.observed_RVs))
assert_no_rvs(mdla.logp())
mdla.debug(fn="logp", verbose=True)
mdla.debug(fn="random", verbose=True)
../_images/1ea15cd4f93d9bbbcc34d9ca6d39a4c0d4b60155874c3a29d5bca4e0fb4fb179.svg 
{'unobserved': [beta_sigma ~ InverseGamma(11, 10),
  beta ~ Normal(0, beta_sigma),
  epsilon ~ InverseGamma(11, 10)],
 'observed': [phcs_hat ~ Normal(f(beta), epsilon)]}

point={'beta_sigma_log__': array(0.), 'beta': array([0., 0., 0.]), 'epsilon_log__': array(0.)}

No problems found
point={'beta_sigma_log__': array(0.), 'beta': array([0., 0., 0.]), 'epsilon_log__': array(0.)}

No problems found

1.2 采样先验预测，查看诊断信息#

with mdla:
    ida = pm.sample_prior_predictive(
        var_names=RVS_PPC + RVS_SIMPLE_COMMON,
        samples=2000,
        return_inferencedata=True,
        random_seed=42,
    )

Sampling: [beta, beta_sigma, epsilon, phcs_hat]

1.2.1 样本内先验 PPC（追溯检查）#

def plot_ppc_retrodictive(idata, group="prior", mdlname="mdla", ynm="y") -> plt.figure:
    """Convenience plot PPC retrodictive KDE"""
    f, axs = plt.subplots(1, 1, figsize=(12, 3))
    _ = az.plot_ppc(idata, group=group, kind="kde", var_names=RVS_PPC, ax=axs, observed=True)
    _ = f.suptitle(f"In-sample {group.title()} PPC Retrodictive KDE on `{ynm}` - `{mdlname}`")
    return f


f = plot_ppc_retrodictive(ida, "prior", "mdla", "phcs")
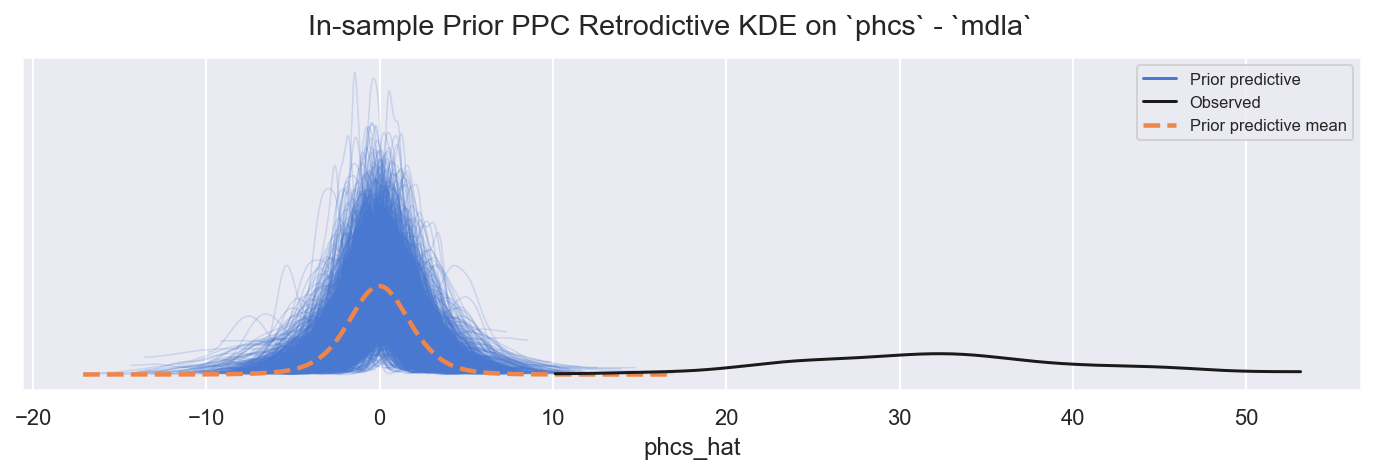
../_images/61fec3699aa82645df4220cd14aa25b7d6553113223e8452da77b7744bb1247a.png

观察

  • 值是错误的，正如预期的那样，但范围是合理的

1.2.2 快速查看选定的先验#

def plot_posterior(
    idata,
    group="prior",
    rvs=RVS_SIMPLE_COMMON,
    coords=None,
    mdlname="mdla",
    n=1,
    nrows=1,
) -> plt.figure:
    """Convenience plot posterior (or prior) KDE"""
    m = int(np.ceil(n / nrows))
    f, axs = plt.subplots(nrows, m, figsize=(2.4 * m, 0.8 + nrows * 1.4))
    _ = az.plot_posterior(idata, group=group, ax=axs, var_names=rvs, coords=coords)
    _ = f.suptitle(f"{group.title()} distributions for rvs {rvs} - `{mdlname}")
    _ = f.tight_layout()
    return f


f = plot_posterior(ida, "prior", rvs=RVS_SIMPLE_COMMON, mdlname="mdla", n=1 + 3 + 1, nrows=1)
../_images/13a76187774943c051e5cdc29be8a027970485d02908c7c5f24e90176a2d7442.png

观察

  • beta_sigma、beta: (levels)、epsilon 都具有指定的合理先验范围

1.3 采样后验，查看诊断信息#

1.3.1 采样后验和 PPC#

with mdla:
    ida.extend(pm.sample(**SAMPLE_KWS), join="right")
    ida.extend(
        pm.sample_posterior_predictive(trace=ida.posterior, var_names=RVS_PPC),
        join="right",
    )

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [beta_sigma, beta, epsilon]





Sampling 4 chains for 2_000 tune and 500 draw iterations (8_000 + 2_000 draws total) took 2 seconds.
Sampling: [phcs_hat]

















1.3.2 迹线#






def plot_traces_and_display_summary(idata, rvs, coords=None, mdlname="mdla") -> plt.figure:
    """Convenience to plot traces and display summary table for rvs"""
    _ = az.plot_trace(idata, var_names=rvs, coords=coords, figsize=(12, 1.4 * len(rvs)))
    f = plt.gcf()
    _ = f.suptitle(f"Posterior traces of {rvs} - `{mdlname}`")
    _ = f.tight_layout()
    _ = az.plot_energy(idata, fill_alpha=(0.8, 0.6), fill_color=("C0", "C8"), figsize=(12, 1.6))
    display(az.summary(idata, var_names=rvs))
    return f


f = plot_traces_and_display_summary(ida, rvs=RVS_SIMPLE_COMMON, mdlname="mdla")

















均值
标准差
hdi_3%
hdi_97%
mcse_mean
mcse_sd
ess_bulk
ess_tail
r_hat






beta_sigma
9.709
2.129
6.372
13.737
0.041
0.032
3311.0
1415.0
1.0




beta[截距]
32.368
0.344
31.719
32.972
0.007
0.005
2221.0
1565.0
1.0




beta[d450_num]
-2.995
0.396
-3.730
-2.246
0.010
0.007
1549.0
1522.0
1.0




beta[d455_num]
-1.790
0.406
-2.592
-1.090
0.010
0.007
1760.0
1470.0
1.0




epsilon
6.925
0.246
6.439
7.360
0.005
0.004
2189.0
1643.0
1.0






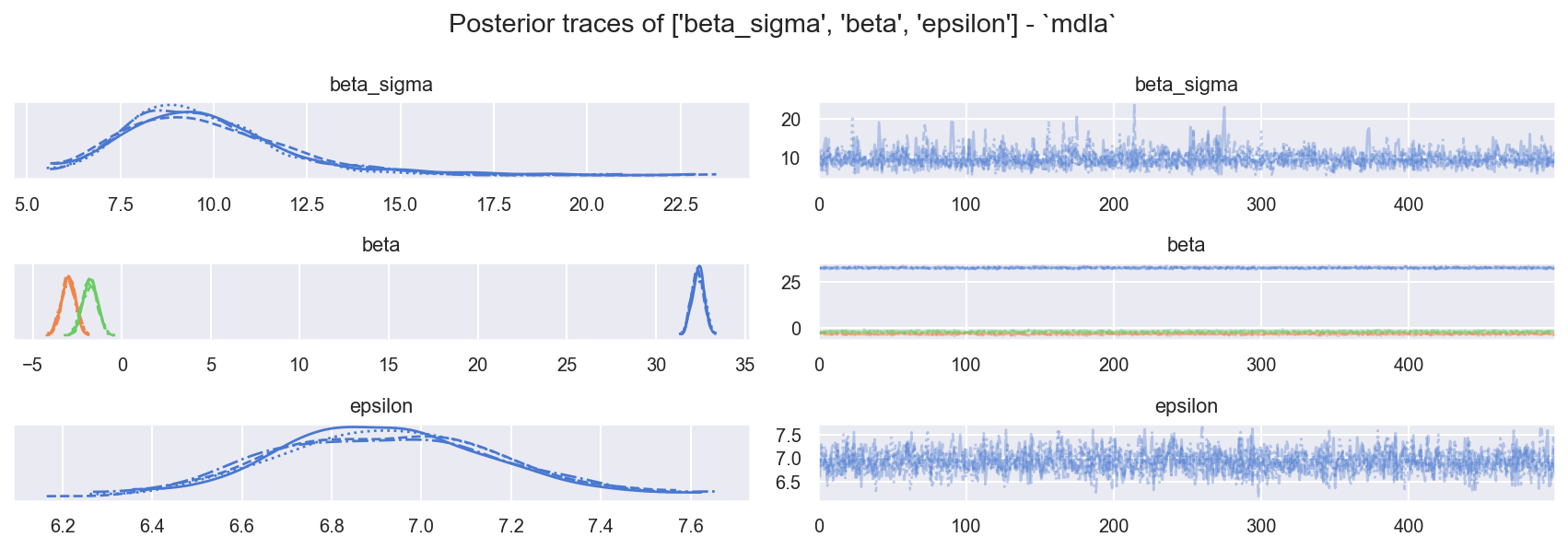
../_images/383fca2fd9138792f903e0967b94888968f4a921c923e101db2881f415198f80.png
../_images/3121114f12207dce8c50e2a3449c00ad60ce73d87ee2a93a8ce2e99e94e0119a.png





观察


    

  • 样本混合良好且表现良好
    

      

    • ess_bulk 良好，r_hat 良好
      • 

    

    • 

  • 边际能量 | 能量跃迁看起来合理
    


    • 







1.3.3 样本内后验 PPC（追溯检查）#






f = plot_ppc_retrodictive(ida, "posterior", "mdla", "phcs")








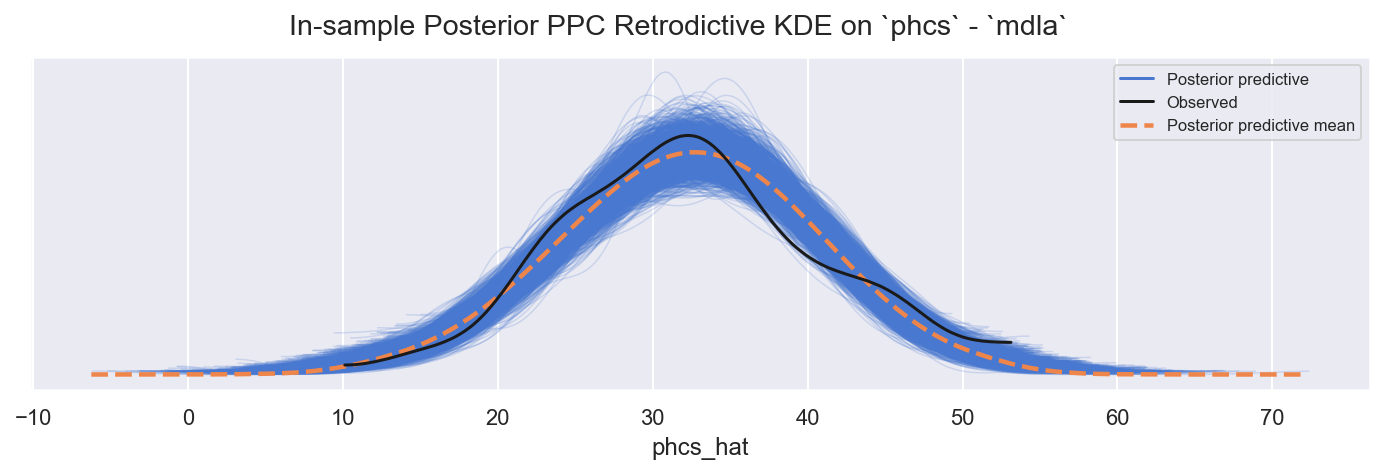
../_images/39132392ed2c01fca4699d9bdcaec78d0741845c538411b38eed6275ee5de0b7.png





观察


    

  • 样本内 PPC phcs_hat 适度地跟踪观察到的 phcs：略微过度分散，也许具有更肥尾部的可能性（例如 StudentT）会更合适
    • 







1.3.4 样本内 PPC LOO-PIT#






def plot_loo_pit(idata, mdlname="mdla", y="phcs_hat", y_hat="phcs_hat"):
    """Convenience plot LOO-PIT KDE and ECDF"""
    f, axs = plt.subplots(1, 2, figsize=(12, 2.4))
    _ = az.plot_loo_pit(idata, y=y, y_hat=y_hat, ax=axs[0])
    _ = az.plot_loo_pit(idata, y=y, y_hat=y_hat, ax=axs[1], ecdf=True)
    _ = axs[0].set_title(f"Predicted `{y_hat}` LOO-PIT")
    _ = axs[1].set_title(f"Predicted `{y_hat}` LOO-PIT cumulative")
    _ = f.suptitle(f"In-sample LOO-PIT `{mdlname}`")
    _ = f.tight_layout()
    return f


f = plot_loo_pit(ida, "mdla")








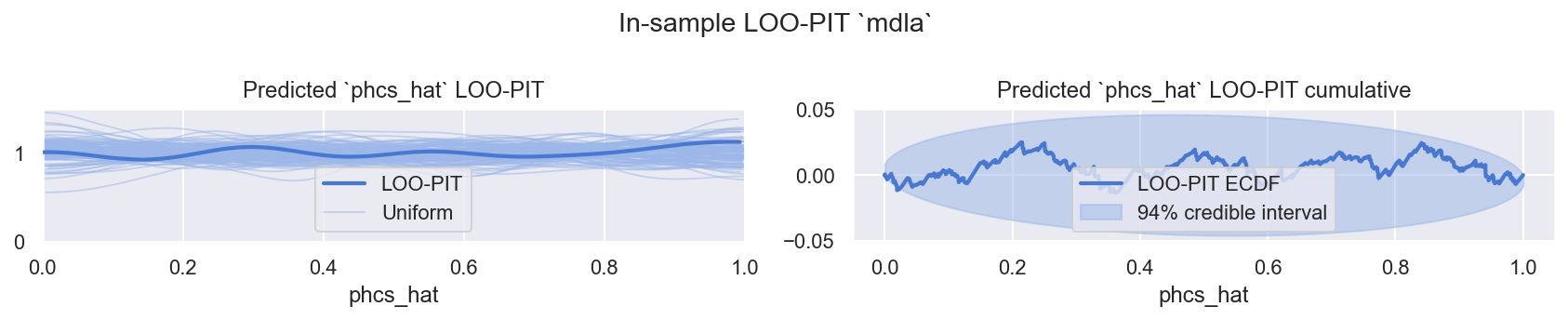
../_images/54d6d7c3f90601515b00527ed3ac8466c2c7dd3639805dc9d9d25e346a872645.png





观察


    

  • LOO-PIT 看起来不错，再次略微过度分散，但可以接受使用
    • 







~~1.3.5 将对数似然与其他模型进行比较~~#






# Nothing to compare yet















1.4 评估后验参数#




1.4.1 单变量#


参数很多，让我们慢慢来






f = plot_posterior(ida, "posterior", rvs=RVS_SIMPLE_COMMON, mdlname="mdla", n=5, nrows=1)








../_images/f38006453bcbbd86bf83a3167aa5a55ae5dd44a09668de95d3e01f0396149763.png





观察


    

  • beta_sigma：E ~ 10 表示需要 beta 位置的高方差
    • 

  • beta: intercept：E ~ 32 证实 beta 位置方差的大部分仅仅是由于将 zscore 值带入 phcs 范围所需的截距偏移，没有问题
    • 

  • beta: d450_num：E ~ -3 负数，HDI94 不跨越 0，效果显着，平滑的中心分布
    

      

    • d450_num 的较高值会减少 phcs_hat
      • 

    

    • 

  • beta: d455_num：E ~ -2 负数，HDI94 不跨越 0，效果显着，平滑的中心分布
    

      

    • d455_num 的较高值会略微减少 phcs_hat
      • 

    

    • 

  • epsilon：E ~ 7 表示数据中仍然存在相当大的方差，尚未通过建模特征处理
    • 









1.5 在简化的 forecast 集上创建 PPC 预测#


仅为了完整性，仅与 Bürkner 论文和 Rochford 的博客文章中的图 3 进行比较。这些图总结为平均值，但这似乎没有必要 - 让我们用完整的样本后验稍微改进一下




用 dffx 替换数据集并重建#






COORDS_F = deepcopy(COORDS)
COORDS_F["oid"] = dffx.index.values
mdla.set_data("y", dffx[ft_y].values, coords=COORDS_F)
mdla.set_data("x", dffx[fts_x].values, coords=COORDS_F)

display(pm.model_to_graphviz(mdla, formatting="plain"))
assert_no_rvs(mdla.logp())
mdla.debug(fn="logp", verbose=True)
mdla.debug(fn="random", verbose=True)








../_images/f7bfa573538510d59d19b862666b1b7b9cb5c52a74c27a6c54bfc4caa7ff823c.svg

point={'beta_sigma_log__': array(0.), 'beta': array([0., 0., 0.]), 'epsilon_log__': array(0.)}

No problems found
point={'beta_sigma_log__': array(0.), 'beta': array([0., 0., 0.]), 'epsilon_log__': array(0.)}

No problems found













with mdla:
    ida_ppc = pm.sample_posterior_predictive(
        trace=ida.posterior, var_names=RVS_PPC, predictions=True
    )









Sampling: [phcs_hat]

















1.5.2 查看预测#






def plot_predicted_phcshat_d450_d455(idata, mdlname) -> plt.Figure:
    """Convenience to plot predicted phcs_hat vs d450 and d455"""
    phcs_hat = (
        az.extract(idata, group="predictions", var_names=["phcs_hat"])
        .to_dataframe()
        .drop(["chain", "draw"], axis=1)
    )
    dfppc = pd.merge(
        phcs_hat.reset_index(),
        dff[["d450", "d455"]].reset_index(),
        how="left",
        on="oid",
    )

    kws = dict(
        y="phcs_hat",
        data=dfppc,
        linestyles=":",
        estimator="mean",
        errorbar=("pi", 94),
        dodge=0.2,
    )

    f, axs = plt.subplots(1, 2, figsize=(12, 6), sharey=True)
    _ = sns.pointplot(x="d450", hue="d455", **kws, ax=axs[0], palette="plasma_r")
    _ = sns.pointplot(x="d455", hue="d450", **kws, ax=axs[1], palette="viridis_r")
    _ = [axs[i].set_title(t) for i, t in enumerate(["d450 x d455", "d455 x d450"])]
    _ = f.suptitle(
        "Domain specific plot of posterior predicted `phcs_hat`"
        + f" vs `d450` and `d455` - `{mdlname}`"
    )
    _ = f.tight_layout()


plot_predicted_phcshat_d450_d455(idata=ida_ppc, mdlname="mdla")








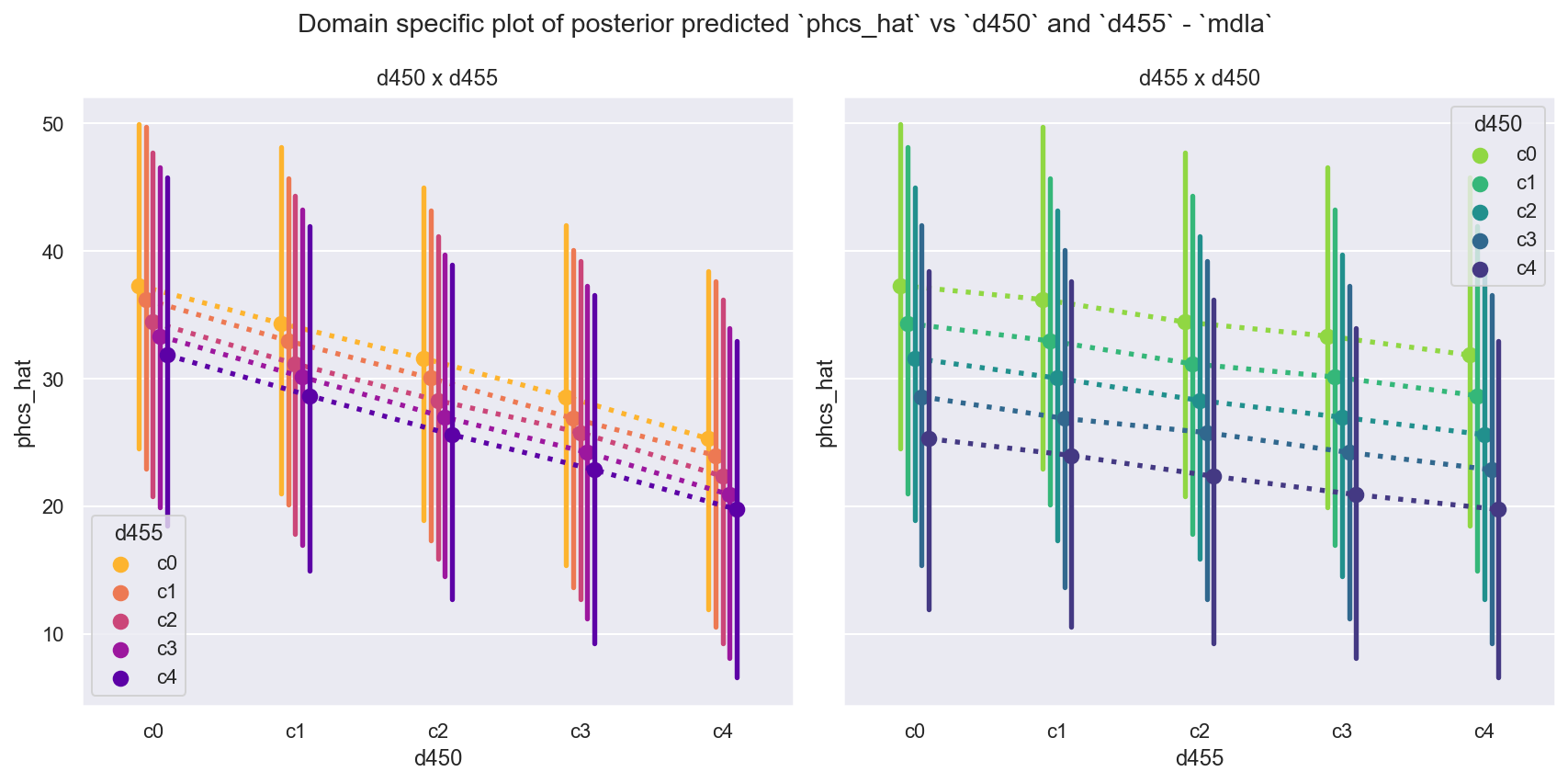
../_images/8c7b81277582b67f5e991fe9f49ffe8a6c71036e69d27489ca4595c7fbc12c8a.png





观察


    

  • 将其与 [Rochford, n.d.] 中的最终图和 [Bürkner P, 2018] 中的图 12 进行比较
    • 

  • 我们看到当 d450 和 d455 被视为数值时，它们的线性响应和相等间距。
    • 

  • 我们还看到 mdla 技术上可以对 d450=c4 进行预测，这在数据中是看不到的。然而，这种预测纯粹是线性外推，虽然在某种意义上有所帮助，但在这种模型设定中可能是完全且具有误导性的错误。
    • 

  • 请注意，这里我们绘制了每个数据点的完整后验分布（而不是总结为均值），这强调了数据和模型中仍然存在大量方差。
    • 















2. 模型 B：更好的方法 - 狄利克雷超先验分配器#


这是一个改进的线性模型，我们承认类别特征是有序的，并且允许有序值具有非相等间距。例如，很可能是 A > B > C，但间距不是度量的：而是 A >>> B > C。我们使用狄利克雷超先验来分配线性系数的非均匀间隔的段来实现这一点。


\[\begin{split} \begin{align} \sigma_{\beta} &\sim \text{InverseGamma}(11, 10) \\ \beta &\sim \text{Normal}(0, \sigma_{\beta}, \text{shape}=j) \\ \\ \beta_{d450} &\sim \text{Normal}(0, \sigma_{\beta}) \\ \chi_{d450} &\sim \text{Dirichlet}(1, \text{shape}=k_{d450}) \\ \nu_{d450} &\sim \beta_{d450} * \sum_{k=0}^{k=k_{d450}}\chi_{d450} \\ \\ \beta_{d455} &\sim \text{Normal}(0, \sigma_{\beta}) \\ \chi_{d455} &\sim \text{Dirichlet}(1, \text{shape}=k_{d455}) \\ \nu_{d455} &\sim \beta_{d455} * \sum_{k=0}^{k=k_{d455}}\chi_{d455} \\ \\ lm &= \beta^{T}\mathbb{x}_{i,j} + \nu_{d450}[x_{i,d450}] + \nu_{d455}[x_{i,d455}]\\ \epsilon &\sim \text{InverseGamma}(11, 10) \\ \hat{y_{i}} &\sim \text{Normal}(\mu=lm, \epsilon) \\ \end{align} \end{split}\]


其中


    

  • 观测值 \(i\) 包含数值特征 \(j\) 和有序类别特征 \(k\) (这里是 d450, d455)，它们各自具有因子值水平 \(k_{d450}, k_{d455}\)，并请注意根据第 0 节，这些都在 [0 - 4] 范围内，如笔记本变量 LVLS_D450_D455 记录的那样。
    • 

  • \(\hat{y_{i}}\) 是我们的估计值，这里是 phcs 的估计值。
    • 

  • 线性子模型 \(lm = \beta^{T}\mathbb{x}_{i,j} + \nu_{d450}[x_{i,d450}] + \nu_{d455}[x_{i,d455}]\) 让我们回归到这些特征。
    • 

  • 值得注意的是
    

      

    • \(\mathbb{x}_{i,d450}\) 被视为有序特征，并用于索引 \(\nu_{d450}[x_{i,d450}]\)。
      • 

    • \(\mathbb{x}_{i,d455}\) 被视为有序特征，并用于索引 \(\nu_{d455}[x_{i,d455}]\)。
      • 

    

    • 

  • 注意：上述规范并非特别优化/向量化/DRY，以帮助解释。
    • 





2.1 构建模型对象#






ft_y = "phcs"
fts_x = ["intercept"]
# NOTE fts_ord = ['d450_idx', 'd455_idx']

COORDS = dict(
    oid=dfx.index.values,
    y_nm=ft_y,
    x_nm=fts_x,
    d450_nm=LVLS_D450_D455,  # not list(df[d450].cat.categories) because c4 missing
    d455_nm=list(df["d455"].cat.categories),
)













with pm.Model(coords=COORDS) as mdlb:
    # NOTE: Spec not particularly optimised / vectorised / DRY to aid explanation

    # 0. create (Mutable)Data containers for obs (Y, X)
    y = pm.Data("y", dfx[ft_y].values, dims="oid")  # (i, )
    x = pm.Data("x", dfx[fts_x].values, dims=("oid", "x_nm"))  # (i, x)
    idx_d450 = pm.Data("idx_d450", dfx["d450_idx"].values, dims="oid")  # (i, )
    idx_d455 = pm.Data("idx_d455", dfx["d455_idx"].values, dims="oid")  # (i, )

    # 1. define priors for numeric exogs
    b_s = pm.InverseGamma("beta_sigma", alpha=11, beta=10)  # (1, )
    b = pm.Normal("beta", mu=0, sigma=b_s, dims="x_nm")  # (x, )

    # 2. define nu
    def _get_nu(nm, dim):
        """Partition continuous prior into ordinal chunks"""
        b0 = pm.Normal(f"beta_{nm}", mu=0, sigma=b_s)  # (1, )
        c0 = pm.Dirichlet(f"chi_{nm}", a=np.ones(len(COORDS[dim])), dims=dim)  # (lvls, )
        return pm.Deterministic(f"nu_{nm}", b0 * c0.cumsum(), dims=dim)  # (lvls, )

    nu_d450 = _get_nu("d450", "d450_nm")
    nu_d455 = _get_nu("d455", "d455_nm")

    # 3. define likelihood
    epsilon = pm.InverseGamma("epsilon", alpha=11, beta=10)
    _ = pm.Normal(
        "phcs_hat",
        mu=pt.dot(x, b.T) + nu_d450[idx_d450] + nu_d455[idx_d455],
        sigma=epsilon,
        observed=y,
        dims="oid",
    )

rvs_simple = RVS_SIMPLE_COMMON + ["beta_d450", "beta_d455"]
rvs_d450 = ["chi_d450", "nu_d450"]
rvs_d455 = ["chi_d455", "nu_d455"]











验证构建的模型结构是否符合我们的意图，并验证参数化。#






display(pm.model_to_graphviz(mdlb, formatting="plain"))
display(dict(unobserved=mdlb.unobserved_RVs, observed=mdlb.observed_RVs))
assert_no_rvs(mdlb.logp())
mdlb.debug(fn="logp", verbose=True)
mdlb.debug(fn="random", verbose=True)








../_images/712bd2d2b8c193c6fb8caefee627dda7f3b21c5c3cfbdf5691821b5889bfc0d2.svg

{'unobserved': [beta_sigma ~ InverseGamma(11, 10),
  beta ~ Normal(0, beta_sigma),
  beta_d450 ~ Normal(0, beta_sigma),
  chi_d450 ~ Dirichlet(<constant>),
  beta_d455 ~ Normal(0, beta_sigma),
  chi_d455 ~ Dirichlet(<constant>),
  epsilon ~ InverseGamma(11, 10),
  nu_d450 ~ Deterministic(f(chi_d450, beta_d450)),
  nu_d455 ~ Deterministic(f(chi_d455, beta_d455))],
 'observed': [phcs_hat ~ Normal(f(beta, chi_d455, beta_d455, chi_d450, beta_d450), epsilon)]}





point={'beta_sigma_log__': array(0.), 'beta': array([0.]), 'beta_d450': array(0.), 'chi_d450_simplex__': array([0., 0., 0., 0.]), 'beta_d455': array(0.), 'chi_d455_simplex__': array([0., 0., 0., 0.]), 'epsilon_log__': array(0.)}

No problems found
point={'beta_sigma_log__': array(0.), 'beta': array([0.]), 'beta_d450': array(0.), 'chi_d450_simplex__': array([0., 0., 0., 0.]), 'beta_d455': array(0.), 'chi_d455_simplex__': array([0., 0., 0., 0.]), 'epsilon_log__': array(0.)}

No problems found















2.2 先验预测抽样，查看诊断结果#






with mdlb:
    idb = pm.sample_prior_predictive(
        var_names=RVS_PPC + rvs_simple + rvs_d450 + rvs_d455,
        samples=2000,
        return_inferencedata=True,
        random_seed=42,
    )









Sampling: [beta, beta_d450, beta_d455, beta_sigma, chi_d450, chi_d455, epsilon, phcs_hat]











2.2.1 样本内先验 PPC（回顾性检查）#






f = plot_ppc_retrodictive(idb, "prior", "mdlb", "phcs")








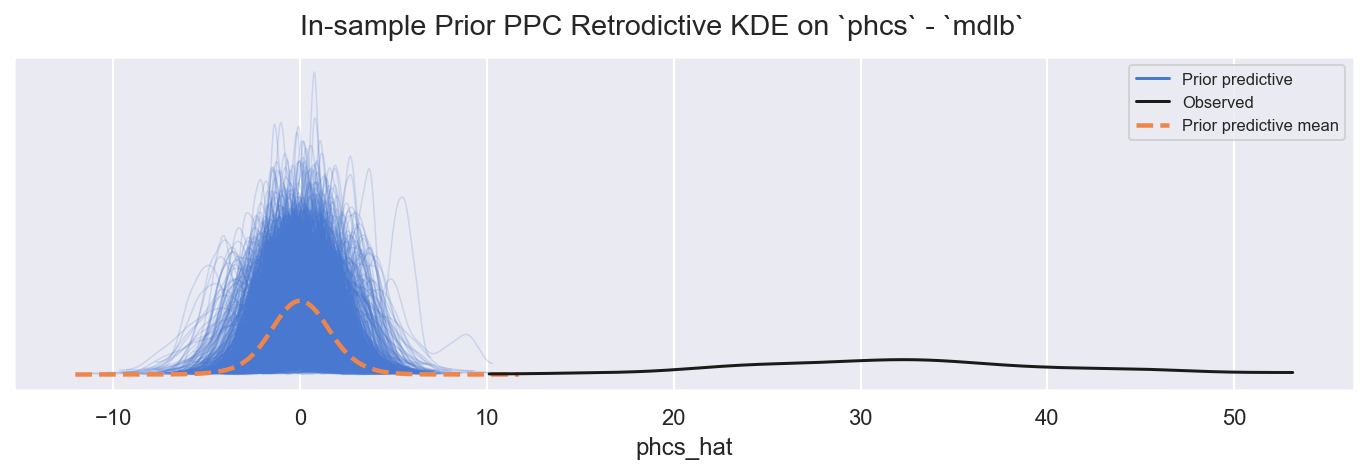
../_images/2143c98e8a36be048efaa89bb1a3c0130783daac23317545c5e06ab88c5f1453.png





观察


    

  • 值是错误的，正如预期的那样，但范围是合理的
    • 







2.2.2 快速查看选定的先验#






f = plot_posterior(idb, "prior", rvs=rvs_simple, mdlname="mdlb", n=5, nrows=1)
f = plot_posterior(idb, "prior", rvs=rvs_d450, mdlname="mdlb", n=5 * 2, nrows=2)
f = plot_posterior(idb, "prior", rvs=rvs_d455, mdlname="mdlb", n=5 * 2, nrows=2)








../_images/52fb04d4e71740b4e5b2c080d1adf8937dfff76e4030d91dbd6eea647ebdb186.png
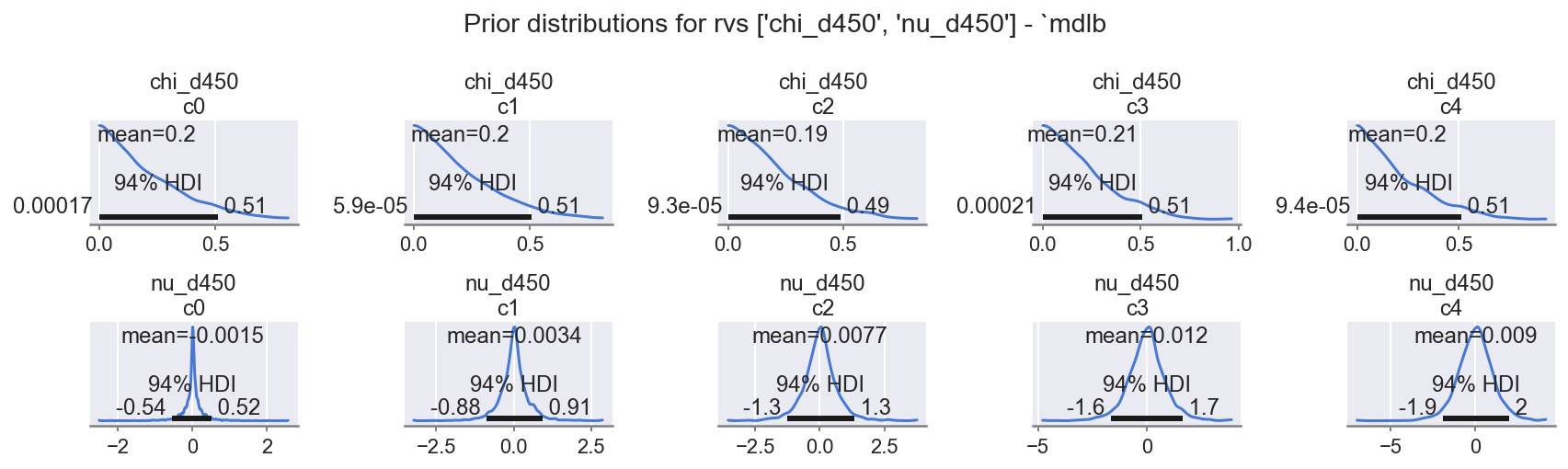
../_images/f5ab1bf70daa1dd04d60f3d3477cb1f887e683fd9e82e3609e4afce389e7b009.png
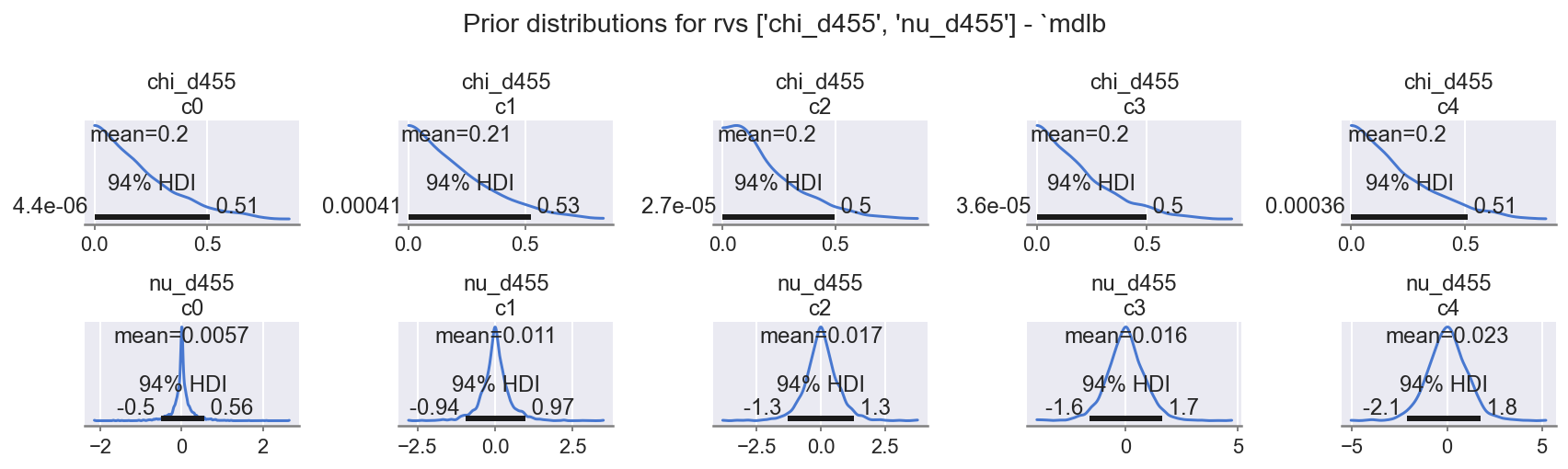
../_images/04334a5e5d9347c01b2ab4fe7c6da1c82bb99c036701c898b9c5c153d37c18a9.png





观察


    

  • 几个新参数！
    • 

  • beta_sigma、beta: (levels)、epsilon：都具有合理的先验范围，如指定的那样。
    • 

  • *_d450:
    

      

    • chi_*：遵守狄利克雷分布的单纯形约束并跨越范围。
      • 

    • nu_*：所有都如指定的那样合理，请注意先验中已存在的排序。
      • 

    

    • 

  • *_d455:
    

      

    • chi_*：遵守狄利克雷分布的单纯形约束并跨越范围。
      • 

    • nu_*：所有都如指定的那样合理，请注意先验中已存在的排序。
      • 

    

    • 









2.3 后验抽样，查看诊断结果#




2.3.1 后验抽样和 PPC#






SAMPLE_KWS["target_accept"] = 0.9  # raise to mitigate some minor divergences
with mdlb:
    idb.extend(pm.sample(**SAMPLE_KWS), join="right")
    idb.extend(
        pm.sample_posterior_predictive(trace=idb.posterior, var_names=RVS_PPC),
        join="right",
    )









Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [beta_sigma, beta, beta_d450, chi_d450, beta_d455, chi_d455, epsilon]









Sampling 4 chains for 2_000 tune and 500 draw iterations (8_000 + 2_000 draws total) took 17 seconds.
Sampling: [phcs_hat]

















2.3.2 迹线图#






f = plot_traces_and_display_summary(idb, rvs=rvs_simple + rvs_d450 + rvs_d455, mdlname="mdlb")

















均值
标准差
hdi_3%
hdi_97%
mcse_mean
mcse_sd
ess_bulk
ess_tail
r_hat






beta_sigma
12.471
2.620
8.293
17.221
0.081
0.058
1180.0
1215.0
1.00




beta[截距]
40.668
2.134
37.460
44.760
0.085
0.061
758.0
577.0
1.00




epsilon
6.858
0.239
6.442
7.350
0.006
0.004
1669.0
1214.0
1.01




beta_d450
-11.531
3.144
-17.884
-6.711
0.111
0.082
884.0
729.0
1.01




beta_d455
-7.317
2.010
-11.477
-4.036
0.071
0.054
957.0
676.0
1.00




chi_d450[c0]
0.114
0.097
0.000
0.294
0.003
0.002
862.0
791.0
1.00




chi_d450[c1]
0.392
0.116
0.175
0.601
0.003
0.002
1135.0
1254.0
1.00




chi_d450[c2]
0.187
0.095
0.013
0.350
0.003
0.002
1194.0
723.0
1.00




chi_d450[c3]
0.131
0.084
0.001
0.280
0.002
0.002
971.0
731.0
1.00




chi_d450[c4]
0.177
0.141
0.000
0.443
0.004
0.003
1324.0
1140.0
1.00




nu_d450[c0]
-1.389
1.419
-3.865
-0.000
0.057
0.046
752.0
765.0
1.00




nu_d450[c1]
-5.658
1.708
-9.063
-3.088
0.061
0.049
1055.0
860.0
1.01




nu_d450[c2]
-7.688
1.691
-10.774
-5.055
0.059
0.046
1080.0
860.0
1.01




nu_d450[c3]
-9.194
1.880
-12.915
-6.119
0.065
0.050
1056.0
814.0
1.01




nu_d450[c4]
-11.531
3.144
-17.884
-6.711
0.111
0.082
884.0
729.0
1.01




chi_d455[c0]
0.145
0.122
0.000
0.381
0.004
0.003
821.0
817.0
1.00




chi_d455[c1]
0.324
0.116
0.112
0.545
0.003
0.002
1326.0
932.0
1.00




chi_d455[c2]
0.059
0.058
0.000
0.161
0.002
0.001
963.0
680.0
1.00




chi_d455[c3]
0.310
0.133
0.073
0.552
0.004
0.003
1104.0
1133.0
1.00




chi_d455[c4]
0.162
0.111
0.000
0.353
0.002
0.002
1744.0
1283.0
1.00




nu_d455[c0]
-1.200
1.331
-3.583
-0.001
0.053
0.040
751.0
744.0
1.00




nu_d455[c1]
-3.519
1.671
-6.616
-0.768
0.061
0.047
913.0
770.0
1.00




nu_d455[c2]
-3.921
1.667
-7.013
-1.082
0.060
0.047
985.0
723.0
1.00




nu_d455[c3]
-6.121
1.855
-9.777
-3.095
0.065
0.050
986.0
740.0
1.00




nu_d455[c4]
-7.317
2.010
-11.477
-4.036
0.071
0.054
957.0
676.0
1.00






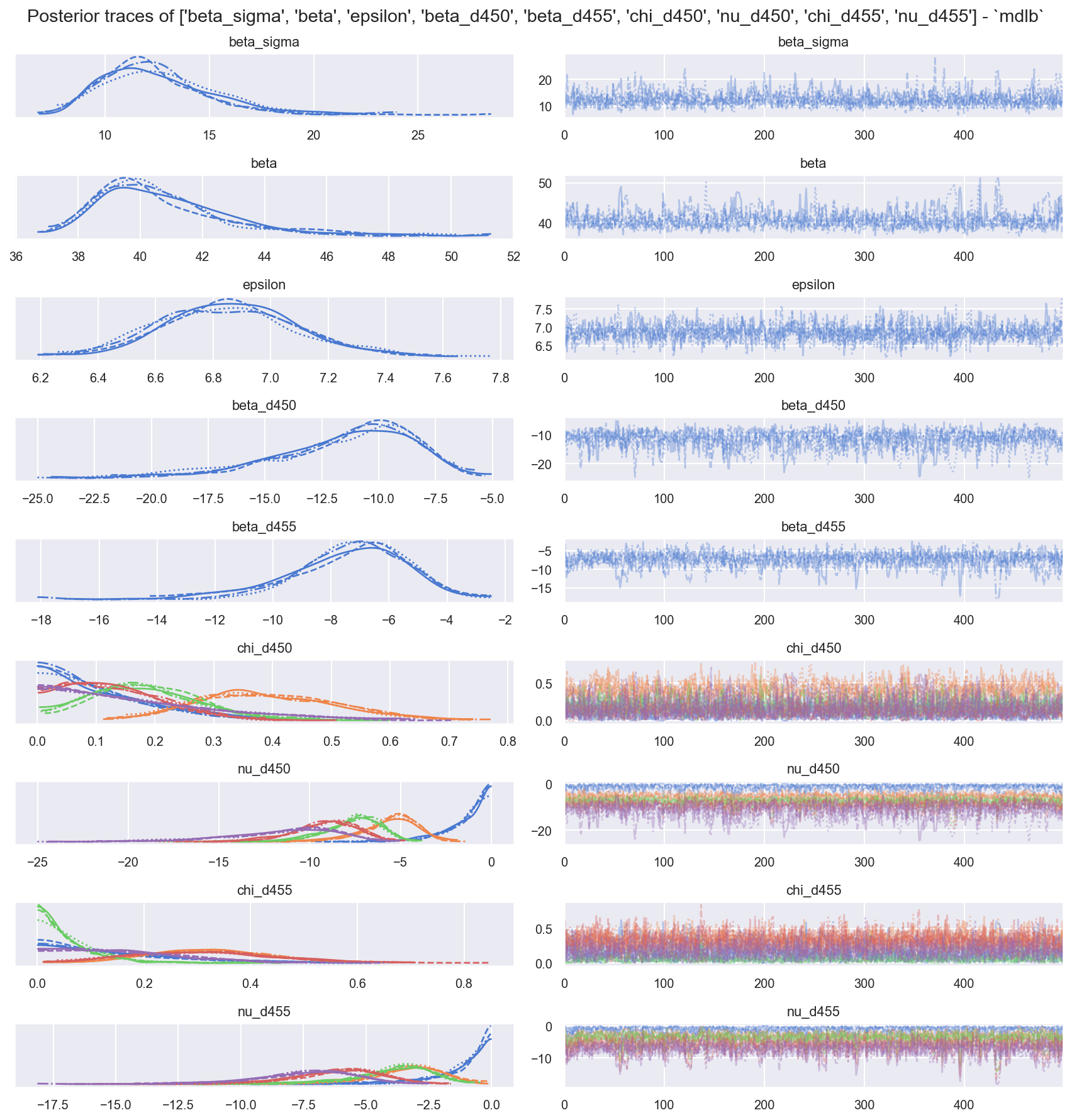
../_images/b7c35a765924250aba30cea9799be6bef9b2a0ff036694356cfe65aa6e5f49e0.png
../_images/83bf95c73e016fc77436198ddec591cf809f76946b083282ad9cf0f6d5640b0e.png





观察


    

  • 样本混合良好且表现良好，但请注意，我们提高了 target_accept=0.9 以减轻/避免在 0.8 时看到的发散。
    

      

    • ess_bulk 有点低，r_hat 还可以。
      • 

    

    • 

  • 边际能量 | 能量跃迁看起来合理
    


    • 







2.3.3 样本内后验 PPC（回顾性检查）#






f = plot_ppc_retrodictive(idb, "posterior", "mdlb", "phcs")








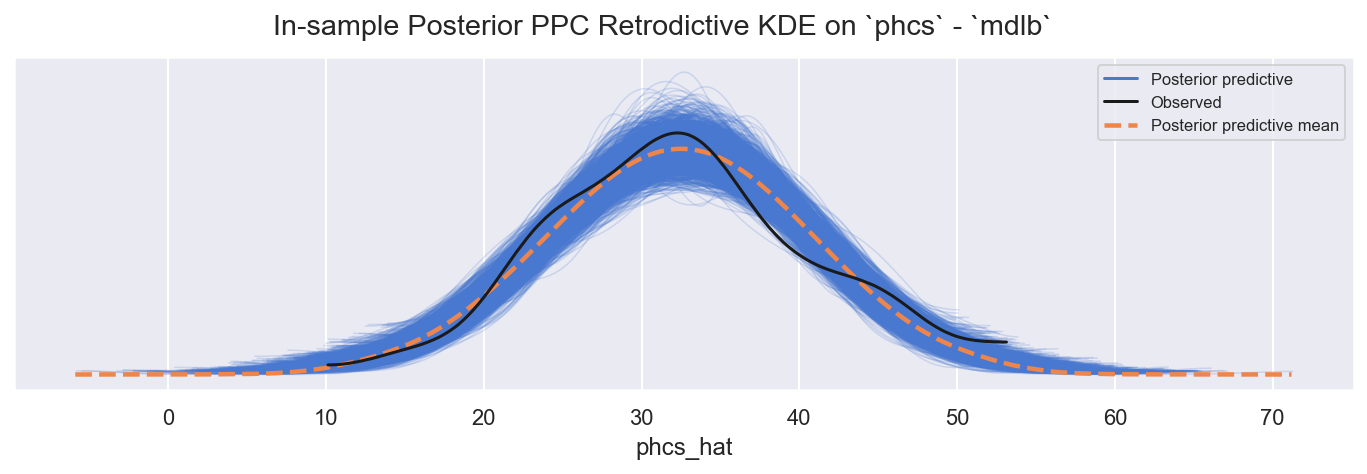
../_images/e4d47865121634c7855f143894e4fbfb47df8e9373b8d19756731dfe0927b5e0.png





观察


    

  • 样本内 PPC phcs_hat 适度地跟踪观察到的 phcs：略微过度分散，也许具有更肥尾部的可能性（例如 StudentT）会更合适
    • 







2.3.4 样本内 PPC LOO-PIT#






f = plot_loo_pit(idb, "mdlb")








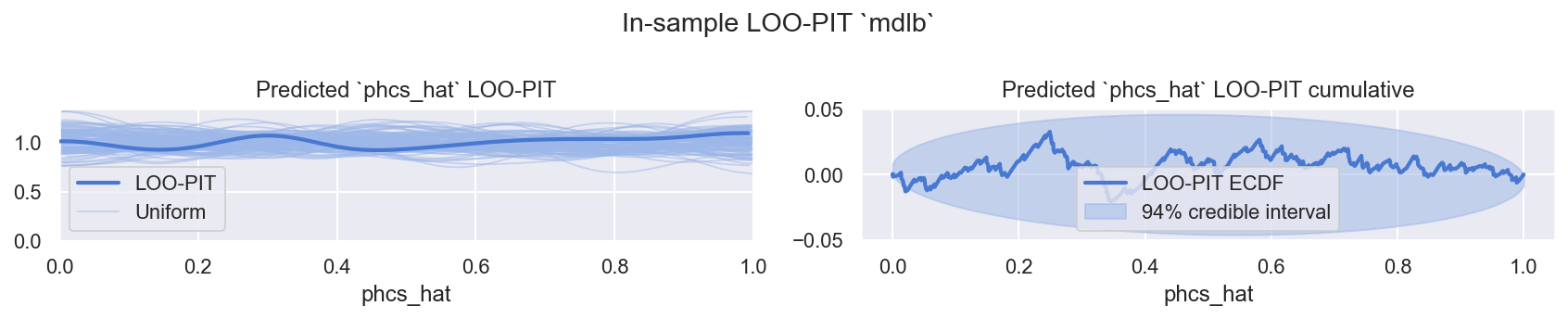
../_images/77d9d5f3bdeea66b8787533121198b44f8307a0346237c9686e003b1c7e28a52.png





观察


    

  • LOO-PIT 看起来不错，再次略微过度分散，但可以接受使用
    • 







2.3.5 比较对数似然与其他模型#






def plot_compare_log_likelihood(idata_dict={}, y_hat="phcs_hat") -> plt.figure:
    """Convenience to plot comparison for a dict of idatas"""
    dfcomp = az.compare(idata_dict, var_name=y_hat, ic="loo", method="stacking", scale="log")
    f, axs = plt.subplots(1, 1, figsize=(12, 2.4 + 0.3 * len(idata_dict)))
    _ = az.plot_compare(dfcomp, ax=axs, title=False, textsize=10, legend=False)
    _ = f.suptitle(
        "Model Performance Comparison: ELPD via In-Sample LOO-PIT "
        + " vs ".join(list(idata_dict.keys()))
        + "\n(higher & narrower is better)"
    )
    _ = f.tight_layout()
    display(dfcomp)
    return f


f = plot_compare_log_likelihood(idata_dict={"mdla": ida, "mdlb": idb})

















rank
elpd_loo
p_loo
elpd_diff
weight
se
dse
warning
scale






mdlb
0
-1412.760828
6.526971
0.000000
0.955269
14.869062
0.000000
False
log




mdla
1
-1415.230697
3.864788
2.469869
0.044731
14.858536
2.309562
False
log






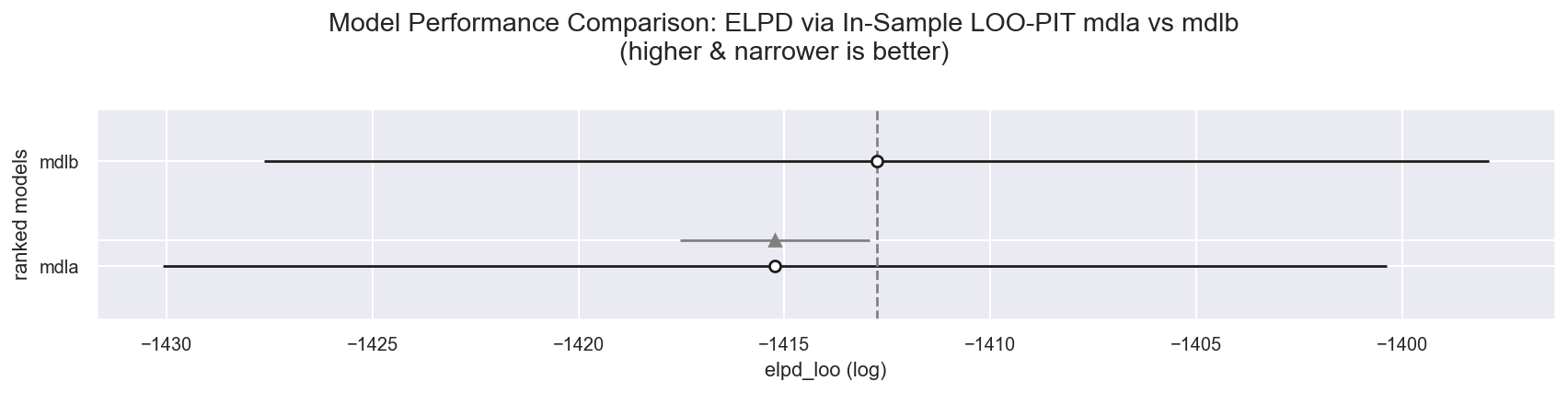
../_images/c05225109ad3a904616c7f30d117aa8099a62dd3aa025545a8ecf2dbe7217c96.png





观察


    

  • 我们新的尊重序数的 mdlb 似乎是赢家，几乎占据了所有权重和更高的 elpd_loo。
    • 









2.4 评估后验参数#




2.4.1 单变量#


参数很多，让我们慢慢来






f = plot_posterior(idb, "posterior", rvs=rvs_simple, mdlname="mdlb", n=5, nrows=1)








../_images/cf704f5cbe0266c0df6f783e12c4f7b5b6a7f75d7ea1ef752e52e2f2a731501f.png





观察


    

  • beta_sigma：E ~ 12 表明需要 beta 的位置具有高方差。
    • 

  • beta: intercept：E ~ 41 确认了 beta 的位置中的大部分方差仅仅是由于截距偏移，需要将 z 评分值放入 phcs 的范围内，没问题。
    • 

  • epsilon：E ~ 7 表示数据中仍然存在相当大的方差，尚未通过建模特征处理
    • 

  • beta: d450：E ~ -12 负数，HDI94 不跨越 0，影响显著，平滑的中心分布。
    

      

    • d450_idx 的更高索引会减少 phcs_hat。
      • 

    

    • 

  • beta: d455：E ~ -7 负数，HDI94 不跨越 0，影响显著，平滑的中心分布。
    

      

    • d455_idx 的更高索引会减少 phcs_hat。
      • 

    

    • 



总的来说，这里更大的系数（与 mdla 相比）表明数据中值之间有更好的区分度，并且性能更好。






f = plot_posterior(idb, "posterior", rvs=rvs_d450, mdlname="mdlb", n=5 * 2, nrows=2)








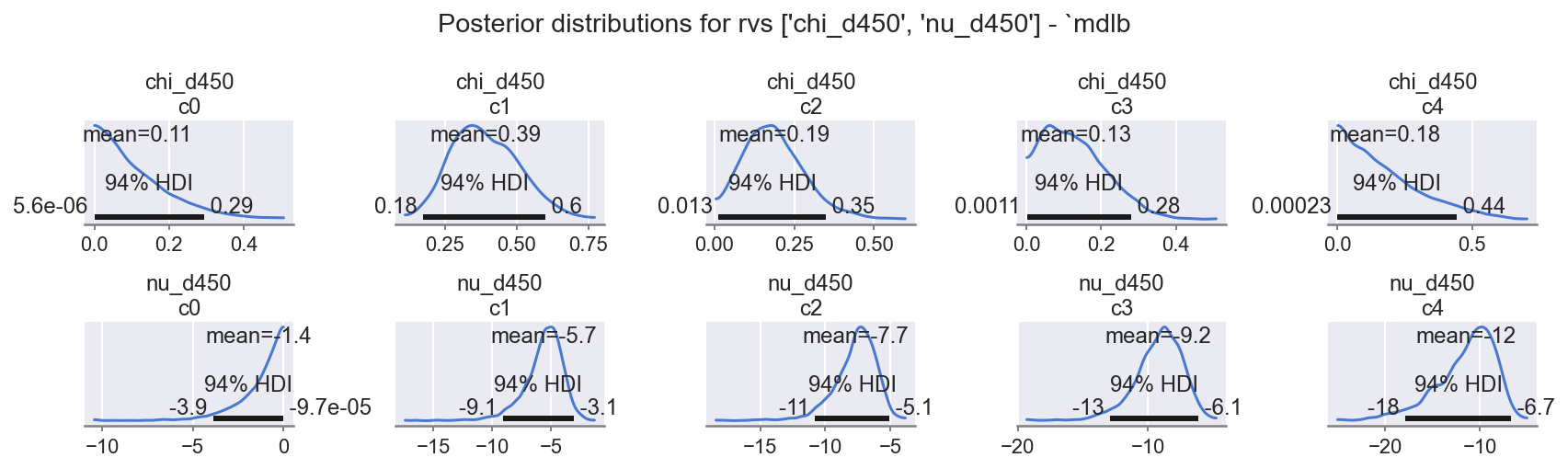
../_images/777919832b5b43946d2d95baa54e37ecd4865d269df2b9e69376245df137c32c.png





观察


有趣的模式


    

  • chi_d450：贯穿整个范围的非线性响应。
    • 

  • nu_d450：非线性效应 beta * chi.csum() 很明显，特别是 c0 远偏离 c1, c2, c3 的趋势。
    • 



特别注意，chi_d450 = c4 的后验分布几乎与其先验值完全相同，因为它在数据集中没有被证实。狄利克雷分布的约束反过来缩放了 chi_d450 = c0 至 c3 的值、beta_450 的尺度，以及对 nu_d450 = c4 的下游影响。


为了比较，您可以通过在第 2.1 节的模型规范中设置 COORDS['d450_nm']=list(df[d450].cat.categories) 并重新运行，看看会发生什么，来尝试较差的替代方案。






f = plot_posterior(idb, "posterior", rvs=rvs_d455, mdlname="mdlb", n=5 * 2, nrows=2)








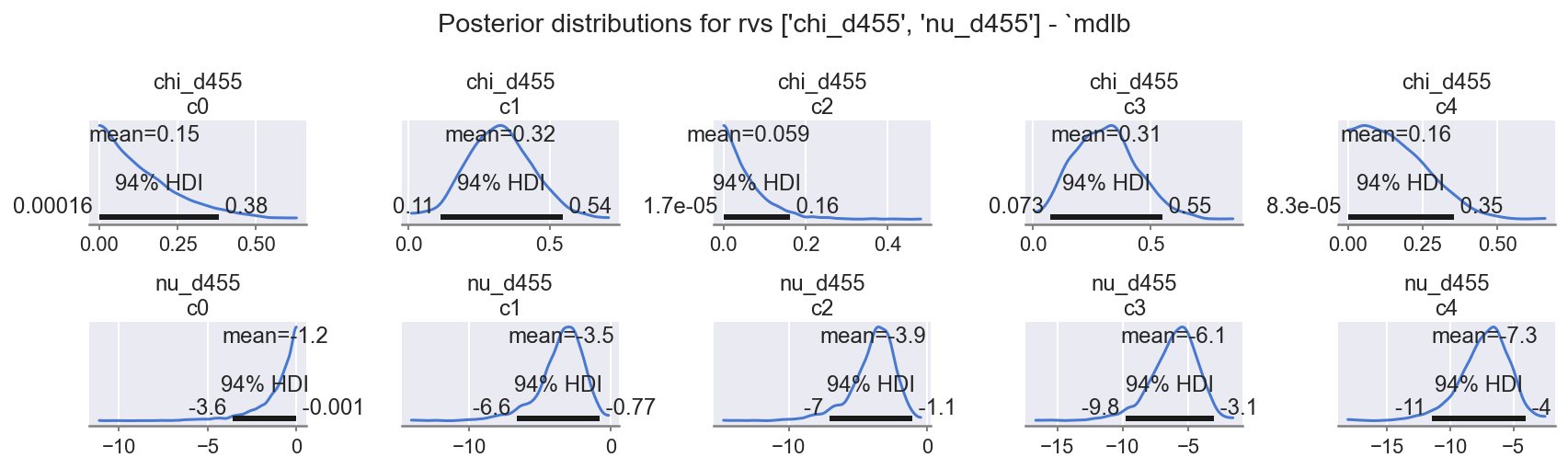
../_images/6cc18407626b7f27f8d0ce75cb1e5267fdf8eb74667c863e6c334242b27b2621.png





观察


有趣的模式


    

  • chi_d455：贯穿整个范围的非线性响应。
    • 

  • nu_d455：非线性效应 beta * chi.csum() 很明显，特别是 c2 几乎与 c1 相同。
    • 





让我们看看这些水平的森林图，以使其更加清晰。






单调先验森林图#






def plot_posterior_forest(idata, group="posterior", rv="beta", mdlname="mdla"):
    """Convenience forestplot posterior (or prior) KDE"""
    f, axs = plt.subplots(1, 1, figsize=(12, 2.4))
    _ = az.plot_forest(idata[group], var_names=[rv], ax=axs, combined=True)
    _ = f.suptitle(f"Forestplot of {group.title()} level values for `{rv}` - `{mdlname}`")
    _ = f.tight_layout()
    return f


f = plot_posterior_forest(idb, "posterior", "nu_d450", "mdlb")
f = plot_posterior_forest(idb, "posterior", "nu_d455", "mdlb")








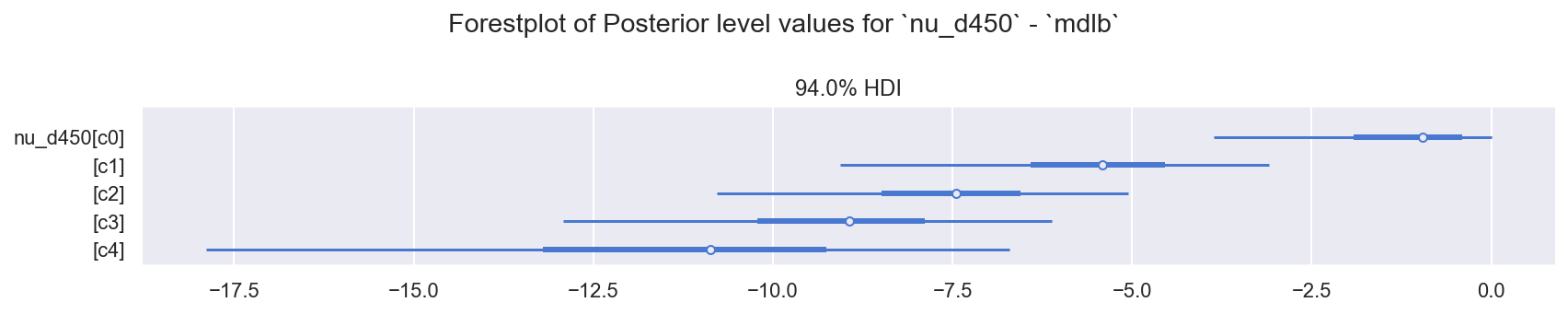
../_images/524d42cac23fd5af4216ea85c2cfa1a2c78107a29eaecb65e2552f0a61414243.png
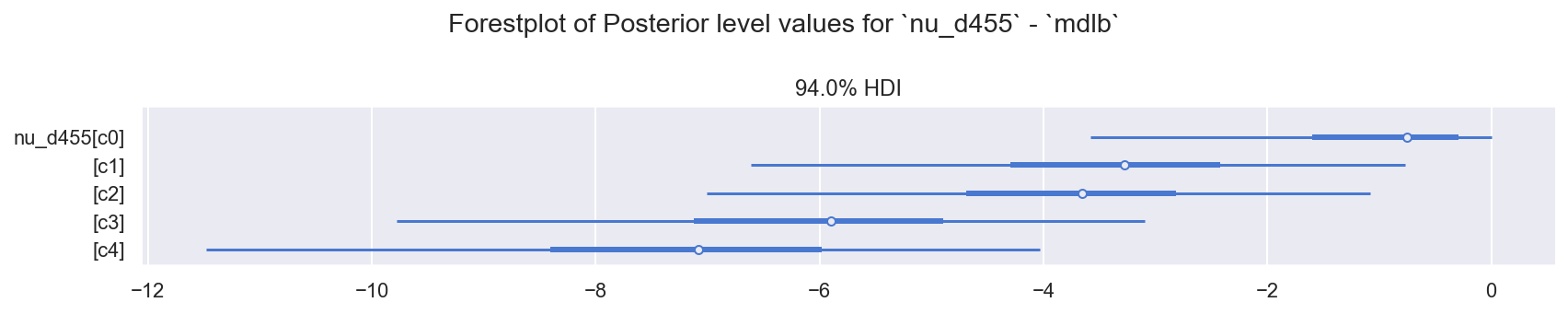
../_images/c4c05653261693090a74e7eb65d22ead412a22d513bf08f51f4e9be9d756a038.png





观察


在这里，我们更详细地看到了相同的模式，特别是：


    

  • nu_d450:
    

      

    • c0 是一个异常值，其影响不成比例地小于 c1, c2, c3。
      • 

    • c4 已被自动填补，并采用先验值，该先验值在线性外推周围具有非常大的方差。
      • 

    

    • 

  • nu_d455：c1, c2 强烈重叠，因此彼此之间的影响非常相似。
    • 











2.5 在简化的 forecast 集上创建 PPC 预测#


仅为了完整性，只需与 Bürkner 论文和 Rochford 的博客文章中的图 3 进行比较。


这些图表总结为均值，但这似乎是不必要的 - 让我们稍微改进一下。




2.5.1 将数据集替换为 dffx，重建并抽样 PPC#






COORDS_F = deepcopy(COORDS)
COORDS_F["oid"] = dffx.index.values
mdlb.set_data("y", dffx[ft_y].values, coords=COORDS_F)
mdlb.set_data("x", dffx[fts_x].values, coords=COORDS_F)
mdlb.set_data("idx_d450", dffx["d450_idx"].values, coords=COORDS_F)
mdlb.set_data("idx_d455", dffx["d455_idx"].values, coords=COORDS_F)

display(pm.model_to_graphviz(mdlb, formatting="plain"))
assert_no_rvs(mdlb.logp())
mdlb.debug(fn="logp", verbose=True)
mdlb.debug(fn="random", verbose=True)








../_images/987df48d08a1faf62bd9de2623ca5ac16164553f2e7de3d0a44569201cdbb2a8.svg

point={'beta_sigma_log__': array(0.), 'beta': array([0.]), 'beta_d450': array(0.), 'chi_d450_simplex__': array([0., 0., 0., 0.]), 'beta_d455': array(0.), 'chi_d455_simplex__': array([0., 0., 0., 0.]), 'epsilon_log__': array(0.)}

No problems found
point={'beta_sigma_log__': array(0.), 'beta': array([0.]), 'beta_d450': array(0.), 'chi_d450_simplex__': array([0., 0., 0., 0.]), 'beta_d455': array(0.), 'chi_d455_simplex__': array([0., 0., 0., 0.]), 'epsilon_log__': array(0.)}

No problems found













with mdlb:
    idb_ppc = pm.sample_posterior_predictive(
        trace=idb.posterior, var_names=RVS_PPC, predictions=True
    )









Sampling: [phcs_hat]

















2.5.2 查看预测结果#






plot_predicted_phcshat_d450_d455(idata=idb_ppc, mdlname="mdlb")








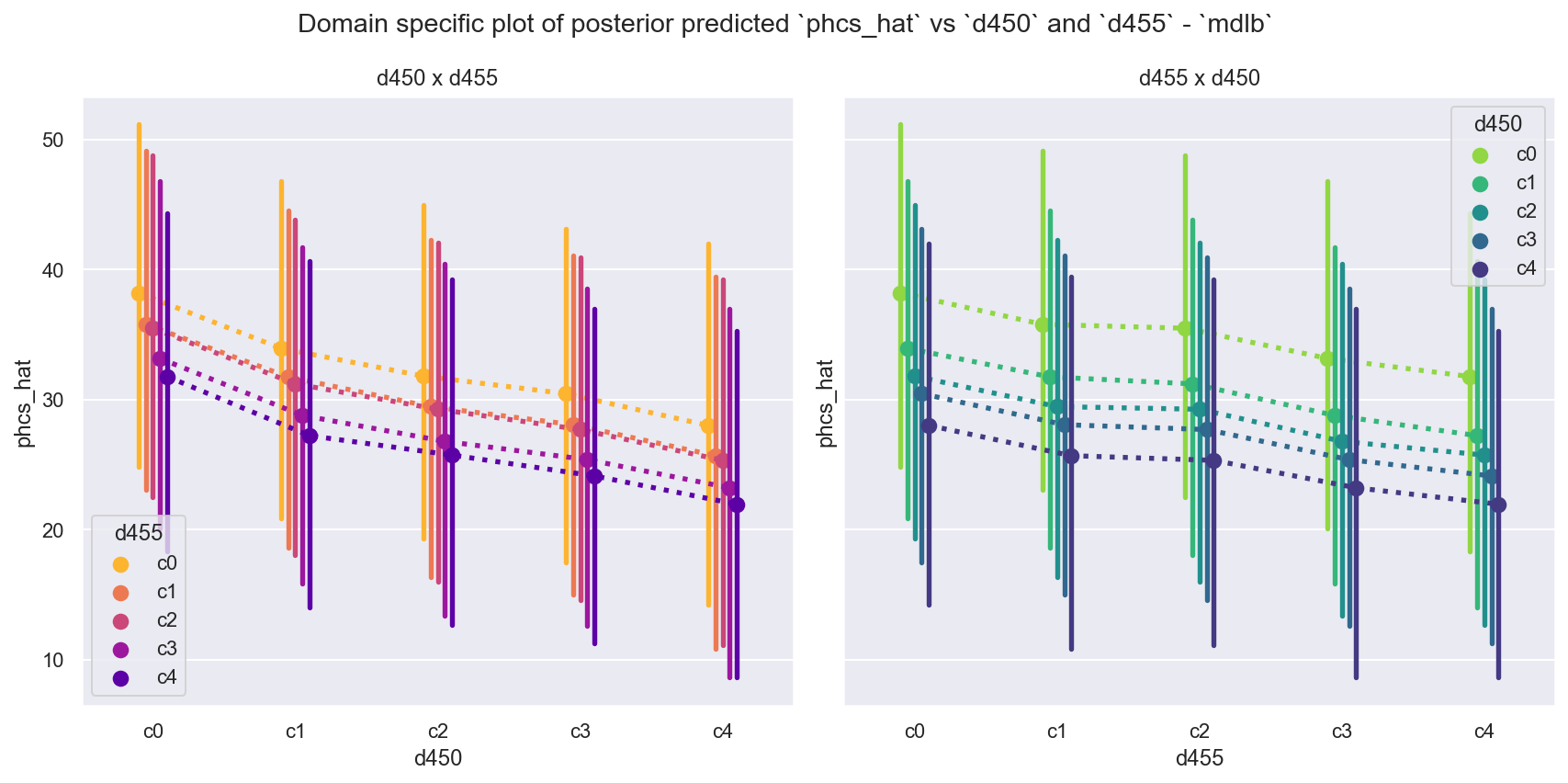
../_images/f4c20ecffcc7163042ffe3ec305cc730b336a362f58b22a242e1373ad6e42b4b.png





观察


    

  • 将其与 [Rochford，无日期] 中的最终图表和 [Bürkner P，2018] 中的图 12 进行比较。
    • 

  • 我们看到当 d450 和 d455 被视为有序类别时，它们的非线性响应和非相等间距。
    • 

  • 特别是，请注意我们在后验图中已经看到的行为。
    

      

    • 左侧图 d450：c0 的所有点都高于第 1.5.2 节中的图（另请注意阴影点中 d455: c1, c2 水平的重叠）。
      • 

    • 右侧图 d455：c1, c2 的所有点都强烈重叠（另请注意 d455 c0 离群）。
      • 

    

    • 

  • 我们还看到 mdlb 可以对 d450=c4 进行预测，这在数据中是看不到的。
    • 

  • 请注意，这里我们绘制了每个数据点的完整后验分布（而不是总结为均值），这强调了数据和模型中仍然存在大量方差。
    • 















勘误#




作者#







参考文献#







[1]

Andrew Gelman、Aki Vehtari、Daniel Simpson、Charles C Margossian、Bob Carpenter、Yuling Yao、Lauren Kennedy、Jonah Gabry、Paul-Christian Bürkner 和 Martin Modrák。 Bayesian workflow。《arXiv 预印本 arXiv:2011.01808》，2020 年。URL： https://arxiv.org/abs/2011.01808。





[2]
(1,2,3,4,5,6)

& Charpentier E Bürkner P。 Modeling monotonic effects of ordinal predictors in bayesian regression models。《PsyArXiv》，2018 年。URL： https://doi.org/10.31234/osf.io/9qkhj，doi:doi:10.31234/osf.io/9qkhj。













水印#






# tested running on Google Colab 2024-10-28
%load_ext watermark
%watermark -n -u -v -iv -w









Last updated: Mon Nov 04 2024

Python implementation: CPython
Python version       : 3.11.9
IPython version      : 8.26.0

pyreadr   : 0.5.2
pytensor  : 2.25.2
numpy     : 1.26.4
pymc      : 5.16.2
tarfile   : 0.9.0
arviz     : 0.19.0
matplotlib: 3.9.1
pandas    : 2.2.2
seaborn   : 0.12.2

Watermark: 2.4.3













许可声明#


此示例库中的所有笔记本均根据 MIT 许可证 提供，该许可证允许修改和再分发用于任何用途，前提是保留版权和许可声明。






引用 PyMC 示例#


要引用此笔记本，请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。




重要提示


许多笔记本改编自其他来源：博客、书籍……在这种情况下，您也应该引用原始来源。


另请记住引用您的代码使用的相关库。




这是一个 bibtex 格式的引用模板


@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}





渲染后可能看起来像