贝叶斯缺失数据插补#
import random
import arviz as az
import matplotlib.cm as cm
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import scipy.optimize
from matplotlib.lines import Line2D
from pymc.sampling.jax import sample_blackjax_nuts, sample_numpyro_nuts
from scipy.stats import multivariate_normal
/Users/nathanielforde/opt/miniconda3/envs/missing_data_clean/lib/python3.11/site-packages/pymc/sampling/jax.py:39: UserWarning: This module is experimental.
warnings.warn("This module is experimental.")
贝叶斯插补和缺失程度#
对具有缺失值的数据进行分析是进入因果推断研究的门户。
任何受缺失数据困扰的分析的关键特征之一是假设,该假设支配着缺失的性质,即数据中出现空白的原因是什么?我们可以忽略它们吗?我们应该担心原因吗?在本笔记本中,我们将看到如何使用最大似然估计和贝叶斯插补技术处理缺失数据的示例。这将引出关于在存在缺失数据的情况下进行推断以及在反事实情况下进行推断的假设的问题。
我们将通过考虑员工满意度调查的示例分析,以及不同的工作条件如何影响我们在数据中看到的响应和无响应,使讨论具体化。
%config InlineBackend.figure_format = 'retina' # high resolution figures
az.style.use("arviz-darkgrid")
rng = np.random.default_rng(42)
缺失数据分类#
鲁宾著名的分类法将问题分解为三个基本选项的选择
完全随机缺失 (MCAR)
随机缺失 (MAR)
非随机缺失 (MNAR)
这些范式中的每一个都可以简化为关于缺失数据模式的条件概率的显式定义。第一种模式是最不令人担忧的。(MCAR) 假设指出,数据的缺失方式与已实现数据的观测部分和未观测部分均无关。它的缺失是由于世界\(\phi\)的偶然情况。
而第二种模式 (MAR) 允许缺失的原因可能是观测数据和世界环境的函数。有时这被称为可忽略的缺失情况,因为估计可以基于观测数据认真进行。可能会有精度损失,但推断应该是可靠的。
最恶劣的缺失数据类型是当缺失是观测数据之外的某些事物的函数时,并且方程无法进一步简化。在这种最终情况下,由于存在混淆的风险,插补和更一般的估计工作可能会变得更加困难。这是不可忽略的缺失情况。
这些假设是在任何分析开始之前做出的。它们本质上是无法验证的。您的分析的成败将取决于每个假设在您寻求应用它们的上下文中是否合理。例如,另一种类型的缺失数据是由系统性删失引起的,如截断或删失数据的贝叶斯回归中所讨论的那样。在这种情况下,删失的原因决定了缺失模式。
员工满意度调查#
我们将遵循 Craig Enders 的著作应用缺失数据分析 Enders K [2022] 的介绍,并使用员工满意度数据集。该数据集包含一些综合指标,报告员工的工作条件和满意度。特别值得注意的是赋权感 (empower)、工作满意度 (worksat) 以及两个综合调查评分,记录员工的领导氛围 (climate) 以及与主管 lmx 的关系质量。
关键问题是什么假设支配着我们的缺失数据模式。
try:
df_employee = pd.read_csv("../data/employee.csv")
except FileNotFoundError:
df_employee = pd.read_csv(pm.get_data("employee.csv"))
df_employee.head()
| 员工 | 团队 | 离职率 | 男性 | 赋权感 | lmx | 工作满意度 | 氛围 | 凝聚力 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 0.0 | 1 | 32.0 | 11.0 | 3.0 | 18.0 | 3.5 |
| 1 | 2 | 1 | 1.0 | 1 | NaN | 13.0 | 4.0 | 18.0 | 3.5 |
| 2 | 3 | 1 | 1.0 | 1 | 30.0 | 9.0 | 4.0 | 18.0 | 3.5 |
| 3 | 4 | 1 | 1.0 | 1 | 29.0 | 8.0 | 3.0 | 18.0 | 3.5 |
| 4 | 5 | 1 | 1.0 | 0 | 26.0 | 7.0 | 4.0 | 18.0 | 3.5 |
# Percentage Missing
df_employee[["worksat", "empower", "lmx"]].isna().sum() / len(df_employee)
worksat 0.047619
empower 0.161905
lmx 0.041270
dtype: float64
# Patterns of missing Data
df_employee[["worksat", "empower", "lmx"]].isnull().drop_duplicates().reset_index(drop=True)
| 工作满意度 | 赋权感 | lmx | |
|---|---|---|---|
| 0 | False | False | False |
| 1 | False | True | False |
| 2 | True | True | False |
| 3 | False | False | True |
| 4 | True | False | False |
fig, ax = plt.subplots(figsize=(20, 7))
ax.hist(df_employee["empower"], bins=30, ec="black", color="cyan", label="Empowerment")
ax.hist(df_employee["lmx"], bins=30, ec="black", color="yellow", label="LMX")
ax.hist(df_employee["worksat"], bins=30, ec="black", color="green", label="Work Satisfaction")
ax.set_title("Employee Satisfaction Survey Results", fontsize=20)
ax.legend();
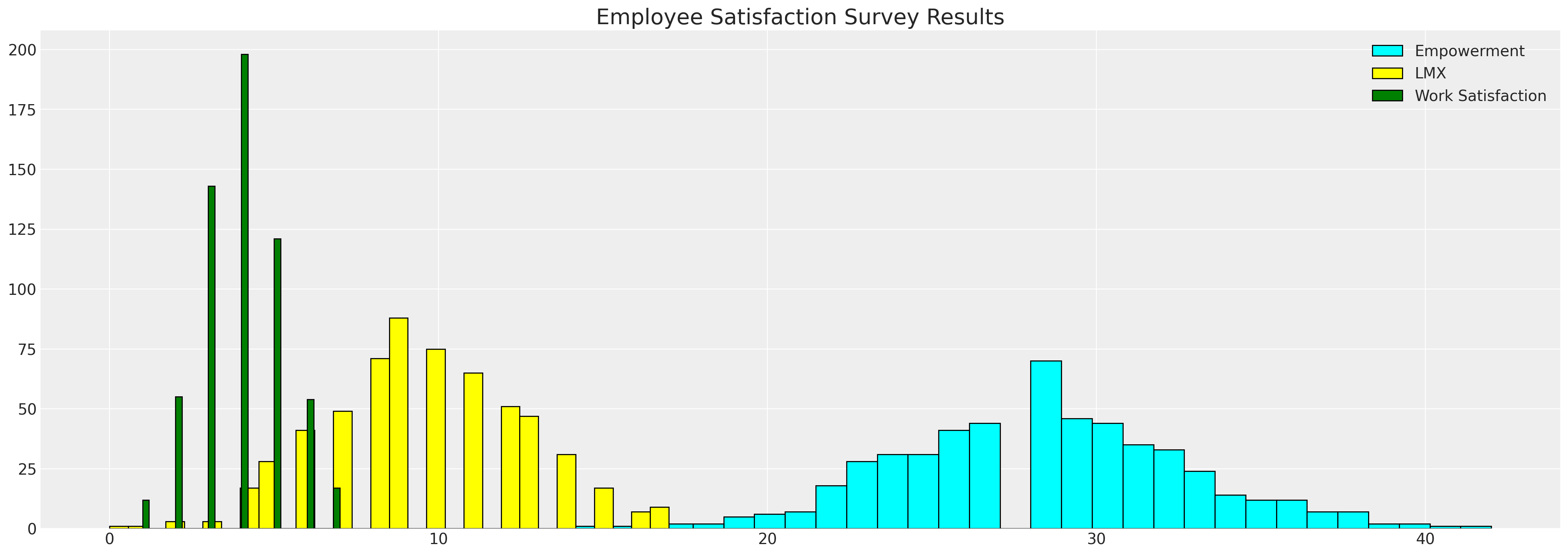
我们在这里看到了员工指标的直方图。我们希望插补数据中的空白,以更好地理解变量之间的关系以及一个变量中的空白如何被另一个变量的值驱动。
FIML:全信息最大似然法#
这种处理缺失数据的方法不是一种插补方法。它使用最大似然估计来估计多元正态分布的参数,该分布可以最好地说是生成了我们的观测数据。它比直接的 MLE 方法稍微复杂一些,因为它尊重了我们的原始数据集中存在缺失数据的事实,但从根本上来说,它是相同的想法。我们希望优化我们的多元正态分布的参数,以最好地拟合观测数据。
该过程的工作原理是将数据划分为其“缺失性”模式,并将每个分区视为对我们想要最大化的最终对数似然项做出贡献。我们结合它们的贡献来估计多元正态分布的拟合。
data = df_employee[["worksat", "empower", "lmx"]]
def split_data_by_missing_pattern(data):
# We want to extract our the pattern of missing-ness in our dataset
# and save each sub-set of our data in a structure that can be used to feed into a log-likelihood function
grouped_patterns = []
patterns = data.notnull().drop_duplicates().values
# A pattern is whether the values in each column e.g. [True, True, True] or [True, True, False]
observed = data.notnull()
for p in range(len(patterns)):
temp = observed[
(observed["worksat"] == patterns[p][0])
& (observed["empower"] == patterns[p][1])
& (observed["lmx"] == patterns[p][2])
]
grouped_patterns.append([patterns[p], temp.index, data.iloc[temp.index].dropna(axis=1)])
return grouped_patterns
def reconstitute_params(params_vector, n_vars):
# Convenience numpy function to construct mirrored COV matrix
# From flattened params_vector
mus = params_vector[0:n_vars]
cov_flat = params_vector[n_vars:]
indices = np.tril_indices(n_vars)
cov = np.empty((n_vars, n_vars))
for i, j, c in zip(indices[0], indices[1], cov_flat):
cov[i, j] = c
cov[j, i] = c
cov = cov + 1e-25
return mus, cov
def optimise_ll(flat_params, n_vars, grouped_patterns):
mus, cov = reconstitute_params(flat_params, n_vars)
# Check if COV is positive definite
if (np.linalg.eigvalsh(cov) < 0).any():
return 1e100
objval = 0.0
for obs_pattern, _, obs_data in grouped_patterns:
# This is the key (tricky) step because we're selecting the variables which pattern
# the full information set within each pattern of "missing-ness"
# e.g. when the observed pattern is [True, True, False] we want the first two variables
# of the mus vector and we want only the covariance relations between the relevant variables from the cov
# in the iteration.
obs_mus = mus[obs_pattern]
obs_cov = cov[obs_pattern][:, obs_pattern]
ll = np.sum(multivariate_normal(obs_mus, obs_cov).logpdf(obs_data))
objval = ll + objval
return -objval
def estimate(data):
n_vars = data.shape[1]
# Initialise
mus0 = np.zeros(n_vars)
cov0 = np.eye(n_vars)
# Flatten params for optimiser
params0 = np.append(mus0, cov0[np.tril_indices(n_vars)])
# Process Data
grouped_patterns = split_data_by_missing_pattern(data)
# Run the Optimiser.
try:
result = scipy.optimize.minimize(
optimise_ll, params0, args=(n_vars, grouped_patterns), method="Powell"
)
except Exception as e:
raise e
mean, cov = reconstitute_params(result.x, n_vars)
return mean, cov
fiml_mus, fiml_cov = estimate(data)
print("Full information Maximum Likelihood Estimate Mu:")
display(pd.DataFrame(fiml_mus, index=data.columns).T)
print("Full information Maximum Likelihood Estimate COV:")
pd.DataFrame(fiml_cov, columns=data.columns, index=data.columns)
Full information Maximum Likelihood Estimate Mu:
| 工作满意度 | 赋权感 | lmx | |
|---|---|---|---|
| 0 | 3.983351 | 28.595211 | 9.624485 |
Full information Maximum Likelihood Estimate COV:
| 工作满意度 | 赋权感 | lmx | |
|---|---|---|---|
| 工作满意度 | 1.568676 | 1.599817 | 1.547433 |
| 赋权感 | 1.599817 | 19.138522 | 5.428954 |
| lmx | 1.547433 | 5.428954 | 8.934030 |
从隐含分布中抽样#
然后,我们可以从隐含分布中抽样,以估计感兴趣的其他特征并针对观测数据进行测试。
mle_fit = multivariate_normal(fiml_mus, fiml_cov)
mle_sample = mle_fit.rvs(10000)
mle_sample = pd.DataFrame(mle_sample, columns=["worksat", "empower", "lmx"])
mle_sample.head()
| 工作满意度 | 赋权感 | lmx | |
|---|---|---|---|
| 0 | 4.467296 | 31.568011 | 12.418765 |
| 1 | 4.713191 | 30.329419 | 10.651786 |
| 2 | 5.699765 | 35.770312 | 12.558135 |
| 3 | 4.067691 | 27.874578 | 6.271341 |
| 4 | 3.580109 | 28.799105 | 9.704713 |
这使我们能够将隐含分布与观测数据进行比较
fig, ax = plt.subplots(figsize=(20, 7))
ax.hist(
mle_sample["empower"],
bins=30,
ec="black",
color="cyan",
alpha=0.2,
label="Inferred Empowerment",
)
ax.hist(mle_sample["lmx"], bins=30, ec="black", color="yellow", alpha=0.2, label="Inferred LMX")
ax.hist(
mle_sample["worksat"],
bins=30,
ec="black",
color="green",
alpha=0.2,
label="Inferred Work Satisfaction",
)
ax.hist(data["empower"], bins=30, ec="black", color="cyan", label="Observed Empowerment")
ax.hist(data["lmx"], bins=30, ec="black", color="yellow", label="Observed LMX")
ax.hist(data["worksat"], bins=30, ec="black", color="green", label="Observed Work Satisfaction")
ax.set_title("Inferred from MLE fit: Employee Satisfaction Survey Results", fontsize=20)
ax.legend()
<matplotlib.legend.Legend at 0x1914bce50>
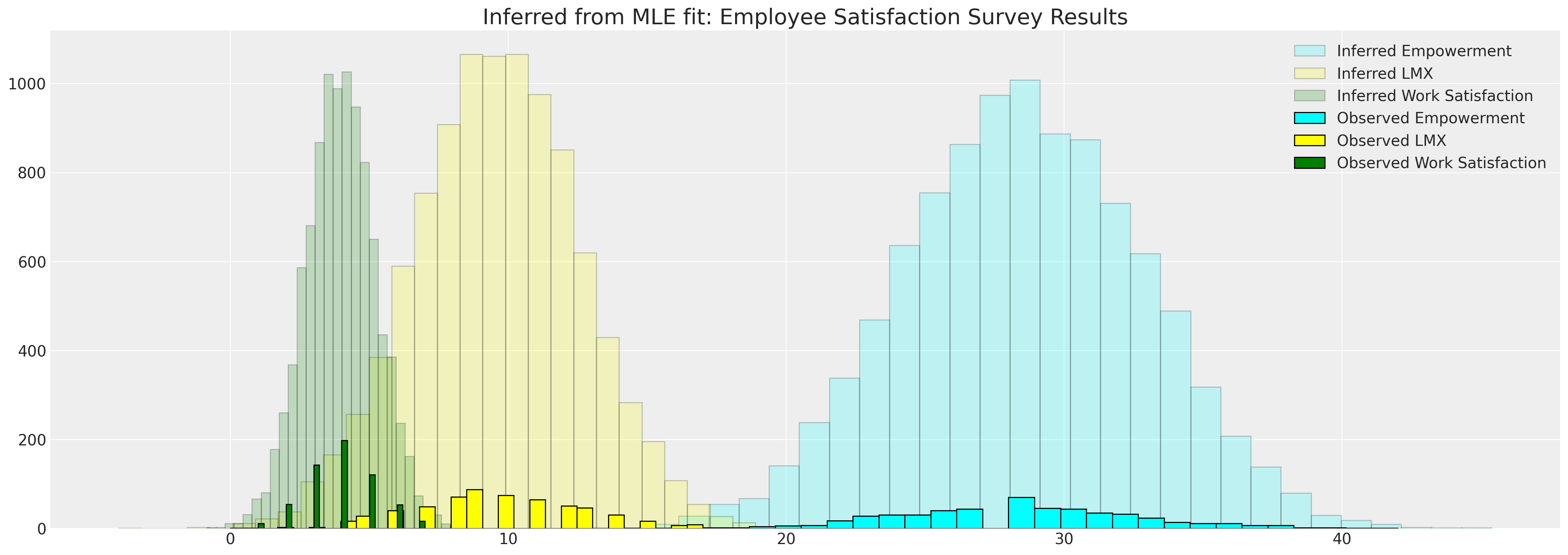
插补指标数据之间的相关性#
我们还可以从我们的样本中计算感兴趣的其他特征。例如,我们可能想知道相关变量之间的相关性。
pd.DataFrame(mle_sample.corr(), columns=data.columns, index=data.columns)
| 工作满意度 | 赋权感 | lmx | |
|---|---|---|---|
| 工作满意度 | 1.000000 | 0.300790 | 0.409996 |
| 赋权感 | 0.300790 | 1.000000 | 0.410874 |
| lmx | 0.409996 | 0.410874 | 1.000000 |
自举敏感性分析#
我们可能还想在不同的缺失性规范下针对自举样本验证估计的参数。
data_200 = df_employee[["worksat", "empower", "lmx"]].dropna().sample(200)
data_200.reset_index(inplace=True, drop=True)
sensitivity = {}
n_missing = np.linspace(30, 100, 5) # Change or alter the range as desired
bootstrap_iterations = 100 # change to large number running a real analysis in this case
for n in n_missing:
sensitivity[int(n)] = {}
sensitivity[int(n)]["mus"] = []
sensitivity[int(n)]["cov"] = []
for i in range(bootstrap_iterations):
temp = data_200.copy()
for m in range(int(n)):
i = random.choice(range(200))
j = random.choice(range(3))
temp.iloc[i, j] = np.nan
try:
fiml_mus, fiml_cov = estimate(temp)
sensitivity[int(n)]["mus"].append(fiml_mus)
sensitivity[int(n)]["cov"].append(fiml_cov)
except Exception as e:
next
在这里,我们绘制了最大似然参数估计值与各种缺失数据方案的对比图。这种方法可以应用于任何插补方法。
fig, axs = plt.subplots(1, 3, figsize=(20, 7))
for n in sensitivity.keys():
temp = pd.DataFrame(sensitivity[n]["mus"], columns=["worksat", "empower", "lmx"])
for col, ax in zip(temp.columns, axs):
ax.hist(
temp[col], alpha=0.1, ec="black", label=f"Missing: {np.round(n/200, 2)}, Mean: {col}"
)
ax.legend()
ax.set_title(f"Bootstrap Distribution for Mean:\n{col}")

fig, axs = plt.subplots(2, 3, figsize=(20, 14))
axs = axs.flatten()
for n in sensitivity.keys():
length = len(sensitivity[n]["cov"])
temp = pd.DataFrame(
[sensitivity[n]["cov"][i][np.tril_indices(3)] for i in range(length)],
columns=[
"var(worksat)",
"cov(worksat, empower)",
"var(empower)",
"cov(worksat, lmx)",
"cov(lmx, empower)",
"var(lmx)",
],
)
for col, ax in zip(temp.columns, axs):
ax.hist(
temp[col], alpha=0.1, ec="black", label=f"Missing: {np.round(n/200, 2)}, Mean: {col}"
)
ax.legend()
ax.set_title(f"Bootstrap Distribution for Expected:\n{col}")
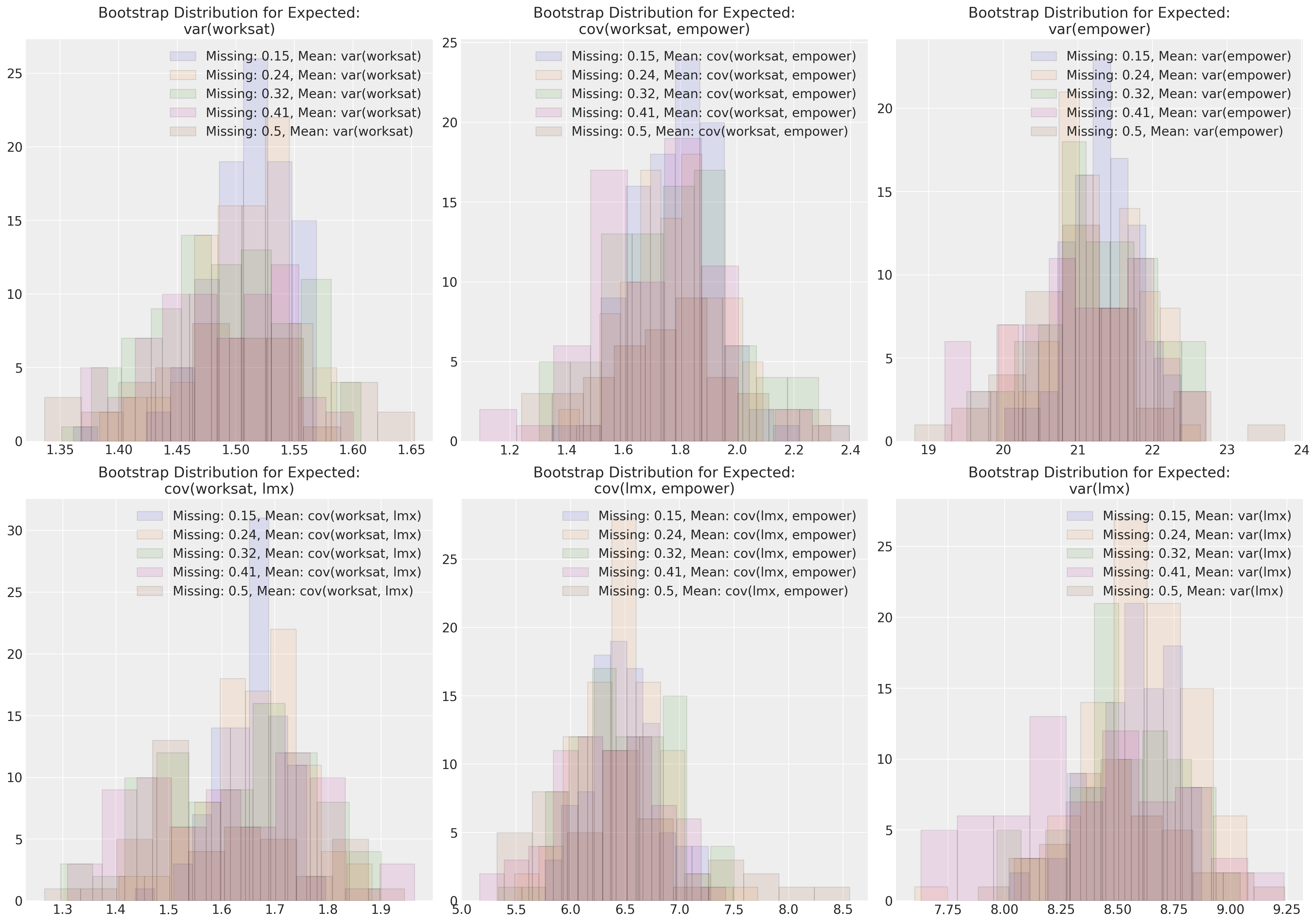
这些图显示,在 (MCAR) 下,我们的多元正态分布的参数估计值对于不同程度的缺失数据相当稳健。尝试在其他缺失数据方案下进行类似的模拟练习是一个有益的练习。
贝叶斯插补#
接下来,我们将应用贝叶斯方法来解决相同的问题。但在这里,我们将看到使用后验预测分布直接插补缺失值。贝叶斯插补方法与我们上面看到的方法不同。我们不仅仅是学习数据生成分布的参数(尽管我们也在这样做),贝叶斯过程通过 MCMC 抽样过程直接插补特定缺失条目的缺失值。
import pytensor.tensor as pt
with pm.Model() as model:
# Priors
mus = pm.Normal("mus", 0, 1, size=3)
cov_flat_prior, _, _ = pm.LKJCholeskyCov("cov", n=3, eta=1.0, sd_dist=pm.Exponential.dist(1))
# Create a vector of flat variables for the unobserved components of the MvNormal
x_unobs = pm.Uniform("x_unobs", 0, 100, shape=(np.isnan(data.values).sum(),))
# Create the symbolic value of x, combining observed data and unobserved variables
x = pt.as_tensor(data.values)
x = pm.Deterministic("x", pt.set_subtensor(x[np.isnan(data.values)], x_unobs))
# Add a Potential with the logp of the variable conditioned on `x`
pm.Potential("x_logp", pm.logp(rv=pm.MvNormal.dist(mus, chol=cov_flat_prior), value=x))
idata = pm.sample_prior_predictive()
idata = pm.sample()
idata.extend(pm.sample(random_seed=120))
pm.sample_posterior_predictive(idata, extend_inferencedata=True)
pm.model_to_graphviz(model)
/var/folders/99/gp2xl6x513s0tvl3cx79zf7m0000gn/T/ipykernel_96943/3865616598.py:16: UserWarning: The effect of Potentials on other parameters is ignored during prior predictive sampling. This is likely to lead to invalid or biased predictive samples.
idata = pm.sample_prior_predictive()
Sampling: [cov, mus, x_unobs]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [mus, cov, x_unobs]
/Users/nathanielforde/opt/miniconda3/envs/missing_data_clean/lib/python3.11/site-packages/pytensor/compile/function/types.py:972: RuntimeWarning: invalid value encountered in accumulate
self.vm()
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 98 seconds.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [mus, cov, x_unobs]
/Users/nathanielforde/opt/miniconda3/envs/missing_data_clean/lib/python3.11/site-packages/pytensor/compile/function/types.py:972: RuntimeWarning: invalid value encountered in accumulate
self.vm()
/Users/nathanielforde/opt/miniconda3/envs/missing_data_clean/lib/python3.11/site-packages/pytensor/compile/function/types.py:972: RuntimeWarning: invalid value encountered in accumulate
self.vm()
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 99 seconds.
/var/folders/99/gp2xl6x513s0tvl3cx79zf7m0000gn/T/ipykernel_96943/3865616598.py:19: UserWarning: The effect of Potentials on other parameters is ignored during posterior predictive sampling. This is likely to lead to invalid or biased predictive samples.
pm.sample_posterior_predictive(idata, extend_inferencedata=True)
az.plot_posterior(idata, var_names=["mus", "cov"]);
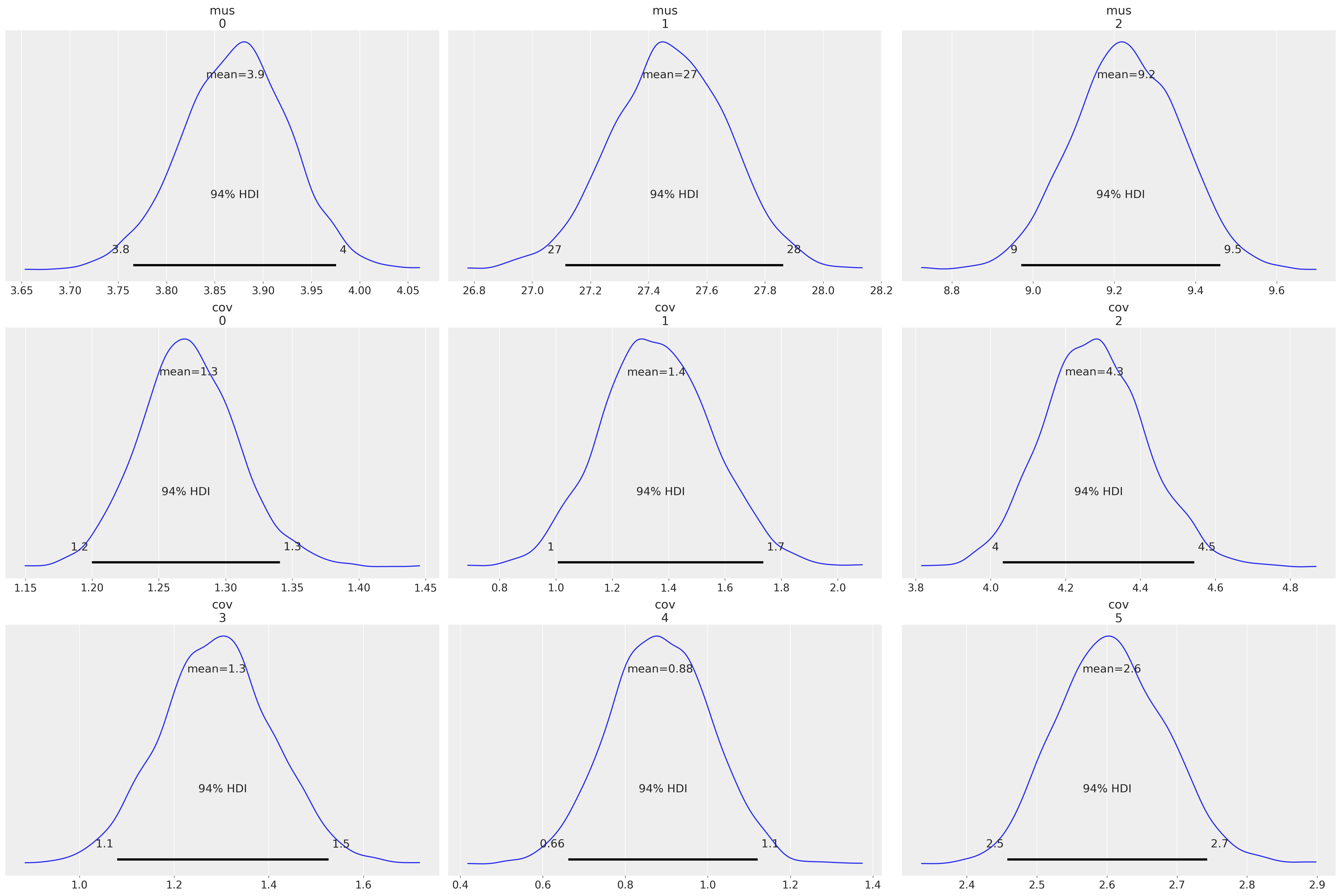
az.summary(idata, var_names=["mus", "cov", "x_unobs"])
| 均值 | 标准差 | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| mus[0] | 3.871 | 0.056 | 3.766 | 3.976 | 0.001 | 0.001 | 6110.0 | 3277.0 | 1.0 |
| mus[1] | 27.473 | 0.200 | 27.114 | 27.863 | 0.003 | 0.002 | 5742.0 | 3320.0 | 1.0 |
| mus[2] | 9.229 | 0.132 | 8.971 | 9.461 | 0.002 | 0.001 | 6154.0 | 3271.0 | 1.0 |
| cov[0] | 1.272 | 0.037 | 1.200 | 1.341 | 0.000 | 0.000 | 6235.0 | 2754.0 | 1.0 |
| cov[1] | 1.356 | 0.197 | 1.007 | 1.736 | 0.003 | 0.002 | 5373.0 | 3750.0 | 1.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| x_unobs[153] | 29.836 | 4.205 | 21.820 | 37.745 | 0.044 | 0.031 | 9232.0 | 2929.0 | 1.0 |
| x_unobs[154] | 2.559 | 1.107 | 0.356 | 4.483 | 0.018 | 0.013 | 3564.0 | 1634.0 | 1.0 |
| x_unobs[155] | 30.071 | 4.029 | 22.614 | 37.652 | 0.039 | 0.028 | 10697.0 | 3078.0 | 1.0 |
| x_unobs[156] | 29.654 | 4.017 | 22.079 | 37.411 | 0.039 | 0.027 | 10626.0 | 2867.0 | 1.0 |
| x_unobs[157] | 27.420 | 4.066 | 19.595 | 34.915 | 0.046 | 0.033 | 7784.0 | 2226.0 | 1.0 |
167 行 × 9 列
imputed_dims = data.shape
imputed = data.values.flatten()
imputed[np.isnan(imputed)] = az.summary(idata, var_names=["x_unobs"])["mean"].values
imputed = imputed.reshape(imputed_dims[0], imputed_dims[1])
imputed = pd.DataFrame(imputed, columns=[col + "_imputed" for col in data.columns])
imputed.head(10)
| worksat_imputed | empower_imputed | lmx_imputed | |
|---|---|---|---|
| 0 | 3.000 | 32.000 | 11.000 |
| 1 | 4.000 | 29.431 | 13.000 |
| 2 | 4.000 | 30.000 | 9.000 |
| 3 | 3.000 | 29.000 | 8.000 |
| 4 | 4.000 | 26.000 | 7.000 |
| 5 | 3.995 | 27.915 | 10.000 |
| 6 | 5.000 | 28.984 | 11.000 |
| 7 | 3.000 | 22.000 | 9.000 |
| 8 | 2.000 | 23.000 | 6.835 |
| 9 | 4.000 | 32.000 | 9.000 |
fig, axs = plt.subplots(1, 3, figsize=(20, 7))
axs = axs.flatten()
for col, col_i, ax in zip(data.columns, imputed.columns, axs):
ax.hist(data[col], color="red", label=col, ec="black", bins=30)
ax.hist(imputed[col_i], color="cyan", alpha=0.3, label=col_i, ec="black", bins=30)
ax.legend()
ax.set_title(f"Imputed Distribution and Observed for {col}")
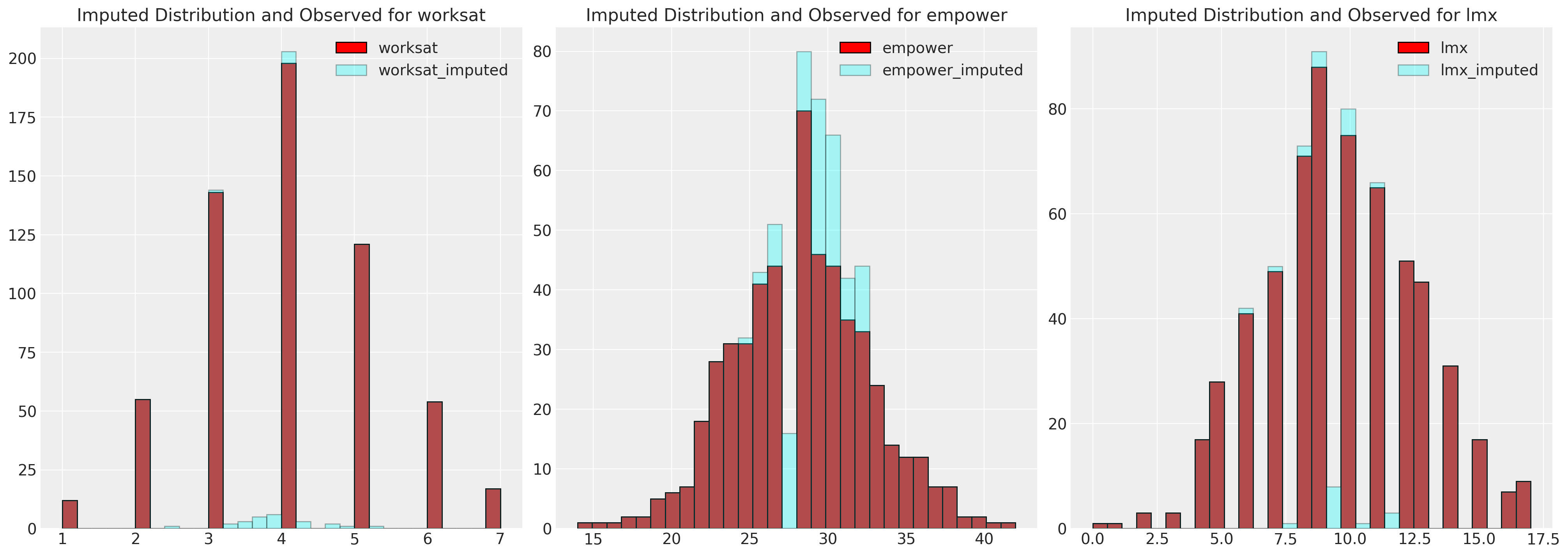
pd.DataFrame(az.summary(idata, var_names=["cov_corr"])["mean"].values.reshape(3, 3))
/Users/nathanielforde/opt/miniconda3/envs/missing_data_clean/lib/python3.11/site-packages/arviz/stats/diagnostics.py:584: RuntimeWarning: invalid value encountered in scalar divide
(between_chain_variance / within_chain_variance + num_samples - 1) / (num_samples)
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 1.000 | 0.302 | 0.423 |
| 1 | 0.302 | 1.000 | 0.405 |
| 2 | 0.423 | 0.405 | 1.000 |
这些结果与上面的 FIML 方法以及 Ender 的应用缺失数据分析中报告的结果一致。
通过链式方程进行贝叶斯插补#
到目前为止,我们已经看到了处理数据集中每个变量作为来自同一分布的集合的多元插补方法。然而,当存在我们感兴趣分析的特定焦点关系时,一种更灵活的方法通常很有用。
继续使用员工数据集,我们将在此处检查 lmx、climate、male 和 empower 之间的关系,其中我们的重点是什么驱动赋权感。回想一下,我们的性别变量 male 是完全指定的,不需要插补。因此,我们有一个可以分解的联合分布
可以将其分解为各个回归方程,或者更一般地分解为每个所需条件模型的组件模型。
我们可以依次插补这些方程中的每一个,保存插补后的数据集并将其馈送到下一个建模练习中。这增加了一些复杂性,因为某些变量将出现两次。一次是在我们的焦点回归中作为预测变量,一次是在其自身组件模型中作为似然项。
PyMC 插补#
正如我们上面看到的,我们可以使用 PyMC 通过使用特定的抽样分布来插补缺失数据的值。在链式方程的情况下,这变得有点棘手,因为我们可能希望同时使用 lmx 的数据作为一个方程中的回归量,并在另一个方程中使用观测数据作为似然。
我们如何指定将用于插补缺失数据的抽样分布也很重要。我们将在此处展示一个示例,其中我们交替使用均匀分布和正态抽样分布来插补焦点回归中的预测项。
data = df_employee[["lmx", "empower", "climate", "male"]]
lmx_mean = data["lmx"].mean()
lmx_min = data["lmx"].min()
lmx_max = data["lmx"].max()
lmx_sd = data["lmx"].std()
cli_mean = data["climate"].mean()
cli_min = data["climate"].min()
cli_max = data["climate"].max()
cli_sd = data["climate"].std()
priors = {
"climate": {"normal": [lmx_mean, lmx_sd, lmx_sd], "uniform": [lmx_min, lmx_max]},
"lmx": {"normal": [cli_mean, cli_sd, cli_sd], "uniform": [cli_min, cli_max]},
}
def make_model(priors, normal_pred_assumption=True):
coords = {
"alpha_dim": ["lmx_imputed", "climate_imputed", "empower_imputed"],
"beta_dim": [
"lmxB_male",
"lmxB_climate",
"climateB_male",
"empB_male",
"empB_climate",
"empB_lmx",
],
}
with pm.Model(coords=coords) as model:
# Priors
beta = pm.Normal("beta", 0, 1, size=6, dims="beta_dim")
alpha = pm.Normal("alphas", 10, 5, size=3, dims="alpha_dim")
sigma = pm.HalfNormal("sigmas", 5, size=3, dims="alpha_dim")
if normal_pred_assumption:
mu_climate = pm.Normal(
"mu_climate", priors["climate"]["normal"][0], priors["climate"]["normal"][1]
)
sigma_climate = pm.HalfNormal("sigma_climate", priors["climate"]["normal"][2])
climate_pred = pm.Normal(
"climate_pred", mu_climate, sigma_climate, observed=data["climate"].values
)
else:
climate_pred = pm.Uniform("climate_pred", 0, 40, observed=data["climate"].values)
if normal_pred_assumption:
mu_lmx = pm.Normal("mu_lmx", priors["lmx"]["normal"][0], priors["lmx"]["normal"][1])
sigma_lmx = pm.HalfNormal("sigma_lmx", priors["lmx"]["normal"][2])
lmx_pred = pm.Normal("lmx_pred", mu_lmx, sigma_lmx, observed=data["lmx"].values)
else:
lmx_pred = pm.Uniform("lmx_pred", 0, 40, observed=data["lmx"].values)
# Likelihood(s)
lmx_imputed = pm.Normal(
"lmx_imputed",
alpha[0] + beta[0] * data["male"] + beta[1] * climate_pred,
sigma[0],
observed=data["lmx"].values,
)
climate_imputed = pm.Normal(
"climate_imputed",
alpha[1] + beta[2] * data["male"],
sigma[1],
observed=data["climate"].values,
)
empower_imputed = pm.Normal(
"emp_imputed",
alpha[2] + beta[3] * data["male"] + beta[4] * climate_pred + beta[5] * lmx_pred,
sigma[2],
observed=data["empower"].values,
)
idata = pm.sample_prior_predictive()
idata.extend(pm.sample(random_seed=120))
pm.sample_posterior_predictive(idata, extend_inferencedata=True)
return idata, model
idata_uniform, model_uniform = make_model(priors, normal_pred_assumption=False)
idata_normal, model_normal = make_model(priors, normal_pred_assumption=True)
pm.model_to_graphviz(model_uniform)
/Users/nathanielforde/opt/miniconda3/envs/missing_data_clean/lib/python3.11/site-packages/pymc/model.py:1400: ImputationWarning: Data in climate_pred contains missing values and will be automatically imputed from the sampling distribution.
warnings.warn(impute_message, ImputationWarning)
/Users/nathanielforde/opt/miniconda3/envs/missing_data_clean/lib/python3.11/site-packages/pymc/model.py:1400: ImputationWarning: Data in lmx_pred contains missing values and will be automatically imputed from the sampling distribution.
warnings.warn(impute_message, ImputationWarning)
/Users/nathanielforde/opt/miniconda3/envs/missing_data_clean/lib/python3.11/site-packages/pymc/model.py:1400: ImputationWarning: Data in lmx_imputed contains missing values and will be automatically imputed from the sampling distribution.
warnings.warn(impute_message, ImputationWarning)
/Users/nathanielforde/opt/miniconda3/envs/missing_data_clean/lib/python3.11/site-packages/pymc/model.py:1400: ImputationWarning: Data in climate_imputed contains missing values and will be automatically imputed from the sampling distribution.
warnings.warn(impute_message, ImputationWarning)
/Users/nathanielforde/opt/miniconda3/envs/missing_data_clean/lib/python3.11/site-packages/pymc/model.py:1400: ImputationWarning: Data in emp_imputed contains missing values and will be automatically imputed from the sampling distribution.
warnings.warn(impute_message, ImputationWarning)
Sampling: [alphas, beta, climate_imputed_missing, climate_imputed_observed, climate_pred_missing, climate_pred_observed, emp_imputed_missing, emp_imputed_observed, lmx_imputed_missing, lmx_imputed_observed, lmx_pred_missing, lmx_pred_observed, sigmas]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [beta, alphas, sigmas, climate_pred_missing, lmx_pred_missing, lmx_imputed_missing, climate_imputed_missing, emp_imputed_missing]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 96 seconds.
Sampling: [climate_imputed_observed, climate_pred_observed, emp_imputed_missing, emp_imputed_observed, lmx_imputed_missing, lmx_imputed_observed, lmx_pred_observed]
/Users/nathanielforde/opt/miniconda3/envs/missing_data_clean/lib/python3.11/site-packages/pymc/model.py:1400: ImputationWarning: Data in climate_pred contains missing values and will be automatically imputed from the sampling distribution.
warnings.warn(impute_message, ImputationWarning)
/Users/nathanielforde/opt/miniconda3/envs/missing_data_clean/lib/python3.11/site-packages/pymc/model.py:1400: ImputationWarning: Data in lmx_pred contains missing values and will be automatically imputed from the sampling distribution.
warnings.warn(impute_message, ImputationWarning)
/Users/nathanielforde/opt/miniconda3/envs/missing_data_clean/lib/python3.11/site-packages/pymc/model.py:1400: ImputationWarning: Data in lmx_imputed contains missing values and will be automatically imputed from the sampling distribution.
warnings.warn(impute_message, ImputationWarning)
/Users/nathanielforde/opt/miniconda3/envs/missing_data_clean/lib/python3.11/site-packages/pymc/model.py:1400: ImputationWarning: Data in climate_imputed contains missing values and will be automatically imputed from the sampling distribution.
warnings.warn(impute_message, ImputationWarning)
/Users/nathanielforde/opt/miniconda3/envs/missing_data_clean/lib/python3.11/site-packages/pymc/model.py:1400: ImputationWarning: Data in emp_imputed contains missing values and will be automatically imputed from the sampling distribution.
warnings.warn(impute_message, ImputationWarning)
Sampling: [alphas, beta, climate_imputed_missing, climate_imputed_observed, climate_pred_missing, climate_pred_observed, emp_imputed_missing, emp_imputed_observed, lmx_imputed_missing, lmx_imputed_observed, lmx_pred_missing, lmx_pred_observed, mu_climate, mu_lmx, sigma_climate, sigma_lmx, sigmas]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [beta, alphas, sigmas, mu_climate, sigma_climate, climate_pred_missing, mu_lmx, sigma_lmx, lmx_pred_missing, lmx_imputed_missing, climate_imputed_missing, emp_imputed_missing]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 106 seconds.
Sampling: [climate_imputed_observed, climate_pred_observed, emp_imputed_missing, emp_imputed_observed, lmx_imputed_missing, lmx_imputed_observed, lmx_pred_observed]
idata_normal
-
<xarray.Dataset> Dimensions: (chain: 4, draw: 1000, beta_dim: 6, alpha_dim: 3, climate_pred_missing_dim_0: 60, lmx_pred_missing_dim_0: 26, lmx_imputed_missing_dim_0: 26, climate_imputed_missing_dim_0: 60, emp_imputed_missing_dim_0: 102, climate_pred_dim_0: 630, lmx_pred_dim_0: 630, lmx_imputed_dim_0: 630, climate_imputed_dim_0: 630, emp_imputed_dim_0: 630) Coordinates: (12/14) * chain (chain) int64 0 1 2 3 * draw (draw) int64 0 1 2 3 4 ... 996 997 998 999 * beta_dim (beta_dim) <U13 'lmxB_male' ... 'empB_lmx' * alpha_dim (alpha_dim) <U15 'lmx_imputed' ... 'empowe... * climate_pred_missing_dim_0 (climate_pred_missing_dim_0) int64 0 1 ... 59 * lmx_pred_missing_dim_0 (lmx_pred_missing_dim_0) int64 0 1 ... 24 25 ... ... * emp_imputed_missing_dim_0 (emp_imputed_missing_dim_0) int64 0 1 ... 101 * climate_pred_dim_0 (climate_pred_dim_0) int64 0 1 2 ... 628 629 * lmx_pred_dim_0 (lmx_pred_dim_0) int64 0 1 2 ... 627 628 629 * lmx_imputed_dim_0 (lmx_imputed_dim_0) int64 0 1 2 ... 628 629 * climate_imputed_dim_0 (climate_imputed_dim_0) int64 0 1 ... 628 629 * emp_imputed_dim_0 (emp_imputed_dim_0) int64 0 1 2 ... 628 629 Data variables: (12/17) beta (chain, draw, beta_dim) float64 0.5683 ...... alphas (chain, draw, alpha_dim) float64 9.008 ...... mu_climate (chain, draw) float64 19.98 20.11 ... 20.12 climate_pred_missing (chain, draw, climate_pred_missing_dim_0) float64 ... mu_lmx (chain, draw) float64 9.514 9.723 ... 9.586 lmx_pred_missing (chain, draw, lmx_pred_missing_dim_0) float64 ... ... ... sigma_lmx (chain, draw) float64 3.027 3.152 ... 3.004 climate_pred (chain, draw, climate_pred_dim_0) float64 ... lmx_pred (chain, draw, lmx_pred_dim_0) float64 11.0... lmx_imputed (chain, draw, lmx_imputed_dim_0) float64 1... climate_imputed (chain, draw, climate_imputed_dim_0) float64 ... emp_imputed (chain, draw, emp_imputed_dim_0) float64 3... Attributes: created_at: 2023-02-02T07:57:06.498924 arviz_version: 0.14.0 inference_library: pymc inference_library_version: 5.0.1 sampling_time: 106.22190403938293 tuning_steps: 1000 -
<xarray.Dataset> Dimensions: (chain: 4, draw: 1000, climate_pred_observed_dim_2: 570, lmx_pred_observed_dim_2: 604, lmx_imputed_observed_dim_2: 604, climate_imputed_observed_dim_2: 570, emp_imputed_observed_dim_2: 528, climate_pred_dim_2: 630, lmx_pred_dim_2: 630, lmx_imputed_dim_2: 630, climate_imputed_dim_2: 630, emp_imputed_dim_2: 630) Coordinates: * chain (chain) int64 0 1 2 3 * draw (draw) int64 0 1 2 3 4 ... 996 997 998 999 * climate_pred_observed_dim_2 (climate_pred_observed_dim_2) int64 0 ...... * lmx_pred_observed_dim_2 (lmx_pred_observed_dim_2) int64 0 1 ... 603 * lmx_imputed_observed_dim_2 (lmx_imputed_observed_dim_2) int64 0 ... 603 * climate_imputed_observed_dim_2 (climate_imputed_observed_dim_2) int64 0 ... * emp_imputed_observed_dim_2 (emp_imputed_observed_dim_2) int64 0 ... 527 * climate_pred_dim_2 (climate_pred_dim_2) int64 0 1 2 ... 628 629 * lmx_pred_dim_2 (lmx_pred_dim_2) int64 0 1 2 ... 627 628 629 * lmx_imputed_dim_2 (lmx_imputed_dim_2) int64 0 1 2 ... 628 629 * climate_imputed_dim_2 (climate_imputed_dim_2) int64 0 1 ... 629 * emp_imputed_dim_2 (emp_imputed_dim_2) int64 0 1 2 ... 628 629 Data variables: climate_pred_observed (chain, draw, climate_pred_observed_dim_2) float64 ... lmx_pred_observed (chain, draw, lmx_pred_observed_dim_2) float64 ... lmx_imputed_observed (chain, draw, lmx_imputed_observed_dim_2) float64 ... climate_imputed_observed (chain, draw, climate_imputed_observed_dim_2) float64 ... emp_imputed_observed (chain, draw, emp_imputed_observed_dim_2) float64 ... climate_pred (chain, draw, climate_pred_dim_2) float64 ... lmx_pred (chain, draw, lmx_pred_dim_2) float64 8.6... lmx_imputed (chain, draw, lmx_imputed_dim_2) float64 ... climate_imputed (chain, draw, climate_imputed_dim_2) float64 ... emp_imputed (chain, draw, emp_imputed_dim_2) float64 ... Attributes: created_at: 2023-02-02T07:57:11.095286 arviz_version: 0.14.0 inference_library: pymc inference_library_version: 5.0.1 -
<xarray.Dataset> Dimensions: (chain: 4, draw: 1000) Coordinates: * chain (chain) int64 0 1 2 3 * draw (draw) int64 0 1 2 3 4 5 ... 994 995 996 997 998 999 Data variables: (12/17) n_steps (chain, draw) float64 31.0 31.0 31.0 ... 31.0 31.0 max_energy_error (chain, draw) float64 -0.3783 -0.1605 ... 0.6239 diverging (chain, draw) bool False False False ... False False reached_max_treedepth (chain, draw) bool False False False ... False False acceptance_rate (chain, draw) float64 0.9975 0.9587 ... 0.6311 0.7695 process_time_diff (chain, draw) float64 0.02338 0.02421 ... 0.01917 ... ... perf_counter_start (chain, draw) float64 4.427e+05 ... 4.427e+05 energy (chain, draw) float64 8.642e+03 ... 8.615e+03 lp (chain, draw) float64 -8.501e+03 ... -8.471e+03 energy_error (chain, draw) float64 -0.1605 0.1162 ... -0.08054 largest_eigval (chain, draw) float64 nan nan nan nan ... nan nan nan tree_depth (chain, draw) int64 5 5 5 5 5 5 5 5 ... 5 5 5 5 5 5 5 Attributes: created_at: 2023-02-02T07:57:06.518637 arviz_version: 0.14.0 inference_library: pymc inference_library_version: 5.0.1 sampling_time: 106.22190403938293 tuning_steps: 1000 -
<xarray.Dataset> Dimensions: (chain: 1, draw: 500, alpha_dim: 3, beta_dim: 6, climate_pred_missing_dim_0: 60, climate_imputed_missing_dim_0: 60, emp_imputed_dim_0: 630, climate_imputed_dim_0: 630, lmx_pred_dim_0: 630, lmx_imputed_missing_dim_0: 26, emp_imputed_missing_dim_0: 102, lmx_pred_missing_dim_0: 26, lmx_imputed_dim_0: 630, climate_pred_dim_0: 630) Coordinates: (12/14) * chain (chain) int64 0 * draw (draw) int64 0 1 2 3 4 ... 496 497 498 499 * alpha_dim (alpha_dim) <U15 'lmx_imputed' ... 'empowe... * beta_dim (beta_dim) <U13 'lmxB_male' ... 'empB_lmx' * climate_pred_missing_dim_0 (climate_pred_missing_dim_0) int64 0 1 ... 59 * climate_imputed_missing_dim_0 (climate_imputed_missing_dim_0) int64 0 ..... ... ... * lmx_pred_dim_0 (lmx_pred_dim_0) int64 0 1 2 ... 627 628 629 * lmx_imputed_missing_dim_0 (lmx_imputed_missing_dim_0) int64 0 1 ... 25 * emp_imputed_missing_dim_0 (emp_imputed_missing_dim_0) int64 0 1 ... 101 * lmx_pred_missing_dim_0 (lmx_pred_missing_dim_0) int64 0 1 ... 24 25 * lmx_imputed_dim_0 (lmx_imputed_dim_0) int64 0 1 2 ... 628 629 * climate_pred_dim_0 (climate_pred_dim_0) int64 0 1 2 ... 628 629 Data variables: (12/17) alphas (chain, draw, alpha_dim) float64 11.45 ...... sigma_climate (chain, draw) float64 1.15 0.4145 ... 0.8882 beta (chain, draw, beta_dim) float64 1.199 ... ... climate_pred_missing (chain, draw, climate_pred_missing_dim_0) float64 ... climate_imputed_missing (chain, draw, climate_imputed_missing_dim_0) float64 ... emp_imputed (chain, draw, emp_imputed_dim_0) float64 8... ... ... sigmas (chain, draw, alpha_dim) float64 6.3 ... 1... lmx_pred_missing (chain, draw, lmx_pred_missing_dim_0) float64 ... sigma_lmx (chain, draw) float64 1.127 5.054 ... 6.724 lmx_imputed (chain, draw, lmx_imputed_dim_0) float64 2... mu_climate (chain, draw) float64 4.559 9.647 ... 9.476 climate_pred (chain, draw, climate_pred_dim_0) float64 ... Attributes: created_at: 2023-02-02T07:54:57.199499 arviz_version: 0.14.0 inference_library: pymc inference_library_version: 5.0.1 -
<xarray.Dataset> Dimensions: (chain: 1, draw: 500, lmx_pred_observed_dim_0: 604, emp_imputed_observed_dim_0: 528, lmx_imputed_observed_dim_0: 604, climate_imputed_observed_dim_0: 570, climate_pred_observed_dim_0: 570) Coordinates: * chain (chain) int64 0 * draw (draw) int64 0 1 2 3 4 ... 496 497 498 499 * lmx_pred_observed_dim_0 (lmx_pred_observed_dim_0) int64 0 1 ... 603 * emp_imputed_observed_dim_0 (emp_imputed_observed_dim_0) int64 0 ... 527 * lmx_imputed_observed_dim_0 (lmx_imputed_observed_dim_0) int64 0 ... 603 * climate_imputed_observed_dim_0 (climate_imputed_observed_dim_0) int64 0 ... * climate_pred_observed_dim_0 (climate_pred_observed_dim_0) int64 0 ...... Data variables: lmx_pred_observed (chain, draw, lmx_pred_observed_dim_0) float64 ... emp_imputed_observed (chain, draw, emp_imputed_observed_dim_0) float64 ... lmx_imputed_observed (chain, draw, lmx_imputed_observed_dim_0) float64 ... climate_imputed_observed (chain, draw, climate_imputed_observed_dim_0) float64 ... climate_pred_observed (chain, draw, climate_pred_observed_dim_0) float64 ... Attributes: created_at: 2023-02-02T07:54:57.206651 arviz_version: 0.14.0 inference_library: pymc inference_library_version: 5.0.1 -
<xarray.Dataset> Dimensions: (climate_pred_observed_dim_0: 570, lmx_pred_observed_dim_0: 604, lmx_imputed_observed_dim_0: 604, climate_imputed_observed_dim_0: 570, emp_imputed_observed_dim_0: 528) Coordinates: * climate_pred_observed_dim_0 (climate_pred_observed_dim_0) int64 0 ...... * lmx_pred_observed_dim_0 (lmx_pred_observed_dim_0) int64 0 1 ... 603 * lmx_imputed_observed_dim_0 (lmx_imputed_observed_dim_0) int64 0 ... 603 * climate_imputed_observed_dim_0 (climate_imputed_observed_dim_0) int64 0 ... * emp_imputed_observed_dim_0 (emp_imputed_observed_dim_0) int64 0 ... 527 Data variables: climate_pred_observed (climate_pred_observed_dim_0) float64 18.... lmx_pred_observed (lmx_pred_observed_dim_0) float64 11.0 ..... lmx_imputed_observed (lmx_imputed_observed_dim_0) float64 11.0... climate_imputed_observed (climate_imputed_observed_dim_0) float64 ... emp_imputed_observed (emp_imputed_observed_dim_0) float64 32.0... Attributes: created_at: 2023-02-02T07:54:57.209280 arviz_version: 0.14.0 inference_library: pymc inference_library_version: 5.0.1
模型拟合#
接下来,我们将检查回归模型的参数拟合,并观察它们如何依赖于插补方案中的先验规范。
az.summary(idata_normal, var_names=["alphas", "beta", "sigmas"], stat_focus="median")
| 中位数 | mad | eti_3% | eti_97% | mcse_median | ess_median | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|
| alphas[lmx_imputed] | 9.057 | 0.446 | 7.854 | 10.263 | 0.011 | 3920.446 | 3077.0 | 1.00 |
| alphas[climate_imputed] | 19.776 | 0.158 | 19.345 | 20.213 | 0.005 | 4203.071 | 3452.0 | 1.00 |
| alphas[empower_imputed] | 17.928 | 0.689 | 16.016 | 19.851 | 0.022 | 3143.699 | 3063.0 | 1.00 |
| beta[lmxB_male] | 0.437 | 0.157 | -0.005 | 0.894 | 0.003 | 7104.804 | 3102.0 | 1.00 |
| beta[lmxB_climate] | 0.018 | 0.022 | -0.042 | 0.076 | 0.001 | 3670.069 | 2911.0 | 1.00 |
| beta[climateB_male] | 0.696 | 0.214 | 0.092 | 1.286 | 0.006 | 4471.550 | 3328.0 | 1.00 |
| beta[empB_male] | 1.656 | 0.214 | 1.043 | 2.254 | 0.005 | 5282.112 | 3361.0 | 1.00 |
| beta[empB_climate] | 0.203 | 0.030 | 0.121 | 0.286 | 0.001 | 3395.600 | 3068.0 | 1.00 |
| beta[empB_lmx] | 0.598 | 0.039 | 0.489 | 0.710 | 0.001 | 4541.732 | 2991.0 | 1.00 |
| sigmas[lmx_imputed] | 3.023 | 0.059 | 2.865 | 3.199 | 0.001 | 5408.426 | 3360.0 | 1.00 |
| sigmas[climate_imputed] | 4.021 | 0.077 | 3.812 | 4.251 | 0.002 | 5084.700 | 3347.0 | 1.01 |
| sigmas[empower_imputed] | 3.815 | 0.079 | 3.598 | 4.052 | 0.002 | 4530.686 | 3042.0 | 1.00 |
az.summary(idata_uniform, var_names=["alphas", "beta", "sigmas"], stat_focus="median")
| 中位数 | mad | eti_3% | eti_97% | mcse_median | ess_median | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|
| alphas[lmx_imputed] | 9.159 | 0.402 | 8.082 | 10.230 | 0.015 | 3450.523 | 3292.0 | 1.0 |
| alphas[climate_imputed] | 19.781 | 0.159 | 19.339 | 20.219 | 0.004 | 4512.068 | 3360.0 | 1.0 |
| alphas[empower_imputed] | 18.855 | 0.645 | 17.070 | 20.708 | 0.026 | 2292.646 | 2706.0 | 1.0 |
| beta[lmxB_male] | 0.433 | 0.166 | 0.013 | 0.867 | 0.003 | 6325.253 | 3040.0 | 1.0 |
| beta[lmxB_climate] | 0.013 | 0.019 | -0.039 | 0.065 | 0.001 | 3197.124 | 3042.0 | 1.0 |
| beta[climateB_male] | 0.689 | 0.224 | 0.067 | 1.284 | 0.006 | 4576.652 | 3231.0 | 1.0 |
| beta[empB_male] | 1.625 | 0.215 | 1.025 | 2.230 | 0.005 | 6056.623 | 3056.0 | 1.0 |
| beta[empB_climate] | 0.206 | 0.025 | 0.130 | 0.275 | 0.001 | 3166.040 | 2923.0 | 1.0 |
| beta[empB_lmx] | 0.488 | 0.044 | 0.363 | 0.608 | 0.001 | 2428.278 | 2756.0 | 1.0 |
| sigmas[lmx_imputed] | 3.020 | 0.058 | 2.874 | 3.186 | 0.001 | 7159.549 | 3040.0 | 1.0 |
| sigmas[climate_imputed] | 4.018 | 0.081 | 3.808 | 4.252 | 0.002 | 6092.150 | 2921.0 | 1.0 |
| sigmas[empower_imputed] | 3.783 | 0.082 | 3.572 | 4.029 | 0.002 | 4046.865 | 2845.0 | 1.0 |
我们可以看到抽样分布的选择如何在我们的两个模型中引起 beta 系数的不同参数估计。这两个插补在参数水平上大致一致,但它们在含义上存在有意义的差异。
az.plot_forest(
[idata_normal, idata_uniform],
var_names=["beta"],
kind="ridgeplot",
model_names=["Gaussian Sampling Distribution", "Uniform Sampling Distribution"],
figsize=(10, 8),
)
array([<AxesSubplot: >], dtype=object)
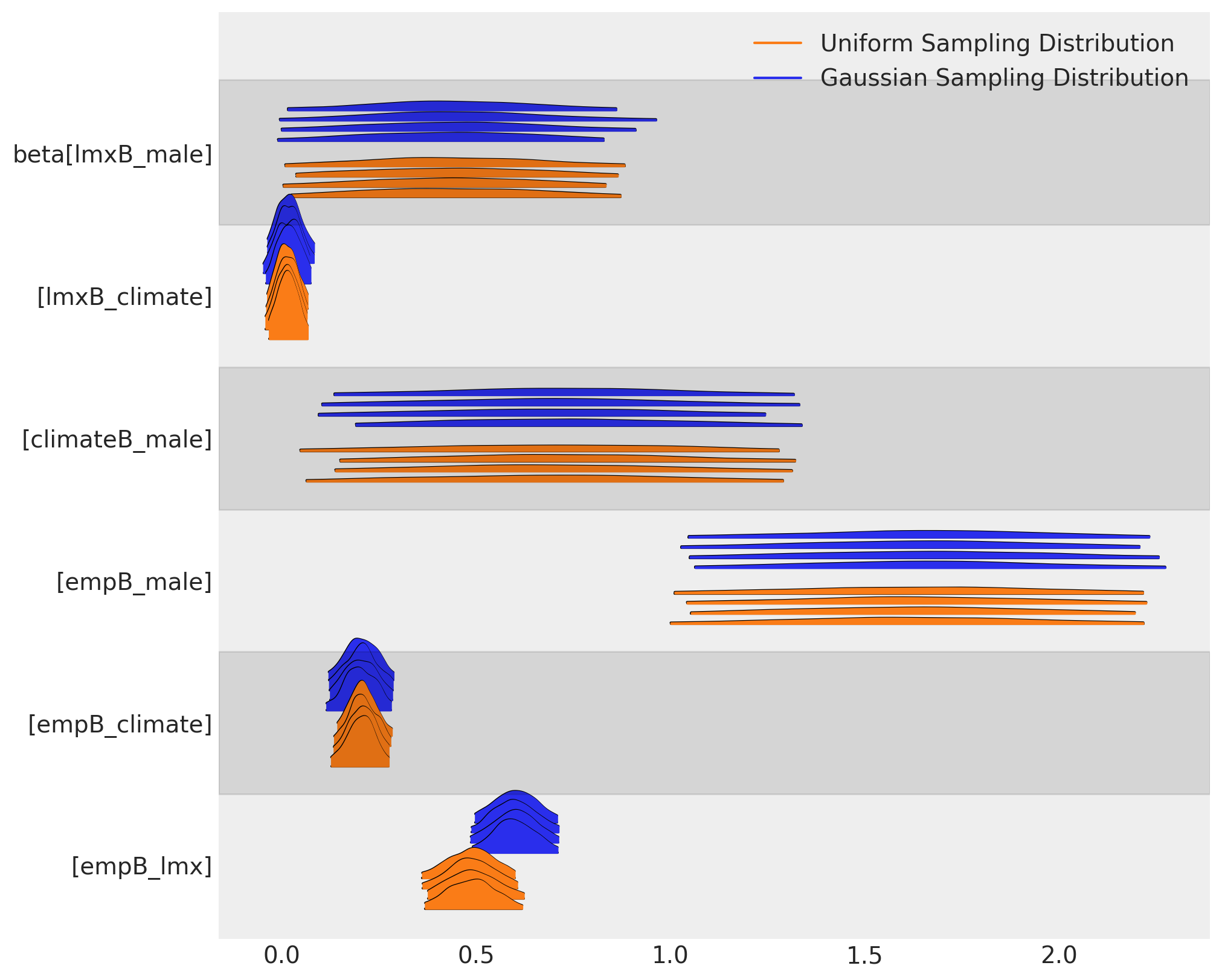
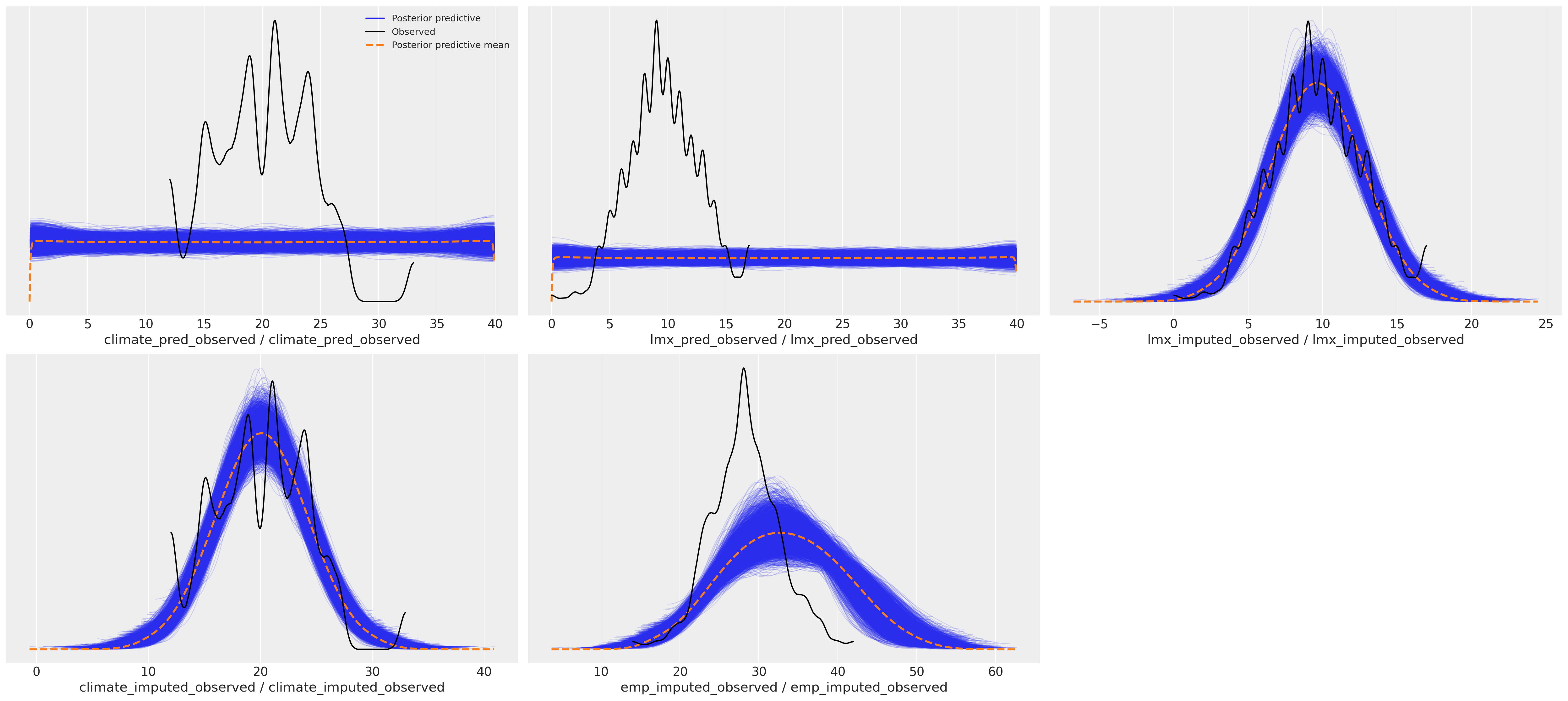
这种差异对后验预测分布具有下游影响。我们可以在这里看到预测项的抽样分布如何影响我们焦点回归方程的后验预测拟合。
后验预测分布#
az.plot_ppc(idata_uniform)
array([[<AxesSubplot: xlabel='climate_pred_observed / climate_pred_observed'>,
<AxesSubplot: xlabel='lmx_pred_observed / lmx_pred_observed'>,
<AxesSubplot: xlabel='lmx_imputed_observed / lmx_imputed_observed'>],
[<AxesSubplot: xlabel='climate_imputed_observed / climate_imputed_observed'>,
<AxesSubplot: xlabel='emp_imputed_observed / emp_imputed_observed'>,
<AxesSubplot: >]], dtype=object)
az.plot_ppc(idata_normal)
array([[<AxesSubplot: xlabel='climate_pred_observed / climate_pred_observed'>,
<AxesSubplot: xlabel='lmx_pred_observed / lmx_pred_observed'>,
<AxesSubplot: xlabel='lmx_imputed_observed / lmx_imputed_observed'>],
[<AxesSubplot: xlabel='climate_imputed_observed / climate_imputed_observed'>,
<AxesSubplot: xlabel='emp_imputed_observed / emp_imputed_observed'>,
<AxesSubplot: >]], dtype=object)
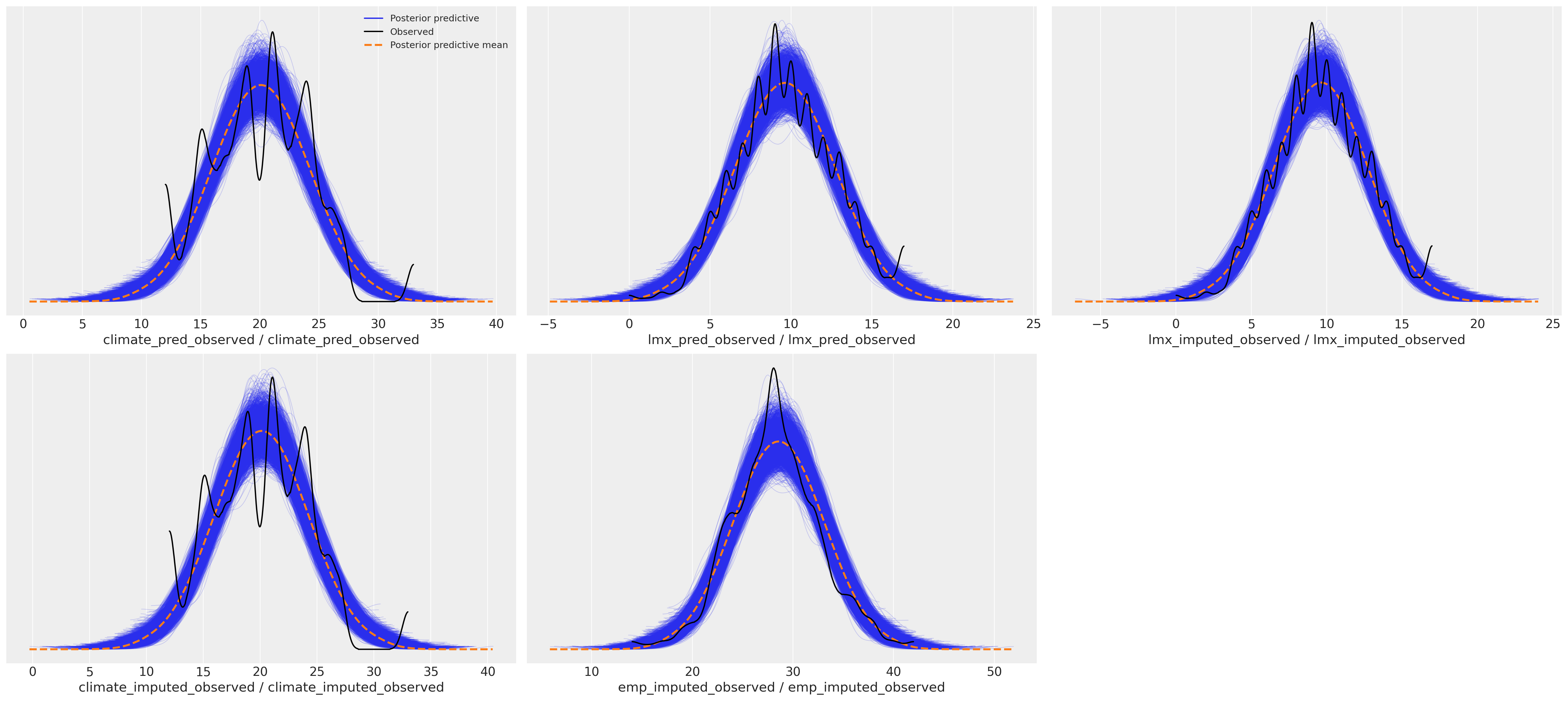
处理后验预测分布#
上面我们在单个 PyMC 模型上下文中估计了许多似然项。这些似然约束了超参数,这些超参数确定了在我们的焦点回归方程中用作预测变量的变量中缺失项的插补值 empower。但是我们也可以执行更手动的顺序插补,其中我们分别对每个从属回归方程进行建模,并依次提取每个变量的插补值,然后在焦点回归方程的插补值上运行一个简单的回归。
我们在这里展示了如何提取每个回归方程的插补值并扩充观测数据。
def get_imputed(idata, data):
imputed_data = data.copy()
imputed_climate = az.extract(idata, group="posterior_predictive", num_samples=1000)[
"climate_imputed"
].mean(axis=1)
mask = imputed_data["climate"].isnull()
imputed_data.loc[mask, "climate"] = imputed_climate.values[imputed_data[mask].index]
imputed_lmx = az.extract(idata, group="posterior_predictive", num_samples=1000)[
"lmx_imputed"
].mean(axis=1)
mask = imputed_data["lmx"].isnull()
imputed_data.loc[mask, "lmx"] = imputed_lmx.values[imputed_data[mask].index]
imputed_emp = az.extract(idata, group="posterior_predictive", num_samples=1000)[
"emp_imputed"
].mean(axis=1)
mask = imputed_data["empower"].isnull()
imputed_data.loc[mask, "empower"] = imputed_emp.values[imputed_data[mask].index]
assert imputed_data.isnull().sum().to_list() == [0, 0, 0, 0]
imputed_data.columns = ["imputed_" + col for col in imputed_data.columns]
return imputed_data
imputed_data_uniform = get_imputed(idata_uniform, data)
imputed_data_normal = get_imputed(idata_normal, data)
imputed_data_normal.head(5)
| imputed_lmx | imputed_empower | imputed_climate | imputed_male | |
|---|---|---|---|---|
| 0 | 11.0 | 32.000000 | 18.0 | 1 |
| 1 | 13.0 | 29.490539 | 18.0 | 1 |
| 2 | 9.0 | 30.000000 | 18.0 | 1 |
| 3 | 8.0 | 29.000000 | 18.0 | 1 |
| 4 | 7.0 | 26.000000 | 18.0 | 0 |
我们在这里使用均值来插补每个缺失单元格的期望值,但是您可以使用后验预测分布中的许多合理值来执行某种敏感性分析
绘制插补数据集#
现在我们将绘制插补值与其观测值,以显示不同的抽样分布如何影响插补模式。
joined_uniform = pd.concat([imputed_data_uniform, data], axis=1)
joined_normal = pd.concat([imputed_data_normal, data], axis=1)
for col in ["lmx", "empower", "climate"]:
joined_uniform[col + "_missing"] = np.where(joined_uniform[col].isnull(), 1, 0)
joined_normal[col + "_missing"] = np.where(joined_normal[col].isnull(), 1, 0)
def rand_jitter(arr):
stdev = 0.01 * (max(arr) - min(arr))
return arr + np.random.randn(len(arr)) * stdev
fig, axs = plt.subplots(1, 3, figsize=(20, 8))
axs = axs.flatten()
ax = axs[0]
ax1 = axs[1]
ax2 = axs[2]
## Derived from MV norm fit.
z = multivariate_normal(
[lmx_mean, joined_uniform["imputed_empower"].mean()], [[8.9, 5.4], [5.4, 19]]
).pdf(joined_uniform[["imputed_lmx", "imputed_empower"]])
ax.scatter(
rand_jitter(joined_uniform["imputed_lmx"]),
rand_jitter(joined_uniform["imputed_empower"]),
c=joined_uniform["empower_missing"],
cmap=cm.winter,
ec="black",
s=50,
)
ax.set_title("Relationship between LMX and Empowerment \n after Uniform Imputation", fontsize=20)
ax.tricontour(joined_uniform["imputed_lmx"], joined_uniform["imputed_empower"], z)
ax.set_xlabel("Leader-Member-Exchange")
ax.set_ylabel("Empowerment")
custom_lines = [
Line2D([0], [0], color=cm.winter(0.0), lw=4),
Line2D([0], [0], color=cm.winter(0.9), lw=4),
]
ax.legend(custom_lines, ["Observed", "Missing - Imputed Empowerment Values"])
z = multivariate_normal(
[lmx_mean, joined_normal["imputed_empower"].mean()], [[8.9, 5.4], [5.4, 19]]
).pdf(joined_normal[["imputed_lmx", "imputed_empower"]])
ax2.scatter(
rand_jitter(joined_normal["imputed_lmx"]),
rand_jitter(joined_normal["imputed_empower"]),
c=joined_normal["empower_missing"],
cmap=cm.autumn,
ec="black",
s=50,
)
ax2.set_title("Relationship between LMX and Empowerment \n after Gaussian Imputation", fontsize=20)
ax2.tricontour(joined_normal["imputed_lmx"], joined_normal["imputed_empower"], z)
ax2.set_xlabel("Leader-Member-Exchange")
ax2.set_ylabel("Empowerment")
custom_lines = [
Line2D([0], [0], color=cm.autumn(0.0), lw=4),
Line2D([0], [0], color=cm.autumn(0.9), lw=4),
]
ax2.legend(custom_lines, ["Observed", "Missing - Imputed Empowerment Values"])
ax1.hist(
joined_normal["imputed_empower"],
label="Gaussian Imputed Empowerment",
bins=30,
color="slateblue",
ec="black",
)
ax1.hist(
joined_uniform["imputed_empower"],
label="Uniform Imputed Empowerment",
bins=30,
color="cyan",
ec="black",
)
ax1.hist(
joined_normal["empower"], label="Observed Empowerment", bins=30, color="magenta", ec="black"
)
ax1.legend()
ax1.set_title("Imputed & Observed Empowerment", fontsize=20);
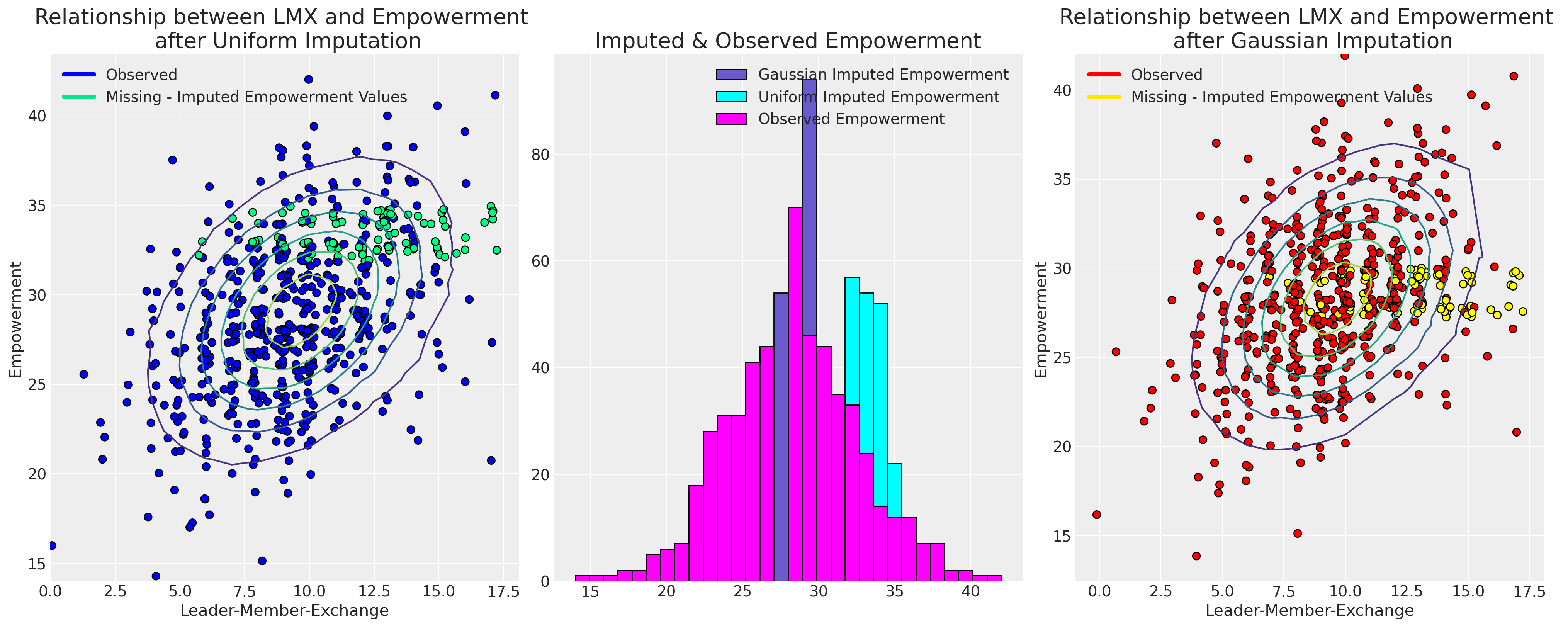
最终,我们对抽样分布的选择导致了不同的合理插补。选择哪个模型将由支配我们数据中缺失原因的假设驱动。
分层结构和数据插补#
我们的员工数据集具有比我们迄今为止检查的更精细的结构。特别是,我们的员工库由大约 100 个团队组成,我们可能想知道满意度倾向或不完整的调查评分在多大程度上是由于当地团队环境造成的?这可能是我们缺失数据模式的一个因素吗?我们将按团队检查报告的赋权感得分,并绘制回归线,这些回归线由每个团队在其报告的 lmx 得分中预测。
heatmap = df_employee.pivot("employee", "team", "empower").dropna(how="all")
heatmap = pd.concat(
[heatmap[~heatmap[col].isnull()][col].reset_index(drop=True) for col in heatmap.columns], axis=1
)
with pd.option_context("format.precision", 2):
display(heatmap.style.background_gradient(cmap="Blues"));
/var/folders/99/gp2xl6x513s0tvl3cx79zf7m0000gn/T/ipykernel_96943/1805800404.py:1: FutureWarning: In a future version of pandas all arguments of DataFrame.pivot will be keyword-only.
heatmap = df_employee.pivot("employee", "team", "empower").dropna(how="all")
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 32.00 | 22.00 | 16.00 | 26.00 | 33.00 | 21.00 | 29.00 | 26.00 | 27.00 | 33.00 | 28.00 | 36.00 | 24.00 | 24.00 | 34.00 | 28.00 | 29.00 | 22.00 | 28.00 | 23.00 | 25.00 | 39.00 | 28.00 | 28.00 | 26.00 | 29.00 | 34.00 | 25.00 | 30.00 | 26.00 | 28.00 | 23.00 | 32.00 | 27.00 | 38.00 | 22.00 | 36.00 | 30.00 | 30.00 | 30.00 | 30.00 | 28.00 | 27.00 | 28.00 | 25.00 | 21.00 | 37.00 | 24.00 | 31.00 | 27.00 | 28.00 | 32.00 | 27.00 | 30.00 | 28.00 | 26.00 | 29.00 | 20.00 | 30.00 | 27.00 | 32.00 | 22.00 | 32.00 | 31.00 | 26.00 | 29.00 | 24.00 | 23.00 | 33.00 | 29.00 | 35.00 | 25.00 | 33.00 | 23.00 | 32.00 | 27.00 | 31.00 | 28.00 | 27.00 | 28.00 | 25.00 | 31.00 | 28.00 | 31.00 | 28.00 | 32.00 | 24.00 | 29.00 | 28.00 | 30.00 | 33.00 | 23.00 | 28.00 | 21.00 | 25.00 | 39.00 | 25.00 | 31.00 | 30.00 | 24.00 | 29.00 | 25.00 | 20.00 | 28.00 | 28.00 |
| 1 | 30.00 | 23.00 | 25.00 | 27.00 | 37.00 | 29.00 | 26.00 | 25.00 | 28.00 | 27.00 | 26.00 | 32.00 | 23.00 | 30.00 | 24.00 | 24.00 | 26.00 | 28.00 | 33.00 | 22.00 | 17.00 | 31.00 | 22.00 | 36.00 | 34.00 | 23.00 | 32.00 | 30.00 | 30.00 | 22.00 | 22.00 | 28.00 | 31.00 | 30.00 | 32.00 | 23.00 | 32.00 | 36.00 | 23.00 | 26.00 | 24.00 | 32.00 | 36.00 | 26.00 | 25.00 | 35.00 | 32.00 | 28.00 | 24.00 | 28.00 | 35.00 | 28.00 | 32.00 | 24.00 | 26.00 | 23.00 | 26.00 | 29.00 | 28.00 | 28.00 | 33.00 | 29.00 | 25.00 | 28.00 | 27.00 | 29.00 | 24.00 | 34.00 | 27.00 | 28.00 | 31.00 | 27.00 | 25.00 | 30.00 | 28.00 | 20.00 | 28.00 | 32.00 | 23.00 | 15.00 | 29.00 | 31.00 | 31.00 | 28.00 | 30.00 | 28.00 | 40.00 | 30.00 | 26.00 | 19.00 | 25.00 | 23.00 | 32.00 | 27.00 | 30.00 | 26.00 | 35.00 | 24.00 | 25.00 | 23.00 | 28.00 | 34.00 | 26.00 | 28.00 | 17.00 |
| 2 | 29.00 | 32.00 | 31.00 | 42.00 | 29.00 | 25.00 | 26.00 | 29.00 | 26.00 | 29.00 | 30.00 | 30.00 | 25.00 | 22.00 | 21.00 | 34.00 | 33.00 | 32.00 | 26.00 | 29.00 | 35.00 | 32.00 | 33.00 | 27.00 | 26.00 | 22.00 | 29.00 | 29.00 | 32.00 | 30.00 | 35.00 | 29.00 | 33.00 | 30.00 | 30.00 | 31.00 | 26.00 | 28.00 | 40.00 | 25.00 | 41.00 | 27.00 | 23.00 | 31.00 | 29.00 | 28.00 | 27.00 | 23.00 | 36.00 | 28.00 | 23.00 | 31.00 | 29.00 | 33.00 | 27.00 | 19.00 | 25.00 | 33.00 | 29.00 | 27.00 | 23.00 | 28.00 | 31.00 | 26.00 | 22.00 | 37.00 | 24.00 | 33.00 | 37.00 | 29.00 | 29.00 | 26.00 | 27.00 | 31.00 | 23.00 | 14.00 | 28.00 | 30.00 | 29.00 | 28.00 | 36.00 | 27.00 | 28.00 | 35.00 | 29.00 | 38.00 | 26.00 | 38.00 | 30.00 | 34.00 | 38.00 | 28.00 | 34.00 | 28.00 | 28.00 | 30.00 | 31.00 | 27.00 | 29.00 | 24.00 | 33.00 | 30.00 | 28.00 | 26.00 | 28.00 |
| 3 | 26.00 | 36.00 | 27.00 | 24.00 | 32.00 | 36.00 | 26.00 | 27.00 | 29.00 | 36.00 | 28.00 | 30.00 | 27.00 | 27.00 | 33.00 | 34.00 | 29.00 | 27.00 | 33.00 | 26.00 | 26.00 | 33.00 | 30.00 | 26.00 | 28.00 | 31.00 | 20.00 | 30.00 | 23.00 | 30.00 | 28.00 | 25.00 | 32.00 | 31.00 | 18.00 | 29.00 | 26.00 | 26.00 | 27.00 | nan | 28.00 | nan | 29.00 | 25.00 | 22.00 | 33.00 | 33.00 | 30.00 | 33.00 | 34.00 | nan | 37.00 | 29.00 | 27.00 | 28.00 | 23.00 | 25.00 | 32.00 | 21.00 | 24.00 | 30.00 | 29.00 | 28.00 | 27.00 | 24.00 | 38.00 | 24.00 | 19.00 | 30.00 | 35.00 | 32.00 | 28.00 | 38.00 | 31.00 | 27.00 | 23.00 | 30.00 | 27.00 | 27.00 | 27.00 | 32.00 | 27.00 | 29.00 | 26.00 | 24.00 | 29.00 | 28.00 | 31.00 | 25.00 | 25.00 | 30.00 | 29.00 | 34.00 | 32.00 | 31.00 | 26.00 | nan | 34.00 | 27.00 | 21.00 | 24.00 | 25.00 | 28.00 | 23.00 | 32.00 |
| 4 | nan | nan | 30.00 | 37.00 | 24.00 | nan | 31.00 | nan | 28.00 | 24.00 | 28.00 | 34.00 | 24.00 | 38.00 | 35.00 | nan | nan | nan | nan | 29.00 | 37.00 | 32.00 | nan | 24.00 | nan | 26.00 | 29.00 | 26.00 | 35.00 | 29.00 | nan | 29.00 | nan | nan | nan | 20.00 | 23.00 | 31.00 | 22.00 | nan | nan | nan | 23.00 | nan | 19.00 | nan | 32.00 | 22.00 | 31.00 | 27.00 | nan | nan | nan | nan | 24.00 | nan | 27.00 | 28.00 | 26.00 | 25.00 | 30.00 | 22.00 | 30.00 | 28.00 | 32.00 | 29.00 | 28.00 | nan | nan | 28.00 | 30.00 | nan | 28.00 | 26.00 | 25.00 | nan | 27.00 | 35.00 | 24.00 | 29.00 | 24.00 | nan | 33.00 | 28.00 | 34.00 | 31.00 | 22.00 | nan | 26.00 | 18.00 | 32.00 | 22.00 | nan | 31.00 | 33.00 | nan | nan | 32.00 | 28.00 | 21.00 | 35.00 | 36.00 | 31.00 | 27.00 | nan |
| 5 | nan | nan | 23.00 | nan | 31.00 | nan | 33.00 | nan | 25.00 | 22.00 | 25.00 | nan | nan | 30.00 | 23.00 | nan | nan | nan | nan | 24.00 | nan | 31.00 | nan | nan | nan | nan | nan | nan | nan | 32.00 | nan | 25.00 | nan | nan | nan | 20.00 | 31.00 | 25.00 | nan | nan | nan | nan | nan | nan | 28.00 | nan | nan | 27.00 | 27.00 | nan | nan | nan | nan | nan | 27.00 | nan | 31.00 | 29.00 | nan | 31.00 | nan | 30.00 | nan | nan | nan | nan | nan | nan | nan | nan | 28.00 | nan | nan | nan | nan | nan | 33.00 | 30.00 | 19.00 | 23.00 | nan | nan | 26.00 | 28.00 | 26.00 | nan | nan | nan | 28.00 | 30.00 | 36.00 | 24.00 | nan | nan | 29.00 | nan | nan | nan | 28.00 | 27.00 | 28.00 | 31.00 | 24.00 | nan | nan |
fits = []
x = np.linspace(0, 20, 100)
fig, ax = plt.subplots(figsize=(20, 7))
for team in df_employee["team"].unique():
temp = df_employee[df_employee["team"] == team][["lmx", "empower"]].dropna()
fit = np.polyfit(temp["lmx"], temp["empower"], 1)
y = fit[0] * x + fit[1]
fits.append(fit)
ax.plot(x, y, alpha=0.6)
ax.scatter(rand_jitter(temp["lmx"]), rand_jitter(temp["empower"]), color="black", ec="white")
ax.set_title("Simple Regression fits by Team \n Empower ~ LMX", fontsize=20)
ax.set_xlabel("Leader-Member-Exchange (LMX)")
ax.set_ylabel("Empowerment")
ax.set_ylim(0, 45);
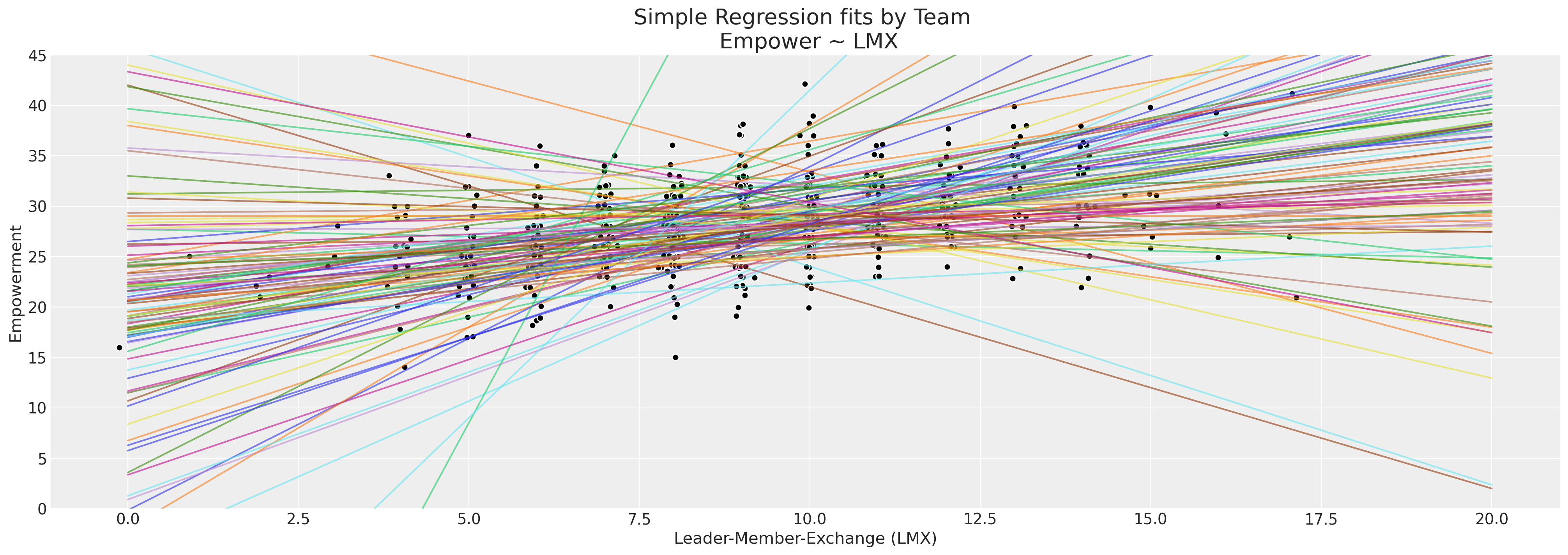
回归线中有足够的散布,至少表明在不同团队之间,赋权感与工作环境之间存在异构关系,但每个团队的观察结果有限。这是分层贝叶斯模型的完美用例。
team_idx, teams = pd.factorize(df_employee["team"], sort=True)
employee_idx, _ = pd.factorize(df_employee["employee"], sort=True)
coords = {"team": teams, "employee": np.arange(len(df_employee))}
with pm.Model(coords=coords) as hierarchical_model:
# Priors
company_beta_lmx = pm.Normal("company_beta_lmx", 0, 1)
company_beta_male = pm.Normal("company_beta_male", 0, 1)
company_alpha = pm.Normal("company_alpha", 20, 2)
team_alpha = pm.Normal("team_alpha", 0, 1, dims="team")
team_beta_lmx = pm.Normal("team_beta_lmx", 0, 1, dims="team")
sigma = pm.HalfNormal("sigma", 4, dims="employee")
# Imputed Predictors
mu_lmx = pm.Normal("mu_lmx", 10, 5)
sigma_lmx = pm.HalfNormal("sigma_lmx", 5)
lmx_pred = pm.Normal("lmx_pred", mu_lmx, sigma_lmx, observed=df_employee["lmx"].values)
# Combining Levels
alpha_global = pm.Deterministic("alpha_global", company_alpha + team_alpha[team_idx])
beta_global_lmx = pm.Deterministic(
"beta_global_lmx", company_beta_lmx + team_beta_lmx[team_idx]
)
beta_global_male = pm.Deterministic("beta_global_male", company_beta_male)
# Likelihood
mu = pm.Deterministic(
"mu",
alpha_global + beta_global_lmx * lmx_pred + beta_global_male * df_employee["male"].values,
)
empower_imputed = pm.Normal(
"emp_imputed",
mu,
sigma,
observed=df_employee["empower"].values,
)
idata_hierarchical = pm.sample_prior_predictive()
# idata_hierarchical.extend(pm.sample(random_seed=1200, target_accept=0.99))
idata_hierarchical.extend(
sample_blackjax_nuts(draws=20_000, random_seed=500, target_accept=0.99)
)
pm.sample_posterior_predictive(idata_hierarchical, extend_inferencedata=True)
pm.model_to_graphviz(hierarchical_model)
/Users/nathanielforde/opt/miniconda3/envs/missing_data_clean/lib/python3.11/site-packages/pymc/model.py:1400: ImputationWarning: Data in lmx_pred contains missing values and will be automatically imputed from the sampling distribution.
warnings.warn(impute_message, ImputationWarning)
/Users/nathanielforde/opt/miniconda3/envs/missing_data_clean/lib/python3.11/site-packages/pymc/model.py:1400: ImputationWarning: Data in emp_imputed contains missing values and will be automatically imputed from the sampling distribution.
warnings.warn(impute_message, ImputationWarning)
Sampling: [company_alpha, company_beta_lmx, company_beta_male, emp_imputed_missing, emp_imputed_observed, lmx_pred_missing, lmx_pred_observed, mu_lmx, sigma, sigma_lmx, team_alpha, team_beta_lmx]
Compiling...
Compilation time = 0:00:04.523249
Sampling...
Sampling time = 0:00:12.370856
Transforming variables...
Transformation time = 0:12:51.685820
Sampling: [emp_imputed_missing, emp_imputed_observed, lmx_pred_observed]
idata_hierarchical
-
<xarray.Dataset> Dimensions: (chain: 4, draw: 20000, team: 105, lmx_pred_missing_dim_0: 26, emp_imputed_missing_dim_0: 102, employee: 630, lmx_pred_dim_0: 630, alpha_global_dim_0: 630, beta_global_lmx_dim_0: 630, mu_dim_0: 630, emp_imputed_dim_0: 630) Coordinates: * chain (chain) int64 0 1 2 3 * draw (draw) int64 0 1 2 3 ... 19996 19997 19998 19999 * team (team) int64 1 2 3 4 5 6 ... 101 102 103 104 105 * lmx_pred_missing_dim_0 (lmx_pred_missing_dim_0) int64 0 1 2 ... 23 24 25 * emp_imputed_missing_dim_0 (emp_imputed_missing_dim_0) int64 0 1 ... 100 101 * employee (employee) int64 0 1 2 3 4 ... 626 627 628 629 * lmx_pred_dim_0 (lmx_pred_dim_0) int64 0 1 2 3 ... 627 628 629 * alpha_global_dim_0 (alpha_global_dim_0) int64 0 1 2 ... 627 628 629 * beta_global_lmx_dim_0 (beta_global_lmx_dim_0) int64 0 1 2 ... 628 629 * mu_dim_0 (mu_dim_0) int64 0 1 2 3 4 ... 626 627 628 629 * emp_imputed_dim_0 (emp_imputed_dim_0) int64 0 1 2 3 ... 627 628 629 Data variables: (12/16) company_beta_lmx (chain, draw) float64 0.6299 0.6698 ... 0.7356 company_beta_male (chain, draw) float64 0.8914 0.9321 ... 0.9751 company_alpha (chain, draw) float64 21.29 21.02 ... 20.83 20.77 team_alpha (chain, draw, team) float64 -1.535 ... 0.1378 team_beta_lmx (chain, draw, team) float64 0.3924 ... -0.1927 mu_lmx (chain, draw) float64 9.773 9.815 ... 9.797 9.764 ... ... lmx_pred (chain, draw, lmx_pred_dim_0) float64 11.0 ...... alpha_global (chain, draw, alpha_global_dim_0) float64 19.7... beta_global_lmx (chain, draw, beta_global_lmx_dim_0) float64 1... beta_global_male (chain, draw) float64 0.8914 0.9321 ... 0.9751 mu (chain, draw, mu_dim_0) float64 31.89 ... 24.59 emp_imputed (chain, draw, emp_imputed_dim_0) float64 32.0 ... Attributes: created_at: 2023-02-02T08:13:38.333014 arviz_version: 0.14.0 -
<xarray.Dataset> Dimensions: (chain: 4, draw: 20000, lmx_pred_observed_dim_2: 604, emp_imputed_observed_dim_2: 528, lmx_pred_dim_2: 630, mu_dim_2: 630, emp_imputed_dim_2: 630) Coordinates: * chain (chain) int64 0 1 2 3 * draw (draw) int64 0 1 2 3 ... 19996 19997 19998 19999 * lmx_pred_observed_dim_2 (lmx_pred_observed_dim_2) int64 0 1 ... 602 603 * emp_imputed_observed_dim_2 (emp_imputed_observed_dim_2) int64 0 1 ... 527 * lmx_pred_dim_2 (lmx_pred_dim_2) int64 0 1 2 3 ... 627 628 629 * mu_dim_2 (mu_dim_2) int64 0 1 2 3 4 ... 626 627 628 629 * emp_imputed_dim_2 (emp_imputed_dim_2) int64 0 1 2 ... 627 628 629 Data variables: lmx_pred_observed (chain, draw, lmx_pred_observed_dim_2) float64 ... emp_imputed_observed (chain, draw, emp_imputed_observed_dim_2) float64 ... lmx_pred (chain, draw, lmx_pred_dim_2) float64 14.09 .... mu (chain, draw, mu_dim_2) float64 35.05 ... 24.5 emp_imputed (chain, draw, emp_imputed_dim_2) float64 34.7... Attributes: created_at: 2023-02-02T08:14:02.072909 arviz_version: 0.14.0 inference_library: pymc inference_library_version: 5.0.1 -
<xarray.Dataset> Dimensions: (chain: 4, draw: 20000) Coordinates: * chain (chain) int64 0 1 2 3 * draw (draw) int64 0 1 2 3 4 5 ... 19995 19996 19997 19998 19999 Data variables: lp (chain, draw) float64 4.1e+03 4.134e+03 ... 4.072e+03 diverging (chain, draw) bool False False False ... False False False energy (chain, draw) float64 4.569e+03 4.597e+03 ... 4.562e+03 tree_depth (chain, draw) int64 10 10 10 10 10 10 ... 10 10 10 10 10 10 n_steps (chain, draw) int64 1023 1023 1023 1023 ... 1023 1023 1023 acceptance_rate (chain, draw) float64 0.9823 0.9843 ... 0.9916 0.9895 Attributes: created_at: 2023-02-02T08:13:38.402578 arviz_version: 0.14.0 -
<xarray.Dataset> Dimensions: (chain: 1, draw: 500, lmx_pred_missing_dim_0: 26, lmx_pred_dim_0: 630, team: 105, alpha_global_dim_0: 630, beta_global_lmx_dim_0: 630, emp_imputed_missing_dim_0: 102, mu_dim_0: 630, employee: 630, emp_imputed_dim_0: 630) Coordinates: * chain (chain) int64 0 * draw (draw) int64 0 1 2 3 4 5 ... 495 496 497 498 499 * lmx_pred_missing_dim_0 (lmx_pred_missing_dim_0) int64 0 1 2 ... 23 24 25 * lmx_pred_dim_0 (lmx_pred_dim_0) int64 0 1 2 3 ... 627 628 629 * team (team) int64 1 2 3 4 5 6 ... 101 102 103 104 105 * alpha_global_dim_0 (alpha_global_dim_0) int64 0 1 2 ... 627 628 629 * beta_global_lmx_dim_0 (beta_global_lmx_dim_0) int64 0 1 2 ... 628 629 * emp_imputed_missing_dim_0 (emp_imputed_missing_dim_0) int64 0 1 ... 100 101 * mu_dim_0 (mu_dim_0) int64 0 1 2 3 4 ... 626 627 628 629 * employee (employee) int64 0 1 2 3 4 ... 626 627 628 629 * emp_imputed_dim_0 (emp_imputed_dim_0) int64 0 1 2 3 ... 627 628 629 Data variables: (12/16) company_alpha (chain, draw) float64 18.23 21.82 ... 23.99 18.59 beta_global_male (chain, draw) float64 -1.439 -0.3283 ... -0.8552 lmx_pred_missing (chain, draw, lmx_pred_missing_dim_0) float64 ... company_beta_lmx (chain, draw) float64 -0.008152 1.042 ... 0.29 lmx_pred (chain, draw, lmx_pred_dim_0) float64 13.11 ..... team_alpha (chain, draw, team) float64 1.207 ... 0.9462 ... ... emp_imputed_missing (chain, draw, emp_imputed_missing_dim_0) float64 ... mu (chain, draw, mu_dim_0) float64 43.46 ... 25.64 team_beta_lmx (chain, draw, team) float64 1.951 ... 0.2287 sigma (chain, draw, employee) float64 5.371 ... 4.738 emp_imputed (chain, draw, emp_imputed_dim_0) float64 35.27... mu_lmx (chain, draw) float64 13.31 13.64 ... 9.915 9.307 Attributes: created_at: 2023-02-02T08:00:29.477993 arviz_version: 0.14.0 inference_library: pymc inference_library_version: 5.0.1 -
<xarray.Dataset> Dimensions: (chain: 1, draw: 500, lmx_pred_observed_dim_0: 604, emp_imputed_observed_dim_0: 528) Coordinates: * chain (chain) int64 0 * draw (draw) int64 0 1 2 3 4 5 ... 495 496 497 498 499 * lmx_pred_observed_dim_0 (lmx_pred_observed_dim_0) int64 0 1 ... 602 603 * emp_imputed_observed_dim_0 (emp_imputed_observed_dim_0) int64 0 1 ... 527 Data variables: lmx_pred_observed (chain, draw, lmx_pred_observed_dim_0) float64 ... emp_imputed_observed (chain, draw, emp_imputed_observed_dim_0) float64 ... Attributes: created_at: 2023-02-02T08:00:29.484585 arviz_version: 0.14.0 inference_library: pymc inference_library_version: 5.0.1 -
<xarray.Dataset> Dimensions: (lmx_pred_observed_dim_0: 604, emp_imputed_observed_dim_0: 528) Coordinates: * lmx_pred_observed_dim_0 (lmx_pred_observed_dim_0) int64 0 1 ... 602 603 * emp_imputed_observed_dim_0 (emp_imputed_observed_dim_0) int64 0 1 ... 527 Data variables: lmx_pred_observed (lmx_pred_observed_dim_0) float64 11.0 ... 5.0 emp_imputed_observed (emp_imputed_observed_dim_0) float64 32.0 ...... Attributes: created_at: 2023-02-02T08:00:29.485965 arviz_version: 0.14.0 inference_library: pymc inference_library_version: 5.0.1
一些收敛性检查#
az.plot_trace(
idata_hierarchical,
var_names=["company_alpha", "team_alpha", "company_beta_lmx", "team_beta_lmx"],
kind="rank_vlines",
);
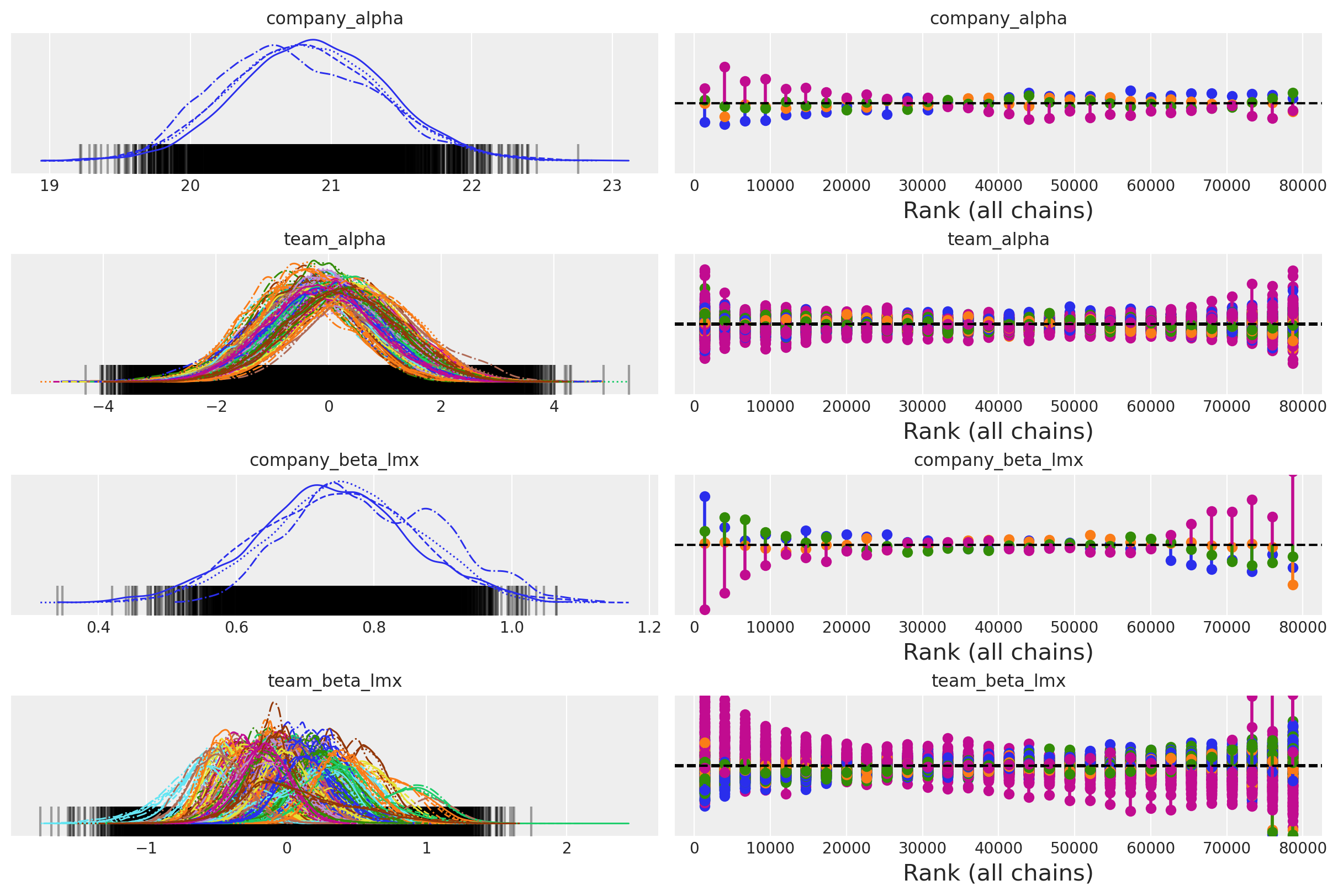
az.plot_energy(idata_hierarchical, figsize=(20, 7));
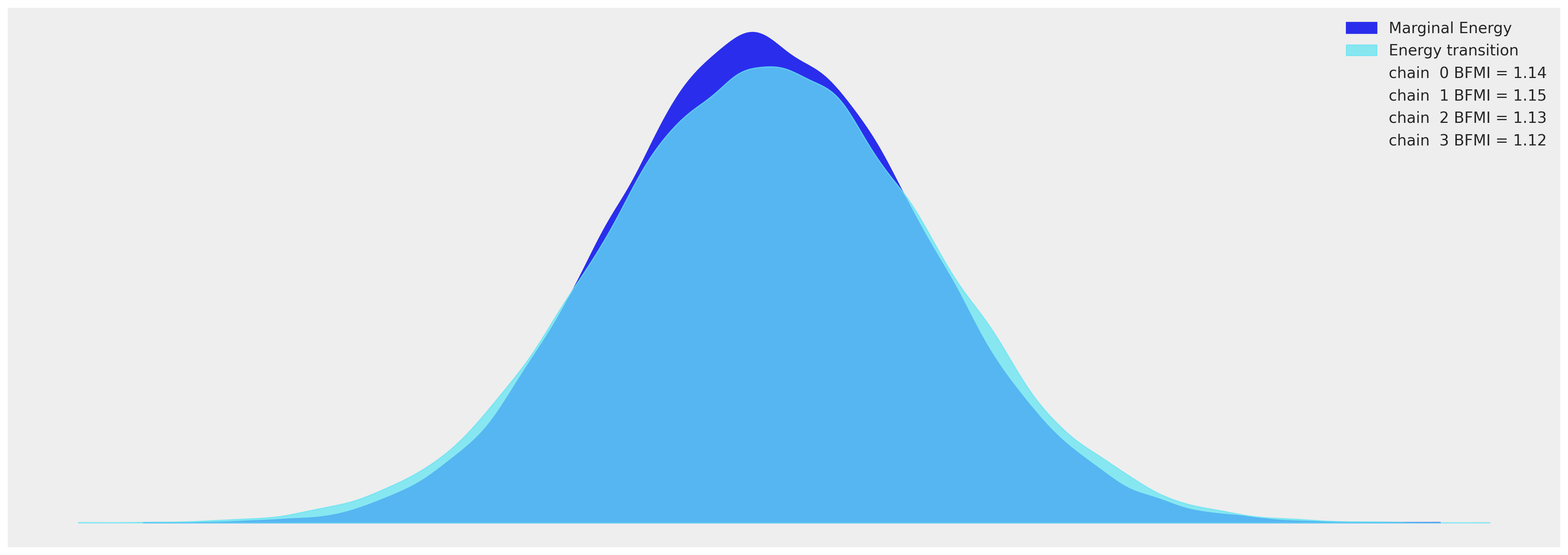
检查模型拟合#
summary = az.summary(
idata_hierarchical,
var_names=[
"company_alpha",
"team_alpha",
"company_beta_lmx",
"company_beta_male",
"team_beta_lmx",
],
)
summary
| 均值 | 标准差 | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| company_alpha | 20.818 | 0.545 | 19.806 | 21.840 | 0.029 | 0.020 | 358.0 | 1316.0 | 1.02 |
| team_alpha[1] | -0.214 | 0.955 | -1.975 | 1.604 | 0.030 | 0.021 | 1043.0 | 2031.0 | 1.00 |
| team_alpha[2] | -0.067 | 0.995 | -1.975 | 1.772 | 0.026 | 0.018 | 1496.0 | 2572.0 | 1.00 |
| team_alpha[3] | -0.568 | 0.931 | -2.271 | 1.250 | 0.027 | 0.019 | 1144.0 | 2135.0 | 1.00 |
| team_alpha[4] | -0.228 | 0.993 | -2.085 | 1.630 | 0.025 | 0.018 | 1552.0 | 4305.0 | 1.00 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| team_beta_lmx[101] | 0.157 | 0.207 | -0.226 | 0.550 | 0.010 | 0.007 | 436.0 | 872.0 | 1.01 |
| team_beta_lmx[102] | 0.407 | 0.198 | 0.042 | 0.785 | 0.011 | 0.008 | 338.0 | 876.0 | 1.01 |
| team_beta_lmx[103] | -0.146 | 0.213 | -0.549 | 0.253 | 0.014 | 0.010 | 215.0 | 835.0 | 1.03 |
| team_beta_lmx[104] | -0.167 | 0.187 | -0.517 | 0.186 | 0.010 | 0.007 | 338.0 | 1346.0 | 1.01 |
| team_beta_lmx[105] | 0.071 | 0.393 | -0.562 | 0.902 | 0.021 | 0.015 | 390.0 | 476.0 | 1.01 |
213 行 × 9 列
az.plot_ppc(
idata_hierarchical, var_names=["emp_imputed_observed"], figsize=(20, 7), num_pp_samples=1000
)
<AxesSubplot: xlabel='emp_imputed_observed / emp_imputed_observed'>

异构插补模式#
正如我们在考虑因果推断问题并关注局部因素的混淆影响时一样,我们在进行插补时也需要这样做。我们在这里展示了一些团队特定的截距项,这些项表明,属于特定团队可以将您的赋权感向上或向下移动到公司级别截距项的总体均值之上或之下。环境的这些局部效应是我们寻求在插补缺失值时考虑的因素。
ax = az.plot_forest(
idata_hierarchical,
var_names=["team_beta_lmx"],
coords={"team": [1, 20, 22, 30, 50, 70, 76, 80, 100]},
figsize=(20, 15),
kind="ridgeplot",
combined=True,
ridgeplot_alpha=0.4,
hdi_prob=True,
)
ax[0].axvline(0)
ax[0].set_title("Team Contribution to the marginal effect of LMX on Empowerment", fontsize=20);
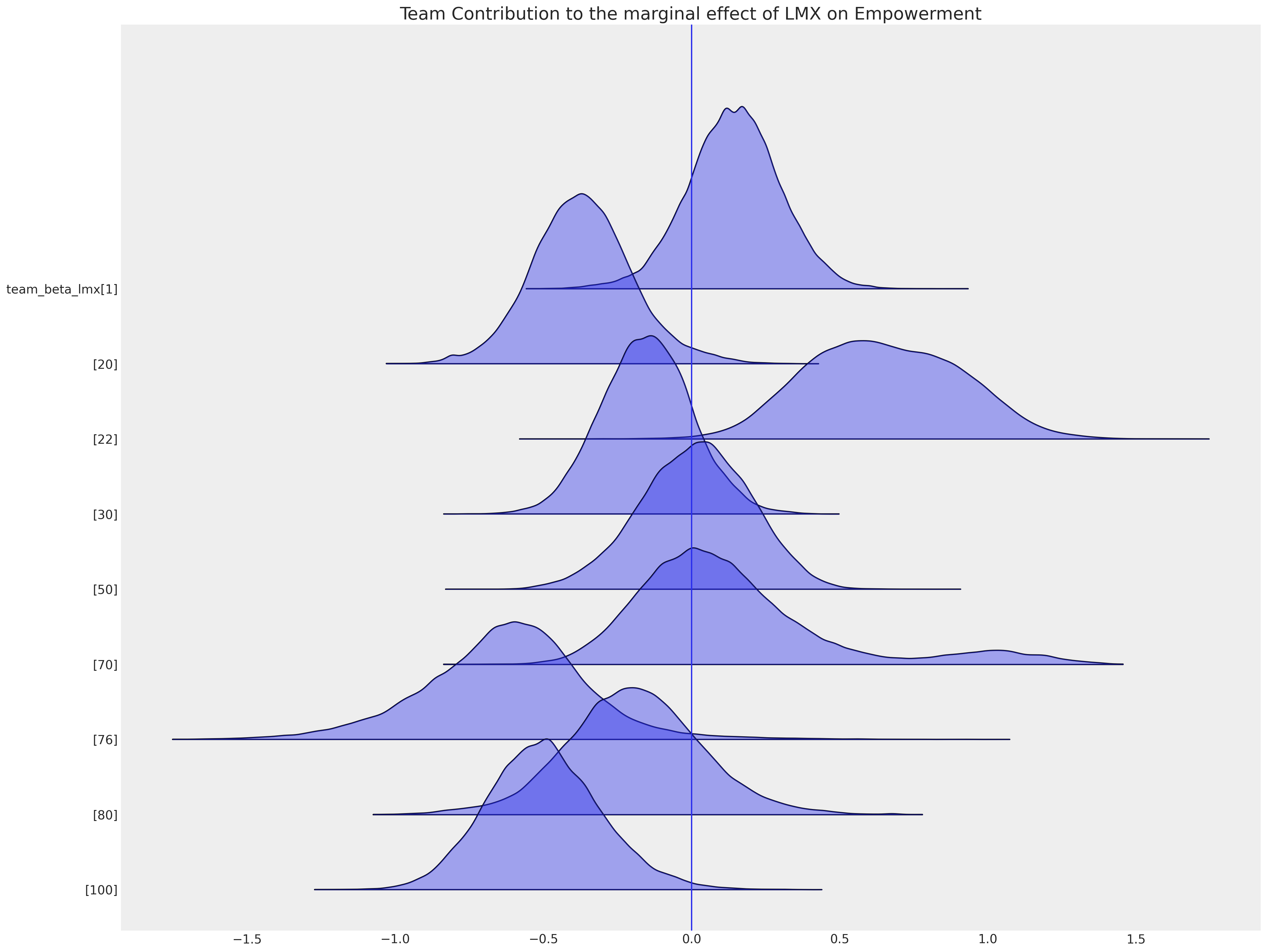
捕获这种局部变化的能力也会影响插补值的模式。
imputed_data = df_employee[["lmx", "empower", "climate"]]
imputed_lmx = az.extract(idata_hierarchical, group="posterior_predictive", num_samples=1000)[
"lmx_pred"
].mean(axis=1)
mask = imputed_data["lmx"].isnull()
imputed_data.loc[mask, "lmx"] = imputed_lmx.values[imputed_data[mask].index]
imputed_emp = az.extract(idata_hierarchical, group="posterior_predictive", num_samples=1000)[
"emp_imputed"
].mean(axis=1)
mask = imputed_data["empower"].isnull()
imputed_data.loc[mask, "empower"] = imputed_emp.values[imputed_data[mask].index]
imputed_data.columns = ["imputed_" + col for col in imputed_data.columns]
joined = pd.concat([imputed_data, df_employee], axis=1)
joined["check"] = np.where(joined["empower"].isnull(), 1, 0)
mosaic = """AAAABB"""
fig, axs = plt.subplot_mosaic(mosaic, sharex=False, figsize=(20, 7))
axs = [axs[k] for k in axs.keys()]
axs[0].scatter(
joined["imputed_lmx"],
joined["imputed_empower"],
c=joined["check"],
cmap=cm.winter,
ec="black",
s=40,
)
z = multivariate_normal([10, joined["imputed_empower"].mean()], [[8.9, 5.4], [5.4, 19]]).pdf(
joined[["imputed_lmx", "imputed_empower"]]
)
axs[0].tricontour(joined["imputed_lmx"], joined["imputed_empower"], z)
axs[1].hist(joined["imputed_empower"], ec="black", label="Imputed", color="limegreen", bins=30)
axs[1].hist(joined["empower"], ec="black", label="observed", color="blue", bins=30)
axs[1].set_title("Empowerment Distributions Imputed \n with Team Informed Estimates", fontsize=20)
axs[0].set_xlabel("Leader Member Exchange - LMX")
axs[0].set_ylabel("Empowerment")
axs[0].set_title("Empowerment Imputed \n with Team Informed Estimates", fontsize=20)
axs[1].legend();
/var/folders/99/gp2xl6x513s0tvl3cx79zf7m0000gn/T/ipykernel_96943/3267370214.py:7: SettingWithCopyWarning:
A value is trying to be set on a copy of a slice from a DataFrame
See the caveats in the documentation: https://pandas.ac.cn/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy
imputed_data.loc[mask, "lmx"] = imputed_lmx.values[imputed_data[mask].index]
/var/folders/99/gp2xl6x513s0tvl3cx79zf7m0000gn/T/ipykernel_96943/3267370214.py:13: SettingWithCopyWarning:
A value is trying to be set on a copy of a slice from a DataFrame
See the caveats in the documentation: https://pandas.ac.cn/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy
imputed_data.loc[mask, "empower"] = imputed_emp.values[imputed_data[mask].index]
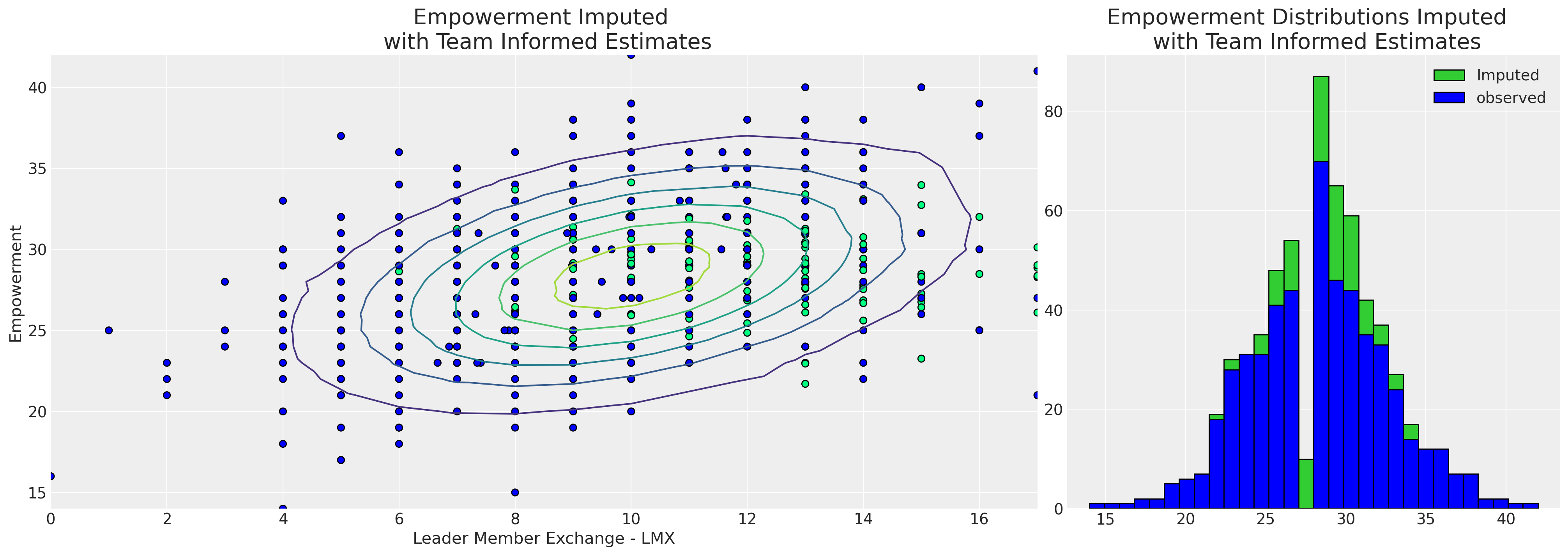
从分层模型中可以清楚地看出,团队特定信息使我们能够插补更广泛的赋权感值,并具有更广泛的分布,这是 lmx 和 male 的函数。这更具说服力,因为所有政治都是地方性的,而后一个模型是由每位员工的工作条件告知的。因此,我们的分层模型能够对缺失报告的可能赋权感值赋予更细致的看法。分层插补模型以两种方式“借用信息”:(i) 单个团队的估计值被拉向全局估计值,并且 (ii) 缺失值是根据我们对团队动态的度量进行插补的。
结论#
我们现在已经看到了多种缺失数据插补方法。我们重点关注了一个示例,在该示例中,由于不同的员工可能有不同的原因来低估他们与管理层的关系,因此缺失数据的原因并不立即显而易见。但是,此处应用的技术非常通用。
多元正态方法在许多情况下插补效果出奇地好,但更前沿的方法是链式方程的顺序规范。这里的贝叶斯方法是最先进的,因为我们可以非常自由地使用不仅仅是简单的回归模型作为我们插补方程的组件模型。对于每个方程,我们可以自由选择似然项以及我们允许在抽样分布上的先验。我们还可以添加分层结构,以尊重数据中的自然聚类,只要它们约束缺失数据的模式即可。
这个一般观点很重要 - 贝叶斯方法的灵活性可以根据我们关于数据缺失原因的理论的适当复杂性进行定制。类似的考虑因素适用于反事实推断中涉及的估计程序。我们关于数据缺失原因(世界为何如此,而不是另一种方式)的理论越发达,我们就越需要灵活的建模框架来捕捉理论的细微之处。贝叶斯建模是理论构建和评估循环的绝佳工具。
参考文献#
Craig Enders K. 应用缺失数据分析。The Guilford Press, 2022.
水印#
%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor
Last updated: Thu Feb 02 2023
Python implementation: CPython
Python version : 3.11.0
IPython version : 8.8.0
pytensor: 2.8.11
sys : 3.11.0 | packaged by conda-forge | (main, Jan 15 2023, 05:44:48) [Clang 14.0.6 ]
pytensor : 2.8.11
scipy : 1.10.0
pymc : 5.0.1
numpy : 1.24.1
matplotlib: 3.6.3
arviz : 0.14.0
pandas : 1.5.2
Watermark: 2.3.1