边缘化高斯混合模型

import arviz as az
import numpy as np
import pymc3 as pm
import seaborn as sns

from matplotlib import pyplot as plt

print(f"Running on PyMC3 v{pm.__version__}")

Running on PyMC3 v3.11.2

%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")

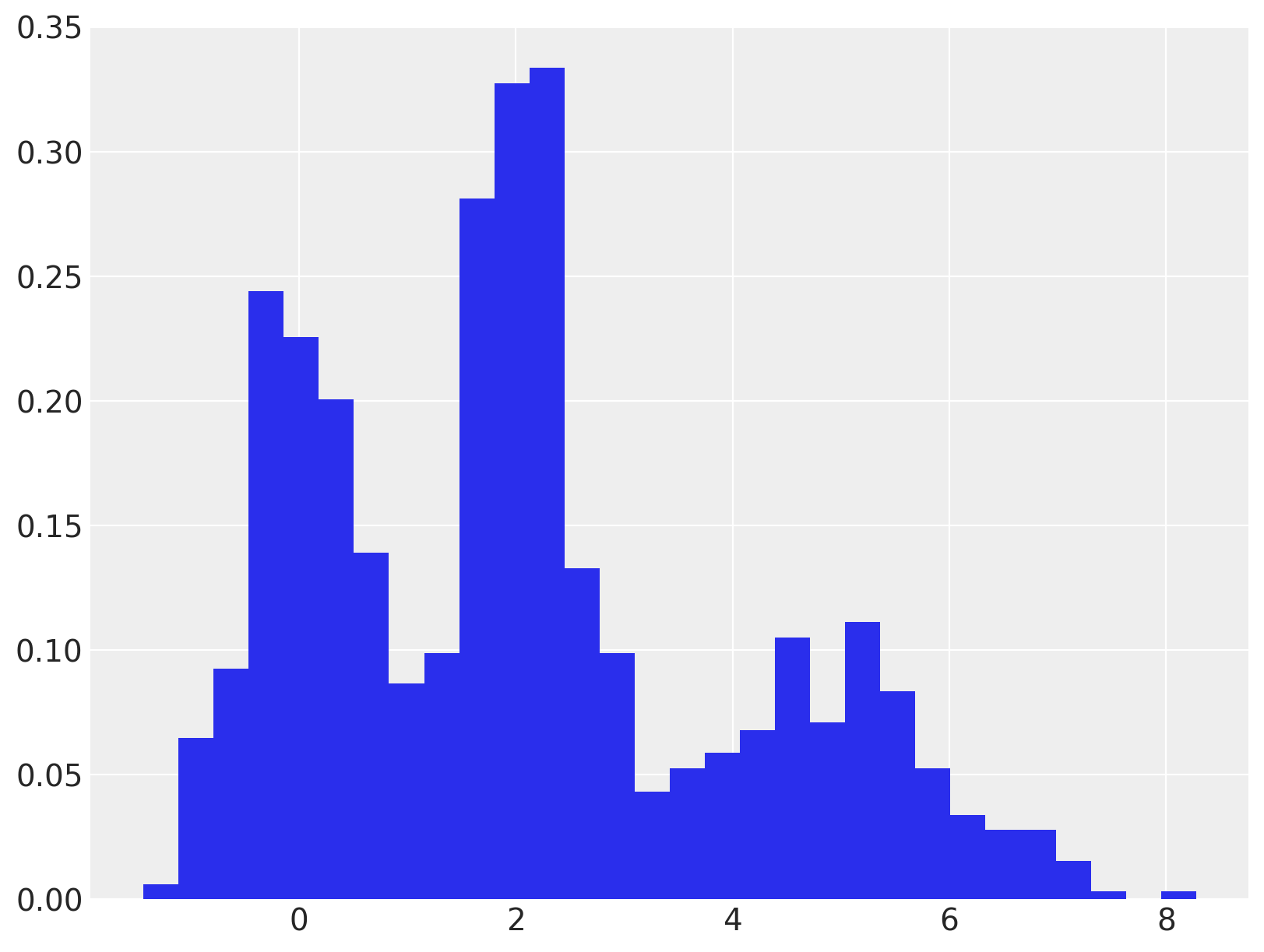
高斯混合模型是一类灵活的模型，适用于表现出亚群体异质性的数据。下面显示了此类数据集的玩具示例。

N = 1000

W = np.array([0.35, 0.4, 0.25])

MU = np.array([0.0, 2.0, 5.0])
SIGMA = np.array([0.5, 0.5, 1.0])

component = rng.choice(MU.size, size=N, p=W)
x = rng.normal(MU[component], SIGMA[component], size=N)

fig, ax = plt.subplots(figsize=(8, 6))

ax.hist(x, bins=30, density=True, lw=0);

高斯混合模型的自然参数化是潜在变量模型

\[\begin{split} \begin{align*} \mu_1, \ldots, \mu_K & \sim N(0, \sigma^2) \\ \tau_1, \ldots, \tau_K & \sim \textrm{Gamma}(a, b) \\ \boldsymbol{w} & \sim \textrm{Dir}(\boldsymbol{\alpha}) \\ z\ |\ \boldsymbol{w} & \sim \textrm{Cat}(\boldsymbol{w}) \\ x\ |\ z & \sim N(\mu_z, \tau^{-1}_z). \end{align*} \end{split}\]

PyMC3 中此参数化的实现可在高斯混合模型中找到。此参数化的缺点是其后验依赖于对离散潜在变量 \(z\) 进行采样。这种依赖性可能导致混合缓慢以及对分布尾部探索的效率低下。

解决这些问题的另一种等效参数化是对 \(z\) 进行边缘化。边缘化模型是

\[\begin{split} \begin{align*} \mu_1, \ldots, \mu_K & \sim N(0, \sigma^2) \\ \tau_1, \ldots, \tau_K & \sim \textrm{Gamma}(a, b) \\ \boldsymbol{w} & \sim \textrm{Dir}(\boldsymbol{\alpha}) \\ f(x\ |\ \boldsymbol{w}) & = \sum_{i = 1}^K w_i\ N(x\ |\ \mu_i, \tau^{-1}_i), \end{align*} \end{split}\]

其中

\[N(x\ |\ \mu, \sigma^2) = \frac{1}{\sqrt{2 \pi} \sigma} \exp\left(-\frac{1}{2 \sigma^2} (x - \mu)^2\right)\]

是正态分布的概率密度函数。

将 \(z\) 从模型中边缘化通常会导致更快的混合和对后验分布尾部更好的探索。对离散参数进行边缘化是 Stan 社区中常用的技巧，因为 Stan 不支持从离散分布中采样。有关边缘化的更多详细信息和几个工作示例，请参阅Stan 用户指南和参考手册。

PyMC3 通过其 NormalMixture 类支持边缘化高斯混合模型。（它还通过其 Mixture 类支持边缘化通用混合模型）下面我们在 PyMC3 中指定并将边缘化高斯混合模型拟合到此数据。

with pm.Model(coords={"cluster": np.arange(len(W)), "obs_id": np.arange(N)}) as model:
    w = pm.Dirichlet("w", np.ones_like(W))

    mu = pm.Normal(
        "mu",
        np.zeros_like(W),
        1.0,
        dims="cluster",
        transform=pm.transforms.ordered,
        testval=[1, 2, 3],
    )
    tau = pm.Gamma("tau", 1.0, 1.0, dims="cluster")

    x_obs = pm.NormalMixture("x_obs", w, mu, tau=tau, observed=x, dims="obs_id")

with model:
    trace = pm.sample(5000, n_init=10000, tune=1000, return_inferencedata=True)

    # sample posterior predictive samples
    ppc_trace = pm.sample_posterior_predictive(trace, var_names=["x_obs"], keep_size=True)

trace.add_groups(posterior_predictive=ppc_trace)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [tau, mu, w]

100.00% [24000/24000 00:27<00:00 Sampling 4 chains, 0 divergences]

Sampling 4 chains for 1_000 tune and 5_000 draw iterations (4_000 + 20_000 draws total) took 28 seconds.

0, dim: obs_id, 1000 =? 1000

100.00% [20000/20000 11:34<00:00]

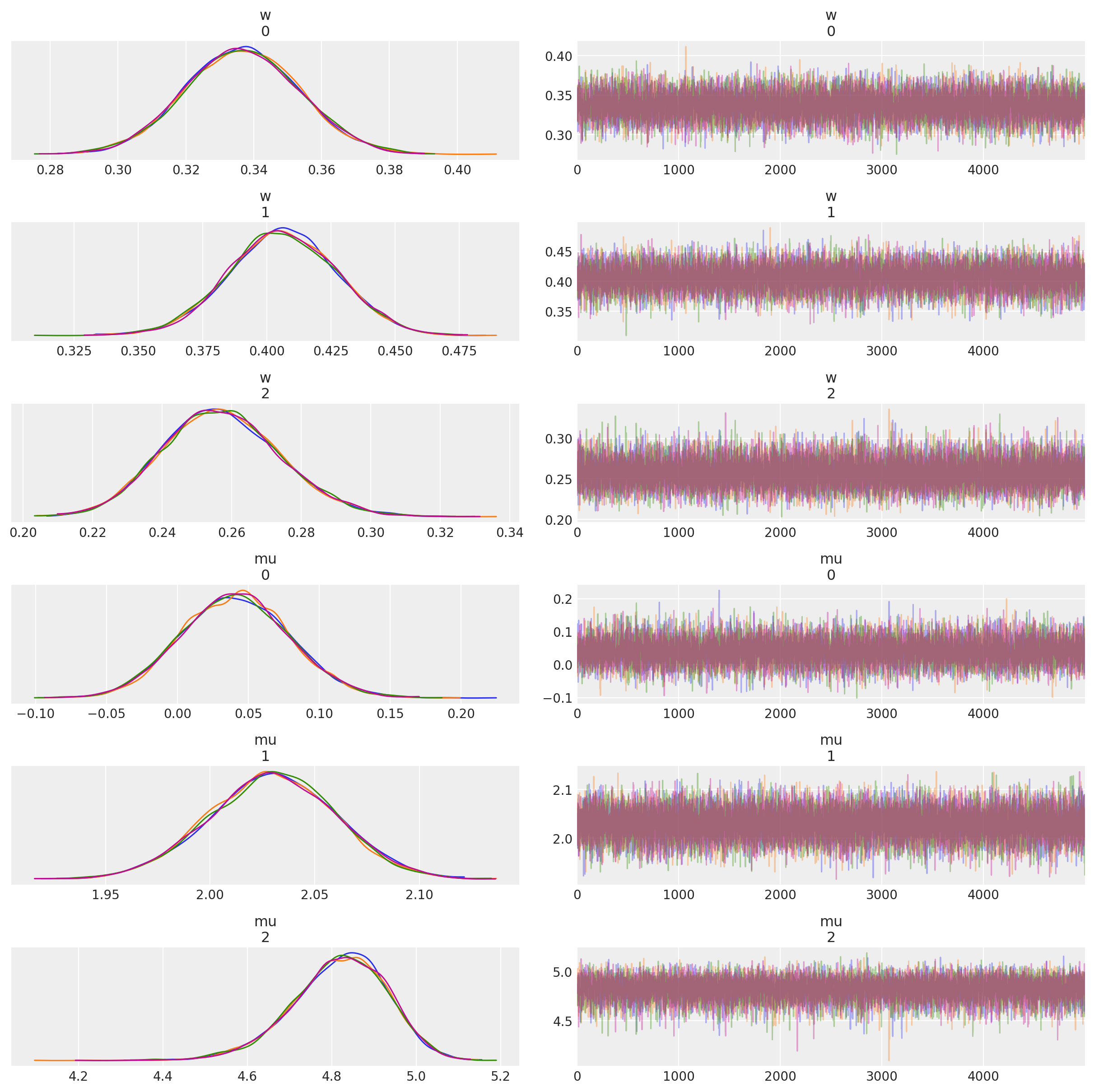
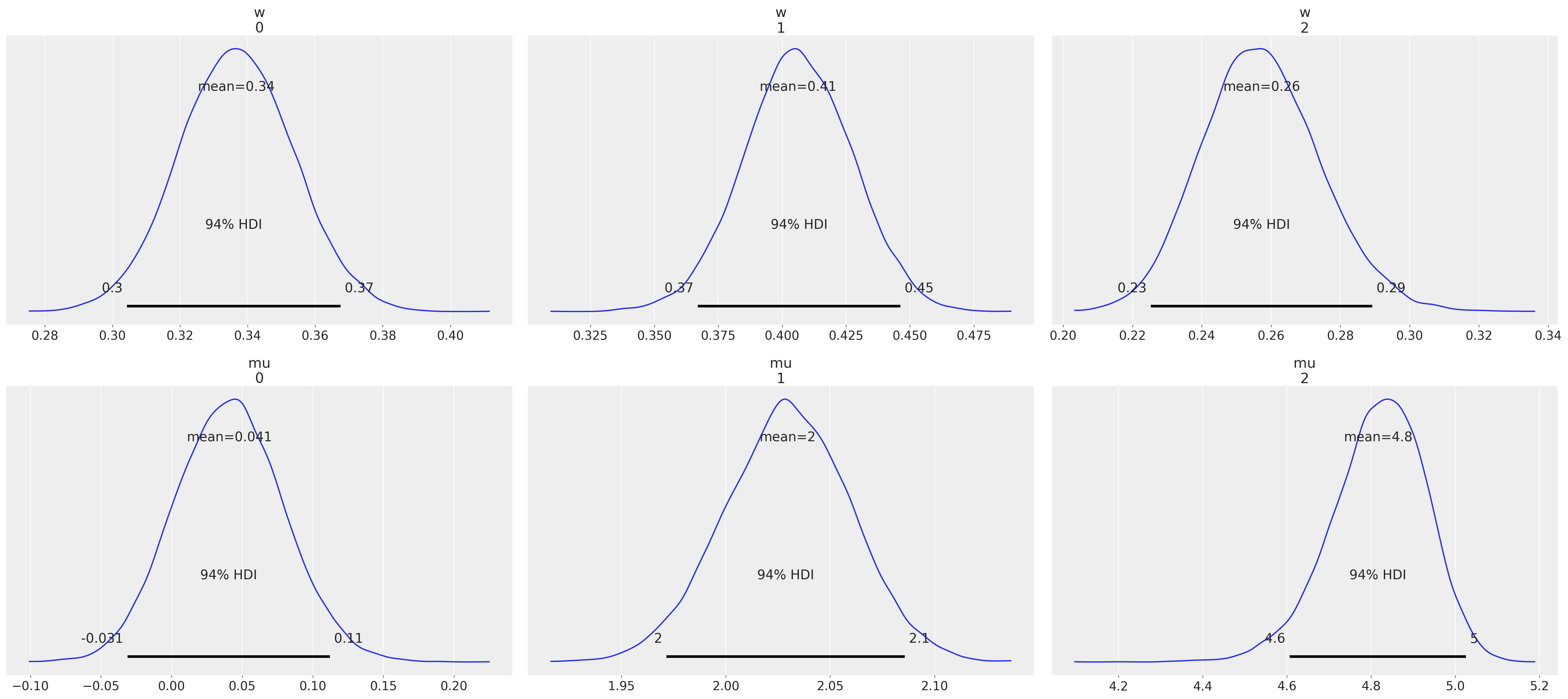
我们在以下图中看到，权重和分量均值的后验分布很好地捕获了真实值。

az.plot_trace(trace, var_names=["w", "mu"], compact=False);

az.plot_posterior(trace, var_names=["w", "mu"]);

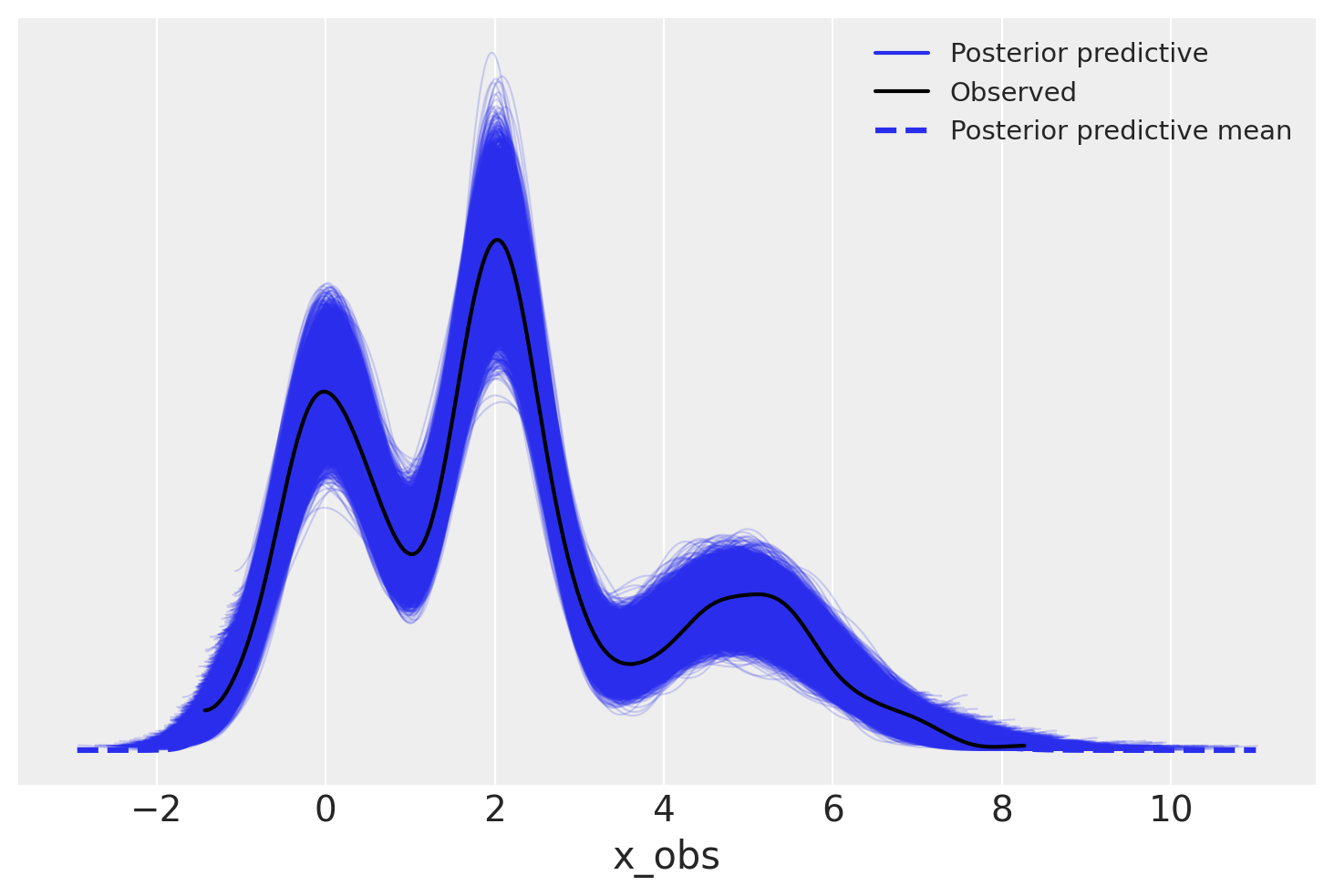
我们看到后验预测样本的分布与观测数据的分布非常接近。

az.plot_ppc(trace);

作者：Austin Rochford

水印

%load_ext watermark
%watermark -n -u -v -iv -w -p theano,xarray

Last updated: Mon Aug 30 2021

Python implementation: CPython
Python version       : 3.8.10
IPython version      : 7.25.0

theano: 1.1.2
xarray: 0.17.0

matplotlib: 3.3.4
numpy     : 1.21.0
seaborn   : 0.11.1
pymc3     : 3.11.2
arviz     : 0.11.2

Watermark: 2.2.0