变分推断：贝叶斯神经网络#

PyMC 中的贝叶斯神经网络#

生成数据#

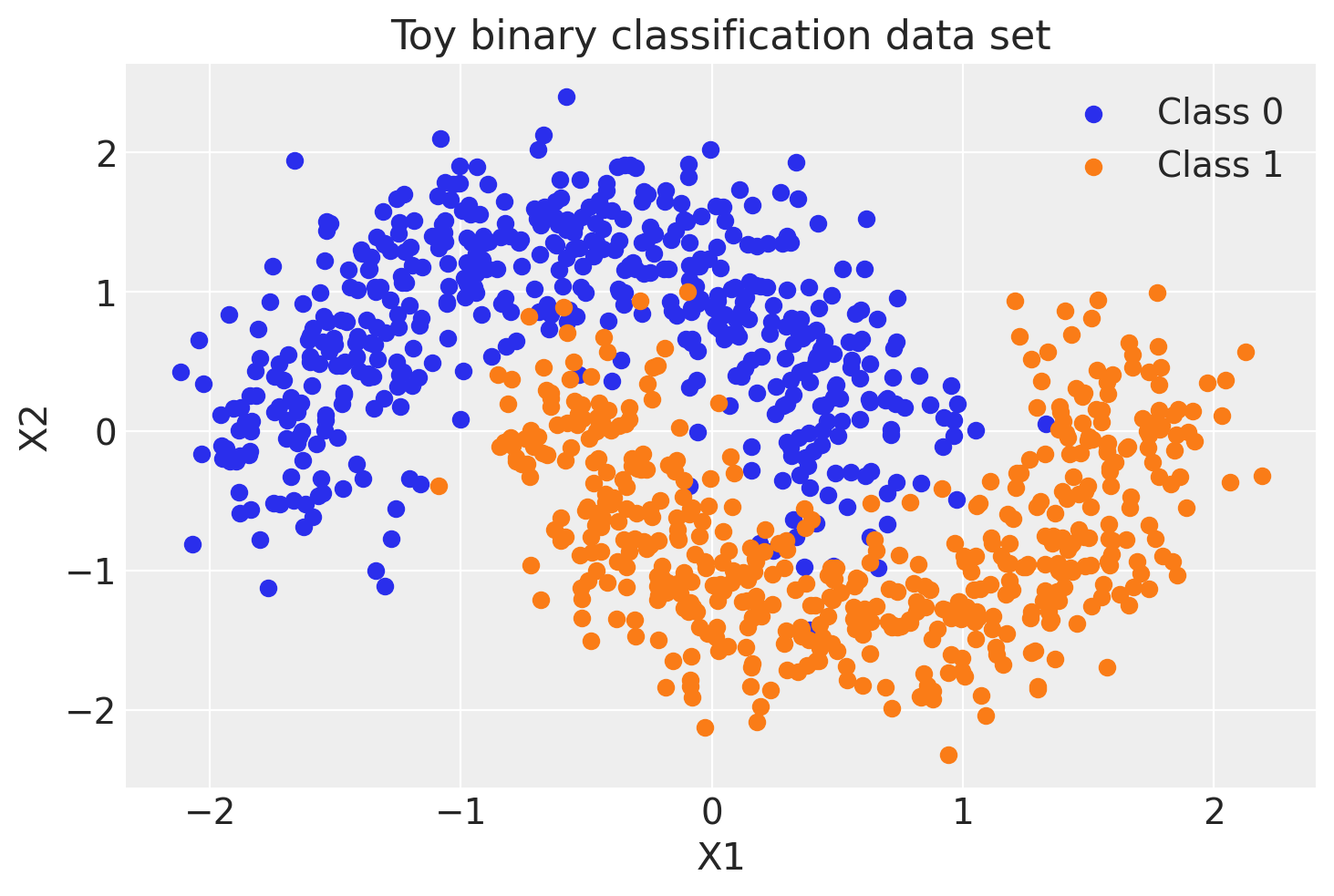
首先，让我们生成一些玩具数据——一个简单的二元分类问题，它是线性不可分的。

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import pytensor
import seaborn as sns

from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import scale

%config InlineBackend.figure_format = 'retina'
floatX = pytensor.config.floatX
RANDOM_SEED = 9927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")

X, Y = make_moons(noise=0.2, random_state=0, n_samples=1000)
X = scale(X)
X = X.astype(floatX)
Y = Y.astype(floatX)
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.5)

fig, ax = plt.subplots()
ax.scatter(X[Y == 0, 0], X[Y == 0, 1], color="C0", label="Class 0")
ax.scatter(X[Y == 1, 0], X[Y == 1, 1], color="C1", label="Class 1")
sns.despine()
ax.legend()
ax.set(xlabel="X1", ylabel="X2", title="Toy binary classification data set");
../_images/3b3c7b7f2b102622afff197b92409716a7f42a91ffb1dc8132d276ff6362069f.png

模型规范#

神经网络非常简单。基本单元是感知器，它只不过是逻辑回归。我们并行使用许多这些，然后将它们堆叠起来以获得隐藏层。这里我们将使用 2 个隐藏层，每个隐藏层有 5 个神经元，这对于如此简单的问题来说已经足够了。

def construct_nn(batch_size=50):
    n_hidden = 5

    # Initialize random weights between each layer
    init_1 = rng.standard_normal(size=(X_train.shape[1], n_hidden)).astype(floatX)
    init_2 = rng.standard_normal(size=(n_hidden, n_hidden)).astype(floatX)
    init_out = rng.standard_normal(size=n_hidden).astype(floatX)

    coords = {
        "hidden_layer_1": np.arange(n_hidden),
        "hidden_layer_2": np.arange(n_hidden),
        "train_cols": np.arange(X_train.shape[1]),
        "obs_id": np.arange(X_train.shape[0]),
    }

    with pm.Model(coords=coords) as neural_network:

        # Define data variables using minibatches
        X_data = pm.Data("X_data", X_train, dims=("obs_id", "train_cols"))
        Y_data = pm.Data("Y_data", Y_train, dims="obs_id")

        # Define minibatch variables
        ann_input, ann_output = pm.Minibatch(X_data, Y_data, batch_size=batch_size)

        # Weights from input to hidden layer
        weights_in_1 = pm.Normal(
            "w_in_1", 0, sigma=1, initval=init_1, dims=("train_cols", "hidden_layer_1")
        )

        # Weights from 1st to 2nd layer
        weights_1_2 = pm.Normal(
            "w_1_2", 0, sigma=1, initval=init_2, dims=("hidden_layer_1", "hidden_layer_2")
        )

        # Weights from hidden layer to output
        weights_2_out = pm.Normal("w_2_out", 0, sigma=1, initval=init_out, dims="hidden_layer_2")

        # Build neural-network using tanh activation function
        act_1 = pm.math.tanh(pm.math.dot(ann_input, weights_in_1))
        act_2 = pm.math.tanh(pm.math.dot(act_1, weights_1_2))
        act_out = pm.math.sigmoid(pm.math.dot(act_2, weights_2_out))

        # Binary classification -> Bernoulli likelihood
        out = pm.Bernoulli(
            "out",
            act_out,
            observed=ann_output,
            total_size=X_train.shape[0],  # IMPORTANT for minibatches
        )
    return neural_network


# Create the neural network model
neural_network = construct_nn()

还不错。Normal 先验有助于正则化权重。通常我们会向输入添加一个常数 b，但我在这里省略了它以保持代码更简洁。

变分推断：扩展模型复杂度#

我们现在可以像 pymc.NUTS 一样运行 MCMC 采样器，它在这种情况下效果很好，但正如已经提到的，当我们扩展模型以获得具有更多层的更深层架构时，这将变得非常缓慢。

相反，我们将使用 pymc.ADVI 变分推断算法。这要快得多，并且可以更好地扩展。请注意，这是一种平均场近似，因此我们忽略了后验中的相关性。

小批量 ADVI#

虽然这个模拟数据集足够小，可以一次性拟合所有数据，但它无法扩展到像 ImageNet 这样大的数据集。在上面的模型中，我们设置了小批量，这将允许扩展到更大的数据集。此外，对小批量数据进行训练（随机梯度下降）可以避免局部最小值，并可以加快收敛速度。

%%time

with neural_network:
    approx = pm.fit(n=30_000)



Finished [100%]: Average Loss = 12.793





CPU times: user 6.77 s, sys: 240 ms, total: 7.01 s
Wall time: 8.12 s









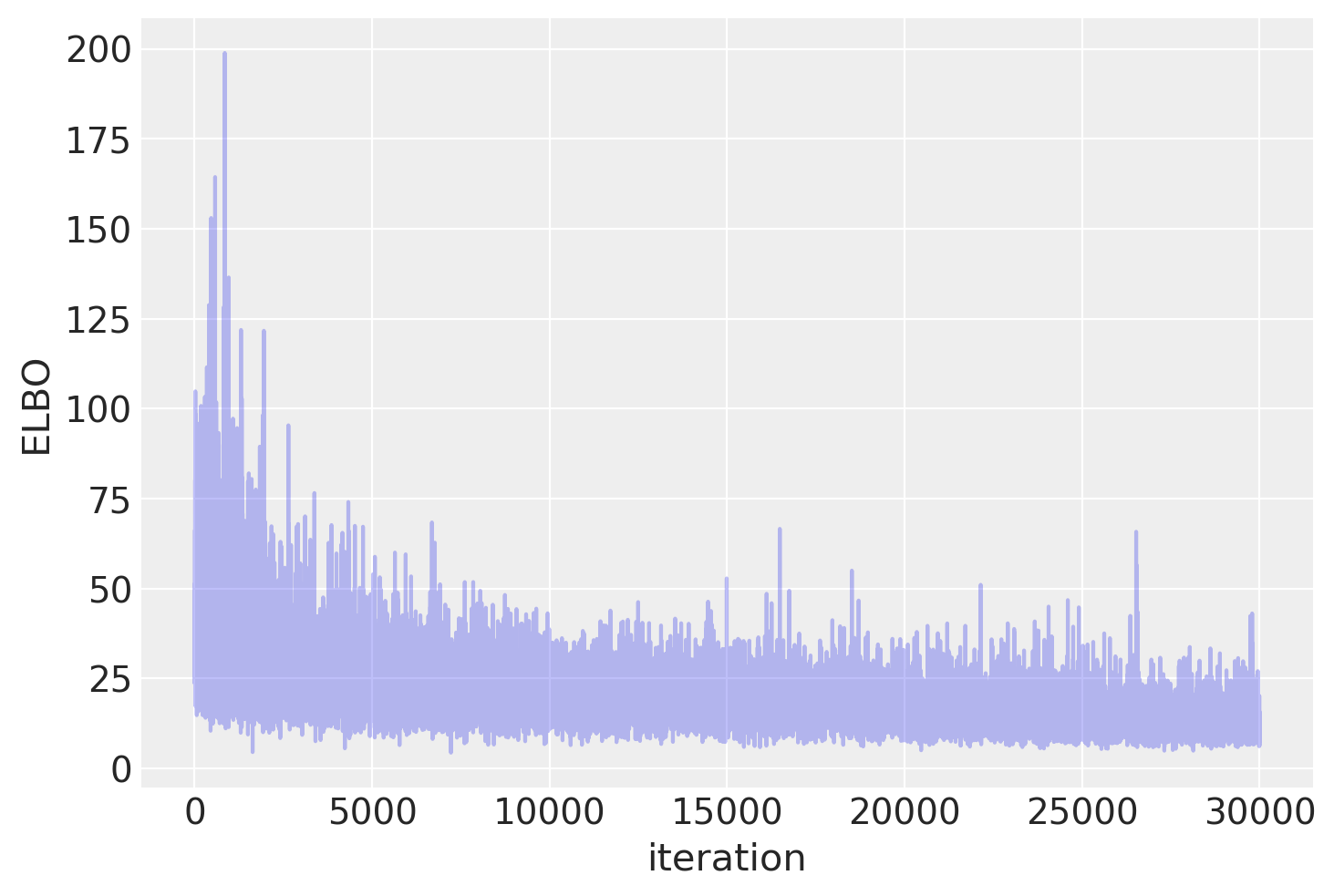
绘制目标函数 (ELBO)，我们可以看到优化迭代地改进了拟合。






plt.plot(approx.hist, alpha=0.3)
plt.ylabel("ELBO")
plt.xlabel("iteration");








../_images/b04c85f23566dc71058d97a790d68044961eca9f377d042c20cb5c257f3f83c4.png









trace = approx.sample(draws=5000)









现在我们已经训练了我们的模型，让我们使用后验预测检查 (PPC) 对保留集进行预测。我们可以使用 pymc.sample_posterior_predictive() 从后验（从变分估计中采样）生成新数据（在本例中为类预测）。


为了预测整个测试集（而不仅仅是小批量），我们需要创建一个新的模型对象来删除小批量。请注意，我们正在使用我们拟合的 trace 从后验预测分布中采样，使用来自原始模型的后验估计。这里没有新的推断，我们只是使用相同的模型和相同的后验估计来生成预测。Flat 分布只是一个占位符，使模型能够工作；实际值是从后验中采样的。






def sample_posterior_predictive(X_test, Y_test, trace, n_hidden=5):
    coords = {
        "hidden_layer_1": np.arange(n_hidden),
        "hidden_layer_2": np.arange(n_hidden),
        "train_cols": np.arange(X_test.shape[1]),
        "obs_id": np.arange(X_test.shape[0]),
    }
    with pm.Model(coords=coords):

        ann_input = X_test
        ann_output = Y_test

        weights_in_1 = pm.Flat("w_in_1", dims=("train_cols", "hidden_layer_1"))
        weights_1_2 = pm.Flat("w_1_2", dims=("hidden_layer_1", "hidden_layer_2"))
        weights_2_out = pm.Flat("w_2_out", dims="hidden_layer_2")

        # Build neural-network using tanh activation function
        act_1 = pm.math.tanh(pm.math.dot(ann_input, weights_in_1))
        act_2 = pm.math.tanh(pm.math.dot(act_1, weights_1_2))
        act_out = pm.math.sigmoid(pm.math.dot(act_2, weights_2_out))

        # Binary classification -> Bernoulli likelihood
        out = pm.Bernoulli("out", act_out, observed=ann_output)
        return pm.sample_posterior_predictive(trace)


ppc = sample_posterior_predictive(X_test, Y_test, trace)









Sampling: [out]











我们可以平均每个观测值的预测，以估计类别 1 的潜在概率。






pred = ppc.posterior_predictive["out"].mean(("chain", "draw")) > 0.5













fig, ax = plt.subplots()
ax.scatter(X_test[pred == 0, 0], X_test[pred == 0, 1], color="C0", label="Predicted 0")
ax.scatter(X_test[pred == 1, 0], X_test[pred == 1, 1], color="C1", label="Predicted 1")
sns.despine()
ax.legend()
ax.set(title="Predicted labels in testing set", xlabel="X1", ylabel="X2");








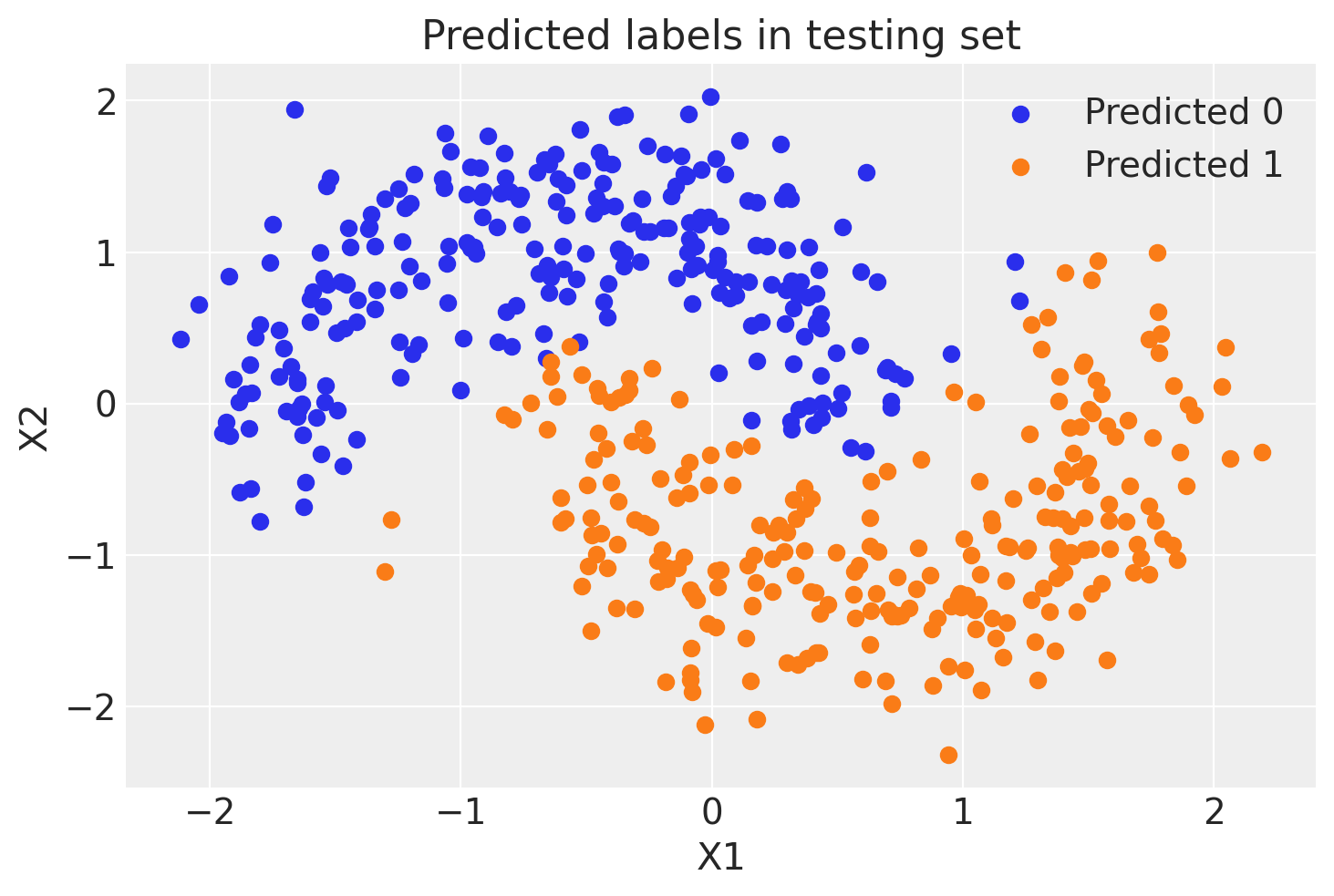
../_images/499495bbb01dce65cc5d6055cdb05a816684143eaa52bd0d20cde183c0325a36.png









print(f"Accuracy = {(Y_test == pred.values).mean() * 100:.2f}%")









Accuracy = 94.40%









嘿，我们的神经网络做得不错！








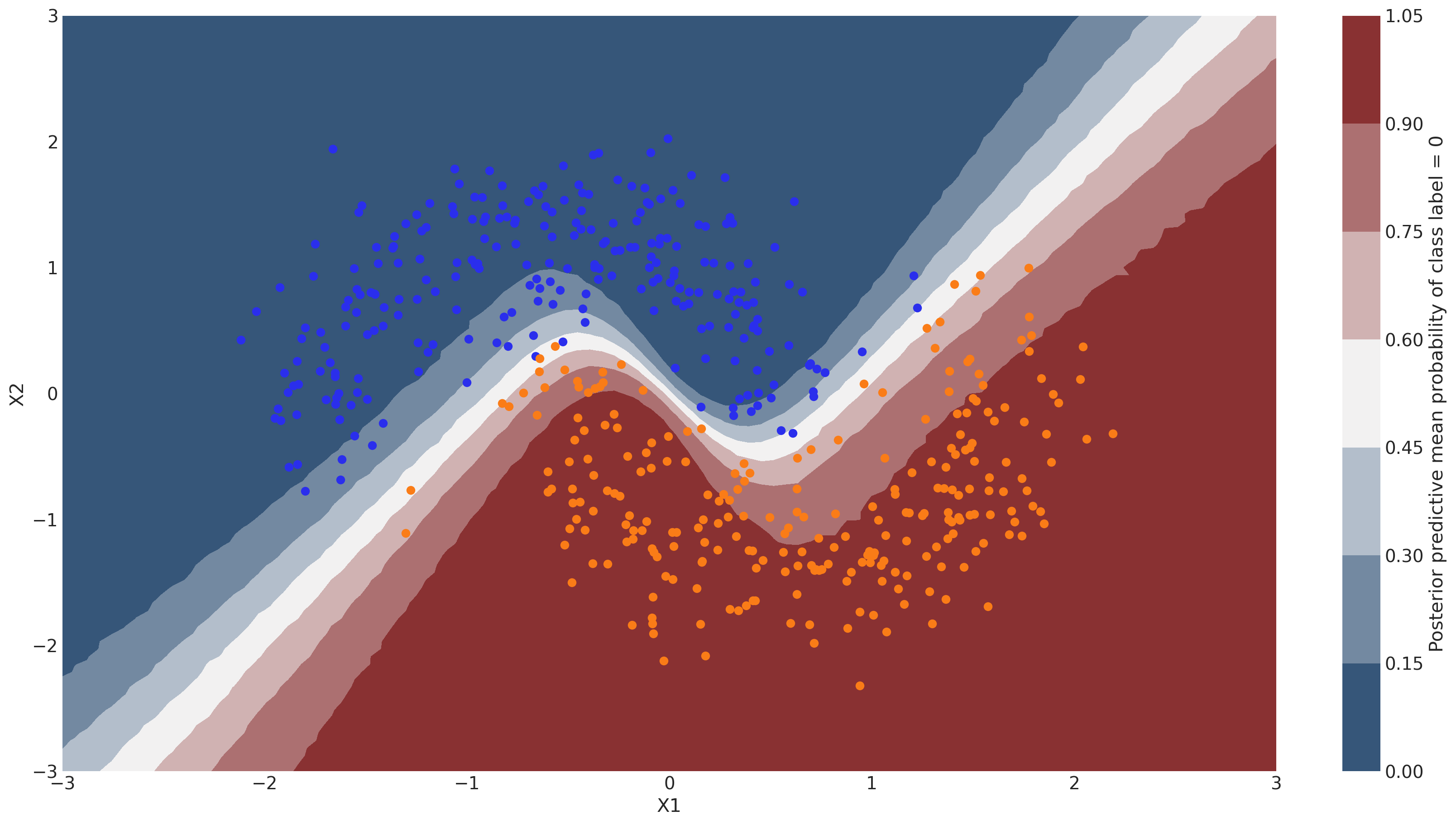
让我们看看分类器学到了什么#


为此，我们在整个输入空间上的网格上评估类别概率预测。






grid = pm.floatX(np.mgrid[-3:3:100j, -3:3:100j])
grid_2d = grid.reshape(2, -1).T
dummy_out = np.ones(grid_2d.shape[0], dtype=np.int8)













ppc = sample_posterior_predictive(grid_2d, dummy_out, trace)









Sampling: [out]















y_pred = ppc.posterior_predictive["out"]











概率曲面#






cmap = sns.diverging_palette(250, 12, s=85, l=25, as_cmap=True)
fig, ax = plt.subplots(figsize=(16, 9))
contour = ax.contourf(
    grid[0], grid[1], y_pred.mean(("chain", "draw")).values.reshape(100, 100), cmap=cmap
)
ax.scatter(X_test[pred == 0, 0], X_test[pred == 0, 1], color="C0")
ax.scatter(X_test[pred == 1, 0], X_test[pred == 1, 1], color="C1")
cbar = plt.colorbar(contour, ax=ax)
_ = ax.set(xlim=(-3, 3), ylim=(-3, 3), xlabel="X1", ylabel="X2")
cbar.ax.set_ylabel("Posterior predictive mean probability of class label = 0");








../_images/c8af7c38f668694054fbd84ff90bf84ea5541216f3f15059011175f93facaee6.png









预测值中的不确定性#


请注意，我们可以使用非贝叶斯神经网络完成以上所有操作。每个类别标签的后验预测的平均值应与最大似然预测值相同。但是，我们也可以查看后验预测的标准差，以了解我们预测中的不确定性。这是它的样子






cmap = sns.cubehelix_palette(light=1, as_cmap=True)
fig, ax = plt.subplots(figsize=(16, 9))
contour = ax.contourf(
    grid[0], grid[1], y_pred.squeeze().values.std(axis=0).reshape(100, 100), cmap=cmap
)
ax.scatter(X_test[pred == 0, 0], X_test[pred == 0, 1], color="C0")
ax.scatter(X_test[pred == 1, 0], X_test[pred == 1, 1], color="C1")
cbar = plt.colorbar(contour, ax=ax)
_ = ax.set(xlim=(-3, 3), ylim=(-3, 3), xlabel="X1", ylabel="X2")
cbar.ax.set_ylabel("Uncertainty (posterior predictive standard deviation)");








../_images/8d8c0f6c12ab482b75ddbe616a6deecf21392db1018c26c26819156ab601d4fb.png





我们可以看到，非常靠近决策边界，我们对预测哪个标签的不确定性最高。您可以想象，将预测与不确定性相关联对于许多应用（如医疗保健）来说至关重要。为了进一步最大化准确性，我们可能希望主要在来自高不确定性区域的样本上训练模型。


为了好玩，我们还可以查看 trace。重点是我们也获得了神经网络权重的不确定性。






az.plot_trace(trace);








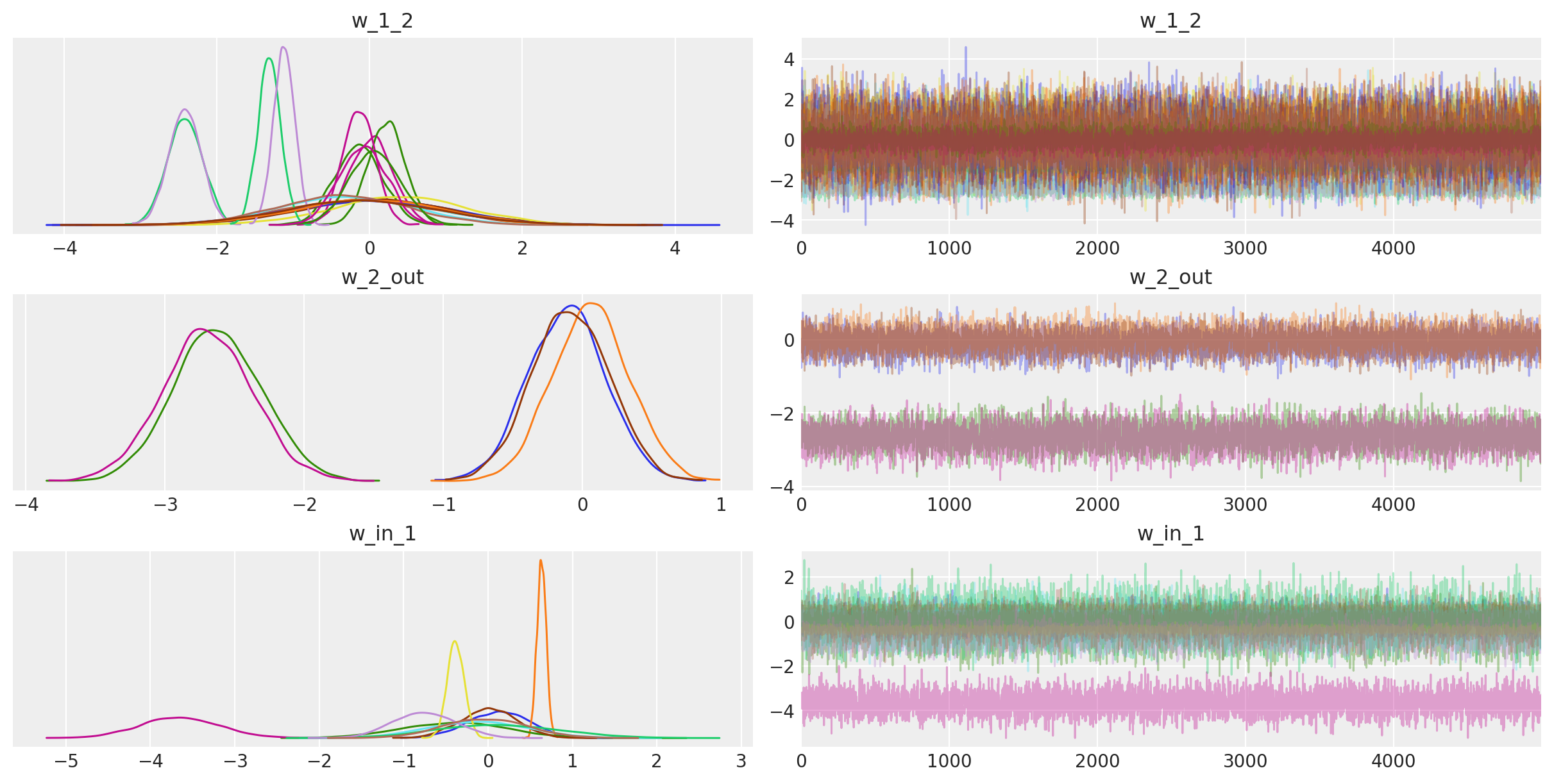
../_images/efbeee3c9a9632a5589de1b9c4cce6ac662111110462ad1bd3f7c2abcefdb352.png





您可能会争辩说，上面的网络并不是真正的深度网络，但请注意，我们可以轻松地扩展它以具有更多层，包括卷积层，以在更具挑战性的数据集上进行训练。








致谢#


Taku Yoshioka 在 PyMC3 中对 ADVI 做了大量工作，包括小批量实现以及从变分后验中采样。我还要感谢 Stan 团队（特别是 Alp Kucukelbir 和 Daniel Lee）推导 ADVI 并教我们了解它。还要感谢 Chris Fonnesbeck、Andrew Campbell、Taku Yoshioka 和 Peadar Coyle 对早期草稿的有用评论。






参考文献#







[1]

Alp Kucukelbir、Rajesh Ranganath、Andrew Gelman 和 David M. Blei。Stan 中的自动变分推断。2015 年。arXiv:1506.03431。





[2]

Volodymyr Mnih、Koray Kavukcuoglu、David Silver、Alex Graves、Ioannis Antonoglou、Daan Wierstra 和 Martin Riedmiller。使用深度强化学习玩 Atari 游戏。2013 年。arXiv:1312.5602。





[3]

C. Maddison 等人。D. Silver、A. Huang。掌握围棋游戏与深度神经网络和树搜索。《自然》，529:484–489，2016 年。网址：https://doi.org/10.1038/nature16961。





[4]

Diederik P Kingma 和 Max Welling。自动编码变分贝叶斯。2014 年。arXiv:1312.6114。





[5]

Christian Szegedy、Wei Liu、Yangqing Jia、Pierre Sermanet、Scott Reed、Dragomir Anguelov、Dumitru Erhan、Vincent Vanhoucke 和 Andrew Rabinovich。使用卷积进行更深入的研究。2014 年。arXiv:1409.4842。












作者#


    

  • 此笔记本最初由 Thomas Wiecki 于 2016 年撰写为博文
    • 

  • 由 Chris Fonnesbeck 于 2022 年为 PyMC v4 更新
    • 

  • 由 Oriol Abril-Pla 和 Earl Bellinger 于 2023 年更新
    • 

  • 由 Chris Fonnesbeck 于 2024 年更新
    • 







水印#






%load_ext watermark
%watermark -n -u -v -iv -w -p xarray









Last updated: Tue Feb 11 2025

Python implementation: CPython
Python version       : 3.12.8
IPython version      : 8.32.0

xarray: 2025.1.2

pytensor  : 2.27.1
pymc      : 5.20.1
arviz     : 0.19.0
numpy     : 1.26.4
seaborn   : 0.13.2
sklearn   : 1.6.1
matplotlib: 3.10.0

Watermark: 2.5.0













许可声明#


此示例库中的所有笔记本均根据 MIT 许可证提供，该许可证允许修改和再分发以用于任何用途，前提是保留版权和许可声明。






引用 PyMC 示例#


要引用此笔记本，请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。




重要提示


许多笔记本改编自其他来源：博客、书籍……在这种情况下，您也应该引用原始来源。


另请记住引用您的代码使用的相关库。




这是一个 BibTeX 引用模板


@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}





渲染后可能如下所示