辛普森悖论#

辛普森悖论描述了一种情况，即在组内两个变量之间可能存在负相关关系，但是当来自多个组的数据合并时，这种关系可能会消失甚至反转符号。下面的 gif 动画（来自辛普森悖论维基百科页面）非常出色地演示了这一点。

描述这种情况的另一种方式是，我们希望估计因果关系 \(x \rightarrow y\)。表面上显而易见的方法是对 y ~ 1 + x 进行建模，这将导致我们得出结论（在上述情况下），增加 \(x\) 会导致 \(y\) 减少（参见下面的模型 1）。但是，\(x\) 和 \(y\) 之间的关系受到组 membership 变量 \(group\) 的混淆。此组 membership 变量未包含在模型中，因此 \(x\) 和 \(y\) 之间的关系存在偏差。如果我们现在考虑 \(group\) 的影响，在某些情况下（例如，上面的图像），这可能会导致我们完全反转对 \(x \rightarrow y\) 的估计符号，现在估计增加 \(x\) 会导致 \(y\) 增加。

简而言之，这种“悖论”（或简称为遗漏变量偏差）可以通过假设一个因果 DAG 来解决，该 DAG 包括主要预测变量和组 membership（混淆变量）如何影响结果变量。我们演示了一个示例，其中我们没有纳入组 membership（因此我们的因果 DAG 是错误的，或者换句话说，我们的模型是错误指定的；模型 1）。然后，我们展示了通过将组 membership 作为对 \(x\) 和 \(y\) 的因果影响来解决此问题的 2 种方法。这在非合并模型（模型 2）和分层模型（模型 3）中显示。

import arviz as az
import graphviz as gr
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import seaborn as sns
import xarray as xr

%config InlineBackend.figure_format = 'retina'
az.style.use("arviz-darkgrid")
figsize = [12, 4]
plt.rcParams["figure.figsize"] = figsize
rng = np.random.default_rng(1234)

生成数据#

此数据生成受到此 stackexchange 问题的启发。它将包含来自 \(G=5\) 组的观察结果。构建数据使得在每个组内 \(x\) 和 \(y\) 之间存在负相关关系，但是当所有组组合在一起时，关系是正相关的。

def generate():
    group_list = ["one", "two", "three", "four", "five"]
    trials_per_group = 20
    group_intercepts = rng.normal(0, 1, len(group_list))
    group_slopes = np.ones(len(group_list)) * -0.5
    group_mx = group_intercepts * 2
    group = np.repeat(group_list, trials_per_group)
    subject = np.concatenate(
        [np.ones(trials_per_group) * i for i in np.arange(len(group_list))]
    ).astype(int)
    intercept = np.repeat(group_intercepts, trials_per_group)
    slope = np.repeat(group_slopes, trials_per_group)
    mx = np.repeat(group_mx, trials_per_group)
    x = rng.normal(mx, 1)
    y = rng.normal(intercept + (x - mx) * slope, 1)
    data = pd.DataFrame({"group": group, "group_idx": subject, "x": x, "y": y})
    return data, group_list


data, group_list = generate()

为了继续进行，清楚地理解数据的形式很有用。这是长格式数据（也称为窄数据），因为每一行代表一个观察结果。我们有一个 group 列，其中包含组标签，以及一个随附的数值 group_idx 列。这在建模时非常有用，因为我们可以将其用作索引来查找组级别参数估计值。最后，我们有预测变量 x 和结果 y 的核心观察结果。

display(data)

	group	group_idx	x	y
0	one	0	-0.294574	-2.338519
1	one	0	-4.686497	-1.448057
2	one	0	-2.262201	-1.393728
3	one	0	-4.873809	-0.265403
4	one	0	-2.863929	-0.774251
...	...	...	...	...
95	five	4	3.981413	0.467970
96	five	4	1.889102	0.553290
97	five	4	2.561267	2.590966
98	five	4	0.147378	2.050944
99	five	4	2.738073	0.517918

100 行 × 4 列

我们可以将其可视化如下。

fig, ax = plt.subplots(figsize=(8, 6))
sns.scatterplot(data=data, x="x", y="y", hue="group", ax=ax);

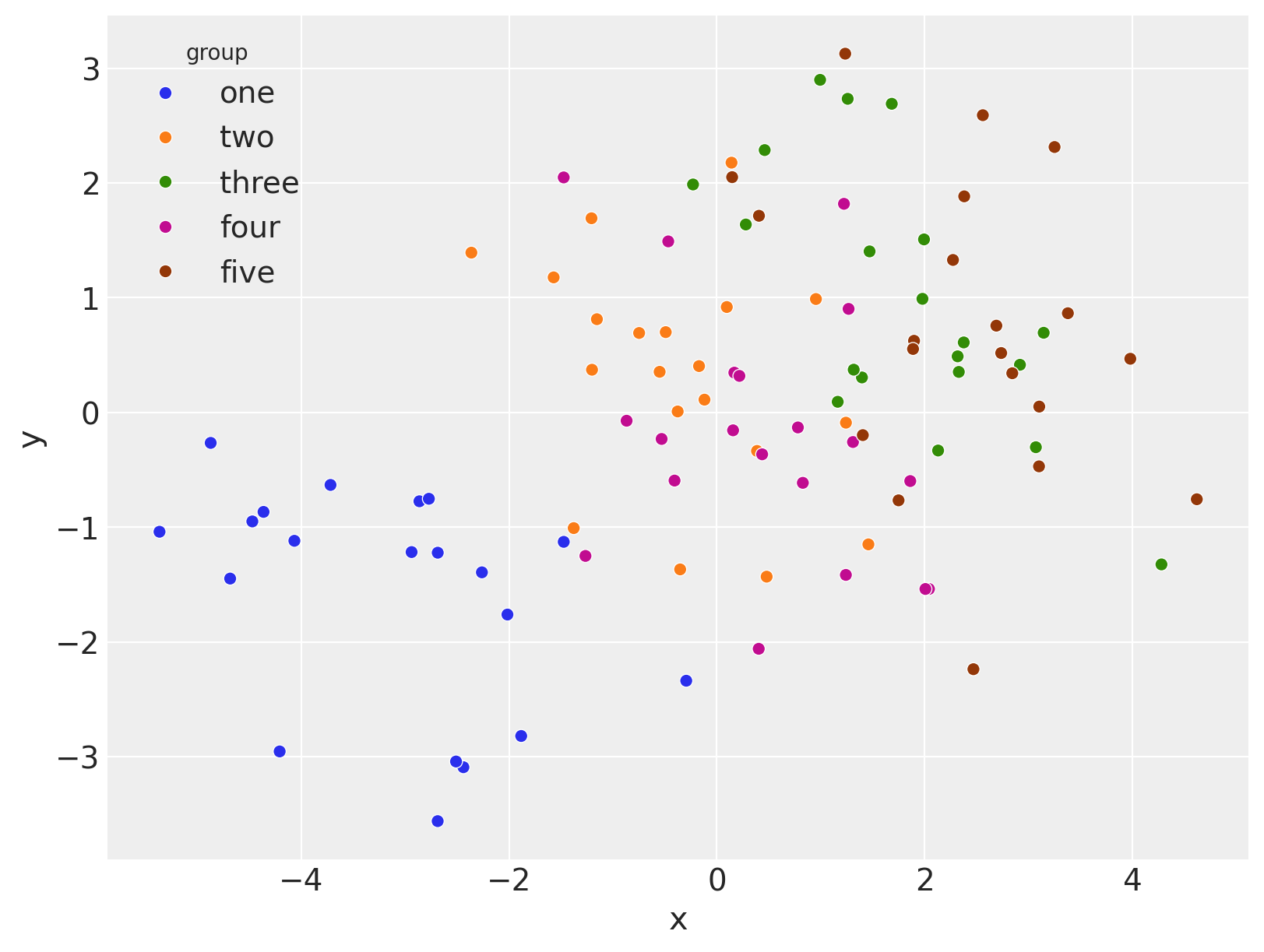
../_images/556007bb19d7e59adda7f74341718f19e393d830f264f18bf0f1dd60c0477781.png

笔记本的其余部分将介绍使用线性模型分析此数据的不同方法。

模型 1：合并回归#

首先，我们检查最简单的模型 - 普通线性回归，它合并所有数据，并且不知道数据的组/多级结构。

从因果角度来看，这种方法体现了以下信念：\(x\) 导致 \(y\)，并且这种关系在所有组中都是恒定的，或者根本不考虑组。这可以在下面的因果 DAG 中显示。

../_images/67de9408d15eb4738028d08cd4861f8ec8c989c214d96b1626ab835656111a3a.svg

我们可以用数学方式将此模型描述为

\[\begin{split} \begin{aligned} \beta_0, \beta_1 &\sim \text{Normal}(0, 5) \\ \sigma &\sim \text{Gamma}(2, 2) \\ \mu_i &= \beta_0 + \beta_1 x_i \\ y_i &\sim \text{Normal}(\mu_i, \sigma) \end{aligned} \end{split}\]

注意

我们还可以使用 Wilkinson 符号将模型 1 表示为 y ~ 1 + x，这等效于 y ~ x，因为默认情况下包含截距。

1 项对应于截距项 \(\beta_0\)。
x 项对应于斜率项 \(\beta_1\)。

现在我们可以将其表示为 PyMC 模型。我们可以注意到模型语法与上面的数学符号有多么相似。

with pm.Model() as model1:
    β0 = pm.Normal("β0", 0, sigma=5)
    β1 = pm.Normal("β1", 0, sigma=5)
    sigma = pm.Gamma("sigma", 2, 2)
    x = pm.Data("x", data.x, dims="obs_id")
    μ = pm.Deterministic("μ", β0 + β1 * x, dims="obs_id")
    pm.Normal("y", mu=μ, sigma=sigma, observed=data.y, dims="obs_id")

我们可以可视化 DAG，这可能是检查我们的模型是否正确指定的有用方法。

pm.model_to_graphviz(model1)

../_images/852847856bacd9b43ed0e5b47b52780a18b9d5cc4d52908995ce1a54b2a474f0.svg

进行推断#

with model1:
    idata1 = pm.sample(random_seed=rng)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [β0, β1, sigma]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.

az.plot_trace(idata1, var_names=["~μ"]);

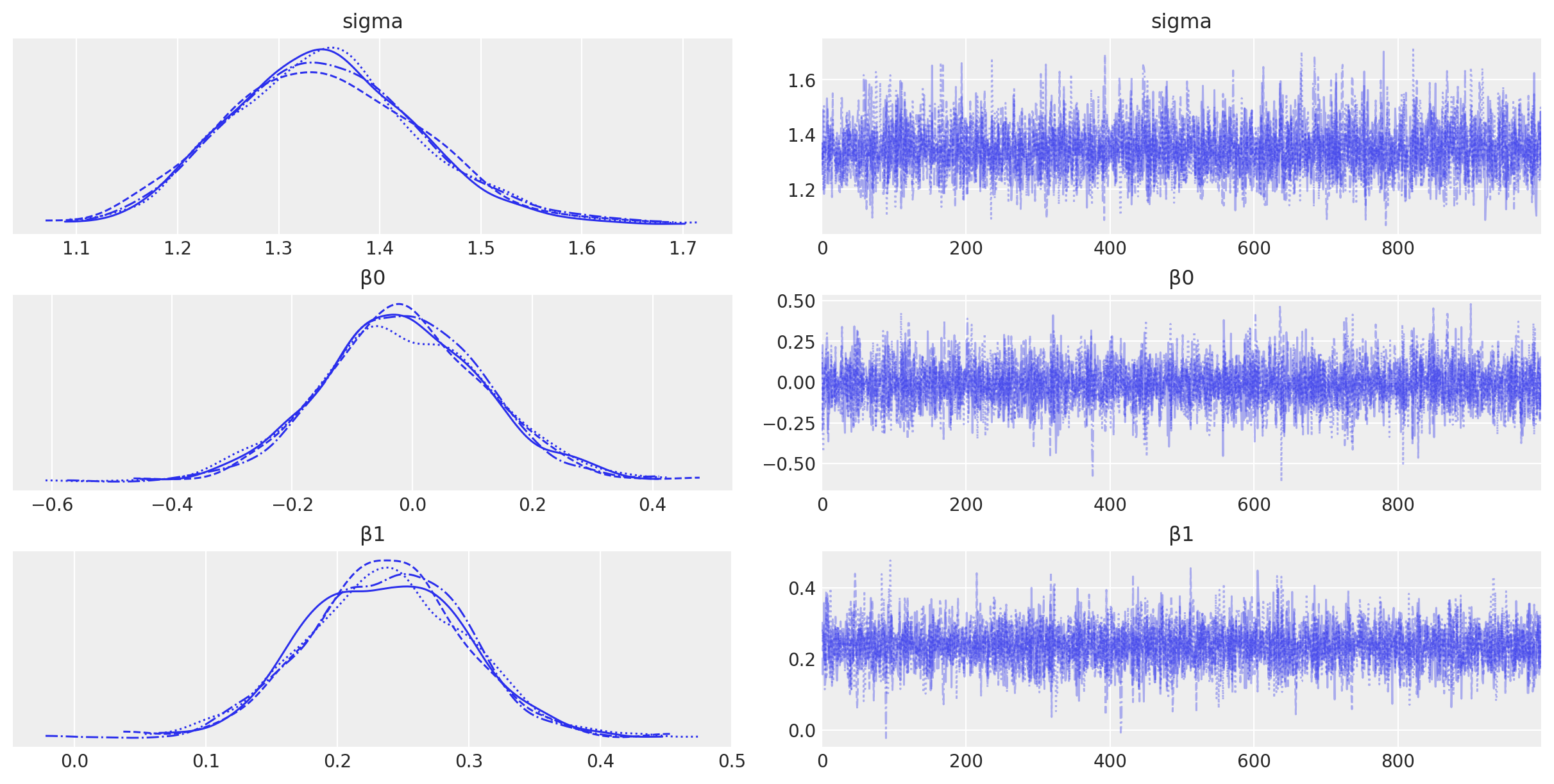
../_images/517c7f1b2f63ba65f6a03a157ba919d120e16e39f0a0989a07d0e8cdbfc01d3b.png

可视化#

首先，我们将定义一个方便的预测函数，它将为我们进行样本外预测。这在可视化模型拟合时会很方便。

def predict(model: pm.Model, idata: az.InferenceData, predict_at: dict) -> az.InferenceData:
    """Do posterior predictive inference at a set of out of sample points specified by `predict_at`."""
    with model:
        pm.set_data(predict_at)
        idata.extend(pm.sample_posterior_predictive(idata, var_names=["y", "μ"], random_seed=rng))
    return idata

现在让我们使用 predict 函数进行样本外预测，我们将使用它进行可视化。

xi = np.linspace(data.x.min(), data.x.max(), 20)

idata1 = predict(
    model=model1,
    idata=idata1,
    predict_at={"x": xi},
)

最后，我们现在可以将模型拟合到数据以及参数空间中的后验进行可视化。

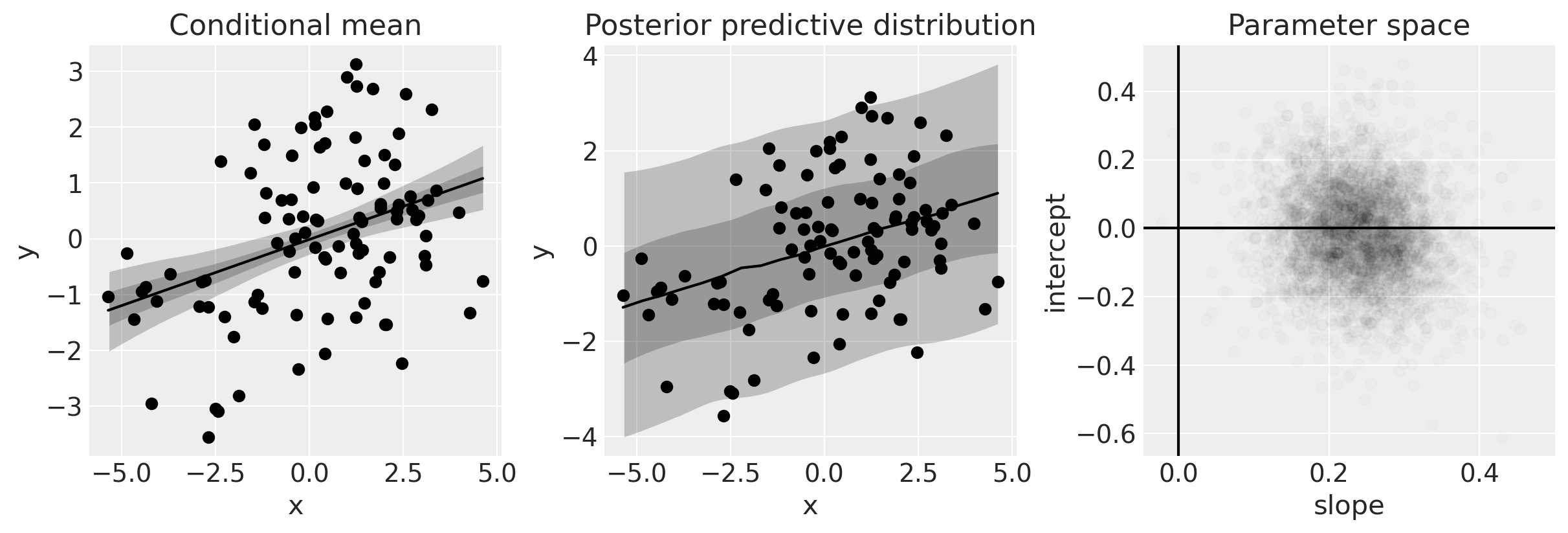
../_images/55da83c67c679438d01dea38642f885d3eb7827eccd587b56ffc6a1732e6eb8f.png

左侧的图显示了数据和条件均值的后验。对于给定的 \(x\)，我们得到模型（即 \(\mu\)）的后验分布。

中间的图显示了条件后验预测分布，它给出了关于我们期望看到的数据的陈述。直观地，这可以理解为不仅合并了我们对模型的了解（左图），还合并了我们对误差分布的了解。

右侧的图显示了我们在参数空间中的后验信念。

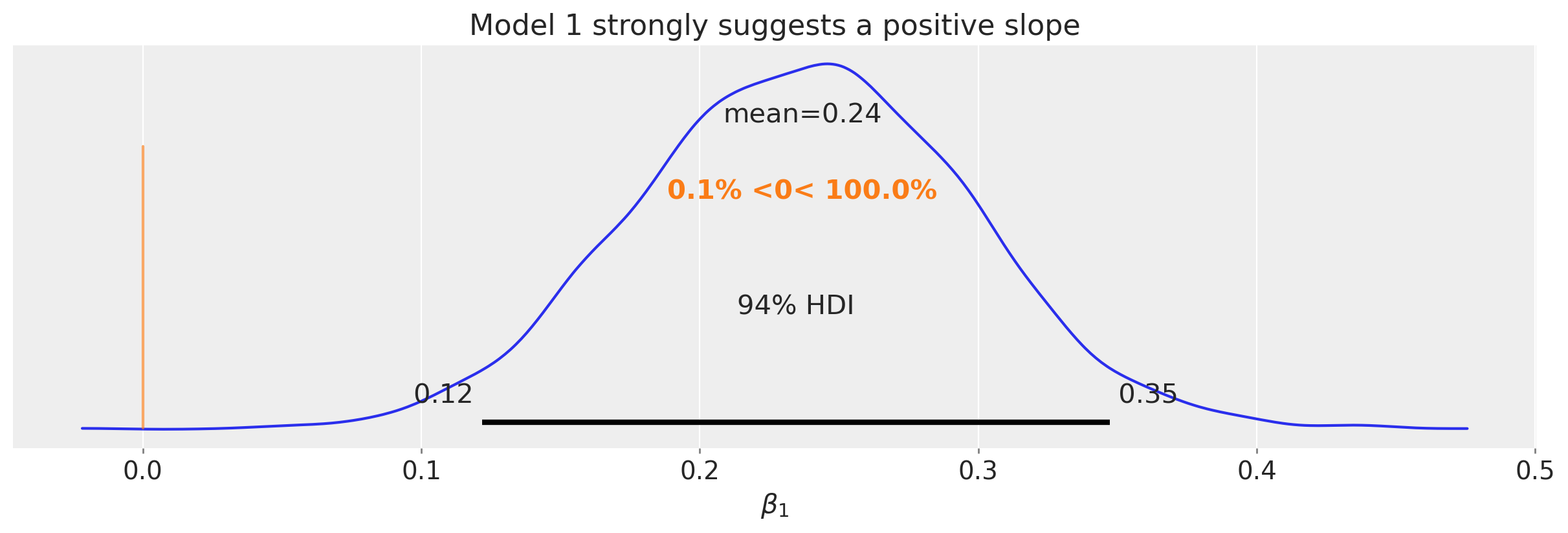
此分析的明确之处之一是我们有可靠的证据表明 \(x\) 和 \(y\) 是正相关的。我们可以从斜率的后验（参见上图中的右侧面板）中看到这一点，我们在下面的图中将其隔离出来。

../_images/7edc1147f4a6fcdca53a73b541b5a1f4822f984a099aa23b06261591342623e9.png

模型 2：包含混淆因素的非合并回归#

我们将在本分析中使用相同的数据，但是这次我们将使用我们对数据来自组的了解。从因果角度来看，我们正在探索 \(x\) 和 \(y\) 都受组 membership 影响的概念。这可以在下面的因果有向无环图 (DAG) 中显示。

../_images/6c09ba19f6176cd619b0e1d946d9d2df19844153f493daa7bb727a0621bac230.svg

因此我们可以看到 \(group\) 是一个混淆变量。因此，如果我们试图发现 \(x\) 对 \(y\) 的因果关系，则需要考虑混淆变量 \(group\)。模型 1 没有这样做，因此得出了错误的结论。但是模型 2 将对此进行说明。

更具体地说，我们基本上将独立的回归拟合到每个组内的数据。这也可以描述为非合并模型。我们可以用数学方式将此模型描述为

\[\begin{split} \begin{aligned} \vec{\beta_0}, \vec{\beta_1} &\sim \text{Normal}(0, 5) \\ \sigma &\sim \text{Gamma}(2, 2) \\ \mu_i &= \vec{\beta_0}[g_i] + \vec{\beta_1}[g_i] x_i \\ y_i &\sim \text{Normal}(\mu_i, g_i) \end{aligned} \end{split}\]

其中 \(g_i\) 是观察 \(i\) 的组索引。因此，参数 \(\vec{\beta_0}\) 和 \(\vec{\beta_1}\) 现在是长度为 \(G\) 的向量，而不是标量。并且 \([g_i]\) 充当索引，用于查找第 \(i^\text{th}\) 个观察的组。

注意

我们还可以使用 Wilkinson 符号将模型 2 表示为 y ~ 0 + g + x:g。

g 项捕获组特定的截距 \(\beta_0[g_i]\) 参数。
0 表示我们没有全局截距项，仅留下组特定的截距作为唯一截距。
x:g 项捕获组特定的斜率 \(\beta_1[g_i]\) 参数。

让我们用 PyMC 代码表示模型 2。

coords = {"group": group_list}

with pm.Model(coords=coords) as model2:
    # Define priors
    β0 = pm.Normal("β0", 0, sigma=5, dims="group")
    β1 = pm.Normal("β1", 0, sigma=5, dims="group")
    sigma = pm.Gamma("sigma", 2, 2)
    # Data
    x = pm.Data("x", data.x, dims="obs_id")
    g = pm.Data("g", data.group_idx, dims="obs_id")
    # Linear model
    μ = pm.Deterministic("μ", β0[g] + β1[g] * x, dims="obs_id")
    # Define likelihood
    pm.Normal("y", mu=μ, sigma=sigma, observed=data.y, dims="obs_id")

通过绘制此模型的 DAG，可以清楚地看到我们现在为每个组都有单独的截距和斜率参数。

pm.model_to_graphviz(model2)

../_images/8a3e89a0a33eea65bdad564d71c25a89a64b3bec5dd4280da0cda0cdfbc43aae.svg

进行推断#

with model2:
    idata2 = pm.sample(random_seed=rng)

az.plot_trace(idata2, var_names=["~μ"]);

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [β0, β1, sigma]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 2 seconds.

../_images/32dc7f9fe8dc6e74a4c09705a1dbe7bfe3e017ee619cebdbb6d5e51d4269633d.png

可视化#

# Generate values of xi and g for posterior prediction
n_points = 10
n_groups = len(data.group.unique())
# Generate xi values for each group and concatenate them
xi = np.concatenate(
    [
        np.linspace(group[1].x.min(), group[1].x.max(), n_points)
        for group in data.groupby("group_idx")
    ]
)
# Generate the group indices array g and cast it to integers
g = np.concatenate([[i] * n_points for i in range(n_groups)]).astype(int)
predict_at = {"x": xi, "g": g}

idata2 = predict(
    model=model2,
    idata=idata2,
    predict_at=predict_at,
)

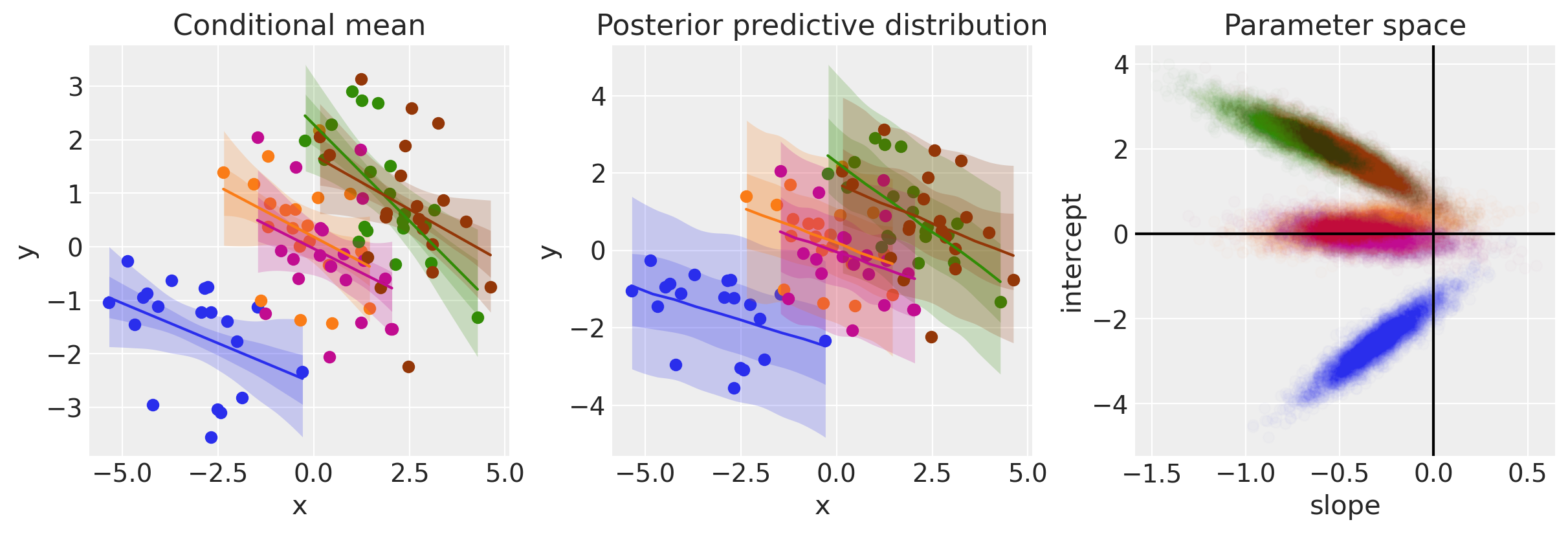
../_images/6b57cdc52bee47deb143971dfc654f54d446de92dbd264e0f4820a41a089bc4d.png

与模型 1 相比，当我们考虑组时，我们可以看到现在的证据指向 \(x\) 和 \(y\) 之间存在负相关关系。我们可以从上图左侧和中间面板中的负斜率以及上面左侧面板中斜率参数的大多数后验样本为负值中看到这一点。

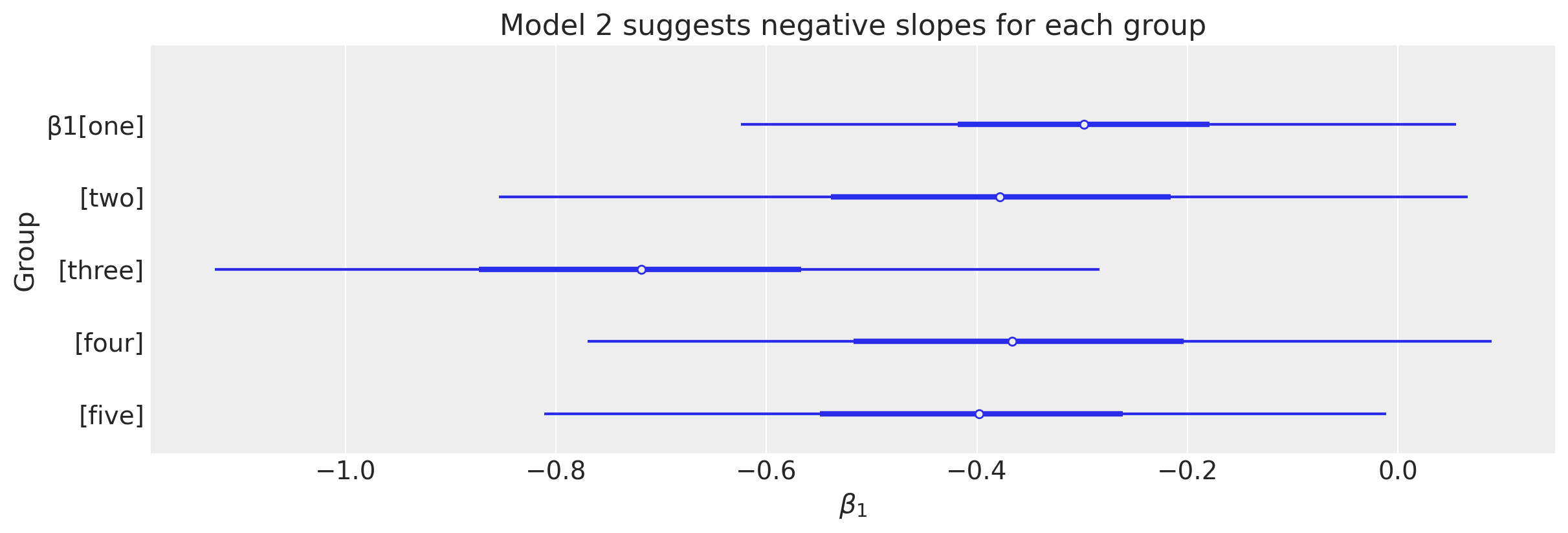
下图更仔细地查看了组级别斜率参数。

../_images/a359c0eb7a3ef3fe23e61d6dab99fdd3c321c69004026b0f678025145d61d653.png

模型 3：包含混淆因素的部分合并模型#

模型 3 假设与模型 2 相同的因果 DAG（见上文）。但是，我们可以进一步深入，并纳入更多关于数据结构的知识。与其将每个组视为完全独立，不如使用我们对这些组是从总体级别分布中抽取的知识。我们可以将其形式化为，组级别斜率和截距被建模为与总体级别斜率和截距的偏差。

我们可以用数学方式将此模型描述为

\[\begin{split} \begin{aligned} \beta_0 &\sim \text{Normal}(0, 5) \\ \beta_1 &\sim \text{Normal}(0, 5) \\ p_{0\sigma}, p_{1\sigma} &\sim \text{Gamma}(2, 2) \\ \vec{u_0} &\sim \text{Normal}(0, p_{0\sigma}) \\ \vec{u_1} &\sim \text{Normal}(0, p_{1\sigma}) \\ \sigma &\sim \text{Gamma}(2, 2) \\ \mu_i &= \overbrace{ \left( \underbrace{\beta_0}_{\text{pop}} + \underbrace{\vec{u_0}[g_i]}_{\text{group}} \right) }^{\text{intercept}} + \overbrace{ \left( \underbrace{\beta_1 \cdot x_i}_{\text{pop}} + \underbrace{\vec{u_1}[g_i] \cdot x_i}_{\text{group}} \right) }^{\text{slope}} \\ y_i &\sim \text{Normal}(\mu_i, \sigma) \end{aligned} \end{split}\]

其中

\(\beta_0\) 和 \(\beta_1\) 分别是总体级别截距和斜率。
\(\vec{u_0}\) 和 \(\vec{u_1}\) 是与总体级别参数的组级别偏差。
\(p_{0\sigma}, p_{1\sigma}\) 是截距和斜率偏差的标准差，可以被认为是“收缩参数”。
- 在 \(p_{0\sigma}, p_{1\sigma} \rightarrow \infty\) 的极限中，我们恢复了非合并模型。
- 在 \(p_{0\sigma}, p_{1\sigma} \rightarrow 0\) 的极限中，我们恢复了合并模型。

注意

我们还可以使用 Wilkinson 符号将模型 3 表示为 1 + x + (1 + x | g)。

1 捕获全局截距 \(\beta_0\)。
x 捕获全局斜率 \(\beta_1\)。
(1 + x | g) 项捕获截距和斜率的组特定项。
- 1 | g 捕获组特定的截距偏差 \(\vec{u_0}\) 参数。
- x | g 捕获组特定的斜率偏差 \(\vec{u_1}[g_i]\) 参数。

with pm.Model(coords=coords) as model3:
    # Population level priors
    β0 = pm.Normal("β0", 0, 5)
    β1 = pm.Normal("β1", 0, 5)
    # Group level shrinkage
    intercept_sigma = pm.Gamma("intercept_sigma", 2, 2)
    slope_sigma = pm.Gamma("slope_sigma", 2, 2)
    # Group level deflections
    u0 = pm.Normal("u0", 0, intercept_sigma, dims="group")
    u1 = pm.Normal("u1", 0, slope_sigma, dims="group")
    # observations noise prior
    sigma = pm.Gamma("sigma", 2, 2)
    # Data
    x = pm.Data("x", data.x, dims="obs_id")
    g = pm.Data("g", data.group_idx, dims="obs_id")
    # Linear model
    μ = pm.Deterministic("μ", (β0 + u0[g]) + (β1 * x + u1[g] * x), dims="obs_id")
    # Define likelihood
    pm.Normal("y", mu=μ, sigma=sigma, observed=data.y, dims="obs_id")

此模型的 DAG 突出了标量总体级别参数 \(\beta_0\) 和 \(\beta_1\) 以及组级别参数 \(\vec{u_0}\) 和 \(\vec{u_1}\)。

pm.model_to_graphviz(model3)

../_images/9fee0f282a87ce7f02f446045676cc44ba51b0546df5a5e0ce3d79d4c171dc4a.svg

注意

为了完整起见，还有另一种等效的方式来编写此模型。

\[\begin{split} \begin{aligned} p_{0\mu}, p_{1\mu} &\sim \text{Normal}(0, 5) \\ p_{0\sigma}, p_{1\sigma} &\sim \text{Gamma}(2, 2) \\ \vec{\beta_0} &\sim \text{Normal}(p_{0\mu}, p_{0\sigma}) \\ \vec{\beta_1} &\sim \text{Normal}(p_{1\mu}, p_{1\sigma}) \\ \sigma &\sim \text{Gamma}(2, 2) \\ \mu_i &= \vec{\beta_0}[g_i] + \vec{\beta_1}[g_i] \cdot x_i \\ y_i &\sim \text{Normal}(\mu_i, \sigma) \end{aligned} \end{split}\]

其中 \(\vec{\beta_0}\) 和 \(\vec{\beta_1}\) 是组级别参数。这些组级别参数可以被认为是来自总体级别截距分布 \(\text{Normal}(p_{0\mu}, p_{0\sigma})\) 和总体级别斜率分布 \(\text{Normal}(p_{1\mu}, p_{1\sigma})\) 的样本。因此，这些分布将代表我们可能期望在某些尚未观察到的组中观察到的内容。

但是，此模型公式与 Wilkinson 符号的映射不太清晰。因此，我们选择以以上给出的形式呈现模型。有关此主题的有趣讨论，请参见 bambi 存储库中的 Discussion #808。

另请参阅

我们正在考虑的分层模型包含一个简化，即假设总体级别斜率和截距是独立的。可以放宽此假设，并通过使用多元正态分布对这些参数之间的任何相关性进行建模。有关更多详细信息，请参见多元正态模型的 LKJ Cholesky 协方差先验笔记本。

另请参阅

在某种意义上，从模型 2 到模型 3 的转变可以看作是添加参数，因此增加了模型复杂性。但是，在另一种意义上，添加关于数据嵌套结构的知识实际上为参数空间提供了约束。可以进行模型比较以仲裁这些模型之间 - 例如，请参见 GLM：模型选择笔记本以获取更多详细信息。

进行推断#

with model3:
    idata3 = pm.sample(target_accept=0.95, random_seed=rng)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [β0, β1, intercept_sigma, slope_sigma, u0, u1, sigma]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 9 seconds.
There were 6 divergences after tuning. Increase `target_accept` or reparameterize.

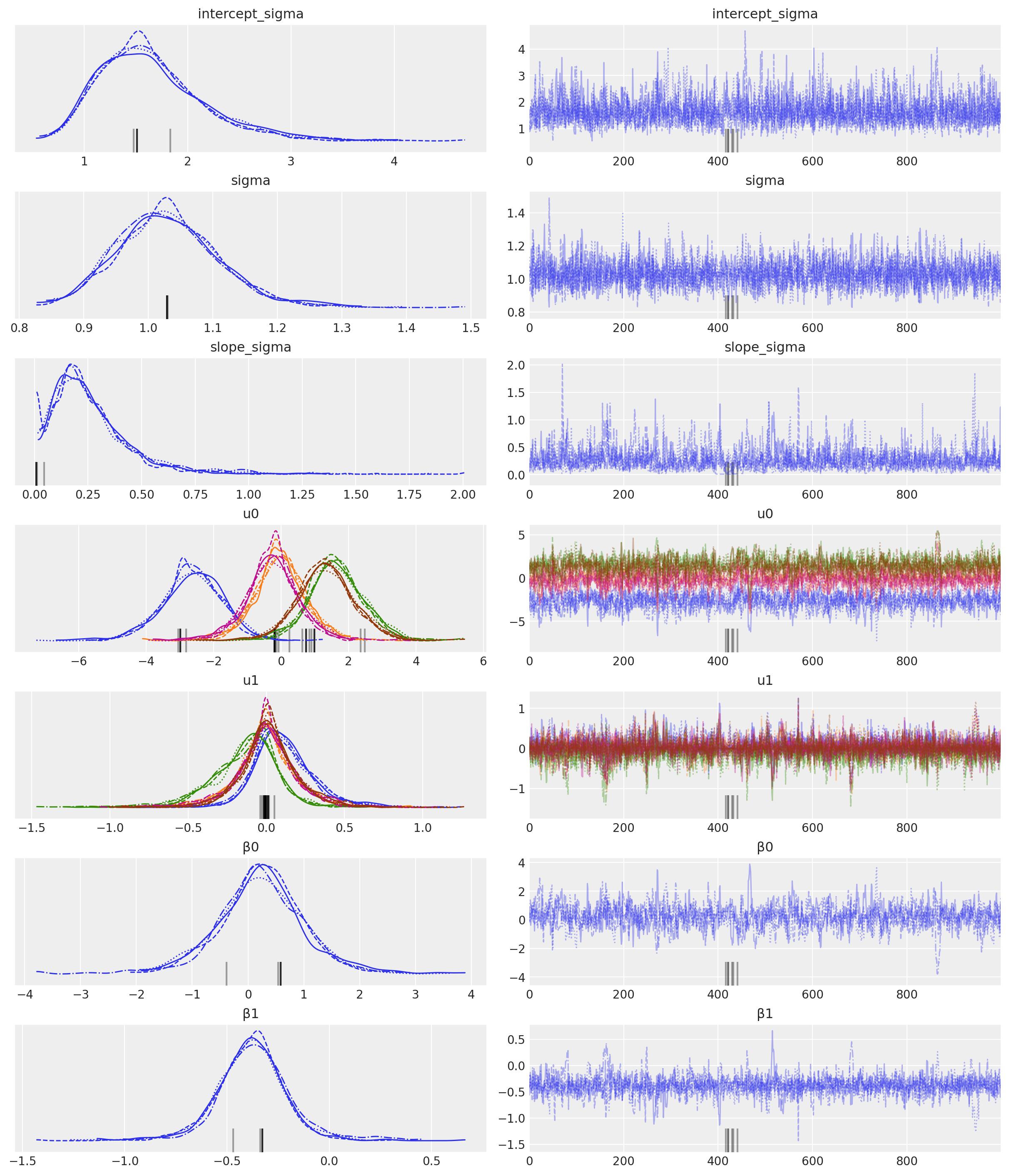
az.plot_trace(idata3, var_names=["~μ"]);

../_images/25b9afec2e8b2fe87368487eb6c7845ec66733b7e8b6d3e3dc8c0899d01c476e.png

可视化#

# Generate values of xi and g for posterior prediction
n_points = 10
n_groups = len(data.group.unique())
# Generate xi values for each group and concatenate them
xi = np.concatenate(
    [
        np.linspace(group[1].x.min(), group[1].x.max(), n_points)
        for group in data.groupby("group_idx")
    ]
)
# Generate the group indices array g and cast it to integers
g = np.concatenate([[i] * n_points for i in range(n_groups)]).astype(int)
predict_at = {"x": xi, "g": g}

idata3 = predict(
    model=model3,
    idata=idata3,
    predict_at=predict_at,
)

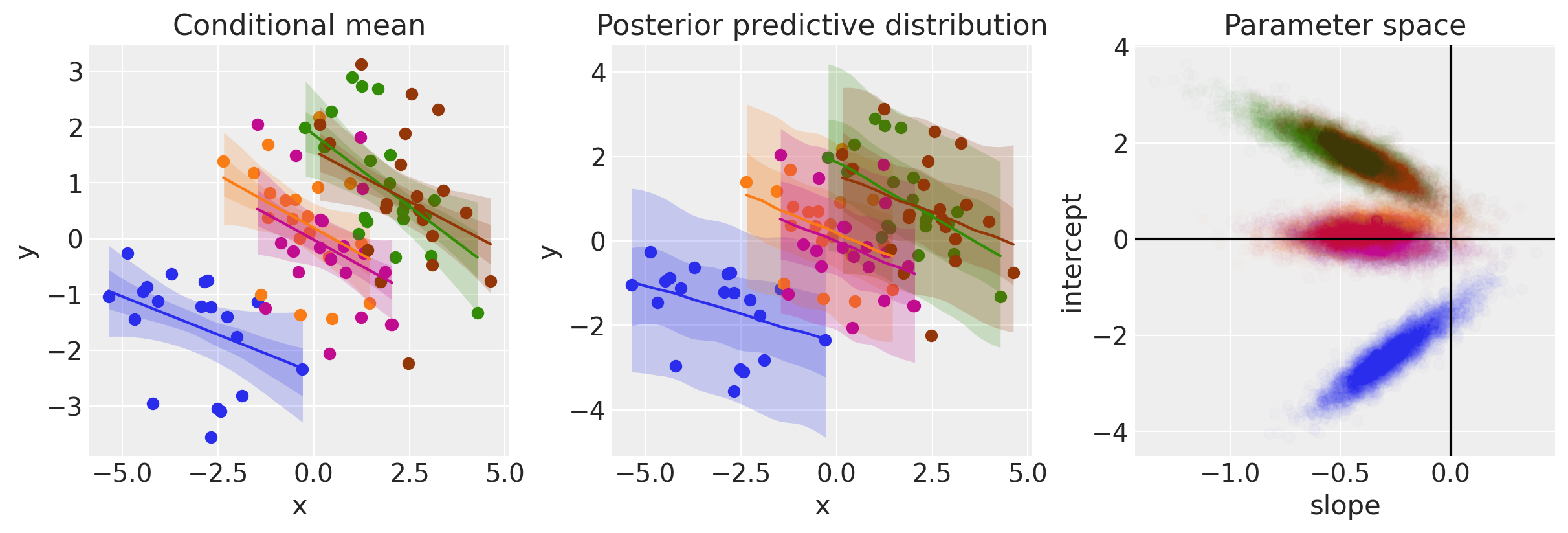
../_images/f1d789c87b8a4d6bb0c429c840c9a094fcd48c8c038a6287eb304f99c933e55d.png

右侧面板显示了斜率和截距参数的组级别后验，如轮廓图所示。我们也可以只绘制下面的边际分布，以查看我们对斜率小于零的信念有多少。

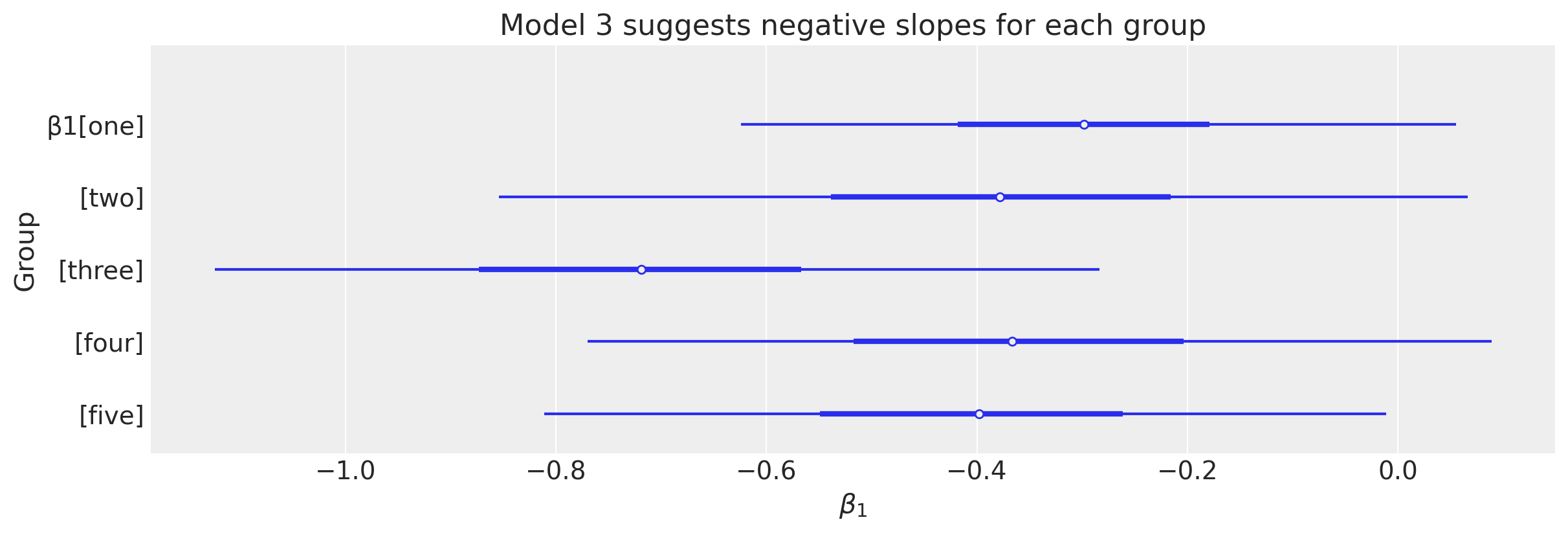
../_images/c2e813c6b28cfc78196905210673e9e1aed36054701d5d54c5d54c0809fbfd8c.png

总结#

使用辛普森悖论，我们已经完成了 3 个不同的模型。第一个是简单的线性回归，它将所有数据视为来自一个组。这相当于一个因果 DAG，断言 \(x\) 因果关系影响 \(y\)，并且忽略了 \(\text{group}\) （即，假设与 \(x\) 或 \(y\) 没有因果关系）。我们看到这导致我们相信回归斜率为正。

虽然这不一定错，但当我们看到组内数据的回归斜率为负时，这才是悖论。

通过更新我们的因果 DAG 以包含组变量，可以解决此悖论。这就是我们在第二个和第三个模型中所做的。模型 2 是一个非合并模型，我们基本上为每个组拟合单独的回归。

模型 3 假设相同的因果 DAG，但添加了每个组都从总体中抽样的知识。这增加了不仅可以对组级别的回归参数进行推断，还可以对总体级别的回归参数进行推断的能力。

作者#

由 Benjamin T. Vincent 于 2021 年 7 月撰写
由 Benjamin T. Vincent 于 2022 年 4 月更新
由 Benjamin T. Vincent 于 2023 年 2 月更新以在 PyMC v5 上运行
由 Benjamin T. Vincent 于 2023 年 2 月更新为使用 az.extract (pymc-examples#522)
由 Benjamin T. Vincent 于 2024 年 9 月更新 (pymc-examples#697 和 pymc-examples#709)

水印#

%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,xarray

Last updated: Sun Sep 22 2024

Python implementation: CPython
Python version       : 3.12.6
IPython version      : 8.27.0

pytensor: 2.25.4
xarray  : 2024.9.0

matplotlib: 3.9.2
arviz     : 0.19.0
pymc      : 5.16.2
numpy     : 1.26.4
xarray    : 2024.9.0
graphviz  : 0.20.3
pandas    : 2.2.3
seaborn   : 0.13.2

Watermark: 2.5.0

许可证声明#

此示例库中的所有笔记本均根据 MIT 许可证提供，该许可证允许修改和重新分发用于任何用途，前提是保留版权和许可证声明。

引用 PyMC 示例#

要引用此笔记本，请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。

重要提示

许多笔记本改编自其他来源：博客、书籍……在这种情况下，您也应该引用原始来源。

还请记住引用您的代码使用的相关库。

这是一个 bibtex 中的引用模板

@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}

渲染后可能看起来像

分类

标签

辛普森悖论#

生成数据#

模型 1：合并回归#

进行推断#

可视化#

模型 2：包含混淆因素的非合并回归#

进行推断#

可视化#

模型 3：包含混淆因素的部分合并模型#

进行推断#

可视化#

总结#

作者#

水印#

许可证声明#

引用 PyMC 示例#