GLM-缺失值-在协变量中#

最小可复现示例：处理多个协变量（数值预测特征）中缺失值的工作流程

协变量中缺失值的自动插补：贝叶斯工作流程的实践示例#

在此，我们演示多个协变量（数值预测特征）中缺失值的自动插补

y ~ x + e
y: Numeric target
x: Numeric with missing values in covariates (numeric predictor features)

免责声明

  • 本 Notebook 仅为实践示例，并非旨在作为学术参考

  • 理论和数学可能不正确、符号不正确或使用不当

  • 代码可能包含错误、效率低下、遗留方法，文本中可能存在拼写错误

  • 使用风险自负！

目录#

讨论#

问题陈述#

我们经常遇到真实世界的情况和数据集，其中预测特征是数值型的，并且观测值在该特征中包含缺失值。

缺失值会破坏模型推断，因为无法计算这些观测值的对数似然值。

我们有几种选择来缓解这种情况

  • 首先，我们应该始终尝试了解值为什么缺失。如果它们不是完全随机缺失 (MCAR) [Enders K, 2022] 并且包含关于有偏差或有损数据生成过程的潜在信息，那么我们可能会选择删除具有缺失值的观测值或忽略包含缺失值的特征

  • 如果我们认为这些值是完全随机缺失 (MCAR)，那么我们可能会选择自动插补缺失值，以便我们可以利用所有可用的观测值。当我们观测值很少和/或缺失程度很高时，这一点尤为重要。

在此，我们演示了作为 pymc 后验抽样过程一部分的自动插补缺失值的方法。我们像往常一样获得推断和预测，但也获得了缺失值的自动插补值。非常棒！

数据和模型演示#

我们的问题陈述是，当面对具有缺失值的数据时，我们希望

  1. 推断样本内数据集中缺失值并抽样完整的后验参数

  2. 预测样本外数据集的内生特征和缺失值

本 notebook 提供了机会来

  • 演示一种使用自动插补的通用方法，该方法经常在 pymc 传说中被提及，但很少完整展示。PyMCon2020 演讲：[Lao, 2020] 提供了一个有用的入门知识和相关讨论

  • 演示一个相当完整的贝叶斯工作流程 [Gelman et al., 2020]，包括数据创建

本 notebook 是另一个 pymc-examples notebook Missing_Data_Imputation.ipynb 的伙伴，后者更详细地介绍了分类法和一个更复杂的数据集和教程风格的实践示例。

设置#

注意

本 notebook 使用的库不是 PyMC 的依赖项，因此需要专门安装才能运行本 notebook。打开下面的下拉菜单以获取更多指导。

额外的依赖项安装说明

为了运行本 notebook（本地或在 binder 上），您不仅需要安装可用的 PyMC 以及所有可选依赖项，还需要安装一些额外的依赖项。有关安装 PyMC 本身的建议，请参阅 安装

您可以使用您喜欢的包管理器安装这些依赖项，我们提供了 pip 和 conda 命令作为示例，如下所示。

$ pip install

请注意，如果您想（或需要）从 notebook 内部而不是命令行安装软件包，您可以通过运行 pip 命令的变体来安装软件包

import sys

!{sys.executable} -m pip install

您不应运行 !pip install，因为它可能会将软件包安装在不同的环境中，即使已安装，也无法从 Jupyter notebook 中使用。

另一种选择是使用 conda

$ conda install

当使用 conda 安装科学 python 软件包时，我们建议使用 conda forge

# uncomment to install in a Google Colab environment
# !pip install watermark

# suppress seaborn, it's far too chatty
import warnings  # #noqa

from copy import deepcopy

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pytensor.tensor as pt

from pymc.testing import assert_no_rvs

warnings.simplefilter(action="ignore", category=FutureWarning)  # noqa
import seaborn as sns

%matplotlib inline
%config InlineBackend.figure_format = 'retina'

sns.set_theme(
    style="darkgrid",
    palette="muted",
    context="notebook",
    rc={"figure.dpi": 72, "savefig.dpi": 144, "figure.figsize": (12, 4)},
)

SAMPLE_KWS = dict(
    progressbar=True,
    draws=500,
    tune=3000,  # tune a little more than usual
    chains=4,
    idata_kwargs=dict(log_likelihood=True),
)

RNG = np.random.default_rng(seed=42)
KWS_MN = dict(markerfacecolor="w", markeredgecolor="#333333", marker="d", markersize=12)
KWS_BOX = dict(kind="box", showmeans=True, whis=(3, 97), meanprops=KWS_MN)
KWS_PNT = dict(estimator=np.mean, errorbar=("ci", 94), join=False, color="#32CD32")
KWS_SCTR = dict(s=80, color="#32CD32")

0. 整理数据集#

实现说明

  • 如果我们能够与缺失数据的真实值进行比较，自动插补和完整工作流程将最容易演示，这意味着我们必须合成数据集

  • 我们将创建至少 2 个包含缺失值的特征，以便演示 pymc 的自动插补例程的扁平化效果

  • 我们创建的缺失值是随机缺失 (MAR) [Enders K, 2022]

  • 我们还借此机会使缺失成为一个真正的问题，即大量值缺失 (40%)

  • 为了简单起见，我们将假设原始特征都服从正态分布：为了使这个例子更具挑战性，读者可以尝试其他分布

0.1 创建合成数据集#

0.1.0 创建“真实”（未观测）数据集（没有缺失值）#

REFVAL_X_MU = dict(a=1, b=1, c=10, d=2)
REFVAL_X_SIGMA = dict(a=1, b=4, c=1, d=10)
REFVAL_BETA = dict(intercept=-4, a=10, b=-20, c=30, d=5)

N = 40
dfraw = pd.DataFrame(
    {
        "a": RNG.normal(loc=REFVAL_X_MU["a"], scale=REFVAL_X_SIGMA["a"], size=N),
        "b": RNG.normal(loc=REFVAL_X_MU["b"], scale=REFVAL_X_SIGMA["b"], size=N),
        "c": RNG.normal(loc=REFVAL_X_MU["c"], scale=REFVAL_X_SIGMA["c"], size=N),
        "d": RNG.normal(loc=REFVAL_X_MU["d"], scale=REFVAL_X_SIGMA["d"], size=N),
    },
    index=[f"o{str(i).zfill(2)}" for i in range(N)],
)
dfraw.index.name = "oid"
dfraw["y"] = (
    REFVAL_BETA["intercept"]
    + (dfraw * np.array(list(REFVAL_BETA.values()))[1:]).sum(axis=1)
    + RNG.normal(loc=0, scale=1, size=N)
)
dfraw.tail()
a b c d y
oid
o35 2.128972 3.761941 9.470507 19.679299 323.667882
o36 0.886053 -0.709011 10.232676 3.302745 343.178076
o37 0.159844 1.634159 10.021852 11.827395 324.313195
o38 0.175519 3.502362 11.601779 -2.992956 260.791421
o39 1.650593 -0.237386 9.760644 -9.849438 260.662351

0.1.1 强制 2 个特征包含 40% 未观测到的缺失值#

df = dfraw.copy()

prop_missing = 0.4
df.loc[RNG.choice(df.index, int(N * prop_missing), replace=False), "c"] = np.nan
df.loc[RNG.choice(df.index, int(N * prop_missing), replace=False), "d"] = np.nan
idx = df[["c", "d"]].isnull().sum(axis=1) > 0
display(df.loc[idx])
display(pd.concat((df.describe(include="all").T, df.isnull().sum(), df.dtypes), axis=1))
a b c d y
oid
o00 1.304717 3.973017 NaN NaN 201.150103
o03 1.940565 1.928645 NaN NaN 342.518597
o04 -0.951035 1.466743 NaN 10.351112 273.873646
o06 1.127840 4.485715 NaN 16.633029 287.578749
o08 0.983199 3.715654 NaN NaN 223.797089
o09 0.146956 1.270316 10.446531 NaN 249.089611
o10 1.879398 2.156478 NaN NaN 281.480703
o14 1.467509 -0.881491 8.312666 NaN 212.866620
o15 0.140708 -1.555511 8.552888 NaN 244.497563
o17 0.041117 6.979765 9.002753 NaN 178.964784
o18 1.878450 -2.463324 NaN NaN 485.762125
o20 0.815138 -5.731479 9.621837 NaN 439.462555
o21 0.319070 -0.339540 NaN -7.895381 305.700832
o23 0.845471 3.344889 NaN NaN 284.174248
o25 0.647866 4.173389 9.794562 NaN 203.615652
o26 1.532309 -0.394900 NaN -4.120968 270.298830
o29 1.430821 0.234783 NaN 3.570486 273.296300
o30 3.141648 -4.102745 NaN 0.413652 426.296015
o31 0.593585 -3.533149 NaN NaN 337.768688
o33 0.186227 2.988643 NaN -2.863079 181.853726
o34 1.615979 1.569703 NaN NaN 289.133447
o35 2.128972 3.761941 9.470507 NaN 323.667882
o36 0.886053 -0.709011 10.232676 NaN 343.178076
o39 1.650593 -0.237386 NaN -9.849438 260.662351
count mean std min 25% 50% 75% max 0 1
a 40.0 1.038265 0.825850 -0.951035 0.445586 1.024615 1.624633 3.141648 0 float64
b 40.0 1.052709 2.918529 -5.731479 -0.744110 1.601931 3.508059 6.979765 0 float64
c 24.0 9.680004 0.737447 8.312666 9.277186 9.640341 10.014834 11.601779 16 float64
d 24.0 1.018293 11.149556 -19.320463 -6.570904 0.502871 6.264410 31.138625 16 float64
y 40.0 285.251112 75.686022 166.591767 228.845718 282.827475 323.829210 485.762125 0 float64

观察

  • 特征 a 和 b 是完整的，没有缺失值

  • 特征 c 和 d 包含缺失值，其中观测值甚至可能包含这两个特征的缺失值

注意我们不需要任何进一步的步骤来准备数据集（例如，清理观测值和特征，强制数据类型，设置索引等），因此我们将直接进入 EDA 和模型输入的转换

0.2 非常有限的快速 EDA#

0.2.1 单变量：目标 y#

def plot_univariate_violin(df: pd.DataFrame, fts: list):
    v_kws = dict(data=df, cut=0)
    cs = sns.color_palette(n_colors=len(fts))
    height_bump = 2 if len(fts) == 1 else 1
    f, axs = plt.subplots(
        len(fts), 1, figsize=(12, 0.8 + height_bump * 1.2 * len(fts)), squeeze=False, sharex=True
    )
    for i, ft in enumerate(fts):
        ax = sns.violinplot(x=ft, **v_kws, ax=axs[i][0], color=cs[i])
        n_nans = pd.isnull(df[ft]).sum()
        _ = ax.text(
            0.993,
            0.93,
            f"NaNs: {n_nans}",
            transform=ax.transAxes,
            ha="right",
            va="top",
            backgroundcolor="w",
            fontsize=10,
        )
        _ = ax.set_title(f"ft: {ft}")
    _ = f.suptitle("Univariate numerics with NaN count noted")
    _ = f.tight_layout()


plot_univariate_violin(df, fts=["y"])
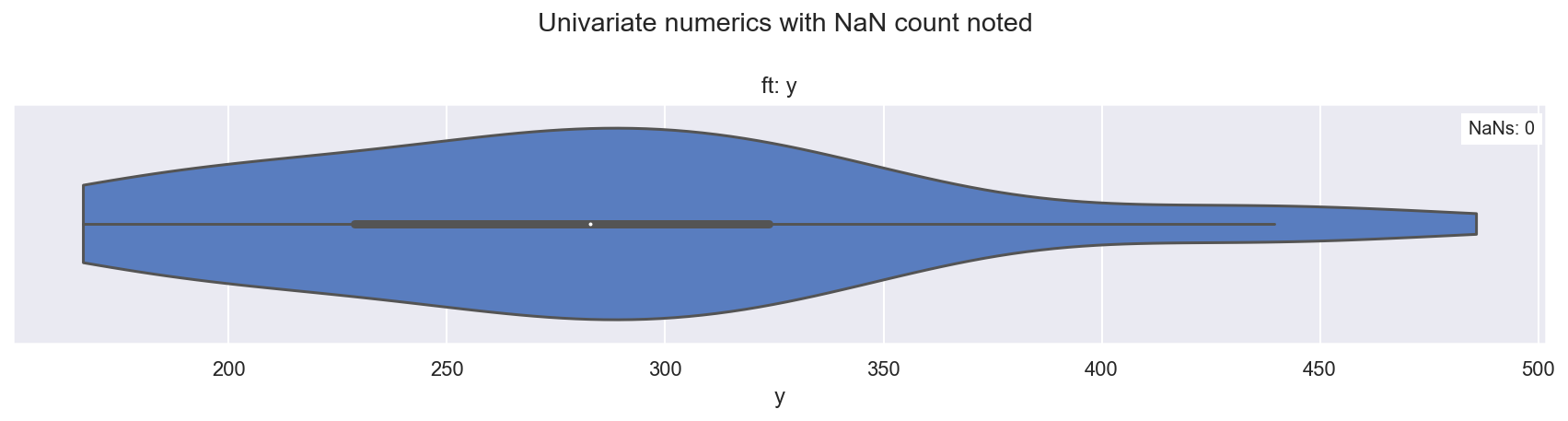
../_images/913658f33469c28d58598eeadec2fd6d0f36d5be40dd0d554e534a0cb83d48fc.png

观察

  • y 看起来平滑，相当中心，可能可以用正态似然建模

0.2.2 单变量：预测变量 a, b, c, d#

plot_univariate_violin(df, fts=["a", "b", "c", "d"])
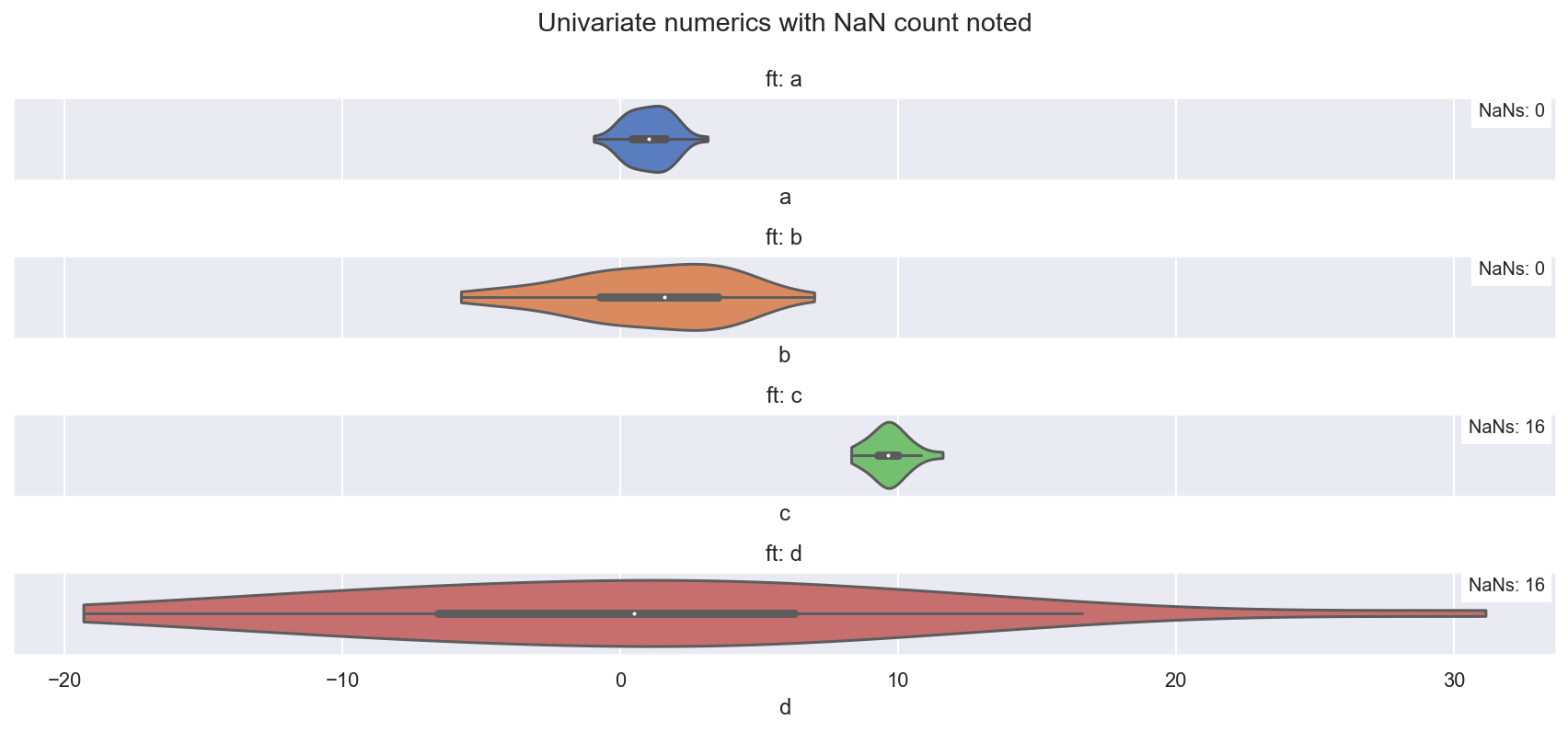
../_images/39b62e02913b56f54c4c218aca75b41ef2510bb5a77d80c74a436d545d569b9b.png

观察

  • a、b、c、d 在范围内变化，但都相当中心，可能可以用正态分布建模

  • c、d 各自包含 16 个 NaN 值

0.2.3 双变量：目标 vs 预测变量#

dfp = df.reset_index().melt(id_vars=["oid", "y"], var_name="ft")
g = sns.lmplot(
    y="y",
    x="value",
    hue="ft",
    col="ft",
    data=dfp,
    fit_reg=True,
    height=4,
    aspect=0.75,
    facet_kws={"sharex": False},
)
_ = g.fig.suptitle("Bivariate plots of `y` vs fts `a`, `b`, `c`, `d`")
_ = g.fig.tight_layout()
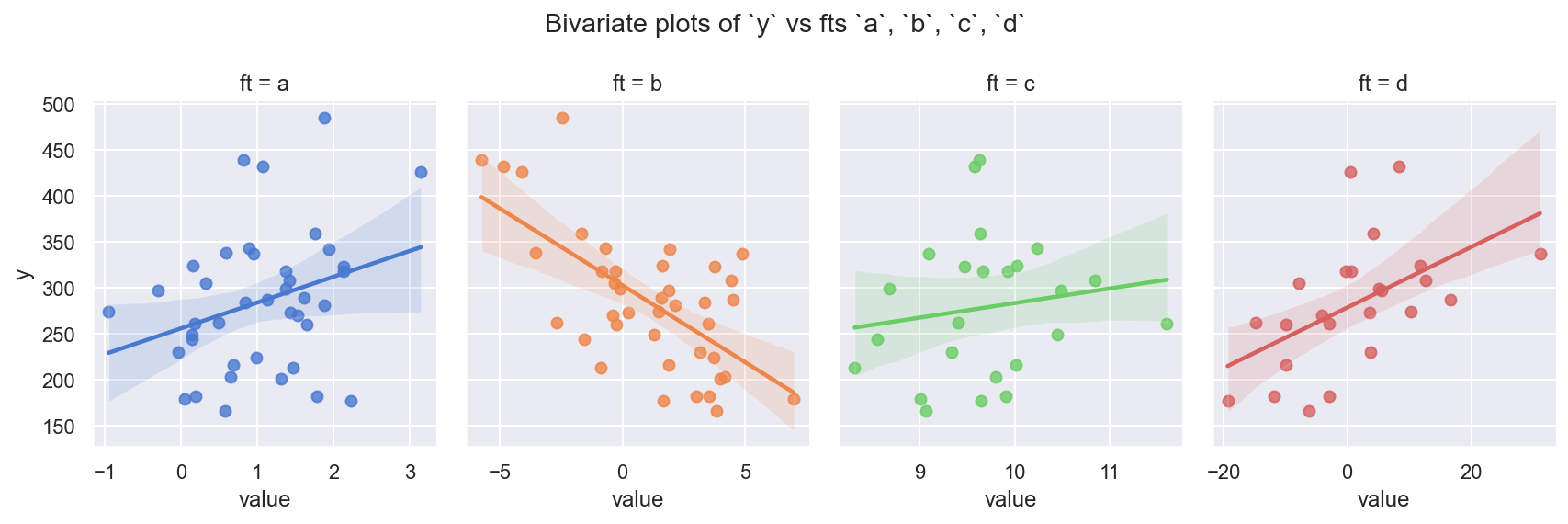
../_images/b0ec3138bad52db40be012e678c2a4f76ed63a37f54743fa405df64b553e035a.png

观察

  • 特征 a、b、c、d 中的每一个都与 y 相关，有些更强，有些更弱

  • 这看起来相当真实

0.3 将数据集转换为 dfx 以用于模型输入#

重要提示

  • 提醒一下，贝叶斯推断方法不需要 test 数据集（或 k 折交叉验证）来拟合参数。

  • 我们也不需要 holdout（样本外）数据集（包含目标 y 值）来评估模型性能，因为我们可以使用样本内 PPC、LOO-PIT 和 ELPD 评估

  • 根据真实世界的模型实现，我们可能会

    • 创建一个单独的 holdout 集（即使我们不需要它）来简单地目测预测输出的行为

    • 创建一个 forecast 集（不包含目标 y 值）来演示我们将如何在生产中使用模型及其预测输出来处理未来的新数据

  • 在这里，我们确实采用了 holdout 集，以便目测预测输出，并目测自动插补的缺失值与真实的合成数据进行比较。这仅仅是因为我们在上面合成了真实数据。

  • 按照以下术语，上面创建的 df 是我们的“工作”数据集，我们将将其划分为“训练集”和“保留集”

数据集术语/划分/目的

|<---------- Relevant domain of all data for our analyses & models ---------->|
|<----- "Observed" historical target ------>||<- "Unobserved" future target ->|
|<----------- "Working" dataset ----------->||<----- "Forecast" dataset ----->|
|<- Training/CrossVal ->||<- Test/Holdout ->|

0.3.1 分离 df_train 和 df_holdout#

注意

  • 我们可以完全控制在 df 中创建多少观测值，因此这种拆分的比例并不重要，我们将安排在保留集中有 10 个观测值

  • 目测以下表格中非空值的 count，以确保我们在 train 和 holdout 数据集中特征 c 和 d 中都有缺失值

df_train = df.sample(n=len(df) - 10, replace=False).sort_index()
print(df_train.shape)
display(
    pd.concat(
        (df_train.describe(include="all").T, df_train.isnull().sum(), df_train.dtypes), axis=1
    )
)

(30, 5)
count mean std min 25% 50% 75% max 0 1
a 30.0 0.986483 0.869626 -0.951035 0.219438 0.934626 1.578862 3.141648 0 float64
b 30.0 0.868533 2.838965 -4.828623 -0.873470 1.518223 3.126624 6.979765 0 float64
c 18.0 9.663899 0.818891 8.312666 9.134305 9.640341 10.019513 11.601779 12 float64
d 18.0 0.549915 9.740175 -19.320463 -5.345297 0.502871 7.547417 16.633029 12 float64
y 30.0 287.402426 76.524934 166.591767 234.020837 285.876498 322.786791 485.762125 0 float64 
df_holdout = df.loc[list(set(df.index.values) - set(df_train.index.values))].copy().sort_index()
print(df_holdout.shape)
display(
    pd.concat(
        (df_holdout.describe(include="all").T, df_holdout.isnull().sum(), df_holdout.dtypes), axis=1
    )
)

(10, 5)
count mean std min 25% 50% 75% max 0 1
a 10.0 1.193610 0.694911 -0.302180 0.848872 1.367769 1.621022 2.128972 0 float64
b 10.0 1.605238 3.238522 -5.731479 -0.119344 2.699954 3.920248 4.873113 0 float64
c 6.0 9.728319 0.466786 9.094521 9.508340 9.708200 9.874776 10.486972 4 float64
d 6.0 2.423426 15.688134 -11.766861 -8.417320 -0.275241 5.069154 31.138625 4 float64
y 10.0 278.797170 76.757413 181.932062 217.877327 271.797565 317.009141 439.462555 0 float64

0.3.2 创建 dfx_train#

转换（z 分数和缩放）数值

FTS_NUM = ["a", "b", "c", "d"]
FTS_NON_NUM = []
FTS_Y = ["y"]
MNS = np.nanmean(df_train[FTS_NUM], axis=0)
SDEVS = np.nanstd(df_train[FTS_NUM], axis=0)

dfx_train_num = (df_train[FTS_NUM] - MNS) / SDEVS
icpt = pd.Series(np.ones(len(df_train)), name="intercept", index=dfx_train_num.index)

# concat including y which will be used as observed
dfx_train = pd.concat((df_train[FTS_Y], icpt, df_train[FTS_NON_NUM], dfx_train_num), axis=1)
display(dfx_train.describe().T)
count mean std min 25% 50% 75% max
y 30.0 2.874024e+02 76.524934 166.591767 234.020837 285.876498 322.786791 485.762125
截距 30.0 1.000000e+00 0.000000 1.000000 1.000000 1.000000 1.000000 1.000000
a 30.0 -1.073216e-16 1.017095 -2.266079 -0.897119 -0.060651 0.692833 2.520633
b 30.0 -9.251859e-17 1.017095 -2.041078 -0.624095 0.232760 0.808990 2.189426
c 18.0 7.401487e-16 1.028992 -1.697915 -0.665470 -0.029602 0.446852 2.435075
d 18.0 4.317534e-17 1.028992 -2.099187 -0.622794 -0.004970 0.739244 1.699085

0.3.3 创建 dfx_holdout#

dfx_holdout_num = (df_holdout[FTS_NUM] - MNS) / SDEVS
icpt = pd.Series(np.ones(len(df_holdout)), name="intercept", index=dfx_holdout_num.index)

# concat including y which will be used as observed
dfx_holdout = pd.concat((df_holdout[FTS_Y], icpt, df_holdout[FTS_NON_NUM], dfx_holdout_num), axis=1)
display(dfx_holdout.describe().T)
count mean std min 25% 50% 75% max
y 10.0 278.797170 76.757413 181.932062 217.877327 271.797565 317.009141 439.462555
截距 10.0 1.000000 0.000000 1.000000 1.000000 1.000000 1.000000 1.000000
a 10.0 0.242251 0.812752 -1.507192 -0.160947 0.445944 0.742143 1.336230
b 10.0 0.263934 1.160242 -2.364538 -0.353919 0.656130 1.093316 1.434692
c 6.0 0.080948 0.586548 -0.715462 -0.195471 0.055667 0.264981 1.034246
d 6.0 0.197925 1.657358 -1.301194 -0.947335 -0.087173 0.477431 3.231515

1. Model0：没有缺失值的基线模型#

本节可能看起来不寻常或不必要，但希望为一般行为提供有用的比较，并有助于进一步解释 ModelA 中使用的模型架构。

我们将使用相同的广义线性模型创建 Model0，该模型在没有任何缺失值的 dfrawx_train 数据集上运行

\[\begin{split} \begin{align} \sigma_{\beta} &\sim \text{InverseGamma}(11, 10) \\ \beta_{j} &\sim \text{Normal}(0, \sigma_{\beta}, \text{shape}=j) \\ \\ \epsilon &\sim \text{InverseGamma}(11, 10) \\ \hat{y_{i}} &\sim \text{Normal}(\mu=\beta_{j}^{T}\mathbb{x}_{ij}, \sigma=\epsilon) \\ \end{align} \end{split}\]

其中

  • 观测值 \(i\)（observation_id 又名 oid）包含具有完整值的数值特征 \(j\)（这是所有特征 a、b、c、d）

  • 我们的目标是 \(\hat{y_{i}}\)，这里是 y，具有线性子模型 \(\beta_{j}^{T}\mathbb{x}_{ij}\)，用于回归到这些特征上

1.0 基于 dfraw 快速准备非缺失数据集#

这是上面 \(\S0.3\) 中相同逻辑/工作流程的轻微简化副本。我们不会在这里占用更多空间进行 EDA，唯一的区别是 c 和 d 现在是完整的

将 dfraw 分区为 dfraw_train 和 dfraw_holdout，使用与 df_train 和 df_holdout 相同的索引

dfraw_train = dfraw.loc[df_train.index].copy()
dfraw_holdout = dfraw.loc[df_holdout.index].copy()
dfraw_holdout.tail()
a b c d y
oid
o25 0.647866 4.173389 9.794562 -2.153573 203.615652
o26 1.532309 -0.394900 9.049978 -4.120968 270.298830
o29 1.430821 0.234783 8.272680 3.570486 273.296300
o35 2.128972 3.761941 9.470507 19.679299 323.667882
o39 1.650593 -0.237386 9.760644 -9.849438 260.662351

创建 dfrawx_train：转换（z 分数和缩放）数值

MNS_RAW = np.nanmean(dfraw_train[FTS_NUM], axis=0)
SDEVS_RAW = np.nanstd(dfraw_train[FTS_NUM], axis=0)

dfrawx_train_num = (dfraw_train[FTS_NUM] - MNS_RAW) / SDEVS_RAW
icpt = pd.Series(np.ones(len(dfraw_train)), name="intercept", index=dfrawx_train_num.index)

# concat including y which will be used as observed
dfrawx_train = pd.concat(
    (dfraw_train[FTS_Y], icpt, dfraw_train[FTS_NON_NUM], dfrawx_train_num), axis=1
)
display(dfrawx_train.describe().T)
count mean std min 25% 50% 75% max
y 30.0 2.874024e+02 76.524934 166.591767 234.020837 285.876498 322.786791 485.762125
截距 30.0 1.000000e+00 0.000000 1.000000 1.000000 1.000000 1.000000 1.000000
a 30.0 -1.073216e-16 1.017095 -2.266079 -0.897119 -0.060651 0.692833 2.520633
b 30.0 -9.251859e-17 1.017095 -2.041078 -0.624095 0.232760 0.808990 2.189426
c 30.0 -1.021405e-15 1.017095 -1.866273 -0.580940 -0.043790 0.739403 2.189560
d 30.0 -3.700743e-17 1.017095 -2.069592 -0.801472 -0.032248 0.691756 2.173761

创建 dfrawx_holdout

dfrawx_holdout_num = (dfraw_holdout[FTS_NUM] - MNS_RAW) / SDEVS_RAW
icpt = pd.Series(np.ones(len(dfraw_holdout)), name="intercept", index=dfrawx_holdout_num.index)

# concat including y which will be used as observed
dfrawx_holdout = pd.concat(
    (dfraw_holdout[FTS_Y], icpt, dfraw_holdout[FTS_NON_NUM], dfrawx_holdout_num), axis=1
)
display(dfrawx_holdout.describe().T)
count mean std min 25% 50% 75% max
y 10.0 278.797170 76.757413 181.932062 217.877327 271.797565 317.009141 439.462555
截距 10.0 1.000000 0.000000 1.000000 1.000000 1.000000 1.000000 1.000000
a 10.0 0.242251 0.812752 -1.507192 -0.160947 0.445944 0.742143 1.336230
b 10.0 0.263934 1.160242 -2.364538 -0.353919 0.656130 1.093316 1.434692
c 10.0 -0.289949 0.823264 -1.915581 -0.786253 -0.166341 0.059979 0.814883
d 10.0 0.224142 1.401435 -1.293270 -0.824576 -0.011119 0.532746 3.116343

请注意 MNS 与 MNS_RAW 和 SDEVS 与 SDEVS_RAW 之间不可避免的（但轻微的）差异

print(MNS)
print(MNS_RAW)
print(SDEVS)
print(SDEVS_RAW)

[0.98648324 0.86853301 9.66389924 0.54991532]
[0.98648324 0.86853301 9.82613624 0.81663988]
[0.85500914 2.7912481  0.79581928 9.46574849]
[0.85500914 2.7912481  0.81095867 9.72998886]

1.1 构建模型对象#

ft_y = "y"
FTS_XJ = ["intercept", "a", "b", "c", "d"]

COORDS = dict(
    xj_nm=FTS_XJ,  # these are the names of the features
    oid=dfrawx_train.index.values,  # these are the observation_ids
)

with pm.Model(coords=COORDS) as mdl0:
    # 0. create (Mutable)Data containers for obs (Y, X)
    y = pm.Data("y", dfrawx_train[ft_y].values, dims="oid")
    xj = pm.Data("xj", dfrawx_train[FTS_XJ].values, dims=("oid", "xj_nm"))

    # 2. define priors for contiguous data
    b_s = pm.Gamma("beta_sigma", alpha=10, beta=10)  # E ~ 1
    bj = pm.Normal("beta_j", mu=0, sigma=b_s, dims="xj_nm")

    # 4. define evidence
    epsilon = pm.Gamma("epsilon", alpha=50, beta=50)  # encourage E ~ 1
    lm = pt.dot(xj, bj.T)
    _ = pm.Normal("yhat", mu=lm, sigma=epsilon, observed=y, dims="oid")

RVS_PPC = ["yhat"]
RVS_PRIOR = ["epsilon", "beta_sigma", "beta_j"]

验证构建的模型结构是否符合我们的意图，并验证参数化#

display(pm.model_to_graphviz(mdl0, formatting="plain"))
display(dict(unobserved=mdl0.unobserved_RVs, observed=mdl0.observed_RVs))
assert_no_rvs(mdl0.logp())
mdl0.debug(fn="logp", verbose=True)
mdl0.debug(fn="random", verbose=True)
../_images/985e3771701853b6c582c314da571199130d76599e4bdfa48dea7f1285ab550f.svg 
{'unobserved': [beta_sigma ~ Gamma(10, f()),
  beta_j ~ Normal(0, beta_sigma),
  epsilon ~ Gamma(50, f())],
 'observed': [yhat ~ Normal(f(beta_j), epsilon)]}

point={'beta_sigma_log__': array(0.), 'beta_j': array([0., 0., 0., 0., 0.]), 'epsilon_log__': array(0.)}

No problems found
point={'beta_sigma_log__': array(0.), 'beta_j': array([0., 0., 0., 0., 0.]), 'epsilon_log__': array(0.)}

No problems found

观察

  • 这是一个非常简单的模型

1.2 抽样先验预测，查看诊断#

GRP = "prior"
kws = dict(samples=2000, return_inferencedata=True, random_seed=42)
with mdl0:
    id0 = pm.sample_prior_predictive(var_names=RVS_PPC + RVS_PRIOR, **kws)

Sampling: [beta_j, beta_sigma, epsilon, yhat]

1.2.1 样本内先验 PPC（回顾性检查）#

def plot_ppc_retrodictive(
    idata: az.InferenceData,
    grp: str = "posterior",
    rvs: list = None,
    mdlnm: str = "mdla",
    ynm: str = "y",
) -> plt.Figure:
    """Convenience plot prior or posterior PPC retrodictive KDE"""
    f, axs = plt.subplots(1, 1, figsize=(12, 3))
    _ = az.plot_ppc(idata, group=grp, kind="kde", var_names=rvs, ax=axs, observed=True)
    _ = f.suptitle(f"In-sample {grp.title()} PPC Retrodictive KDE on `{ynm}` - `{mdlnm}`")
    return f


f = plot_ppc_retrodictive(id0, grp=GRP, rvs=["yhat"], mdlnm="mdl0", ynm="y")
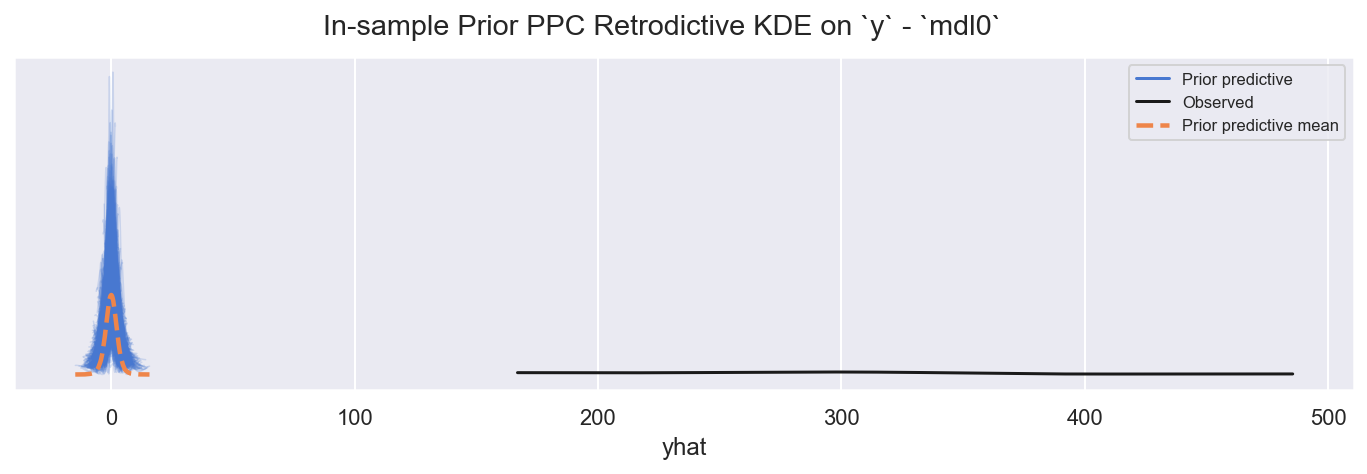
../_images/e5a9e807b3f00672a761f353a86bcf437ab71fcac9bb02e15e01882a9ad6378c.png

观察

  • 先验 PPC 是错误的，正如预期的那样，因为我们设置了相对不提供信息的先验

  • 但是，总体范围和尺度是合理的，并且采样器应该能够轻松找到最高似然潜在空间

1.2.2 快速查看选定的先验#

系数等#

def plot_krushke(
    idata: az.InferenceData,
    group: str = "posterior",
    rvs: list = RVS_PRIOR,
    coords: dict = None,
    ref_vals: list = None,
    mdlnm: str = "mdla",
    n: int = 1,
    nrows: int = 1,
) -> plt.figure:
    """Convenience plot Krushke-style posterior (or prior) KDE"""
    m = int(np.ceil(n / nrows))
    f, axs = plt.subplots(nrows, m, figsize=(3 * m, 0.8 + nrows * 2))
    _ = az.plot_posterior(
        idata, group=group, ax=axs, var_names=rvs, coords=coords, ref_val=ref_vals
    )
    _ = f.suptitle(f"{group.title()} distributions for rvs {rvs} - `{mdlnm}")
    _ = f.tight_layout()
    return f


f = plot_krushke(id0, GRP, rvs=RVS_PRIOR, mdlnm="mdl0", n=1 + 1 + 5, nrows=2)
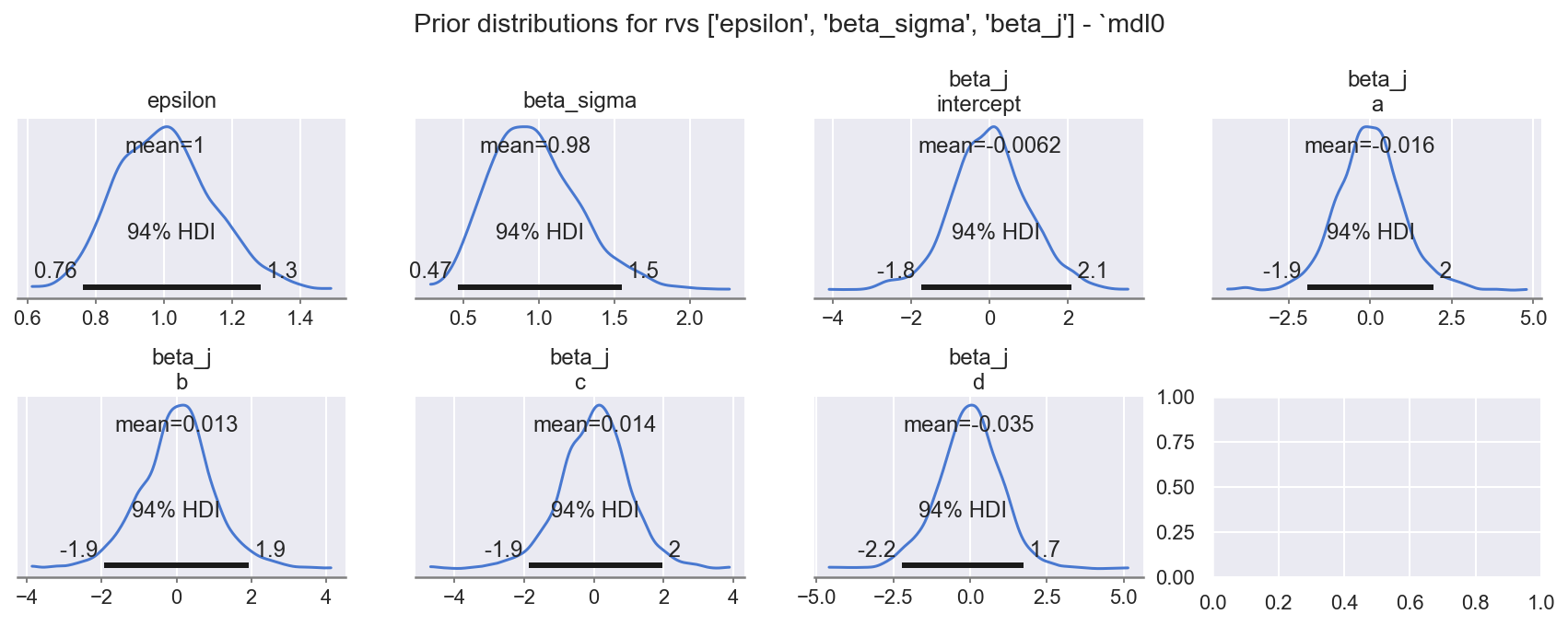
../_images/3cddbd37e2fdd52fb6792b2d527ef6d2a06dd2e522123bd7b310688ebda91e6d.png

观察

  • 模型先验 beta_sigma、beta_j: (levels)、epsilon 都具有合理的先验范围，如指定的

1.3 抽样后验，查看诊断#

1.3.1 抽样后验和 PPC#

GRP = "posterior"
with mdl0:
    id0.extend(pm.sample(**SAMPLE_KWS), join="right")
    id0.extend(
        pm.sample_posterior_predictive(trace=id0.posterior, var_names=RVS_PPC),
        join="right",
    )

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [beta_sigma, beta_j, epsilon]



Sampling 4 chains for 3_000 tune and 500 draw iterations (12_000 + 2_000 draws total) took 7 seconds.
Sampling: [yhat]















1.3.2 查看轨迹图#






def plot_traces_and_display_summary(
    idata: az.InferenceData, rvs: list = None, coords: dict = None, mdlnm="mdla", energy=False
) -> plt.Figure:
    """Convenience to plot traces and display summary table for rvs"""
    _ = az.plot_trace(idata, var_names=rvs, coords=coords, figsize=(12, 0.8 + 1.1 * len(rvs)))
    f = plt.gcf()
    _ = f.suptitle(f"Posterior traces of {rvs} - `{mdlnm}`")
    _ = f.tight_layout()
    if energy:
        _ = az.plot_energy(idata, fill_alpha=(0.8, 0.6), fill_color=("C0", "C8"), figsize=(12, 1.6))
    display(az.summary(idata, var_names=rvs))
    return f


f = plot_traces_and_display_summary(id0, rvs=RVS_PRIOR, mdlnm="mdl0", energy=True)

















mean
sd
hdi_3%
hdi_97%
mcse_mean
mcse_sd
ess_bulk
ess_tail
r_hat






epsilon
1.004
0.101
0.808
1.183
0.002
0.002
1694.0
1363.0
1.0




beta_sigma
20.902
0.832
19.305
22.399
0.018
0.013
2064.0
1567.0
1.0




beta_j[intercept]
287.374
0.185
287.008
287.709
0.004
0.003
2442.0
1763.0
1.0




beta_j[a]
8.456
0.202
8.062
8.817
0.005
0.004
1470.0
1604.0
1.0




beta_j[b]
-55.912
0.202
-56.271
-55.539
0.005
0.003
1967.0
1566.0
1.0




beta_j[c]
24.226
0.186
23.886
24.569
0.004
0.003
2100.0
1508.0
1.0




beta_j[d]
48.753
0.188
48.412
49.096
0.004
0.003
2369.0
1163.0
1.0






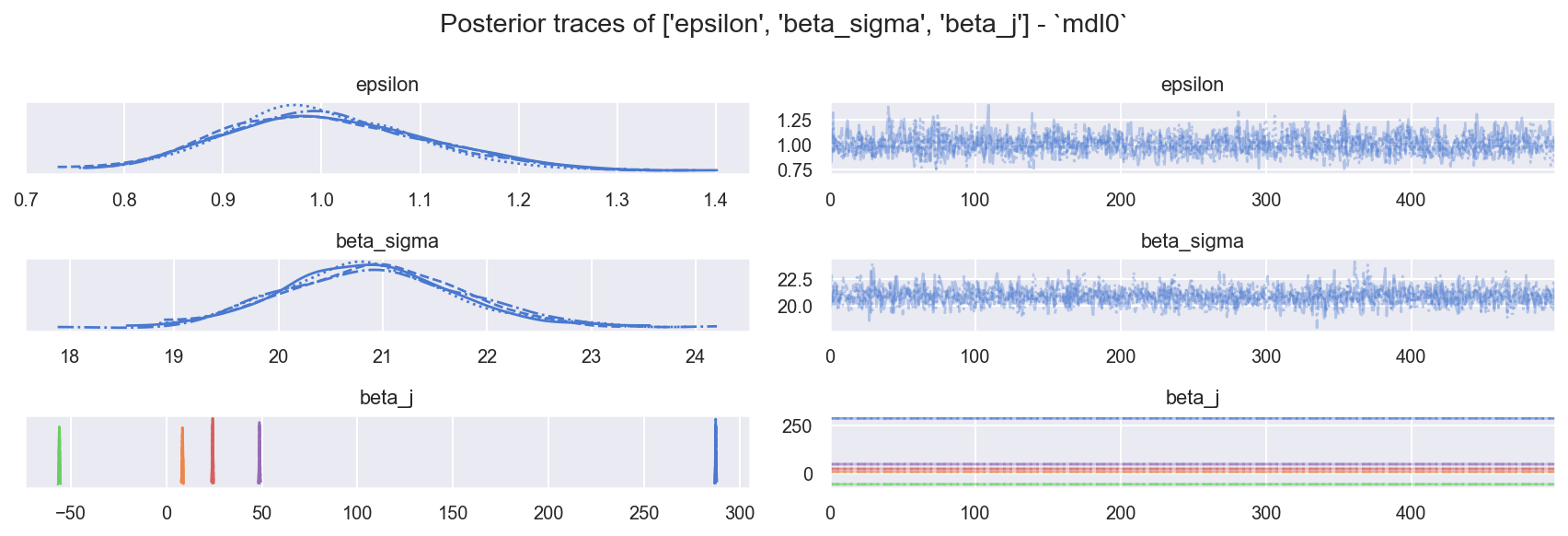
../_images/4d55907c6a11aa18057d1962e223dbe2fd60366d12a89a8a858af23d5dd60417.png
../_images/14b615c98cafc1327f7a3bf22807ddaaa55bfdd1c7b51198ddb1228604f48111.png





观察


    

  • 样本混合良好且行为良好：ess_bulk 良好，r_hat 良好
    • 

  • 边际能量 | 能量跃迁看起来有点不匹配，但 E-BFMI >> 0.3 因此 显然是合理的
    • 







1.3.3 样本内后验 PPC（回顾性检查）#






f = plot_ppc_retrodictive(id0, grp=GRP, rvs=["yhat"], mdlnm="mdl0", ynm="y")








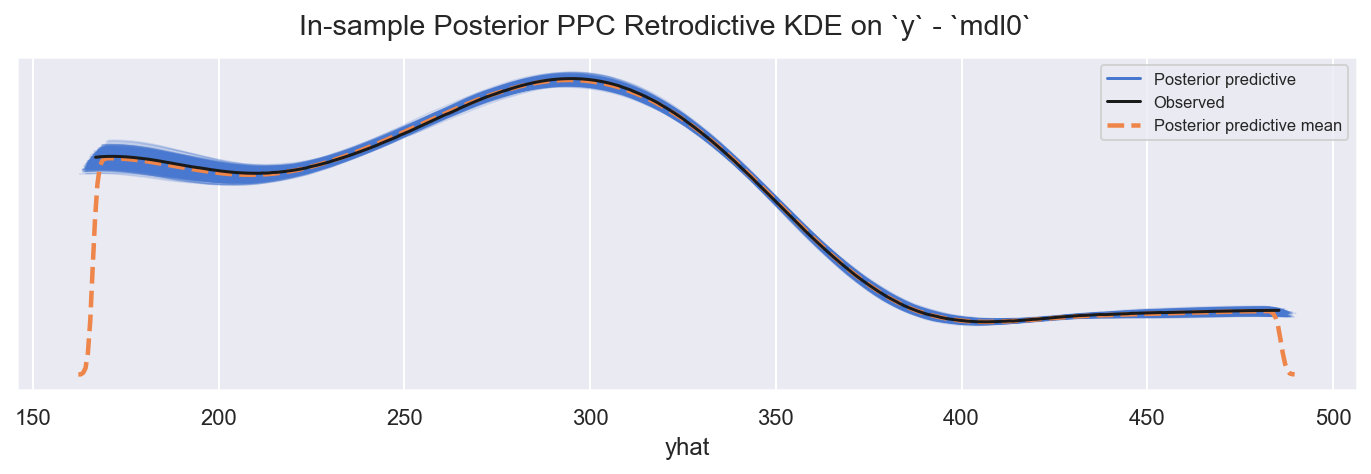
../_images/c3e16f83f4fe52f0de8ac528c80568a8a411a43a19d88caeaa744623a13fd237.png





观察


    

  • 样本内 PPC yhat 非常紧密地跟踪观测到的 y
    • 







1.3.4 样本内 PPC LOO-PIT#






def plot_loo_pit(
    idata: az.InferenceData, mdlname: str = "mdla", y: str = "yhat", y_hat: str = "yhat"
) -> plt.Figure:
    """Convenience plot LOO-PIT KDE and ECDF"""
    f, axs = plt.subplots(1, 2, figsize=(12, 2.4))
    _ = az.plot_loo_pit(idata, y=y, y_hat=y_hat, ax=axs[0])
    _ = az.plot_loo_pit(idata, y=y, y_hat=y_hat, ax=axs[1], ecdf=True)
    _ = axs[0].set_title(f"Predicted `{y_hat}` LOO-PIT")
    _ = axs[1].set_title(f"Predicted `{y_hat}` LOO-PIT cumulative")
    _ = f.suptitle(f"In-sample LOO-PIT `{mdlname}`")
    _ = f.tight_layout()
    return f


f = plot_loo_pit(id0, "mdla")








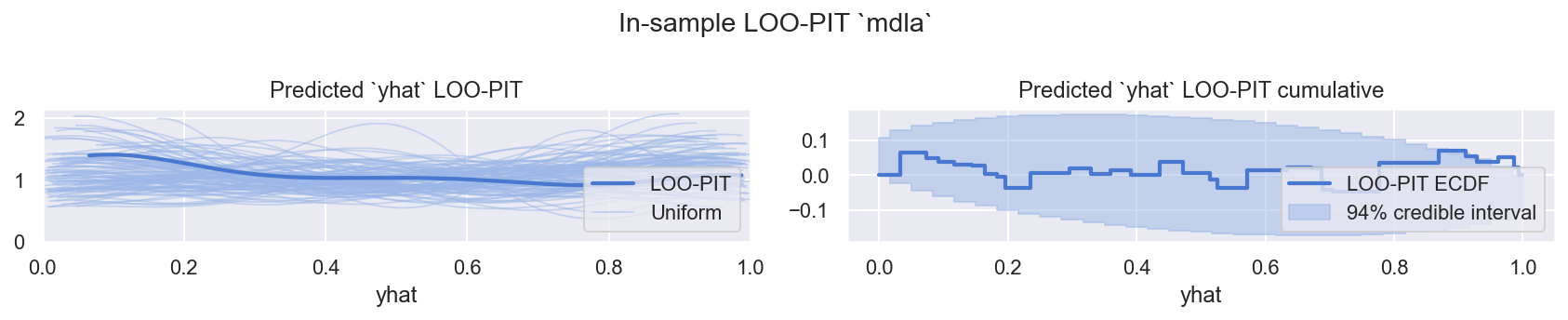
../_images/e259a8da7070669c7c3e3a08e4d367c830e4071b65ea17d95a79000a23b317cc.png





观察


    

  • LOO-PIT 看起来不错，稍微过度分散，但对于使用来说完全可以接受
    • 









1.4 评估后验参数#




1.4.1 系数等#






f = plot_krushke(id0, GRP, RVS_PRIOR, mdlnm="mdl0", n=1 + 1 + 5, nrows=2)








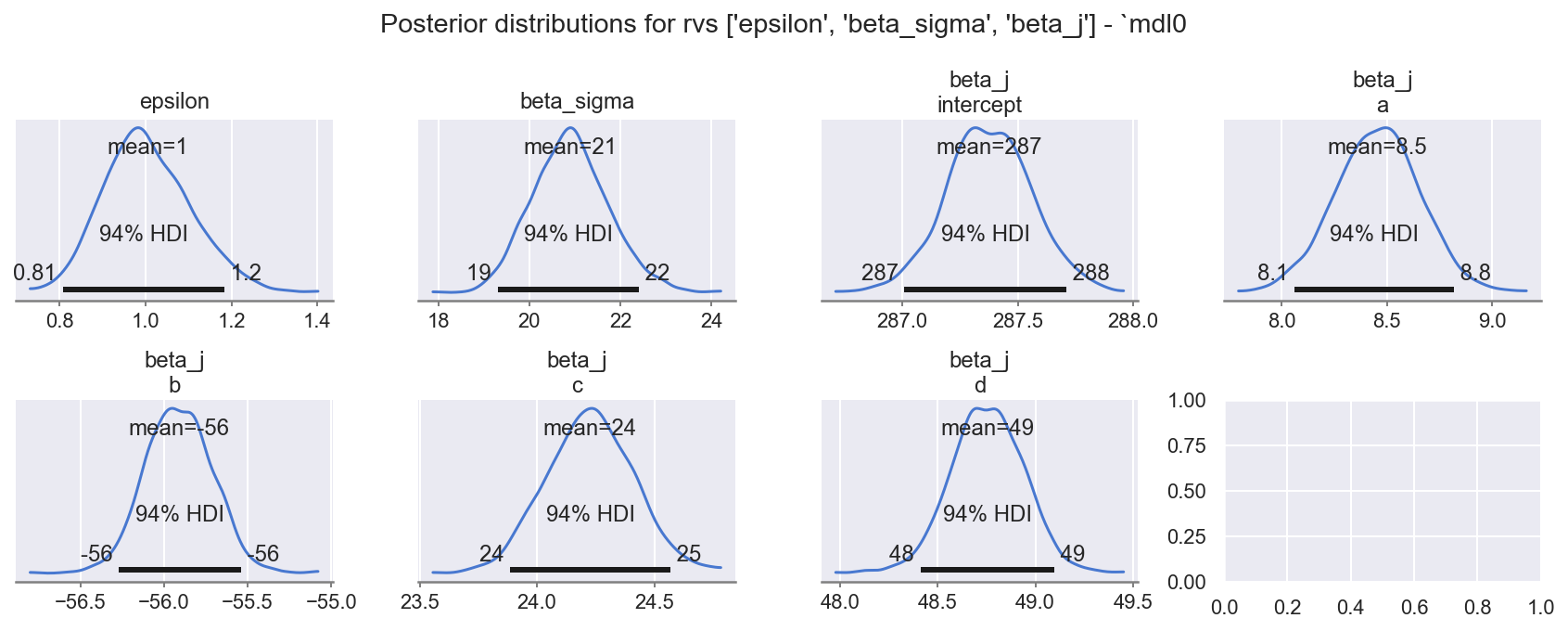
../_images/dd75904f7f776564d6d372412c8617ec6eae9f79941c1b88f4ca1bcde3cd5ede.png





观察


    

  • 模型系数 beta_sigma、beta_j: (levels)、epsilon 的后验都平滑且中心，如指定的
    • 





为了趣味性，绘制 beta_j 水平的森林图，以比较相对效应#






def plot_forest(
    idata: az.InferenceData, grp: str = "posterior", rvs: list = None, mdlnm="mdla"
) -> plt.Figure:
    """Convenience forestplot posterior (or prior) KDE"""

    n = sum([idata[grp][rv].shape[-1] for rv in rvs])
    f, axs = plt.subplots(1, 1, figsize=(12, 0.6 + 0.3 * n))
    _ = az.plot_forest(idata[grp], var_names=rvs, ax=axs, combined=True)
    _ = f.suptitle(f"Forestplot of {grp.title()} level values for `{rvs}` - `{mdlnm}`")
    _ = f.tight_layout()
    return f


f = plot_forest(id0, grp=GRP, rvs=["beta_j"], mdlnm="mdl0")








../_images/4e3cf64303121ea2b82ac392ec0f38970483c4dfd057e1cb14823268bf3a9645.png





观察


    

  • 非常紧凑且独特的后验分布
    • 

  • 这些水平大致对应于我们期望看到的，考虑到合成数据的创建
    • 











1.5 在 dfrawx_holdout 集上创建 PPC 预测#




1.5.1 将数据集替换为 dfrawx_holdout#






COORDS_F = deepcopy(COORDS)
COORDS_F["oid"] = dfrawx_holdout.index.values
mdl0.set_data("xj", dfrawx_holdout[FTS_XJ].values, coords=COORDS_F)













1.5.2 为 yhat 抽样 PPC#






with mdl0:
    id0_h = pm.sample_posterior_predictive(trace=id0.posterior, var_names=RVS_PPC, predictions=True)









Sampling: [yhat]















1.5.3 样本外：将预测的 yhat 与已知的真实值 y 进行比较#




从 PPC idata 中提取 yhat，并附加真实值（仅在它是 holdout 集时可用）#






dfraw_h_y = (
    az.extract(id0_h, group="predictions", var_names=["yhat"])
    .to_dataframe()
    .drop(["chain", "draw"], axis=1)
    .reset_index()
    .set_index(["oid"])
)
dfraw_h_y = pd.merge(dfraw_h_y, dfraw_holdout[["y"]], how="left", left_index=True, right_index=True)
dfraw_h_y.describe().T

















count
mean
std
min
25%
50%
75%
max






chain
20000.0
1.500000
1.118062
0.000000
0.750000
1.500000
2.250000
3.000000




draw
20000.0
249.500000
144.340887
0.000000
124.750000
249.500000
374.250000
499.000000




yhat
20000.0
278.561418
72.901021
177.512164
202.607237
271.000294
324.595923
442.744943




y
20000.0
278.797170
72.820296
181.932062
203.615652
271.797565
323.667882
439.462555














绘制后验 yhat 与已知的真实值 y 的关系图（仅在它是 holdout 集时可用）#






def plot_yhat_vs_y(
    df_h: pd.DataFrame, yhat: str = "yhat", y: str = "y", mdlnm: str = "mdla"
) -> plt.Figure:
    """Convenience plot forecast yhat with overplotted y from holdout set"""
    g = sns.catplot(x=yhat, y="oid", data=df_h.reset_index(), **KWS_BOX, height=4, aspect=3)
    _ = g.map(sns.scatterplot, y, "oid", **KWS_SCTR, zorder=100)
    _ = g.fig.suptitle(
        f"Out-of-sample: boxplots of posterior `{yhat}` with overplotted actual `{y}` values"
        + f" per observation `oid` (green dots) - `{mdlnm}`"
    )
    _ = g.tight_layout()
    return g.fig


_ = plot_yhat_vs_y(dfraw_h_y, mdlnm="mdl0")








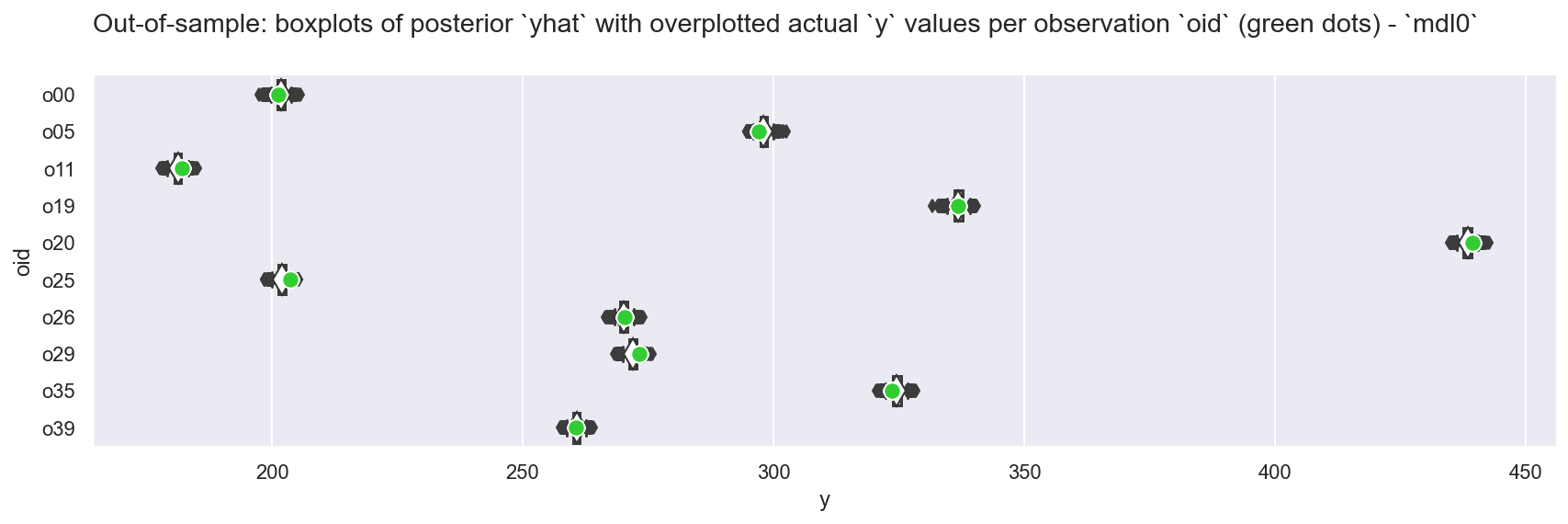
../_images/5c8b0315df9ab51478967c35a4d3edab43a56ba03548b3e13ed1badfc9b7f031.png





观察


    

  • 预测 yhat 看起来非常接近真实值 y，通常在 \(HDI_{94}\) 和 \(HDI_{50}\) 范围内
    • 

  • 正如我们所期望的那样，yhat 的分布也很有用：量化预测中的不确定性，并让我们据此做出更好的决策。
    • 

















2. ModelA：自动插补缺失值#


现在我们继续处理缺失值！


ModelA 是 Model0 的扩展，具有一个简单的线性子模型，该模型在具有缺失值的特征 \(k\) 的数据上具有分层先验


\[\begin{split} \begin{align} \sigma_{\beta} &\sim \text{InverseGamma}(11, 10) \\ \beta_{j} &\sim \text{Normal}(0, \sigma_{\beta}, \text{shape}=j) \\ \beta_{k} &\sim \text{Normal}(0, \sigma_{\beta}, \text{shape}=k) \\ \\ \mu_{k} &\sim \text{Normal}(0, 1, \text{shape}=k) \\ \mathbb{x}_{ik} &\sim \text{Normal}(\mu_{k}, 1, \text{shape}=(i,k)) \\ \\ \epsilon &\sim \text{InverseGamma}(11, 10) \\ \hat{y_{i}} &\sim \text{Normal}(\mu=\beta_{j}^{T}\mathbb{x}_{ij} + \beta_{k}^{T}\mathbb{x}_{ik}, \sigma=\epsilon) \\ \end{align} \end{split}\]


其中


    

  • 观测值 \(i\) 包含具有完整值的数值特征 \(j\)，以及包含缺失值的数值特征 \(k\)
    • 

  • 为了本示例的目的，我们假设将来特征 \(j\) 将始终是完整的，并且缺失值可能发生在 \(k\) 中，并据此设计模型
    • 

  • 这是一个很大的假设，因为理论上缺失值可能发生在任何特征中，但我们扩展了示例以假设我们始终要求特征 \(j\) 是完整的
    • 

  • 我们将数据 \(\mathbb{x}_{ik}\) 视为随机变量，并“观测”非缺失值。
    • 

  • 我们将假设缺失数据值具有均值 \(\mu_{k}\) 的正态分布 - 这是合理的，因为我们对 dfx 数据进行了 z 分数标准化，并且可以预期围绕 0 具有一定的中心性。当然，\(\mathbb{x}_{ik}\) 中数据的实际分布可能高度偏斜，因此正态分布不一定是最佳选择，但这是一个好的开始
    • 

  • 我们的目标是 \(\hat{y_{i}}\)，这里是 y，具有线性子模型 \(\beta_{j}^{T}\mathbb{x}_{ij}\) 和 \(\beta_{k}^{T}\mathbb{x}_{ik}\)，用于回归到这些特征上
    • 



实现说明


在 pymc 中有几种处理缺失值的方法。在 ModelA 中，我们使用了 pymc “自动插补”，我们指示模型“观测”包含缺失值的特征的数据集 dfx_train[FTS_XK] 的一部分，并且 pymc 构建过程将非常友好地处理缺失值并在元素级别提供自动插补。


这在模型规范中既方便又简洁，但确实需要进一步操作模型和 idata 才能创建样本外预测，详见 \(\S 2.5\)


特别是


    

  • 自动插补例程将为我们创建扁平化的 xk_observed 和 xk_unobserved RV，基于 xk 的（单个）指定分布，以及具有正确维度的 xk 的最终 Deterministic
    • 

  • 但是，一个重要的限制是，目前，pm.Data 不能包含 NaNs（或 masked_array），因此我们不能使用通常的工作流程 mdl.set_data() 将样本内数据集替换为样本外数据集来进行预测！
    • 

  • 例如，以下两种构造都不可能
    

      

    1. 无法将 NaNs 插入到 pm.Data 中
      

      xk_data = pm.Data('xk_data', dfx_train[FTS_XK].values, dims=('oid', 'xk_nm'))
xk_ma = np.ma.masked_array(xk_data, mask=np.isnan(xk_data.values))

      

      

      2. 

    2. 无法将 masked_array 插入到 pm.Data 中
      

      xk_ma = pm.Data('xk_ma', np.ma.masked_array(dfx_train[FTS_XK].values, mask=np.isnan(dfx_train[FTS_XK].values)))

      

      

      3. 

    

    • 

  • 另请参阅 pymc issue #6626 和 拟议的新功能 #7204 中的进一步讨论
    • 

  • 最后，请注意，一些早期的自动插补示例涉及创建 np.ma.masked_array 并将其传递到观测到的 RV 中。截至 2024 年 12 月，这似乎不再必要，我们可以直接传入 dataframe
    

    例如，这个
    

    xk_ma = np.ma.masked_array(dfx_train[FTS_XK].values, mask=np.isnan(dfx_train[FTS_XK].values))
xk = pm.Normal("xk", mu=xk_mu, sigma=1.0, observed=xk_ma, dims=("oid", "xk_nm"))

    

    

    现在可以简单地表述为
    

    xk = pm.Normal("xk", mu=xk_mu, sigma=1.0, observed=dfx_train[FTS_XK].values, dims=("oid", "xk_nm"))

    

    

    • 





2.1 构建模型对象#






ft_y = "y"
FTS_XJ = ["intercept", "a", "b"]
FTS_XK = ["c", "d"]
COORDS = dict(
    xj_nm=FTS_XJ,  # names of the features j
    xk_nm=FTS_XK,  # names of the features k
    oid=dfx_train.index.values,  # these are the observation_ids
)

with pm.Model(coords=COORDS) as mdla:
    # 0. create (Mutable)Data containers for obs (Y, X)
    y = pm.Data("y", dfx_train[ft_y].values, dims="oid")
    xj = pm.Data("xj", dfx_train[FTS_XJ].values, dims=("oid", "xj_nm"))

    # 1. create auto-imputing likelihood for missing data values
    # NOTE: there's no way to put a nan-containing array (nor a np.masked_array)
    # into a pm.Data, so dfx_train[FTS_XK].values has to go in directly
    xk_mu = pm.Normal("xk_mu", mu=0.0, sigma=1, dims="xk_nm")
    xk = pm.Normal(
        "xk", mu=xk_mu, sigma=1.0, observed=dfx_train[FTS_XK].values, dims=("oid", "xk_nm")
    )

    # 2. define priors for contiguous and auto-imputed data
    b_s = pm.Gamma("beta_sigma", alpha=10, beta=10)  # E ~ 1
    bj = pm.Normal("beta_j", mu=0, sigma=b_s, dims="xj_nm")
    bk = pm.Normal("beta_k", mu=0, sigma=b_s, dims="xk_nm")

    # 4. define evidence
    epsilon = pm.Gamma("epsilon", alpha=50, beta=50)  # encourage E ~ 1
    lm = pt.dot(xj, bj.T) + pt.dot(xk, bk.T)
    _ = pm.Normal("yhat", mu=lm, sigma=epsilon, observed=y, dims="oid")

RVS_PPC = ["yhat"]
RVS_PRIOR = ["epsilon", "beta_sigma", "beta_j", "beta_k"]
RVS_K = ["xk_mu"]
RVS_XK = ["xk"]
RVS_XK_UNOBS = ["xk_unobserved"]









/Users/jon/miniforge/envs/oreum_survival/lib/python3.11/site-packages/pymc/model/core.py:1366: ImputationWarning: Data in xk contains missing values and will be automatically imputed from the sampling distribution.
  warnings.warn(impute_message, ImputationWarning)











验证构建的模型结构是否符合我们的意图，并验证参数化#






display(pm.model_to_graphviz(mdla, formatting="plain"))
display(dict(unobserved=mdla.unobserved_RVs, observed=mdla.observed_RVs))
assert_no_rvs(mdla.logp())
mdla.debug(fn="logp", verbose=True)
mdla.debug(fn="random", verbose=True)








../_images/fe97b2f81d1a28eeb414de5b105eaeab46873091f107ff08111f2dbc6978dbc1.svg

{'unobserved': [xk_mu ~ Normal(0, 1),
  xk_unobserved,
  beta_sigma ~ Gamma(10, f()),
  beta_j ~ Normal(0, beta_sigma),
  beta_k ~ Normal(0, beta_sigma),
  epsilon ~ Gamma(50, f()),
  xk ~ Unknown(f(xk_observed, xk_unobserved))],
 'observed': [xk_observed,
  yhat ~ Normal(f(beta_j, beta_k, xk_observed, xk_unobserved), epsilon)]}





point={'xk_mu': array([0., 0.]), 'xk_unobserved': array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
       0., 0., 0., 0., 0., 0., 0.]), 'beta_sigma_log__': array(0.), 'beta_j': array([0., 0., 0.]), 'beta_k': array([0., 0.]), 'epsilon_log__': array(0.)}

No problems found
point={'xk_mu': array([0., 0.]), 'xk_unobserved': array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
       0., 0., 0., 0., 0., 0., 0.]), 'beta_sigma_log__': array(0.), 'beta_j': array([0., 0., 0.]), 'beta_k': array([0., 0.]), 'epsilon_log__': array(0.)}

No problems found









观察


    

  • 我们有两个新的自动创建的节点 xk_observed（观测数据）和 xk_unobserved（未观测到的自由 RV），它们各自具有与我们为 xk 指定的相同的分布
    • 

  • 原始的 xk 现在由一个新的 Deterministic 节点表示，该节点具有这两个节点（连接和重塑）的函数
    • 

  • 特别注意 xk_unobserved 具有新的扁平化形状，其长度等于相关特征 \(k\) 中 NaN 的计数，并且它丢失了我们分配给 xk 的 dims。这是一个目前无益的限制，这意味着我们必须进行一些索引才能稍后恢复 PPC 值
    • 









2.2 抽样先验预测，查看诊断#






GRP = "prior"
kws = dict(samples=2000, return_inferencedata=True, random_seed=42)
with mdla:
    ida = pm.sample_prior_predictive(
        var_names=RVS_PPC + RVS_PRIOR + RVS_K + RVS_XK + RVS_XK_UNOBS, **kws
    )









Sampling: [beta_j, beta_k, beta_sigma, epsilon, xk_mu, xk_observed, xk_unobserved, yhat]











2.2.1 样本内先验 PPC（回顾性检查）#






f = plot_ppc_retrodictive(ida, grp=GRP, rvs=["yhat"], mdlnm="mdla", ynm="y")








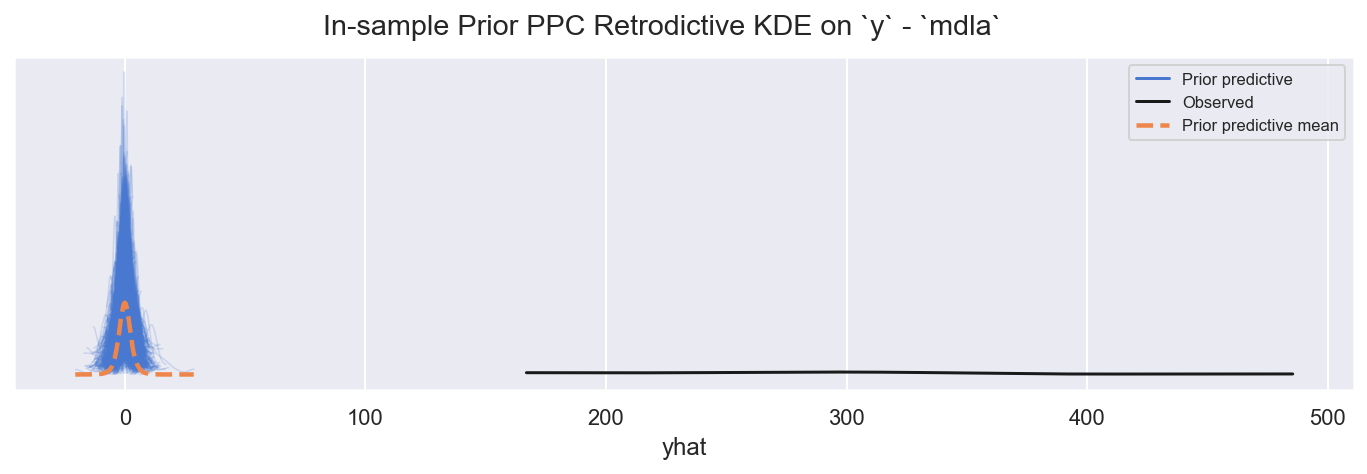
../_images/50fab962c684a8423c651f9f8bde76fc42a7e22e941156c46bfa1919bdfe7e03.png





观察


    

  • 值是错误的，正如预期的那样，但范围是合理的
    • 







2.2.2 快速查看选定的先验#




系数等#






f = plot_krushke(ida, GRP, rvs=RVS_PRIOR, mdlnm="mdla", n=1 + 1 + 3 + 2, nrows=2)








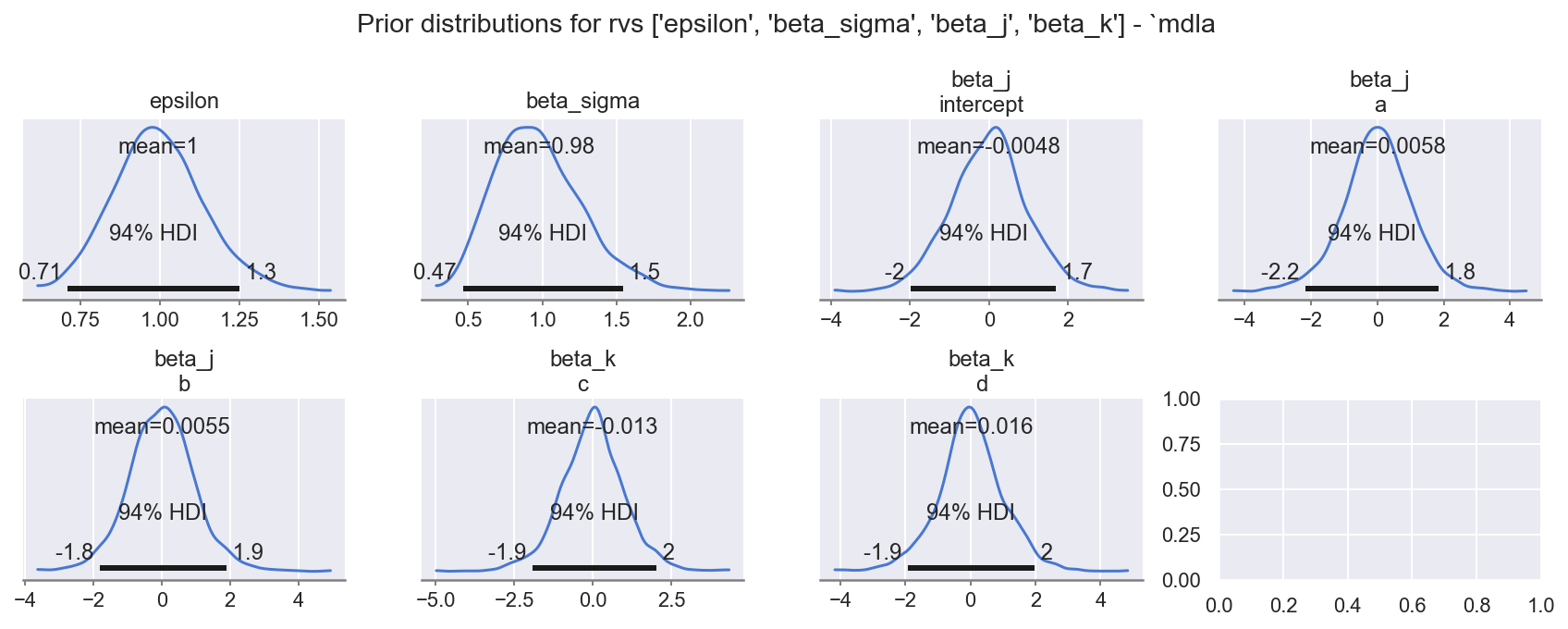
../_images/9c668d4adbb11cf79b5f88cf0443c8e961f3e2f6ca6dd6709131fb9833478e3a.png





观察


    

  • 模型先验 beta_sigma、beta_j: (levels)、beta_k: (levels)、epsilon 都具有合理的先验范围，如指定的
    • 







缺失数据 \(\mathbb{x}_{k}\) 的分层值 \(\mu_{k}\)#






f = plot_krushke(ida, GRP, RVS_K, mdlnm="mdla", n=2, nrows=1)








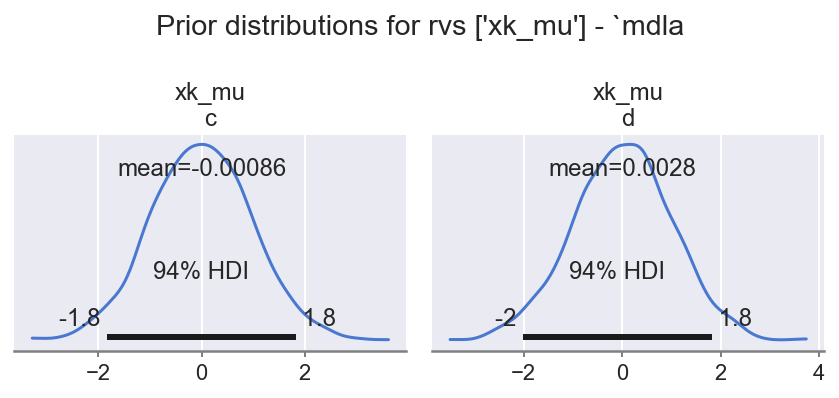
../_images/25c7b0a8fd4a63ee34fb8576746da10c5ad0c2de2fb938b99175555042b067b8.png





观察


    

  • 数据插补分层先验 xk_mu (levels) 具有合理的先验范围，如指定
    • 







\(x_{k}\) 中缺失数据的值 (xk_unobserved)#






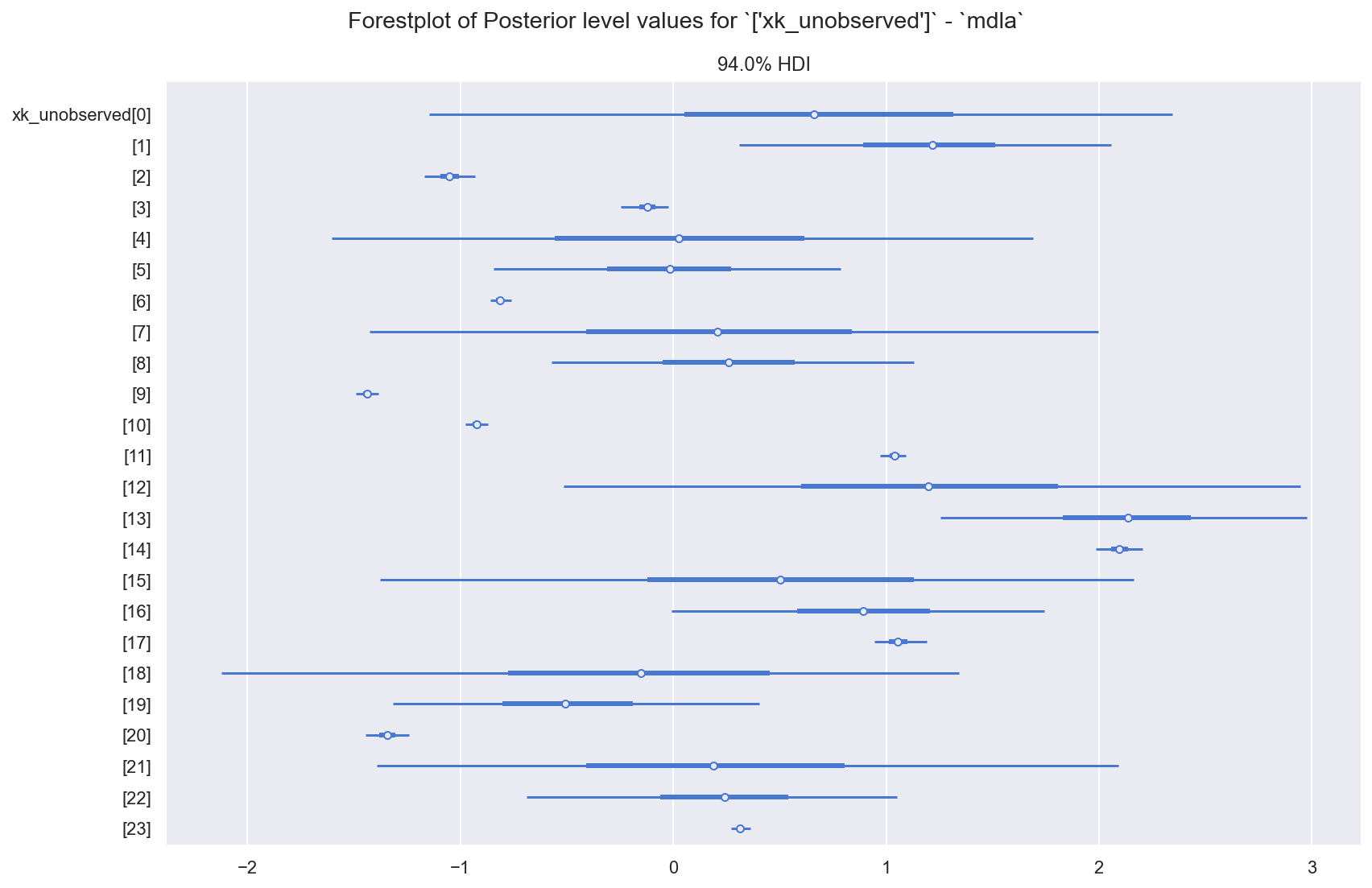
f = plot_forest(ida, GRP, RVS_XK_UNOBS, "mdla")








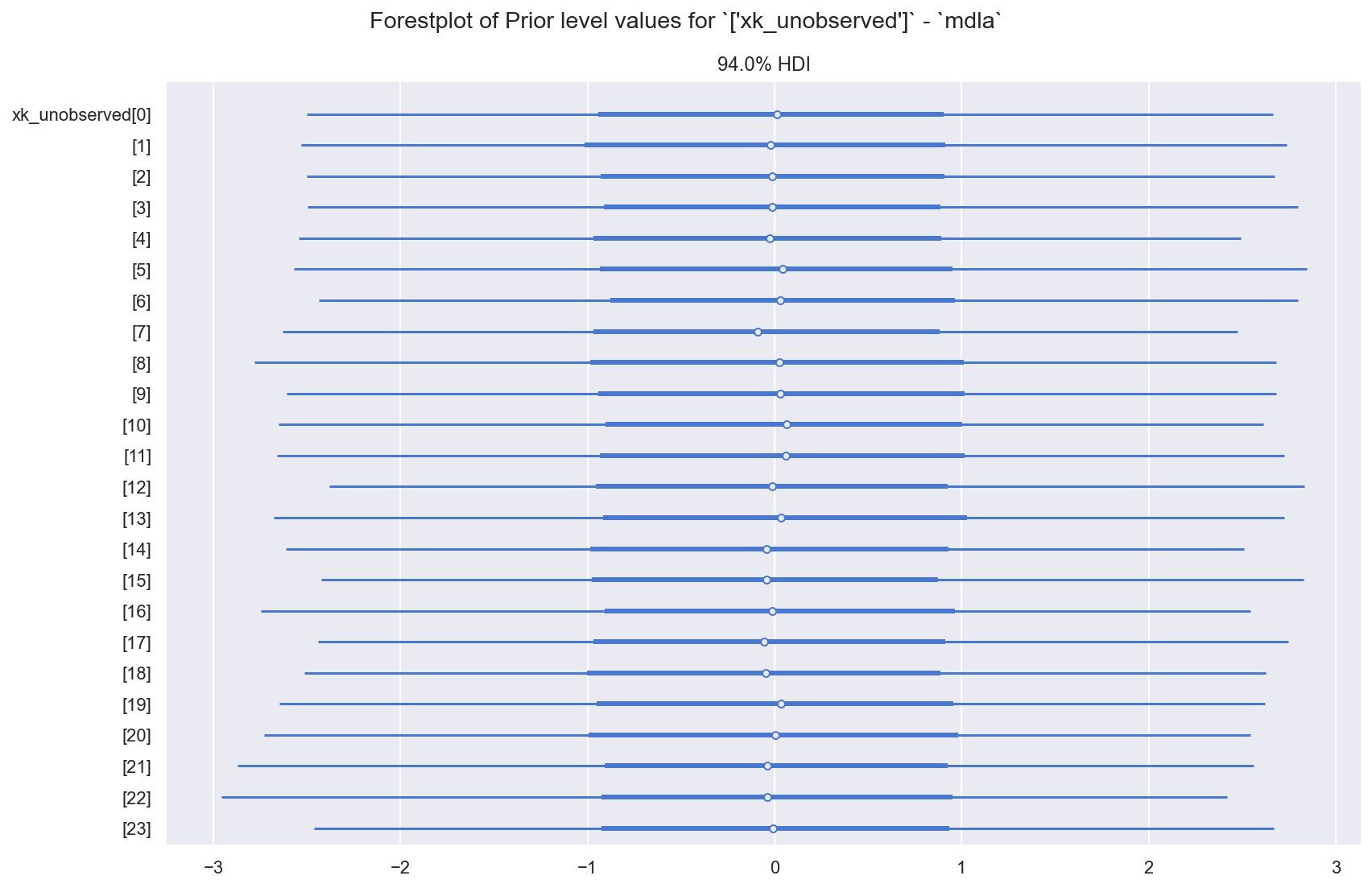
../_images/590489a6aa89cbf0a7c537a5a310530461281136e49db413b8670d2836630616.png





观察


    

  • 自动插补数据 xk_unobserved 的先验值当然都相同，并且在合理的指定范围内
    • 

  • 再次注意，这是一个扁平化的 RV，其长度等于特征 c 和 d 中 NaN 的计数
    • 











2.3 样本后验，查看诊断结果#




2.3.1 样本后验和 PPC#






GRP = "posterior"
with mdla:
    ida.extend(pm.sample(**SAMPLE_KWS), join="right")
    ida.extend(
        pm.sample_posterior_predictive(trace=ida.posterior, var_names=RVS_PPC),
        join="right",
    )









Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [xk_mu, xk_unobserved, beta_sigma, beta_j, beta_k, epsilon]







Sampling 4 chains for 3_000 tune and 500 draw iterations (12_000 + 2_000 draws total) took 181 seconds.
Sampling: [xk_observed, yhat]















2.3.2 查看轨迹图#






f = plot_traces_and_display_summary(ida, rvs=RVS_PRIOR + RVS_K, mdlnm="mdla", energy=True)

















mean
sd
hdi_3%
hdi_97%
mcse_mean
mcse_sd
ess_bulk
ess_tail
r_hat






epsilon
1.060
0.121
0.834
1.284
0.003
0.002
1473.0
1542.0
1.0




beta_sigma
20.614
0.830
19.026
22.100
0.015
0.011
3011.0
1344.0
1.0




beta_j[intercept]
281.014
0.298
280.466
281.596
0.008
0.005
1578.0
1491.0
1.0




beta_j[a]
8.567
0.370
7.883
9.285
0.011
0.008
1181.0
1416.0
1.0




beta_j[b]
-55.839
0.354
-56.470
-55.147
0.009
0.007
1476.0
1375.0
1.0




beta_k[c]
23.532
0.355
22.854
24.207
0.012
0.008
937.0
1111.0
1.0




beta_k[d]
47.316
0.310
46.749
47.879
0.007
0.005
1968.0
1821.0
1.0




xk_mu[c]
0.108
0.204
-0.253
0.498
0.005
0.004
1649.0
1434.0
1.0




xk_mu[d]
0.081
0.187
-0.278
0.415
0.004
0.004
2204.0
1478.0
1.0






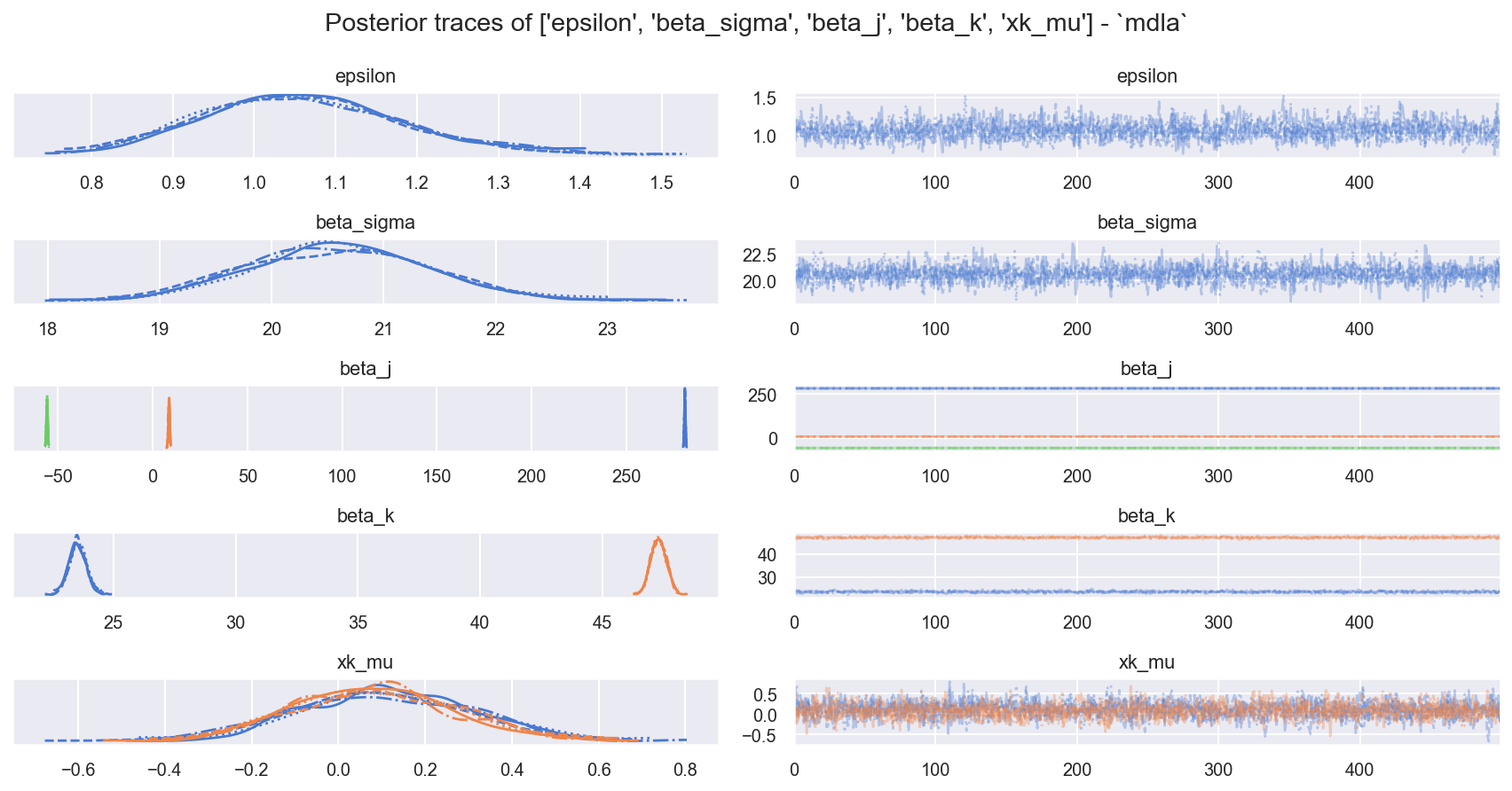
../_images/1eb5bf02983f7d940543a8ea37e75b2004f8a9fe35cc1e801d10a4ecb4522c19.png
../_images/07721209e8eaec9bba4aacf481ca42776603f1c3a38576334d461588113b58d7.png





观察


    

  • 样本混合良好且行为良好：ess_bulk 良好，r_hat 良好
    • 

  • 边际能量 | 能量跃迁看起来有点不匹配：虽然 E-BFMI >> 0.3 (并且 显然是合理的)，但请注意这些值低于 Model0 的值。这是缺失数据的影响。
    • 







2.3.3 样本内后验 PPC（回顾性检查）#






f = plot_ppc_retrodictive(ida, grp=GRP, rvs=["yhat"], mdlnm="mdla", ynm="y")








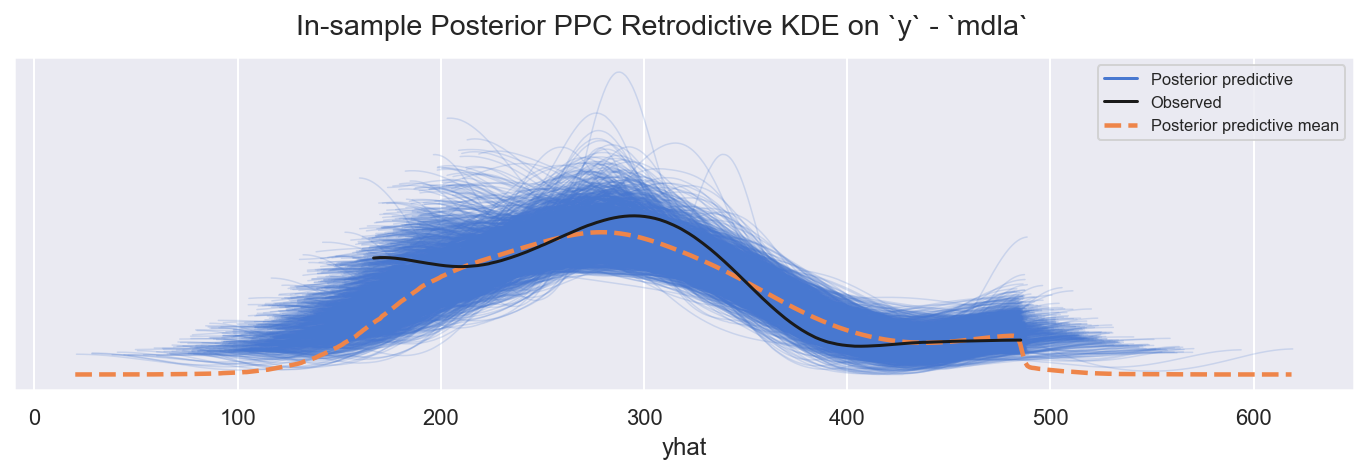
../_images/3c5076436fe9924ef58fd28195ad744e19500b08d9b4b335bcfcca4665367c1f.png





观察


    

  • 样本内 PPC yhat 对观测到的 y 的追踪效果尚可：可能稍微过度分散，或许具有更肥尾分布的似然函数会更合适（例如 StudentT）
    • 







2.3.4 样本内 PPC LOO-PIT#






f = plot_loo_pit(ida, "mdla")








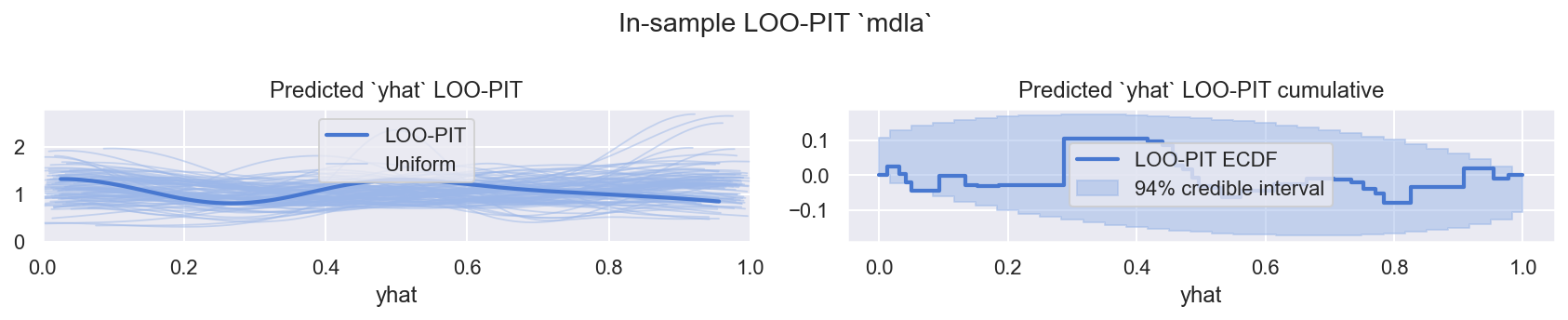
../_images/b19802136881f9c55e7eedf360bf77c0704ccb0acb3520ab694ad851850eba00.png





观察


    

  • LOO-PIT 看起来不错，再次稍微过度分散，但对于使用来说可以接受
    • 







2.3.5 比较对数似然与其它模型#






def plot_compare_log_likelihood(idatad: dict, yhat: str = "yhat") -> plt.Figure:
    """Convenience to plot comparison for a dict of idatas"""
    dfcomp = az.compare(idatad, var_name=yhat, ic="loo", method="stacking", scale="log")
    f, axs = plt.subplots(1, 1, figsize=(12, 2 + 0.3 * len(idatad)))
    _ = az.plot_compare(dfcomp, ax=axs, title=False, textsize=10, legend=False)
    _ = f.suptitle(
        "Model Performance Comparison: ELPD via In-Sample LOO-PIT: `"
        + "` vs `".join(list(idatad.keys()))
        + "`\n(higher & narrower is better)"
    )
    _ = f.tight_layout()
    display(dfcomp)
    return f


f = plot_compare_log_likelihood(idatad={"mdl0": id0, "mdla": ida})









/Users/jon/miniforge/envs/oreum_survival/lib/python3.11/site-packages/arviz/stats/stats.py:795: UserWarning: Estimated shape parameter of Pareto distribution is greater than 0.70 for one or more samples. You should consider using a more robust model, this is because importance sampling is less likely to work well if the marginal posterior and LOO posterior are very different. This is more likely to happen with a non-robust model and highly influential observations.
  warnings.warn(
/Users/jon/miniforge/envs/oreum_survival/lib/python3.11/site-packages/arviz/stats/stats.py:795: UserWarning: Estimated shape parameter of Pareto distribution is greater than 0.70 for one or more samples. You should consider using a more robust model, this is because importance sampling is less likely to work well if the marginal posterior and LOO posterior are very different. This is more likely to happen with a non-robust model and highly influential observations.
  warnings.warn(













rank
elpd_loo
p_loo
elpd_diff
weight
se
dse
warning
scale






mdl0
0
-45.658024
4.860332
0.000000
1.0
3.525409
0.000000
True
log




mdla
1
-59.472497
18.295350
13.814473
0.0
3.059752
3.259371
True
log






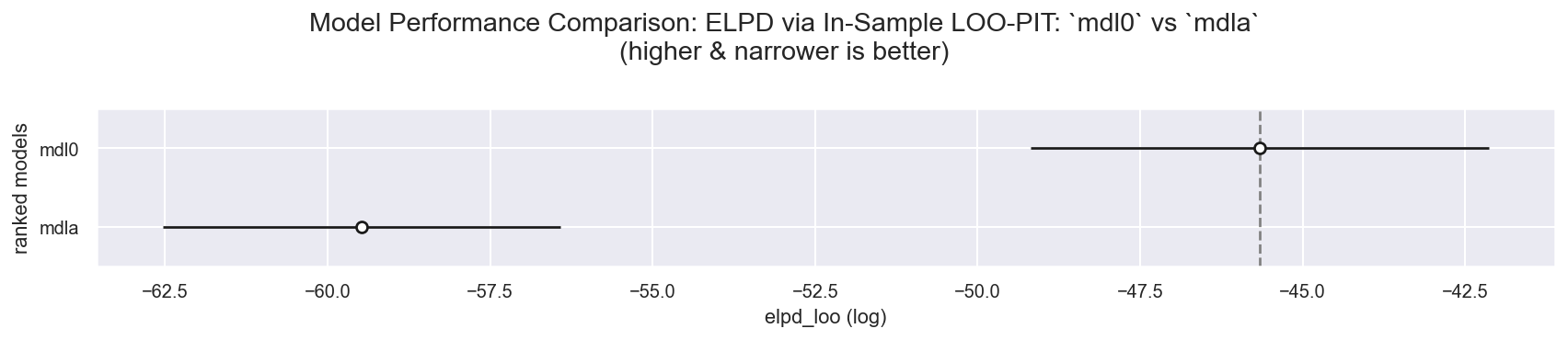
../_images/60640fb7cdf27dbf93578d71c24fcc9e08a3e1c78529e57fb011f066759b5e26.png





观察


    

  • 非常有趣：我们的自动插补 ModelA 与 Model0 相比，效果当然较差，后者受益于完整的数据集（没有缺失值），但也没有差太多，而且（当然）我们已经能够处理样本内数据中的缺失值！
    • 









2.4 评估后验参数#




2.4.1 系数等等#






f = plot_krushke(ida, GRP, RVS_PRIOR, mdlnm="mdla", n=1 + 1 + 3 + 2, nrows=2)








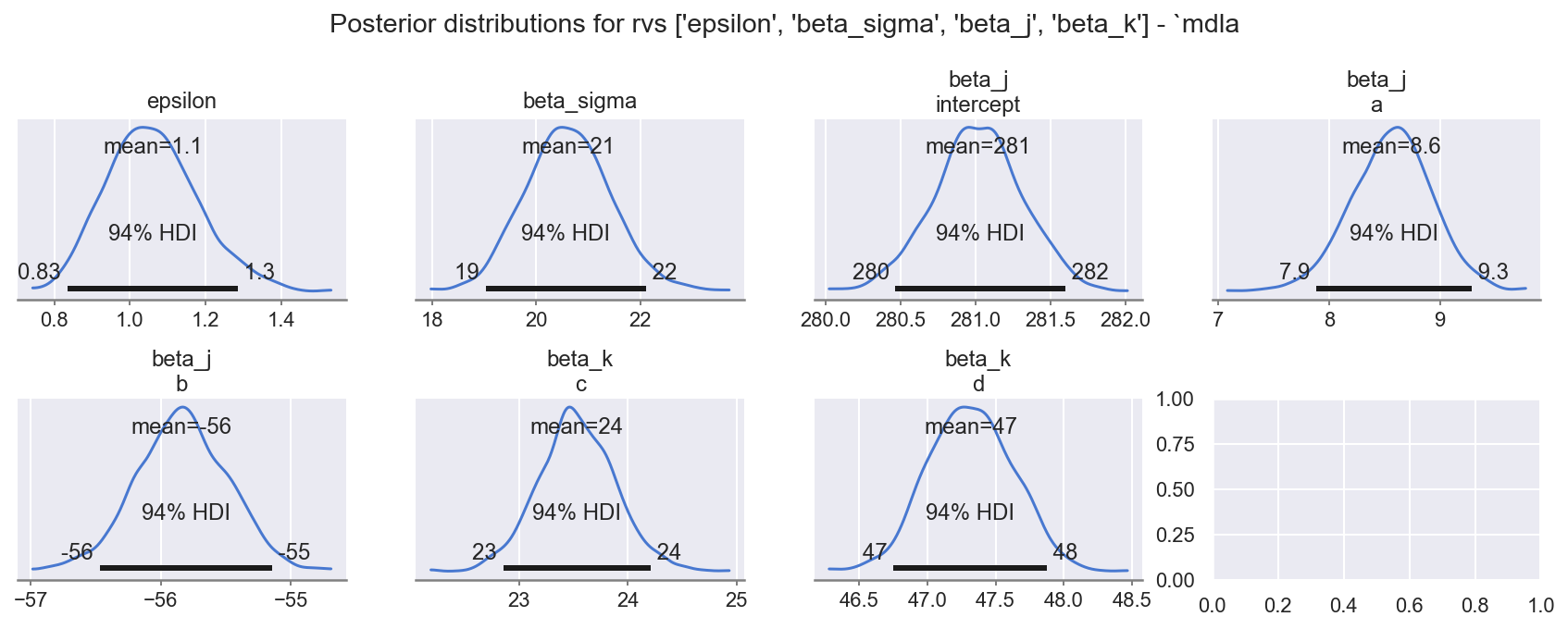
../_images/c9ac1748f424147305e05134d02fd9e7637dd04396bfb7a218e3db7ff3be9d00.png





观察


    

  • 模型系数 beta_sigma、beta_j: (levels)、beta_k: (levels)、epsilon 都具有合理的先验范围，如指定
    • 





为了有趣起见，用森林图绘制 beta_j 和 beta_k 水平，以比较相对效应#






f = plot_forest(ida, grp=GRP, rvs=["beta_j", "beta_k"], mdlnm="mdla")








../_images/94f2e5a5293616592d3c1f82048d0cae6e1103769ce329fdf449eec771f3984a.png





观察


    

  • 非常紧凑且独特的后验分布
    • 

  • 大致将此图与上面 \(\S1.4\) 中 Model0 的相同图进行比较
    • 









2.4.2 缺失数据 \(\mathbb{x}_{k}\) 的分层值#






f = plot_krushke(ida, GRP, RVS_K, mdlnm="mdla", n=2, nrows=1)








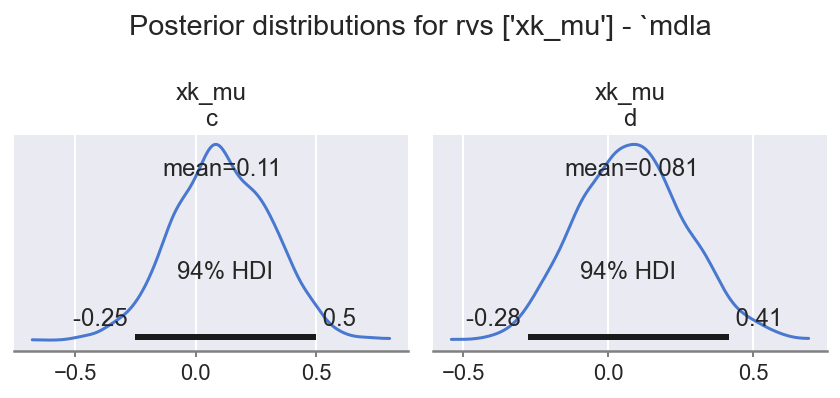
../_images/85fb9dbcd5483b130273ba893c6a8d0671d7ce1944d25b2921b50dc53643b740.png





观察


    

  • 数据插补分层先验没有远离 0，这是合理的，因为缺失是随机的
    • 

  • 然而，它们确实显示出细微的差异，这令人鼓舞，表明它们正在捕捉由于 REFVALS_X_MU 导致的主要原始数据中的固有差异
    • 







2.4.3 查看 \(x_{k}\) 中缺失数据的自动插补值 (xk_unobserved)#






f = plot_forest(ida, GRP, RVS_XK_UNOBS, "mdla")








../_images/99ae577e670e80bb664fd322c8b4db1984542074a294e337dffa44c6d4e6623d.png





观察


    

  • 我们已经使用我们的模型自动插补了 xk_unobserved 中的缺失值，并量化了不确定性
    • 

  • 通过适当的模型后索引，我们可以将这些用作缺失数据真实值的后验预测
    • 

  • 接下来我们将展示索引以及与合成已知值的特殊比较
    • 







2.4.4 样本内：将自动插补值 \(x_{k}\) xk_unobserved 与已知的真实值进行比较#


注意


    

  • 我们只能进行比较，因为它是一个合成数据集，我们在上面的 dfraw 中创建了这些完整（全部）值
    • 





创建索引以从 xk 中提取适当的观测值，因为 xk_unobserved 没有正确的 dims 索引#






dfx_train_xk = (
    dfx_train.loc[:, ["c", "d"]]
    .reset_index()
    .melt(id_vars=["oid"], var_name="xk_nm", value_name="xk")
    .set_index(["oid", "xk_nm"])
)
idx_xk_unobs = dfx_train_xk.loc[dfx_train_xk["xk"].isnull()].index











从 PPC idata 中提取，通过索引隔离，转换回数据域#






df_mns_sdevs = pd.DataFrame({"mn": MNS, "sdev": SDEVS}, index=["a", "b", "c", "d"])
df_mns_sdevs.index.name = "xk_nm"

df_xk_unobs = (
    az.extract(ida, group=GRP, var_names=RVS_XK)
    .to_dataframe()
    .drop(["chain", "draw"], axis=1)
    .reset_index()
    .set_index(["oid", "xk_nm"])
    .loc[idx_xk_unobs]
)
df_xk_unobs = (
    pd.merge(df_xk_unobs.reset_index(), df_mns_sdevs.reset_index(), how="left", on=["xk_nm"])
    .set_index(["oid", "xk_nm"])
    .sort_index()
)
df_xk_unobs["xk_unobs_ppc_data_domain"] = (df_xk_unobs["xk"] * df_xk_unobs["sdev"]) + df_xk_unobs[
    "mn"
]
df_xk_unobs.head()


















chain
draw
xk
mn
sdev
xk_unobs_ppc_data_domain




oid
xk_nm












o03
c
0
0
0.331594
9.663899
0.795819
9.927788




c
0
1
0.263749
9.663899
0.795819
9.873796




c
0
2
0.673567
9.663899
0.795819
10.199937




c
0
3
0.348009
9.663899
0.795819
9.940851




c
0
4
1.751358
9.663899
0.795819
11.057664














附加真实值（仅在合成数据中可用）#






dfraw_xk = (
    dfraw[["c", "d"]]
    .reset_index()
    .melt(id_vars=["oid"], var_name="xk_nm", value_name="xk_unobs_true_val")
    .set_index(["oid", "xk_nm"])
)

df_xk_unobs = pd.merge(
    df_xk_unobs, dfraw_xk.loc[idx_xk_unobs], how="left", left_index=True, right_index=True
)
df_xk_unobs.head()


















chain
draw
xk
mn
sdev
xk_unobs_ppc_data_domain
xk_unobs_true_val




oid
xk_nm













o03
c
0
0
0.331594
9.663899
0.795819
9.927788
9.618262




c
0
1
0.263749
9.663899
0.795819
9.873796
9.618262




c
0
2
0.673567
9.663899
0.795819
10.199937
9.618262




c
0
3
0.348009
9.663899
0.795819
9.940851
9.618262




c
0
4
1.751358
9.663899
0.795819
11.057664
9.618262














强制用于绘图的 dtypes#






df_xk_unobs = df_xk_unobs.reset_index()
df_xk_unobs["oid"] = pd.Categorical(df_xk_unobs["oid"])
df_xk_unobs["xk_nm"] = pd.Categorical(df_xk_unobs["xk_nm"])
df_xk_unobs.set_index(["oid", "xk_nm"], inplace=True)
df_xk_unobs.head()


















chain
draw
xk
mn
sdev
xk_unobs_ppc_data_domain
xk_unobs_true_val




oid
xk_nm













o03
c
0
0
0.331594
9.663899
0.795819
9.927788
9.618262




c
0
1
0.263749
9.663899
0.795819
9.873796
9.618262




c
0
2
0.673567
9.663899
0.795819
10.199937
9.618262




c
0
3
0.348009
9.663899
0.795819
9.940851
9.618262




c
0
4
1.751358
9.663899
0.795819
11.057664
9.618262














绘制后验 xk_unobserved 与已知的真实值（仅在此合成示例中可能）#






def plot_xkhat_vs_xk(
    df_xk: pd.DataFrame,
    xkhat: str = "xk_unobs_ppc_data_domain",
    x: str = "xk_unobs_true_val",
    mdlnm: str = "mdla",
    in_samp: bool = True,
) -> plt.Figure:
    """Convenience plot forecast xkhat with overplotted x true val (from synthetic set)"""
    g = sns.catplot(
        x=xkhat,
        y="oid",
        col="xk_nm",
        data=df_xk.reset_index(),
        **KWS_BOX,
        height=5,
        aspect=1.5,
        sharex=False,
    )
    _ = g.map(sns.scatterplot, x, "oid", **KWS_SCTR, zorder=100)
    s = "In-sample" if in_samp else "Out-of-sample"
    _ = g.fig.suptitle(
        f"{s}: boxplots of posterior `{xkhat}` with overplotted actual `{x}` values"
        + f" per observation `oid` (green dots) - `{mdlnm}`"
    )
    _ = g.tight_layout()
    return g.fig


_ = plot_xkhat_vs_xk(df_xk_unobs, mdlnm="mdla")








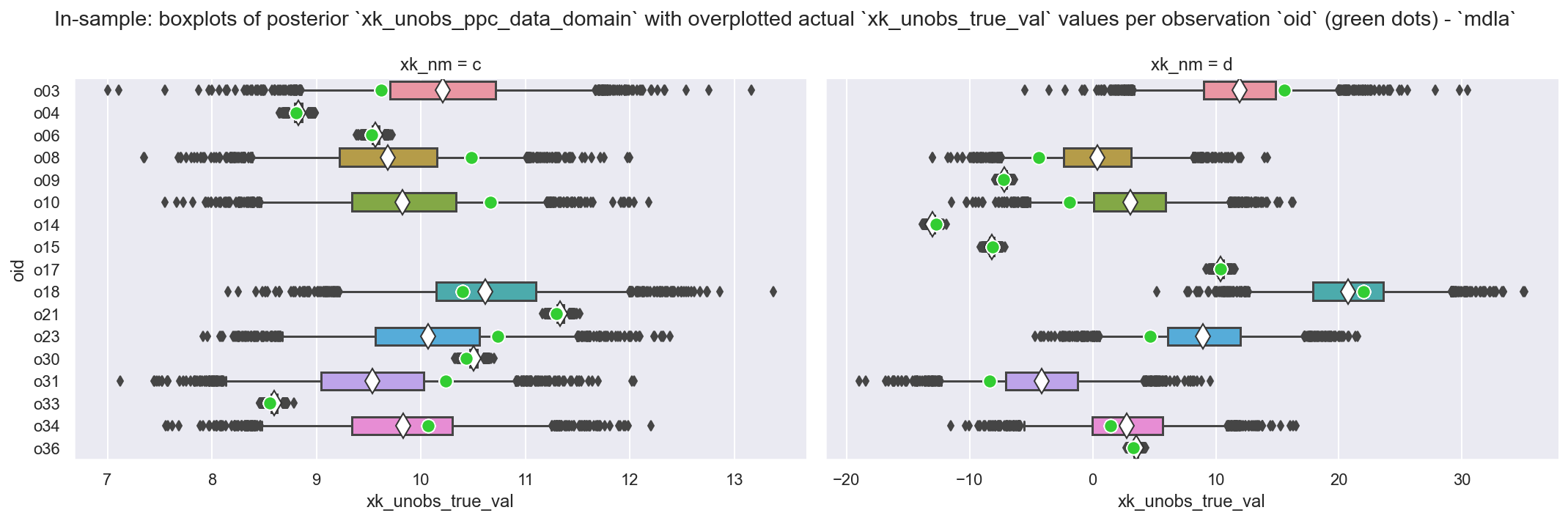
../_images/e0404a045e4de6eb19ad813589fba58a91305d623eb24d1c3c8cc79be4680d2a.png





观察


    

  • 这是我们针对样本内数据集 dfx_train 上的缺失数据的自动插补后验分布（箱线图）
    • 

  • 这些是我们模型构建的（非常有用的！）副作用，让我们能够填补 df_train 中 c 和 d 的真实世界缺失值
    • 

  • 一些观测值（例如 o03）在 c 和 d 中都有缺失值，另一些（例如 o04）只有一个
    • 

  • 我们还叠加绘制了来自合成数据集的已知真实值：并且对于所有值而言，匹配都很接近：通常都在 HDI94 范围内
    • 

  • 在观测值具有多个缺失值的情况下（例如 o00、o8、o10 是很好的例子），我们看到了缺乏可识别性的可能性：这是数据和模型架构的一个有趣且不易避免的副作用，在现实世界中，我们可能会寻求通过移除观测值或特征来缓解这种情况。
    • 













2.5 在 dfx_holdout 集上创建 PPC 预测#


实现说明


以下过程有点像黑客手法


    

  1. 首先：我们需要完全使用 dfx_holdout 重新指定模型，因为（如上文 \(\S 2.1\) 构建模型对象 中所述）我们不能将 NaNs （或 masked_array）放入 pm.Data 中。如果我们可以这样做，那么我们可以简单地使用 pm.set_data()，但我们不能，所以我们不这样做。
    2. 

  2. 其次：对 xk_unobserved 进行 Sample_ppc，因为这是计算 yhat 的先决条件，并且我们无法在 sample_posterior_predictive 中指定条件顺序
    3. 

  3. 第三：使用这些预测来对 yhat 进行 sample_ppc
    4. 



现实情况


    

  • 对于我们想要预测新传入数据的真实世界场景来说，此过程并非最佳，因为我们必须在步骤 1 中不断重新指定模型（这为简单的人为错误创造了机会），并且步骤 2 和 3 涉及对 idata 对象的操作，这很麻烦
    • 

  • 它仍然应该适用于相对较慢的（可能批量处理的）预测过程，其量级为秒，而不是亚秒级响应时间
    • 

  • 无论如何，如果要部署它来处理亚秒级输入流，那么纠正这种情况的更简单方法是确保上游进行适当的数据验证/清理，并要求没有缺失数据！
    • 





2.5.1 首先：完全重建模型，使用 dfx_holdout#






COORDS_H = deepcopy(COORDS)
COORDS_H["oid"] = dfx_holdout.index.values

with pm.Model(coords=COORDS_H) as mdla_h:
    # 0. create (Mutable)Data containers for obs (Y, X)
    # NOTE: You could use mdla.set_data to change these pm.Data containers...
    y = pm.Data("y", dfx_holdout[ft_y].values, dims="oid")
    xj = pm.Data("xj", dfx_holdout[FTS_XJ].values, dims=("oid", "xj_nm"))

    # same code as above for mdla
    # 1. create auto-imputing likelihood for missing data values
    # NOTE: there's no way to put a nan-containing array (nor a np.masked_array)
    # into a pm.Data, so dfx_holdout[FTS_XK].values has to go in directly
    xk_mu = pm.Normal("xk_mu", mu=0.0, sigma=1, dims="xk_nm")
    xk = pm.Normal(
        "xk", mu=xk_mu, sigma=1.0, observed=dfx_holdout[FTS_XK].values, dims=("oid", "xk_nm")
    )

    # 2. define priors for contiguous and auto-imputed data
    b_s = pm.Gamma("beta_sigma", alpha=10, beta=10)  # E ~ 1
    bj = pm.Normal("beta_j", mu=0, sigma=b_s, dims="xj_nm")
    bk = pm.Normal("beta_k", mu=0, sigma=b_s, dims="xk_nm")

    # 4. define evidence
    epsilon = pm.InverseGamma("epsilon", alpha=11, beta=10)
    lm = pt.dot(xj, bj.T) + pt.dot(xk, bk.T)
    _ = pm.Normal("yhat", mu=lm, sigma=epsilon, observed=y, dims="oid")









/Users/jon/miniforge/envs/oreum_survival/lib/python3.11/site-packages/pymc/model/core.py:1366: ImputationWarning: Data in xk contains missing values and will be automatically imputed from the sampling distribution.
  warnings.warn(impute_message, ImputationWarning)













display(pm.model_to_graphviz(mdla_h, formatting="plain"))
assert_no_rvs(mdla_h.logp())
mdla_h.debug(fn="logp", verbose=True)
mdla_h.debug(fn="random", verbose=True)








../_images/f9365ea984f8a9698961a08536cd59d204d709817ff55c85de4342e50d65a8dc.svg

point={'xk_mu': array([0., 0.]), 'xk_unobserved': array([0., 0., 0., 0., 0., 0., 0., 0.]), 'beta_sigma_log__': array(0.), 'beta_j': array([0., 0., 0.]), 'beta_k': array([0., 0.]), 'epsilon_log__': array(0.)}

No problems found
point={'xk_mu': array([0., 0.]), 'xk_unobserved': array([0., 0., 0., 0., 0., 0., 0., 0.]), 'beta_sigma_log__': array(0.), 'beta_j': array([0., 0., 0.]), 'beta_k': array([0., 0.]), 'epsilon_log__': array(0.)}

No problems found













2.5.2 其次：对样本外数据集中的缺失值 xk_unobserved 进行样本 PPC#


注意


    

  • 避免更改 ida，而是进行深拷贝 ida_h，删除不必要的组，我们将使用它
    • 

  • 我们不会创建一个裸 az.InferenceData 然后添加组，因为我们必须向对象添加各种额外的细微信息。复制和删除组更容易
    • 

  • posterior 中的 xarray 索引将是错误的（根据 dfx_train 而不是 dfx_holdout 设置），特别是维度 oid 和坐标 oid。
    • 

  • 在 xarray.Dataset 内部更改此类内容完全是噩梦，因此我们不会尝试更改它们。无论如何，在这种情况下这无关紧要，因为我们不会引用 posterior。
    • 







ida_h = deepcopy(ida)
# leave only posterior
del (
    ida_h.log_likelihood,
    ida_h.sample_stats,
    ida_h.prior,
    ida_h.prior_predictive,
    ida_h.posterior_predictive,
    ida_h.observed_data,
    ida_h.constant_data,
)
ida_h















arviz.InferenceData




    

  • 



    

    

      

      















      <xarray.Dataset> Size: 1MB
Dimensions:              (chain: 4, draw: 500, xk_nm: 2,
                          xk_unobserved_dim_0: 24, xj_nm: 3, oid: 30)
Coordinates:
  * chain                (chain) int64 32B 0 1 2 3
  * draw                 (draw) int64 4kB 0 1 2 3 4 5 ... 495 496 497 498 499
  * xk_nm                (xk_nm) <U1 8B 'c' 'd'
  * xk_unobserved_dim_0  (xk_unobserved_dim_0) int64 192B 0 1 2 3 ... 21 22 23
  * xj_nm                (xj_nm) <U9 108B 'intercept' 'a' 'b'
  * oid                  (oid) <U3 360B 'o01' 'o02' 'o03' ... 'o36' 'o37' 'o38'
Data variables:
    xk_mu                (chain, draw, xk_nm) float64 32kB 0.2089 ... 0.2972
    xk_unobserved        (chain, draw, xk_unobserved_dim_0) float64 384kB 0.3...
    beta_j               (chain, draw, xj_nm) float64 48kB 280.5 ... -55.48
    beta_k               (chain, draw, xk_nm) float64 32kB 23.61 46.93 ... 47.18
    beta_sigma           (chain, draw) float64 16kB 19.33 19.92 ... 21.89 20.18
    epsilon              (chain, draw) float64 16kB 0.9637 1.067 ... 1.014
    xk                   (chain, draw, oid, xk_nm) float64 960kB -0.4094 ... ...
Attributes:
    created_at:                 2024-12-16T10:46:11.401365+00:00
    arviz_version:              0.20.0
    inference_library:          pymc
    inference_library_version:  5.16.2
    sampling_time:              181.2683072090149
    tuning_steps:               3000

      

    

    

    • 













# NOTE for later clarity and to avoid overwriting, temporarily save posterior
# [xk, xk_unobserved] into group `posterior_predictive`` and remove any more
# unnecessary groups

with mdla_h:
    ida_h.extend(
        pm.sample_posterior_predictive(
            trace=ida_h.posterior, var_names=["xk_unobserved", "xk"], predictions=False
        ),
        join="right",
    )

del ida_h.observed_data, ida_h.constant_data
ida_h









Sampling: [xk_observed, xk_unobserved]













arviz.InferenceData




    

  • 



    

    

      

      















      <xarray.Dataset> Size: 1MB
Dimensions:              (chain: 4, draw: 500, xk_nm: 2,
                          xk_unobserved_dim_0: 24, xj_nm: 3, oid: 30)
Coordinates:
  * chain                (chain) int64 32B 0 1 2 3
  * draw                 (draw) int64 4kB 0 1 2 3 4 5 ... 495 496 497 498 499
  * xk_nm                (xk_nm) <U1 8B 'c' 'd'
  * xk_unobserved_dim_0  (xk_unobserved_dim_0) int64 192B 0 1 2 3 ... 21 22 23
  * xj_nm                (xj_nm) <U9 108B 'intercept' 'a' 'b'
  * oid                  (oid) <U3 360B 'o01' 'o02' 'o03' ... 'o36' 'o37' 'o38'
Data variables:
    xk_mu                (chain, draw, xk_nm) float64 32kB 0.2089 ... 0.2972
    xk_unobserved        (chain, draw, xk_unobserved_dim_0) float64 384kB 0.3...
    beta_j               (chain, draw, xj_nm) float64 48kB 280.5 ... -55.48
    beta_k               (chain, draw, xk_nm) float64 32kB 23.61 46.93 ... 47.18
    beta_sigma           (chain, draw) float64 16kB 19.33 19.92 ... 21.89 20.18
    epsilon              (chain, draw) float64 16kB 0.9637 1.067 ... 1.014
    xk                   (chain, draw, oid, xk_nm) float64 960kB -0.4094 ... ...
Attributes:
    created_at:                 2024-12-16T10:46:11.401365+00:00
    arviz_version:              0.20.0
    inference_library:          pymc
    inference_library_version:  5.16.2
    sampling_time:              181.2683072090149
    tuning_steps:               3000

      

    

    

    • 

  • 



    

    

      

      















      <xarray.Dataset> Size: 452kB
Dimensions:              (chain: 4, draw: 500, xk_unobserved_dim_2: 8, oid: 10,
                          xk_nm: 2)
Coordinates:
  * chain                (chain) int64 32B 0 1 2 3
  * draw                 (draw) int64 4kB 0 1 2 3 4 5 ... 495 496 497 498 499
  * xk_unobserved_dim_2  (xk_unobserved_dim_2) int64 64B 0 1 2 3 4 5 6 7
  * oid                  (oid) <U3 120B 'o00' 'o05' 'o11' ... 'o29' 'o35' 'o39'
  * xk_nm                (xk_nm) <U1 8B 'c' 'd'
Data variables:
    xk_unobserved        (chain, draw, xk_unobserved_dim_2) float64 128kB 0.1...
    xk                   (chain, draw, oid, xk_nm) float64 320kB 0.1384 ... 1...
Attributes:
    created_at:                 2024-12-16T10:46:21.721655+00:00
    arviz_version:              0.20.0
    inference_library:          pymc
    inference_library_version:  5.16.2

      

    

    

    • 













2.5.3 第三：将 xk_unobserved 的预测值代入 idata，并对 yhat 进行样本 PPC#






# NOTE overwrite [xk, xk_observed] in group `posterior` and sample yhat into new
# group `predictions`
ida_h.posterior.update({"xk_unobserved": ida_h.posterior_predictive.xk_unobserved})
ida_h.posterior.update({"xk": ida_h.posterior_predictive.xk})

with mdla_h:
    ida_h.extend(
        pm.sample_posterior_predictive(trace=ida_h.posterior, var_names=["yhat"], predictions=True),
        join="right",
    )

# NOTE copy [xk, xk_observed] into group `predictions` to make it clear that these
# dont fit in group `posterior` (the dims / coords issue), and drop groups
# `posterior_predictive` and `posterior`
ida_h.predictions.update({"xk_unobserved": ida_h.posterior_predictive.xk_unobserved})
ida_h.predictions.update({"xk": ida_h.posterior_predictive.xk})

del ida_h.posterior_predictive, ida_h.posterior
ida_h









Sampling: [xk_observed, yhat]













arviz.InferenceData




    

  • 



    

    

      

      















      <xarray.Dataset> Size: 612kB
Dimensions:              (chain: 4, draw: 500, oid: 10, xk_unobserved_dim_2: 8,
                          xk_nm: 2)
Coordinates:
  * chain                (chain) int64 32B 0 1 2 3
  * draw                 (draw) int64 4kB 0 1 2 3 4 5 ... 495 496 497 498 499
  * oid                  (oid) <U3 120B 'o00' 'o05' 'o11' ... 'o29' 'o35' 'o39'
  * xk_unobserved_dim_2  (xk_unobserved_dim_2) int64 64B 0 1 2 3 4 5 6 7
  * xk_nm                (xk_nm) <U1 8B 'c' 'd'
Data variables:
    yhat                 (chain, draw, oid) float64 160kB 216.2 328.5 ... 357.7
    xk_unobserved        (chain, draw, xk_unobserved_dim_2) float64 128kB 0.1...
    xk                   (chain, draw, oid, xk_nm) float64 320kB 0.1384 ... 1...
Attributes:
    created_at:                 2024-12-16T10:46:22.072054+00:00
    arviz_version:              0.20.0
    inference_library:          pymc
    inference_library_version:  5.16.2

      

    

    

    • 

  • 



    

    

      

      















      <xarray.Dataset> Size: 468B
Dimensions:  (oid: 10, xj_nm: 3)
Coordinates:
  * oid      (oid) <U3 120B 'o00' 'o05' 'o11' 'o19' ... 'o26' 'o29' 'o35' 'o39'
  * xj_nm    (xj_nm) <U9 108B 'intercept' 'a' 'b'
Data variables:
    xj       (oid, xj_nm) float64 240B 1.0 0.3722 1.112 ... 1.0 0.7767 -0.3962
Attributes:
    created_at:                 2024-12-16T10:46:22.075888+00:00
    arviz_version:              0.20.0
    inference_library:          pymc
    inference_library_version:  5.16.2

      

    

    

    • 









观察


    

  • 最后，在 ida_h 中，我们拥有 predictions 和 predictions_constant_data 的数据集，就像我们只完成了一个步骤一样
    • 

  • mdla_h 可以安全移除
    • 







2.5.4 样本外：将自动插补值 \(x_{k}\) xk_unobserved 与已知的真实值进行比较#


注意


    

  • 回想一下，我们只能这样做，因为它是一个合成数据集，我们在上面的 dfraw 中创建了这些完整（全部）值
    • 

  • 我们将展示一个可能会让读者感到惊讶的图…
    • 





创建索引以从 xk 中提取适当的观测值，因为 xk_unobserved 没有正确的 dims 索引#






dfx_holdout_xk = (
    dfx_holdout.loc[:, ["c", "d"]]
    .reset_index()
    .melt(id_vars=["oid"], var_name="xk_nm", value_name="xk")
    .set_index(["oid", "xk_nm"])
)
idx_h_xk_unobs = dfx_holdout_xk.loc[dfx_holdout_xk["xk"].isnull()].index













从 PPC idata 中提取 xk_unobserved，通过索引隔离，转换回数据域#






df_h_xk_unobs = (
    az.extract(ida_h, group="predictions", var_names=["xk"])
    .to_dataframe()
    .drop(["chain", "draw"], axis=1)
    .reset_index()
    .set_index(["oid", "xk_nm"])
    .loc[idx_h_xk_unobs]
)
df_h_xk_unobs = (
    pd.merge(df_h_xk_unobs.reset_index(), df_mns_sdevs.reset_index(), how="left", on=["xk_nm"])
    .set_index(["oid", "xk_nm"])
    .sort_index()
)
df_h_xk_unobs["xk_unobs_ppc_data_domain"] = (
    df_h_xk_unobs["xk"] * df_h_xk_unobs["sdev"]
) + df_h_xk_unobs["mn"]













附加真实值（仅在此合成示例中可能）#






df_h_xk_unobs = pd.merge(
    df_h_xk_unobs, dfraw_xk.loc[idx_h_xk_unobs], how="left", left_index=True, right_index=True
)













强制用于绘图的 dtypes#






df_h_xk_unobs = df_h_xk_unobs.reset_index()
df_h_xk_unobs["oid"] = pd.Categorical(df_h_xk_unobs["oid"])
df_h_xk_unobs["xk_nm"] = pd.Categorical(df_h_xk_unobs["xk_nm"])
df_h_xk_unobs.set_index(["oid", "xk_nm"], inplace=True)













绘制后验 xk_unobserved 与已知的真实值（仅在此合成示例中可能）#






_ = plot_xkhat_vs_xk(df_h_xk_unobs, mdlnm="mdla", in_samp=False)








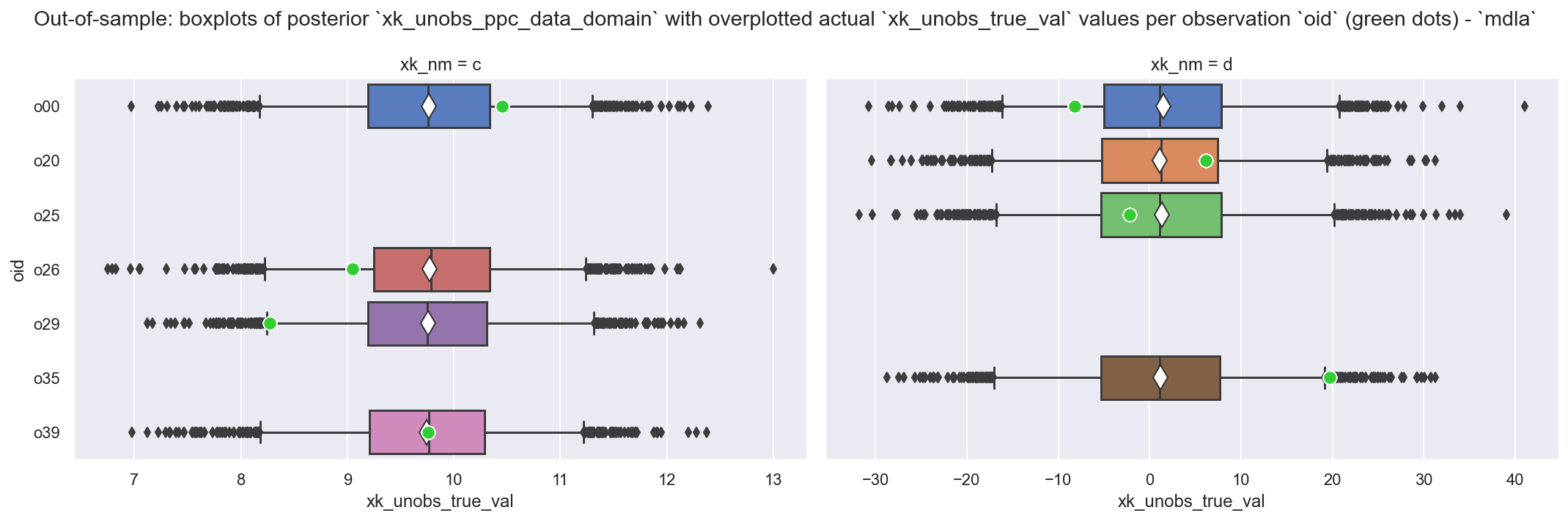
../_images/78c98b5d0c174d0456df109b54b78c6d00269375bf3a22d96738ecb21279c316.png





观察


    

  • 非常好：这看起来我们的预测很糟糕 - 但模型按预期工作，这有助于说明问题
    • 

  • xk_unobserved 的后验值已从分层 xk_mu 分布中提取，并且不以任何其他事物为条件，因此我们几乎获得了所有相同的预测值
    • 

  • 这应该让人深刻理解，虽然从技术上讲，此模型可以处理新的缺失值，并且确实自动插补样本外数据集（此处为 dfx_holdout）中缺失数据的值，但 xk_unobserved 的这些自动插补值不能比分层先验 xk_mu 的后验分布提供更多信息。
    • 









2.5.5 样本外：将预测的 \(\hat{y}\) yhat 与已知的真实值进行比较#




从 PPC idata 中提取 yhat，并附加真实值（仅因为它是 holdout 集才可用）#






df_h_y = (
    az.extract(ida_h, group="predictions", var_names=["yhat"])
    .to_dataframe()
    .drop(["chain", "draw"], axis=1)
    .reset_index()
    .set_index(["oid"])
)
df_h_y = pd.merge(df_h_y, df_holdout[["y"]], how="left", left_index=True, right_index=True)
df_h_y.describe().T

















count
mean
std
min
25%
50%
75%
max






chain
20000.0
1.500000
1.118062
0.000000
0.750000
1.500000
2.250000
3.000000




draw
20000.0
249.500000
144.340887
0.000000
124.750000
249.500000
374.250000
499.000000




yhat
20000.0
274.219714
81.642115
7.298419
216.866769
265.639881
325.320904
607.137715




y
20000.0
278.797170
72.820296
181.932062
203.615652
271.797565
323.667882
439.462555














绘制后验 yhat 与已知的真实值 y（仅因为它是 holdout 集才可用）#






_ = plot_yhat_vs_y(df_h_y)








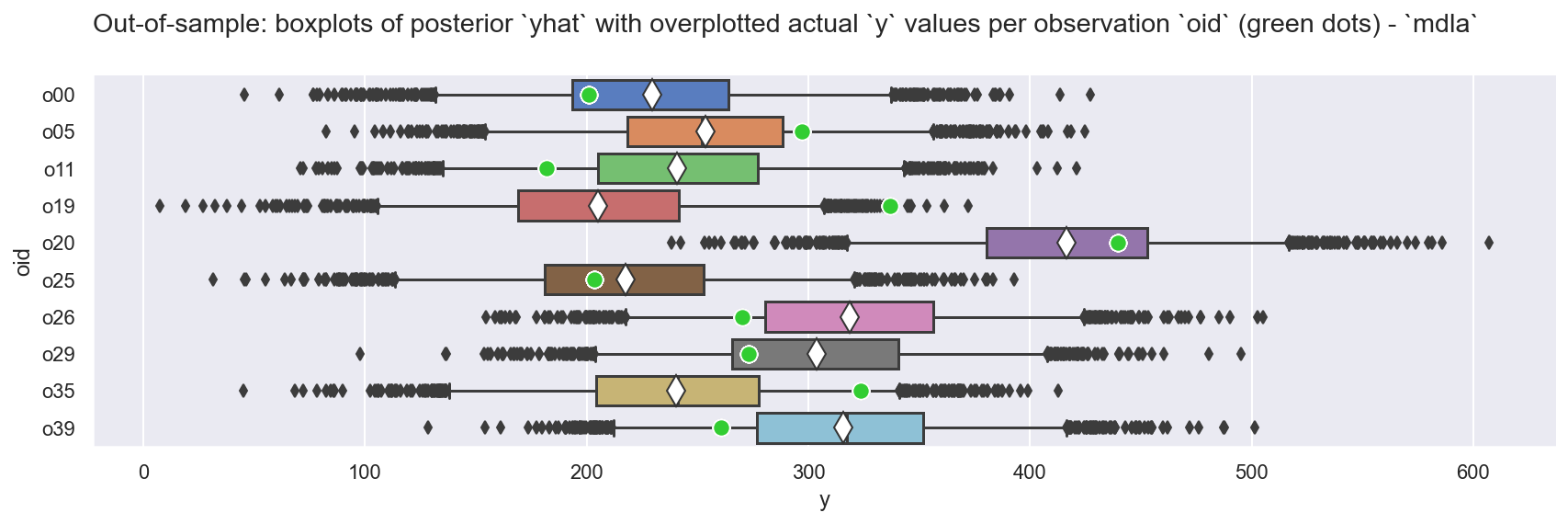
../_images/a4868156159ba4f8d1022310bd0f4824ccfbd99de6b3632f16872f2bff90ed6a.png





观察


    

  • 预测 yhat 看起来非常接近真实值 y，通常都在 \(HDI_{94}\) 范围内
    • 

  • 正如我们所期望的那样，yhat 的分布也很有用：量化预测中的不确定性，并让我们据此做出更好的决策。
    • 

















勘误#




作者#







参考资料#







[1]
(1,2)

Craig Enders K. 应用缺失数据分析。The Guilford Press, 2022.





[2]

Junpeng Lao. 部分缺失多元观测以及如何处理它们. 2020. URL: https://discourse.pymc.io/t/partial-missing-multivariate-observation-and-what-to-do-with-them-by-junpeng-lao/6050 (于 2020-10-01 访问).





[3]

Andrew Gelman, Aki Vehtari, Daniel Simpson, Charles C Margossian, Bob Carpenter, Yuling Yao, Lauren Kennedy, Jonah Gabry, Paul-Christian Bürkner, 和 Martin Modrák. 贝叶斯工作流程. arXiv preprint arXiv:2011.01808, 2020. URL: https://arxiv.org/abs/2011.01808.












水印#






# tested running on Google Colab 2024-12-16
%load_ext watermark
%watermark -n -u -v -iv -w









Last updated: Mon Dec 16 2024

Python implementation: CPython
Python version       : 3.11.10
IPython version      : 8.29.0

pymc      : 5.16.2
matplotlib: 3.9.2
pandas    : 2.2.3
pytensor  : 2.25.5
arviz     : 0.20.0
seaborn   : 0.12.2
numpy     : 1.26.4

Watermark: 2.5.0













许可声明#


本示例库中的所有笔记本均根据 MIT 许可证 提供，该许可证允许修改和再分发以用于任何用途，前提是保留版权和许可声明。






引用 PyMC 示例#


要引用此笔记本，请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。




重要提示


许多笔记本都改编自其他来源：博客、书籍…… 在这种情况下，您也应该引用原始来源。


另请记住引用您的代码使用的相关库。




这是一个 bibtex 中的引用模板


@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}





一旦渲染，它可能看起来像