样条#

简介#

通常，我们想要拟合的模型不是 \(x\) 和 \(y\) 之间的一条完美直线。相反，模型的参数预计会随着 \(x\) 而变化。 有多种方法可以处理这种情况，其中一种是拟合样条。 样条拟合实际上是多个单独曲线（分段多项式）的总和，每个曲线都拟合到 \(x\) 的不同部分，这些曲线在其边界处连接在一起，通常称为节点。

样条实际上是多条单独的线，每条线都拟合到 \(x\) 的不同部分，这些线在其边界处连接在一起，通常称为节点。

下面是如何使用 PyMC 拟合样条的完整工作示例。 数据和模型取自 Statistical Rethinking 2e，作者是 Richard McElreath [McElreath，2018]。

有关这种非线性建模方法的更多信息，我建议从 Bayesian Modeling and Computation in Python 第 5 章 开始阅读 [Martin等，2021]。

from pathlib import Path

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm

from patsy import build_design_matrices, dmatrix

%matplotlib inline
%config InlineBackend.figure_format = "retina"

seed = sum(map(ord, "splines"))
rng = np.random.default_rng(seed)
az.style.use("arviz-darkgrid")

樱花数据#

此示例的数据是每年樱花树开花的日数（doy，代表“一年中的天数”）（year）。 为了方便起见，缺少 doy 的年份被删除（这通常是处理缺失数据的一个坏主意！）。

try:
    blossom_data = pd.read_csv(Path("..", "data", "cherry_blossoms.csv"), sep=";")
except FileNotFoundError:
    blossom_data = pd.read_csv(pm.get_data("cherry_blossoms.csv"), sep=";")


blossom_data.dropna().describe()
year doy temp temp_upper temp_lower
count 787.000000 787.00000 787.000000 787.000000 787.000000
mean 1533.395172 104.92122 6.100356 6.937560 5.263545
std 291.122597 6.25773 0.683410 0.811986 0.762194
min 851.000000 86.00000 4.690000 5.450000 2.610000
25% 1318.000000 101.00000 5.625000 6.380000 4.770000
50% 1563.000000 105.00000 6.060000 6.800000 5.250000
75% 1778.500000 109.00000 6.460000 7.375000 5.650000
max 1980.000000 124.00000 8.300000 12.100000 7.740000 
blossom_data = blossom_data.dropna(subset=["doy"]).reset_index(drop=True)
blossom_data.head(n=10)
year doy temp temp_upper temp_lower
0 812 92.0 NaN NaN NaN
1 815 105.0 NaN NaN NaN
2 831 96.0 NaN NaN NaN
3 851 108.0 7.38 12.10 2.66
4 853 104.0 NaN NaN NaN
5 864 100.0 6.42 8.69 4.14
6 866 106.0 6.44 8.11 4.77
7 869 95.0 NaN NaN NaN
8 889 104.0 6.83 8.48 5.19
9 891 109.0 6.98 8.96 5.00

删除包含缺失数据的行后，有 827 年的数据记录了树木开花的天数。

blossom_data.shape

(827, 5)

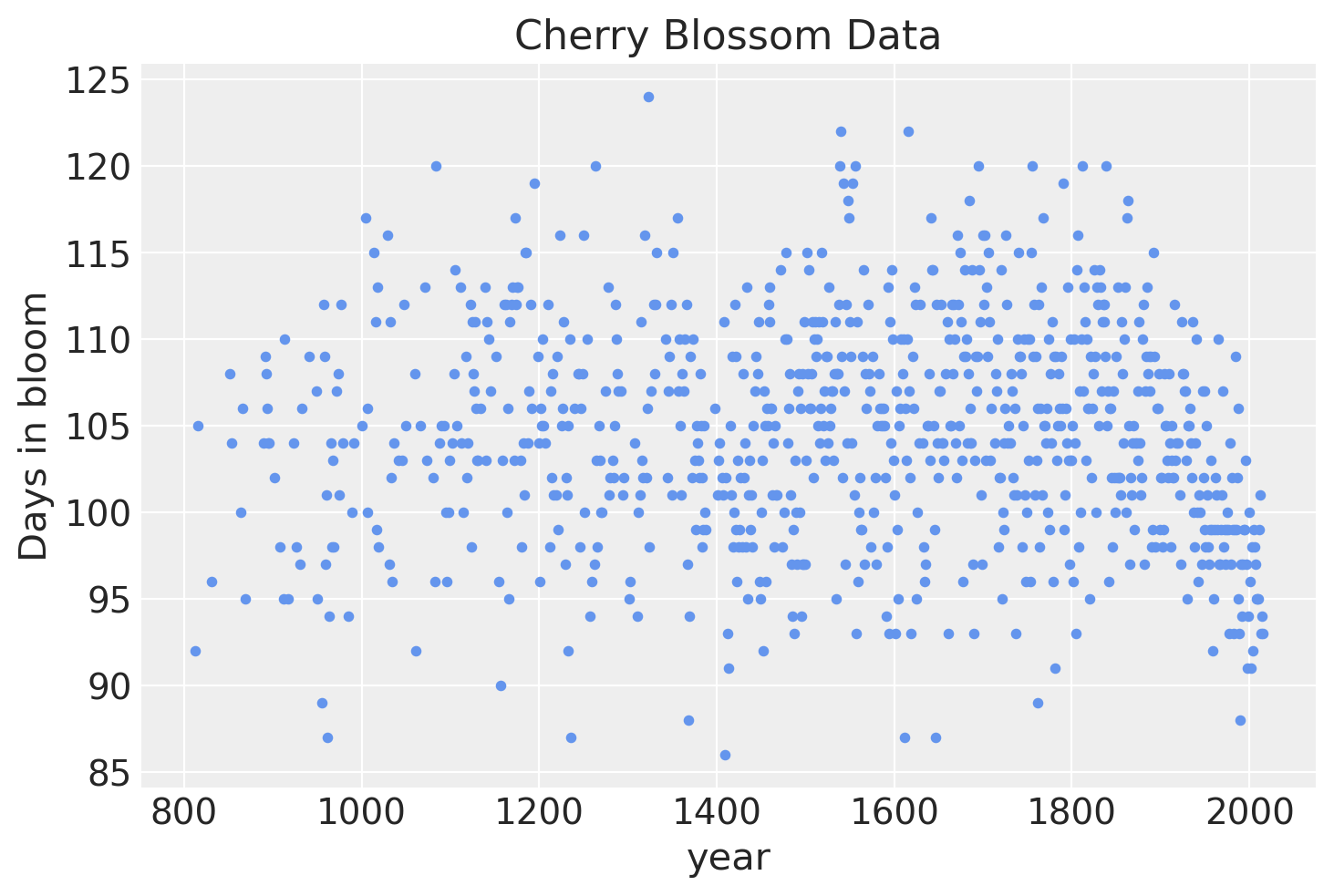
如果我们可视化数据，很明显，每年的变化很大，但有一些证据表明开花天数随时间呈非线性趋势。

blossom_data.plot.scatter(
    "year",
    "doy",
    color="cornflowerblue",
    s=10,
    title="Cherry Blossom Data",
    ylabel="Days in bloom",
);
../_images/016cb0cee1bc2066be9ae62e3da61810e3f301cbe9d103a8a3d0c2cfce6dfe1c.png

模型#

我们将拟合以下模型。

\(D \sim \mathcal{N}(\mu, \sigma)\)
\(\quad \mu = a + Bw\)
\(\qquad a \sim \mathcal{N}(100, 10)\)
\(\qquad w \sim \mathcal{N}(0, 10)\)
\(\quad \sigma \sim \text{Exp}(1)\)

开花天数 \(D\) 将被建模为正态分布，均值为 \(\mu\)，标准差为 \(\sigma\)。 反过来，均值将是一个线性模型，由 y 轴截距 \(a\) 和由基 \(B\) 定义的样条乘以模型参数 \(w\) 组成，其中每个基区域都有一个变量。 两者都具有相对较弱的正态先验。

准备样条#

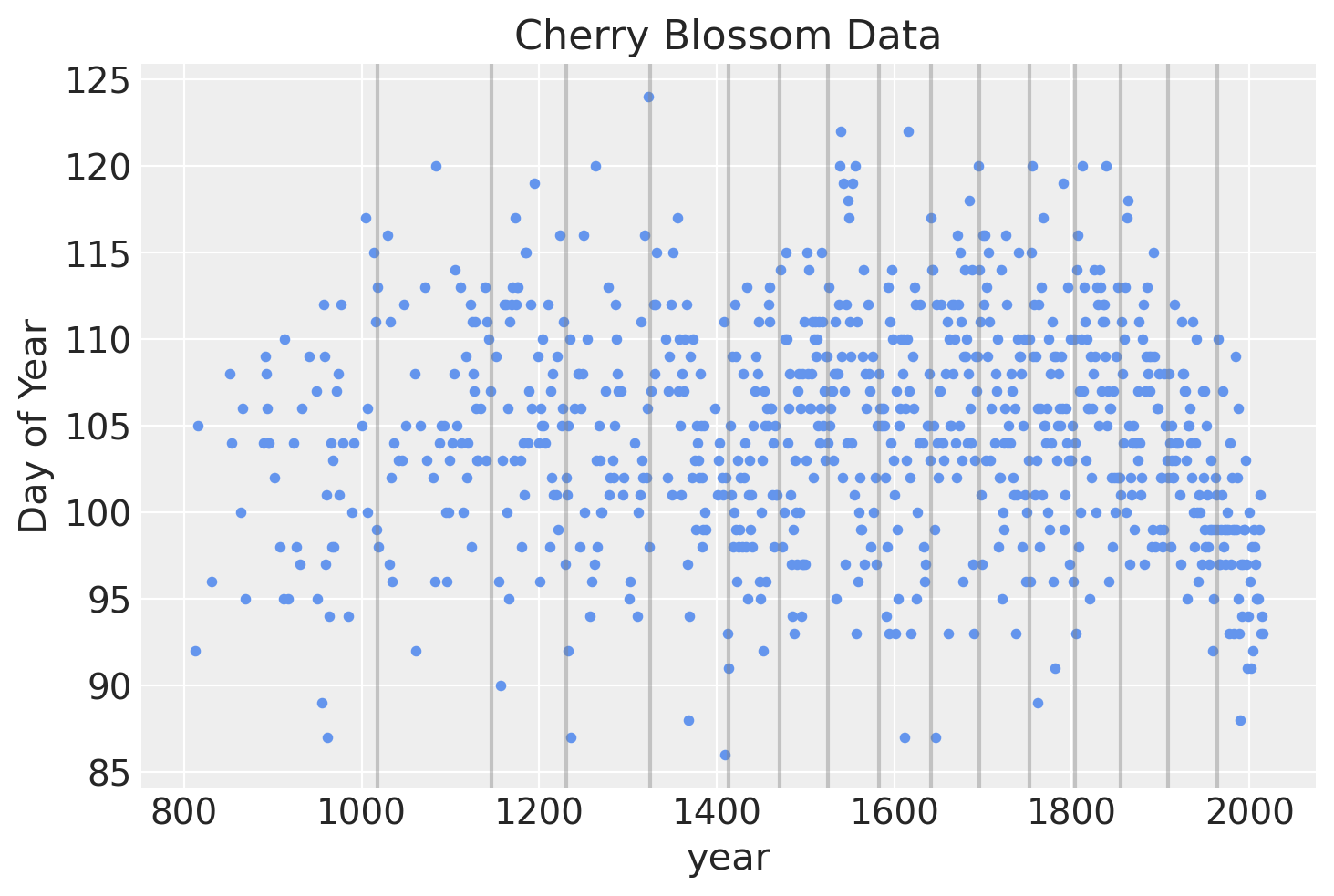
样条将有 15 个节点，将年份分成 16 个部分（包括覆盖我们有数据之前的年份和之后的年份的区域）。 节点是样条的边界，之所以这样命名，是因为各个线将如何在这些边界处连接在一起，形成一条连续且平滑的曲线。 节点将在年份上不均匀分布，以便每个区域具有相同比例的数据。

num_knots = 15
knot_list = np.percentile(blossom_data.year, np.linspace(0, 100, num_knots + 2))[1:-1]
knot_list

array([1017.625, 1146.5  , 1230.875, 1325.   , 1413.25 , 1471.   ,
       1525.375, 1583.   , 1641.625, 1696.25 , 1751.875, 1803.5  ,
       1855.125, 1908.75 , 1963.375])

下面是节点在数据上的位置图。

blossom_data.plot.scatter(
    "year",
    "doy",
    color="cornflowerblue",
    s=10,
    title="Cherry Blossom Data",
    ylabel="Day of Year",
)
for knot in knot_list:
    plt.gca().axvline(knot, color="grey", alpha=0.4)
../_images/f6b26e67aaefdf665fe12f3e54e6fcb36a1feea137e007ada7891472a0a9f2c0.png

我们可以使用 patsy 来创建矩阵 \(B\)，它将是回归的 b 样条基。 次数设置为 3 以创建三次 b 样条。

B = dmatrix(
    "bs(year, knots=knots, degree=3, include_intercept=True) - 1",
    {"year": blossom_data.year.values, "knots": knot_list},
)
B
隐藏代码单元格输出 
DesignMatrix with shape (827, 19)
  Columns:
    ['bs(year, knots=knots, degree=3, include_intercept=True)[0]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[1]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[2]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[3]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[4]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[5]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[6]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[7]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[8]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[9]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[10]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[11]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[12]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[13]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[14]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[15]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[16]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[17]',
     'bs(year, knots=knots, degree=3, include_intercept=True)[18]']
  Terms:
    'bs(year, knots=knots, degree=3, include_intercept=True)' (columns 0:19)
  (to view full data, use np.asarray(this_obj))

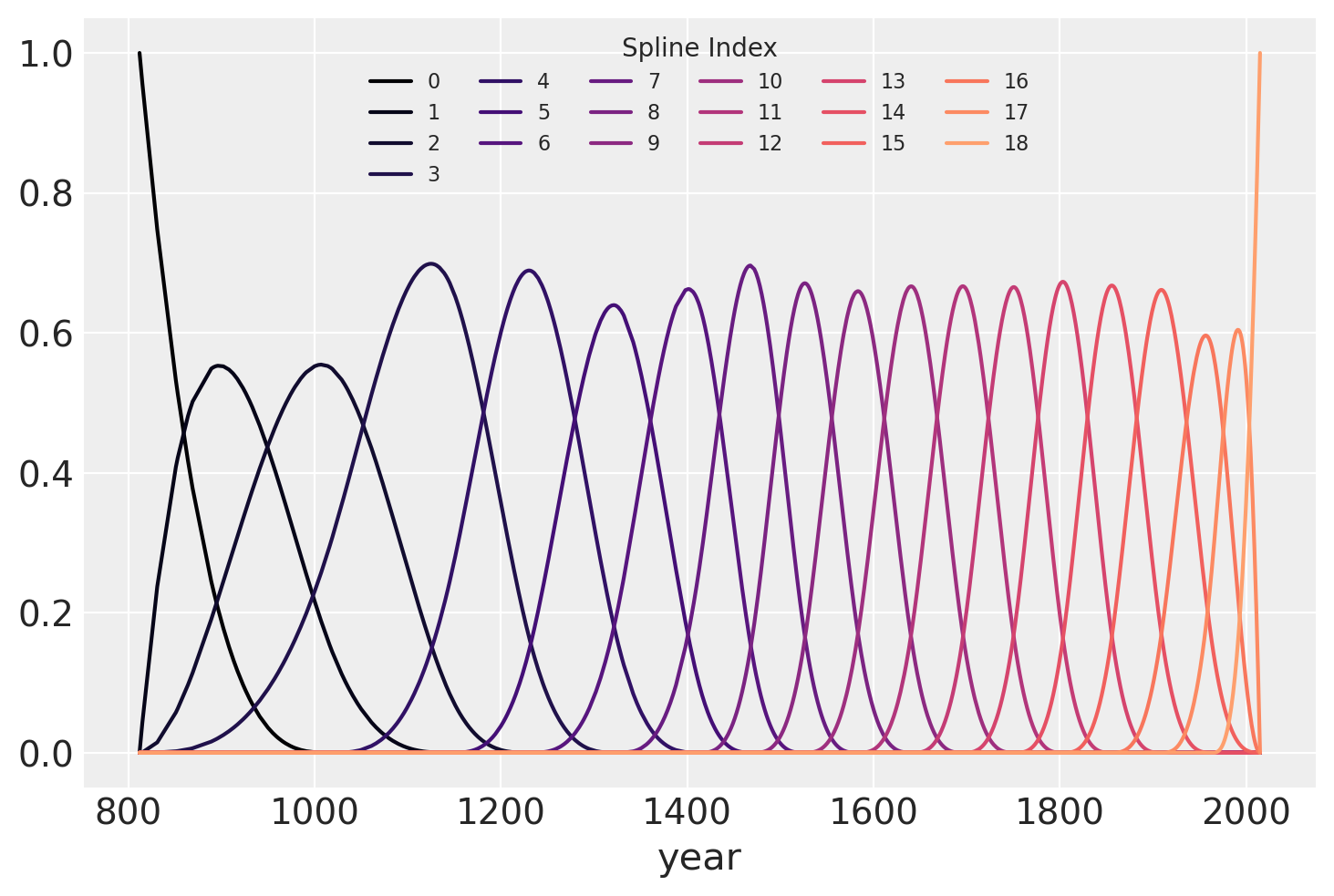
b 样条基绘制在下方，显示样条每个片段的域。 每条曲线的高度表示相应的模型协变量（每个样条区域一个）对模型在该区域的推断的影响程度。 重叠区域表示节点，显示了如何形成从一个区域到下一个区域的平滑过渡。

spline_df = (
    pd.DataFrame(B)
    .assign(year=blossom_data.year.values)
    .melt("year", var_name="spline_i", value_name="value")
)

color = plt.cm.magma(np.linspace(0, 0.80, len(spline_df.spline_i.unique())))

fig = plt.figure()
for i, c in enumerate(color):
    subset = spline_df.query(f"spline_i == {i}")
    subset.plot("year", "value", c=c, ax=plt.gca(), label=i)
plt.legend(title="Spline Index", loc="upper center", fontsize=8, ncol=6);
../_images/fdebc57d7b70df3b2f12b01f949fd362e146a138f0fe511449c88e55ecfcf81b.png

拟合模型#

最后，可以使用 PyMC 构建模型。 图形图显示了模型参数的组织结构（请注意，这需要安装 python-graphviz，我建议在 conda 虚拟环境中执行此操作）。

COORDS = {"splines": np.arange(B.shape[1])}
with pm.Model(coords=COORDS) as spline_model:
    a = pm.Normal("a", 100, 5)
    w = pm.Normal("w", mu=0, sigma=3, size=B.shape[1], dims="splines")

    mu = pm.Deterministic(
        "mu",
        a + pm.math.dot(np.asarray(B, order="F"), w.T),
    )
    sigma = pm.Exponential("sigma", 1)

    D = pm.Normal("D", mu=mu, sigma=sigma, observed=blossom_data.doy)

pm.model_to_graphviz(spline_model)
../_images/900bd34077daf2f54a3a11ebc9c29308d97e962421d7c01c39ac95e217fad1db.svg 
with spline_model:
    idata = pm.sample_prior_predictive()
    idata.extend(
        pm.sample(
            nuts_sampler="nutpie",
            draws=1000,
            tune=1000,
            random_seed=rng,
            chains=4,
        )
    )
    pm.sample_posterior_predictive(idata, extend_inferencedata=True)

Sampling: [D, a, sigma, w]
/Users/alex_andorra/tptm_alex/pymc/pymc/pytensorf.py:1057: FutureWarning: compile_pymc was renamed to compile. Old name will be removed in a future release of PyMC
  warnings.warn(
/Users/alex_andorra/tptm_alex/pymc/pymc/pytensorf.py:1057: FutureWarning: compile_pymc was renamed to compile. Old name will be removed in a future release of PyMC
  warnings.warn(

采样器进度

总链数: 4

活动链数: 0

完成链数: 4

正在采样

预计完成时间: now

进度 抽取 发散 步长 梯度/抽取
2000 0 0.53 7
2000 0 0.52 15
2000 0 0.52 15
2000 0 0.51 15 
Sampling: [D]













分析#


现在我们可以分析模型后验的抽取结果。




参数估计#


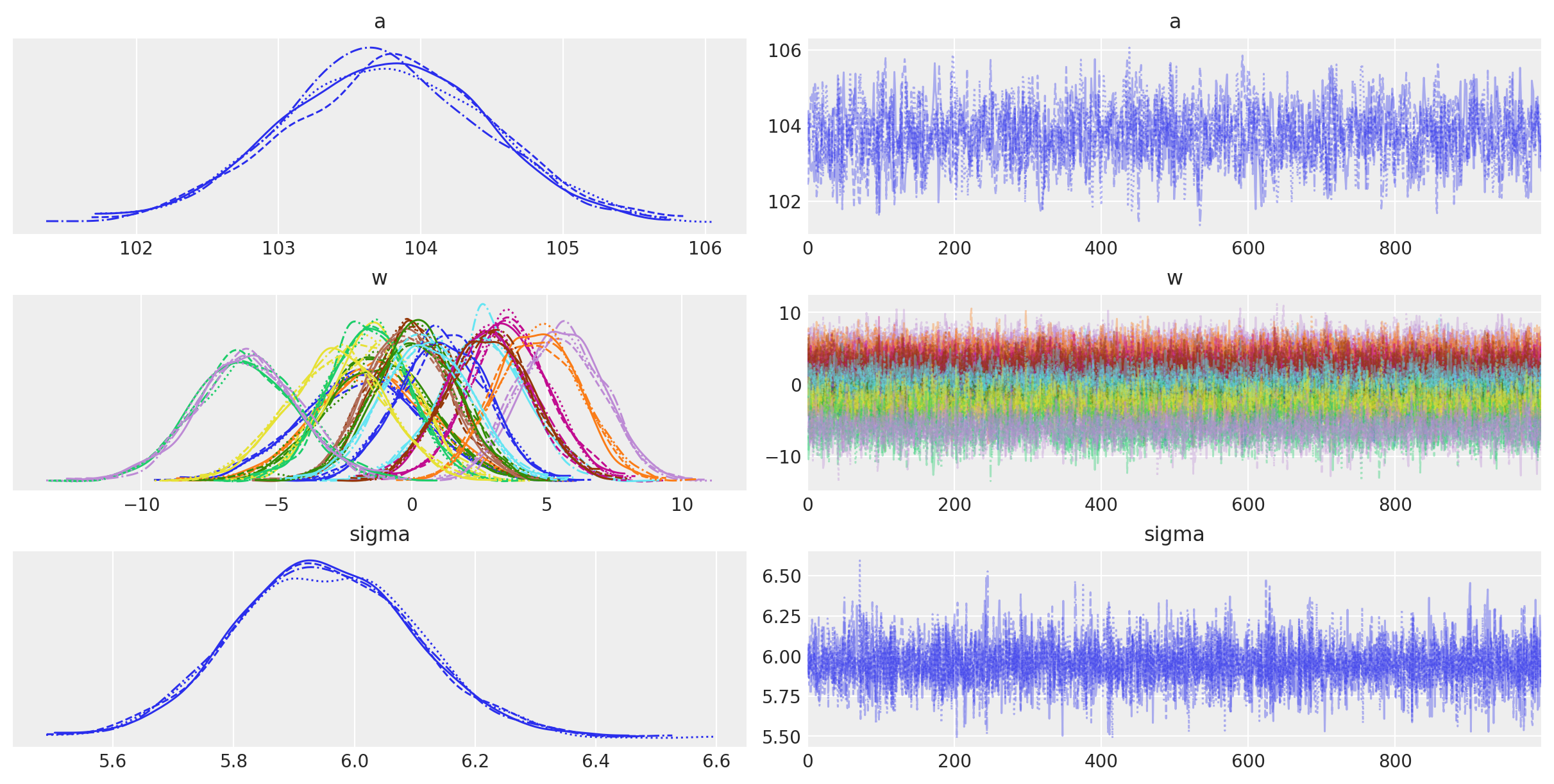
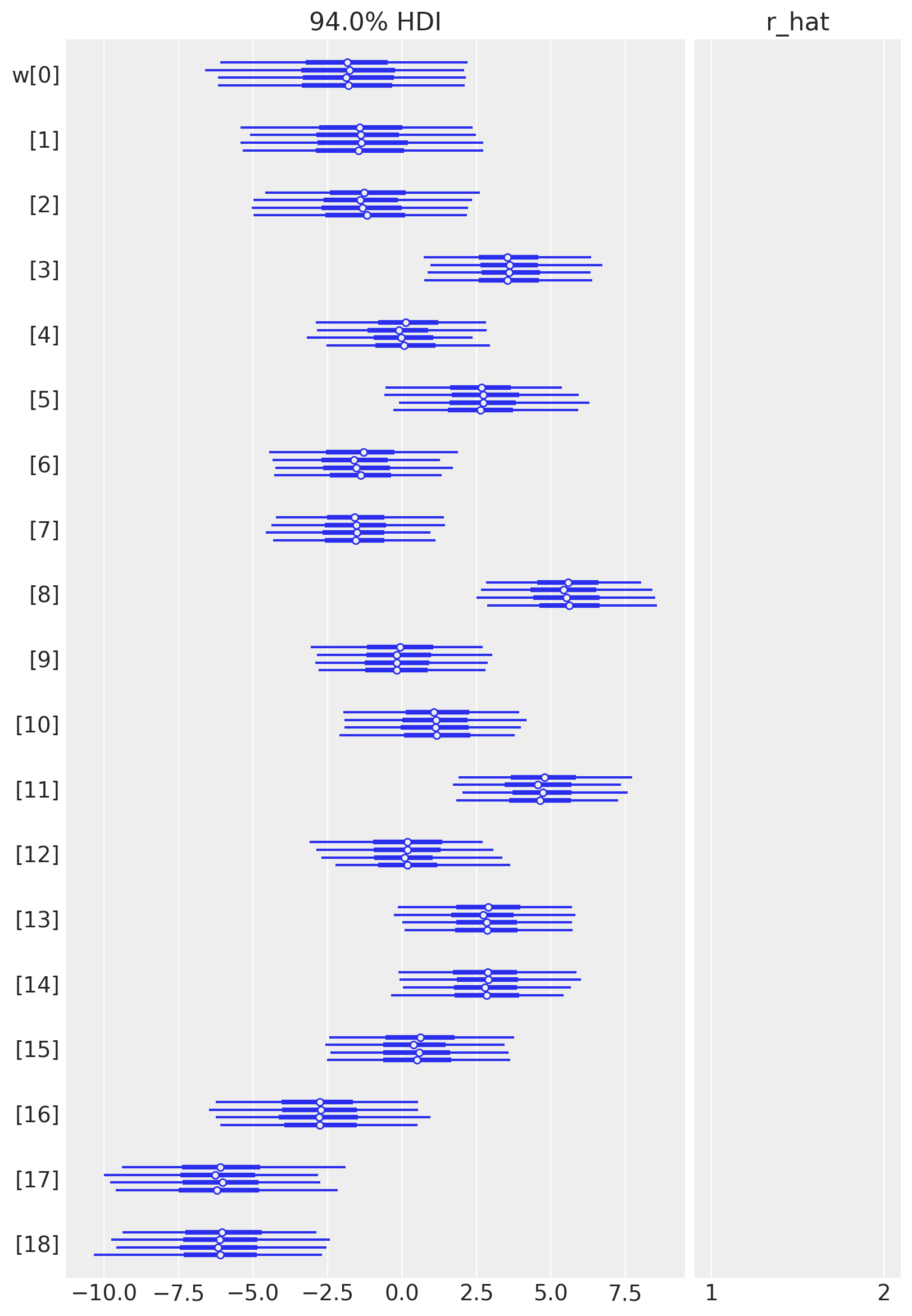
下表总结了模型参数的后验分布。 \(a\) 和 \(\sigma\) 的后验分布非常窄，而 \(w\) 的后验分布则更宽。 这可能是因为所有数据点都用于估计 \(a\) 和 \(\sigma\)，而只有一部分数据点用于 \(w\) 的每个值。 （对这些进行分层建模，允许信息共享并在样条上添加正则化可能会很有趣。） 有效样本大小和 \(\widehat{R}\) 值看起来都不错，表明模型已收敛并从后验分布中良好采样。






az.summary(idata, var_names=["a", "w", "sigma"])

















mean
sd
hdi_3%
hdi_97%
mcse_mean
mcse_sd
ess_bulk
ess_tail
r_hat






a
103.743
0.733
102.370
105.147
0.021
0.015
1276.0
2009.0
1.0




w[0]
-1.827
2.251
-6.169
2.267
0.029
0.028
5907.0
3251.0
1.0




w[1]
-1.397
2.129
-5.272
2.697
0.034
0.027
3952.0
3177.0
1.0




w[2]
-1.294
1.953
-5.002
2.329
0.036
0.026
2938.0
2630.0
1.0




w[3]
3.610
1.492
0.879
6.559
0.028
0.020
2866.0
3473.0
1.0




w[4]
0.037
1.515
-2.648
3.062
0.029
0.020
2736.0
3097.0
1.0




w[5]
2.685
1.673
-0.436
5.924
0.031
0.022
2929.0
3015.0
1.0




w[6]
-1.479
1.596
-4.494
1.409
0.032
0.022
2569.0
3082.0
1.0




w[7]
-1.578
1.505
-4.573
1.134
0.029
0.022
2660.0
2458.0
1.0




w[8]
5.536
1.545
2.757
8.435
0.030
0.021
2690.0
2868.0
1.0




w[9]
-0.126
1.565
-2.918
2.900
0.030
0.022
2637.0
2754.0
1.0




w[10]
1.120
1.614
-1.962
4.012
0.030
0.021
2910.0
2822.0
1.0




w[11]
4.663
1.542
1.739
7.449
0.029
0.020
2844.0
3233.0
1.0




w[12]
0.147
1.587
-2.901
3.083
0.033
0.023
2385.0
3011.0
1.0




w[13]
2.820
1.555
-0.152
5.696
0.028
0.020
3130.0
3304.0
1.0




w[14]
2.839
1.577
-0.085
5.838
0.030
0.021
2800.0
2889.0
1.0




w[15]
0.509
1.642
-2.515
3.596
0.033
0.024
2445.0
2960.0
1.0




w[16]
-2.807
1.859
-6.355
0.548
0.033
0.024
3207.0
3229.0
1.0




w[17]
-6.127
1.951
-9.550
-2.197
0.036
0.025
2959.0
2921.0
1.0




w[18]
-6.111
1.911
-9.586
-2.420
0.030
0.022
4173.0
2946.0
1.0




sigma
5.951
0.148
5.664
6.224
0.002
0.001
6452.0
2891.0
1.0










模型参数的迹图看起来不错（同质且没有趋势迹象），进一步表明链已收敛和混合。






az.plot_trace(idata, var_names=["a", "w", "sigma"]);








../_images/6a1c43b7c2956881ab29d740bd2a82a4efaaecfa738fda60705b1cf879b7b1fe.png









az.plot_forest(idata, var_names=["w"], combined=False, r_hat=True);








../_images/f36320e02c1740f9806842e8e6896111448ce179267ea29adaa2cd1b26789bfa.png





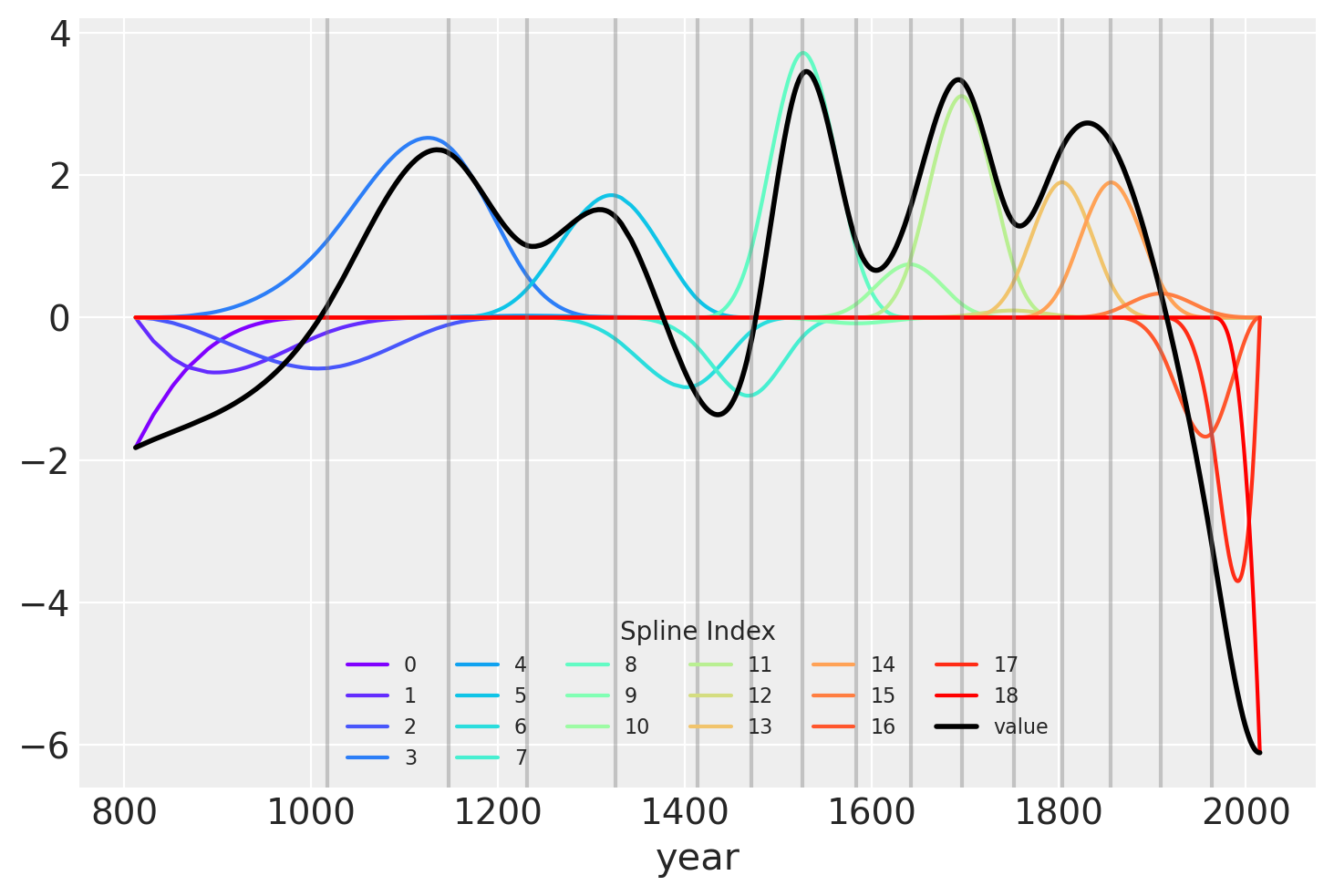
拟合样条值的另一种可视化方法是将它们与基矩阵相乘后绘制出来。 节点边界再次显示为垂直线，但现在样条基与 \(w\) 的值（表示为彩虹色曲线）相乘。 \(B\) 和 \(w\) 的点积（线性模型中的实际计算）以黑色显示。






wp = idata.posterior["w"].mean(("chain", "draw")).values

spline_df = (
    pd.DataFrame(B * wp.T)
    .assign(year=blossom_data.year.values)
    .melt("year", var_name="spline_i", value_name="value")
)

spline_df_merged = (
    pd.DataFrame(np.dot(B, wp.T))
    .assign(year=blossom_data.year.values)
    .melt("year", var_name="spline_i", value_name="value")
)


color = plt.cm.rainbow(np.linspace(0, 1, len(spline_df.spline_i.unique())))
fig = plt.figure()
for i, c in enumerate(color):
    subset = spline_df.query(f"spline_i == {i}")
    subset.plot("year", "value", c=c, ax=plt.gca(), label=i)
spline_df_merged.plot("year", "value", c="black", lw=2, ax=plt.gca())
plt.legend(title="Spline Index", loc="lower center", fontsize=8, ncol=6)

for knot in knot_list:
    plt.gca().axvline(knot, color="grey", alpha=0.4)








../_images/ade5e042db6e43f657ec00f5a0d8b58b94813edad17006cbf4b5e2371e8d22c3.png









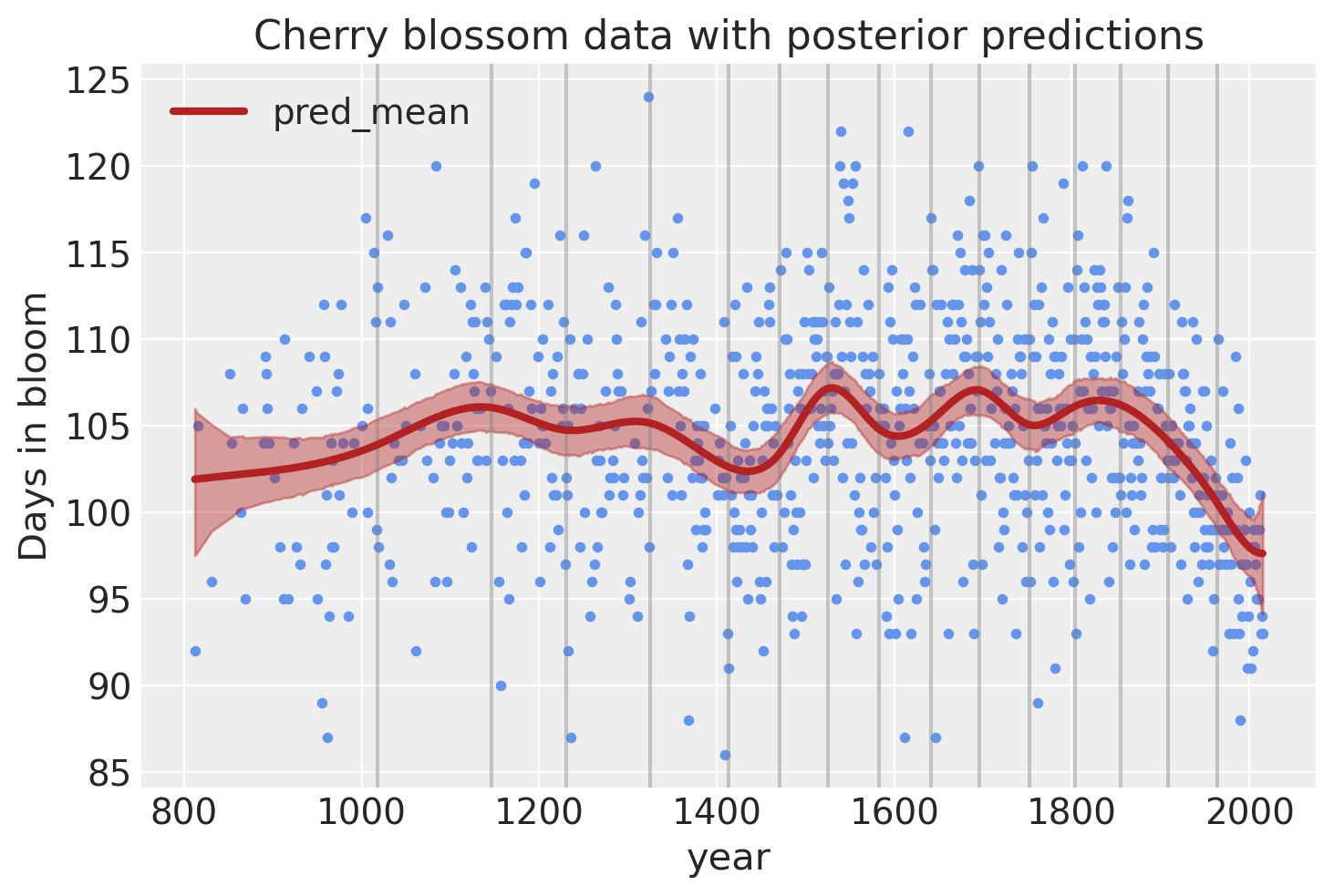
模型预测#


最后，我们可以使用后验预测检查来可视化模型的预测。






post_pred = az.summary(idata, var_names=["mu"]).reset_index(drop=True)
blossom_data_post = blossom_data.copy().reset_index(drop=True)
blossom_data_post["pred_mean"] = post_pred["mean"]
blossom_data_post["pred_hdi_lower"] = post_pred["hdi_3%"]
blossom_data_post["pred_hdi_upper"] = post_pred["hdi_97%"]













blossom_data.plot.scatter(
    "year",
    "doy",
    color="cornflowerblue",
    s=10,
    title="Cherry blossom data with posterior predictions",
    ylabel="Days in bloom",
)
for knot in knot_list:
    plt.gca().axvline(knot, color="grey", alpha=0.4)

blossom_data_post.plot("year", "pred_mean", ax=plt.gca(), lw=3, color="firebrick")
plt.fill_between(
    blossom_data_post.year,
    blossom_data_post.pred_hdi_lower,
    blossom_data_post.pred_hdi_upper,
    color="firebrick",
    alpha=0.4,
);








../_images/a7de6be65712fc4e30b937e0aaa463674833b1978d9814f230af3e23541eea8c.png











预测新数据#


现在假设我们获得了一个新数据集，其年份范围与原始数据集相同，并且我们希望使用拟合模型获得此新数据集的预测。 我们可以使用经典的 PyMC 工作流程 Data 容器和 set_data 方法来做到这一点。


不过，在我们到达那里之前，让我们注意一下，我们没有说新数据集包含新的年份，即样本外年份。 这是有意的，因为样条无法外推到用于拟合模型的数据集范围之外——因此它们在时间序列分析中受到限制。 但是，在之前见过的数据范围内，这没有问题。


撇开这种精确度不谈，让我们重新定义我们的模型，这次添加 Data 容器。






COORDS = {"obs": blossom_data.index}













with pm.Model(coords=COORDS) as spline_model:
    year_data = pm.Data("year", blossom_data.year)
    doy = pm.Data("doy", blossom_data.doy)

    # intercept
    a = pm.Normal("a", 100, 5)

    # Create spline bases & coefficients
    ## Store knots & design matrix for prediction
    spline_model.knots = np.percentile(year_data.eval(), np.linspace(0, 100, num_knots + 2))[1:-1]
    spline_model.dm = dmatrix(
        "bs(x, knots=spline_model.knots, degree=3, include_intercept=False) - 1",
        {"x": year_data.eval()},
    )
    spline_model.add_coords({"spline": np.arange(spline_model.dm.shape[1])})
    splines_basis = pm.Data("splines_basis", np.asarray(spline_model.dm), dims=("obs", "spline"))
    w = pm.Normal("w", mu=0, sigma=3, dims="spline")

    mu = pm.Deterministic(
        "mu",
        a + pm.math.dot(splines_basis, w),
    )
    sigma = pm.Exponential("sigma", 1)

    D = pm.Normal("D", mu=mu, sigma=sigma, observed=doy)













pm.model_to_graphviz(spline_model)








../_images/c9a3a3c80b3d75777a385ccf22a4f7c9f8d42295053a3835621853896ba6232f.svg









with spline_model:
    idata = pm.sample(
        nuts_sampler="nutpie",
        random_seed=rng,
    )
    idata.extend(pm.sample_posterior_predictive(idata, random_seed=rng))









/Users/alex_andorra/tptm_alex/pymc/pymc/pytensorf.py:1057: FutureWarning: compile_pymc was renamed to compile. Old name will be removed in a future release of PyMC
  warnings.warn(
/Users/alex_andorra/tptm_alex/pymc/pymc/pytensorf.py:1057: FutureWarning: compile_pymc was renamed to compile. Old name will be removed in a future release of PyMC
  warnings.warn(












采样器进度


总链数: 4


活动链数: 0


完成链数: 4


正在采样


预计完成时间: now








进度
抽取
发散
步长
梯度/抽取










2000
0
0.52
7








2000
0
0.53
15








2000
0
0.52
7








2000
0
0.53
7









Sampling: [D]











现在我们可以换出数据并使用新数据更新设计矩阵






new_blossom_data = (
    blossom_data.sample(50, random_state=rng).sort_values("year").reset_index(drop=True)
)

# update design matrix with new data
year_data_new = new_blossom_data.year.to_numpy()
dm_new = build_design_matrices([spline_model.dm.design_info], {"x": year_data_new})[0]









使用 set_data 更新模型中的数据






with spline_model:
    pm.set_data(
        new_data={
            "year": year_data_new,
            "doy": new_blossom_data.doy.to_numpy(),
            "splines_basis": np.asarray(dm_new),
        },
        coords={
            "obs": new_blossom_data.index,
        },
    )









剩下的就是从后验预测分布中采样






with spline_model:
    preds = pm.sample_posterior_predictive(idata, var_names=["mu"])









Sampling: []











绘制预测图，检查一切是否顺利






_, axes = plt.subplots(1, 2, figsize=(16, 5), sharex=True, sharey=True)

blossom_data.plot.scatter(
    "year",
    "doy",
    color="cornflowerblue",
    s=10,
    title="Posterior predictions",
    ylabel="Days in bloom",
    ax=axes[0],
)
axes[0].vlines(
    spline_model.knots,
    blossom_data.doy.min(),
    blossom_data.doy.max(),
    color="grey",
    alpha=0.4,
)
axes[0].plot(
    blossom_data.year,
    idata.posterior["mu"].mean(("chain", "draw")),
    color="firebrick",
)
az.plot_hdi(blossom_data.year, idata.posterior["mu"], color="firebrick", ax=axes[0])

new_blossom_data.plot.scatter(
    "year",
    "doy",
    color="cornflowerblue",
    s=10,
    title="Predictions on new data",
    ylabel="Days in bloom",
    ax=axes[1],
)
axes[1].vlines(
    spline_model.knots,
    blossom_data.doy.min(),
    blossom_data.doy.max(),
    color="grey",
    alpha=0.4,
)
axes[1].plot(
    new_blossom_data.year,
    preds.posterior_predictive.mu.mean(("chain", "draw")),
    color="firebrick",
)
az.plot_hdi(new_blossom_data.year, preds.posterior_predictive.mu, color="firebrick", ax=axes[1]);








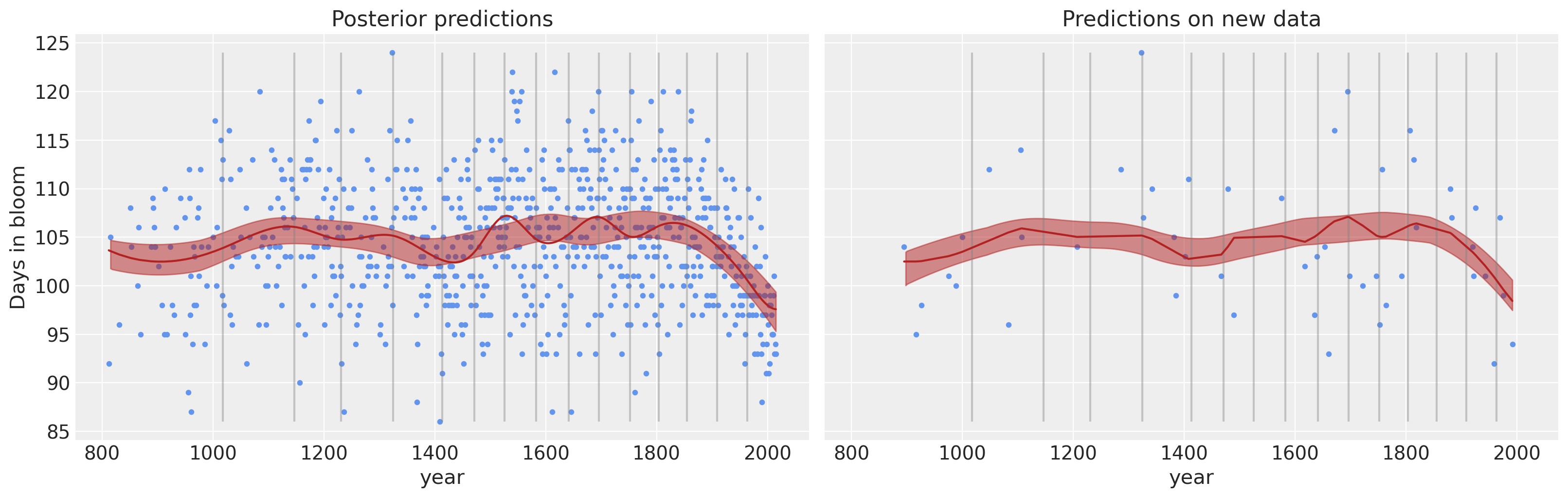
../_images/8b7bc633c30e39e58259c74e61aed76fd404b5db8fb9240b4343a3523c8eb11d.png





还有… 瞧！ 诚然，这个例子不是最现实的例子，但我们相信您可以将其调整为您最疯狂的梦想；）






参考文献#







[1]

Osvaldo A Martin、Ravin Kumar 和 Junpeng Lao. Python 中的贝叶斯建模和计算。 Chapman and Hall/CRC, 2021. doi:10.1201/9781003019169.





[2]

Richard McElreath. Statistical rethinking: A Bayesian course with examples in R and Stan. Chapman and Hall/CRC, 2018.












作者#


    

  • 由 Joshua Cook 创建
    • 

  • 由 Tyler James Burch 更新
    • 

  • 由 Chris Fonnesbeck 更新
    • 

  • 由 Alex Andorra 添加了关于新数据的预测
    • 







水印#






%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,xarray,patsy









Last updated: Mon Feb 03 2025

Python implementation: CPython
Python version       : 3.12.3
IPython version      : 8.22.2

pytensor: 2.27.0
xarray  : 2024.3.0
patsy   : 1.0.1

pandas    : 2.2.1
arviz     : 0.20.0
pymc      : 5.20.0+24.g3b6e35163
matplotlib: 3.8.3
numpy     : 1.26.4

Watermark: 2.4.3













许可声明#


此示例库中的所有笔记本均根据 MIT 许可证 提供，该许可证允许修改和重新分发用于任何用途，前提是保留版权和许可声明。






引用 PyMC 示例#


要引用此笔记本，请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。




重要提示


许多笔记本都改编自其他来源：博客、书籍……在这种情况下，您也应该引用原始来源。


另请记住引用您的代码使用的相关库。




这是一个 bibtex 中的引用模板


@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}





渲染后可能看起来像