干预分布和使用 do 算子的图变异

PyMC 是开源贝叶斯统计生态系统的关键组成部分。它每天都在帮助解决各个行业和学术研究领域的实际问题。并且它之所以能达到这种实用程度，是因为它在解决贝叶斯统计推断问题时易于访问、功能强大且切实有用。

但时代在变化。一场因果革命正在进行中，人们越来越认识到，要回答一些最有趣和最具挑战性的问题，需要我们将因果推理融入到我们的工作中。

PyMC 正在迎接这一挑战！虽然有很多新颖的因果概念需要学习，但贝叶斯学者会发现他们并非从零开始。他们已经非常熟悉有向无环图 (DAG)，因此这为相对容易地进入贝叶斯因果推断的世界提供了一个良好的起点。

本笔记本将介绍因果推理的基础组成部分之一，它已新近引入 PyMC 生态系统，即 \(\operatorname{do}\) 算子。实际上，根据您想使用的定义，将 \(\operatorname{do}\) 算子添加到 PyMC 用户每天构建的那种贝叶斯 DAG 中，使我们达到了构建 因果贝叶斯网络 的状态。

如果这听起来很酷，让我们深入了解一下…

设置笔记本

import arviz as az
import graphviz as gr
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import seaborn as sns

from packaging import version

WARNING (pytensor.configdefaults): g++ not available, if using conda: `conda install m2w64-toolchain`
WARNING (pytensor.configdefaults): g++ not detected!  PyTensor will be unable to compile C-implementations and will default to Python. Performance may be severely degraded. To remove this warning, set PyTensor flags cxx to an empty string.
WARNING (pytensor.tensor.blas): Using NumPy C-API based implementation for BLAS functions.

# import the new functionality
from pymc.model.transform.conditioning import do

RANDOM_SEED = 123
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
%config InlineBackend.figure_format = 'retina'

贝叶斯推断可以做什么？

无论我们构建的是描述性模型还是试图对底层过程建模的模型，贝叶斯学者都非常习惯于构建白盒（即 黑盒 的反义词）、可解释的 数据生成过程 模型。虽然我们使用代码构建 PyMC 模型，但在幕后，这表示为一个 DAG，我们可以使用 graphviz 可视化它。让我们看看这如何使用文档中的示例工作

J = 8
y = np.array([28, 8, -3, 7, -1, 1, 18, 12])
sigma = np.array([15, 10, 16, 11, 9, 11, 10, 18])

with pm.Model() as schools:
    eta = pm.Normal("eta", 0, 1, shape=J)
    mu = pm.Normal("mu", 0, sigma=1e6)
    tau = pm.HalfCauchy("tau", 25)
    theta = mu + tau * eta
    obs = pm.Normal("obs", theta, sigma=sigma, observed=y)

pm.model_to_graphviz(schools)

无论我们使用哪个特定模型或哪些模型，我们都可以执行一系列统计程序

• 我们可以检查先验预测分布，以了解基于我们声明的先验信念和 pymc.sample_prior_predictive，我们在给定的 DAG 中期望看到什么。一个示例用例是当我们想了解我们基于模型结构（例如，国家和国际经济）以及我们对潜在变量的先验信念对未来通胀如何演变的预测时。

• 我们可以通过使用 pymc.sample 从后验分布中采样来进行贝叶斯推断。这将更新我们的信念，以便根据我们观察到的数据，为潜在变量的不同值分配可信度。例如，也许我们向数据集添加了另一个通胀数据点，并且我们想更新我们对经济模型中潜在变量的信念。

• 我们可以使用 pymc.sample_posterior_predictive 检查后验预测分布。这与先验预测分布密切相关，但在我们的运行示例中，它将允许我们在观察到另一个数据点后，创建一套关于未来通胀率的修订预测。

• 如果我们愿意，我们可以使用 GLM：模型选择 来比较不同的模型（数据生成过程）。这可能特别有用，因为我们可能并不完全相信我们知道经济的“真实”模型，即使在粗略的抽象级别上也是如此。因此，我们可以构建多个模型 (DAG)，并评估每个模型生成观察数据的相对可信度。

• 如果我们有许多候选数据生成过程，我们可以通过 模型平均 将我们对数据生成过程的不确定性纳入其中。

如果我们掌握了所有这些步骤，我们可以理所当然地对自己感到非常满意。我们可以通过这些统计和预测程序完成很多工作。

为什么因果关系很重要

但现在是时候让我们这些自鸣得意的贝叶斯学者清醒一下了。正如其他人所论证的那样（例如，Pearl 和 Mackenzie [2018]，Pearl [2000]），完全有可能构建一个相当好的预测模型，但一旦您（或任何其他人）干预系统，该模型可能会彻底失败。这种干预会完全破坏预测建模方法，并让您迅速意识到将因果推理添加到我们的技能组合中的必要性。

在我们的运行示例中，这可能对应于中央银行从预测通胀转变为采取行动并通过例如改变利率来干预系统的情况。突然之间，您可能会面临这样一种情况：经济对您的干预没有像您预测的那样做出反应。

让我们考虑一个看似微不足道的 3 节点示例，看看我们是如何被愚弄的。下图显示了两个不同的因果 DAG。左边我们感兴趣的是 \(X\) 如何因果地影响 \(Y\)，既直接地，也通过中介变量 \(M\) 间接地影响。如果我们采用纯粹的统计方法（例如，贝叶斯中介分析），我们可能会发现数据很可能是由这个 DAG 生成的。这可能会给我们信心对 \(M\) 进行干预，目的是影响我们的目标结果 \(Y\)。但是，当我们在现实世界中进行这种干预并改变 \(M\) 时，我们实际上发现 \(Y\) 绝对没有变化。这是怎么回事？

显示代码单元格源 隐藏代码单元格源

g = gr.Digraph()
# Wrong data generating process
g.node(name="x2", label="X")
g.node(name="y2", label="Y")
g.node(name="m2", label="M")
g.edge(tail_name="x2", head_name="y2")
g.edge(tail_name="x2", head_name="m2")
g.edge(tail_name="m2", head_name="y2")
# Actual causal DAG
g.node(name="x", label="X")
g.node(name="y", label="Y")
g.node(name="m", label="M")
g.node(name="u", label="U", color="lightgrey", style="filled")
g.edge(tail_name="x", head_name="y")
g.edge(tail_name="x", head_name="m")
g.edge(tail_name="m", head_name="y", style="dashed", dir="none")
g.edge(tail_name="u", head_name="m", color="lightgrey")
g.edge(tail_name="u", head_name="y", color="lightgrey")
# Render
g

我们不知道，但实际的数据生成过程是由右侧的 DAG 捕获的。这表明 \(X\) 确实因果地影响 \(M\) 和 \(Y\)，但是 \(M\) 实际上并没有因果地影响 \(Y\)。相反，存在一个未观察到的变量 \(U\)，它因果地影响 \(M\) 和 \(Y\)。这个未观察到的混淆因素创建了一条后门路径，统计关联可能在该路径 \(X \rightarrow M \rightarrow U \rightarrow Y\) 之间流动。所有这些都导致 \(M\) 和 \(Y\) 之间存在统计关联，这使我们的纯粹统计方法误导我们认为 \(M\) 确实因果地影响 \(Y\)，而实际上并非如此。难怪我们的干预未能产生任何效果。

我们的错误是将统计模型解释为因果模型。

统计分布与干预分布

到目前为止，这还是相当高层次的，但让我们试着稍微明确一下。在我们的示例中，如果我们采用纯粹的统计方法，我们可以问“当利率为 2% 时会发生什么？”这是一个统计问题，因为我们基本上是在回顾我们的数据集，并过滤（或条件化）利率为（或非常接近）2% 的时间点。因此，让我们标记一下 - 条件分布是纯粹的统计量。

尽管我们可能想要回答的真正问题是“如果我们过去将利率设定为 2%，会发生什么？”或“如果我们将来将利率设定为 2%，会发生什么？”尽管措辞略有变化，但这现在彻底改变了我们为回答问题必须做的事情。因此，这里的关键点是 干预分布需要因果（而非统计）方法。

干预分布很酷，因为它们允许我们提出假设性问题（或反事实问题）。例如，使用因果 DAG，我们可以提出以下形式的问题：“如果我做 X，我预计未来会发生什么？”或“如果 X 发生过，我预计过去会发生什么？”看看这些类型的问题与纯粹的统计类型的问题有何不同的味道 - 它们更像是“根据我所看到的，我预计会发生什么。”看看这如何具有更被动、观察性的焦点。

从现在开始，本笔记本的主要目的是提供一些关于条件分布和干预分布之间差异的理解和直觉，以及如何使用 PyMC 估计干预分布。正如我们上面所说，我们可以使用 \(\operatorname{do}\) 算子来估计干预分布。因此，让我们深入了解一下，看看它是如何工作的。

干预和 \(\operatorname{do}\) 算子

我们将考虑 Pearl [2000] 中的一个示例，我们在其中检查一个 DAG，该 DAG 是各种因素如何相互影响以导致草地变得湿滑的假定因果解释。左边显示了我们的因果 DAG，右边显示了如果我们考虑打开洒水器的干预（假设的或实际的），DAG 如何变化。\(\operatorname{do}\) 算子实现了我们想要进行的干预。它由 2 个简单的步骤组成

1. 它获取图中的给定节点，并将该节点设置为所需的值。

2. 它通过删除所有进入该节点的传入边来消除其他节点对该节点的任何因果影响。

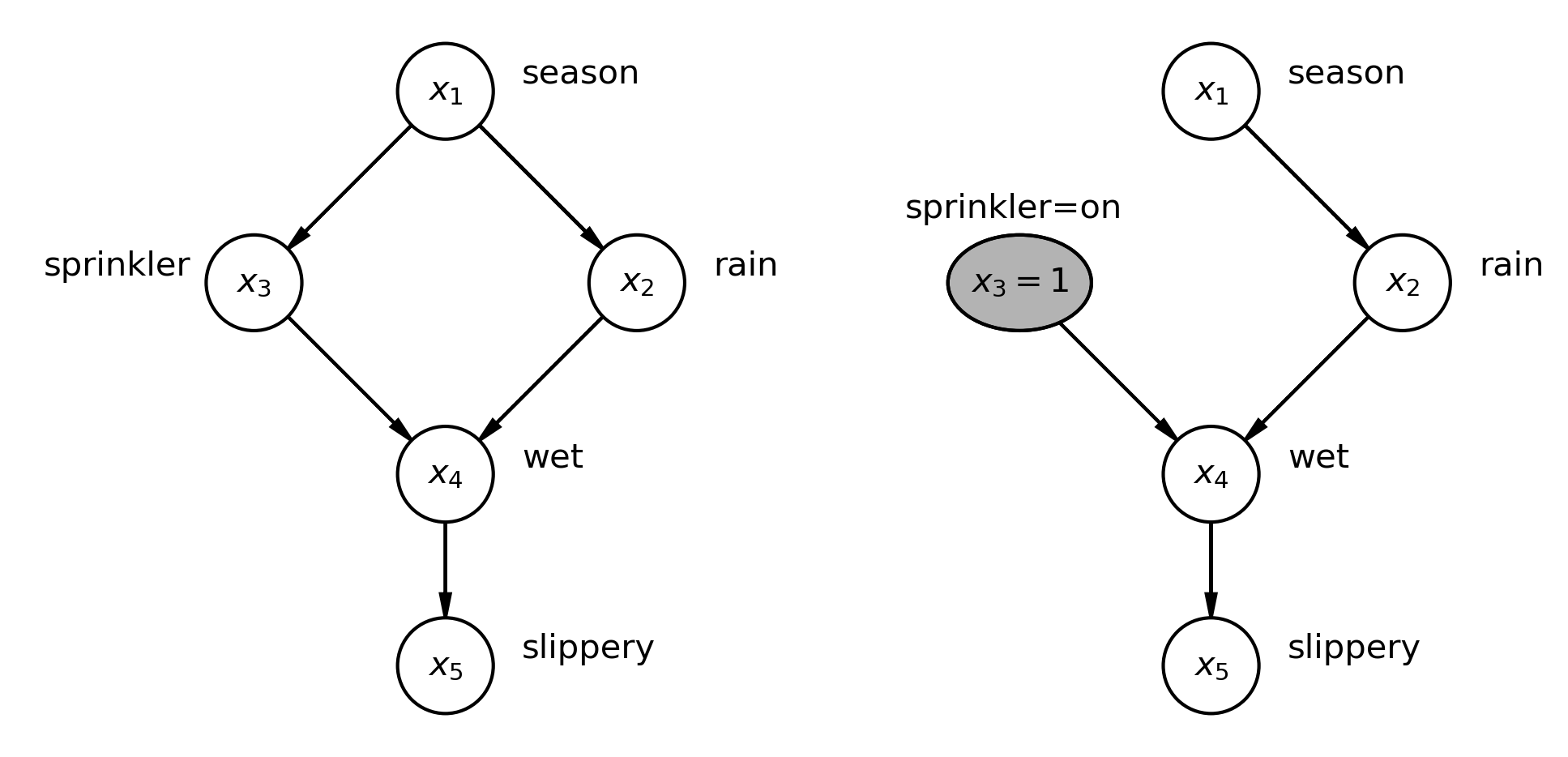
在该图的左侧，我们有一个因果 DAG，描述了季节、洒水器是否已打开、是否下雨、草地是否潮湿以及草地是否湿滑之间的因果关系。

联合分布可以分解为

\[ P(x_1, x_2, x_3, x_4, x_5) = P(x_1) P(x_3|x_1) P(x_2|x_1) P(x_4|x_3, x_2) P(x_5|x_4) \]

分解联合分布

对于 DAG，复杂的联合分布可以分解为条件分布的乘积

\[ P(x_1, x_2, \ldots, x_n) = \prod_i P(x_i|pa_i) \]

其中 \(pa_i\) 是节点 \(x_i\) 的父节点，而 \(i = \{ 1, \ldots, n \}\)。

在该图的右侧，我们应用了 \(\operatorname{do}\) 算子来检查如果我们设置洒水器为开启会发生什么。您可以看到我们现在已经设置了该节点的值 \(x_3=1\)，并且我们删除了季节的传入边（影响），这意味着一旦我们手动打开洒水器，它就不再受季节的影响。

为了描述这种新的干预分布，我们需要截断因子分解

截断因子分解

Pearl [2000] 将截断因子分解描述如下。如果我们在一组 \(V\) 变量上有一个概率分布 \(P(v)\)，则 \(P_x(v)\) 是由 \(\operatorname{do}(X=x)\) 产生的干预分布，它将 \(X\) 变量的子集设置为常数 \(x\)。然后我们可以使用截断因子分解来描述干预分布，如下所示

\[ P_x(v) = \prod_{ \{ i | V_i \notin X \} } P(v_i|pa_i) \]

这实际上非常简单。它可以被认为与联合分布的常规因子分解完全相同，但我们只包括不影响任何干预变量的项。

感兴趣的读者可以参考 Pearl [2000] 关于因果贝叶斯网络的 1.3 节。

将其应用于洒水器示例，我们可以将干预分布定义为

\[ P(x_1, x_2, \operatorname{do}(x_3=1), x_4, x_5) = P(x_1) P(x_2|x_1) P(x_4|x_3=1, x_2) P(x_5|x_4) \]

这里有两个重要的变化

1. 请注意，\(x_3\) 以前是一个随机变量，但由于我们的干预，现在已被“锁定”在特定值 \(x_3=1\)。

2. 请注意缺少 \(P(x_3|x_1)\) 项，因为 \(x_1\) 不再对 \(x_3\) 具有任何因果影响。

因此，总而言之，这非常酷。我们可以使用 \(\operatorname{do}\) 算子对我们的世界模型进行干预。然后，我们可以观察这种干预的后果，并更好地预测当我们积极主动地在世界中进行干预（实际地或假设地）时会发生什么。当然，准确性取决于我们的因果 DAG 在多大程度上反映了世界中的真实过程。

对于那些想要进一步了解 \(\operatorname{do}\) 算子的背景信息（从不同的角度解释）的人，读者应查看图文并茂且解释清晰的博客文章 通过 Do 算子实现的因果效应 [Talebi, 2022]、Pearl 和 Mackenzie [2018] 的科普书籍或 Molak [2023] 的教科书。

三个不同的因果 DAG

注意

本节主要受到帖子 因果推断 2：通过玩具示例说明干预 [Huszár, 2019] 的启发。模仿是最真诚的恭维。

如果我们考虑 2 个变量 \(x\) 和 \(y\) 之间的关系，我们可以提出许多不同的因果 DAG。下面我们仅考虑 3 种可能性，我们将分别标记为 DAG 1、2 和 3。

1. \(x\) 因果地影响 \(y\)

2. \(y\) 因果地影响 \(x\)

3. \(z\) 因果地影响 \(x\) 和 \(y\)

我们也可以在下面更图形化地绘制这些内容

显示代码单元格源 隐藏代码单元格源

g = gr.Digraph()

# DAG 1
g.node(name="x1", label="x")
g.node(name="y1", label="y")
g.edge(tail_name="x1", head_name="y1")

# DAG 2
g.node(name="y2", label="y")
g.node(name="x2", label="x")
g.edge(tail_name="y2", head_name="x2")

# DAG 3
g.node(name="z", label="z")
g.node(name="x", label="x")
g.node(name="y", label="y")
g.edge(tail_name="z", head_name="x")
g.edge(tail_name="z", head_name="y")

g

我们还可以想象在 Python 代码中实现此类因果 DAG 以生成 N 个随机数。这些都将产生特定的联合分布 \(P(x, y)\)，事实上，由于 Ferenc Huszár 在他的博客文章中很聪明，我们稍后会看到这些都将产生相同的联合分布。

DAG 1

x = rng.normal(loc=0, scale=1, size=N)
y = x + 1 + np.sqrt(3) * rng.normal(size=N)

DAG 2

y = 1 + 2 * rng.normal(size=N)
x = (y - 1) / 4 + np.sqrt(3) * rng.normal(size=N) / 2

DAG 3

z = rng.normal(size=N)
y = z + 1 + np.sqrt(3) * rng.normal(size=N)
x = z

注意

这些代码片段很重要，因为它们定义了相同的联合分布 \(P(x,y)\)，但它们具有不同的 DAG 结构。因此，当使用 \(\operatorname{do}\) 算子进行干预时，它们的响应可能会有所不同。值得回顾这些代码片段，以确保您了解它们与上面的 DAG 结构之间的关系，并仔细思考对变量进行干预将如何影响变量 \(x, y, z\) 的值（如果有影响）。

但是，我们将使用 PyMC 的贝叶斯因果 DAG 来实现这些。让我们看看如何做到这一点，然后使用 pm.sample_prior_predictive 从中生成样本。当我们处理每个 DAG 时，我们将提取样本以供稍后绘制，并绘制 PyMC 模型的 graphviz 表示。您将看到，虽然这些在视觉上稍微复杂一些，但它们实际上与我们上面指定的因果 DAG 相匹配。

# number of samples to generate
N = 1_000_000

with pm.Model() as model1:
    x = pm.Normal("x")
    temp = pm.Normal("temp")
    y = pm.Deterministic("y", x + 1 + np.sqrt(3) * temp)
    idata1 = pm.sample_prior_predictive(samples=N, random_seed=rng)

ds1 = az.extract(idata1.prior, var_names=["x", "y"])

pm.model_to_graphviz(model1)

Sampling: [temp, x]

with pm.Model() as model2:
    y = pm.Normal("y", mu=1, sigma=2)
    temp = pm.Normal("temp")
    x = pm.Deterministic("x", (y - 1) / 4 + np.sqrt(3) * temp / 2)
    idata2 = pm.sample_prior_predictive(samples=N, random_seed=rng)

ds2 = az.extract(idata2.prior, var_names=["x", "y"])

pm.model_to_graphviz(model2)

Sampling: [temp, y]

with pm.Model() as model3:
    z = pm.Normal("z")
    temp = pm.Normal("temp")
    y = pm.Deterministic("y", z + 1 + np.sqrt(3) * temp)
    x = pm.Deterministic("x", z)
    idata3 = pm.sample_prior_predictive(samples=N)

ds3 = az.extract(idata3.prior, var_names=["x", "y"])

pm.model_to_graphviz(model3)

Sampling: [temp, z]

联合分布，\(P(x,y)\)

首先，让我们看看每个 DAG 的联合分布，以使我们自己确信这些实际上是相同的。

显示代码单元格源 隐藏代码单元格源

fig, ax = plt.subplots(1, 3, figsize=(12, 8), sharex=True, sharey=True)

for i, ds in enumerate([ds1, ds2, ds3]):
    az.plot_kde(
        ds["x"],
        ds["y"],
        hdi_probs=[0.25, 0.5, 0.75, 0.9, 0.95],
        contour_kwargs={"colors": None},
        contourf_kwargs={"alpha": 0.5},
        ax=ax[i],
    )
    ax[i].set(
        title=f"$P(x, y)$, DAG {i+1}",
        xlim=[-4, 4],
        xticks=np.arange(-4, 4 + 1, step=2),
        ylim=[-6, 8],
        yticks=np.arange(-6, 8 + 1, step=2),
        aspect="equal",
    )
    ax[i].axvline(x=2, ls="--", c="k")

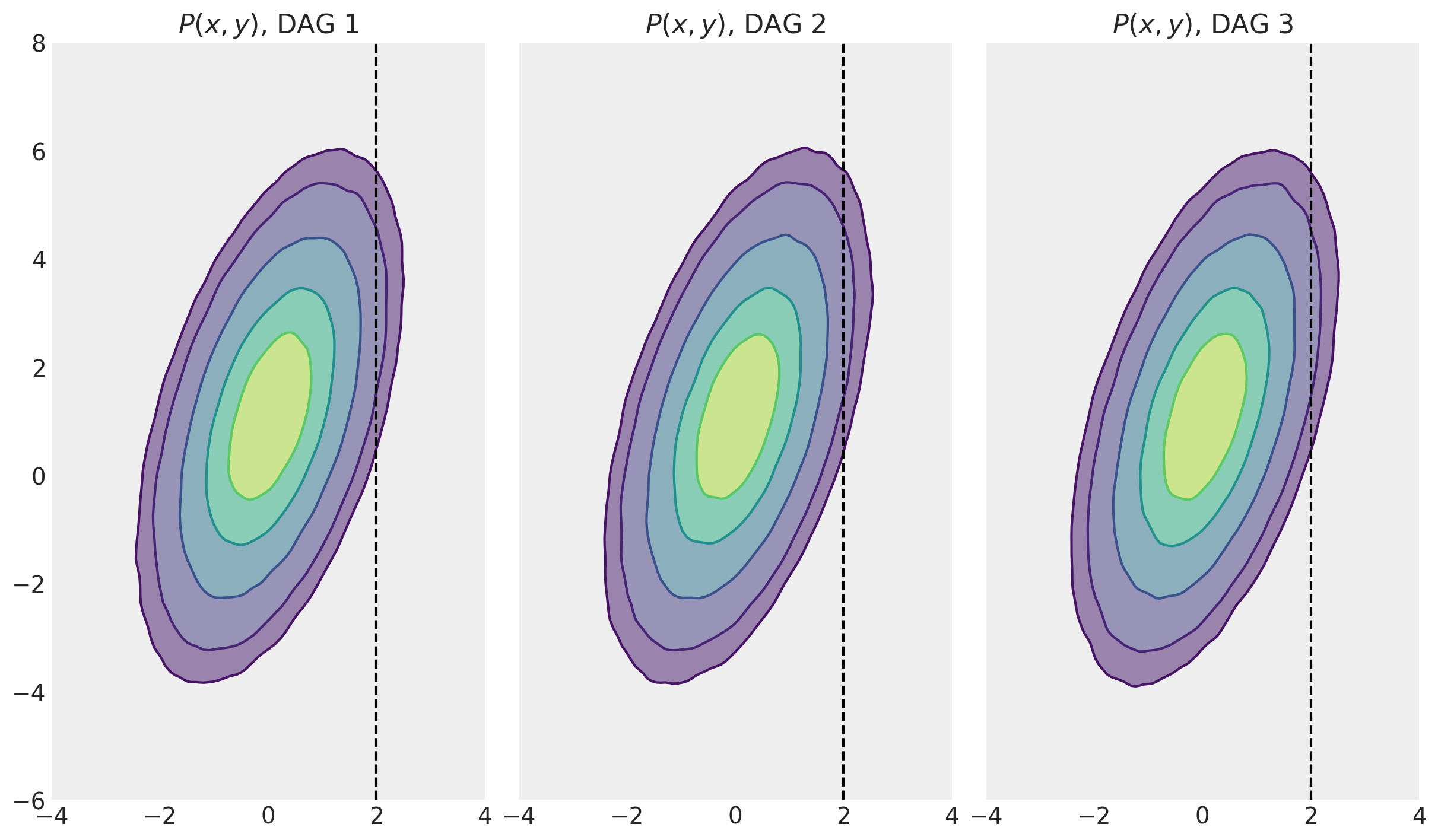
至此，我们已经遇到了 3 个不同的数据生成过程（及其相应的 DAG）。我们从先验分布中抽取了许多 MCMC 样本，并将每个模型的联合分布 \(P(x,y)\) 可视化。我们现在可以回顾条件分布（例如，\(P(y|x=2)\)，请参阅下一节）以及它们如何与干预分布 \(P(y|\operatorname{do}=2)\) 在随后的章节中进行比较。

条件分布，\(P(y|x=2)\)

为了表示样本的概率分布的 MCMC 精神，现在让我们计算条件分布。如果我们选择所有 \(x\) 值恰好为 2 的值，那么我们可能最终根本没有任何样本，因此我们将要做的是围绕 2 提取非常窄的样本切片。因此，这些将是近似值 - 随着样本数量的增加和切片宽度的减小，我们的近似值将变得更加准确。

# Extract samples from P(y|x≈2)
conditional1 = ds1.query(sample="1.99 < x < 2.01")["y"]
conditional2 = ds2.query(sample="1.99 < x < 2.01")["y"]
conditional3 = ds3.query(sample="1.99 < x < 2.01")["y"]

现在我们已经获得了所有 DAG 的 \(P(y|x=2)\) 的 MCMC 估计值。但是您必须稍等片刻才能绘制它们。让我们继续计算 \(P(y|\operatorname{do}(x=2))\)，然后将它们一起绘制，以便我们可以进行比较。

干预分布，\(P(y|\operatorname{do}(x=2))\)

对于 3 个 DAG 中的每一个，让我们依次使用 \(\operatorname{do}\) 算子，设置 \(x=2\)。这将为我们提供一个新的 DAG，我们将绘制 graphviz 表示，然后抽取样本以表示干预分布。

model1_do = do(model1, {"x": 2})
pm.model_to_graphviz(model1_do)

重要提示

让我们花点时间反思一下我们在这里所做的事情！我们采用了一个模型（model1），然后使用了 \(\operatorname{do}\) 函数，并指定了我们想要进行的干预。在本例中，它是将 \(x=2\)。然后，我们获得了一个新模型，其中原始 DAG 已按照我们上面设置的方式发生了变异。即，我们定义了 \(x=2\)并删除了从传入节点到 \(x\) 的边。在第一个 DAG 中，没有传入边，但这在下面的 DAG2 和 DAG 3 中是这种情况。

model2_do = do(model2, {"x": 2})
pm.model_to_graphviz(model2_do)

model3_do = do(model3, {"x": 2})
pm.model_to_graphviz(model3_do)

因此，我们可以看到，在 DAG 1 中，\(x\) 变量仍然对 \(y\) 具有因果影响。但是，在 DAG 2 和 DAG 3 中，\(y\) 不再受 \(x\) 的因果影响。因此，在 DAG 2 和 DAG 3 中，我们的干预 \(\operatorname{do}(x=2)\) 对 \(y\) 没有影响。

接下来，我们将从每个干预分布中采样。请注意，我们正在使用经过修改的模型 model1_do、model2_do 和 model3_do。

with model1_do:
    idata1_do = pm.sample_prior_predictive(samples=N, random_seed=rng)

with model2_do:
    idata2_do = pm.sample_prior_predictive(samples=N, random_seed=rng)

with model3_do:
    idata3_do = pm.sample_prior_predictive(samples=N, random_seed=rng)

Sampling: [temp]
Sampling: [temp, y]
Sampling: [temp, z]

因此，让我们比较所有 3 个 DAG 的条件分布和干预分布。

显示代码单元格源 隐藏代码单元格源

fig, ax = plt.subplots(1, 2, figsize=(10, 4), sharex=True, sharey=True)

az.plot_density(
    [conditional1, conditional2, conditional3],
    data_labels=["DAG 1", "DAG 2", "DAG 3"],
    combine_dims={"sample"},
    ax=ax[0],
    hdi_prob=1.0,
)
ax[0].set(xlabel="y", title="Conditional distributions\n$P(y|x=2)$")

az.plot_density(
    [idata1_do, idata2_do, idata3_do],
    data_labels=["DAG 1", "DAG 2", "DAG 3"],
    group="prior",
    var_names="y",
    ax=ax[1],
    hdi_prob=1.0,
)
ax[1].set(xlabel="y", title="Interventional distributions\n$P(y|\\operatorname{do}(x=2))$");

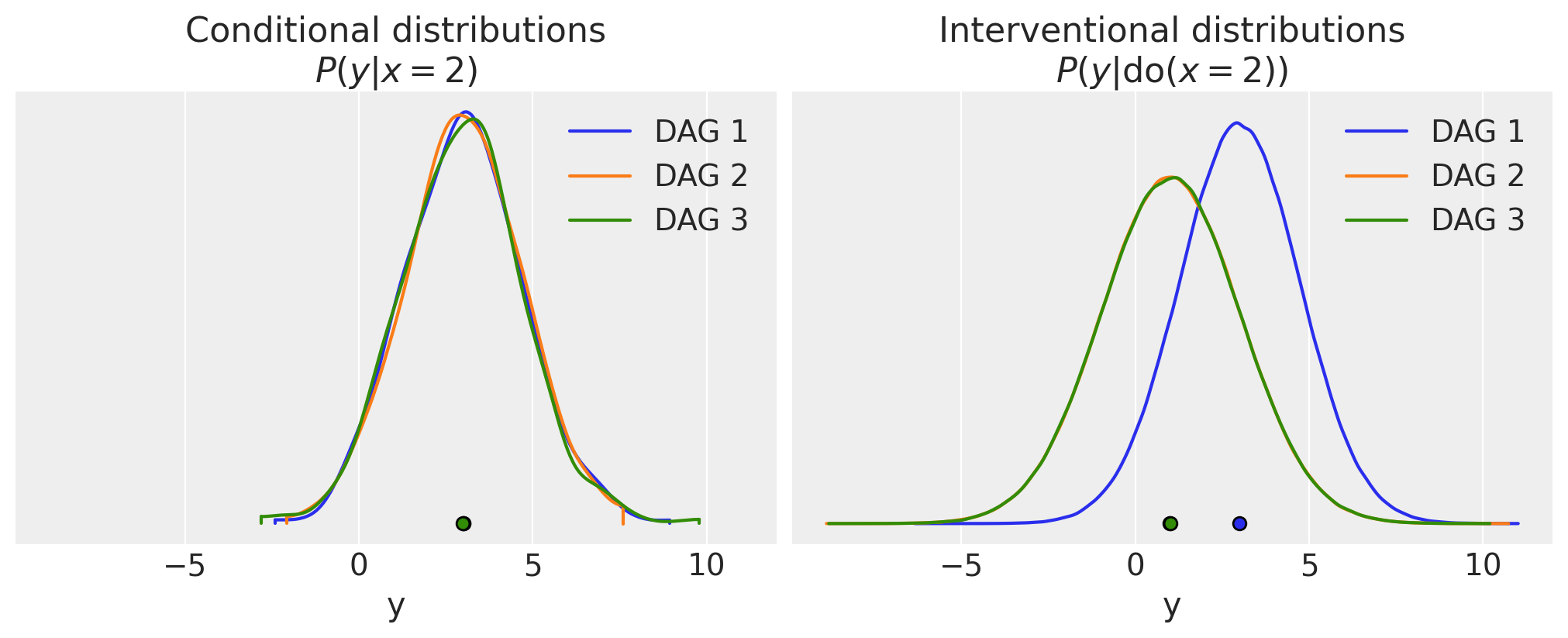
我们可以看到，正如预期的那样，条件分布对于所有 3 个 DAG 都是相同的。请注意，这些分布不是估计参数的后验分布 - 我们在这里没有进行任何参数估计。

然而，对于干预分布，情况有所不同。在这里，DAG 1 是不同的，因为它是唯一一个我们的 \(\operatorname{do}(x=2)\) 干预因果地影响 \(y\) 的 DAG。如果我们进一步思考，由于 \(\operatorname{do}\)对于此 DAG 没有影响结构，因此在本例中 \(P(y|\operatorname{do}(x=2)) = P(y|x=2)\)。然而，这不是可以概括的东西，这只是特定于这个特定简单 DAG 的东西。

在 DAG 2 和 DAG 3 中，干预切断了 \(x\) 对 \(y\) 的任何因果影响。让我们回顾一下经过修改的 DAG 的外观；下面显示了经过修改的 DAG 2，我们可以看到 \(P(y|\operatorname{do}(x=2)) = P(y)\)。

显示代码单元格源 隐藏代码单元格源

g = gr.Digraph()
g.node(name="y2", label="y")
g.node(name="x2", label="x")
g

下面显示了经过修改的 DAG 3。我们可以看到，对于此 DAG，\(P(y|\operatorname{do}(x=2)) = P(y|z)\)。

显示代码单元格源 隐藏代码单元格源

g = gr.Digraph()
g.node(name="z", label="z")
g.node(name="x", label="x")
g.node(name="y", label="y")
g.edge(tail_name="z", head_name="y")
g

DAG 2 和 DAG 3 的 \(P(y|\operatorname{do}(x=2))\) 在这个人为的示例中实际上是相同的，因为细节的安排是为了使所有 DAG 都达到相同的边缘分布 \(P(y)\)。

总结

希望我已经为我们为什么需要将我们的技能组合扩展到仅贝叶斯统计领域之外建立了强有力的论据。虽然这些方法现在和将来都将是 PyMC 的核心，但该生态系统正在拥抱因果推理。

特别是，我们已经了解了如何使用新的 \(\operatorname{do}\) 算子对世界因果模型实施已实现或假设的干预，以获得干预分布。了解底层的因果 DAG 以及干预如何改变此 DAG 是构建我们对因果推理理解的关键组成部分。

令人兴奋的是，还有更多的因果推理思想和概念需要学习。PyMC 正在根据需要进行调整，以支持您的所有贝叶斯因果推断需求。

建议希望了解更多信息的读者查看引用的博客文章以及教科书，Pearl [2000]、Glymour et al. [2016]、McElreath [2018]、Molak [2023]。

作者

• 作者：Benjamin T. Vincent，于 2023 年 7 月

参考文献

[1] (1,2)

Judea Pearl 和 Dana Mackenzie。《为什么之书：因果关系的新科学》。Basic books，2018 年。

[2] (1,2,3,4,5)

Judea Pearl。《因果关系：模型、推理和推断》。Cambridge University Press，2000 年。ISBN 978-0521895606。

[3]

Shawhin Talebi。《通过 do 算子实现的因果效应》。2022 年。网址：https://towardsdatascience.com/causal-effects-via-the-do-operator-5415aefc834a（于 2023-07-01 访问）。

[4] (1,2)

Aleksander Molak。《Python 中的因果推断和发现》。Packt Publishing，2023 年。

[5]

Ferenc Huszár。《因果推断 2：通过玩具示例说明干预》。2019 年。网址：https://www.inference.vc/causal-inference-2-illustrating-interventions-in-a-toy-example/（于 2023-07-01 访问）。

[6]

Madelyn Glymour、Judea Pearl 和 Nicholas P Jewell。《统计学中的因果推断：入门》。John Wiley & Sons，2016 年。

[7]

Richard McElreath。《统计再思考：R 和 Stan 中的贝叶斯课程示例》。Chapman and Hall/CRC，2018 年。

水印

%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,xarray

Last updated: Mon Feb 19 2024

Python implementation: CPython
Python version       : 3.9.13
IPython version      : 8.18.1

pytensor: 2.18.6
xarray  : 2024.1.1

numpy     : 1.26.4
packaging : 23.2
graphviz  : 0.20.1
seaborn   : 0.13.2
arviz     : 0.17.0
pymc      : 5.10.4
matplotlib: 3.8.3

Watermark: 2.4.3