GLM：稳健线性回归#

本教程是关于贝叶斯广义线性模型 (GLM) 的三部分系列文章的第二部分，该系列文章最初出现在 Thomas Wiecki 的博客上

在这篇博文中，我将写关于

少数异常值如何极大地影响线性回归模型的拟合。
如何用 Student T 分布替换正态似然函数以产生稳健回归。

在线性回归教程中，我描述了最小化回归线的平方距离与最大化均值来自回归线的正态分布的似然函数是相同的。后一种概率表达式使我们能够轻松地构建贝叶斯线性回归模型。

这在模拟数据上效果非常好。但是，模拟数据的问题在于它是模拟的。在现实世界中，情况往往更加混乱，并且像正态性这样的假设很容易被少数异常值破坏。

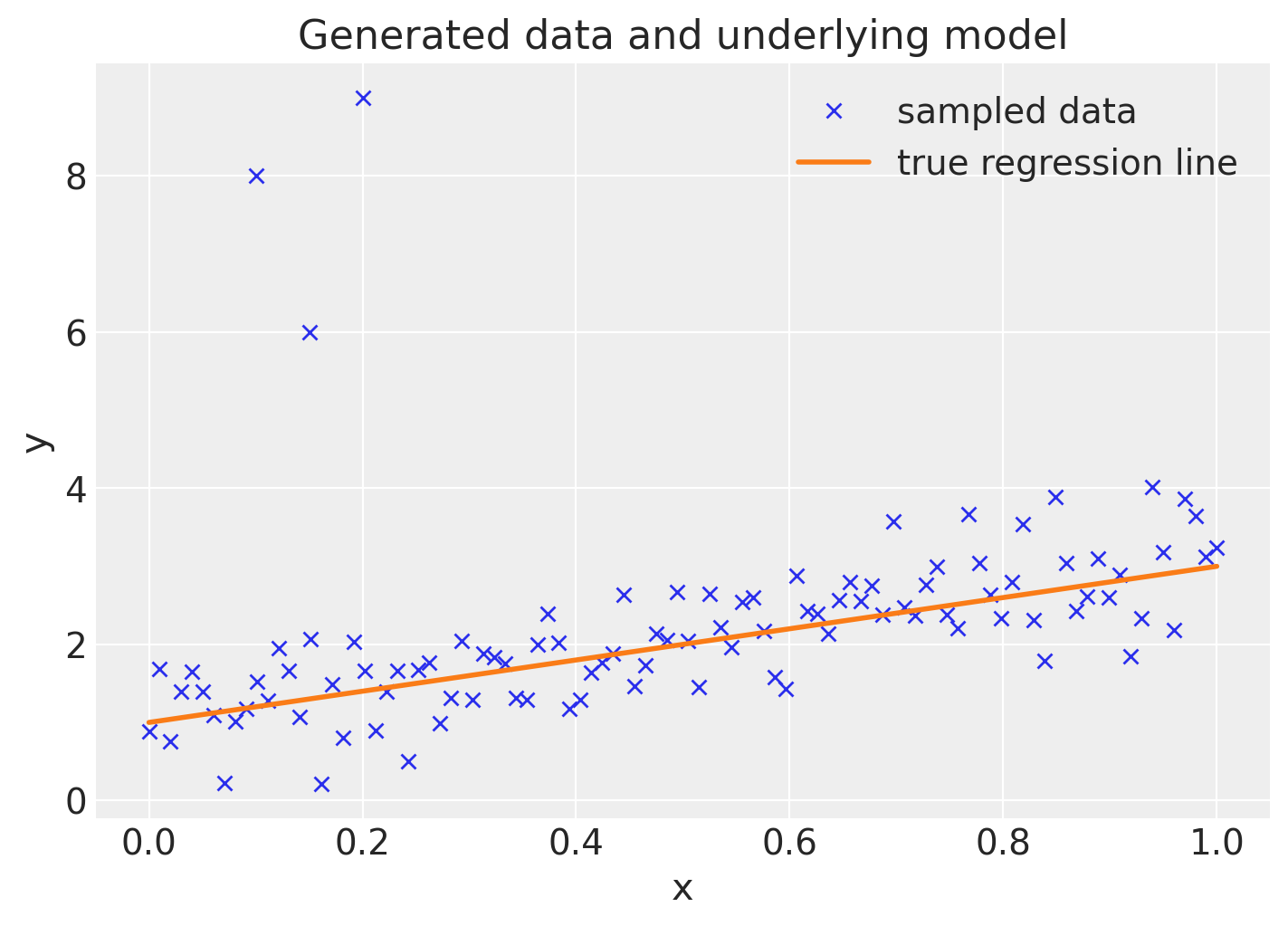
让我们看看如果我们将一些异常值添加到上一篇文章的模拟数据中会发生什么。

首先，让我们导入我们的模块。

%matplotlib inline

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pytensor
import pytensor.tensor as pt
import xarray as xr

RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
%config InlineBackend.figure_format = 'retina'
az.style.use("arviz-darkgrid")

创建一些玩具数据，但也添加一些异常值。

size = 100
true_intercept = 1
true_slope = 2

x = np.linspace(0, 1, size)
# y = a + b*x
true_regression_line = true_intercept + true_slope * x
# add noise
y = true_regression_line + rng.normal(scale=0.5, size=size)

# Add outliers
x_out = np.append(x, [0.1, 0.15, 0.2])
y_out = np.append(y, [8, 6, 9])

data = pd.DataFrame(dict(x=x_out, y=y_out))

将数据与真实回归线一起绘制（左上角的三个点是我们添加的异常值）。

fig = plt.figure(figsize=(7, 5))
ax = fig.add_subplot(111, xlabel="x", ylabel="y", title="Generated data and underlying model")
ax.plot(x_out, y_out, "x", label="sampled data")
ax.plot(x, true_regression_line, label="true regression line", lw=2.0)
plt.legend(loc=0);

../_images/cca03e23e9627b2fb5f4156cb11fa372d2c3f72389827aa6cfb4f0503abc80ab.png

稳健回归#

正态似然函数#

让我们看看如果我们通过拟合具有正态似然函数的回归模型来估计我们的贝叶斯线性回归模型会发生什么。请注意，bambi 库提供了一个易于使用的库，使得可以使用一行代码构建等效模型。使用 Bambi 的相同笔记本的版本可在 bambi 的文档中找到

with pm.Model() as model:
    xdata = pm.ConstantData("x", x_out, dims="obs_id")

    # define priors
    intercept = pm.Normal("intercept", mu=0, sigma=1)
    slope = pm.Normal("slope", mu=0, sigma=1)
    sigma = pm.HalfCauchy("sigma", beta=10)

    mu = pm.Deterministic("mu", intercept + slope * xdata, dims="obs_id")

    # define likelihood
    likelihood = pm.Normal("y", mu=mu, sigma=sigma, observed=y_out, dims="obs_id")

    # inference
    trace = pm.sample(tune=2000)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [intercept, slope, sigma]

100.00% [6000/6000 00:06<00:00 采样 2 个链，0 个发散]

Sampling 2 chains for 2_000 tune and 1_000 draw iterations (4_000 + 2_000 draws total) took 17 seconds.

为了评估拟合度，下面的代码通过从后验分布中获取回归参数并绘制其中 20 个的回归线来计算后验预测回归线。

post = az.extract(trace, num_samples=20)
x_plot = xr.DataArray(np.linspace(x_out.min(), x_out.max(), 100), dims="plot_id")
lines = post["intercept"] + post["slope"] * x_plot

plt.scatter(x_out, y_out, label="data")
plt.plot(x_plot, lines.transpose(), alpha=0.4, color="C1")
plt.plot(x, true_regression_line, label="True regression line", lw=3.0, c="C2")
plt.legend(loc=0)
plt.title("Posterior predictive for normal likelihood");

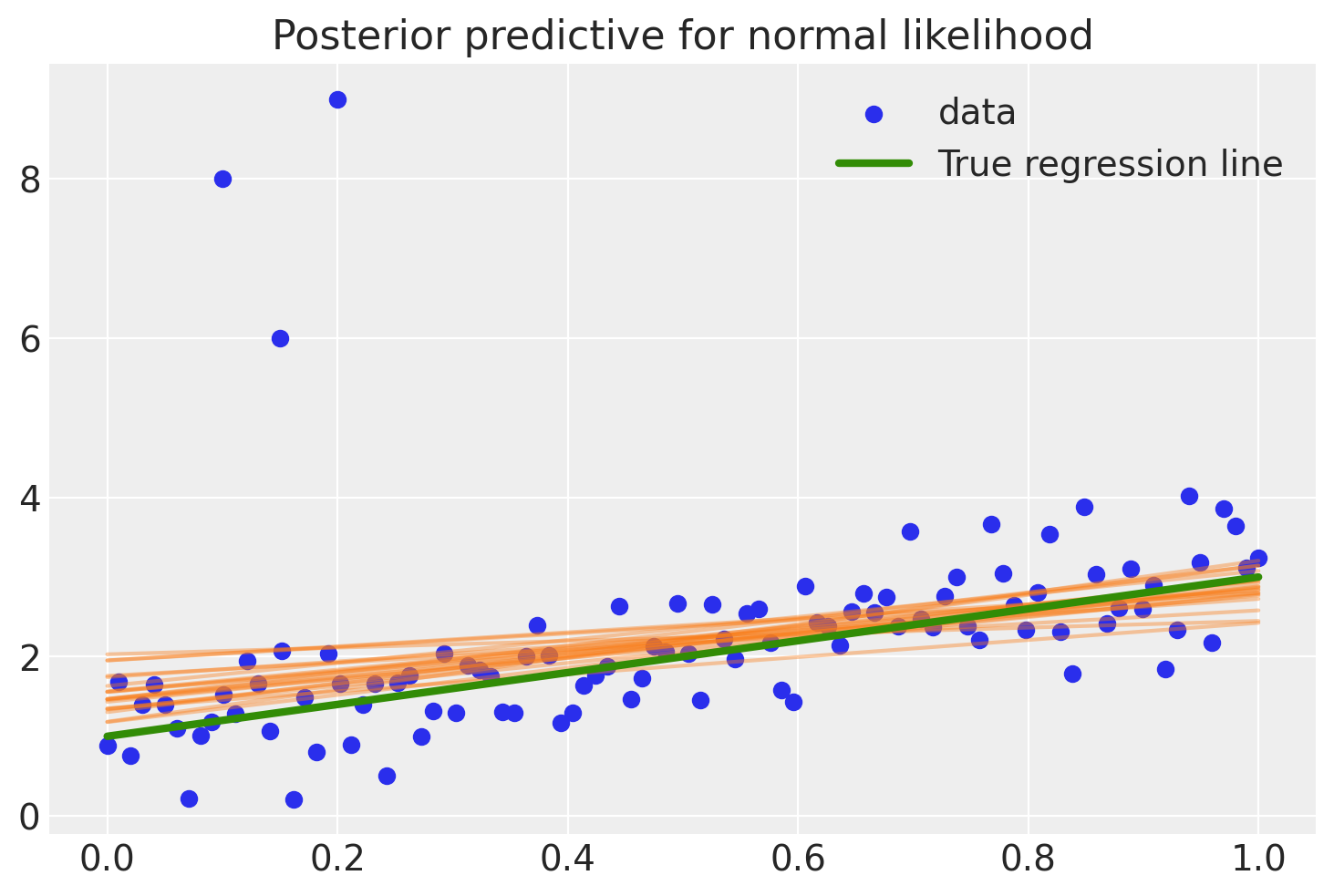
../_images/2a78b97583ee869cae0dd0c05e5342683605d657e6baf4e1169a55644bddf662.png

正如您所见，拟合度非常倾斜，并且我们的估计存在相当大的不确定性，这由不同后验预测回归线的范围广泛表示。这是为什么呢？原因是正态分布在尾部没有太多的质量，因此，异常值会强烈影响拟合度。

频率主义者会估计一个稳健回归并使用非二次距离度量来评估拟合度。

但是贝叶斯主义者该怎么做呢？由于问题是正态分布的轻尾，我们可以假设我们的数据不是正态分布的，而是根据 Student T 分布分布的，该分布具有更重的尾部，如下所示 [Kruschke, 2014, Gelman et al., 2013]。

让我们看一下这两个分布，以了解它们。

normal_dist = pm.Normal.dist(mu=0, sigma=1)
t_dist = pm.StudentT.dist(mu=0, lam=1, nu=1)
x_eval = np.linspace(-8, 8, 300)
plt.plot(x_eval, pm.math.exp(pm.logp(normal_dist, x_eval)).eval(), label="Normal", lw=2.0)
plt.plot(x_eval, pm.math.exp(pm.logp(t_dist, x_eval)).eval(), label="Student T", lw=2.0)
plt.xlabel("x")
plt.ylabel("Probability density")
plt.legend();

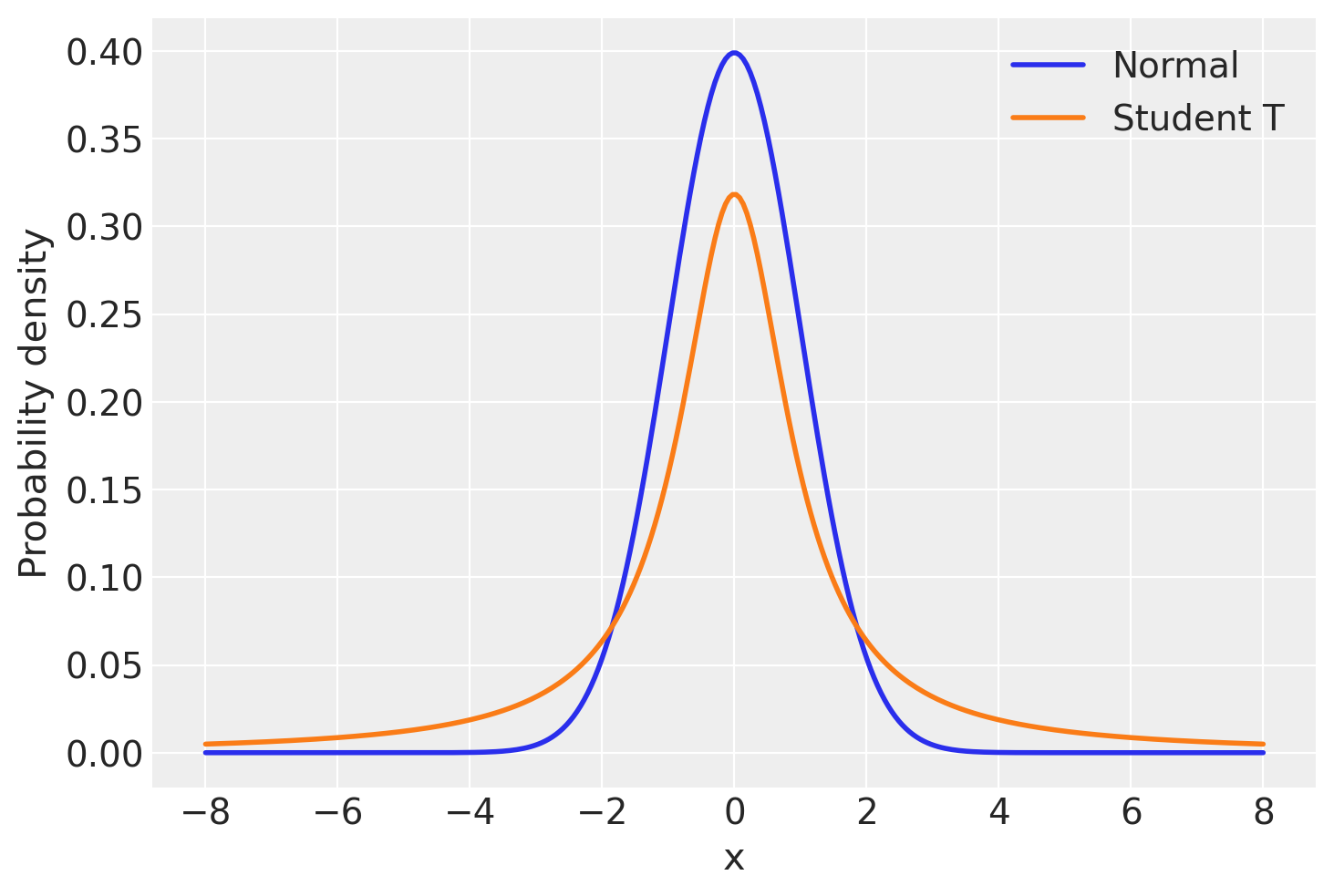
../_images/695eee0cbe3ee92da4619c71c542fc0e7f20906573a87df7292fce4579929b50.png

正如您所见，在 T 分布下，远离均值（在本例中为 0）的值的概率比在正态分布下高得多。

下面是一个 PyMC 模型，其中 likelihood 项遵循自由度为 \(\nu=3\) 的 StudentT 分布，而不是 Normal 分布。

with pm.Model() as robust_model:
    xdata = pm.ConstantData("x", x_out, dims="obs_id")

    # define priors
    intercept = pm.Normal("intercept", mu=0, sigma=1)
    slope = pm.Normal("slope", mu=0, sigma=1)
    sigma = pm.HalfCauchy("sigma", beta=10)

    mu = pm.Deterministic("mu", intercept + slope * xdata, dims="obs_id")

    # define likelihood
    likelihood = pm.StudentT("y", mu=mu, sigma=sigma, nu=3, observed=y_out, dims="obs_id")

    # inference
    robust_trace = pm.sample(tune=4000)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [intercept, slope, sigma]

100.00% [10000/10000 00:16<00:00 采样 2 个链，0 个发散]

Sampling 2 chains for 4_000 tune and 1_000 draw iterations (8_000 + 2_000 draws total) took 24 seconds.

robust_post = az.extract(robust_trace, num_samples=20)
x_plot = xr.DataArray(np.linspace(x_out.min(), x_out.max(), 100), dims="plot_id")
robust_lines = robust_post["intercept"] + robust_post["slope"] * x_plot

plt.scatter(x_out, y_out, label="data")
plt.plot(x_plot, robust_lines.transpose(), alpha=0.4, color="C1")
plt.plot(x, true_regression_line, label="True regression line", lw=3.0, c="C2")
plt.legend(loc=0)
plt.title("Posterior predictive for Student-T likelihood")

Text(0.5, 1.0, 'Posterior predictive for Student-T likelihood')

../_images/2c34339bb4a0baa17ae6065d3143e9f8f765b12e1767458ce0eae2f20283b407.png

好了，好多了！异常值几乎没有影响我们的估计，因为我们的似然函数假设异常值的概率比在正态分布下高得多。

总结#

通过将似然函数从正态分布更改为 Student T 分布（尾部具有更多质量），我们可以执行稳健回归。

扩展:

除了均值和方差之外，Student-T 分布还具有第三个参数，称为自由度，它描述了应该在尾部放置多少质量。这里将其设置为 1，这为尾部提供了最大质量（将其设置为无穷大会导致正态分布！）。可以很容易地将先验放在此参数上，而不是固定它，我将其作为读者的练习；）。
T 分布也可以用作先验。请参阅多层建模贝叶斯方法入门
我们如何测试我们的数据是否正态，或者是否以重要方式违反了该假设？查看 Allen Downey 的这篇精彩博文：可能想太多了。

作者#

改编自 Thomas Wiecki 的博客
由 @fonnesbeck 于 2016 年 9 月更新 (pymc#1378)
由 @chiral-carbon 于 2021 年 8 月更新 (pymc-examples#205)
由 Conor Hassan、Igor Kuvychko、Reshama Shaikh 和 Oriol Abril Pla 于 2022 年更新
由 Reshama Shaikh 于 2023 年 1 月重新运行，使用 PyMC v5

参考文献#

[1]

John Kruschke. Doing Bayesian data analysis: A tutorial with R, JAGS, and Stan. Academic Press, 2014.

[2]

Andrew Gelman, John B. Carlin, Hal S. Stern, David B. Dunson, Aki Vehtari, and Donald B. Rubin. Bayesian Data Analysis. Chapman and Hall/CRC, 2013.

水印#

%load_ext watermark
%watermark -n -u -v -iv -w -p xarray

Last updated: Tue Jan 10 2023

Python implementation: CPython
Python version       : 3.11.0
IPython version      : 8.8.0

xarray: 2022.12.0

matplotlib: 3.6.2
pandas    : 1.5.2
numpy     : 1.24.1
pymc      : 5.0.1
pytensor  : 2.8.11
arviz     : 0.14.0
xarray    : 2022.12.0

Watermark: 2.3.1

许可声明#

此示例库中的所有笔记本均根据 MIT 许可证提供，该许可证允许修改和再分发以用于任何用途，前提是保留版权和许可声明。

引用 PyMC 示例#

要引用此笔记本，请使用 Zenodo 为 pymc-examples 存储库提供的 DOI。

重要提示

许多笔记本改编自其他来源：博客、书籍……在这种情况下，您也应该引用原始来源。

另请记住引用您的代码使用的相关库。

这是一个 bibtex 中的引用模板

@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}

渲染后可能看起来像

分类

标签

GLM：稳健线性回归#

GLM：稳健线性回归#

稳健回归#

正态似然函数#

总结#

作者#

参考文献#

水印#

许可声明#

引用 PyMC 示例#